геометрия – Как найти измерения параллелепипида?
|
Общая длина ребер прямоугольного параллелепипеда равна 612м. Одно из ребер на 54м меньше другого и на 30м больше третьего. Как найти измерения параллелепипеда. Обозначьте ребра буквами a, b, c и составьте систему уравнений. |
1 ответ
|
ребра обозначим $% a; a+54; a-30.$% получим уравнвние: $% 4(а+а+54+а-30) = 612.$% |
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
отмечен:
геометрия
×3,291
задан
10 Дек ’12 23:29
показан
1707 раз
обновлен
11 Дек ’12 11:04
Связанные исследования
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Что такое периметр параллелограмма
Периметр параллелограмма — это сумма длин всех его сторон.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.
Свойства
- противоположные стороны равны и параллельны;
- противоположные углы попарно равны;
- сумма соседних углов равна 180 градусов;
- сумма всех углов равна 360 градусов;
- диагонали фигуры делятся пополам в точке пересечения;
- точка пересечения диагоналей — центр симметрии параллелограмма;
- биссектриса образует равнобедренный треугольник.
Как найти периметр
Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По сумме всех сторон
Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем формулу:
P=2(a+b),
где a и b — это две смежные стороны данного четырехугольника.
По стороне и двум диагоналям
Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:
(a=frac{sqrt{2d_1^2+2d_2^2-4b^2}}2,)
где (d_1) и (d_2) — это обе диагонали фигуры.
Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b).)
По стороне, высоте и синусу угла
В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:
(a=frac{h_b}{sinalpha})
где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.
Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:
(P=2(frac{h_b}{sinalpha}+b))
Примеры решения задач
Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.
Задача 1
Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.
Решение:
Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.
Ответ: 28 см.
Задача 2
Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.
Решение:
Для расчета суммы длин всех сторон используем формулу:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b))
Подставляем известные значения:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(frac{sqrt{2times6^2+2times8^2-4times4^2}}2+4)=2(frac{sqrt{72+128-64}}2+4)=2(frac{2sqrt{34}}2+4)=2sqrt{34}+8) см.
Ответ:( 2sqrt{34}+8) см.
Задача 3
Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6). Найти сумму длин всех сторон фигуры.
Решение:
Для расчета будем использовать уравнение:
(P=2(frac{h_b}{sinalpha}+b))
Подставим известные величины:
(P=2(frac1{sin{displaystylefracpi6}}+2)=2(frac1{displaystylefrac12}+2)=8;)см.
Ответ: 8 см.
Содержание:
- Формула площади параллелограмма:
- Формула периметра параллелограмма:
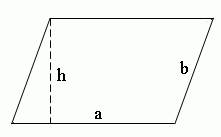
Параллелограмм – это четырёхугольник, у которого противолежащие
стороны попарно параллельны, т.е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник,
квадрат и ромб.
Формула площади параллелограмма:
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц.
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
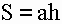
S – площадь параллелограмма
a – длина основания
h – длина высоты
См. также: Программа для расчета площади параллелограмма.
Формула периметра параллелограмма:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).
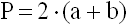
P – периметр параллелограмма
a – длина 1-ой стороны параллелограмма
b – длина 2-ой стороны параллелограмма
См. также: Программа для расчета периметра параллелограмма.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений науки древнего мира.
Считается, что первое достаточно точное определение размеров Земли провёл греческий учёный Эратосфен (276—194 до н. э.), живший в Египте. Идея, положенная в основу измерений Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину её радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: ϕB – ϕA.

Рис. 3.8. Способ Эратосфена
Для того чтобы определить эту разность, Эратосфен сравнил полуденную высоту Солнца в один и тот же день в двух городах, находящихся на одном меридиане. Измерив высоту Солнца hB (рис. 3.8) в полдень 22 июня в Александрии, где он жил, Эратосфен установил, что Солнце отстоит от зенита на 7,2°. В этот день в полдень в городе Сиена (ныне Асуан) Солнце освещает дно самых глубоких колодцев, т. е. находится в зените (hA = 90°). Следовательно, длина дуги составляет 7,2°. Расстояние между Сиеной (A) и Александрией (B) около 5000 греческих стадий — l.
Стадией в Древней Греции считалось расстояние, которое проходит легко вооружённый греческий воин за тот промежуток времени, в течение которого Солнце, коснувшееся горизонта своим нижним краем, целиком скроется за горизонт.
Несмотря на кажущееся неудобство такой единицы и достаточную громоздкость словесного определения, её введение выглядело вполне оправданным, учитывая, что строгая периодичность небесных явлений позволяла использовать их движение для счёта времени.
Обозначив длину окружности земного шара через L, получим такое выражение:
 =
=  ,
,
откуда следует, что длина окружности земного шара равняется 250 тыс. стадий.
Точная величина стадии в современных единицах неизвестна, но, зная, что расстояние между Александрией и Асуаном составляет 800 км, можно полагать, что 1 стадия = 160 м. Результат, полученный Эратосфеном, практически не отличается от современных данных, согласно которым длина окружности Земли составляет 40 тыс. км.
Эратосфен ввёл в практику использование терминов «широта» и «долгота». Видимо, появление этих терминов связано с особенностями формы карт того времени: они повторяли по очертаниям побережье Средиземного моря, которое длиннее по направлению запад—восток (по долготе), чем с севера на юг (по широте).

Рис. 3.9. Параллактическое смещение
Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — BC) и двух углов B и C в треугольнике ABC (рис. 3.9).
Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.
Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.

Рис. 3.10. Схема триангуляции
Для определения длины дуги используется система треугольников — способ триангуляции, который впервые был применён ещё в 1615 г. Пункты в вершинах этих треугольников выбираются по обе стороны дуги на расстоянии 30—40 км друг от друга так, чтобы из каждого пункта были видны по крайней мере два других. Основой для вычисления длин сторон во всех этих треугольниках является размер базиса AC (рис. 3.10). Точность измерения базиса длиной в 10 км составляет около 1 мм. Во всех пунктах устанавливают геодезические сигналы — вышки высотой в несколько десятков метров. С вершины сигнала с помощью угломерного инструмента (теодолита) измеряют углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон. Проводя затем измерение углов из пунктов, расстояние между которыми вычислено, можно узнать длину двух очередных сторон в треугольнике. Зная длину сторон этих треугольников, можно определить длину дуги AB.
В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы Земли Французская академия наук снарядила сразу две экспедиции. Одна из них работала в экваториальных широтах Южной Америки в Перу, другая — вблизи Северного полярного круга на территории Финляндии и Швеции. Измерения показали, что длина одного градуса дуги меридиана на севере больше, чем вблизи экватора. Последующие исследования подтвердили, что длина дуги одного градуса меридиана увеличивается с возрастанием географической широты. Это означало, что форма Земли — не идеальный шар: она сплюснута у полюсов. Её полярный радиус на 21 км короче экваториального.
Для школьного глобуса масштаба 1 : 50 000 000 отличие этих радиусов будет всего 0,4 мм, т. е. совершенно незаметно.
Отношение разности величин экваториального и полярного радиусов Земли к величине экваториального называется сжатием. По современным данным, оно составляет  , или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения.
, или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения.
В XX в. благодаря измерениям, точность которых составила 15 м, выяснилось, что земной экватор также нельзя считать окружностью. Сплюснутость экватора составляет всего  (в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передаёт фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.
(в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передаёт фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.
В настоящее время форму Земли принято характеризовать следующими величинами:
|
сжатие эллипсоида — 1 : 298,25; |
|
средний радиус — 6371,032 км; |
|
длина окружности экватора — 40075,696 км. |
Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.
Горизонтальным параллаксом ( p) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).

Рис. 3.11. Горизонтальный параллакс светила
Из треугольника OAS можно выразить величину — расстояние OS = D:
D =  ,
,
где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.
Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57ʹ. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8ʺ. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.
Известно, что для малых углов sin p ≈ p, если угол p выражен в радианах. В одном радиане содержится 206 265ʺ. Тогда, заменяя sin p на p и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:
D =  R,
R,
или (с достаточной точностью)
D =  R.
R.
Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.
На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9ʺ?
|
Дано: p1 = 0,9ʺ D☉ = 1 а. е. p☉ = 8,8ʺ |
Решение: Известно, что параллакс Солнца на расстоянии в 1 а. е. равен 8,8ʺ. Тогда, написав формулы для расстояния до Солнца и до Сатурна и поделив их одна на другую, получим: |
|
D1 — ? |
 =
=  .
.
Откуда
D1 =  =
=  = 9,8 а. е.
= 9,8 а. е.
Ответ: D1 = 9,8 а. е.

Рис. 3.12. Угловые размеры светила
Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 3.12). Формула, связывающая эти величины, аналогична формуле для определения параллакса:
D =  .
.
Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30ʹ, а все планеты видны невооружённым глазом как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:
D =  и D =
и D =  .
.
Следовательно,
r =  R.
R.
Если расстояние D известно, то
r = Dρ,
где величина ρ выражена в радианах.
Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30ʹ?
|
Дано: D = 400 000 км ρ = 30ʹ |
Решение: Если ρ выразить в радианах, то d = Dρ. Следовательно, |
|
d — ? |
d =  = 3490 км.
= 3490 км.
Ответ: d = 3490 км.

Вопросы 1. Какие измерения, выполненные на Земле, свидетельствуют о её сжатии? 2. Меняется ли и по какой причине горизонтальный параллакс Солнца в течение года? 3. Каким методом определяется расстояние до ближайших планет в настоящее время?

Упражнение 11 1. Чему равен горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если Юпитер в 5 раз дальше от Солнца, чем Земля? 2. Расстояние Луны от Земли в ближайшей к Земле точке орбиты (перигее) 363 000 км, а в наиболее удалённой (апогее) — 405 000 км. Определите горизонтальный параллакс Луны в этих положениях. 3. Во сколько раз Солнце больше, чем Луна, если их угловые диаметры одинаковы, а горизонтальные параллаксы равны 8,8ʺ и 57ʹ соответственно? 4. Чему равен угловой диаметр Солнца, видимого с Нептуна?
Содержание
- – Как определить расстояние в километрах с помощью градусной сетки?
- – Как определить расстояние в километрах и градусах?
- – Как вычислить расстояние по параллели?
- – Как определить расстояние с помощью масштаба?
- – Как определить протяженность по градусной сетке?
- – Что можно узнать с помощью градусной сети карты?
- – Как рассчитать расстояние в километрах по карте?
- – Как можно определить расстояние по глобусу?
- – Как определить расстояние между городами с помощью координат?
- – Как определить расстояние между пунктами расположенными на одной параллели?
- – Как можно узнать по карте полушарий длину дуги 1 градуса параллели?
- – Как определить протяженность материка?
- – Как с помощью масштаба определяется расстояние на плане и карте?
- – Как найти расстояние на карте Если известен масштаб и местность?
- – Как узнать в каком масштабе карта?
Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км.
Как определить расстояние в километрах с помощью градусной сетки?
Длина дуги одного градуса меридиана (или одного градуса на экваторе) равна 111 км.
- Определяем расстояние между ними в градусах (из долготы одного пункта вычитаем долготу другого пункта)
- Далее необходимо число градусов умножить на 111 км.
18 апр. 2020 г.
Как определить расстояние в километрах и градусах?
Чтобы рассчитать расстояние между двумя точками на карте в градусах с севера на юг нужно знать, чему равен 1° по меридиану. Он равен 111 км. То есть находим разницу в градусах между двумя точками и умножаем её на 111 км, получаем расстояние в километрах.
Как вычислить расстояние по параллели?
Алгоритм определения расстояний по параллели: 1) определить значение координат двух точек параллели, расстояние между которыми необходимо рассчитать; 2) определить расстояние между двумя точками параллели в градусной мере (отсчет производится от нулевого меридиана, поэтому значения либо складываются, либо вычитаются); …
Как определить расстояние с помощью масштаба?
Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1 : 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е.
Как определить протяженность по градусной сетке?
Вычислить расстояние с помощью градусной сетки несколько сложнее. Для определения протяженности страны с севера на юг, выясните широты крайних северной и южной точек, определите разницу в градусах и умножьте полученное число на 111,1 км (градус каждого меридиана равен 111,1 км).
Что можно узнать с помощью градусной сети карты?
С помощью градусной сетки на глобусе и карте можно определить стороны горизонта, а также точное местоположение какого-либо объекта по его географическим координатам. Изображение меридианов и параллелей на глобусе и физической карте полушарий различно. На глобусе все меридианы — полуокружности, а параллели — окружности.
Как рассчитать расстояние в километрах по карте?
Как измерить расстояние между точками
- Откройте Google Карты на компьютере. …
- Наведите курсор на начальную точку и нажмите правую кнопку мыши. …
- Выберите Измерить расстояние.
- Укажите на карте вторую точку, нажав левую кнопку мыши. …
- При необходимости вы можете перетащить точку в другое место или удалить, нажав на нее.
Как можно определить расстояние по глобусу?
Чтобы определить расстояние по глобусу надо нитью, или сантиметром, или гибкой линейкой замерить расстояние между искомыми точками на глобусе, затем полученное значение умножить на масштаб глобуса, который можно найти в районе экватора на акватории океана.
Как определить расстояние между городами с помощью координат?
Расстояние между двумя точками равно квадратному корню из суммы квадратов разностей координат по каждой оси. Каждая точка на плоскости характеризуется двумя координатами, а каждая точка в пространстве – тремя. Для того, чтобы определить расстояние между двумя точками на плоскости, надо ввести две координаты двух точек.
Как определить расстояние между пунктами расположенными на одной параллели?
Для определения расстояния в километрах между пунктами, лежащими на одной параллели, число градусов умножают на длину дуги 1° параллели, обозначенную на карте или определенную по таблицам.
Как можно узнать по карте полушарий длину дуги 1 градуса параллели?
Для определения длины одного градуса дуги произвольной параллели нужно умножить 111,3 км (длину дуги экваториальной параллели в 1 градус) на косинус угла, соответствующего искомой параллели.
Как определить протяженность материка?
Итак, чтобы посчитать количество километров в материке с запада на восток, умножьте величину градуса экватора (111,3 км) на косинус угла нужной вам параллели, затем умножьте полученный результат на длину материка в градусах. Найти протяженность материка можно и по определенной параллели либо по определенному меридиану.
Как с помощью масштаба определяется расстояние на плане и карте?
В математике масштаб определяется как отношение расстояния на карте к соответствующему расстоянию на реальной местности. Масштаб 1:100000 означает, что 1 см на карте соответствует 100000 см = 1000 м = 1 км на местности.
Как найти расстояние на карте Если известен масштаб и местность?
Если на карте обозначен масштаб 1:20 000 000, то измерив расстояние между пунктами в сантиметрах и умножив его на 20 000 000, вы получите реальное расстояние между пунктами в сантиметрах. Для упрощения вычислений можно масштаб сразу перевести в километры или метры на местности.
Как узнать в каком масштабе карта?
В этом случае надо измерить по карте линейкой расстояние в сантиметрах от одного населенного пункта до другого и подписанное количество километров разделить на расстояние в сантиметрах. Полученное число будет означать величину масштаба карты (число километров в одном сантиметре).
Интересные материалы:
Кто автор рассказа Лягушка путешественница?
Кто автор рассказа Мороз красный нос?
Кто автор рассказа оловянный солдатик?
Кто автор рассказа тайное становится явным?
Кто автор рассказа телеграмма?
Кто автор рассказа Том Сойер?
Кто автор рассказа Витя Малеев в школе и дома?
Кто автор рассказа железная дорога?
Кто был самым старшим мальчиком в рассказе Бежин луг?
Кто были родители Васютки из рассказа Васюткино озеро?
