|
Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы?
Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так:
И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм:
Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример:
S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим
Ксарфакс 6 лет назад Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле:
N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах.
N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество.
N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.
N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см².
Марина Вологда 3 года назад Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач:
Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника:
Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика:
Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник:
Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2.
Enot-Nina 3 года назад Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам:
Бархатные лапки 3 года назад Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах.
Ann Luka 6 лет назад Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток.
Outline 3 года назад Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника:
Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников:
S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13.
KritikSPb 3 года назад Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ.
127771 3 года назад Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где:
Теперь разберемся на примере, у нас есть такой пример:
Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см.
Бекки Шарп 3 года назад Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где
Вот такая фигура у нас –
Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ? |
![]()
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
ФОРМУЛА ПИКА
Площадь искомой фигуры можно найти по формуле:
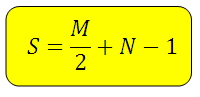
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)


Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)
N = 20 (обозначены синим)


Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)
N = 25 (обозначены синим)


Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)
N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:


Отметим узлы:

M = 11 (обозначены красным)
N = 5 (обозначены синим)

Ответ: 9,5
![]()
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.
Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Григорий Мерзон
«Квантик» №9, 2018
Формула Пика
Как найти площадь многоугольника на клетчатой бумаге? Можно подсчитать число клеток, которые полностью накрыты фигурой, и ещё как-то учесть клетки, накрытые фигурой частично, — скажем, прибавить половину от числа этих клеток. И сказать, что площадь фигуры (в клеточках) приблизительно равна полученной сумме.

А можно вместо клеток, полностью или частично накрытых многоугольником, считать узлы сетки (вершины клеток) строго внутри многоугольника или на его границе.

Действительно, вокруг каждого узла сетки можно нарисовать по единичному квадратику. И если узел лежит на границе многоугольника, то этот квадратик накрыт многоугольником только частично. А если узел лежит внутри, то обычно и квадратик накрыт многоугольником полностью… впрочем, иногда всё же не полностью — но мы и считаем площадь только приближённо.
Но чудесным образом последний рецепт всегда даёт почти правильный ответ! А именно, верна Формула Пика. Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
S
=
i
+
b
2
−
1
,
где i — число узлов сетки строго внутри многоугольника, b — число узлов сетки на его границе.
Подчеркнём, что это уже не приближённая, а точная формула!

Интересно, что хотя длины сторон у многоугольников обычно совершенно не целые, формула Пика гарантирует, что площадь всегда получится целой или полуцелой.

Тающий лёд
Формула Пика известна с XIX века, и с тех пор у неё появилось много доказательств, но большинство из них не такие уж простые. Мы обсудим предложенный в 1997 году швейцарским математиком Кристианом Блаттером мысленный эксперимент с тающим льдом, который сразу объясняет формулу Пика.

Поставим на каждый узел сетки по одинаковому цилиндрическому столбику изо льда. Каждый столбик очень тонкий (пересекается только с теми сторонами многоугольника, которые проходят через центр столбика) и весит 1 грамм.
Построим вокруг каждого столбика забор в виде единичного квадратика, после чего растопим весь лёд (во всех квадратиках вода растекается одинаково и симметрично относительно центра своего квадратика). Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).

С другой стороны, задумаемся, откуда эта вода попала в наш многоугольник. Посмотрим на какую-нибудь конкретную сторону многоугольника. Если через неё внутрь многоугольника втекла вода из какого-то столбика, то точно столько же воды из симметричного столбика (симметричного относительно середины этой стороны) через неё из многоугольника вытекло.

То есть внутри многоугольника ровно столько воды, сколько в нём было льда! А сколько в нём было льда? Каждый из узлов сетки внутри многоугольника даёт вклад 1 грамм, общий вес получается i граммов. Узлы на сторонах обычно дают по
1
2
грамма, но только если это не вершина, для вершины этот вес меньше — так что и общий вес узлов на границе получается не
b
2
граммов, а меньше.

Насколько меньше? Продлим немного каждую сторону, обходя многоугольник вдоль сторон по часовой стрелке. На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.

То есть суммарный вес льда внутри многоугольника равен
i
+
b
2
−
1
, и мы получили формулу Пика!
Художник Мария Усеинова
Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!
• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.
Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.
Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 – 1 = 10 квадратных единиц.

Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника. чтд
К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.

Специально для ЖЖ матфака, Сергей Романов.
Приветствую Вас, уважаемые Читатели! Сегодня хочу рассказать Вам о формуле, которая настолько упрощает решение некоторых задач единого государственного экзамена по математике, что не пользоваться её было бы кощунством. Речь идет о задачах, в которых надо найти площадь многоугольников, начерченных на бумаге в клетку. Поехали!
Итак, необходимо найти площадь многоугольника из рисунка ниже (2 фото):
Да, решение не сложное, но, оказывается, есть намного более короткий путь, который изобрел австрийский математик Георг Пик:
Давайте еще раз внимательно посмотрим на условие задачи:
По формуле Пика необходимо подсчитать количество точек целочисленной решетки внутри фигуры (синим цветом) и на границах фигуры (красным цветом). Таких точек получается по 10 штук. Дальше площадь рассчитывается по формуле:
S = В + Г/2 – 1 = 10 + 10/2 – 1 = 14, где В – точки внутри, Г – на границе.
Без сомнения чудесная формула, однако она работает лишь тогда, когда все вершины многоугольника расположены на узлах решетки, так что знание формул площадей из геометрии всё равно не будет лишним. А что думаете по этому поводу Вы? Пишите в комментариях. Спасибо за внимание!
Читайте также:
- Кирпич Эйлера
- Самый важный из интегралов
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.





















