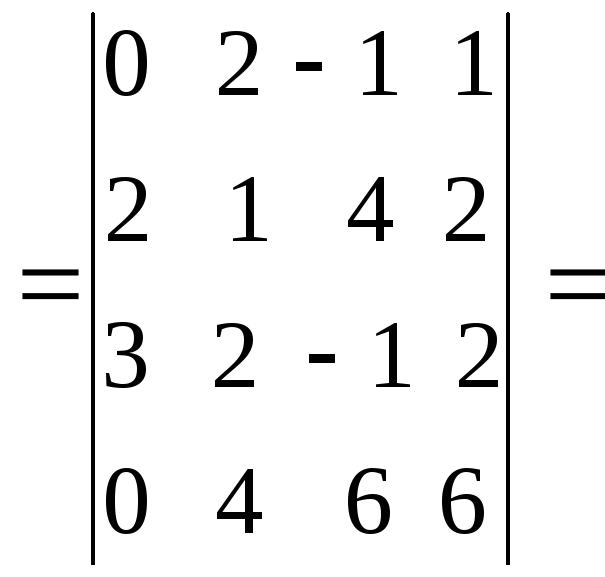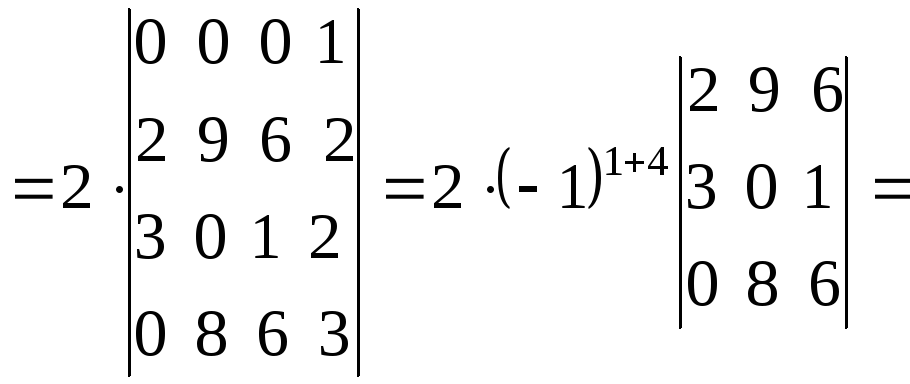Как найти вспомогательные определитель матрицы

(схема 16)

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной,
если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее
свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи
подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она
имеет хотя бы одно решение, и несовместной, если она решений не
имеет.

Совместная система уравнений называется определенной,
если она имеет единственное решение, и неопределенной, если она имеет более
одного решения.

Рассмотрим неоднородную систему линейных
алгебраических уравнений, имеющую при n=m следующий
общий вид:

.                                                                                                                                                  (1.5) 

Главной матрицей A системы
линейных алгебраических уравнений называется матрица, составленная из
коэффициентов, стоящих при неизвестных:

.

Определитель главной матрицы системы называется главным
определителем и обозначается ∆.

Вспомогательный определитель ∆_i  получается
из главного определителя путем замены i-го
столбца на столбец свободных членов.

Теорема 1.1
(теорема Крамера). Если главный
определитель системы линейных алгебраических уравнений отличен от нуля, то
система имеет единственное решение, вычисляемое по формулам:

.                                                                                                                                                                        (1.6)

 Если
главный определитель ∆=0, то система либо 
имеет бесконечное множество решений (при всех нулевых вспомогательных
определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного
из вспомогательных определителей).

В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если
главный определитель системы линейных алгебраических уравнений отличен от нуля,
то система является совместной определенной и при этом ; если главный определитель нулевой, то система является
либо совместной неопределенной (при всех ∆_i=0),
либо несовместной (при отличии хотя бы одного из ∆_i от нуля).

После этого следует провести проверку полученного
решения.

Пример 1.4.  Решить
систему методом Крамера 

Решение.  Так
как главный определитель системы

 отличен от нуля, то система имеет единственное
решение. Вычислим вспомогательные определители

Воспользуемся
формулами Крамера (1.6):
 

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла
и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

                                                                   
                                     Таблица 1.4                                 

Определить стоимость 1 единицы продукции молокоцеха
каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z –
1 кг
творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из
трех дней реализации можно отобразить следующей системой:

.

Решим систему методом Крамера. Найдем главный
определитель системы по формуле (1.2):

         

     Так
как он отличен от нуля, то система имеет единственное решение. Вычислим
вспомогательные определители с помощью формулы (1.2):

        

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1
литра молока равна 44 рубля, 1
кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с
помощью калькулятора трудоемок, поэтому на практике используют персональный
компьютер. Так, для решения систем линейных алгебраических уравнений методом
Крамера в MS Excel высчитывают ее главный и вспомогательные определители
с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек
и элементы матрицы, определитель которой находится.

В MathCAD для
нахождения определителя пользуются палитрой оператора Matrix

Вопросы для
самопроверки

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Второй столбец умножим на третий столбец – на -ый столбец – на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

• Заказать решение задач по высшей математике

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй – при неизвестной у, третий – при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера – Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

Как найти вспомогательный определитель системы линейных уравнений

ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I

§29 Главный и вспомогательный определители системы двух линейных ypaвнений с двумя неизвестными.

Главным определителем системы уравнений

(1)

составленный из коэффициентов при неизвестных х и у. Этот определитель мы будем обозначать греческой буквой Δ (дельта). Очевидно, что

Первым вспомогательным определителем системы уравнений (1) называется определитель

Он получается из главного определителя этой системы уравнений путем замены первого столбца на столбец свободных членов. Этот определитель мы будем обозначать Δ_x. Индекс (то есть значок) х при Δ указывает, что в главном определителе Δ первый столбец, составленный из коэффициентов при х в системе уравнений (1), заменен на столбец свободных членов . Очевидно, что

Вторым вспомогательным определителем системы уравнений (1) называется определитель

‘

который получается из главного определителя этой системы путем замены второго столбца на столбец свободных членов. Этот определитель мы будем обозначать Δ_y. Очевидно, что

Пример. Для системы уравнений

Вопрос о том, какую пользу приносят введенные нами определители Δ , Δ_x и Δ_y при решении системы уравнений (1), мы выясним в следующих параграфах.

Найти главный и вспомогательные определители для следующих систем уравнений:

Вспомогательный определитель

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Системы линейных уравнений

Система уравнений следующего вида:

,

где а ij , b i – числовые коэффициенты, x i – переменные, называется системой линейных уравнений.

Решить систему линейных уравнений – значит указать все решения системы, то есть такие наборы значений переменных, которые обращают уравнения системы в тождества.

Система линейных уравнений называется:

совместной, если она имеет хотя бы одно решение;

несовместной, если она не имеет решений;

определенной, если она имеет единственное решение;

однородной, если все b i = 0;

неоднородной, если все b i ≠ 0.

(Габриель Крамер (1704-1752) швейцарский математик)

Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.

Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

Теорема. (Правило Крамера):

Система из n уравнений с n неизвестными

В случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам:

х i = ;

где  – главный определитель , составленный из числовых коэффициентов при неизвестных, а  i – вспомогательный определитель , получаемый из главного заменой i -го столбца столбцом свободных членов b i .

 i =

Пример. Решить систему, используя правило Крамера.

;

 1 = ;  2 = ;  3 = ;

x 1 = ; x 2 = ; x 3 = ;

Пример. Найти решение системы уравнений:

 = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

x 1 = = 1;

 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

x 2 = = 2;

 3 = = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

x 3 = = 3.

Если система однородна, т.е. b i = 0, то при 0 система имеет единственное нулевое решение x 1 = x 2 = … = x n = 0.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Этот метод удобен для решения систем невысокого порядка. Он основан на применении свойств умножения матриц.

Пусть дана система уравнений:

A = – матрица коэффициентов системы;

B = матрица – столбец свободных членов;

X = – матрица – столбец неизвестных.

Систему уравнений можно записать в матричной форме:

Сделаем следующее преобразование: A -1 AX = A -1 B,

т.к. А -1 А = Е, то ЕХ = А -1 В, получим

Х = А -1  В – решение матричного уравнения

Пример . Решить систему матричным методом

, , .

Получаем матричное уравнение .

Его решение , т.е.

.

(Нахождение обратной матрицы было рассмотрено ранее).

Ответ:

(Карл Фридрих Гаусс (1777-1855) немецкий математик)

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

Определение: Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.

Определение: Матрица называется расширенной матрицей системы, если к матрице А присоединить столбец свободных членов системы.

Расширенная матрица – это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями можно заменить работой со строками матрицы.

Определение: Матрицу А называют ступенчатой, если:

А) любая ее строка имеет хотя бы один отличный от нуля элемент,

Б) первый отличный от нуля элемент каждой ее строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.

Метод Гаусса является эффективным методом решения и исследования систем линейных уравнений. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида, которая легко решается и исследуется. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Разберем идею метода Гаусса на конкретных примерах.

Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы и с помощью элементарных преобразований приведем к виду:

Таким образом, исходная система может быть представлена в виде:

, откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1.

Пример. Решить систему методом Гаусса.

Составим расширенную матрицу системы.

Таким образом, исходная система может быть представлена в виде:

, откуда получаем: z = 3; y = 2; x = 1.

Как найти вспомогательный определитель системы линейных уравнений

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:

Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:

Определитель главной матрицы системы называется главным определителем и обозначается ∆.

Вспомогательный определитель ∆ _i получается из главного определителя путем замены i -го столбца на столбец свободных членов .

Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:

Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).

В свете приведенных выше определений , теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆ _i = 0), либо несовместной (при отличии хотя бы одного из ∆ _i от нуля).

После этого следует провести проверку полученного решения.

Пример 1.4. Решить систему методом Крамера

Решение. Так как главный определитель системы

отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители

Воспользуемся формулами Крамера (1.6):

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

Определить стоимость 1 единицы продукции молокоцеха каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:

Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):

Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.

В MathCAD для нахождения определителя пользуются палитрой оператора Matrix

[spoiler title=”источники:”]

http://gigabaza.ru/doc/42387.html

http://www.sites.google.com/site/vyssaamatem/kupit-sklad/i-3-metod-kramera-resenia-sistem-linejnyh-algebraiceskih-uravnenij

[/spoiler]

ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§29 Главный
и вспомогательный определители системы двух линейных ypaвнений с двумя неизвестными.

Главным определителем системы уравнений

         (1)

называется определитель

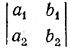
составленный из коэффициентов при неизвестных х и у. Этот определитель мы будем обозначать греческой буквой Δ (дельта). Очевидно, что

Δ= a₁b₂ — a₂b₁

Первым вспомогательным определителем системы уравнений (1) называется определитель

Он получается из главного определителя этой  системы уравнений путем замены первого столбца на столбец свободных членов.   Этот определитель мы будем обозначать   Δ_x. Индекс (то есть значок) х при Δ указывает,   что в главном определителе Δ первый столбец, составленный из коэффициентов при х в системе уравнений (1), заменен на столбец свободных членов . Очевидно, что

Δ_x = c₁b₂ — c₂b₁

Вторым вспомогательным определителем системы уравнений (1) называется определитель

‘

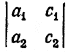который получается из главного определителя этой системы путем замены второго столбца на столбец свободных членов. Этот определитель мы будем обозначать  Δ_y. Очевидно,  что

Δ_y = a₁c₂ — a₂c₁.

Пример. Для системы уравнений

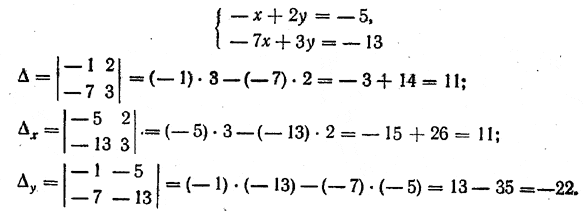
Вопрос о том, какую пользу приносят введенные нами определители Δ , Δ_x и Δ_y при решении системы уравнений (1), мы выясним в следующих параграфах.

Упражнения

Найти  главный и вспомогательные определители для следующих систем уравнений:

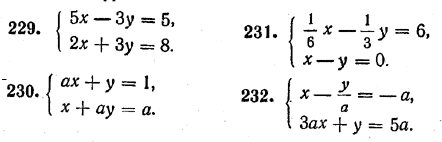
ОТВЕТЫ

231. ¹/₆; —6;—6.    232. 4;   5 — а;   5а+ 3а² (а =/= 0).

1. Определители и системы линейных уравнений

1.1.
Системы двух линейных уравнений и
определители второго порядка

Рассмотрим
систему двух линейных уравнений с двумя
неизвестными:

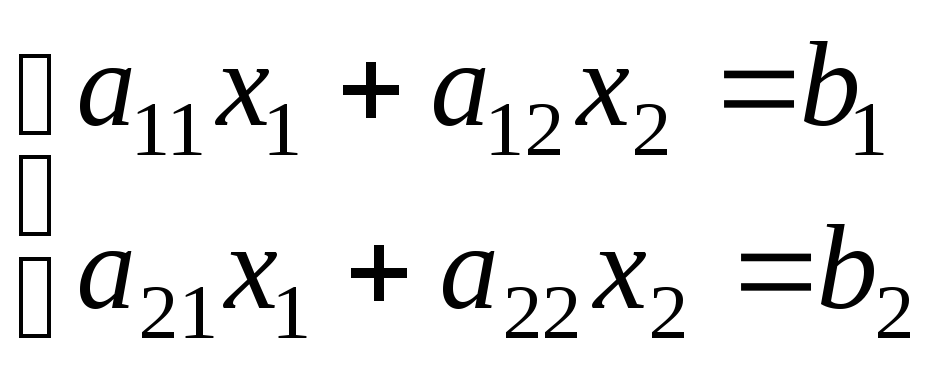
Коэффициенты

при неизвестных
и
имеют два индекса: первый указывает
номер уравнения, второй – номер
переменной.

Главным определителем системы называется таблица, составленная из коэффициентов при неизвестных и заключенная в прямые скобки:

Вспомогательным определителем называют определитель, полученный из главного определителя заменой одного из столбцов на столбец свободных членов:

Главнаядиагональ определителя – это диагональ, направленная из левого верхнего угла в правый нижний угол. Вторая диагональ называетсяпобочной.

Определитель второго порядка равен разности между произведением элементов главной диагонали и произведением элементов побочной диагонали:

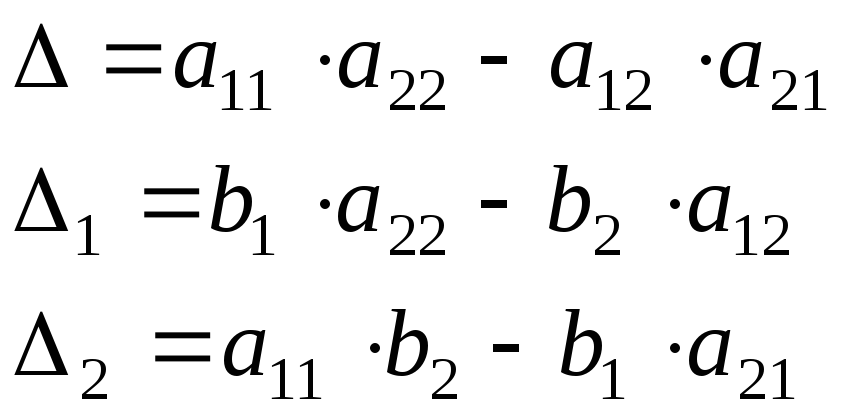
Правило
Крамера: Решение системы находят
путем деления вспомогательных
определителей на главный определитель
системы

,

Замечание
1.Использование правила Крамера
возможно, если определитель системы
не равен нулю.

Замечание
2.Формулы Крамера обобщаются и на
системы большего порядка.

Пример
1. Решить систему:
.

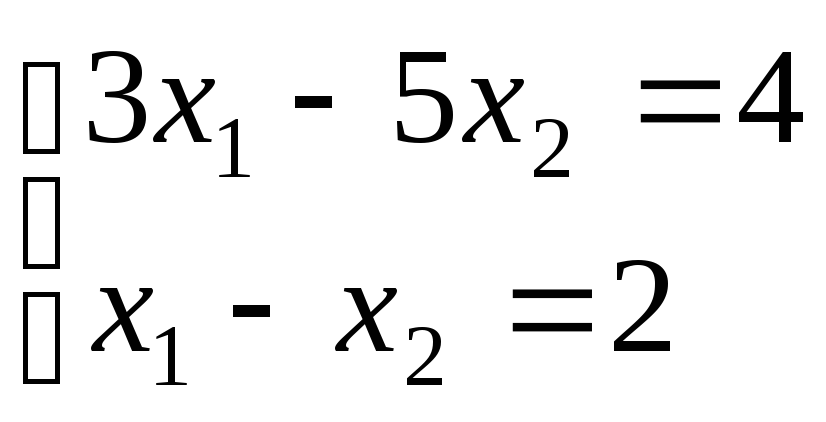Решение.

;

;

;

Проверка:

Вывод:
Система решена верно:
.

1.2. Системы трех линейных уравнений и определители третьего порядка

Рассмотрим
систему трех линейных уравнений с тремя
неизвестными:

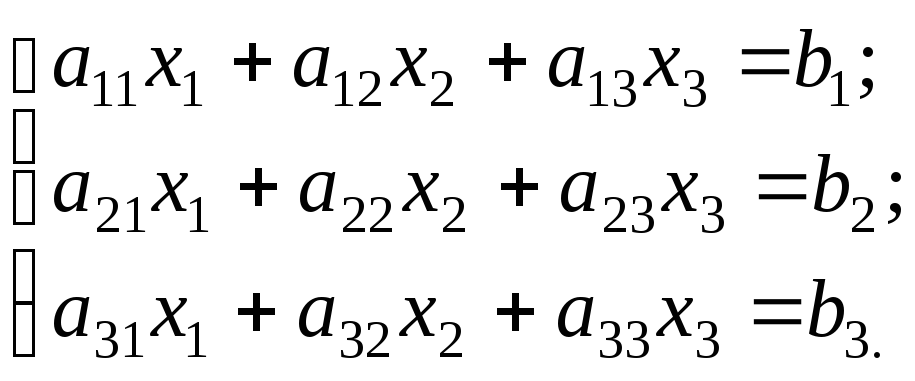
Определитель,
составленный из коэффициентов при
неизвестных, называется определителем
системы или главным определителем:

.

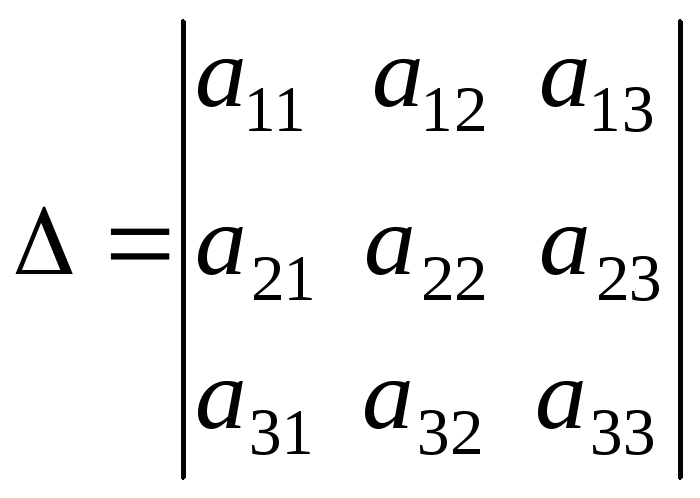Если

то система имеет единственное решение,
которое определяется по формулам
Крамера:

где

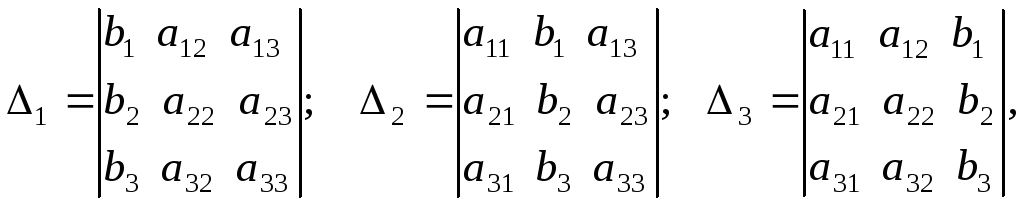
где
определители
– называются вспомогательными и
получаются из определителя
путем замены его первого, второго или
третьего столбца столбцом свободных
членов системы.

Пример
2.Решить систему
.

Сформируем
главный и вспомогательные определители:

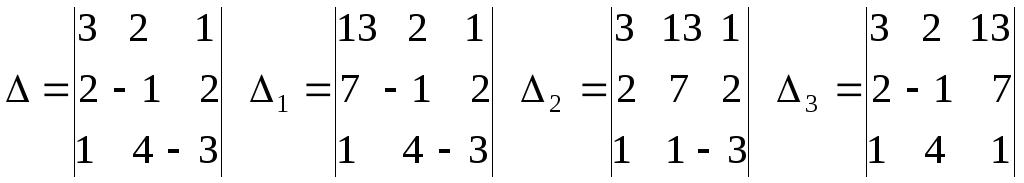
Осталось
рассмотреть правила вычисления
определителей третьего порядка. Их три:
правило дописывания столбцов, правило
Саррюса, правило разложения.

а)
Правило дописывания первых двух столбцов
к основному определителю:

.

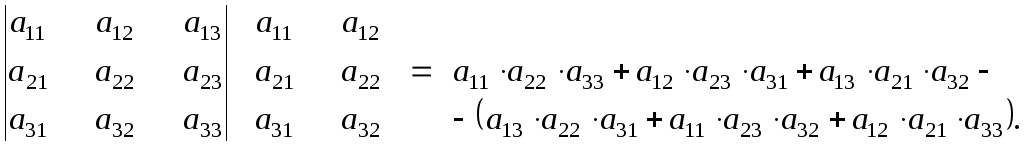
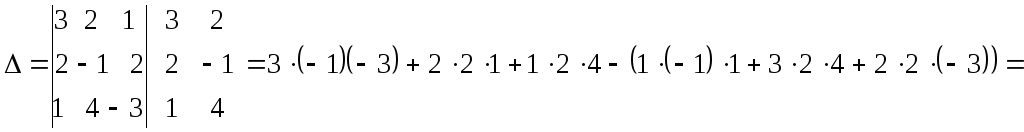
Вычисление
проводятся следующим образом: со своим
знаком идут произведения элементов
главной диагонали и по параллелям к
ней, с обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней.

б)
Правило Саррюса:

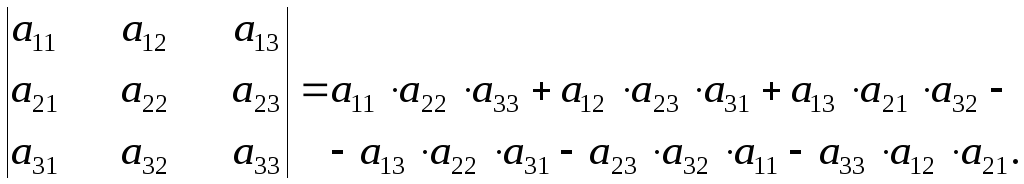
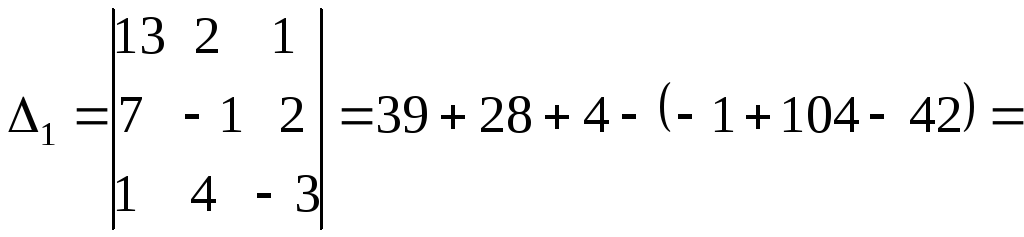
Со
своим знаком берут произведения элементов
главной диагонали и по параллелям к
ней, причем недостающий третий элемент
берут из противоположного угла. С
обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней, третий элемент берут
из противоположного угла.

в)
Правило разложения по элементам строки
или столбца:

Определитель равен сумме произведений элементов какой-нибудь строки (столбца) на их соответствующие алгебраические дополнения.

Если

,
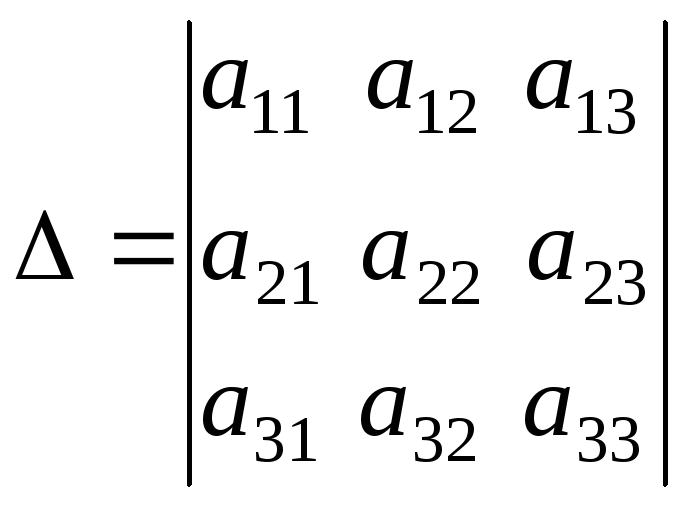тогда
.

Алгебраическое
дополнение– это определитель более
низкого порядка, получаемый путем
вычеркивания соответствующей строки
и столбца и учитывающий знак
,
где– номер строки,– номер столбца.

Например,

,

,
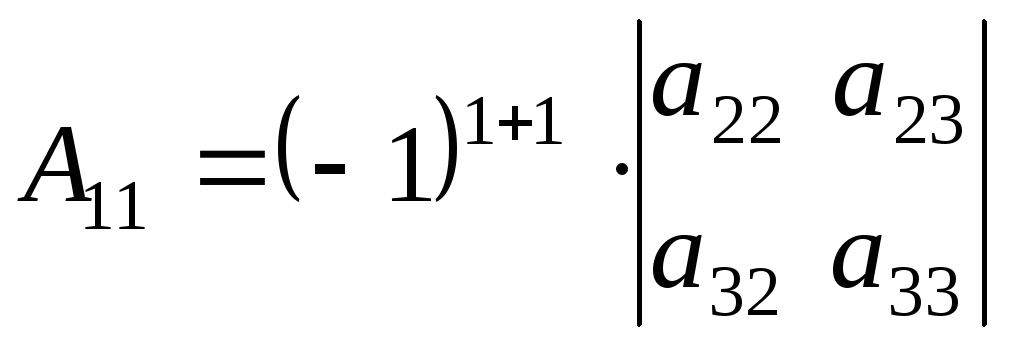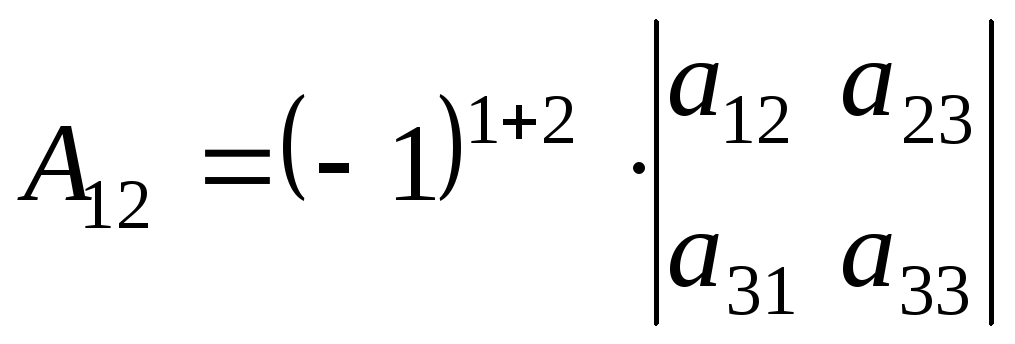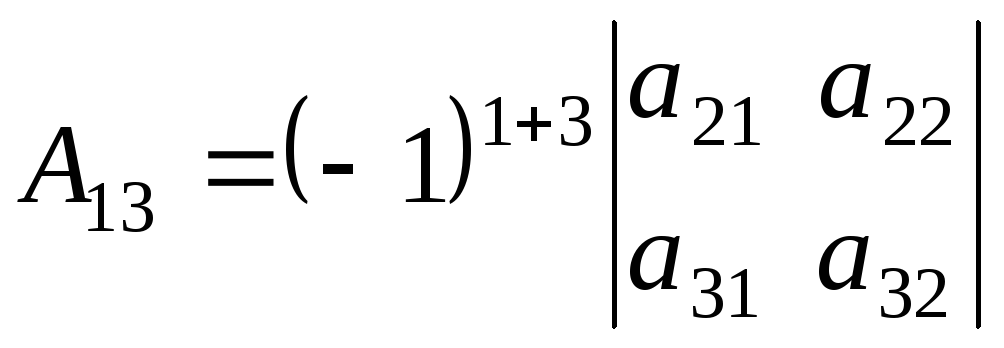и т.д.

Вычислим
по этому правилу вспомогательные
определители
и
,
раскрывая их по элементам первой строки.

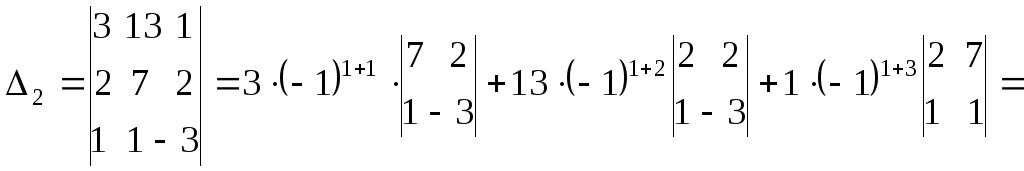
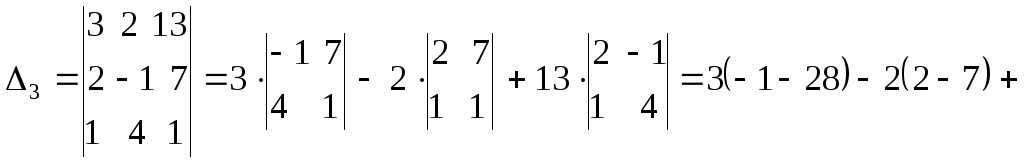
Вычислив
все определители, по правилу Крамера
найдем переменные:

Проверка:

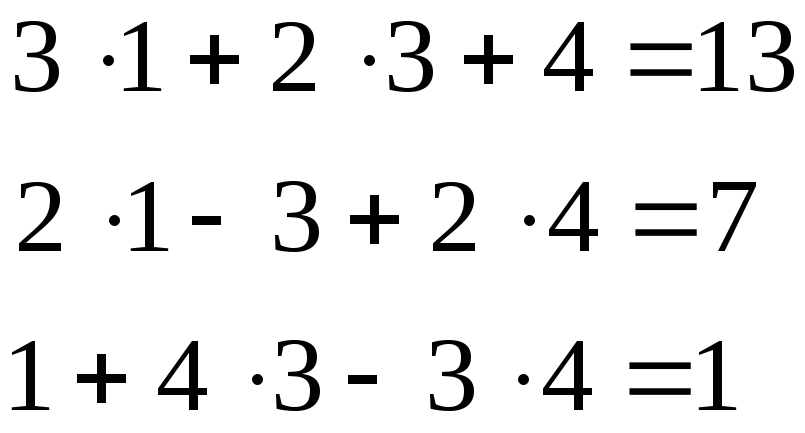
Вывод:
система решена верно:
.

1. Основные
   свойства определителей

Необходимо
помнить, что определитель – это число,
найденное по некоторым правилам. Его
вычисление может быть упрощено, если
пользоваться основными свойствами,
справедливыми для определителей любого
порядка.

Свойство
1.Значение определителя не изменится
от замены всех его строк соответствующими
по номеру столбцами и наоборот.

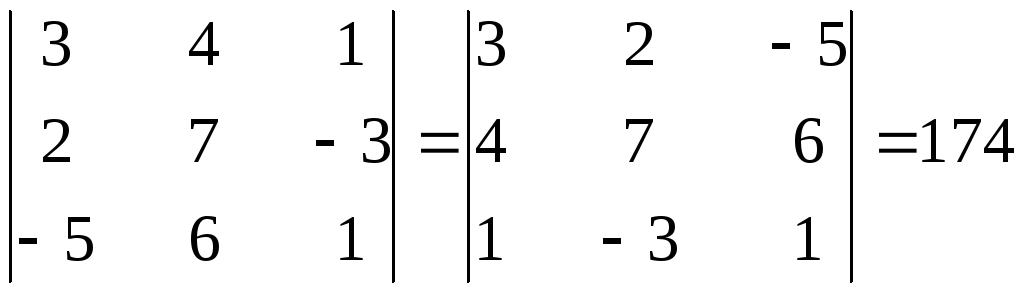
Операция
замены строк столбцами называется
транспонированием. Из этого свойства
вытекает, что всякое утверждение,
справедливое для строк определителя,
будет справедливым и для его столбцов.

Свойство
2.Если в определителе поменять
местами две строки (столбца), то знак
определителя поменяется на противоположный.

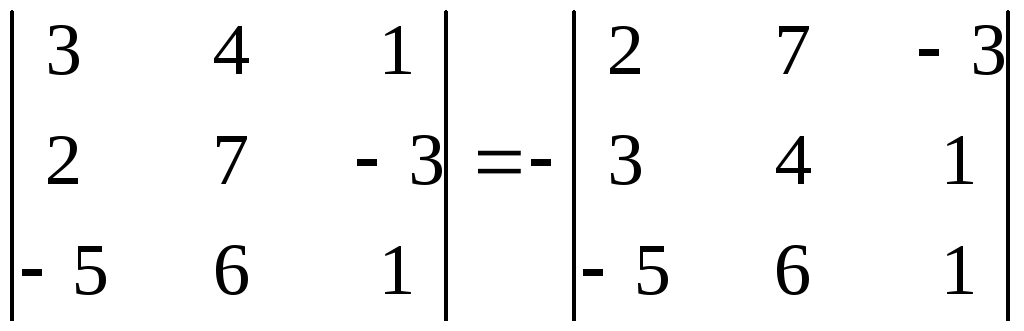
Свойство
3.Если все элементы какой-нибудь
строки определителя равны 0, то определитель
равен 0.

Свойство
4.Если элементы строки определителя
умножить (разделить) на какое-нибудь
число
,
то и значение определителя увеличится
(уменьшится) в
раз.

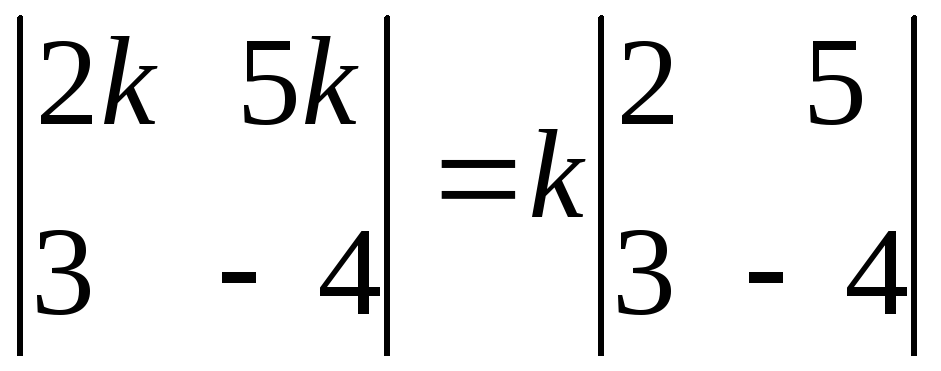
Если
элементы какой-нибудь строки, имеют
общий множитель, то его можно вынести
за знак определителя.

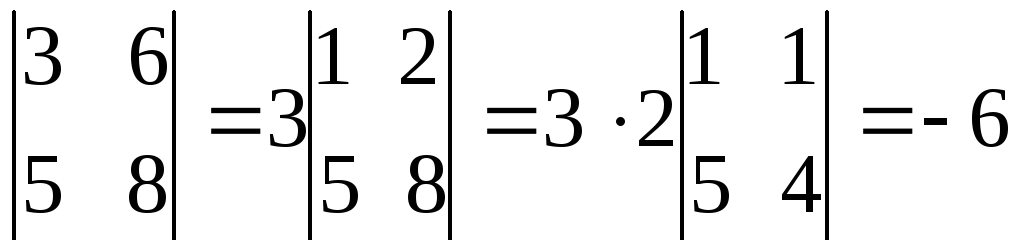
Свойство
5. Если определитель имеет две
одинаковые или пропорциональные строки,
то такой определитель равен 0.

Свойство
6. Если элементы какой-нибудь строки
определителя представляют собой сумму
двух слагаемых, то определитель равен
сумме двух определителей.

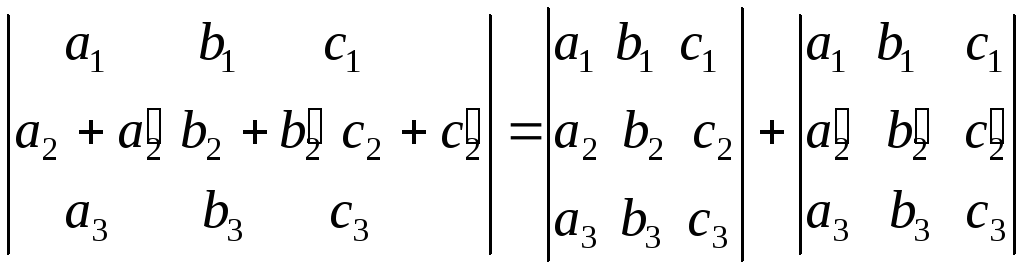
Свойство
7. Значение определителя не изменится,
если к элементам какой-нибудь строки
добавить элементы другой строки,
умноженной на одно и то же число.

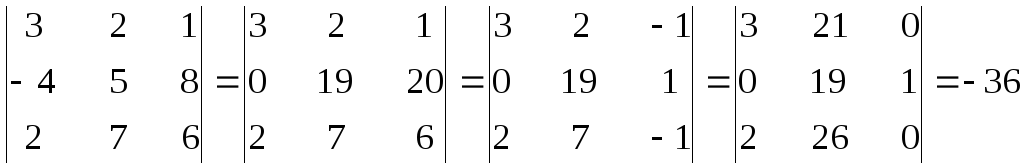
В
этом определителе вначале ко второй
строке прибавили третью, умноженную на
2, затем из третьего столбца вычли второй,
после чего вторую строку прибавили к
первой и третьей, в результате получили
много нулей и упростили подсчет.

Элементарными
преобразованиями определителя
называются упрощения его благодаря
использованию указанных свойств.

Пример
1.Вычислить определитель

Непосредственный
подсчет по одному из рассмотренных выше
правил приводит к громоздким вычислениям.
Поэтому целесообразно воспользоваться
свойствами:

а)
из І строки вычтем вторую, умноженную
на 2;

б)
из ІІ строки вычтем третью, умноженную
на 3.

В
результате получаем:

Разложим
этот определитель по элементам первого
столбца, содержащего лишь один ненулевой
элемент.

.

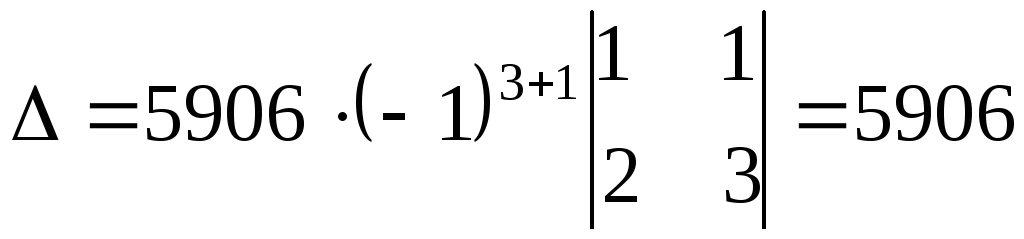1. Системы
   и определители высших порядков

Систему

линейных уравнений с
неизвестными можно записать в таком
виде:

Для
этого случая также можно составить
главный и вспомогательные определители,
а неизвестные определять по правилу
Крамера. Проблема состоит в том, что
определители более высокого порядка
могут быть вычислены только путем
понижения порядка и сведения их к
определителям третьего порядка. Это
может быть осуществлено способом прямого
разложения по элементам строк или
столбцов, а также с помощью предварительных
элементарных преобразований и дальнейшего
разложения.

Пример
4. Вычислить определитель четвертого
порядка

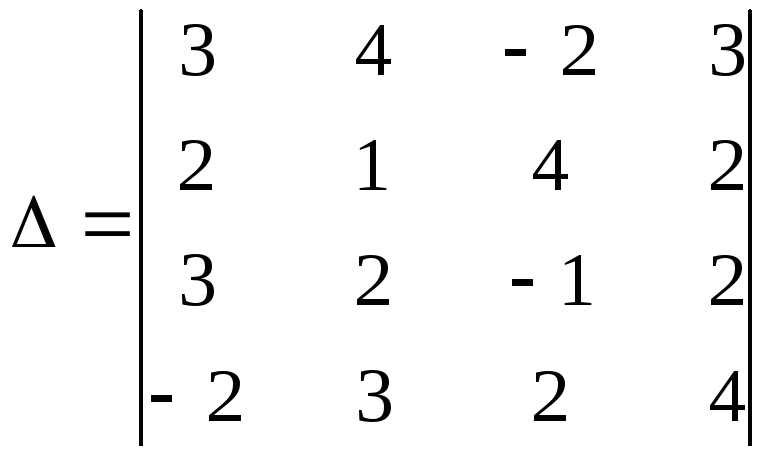
Решение
найдем двумя способами:

а)
путем прямого разложения по элементам
первой строки:

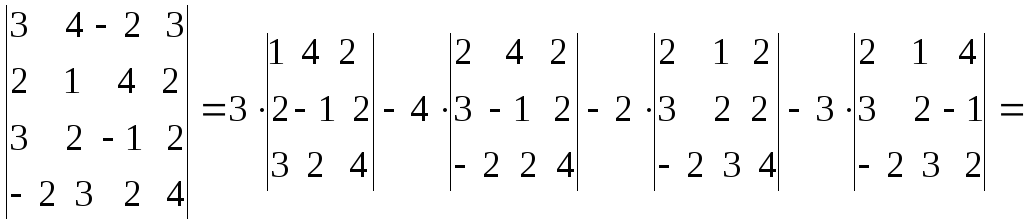
б)
путем предварительных преобразований
и дальнейшего разложения

	а) из І строки вычтем ІІІ
б) ІІ строку прибавим к ІV

а) из IV строки вынесем 2
б) сложим III и IV столбцы
в) умножим на 2 III столбец и прибавим ко II

Пример
5.Вычислить определитель пятого
порядка, получая нули в третьей строке
с помощью четвертого столбца

из первой строки вычтем вторую, из третьей вычтем вторую, из четвертой вычтем вторую, умноженную на 2.

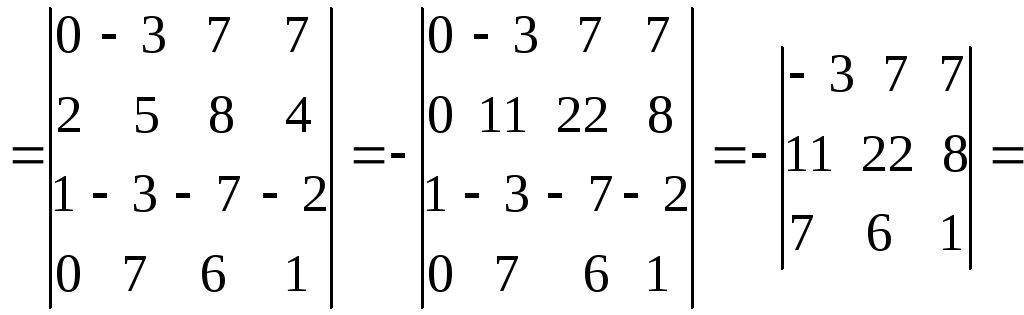
из
второго столбца вычтем третий:

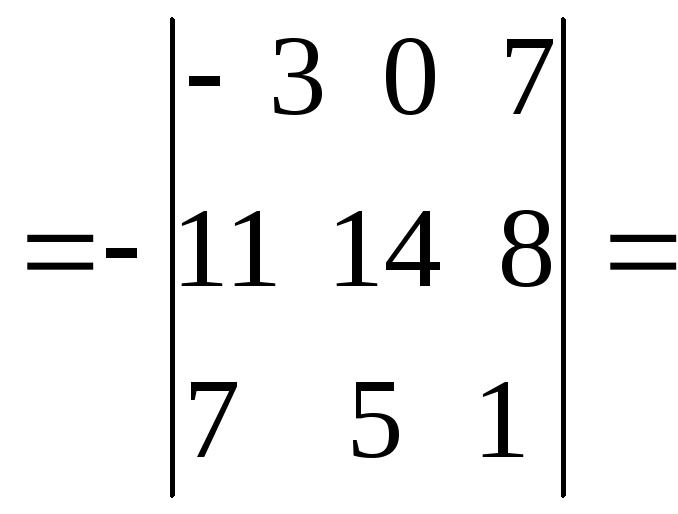
из
второй строки вычтем третью:

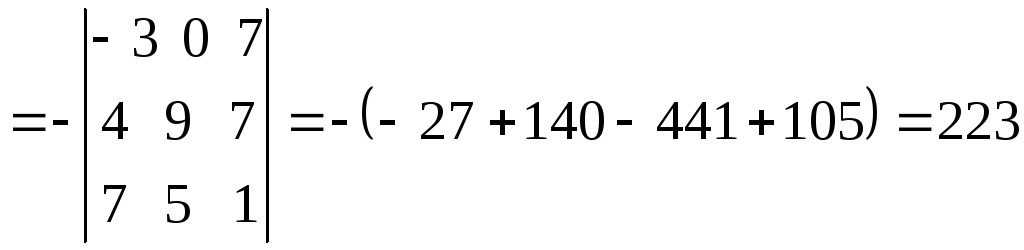
Пример
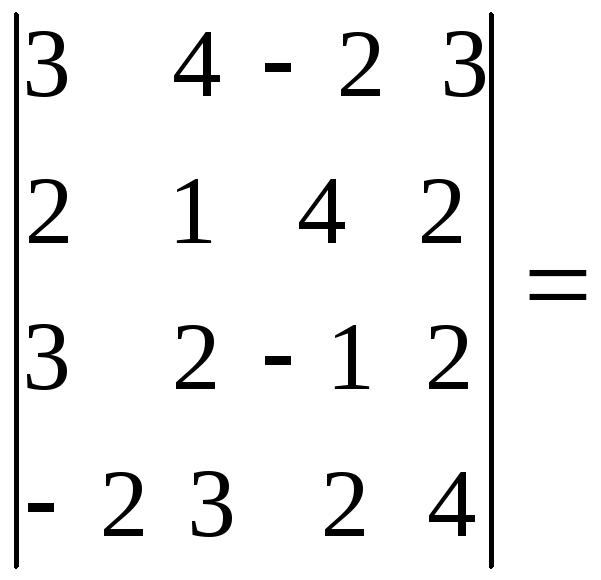
6.Решить систему:

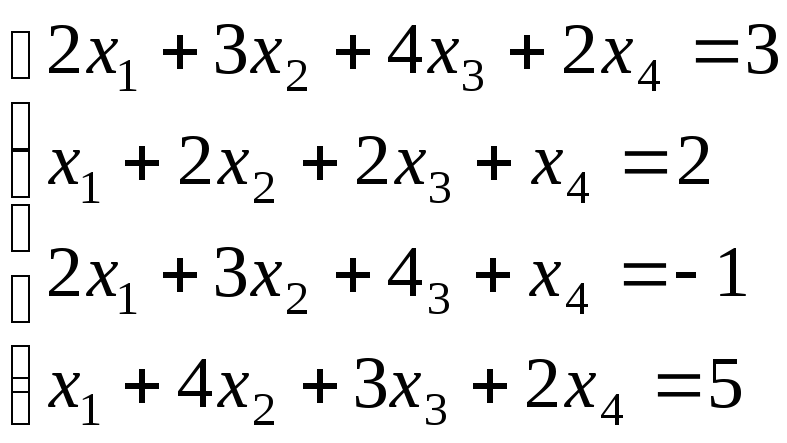
Решение.Составим определитель системы и, применив
свойства определителей, вычислим его:

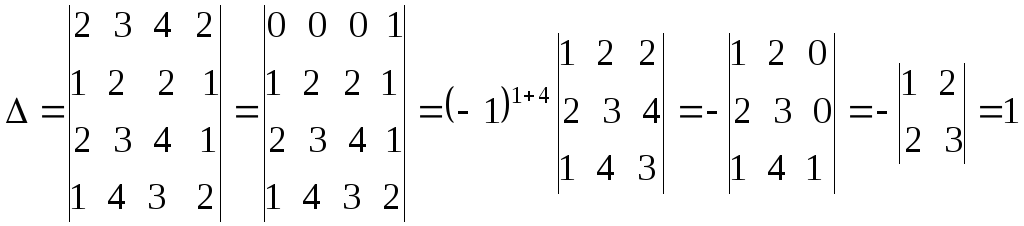
(из
первой строки вычтем третью, а затем в
полученном определителе третьего
порядка из третьего столбца вычитаем
первый, умноженный на 2). Определитель

,
следовательно, формулы Крамера применимы.

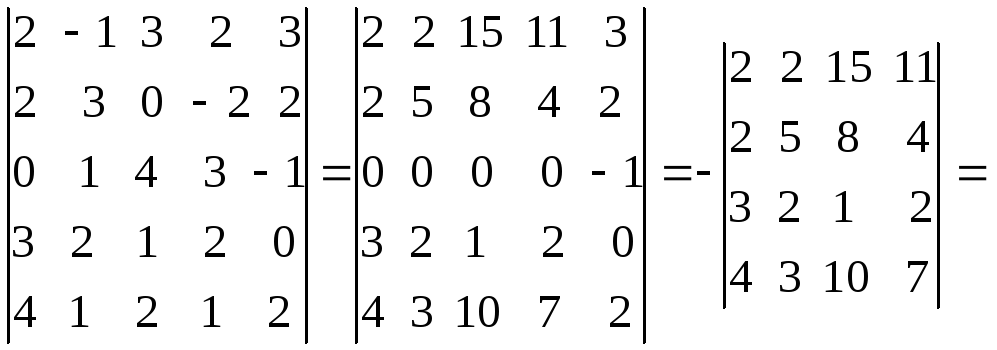
Вычислим
остальные определители:

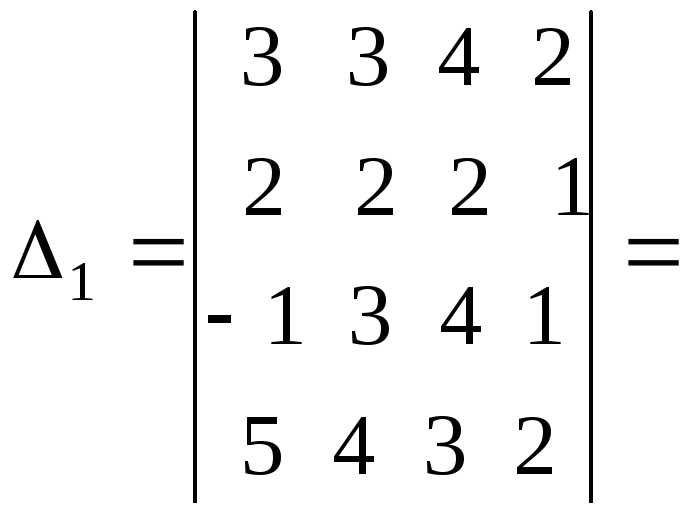
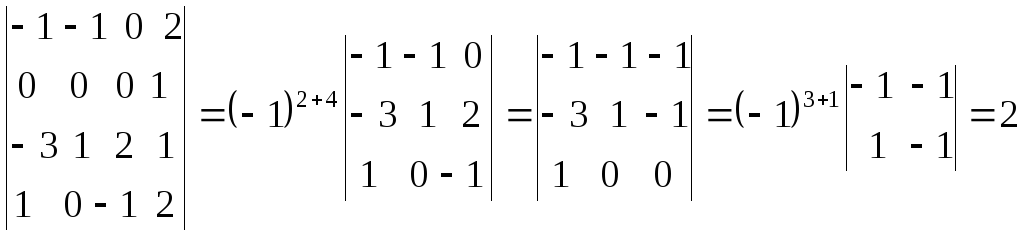
Четвертый
столбец умножили на 2 и вычли из остальных

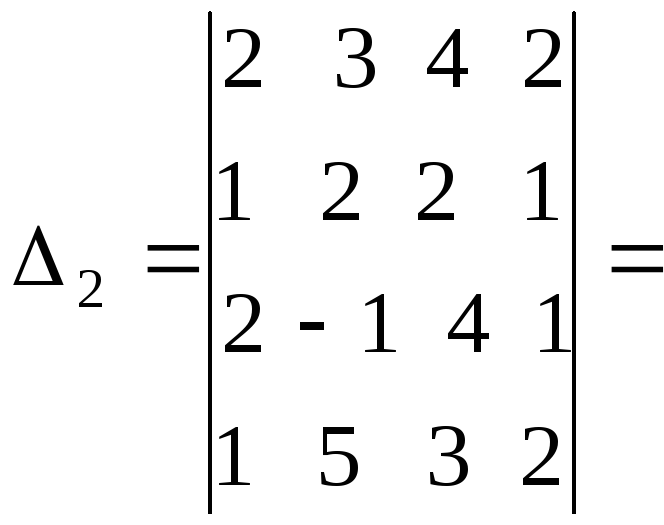
Четвертый
столбец вычли из первого, а затем, умножив
на 2, вычли из второго и третьего столбцов.

.

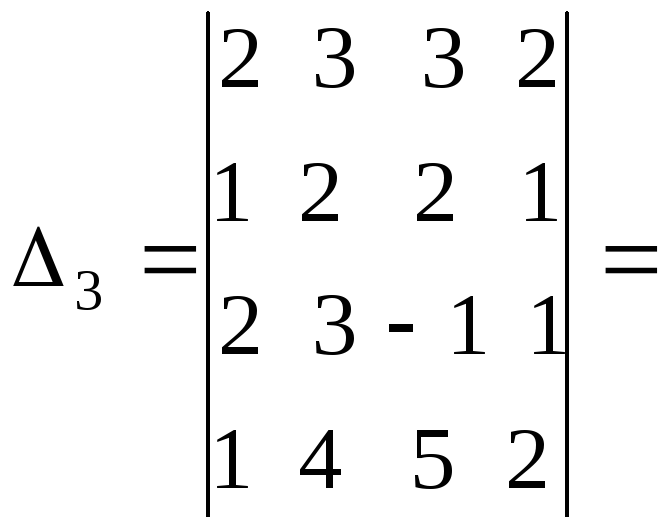
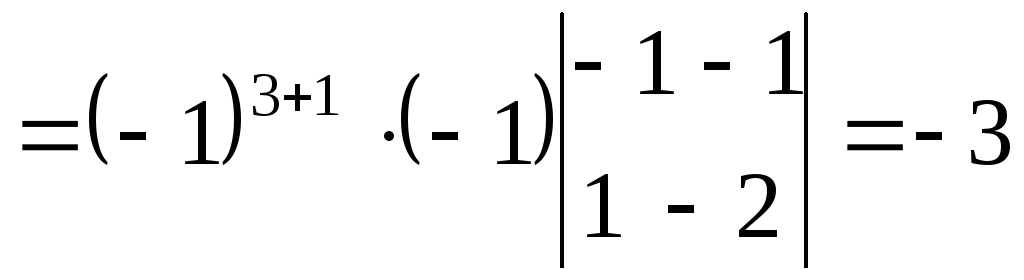Здесь
выполнили те же преобразования, что и
для
.

.

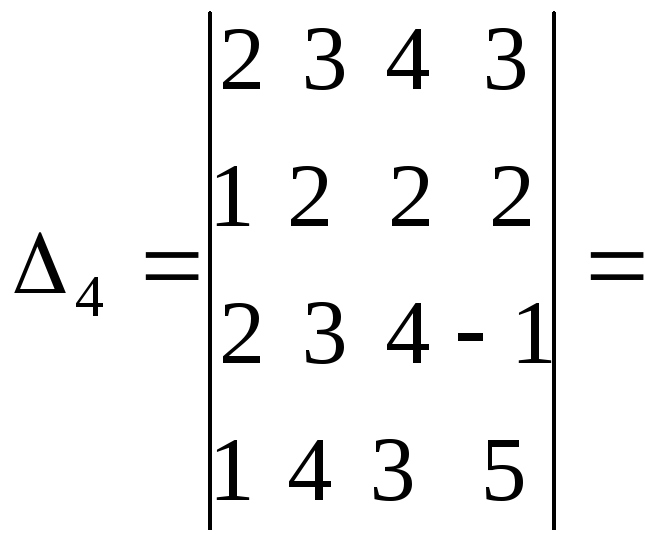
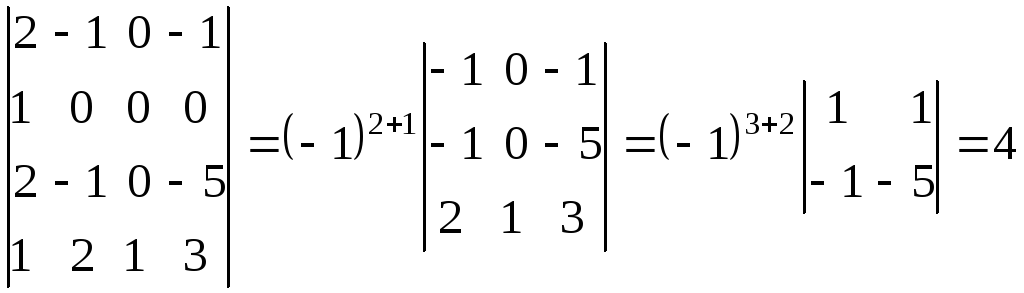При
нахождении
первый столбец умножили на 2 и вычли из
остальных.

По
правилу Крамера имеем:

.

После
подстановки в уравнения найденных
значений убеждаемся в правильности
решения системы.

2.
МАТРИЦЫ и
ИХ
ИСПОЛЬЗОВАНИЕ

В
РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #