Друзья, я знаю, что вы любите задачка с нахождением площади закрашенной области 🙂 В этой заметке разберем очередную такую задачку.
Задача
Дан прямоугольник со сторонами 20 и 10, в который вписано две окружности, которые касаются друг друга. Проведена также диагональ прямоугольника. Найти площадь закрашенной области.
Остановитесь на этом моменте, возьмите карандаш с черновиком, и попробуйте сделать задачу самостоятельно.
Решение:
Изначально можно предположить, что нам понадобится общая формула для площадей сегментов круга. Выведем её из элементарной геометрии:
Если мы начнем применять эту формулу к нашей задаче, сможем выразить площадь желтых сегментов следующим образом:
И дальнейшими манипуляциями сможем дойти до конца… НО, если немного подумать, то такие усложнения не нужны. Потому что диагональю окружности делятся на попарно одинаковые сегменты. А потом из треугольника откусываются два сегмента, которые суммарно составляют цельную одну окружность:
То есть нужно из площади половины прямоугольника (площади прямоугольного треугольника) отнять площадь одного круга. И мы получим площадь закрашенной красным цветом области: 100 – 25π
Задача решена.
Понравилась задачка? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Для начала добавим точки G и H на чертёж, чтобы потом было проще объяснить процесс решения:

Теперь площадь закрашенной фигуры AGCE можно найти, как разность площади целого прямоугольника ABCD и площадей трёх фигур, которые остались не закрашенными, а именно прямоугольной трапеции ABHG, прямоугольного треугольника CGH и прямоугольного треугольника CDE ( впрочем, возможны и другие варианты трапеций и треугольников ).
Площадь прямоугольника ABCD равна произведению длин его сторон:
S(ABCD) = AB * AD = ( AF + BF ) * ( AE + DE ) =
= ( 3 + 2 ) * ( 2 + 2 ) = 5 * 4 = 20 см²
Площадь прямоугольной трапеции ABHG равна половине произведения суммы длин её оснований и её же высоты:
S(ABHG) = ( AB + GH ) * BH / 2 =
= ( AF + FB + FB ) * AE / 2 =
= ( 3 + 2 + 2 ) * 2 / 2 = 7 см²
Площадь прямоугольного треугольника CGH равна половине произведения его катетов CH и GH:
S(CGH) = CH * GH / 2 =
= ED * FB / 2 = 2 * 2 / 2 = 2 см²
Площадь прямоугольного треугольника CDE равна половине произведения его катетов ED и CD:
S(CDE) = ED * DC / 2 =
= ED * ( AF + FB ) / 2 =
= 2 * ( 3 + 2 ) / 2 = 5 см²
Ну, и наконец можно найти площадь закрашенной фигуры AGCE:
S(AGCE) = S(ABCD) – S(ABHG) -S(CGH) – S(CDE) =
= 20 – 7 – 2 – 5 = 6 см²
Ответ: площадь закрашенной фигуры равна В) 6 см²
- 08
Дек 17

Числа от 1 до 100
Умножение и деление
178. 1) Обведи номер прямоугольника, у которого закрашена одна шестая часть, кружком, а у которого закрашена одна восьмая, – квадратом.
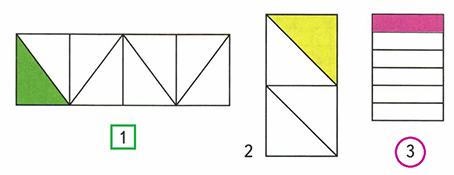
2) Найди площадь каждой закрашенной части в прямоугольниках с номерами 2 и 3.
По измерениям линейкой стороны прямоугольника с номером 2 равны 2 см и 4 см, а с номером 3 – 2 см и 3 см.
1) 2 см • 4 см = 8 см2 – площадь прямоугольника с номером 2
8 см2 : 4 = 2 см2 – площадь четвёртой (закрашенной) части прямоугольника
2) 2 см • 3 см = 6 см2 – площадь прямоугольника с номером 3
6 см2 : 6 = 1 см2 – площадь шестой (закрашенной) части прямоугольника
179.
1 • 25 > 25 • 0 49 • 0 = 0 • 49
67 • 1 = 1 • 67 (16 + 4) • 0 = 0 • (16 – 4)
180.
27 : 1 = 27 0 • (15 + 47) = 0
28 : 4 = 7 (36 – 9) : 1 = 27
6 : 6 = 1 (74 – 20) : 9 = 6
4 • 10 = 40 70 : 7 • 8 = 80
ГДЗ по математике. Рабочая тетрадь. 3 класс. Часть 1. Моро М. И., Волкова С. И.
Математика. 3 класс
3 класс. Рабочая тетрадь №1. Ответы к стр. 66
4.5 (89.58%) от 71 голосующих
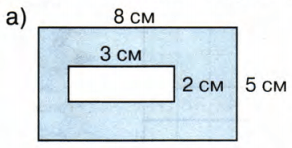
Найди площадь закрашенных фигур:

reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 4. Решение задач. Номер №10
Решение а
1) 8 * 5 = 40
(
с
м
2
)
− площадь всей фигуры;
2) 3 * 2 = 6
(
с
м
2
)
− площадь не закрашенной фигуры;
3) 40 − 6 = 34
(
с
м
2
)
− площадь закрашенной фигуры.
Выражение: 8 * 5 − 3 * 2 = 40 − 6 = 34
Ответ: 34
с
м
2
Решение б
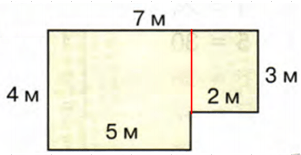
1) 4 * 5 = 20
(
м
2
)
− площадь большого прямоугольника;
2) 2 * 3 = 6
(
м
2
)
− площадь маленького прямоугольника;
3) 20 + 6 = 26
(
м
2
)
− площадь закрашенной фигуры.
Выражение: 4 * 5 + 2 * 3 = 20 + 6 = 26
Ответ: 26
м
2
3 октября 2013
В этом коротком уроке мы научимся считать площади фигур без координатной сетки. Здесь не будет никаких клеточек, никаких пересечений и узлов. Будет только система координат и несколько отмеченных чисел.
Как решать такие задачи? В первую очередь, следует отметить, что у нас все-таки есть линии разметки, а точнее проекции точек на оси координат. И именно они потребуются нам для решения задачи. Причем схема будет даже чуть проще, чем при вычислении площадей методом обводки на координатной сетке. Взгляните на задачу:
Задача B5. Найдите площадь треугольника, изображенного на рисунке.
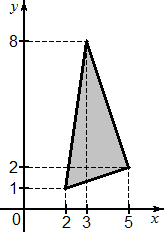
Итак, первый шаг: чертим описанный прямоугольник. Для этого продолжаем линии разметки таким образом, чтобы получилась замкнутая фигура. Это и будет искомый описанный прямоугольник, причем вершины искомой фигуры будут высекать на сторонах этого прямоугольника отдельные отрезки. А значит нам снова нужна формула площади треугольника:
S = 0,5ab
где a и b — катеты (разумеется, речь идет только о прямоугольном треугольнике). А так же пригодится площадь прямоугольника:
S = ab
где a и b — смежные стороны.
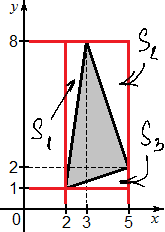
В нашем случае таких треугольников получилось три. Обозначим их S1, S2 и S3. Чтобы сосчитать их площади, нужно сначала найти длину каждого катета. Например, наибольший катер в треугольнике S1 равен a = 8 − 1 = 7, а меньший катет b = 3 − 2 = 1.
Обратите внимание: мы всегда вычитаем из большей абсциссы меньшую, а также из большей ординаты меньшую. Для треугольника S2 верхний катет будет равен a = 5 − 3 = 2, а боковой катет равен b = 8 − 2 = 6. Наконец, для треугольника S3 больший катет будет равен a = 5 − 2 = 3, а меньший катет равен b = 2 − 1 = 1.
Находим площади полученных треугольников:
S1 = 0,5 · 1 · 7 = 3,5;
S2 = 0,5 · 2 · 6 = 6;
S3 = 0,5 · 1 · 3 = 1,5.
Кроме того, нам нужно найти общую площадь описанного прямоугольника. Его стороны равны 7 и 3, а значит площадь равна:
S0 = 7 · 3 = 21.
Осталось выполнить последний шаг. Чтобы найти площадь закрашенной фигуры, нужно из общей площади вычесть площадь дополнительных треугольников, которые мы получили, когда описывали прямоугольник. Получим:
S = S0 − (S1 + S2 + S3) = 21 − (3,5 + 6 + 1,5) = 21 − 11 = 10
Это и является ответом. Площадь закрашенного треугольника равна 10. Как видите, общая схема решения и объем вычислений ничем не отличается от стандартных задач B5 из ЕГЭ по математике, в которых присутствует координатная сетка. Достаточно небольшой тренировки — и вы будете решать эти задачи почти устно.
Смотрите также:
- Задача B5: площадь фигур с вершиной в начале координат

- Опасные ошибки в задачах на площади

- Тест к уроку «Что такое логарифм» (средний)

- Тест к уроку «Площади многоугольников без координатной сетки» (средний)

- Упрощаем решение задач с помощью замены переменной

- Задача B4: расчет времени в пути

