Как найти вебер формула

Как найти вебер формула

Магнитный поток
Phi
Размерность ML2T−2I−1
Единицы измерения
СИ Вб
СГС Мкс
Примечания
Скалярная величина
Классическая электродинамика
VFPt Solenoid correct2.svg
Электричество · Магнетизм

Электростатика

Закон Кулона
Теорема Гаусса
Электрический дипольный момент
Электрический заряд
Электрическая индукция
Электрическое поле
Электростатический потенциал

Магнитостатика

Закон Био — Савара — Лапласа
Закон Ампера
Магнитный момент
Магнитное поле
Магнитный поток
Магнитная индукция

Электродинамика

Векторный потенциал
Диполь
Потенциалы Лиенара — Вихерта
Сила Лоренца
Ток смещения
Униполярная индукция
Уравнения Максвелла
Электрический ток
Электродвижущая сила
Электромагнитная индукция
Электромагнитное излучение
Электромагнитное поле

Электрическая цепь

Закон Ома
Законы Кирхгофа
Индуктивность
Радиоволновод
Резонатор
Электрическая ёмкость
Электрическая проводимость
Электрическое сопротивление
Электрический импеданс

Ковариантная формулировка

Тензор электромагнитного поля
Тензор энергии-импульса
4-потенциал
4-ток

См. также: Портал:Физика

Магни́тный пото́к — поток вектора магнитной индукции mathbf {B} через некоторую поверхность. Для бесконечно малого участка равен произведению модуля {displaystyle |mathbf {B} |} на площадь участка {displaystyle {rm {{d}S}}} и косинус угла alpha между mathbf {B} и нормалью mathbf {n} к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам. Стандартное обозначение — Phi .

Важнейшая физическая формула, в которую входит магнитный поток, — выражение для закона электромагнитной индукции Фарадея.

Определение магнитного потока[править | править код]

Разбиение поверхности на малые участки {displaystyle {rm {d}}S}

Изменение вектора нормали к поверхности

Магнитным потоком через бесконечно малый элемент поверхности {displaystyle {rm {d}}S} называется произведение

{displaystyle {rm {d}}Phi =B,{rm {d}}S,cos alpha =mathbf {B} cdot {rm {d}}mathbf {S} },

где alpha — угол между вектором магнитной индукции mathbf {B} и единичным вектором нормали mathbf {n} к участку поверхности, а векторный элемент dS площади поверхности S определяется как

{displaystyle {rm {d}}mathbf {S} ={rm {d}}S,mathbf {n} }.

Магнитным потоком через поверхность конечной площади называется интеграл от dPhi по поверхности:

{displaystyle Phi =int {rm {d}}Phi =iint limits _{S}mathbf {B} cdot {rm {d}}mathbf {S} }.

Направление вектора mathbf {n} в общем случае непостоянно (см. рис.), магнитное поле также может изменяться вдоль поверхности. Точка в произведениях означает скалярное умножение векторов. Интеграл понимается как предел суммы по малым участкам при стремлении их размеров к нулю. Поверхность может быть незамкнутой (как на рис.) или замкнутой.

В случае однородного поля и плоской поверхности магнитный поток рассчитывается как {displaystyle Phi =B,S,cos alpha }.

Единицы измерения магнитного потока[править | править код]

В СИ единицей магнитного потока является вебер (Вб, размерность — Вб = В·с =
кг·м²·с-2·А-1), в системе СГС — максвелл (Мкс, 1 Вб = 108 Мкс).

Приборы для измерения потока[править | править код]

Прибор для измерения магнитных потоков называется флюксметром (от лат. fluxus — «течение» и греч. metron — мера) или веберметром.

Некоторые свойства магнитного потока[править | править код]

В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции mathbf {B} через любую замкнутую поверхность S равен нулю:

{displaystyle Phi =oint limits _{S}mathbf {B} cdot {text{d}}mathbf {S} =0}.

Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.

В соответствии с теоремой Стокса, магнитный поток Phi через поверхность, «натянутую» на некий контур L, можно выразить через циркуляцию векторного потенциала mathbf {A} магнитного поля по этому контуру:

Phi =oint limits _{L}{mathbf {A}}cdot {mathbf {dl}},

поскольку имеет место связь {displaystyle mathbf {B} ={rm {{rot}mathbf {A} }}}. Этот поток не зависит от конфигурации натянутой поверхности.

Переменный во времени магнитный поток[править | править код]

По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создаётся электродвижущая сила

{displaystyle {mathcal {E}}=-{frac {rm {{d}Phi }}{rm {{d}t}}}}

в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нём возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции mathbf {B} и/или геометрии контура.

Квантование магнитного потока[править | править код]

При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:

{displaystyle Phi _{0}={frac {h}{e}}},

где h — постоянная Планка, e — элементарный заряд.

Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов. Это прямое подтверждение теории БКШ, согласно которой сверхпроводимость обусловлена электронными парами (куперовскими парами):

{displaystyle Phi _{s}={frac {Phi _{0}}{2}}={frac {h}{2e}}=2{,}067833758times 10^{-15}} Вб (в СИ);
{displaystyle Phi _{s}={frac {hc}{2e}}=2,067833636times 10^{-7}} Гаусс·см2 (в СГС), c — скорость света.

Экспериментально квантование магнитного потока было обнаружено в 1961 году.

См. также[править | править код]

  • Уравнения Максвелла
  • Электродвигатель постоянного тока
  • Потокосцепление
  • Индуктивность
Источник

Вебер.

Поделиться в:

Вебер – единица измерения магнитного потока в Международной системе единиц (СИ). Имеет русское обозначение – Вб; международное – Wb.

Вебер, как единица измерения

Применение вебера

Представление вебера в других единицах измерения – формулы

Кратные и дольные единицы

Вебер, как единица измерения:

Вебер – единица измерения магнитного потока в Международной системе единиц (СИ), названная в честь немецкого учёного Вильгельма Эдуарда Вебера.

Вебер имеет русское обозначение – Вб; международное – Wb.

Изменение магнитного потока через замкнутый контур со скоростью один вебер в секунду наводит в этом контуре электродвижущую силу (ЭДС), равную одному вольту (закон Фарадея).

Вб = В · с.

1 Вб = 1 В · 1 с.

1 вебер ‒ магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 ом проходит количество электричества в 1 кулон.

Вб = Ом · Кл.

1 Вб = 1 Ом · 1 Кл.

1 вебер ‒ магнитный поток, созданный магнитным полем индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.

Вб = Тл · м2.

1 Вб = 1 Тл · 1 м2.

Если в однородно магнитном поле при повороте одиночного замкнутого контура с током в один ампер совершается работа в один джоуль, то изменение магнитного потока, охватываемого контуром, равно одному веберу.

Вб = Н · м / А.

1 Вб = 1 Н · 1 м / 1 А.

Название вебер было установлено Международной электротехнической комиссией (МЭК) в 1930 году. В Международную систему единиц вебер введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы вебер пишется со строчной буквы, а её обозначение «Вб» — с заглавной.

Вебер включен в первый раздел Общероссийский классификатор единиц измерения (ОКЕИ) – “Международные единицы измерения, включенные в ОКЕИ“.

Применение вебера:

Вебер применяется для измерения магнитного потока.

Представление вебера в других единицах измерения – формулы:

Через основные и другие единицы измерения СИ вебер выражается следующим образом:

Вб = кг · м2 · с−2 · А−1.

Вб = Н · м / А.

Вб = В · с.

Вб = Гн · А.

Вб = Ом · Кл.

Вб = Дж / А.

Вб = Тл · м2.

где Вб – вебер, кг – килограмм, м – метр, Н – ньютон, В – вольт, с – секунда, Гн – генри, Тл – тесла, А – ампер, Ом – ом, Кл – кулон, Дж – джоуль.

Кратные и дольные единицы:

Кратные и дольные единицы образуются с помощью стандартных приставок СИ.

Кратные Дольные
величина название обозначение величина название обозначение
101 Вб декавебер даВб daWb 10−1 Вб децивебер дВб dWb
102 Вб гектовебер гВб hWb 10−2 Вб сантивебер сВб cWb
103 Вб киловебер кВб kWb 10−3 Вб милливебер мВб mWb
106 Вб мегавебер МВб MWb 10−6 Вб микровебер мкВб µWb
109 Вб гигавебер ГВб GWb 10−9 Вб нановебер нВб nWb
1012 Вб теравебер ТВб TWb 10−12 Вб пиковебер пВб pWb
1015 Вб петавебер ПВб PWb 10−15 Вб фемтовебер фВб fWb
1018 Вб эксавебер ЭВб EWb 10−18 Вб аттовебер аВб aWb
1021 Вб зеттавебер ЗВб ZWb 10−21 Вб зептовебер зВб zWb
1024 Вб иоттавебер ИВб YWb 10−24 Вб иоктовебер иВб yWb

Источник: https://ru.wikipedia.org/wiki/Веббер

Примечание: © Фото https://www.pexels.com, https://pixabay.com

характеристика единица величина измерение физика

Коэффициент востребованности
2 060

Источник

Единица измерения магнитного потока, теория и онлайн калькуляторы

Единица измерения магнитного потока

Определение

Элементарный магнитный поток ($dФ$) сквозь малую поверхность $dS$ равен произведению проекции вектора магнитной
индукции ($B_n$) на нормаль к элементарной площадке $dS$ на величину этой площадки:

[dФ=B_ndS left(1right).]

Полный поток сквозь всю поверхность $S$ будет равен:

[Ф=intlimits_S{B_ndS left(2right).}]

Если поверхность $S$ является плоской, находится она в однородном магнитном поле, причем перпендикулярно линиям индукции поля, то магнитный поток можно найти как:

[Ф=BS left(3right).]

Вебер – единица измерения магнитного потока в системе СИ

Единицу измерения магнитного потока можно определить исходя из выражения (3), как:

[left[Фright]=Тлcdot м^2=Вб.]

Единица измерения магнитного потока имеет собственное наименование – вебер (Вб). 1 Вебер – единица измерения магнитного потока в Международной системе единиц (СИ), это магнитный поток, который создает магнитное поле имеющее индукцию 1Тл через поперечное сечение площадью 1 $м^2$.

Иногда 1 вебер определяют иначе. Вебер (единица измерения магнитного потока) – это магнитный поток, при уменьшении которого до нуля, в сцепленной с ним электрической цепи, имеющей сопротивление один ом сквозь поперечное сечение проводника проходит заряд равный одному кулону. Данное определение вебера основывается на формуле:

[Delta q=frac{Delta Ф}{R}left(4right),]

где $Delta q$ – заряд, который проходит в замкнутой цепи, при изменении магнитного потока $Delta Ф$ сквозь поверхность, которую ограничивает цепь; $R$ – сопротивление рассматриваемой цепи. Исходя из формулы (4) вебер можно считать комбинацией следующих единиц:

[left[Фright]=Вб=Клcdot Ом.]

Производная единица измерения магнитного потока вебер выражается через основные единицы системы СИ как:

[Вб=Тлcdot м^2=frac{кг}{Аcdot с^2}cdot м^2.]

Для обозначения кратных и дольных десятичных единиц измерения магнитного потока используют стандартные приставки системы СИ. Например, мВб (мили вебер): $1 мВб={10}^{-3 }Вб;;$ ГВб (гига вебер) $1 ГВб={10}^{6 }Вб.$

Максвелл – единица измерения магнитного потока в системе СГС

В системе СГС (сантиметр, грамм, секунда) единица измерения магнитного потока, так же как в СИ имеет свое наименование. Она называется максвелл (Мкс). С вебером максвелл соотносится как:

[1Вб={10}^8Мкс.]

Максвелл – единица измерения магнитного потока, получил свое название в честь Дж. К. Максвелла в 1900 г.

[left[Фright]=Мкс=Гсcdot {см}^2.]

Через плоский контур, площадью один квадратный сантиметр, находящийся в однородном магнитном поле с индукцией 1 гаусс (Гс) перпендикулярно направлению вектора магнитной индукции, проходит магнитный поток в один максвелл.

Примеры задач с решением

Пример 1

Задание. Получите вебер, как комбинацию основных единиц Международной системы, основываясь на его определении: $Вб=Клcdot Ом.$

Решение. Используя определение вебера- единицы измерения магнитного потока через произведение кулона на ом, рассмотрим как каждая из этих двух единиц выражается через основные единицы СИ. Так для единицы заряда имеем:

[Кл=Аcdot с left(1.1right).]

Для единицы сопротивления:

[Ом=frac{м^{2cdot }cdot кг}{с^3{cdot А}^2} left(1.2right).]

Используя (1.1) и (1.2) в определении единицы измерения магнитного потока, получаем:

[Вб=Клcdot Ом=А•с cdot frac{м^{2cdot }cdot кг}{с^3cdot А^2}=frac{м^2cdot кг}{с^2cdot А}.]

Ответ. Единица измерения магнитного потока при определении
как $Вб=Клcdot Ом$=$ Тлcdot м^2=frac{м^2cdot кг}{с^2cdot А}$

Пример 2

Задание. Какова величина магнитного потока, пронизывающего плоскую поверхность, площадь которой равна $S=50 {см}^2$, если индукция магнитного поля составляет 0,4 Тл, при этом рассматриваемая поверхность расположена под углом $beta =$300 к направлению вектора магнитной индукции поля? Запишите ответ в единицах системы СГС.

Решение. Сделаем рисунок.

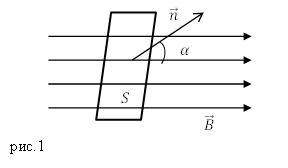
Единица измерения магнитного потока, пример 1

По определению магнитный поток через плоскую поверхность в однородном поле равен:

[Ф=BS{cos alpha }left(2.1right),]

где $alpha $ – угол меду нормалью к плоскости и направлением вектора $overline{B}$. Следует обратить внимание на то, что в условии задачи угол в 300 – это угол между направлением вектора индукции и плоскостью, следовательно, необходимый для решения задачи угол равен:

[alpha =90-beta left(2.2right).]

Так как задачу следует решать в какой-либо, но одной системе единиц, то переведем площадь поверхности в единицы СИ, получим:

[S=50 {см}^2=5cdot {10}^{-3}м^2.]

Проведем вычисления магнитного потока:

[Ф=0,4cdot 5cdot {10}^{-3}{cos left(90-30right)={10}^{-3}left(Вбright). }]

Так как:

[1Вб={10}^8Мкс,]

получаем:

[Ф={10}^{-3}Вб={10}^{-3}cdot {10}^8={10}^5Мкс.]

Ответ. $Ф$=${10}^5Мкс$

Читать дальше: единица измерения магнитной индукции.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Магнитный поток

Магнитный поток это произведение магнитной индукции на площадь поперечного сечения поля.

Единица СИ магнитного потока:

[ [Ф] = вольт cdot секунда = (В cdot с) = вебер enspace (Вб) ]

Если

Ф магнитный поток, Вб
В магнитная индукция, Тесла
Bн нормальная составляющая магнитной индукции, Тесла
S площадь поперечного сечения поля, метр2

то для однородного поля

[ Ф = B_H S ]

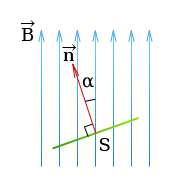
Магнитный поток Вебер

Причем

[ B_H = B cos(α) ]

Здесь α это угол между нормалью площадки S и магнитной индукцией.

Для неоднородного поля, когда индукция меняется по сечению поля

[ Ф = int B_H dS ]

Магнитный поток, Вебер

 стр. 648
Источник

Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.

Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.

Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.

Плоская поверхность в магнитном поле

Рис. 1. Плоская поверхность в магнитном поле. Красным цветом обозначен вектор S, представляющий эту поверхность.

Потоком вектора магнитной индукции ФB через поверхность S называется скалярное произведение векторов B и S.

Формула магнитный поток

Итак можно дать следующее определение термину «магнитный поток»:

Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.

Википедия

Зависимости магнитного потока

Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.

Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.

Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.

В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.

Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.

Единица измерения и обозначение магнитного потока

Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м2 .

Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м2 , то есть [Ф] = Т * м2 . Обозначается магнитный поток как Ф (символ формулы — греческая фи).

Примеры

Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.

  1. В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: ФB = B * S и при этом его значение максимально, так как:

параметры формулы магнитный поток

Поверхность перпендикулярна силовым линиям магнитного поля

Рис. 2. Поверхность перпендикулярна силовым линиям магнитного поля. Векторы B и S параллельны

2. А в каком случае при ненулевой магнитной индукции ФB = 0 ?

Поверхность параллельна силовым линиям магнитного поля

Рис. 3. Поверхность параллельна силовым линиям магнитного поля. Векторы B и S перпендикулярны

Определение магнитного потока показывает, что это тот случай, когда:

Угол поток

потому что cos 90° = 0.

На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.

Обратите внимание, что ФB можно представить как произведение В и S⟂, где S⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).

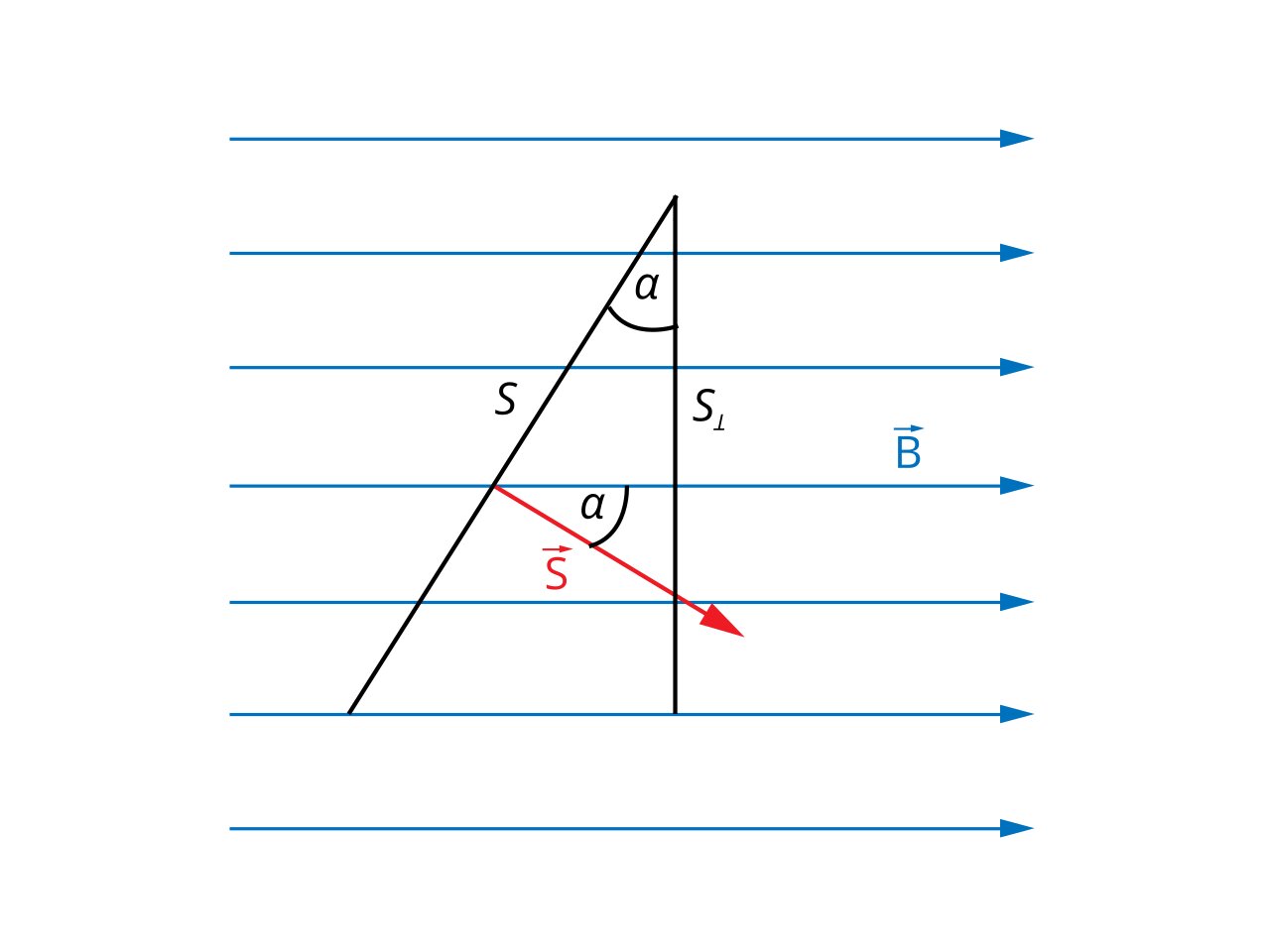
Поверхность S⊥ - это проекция поверхности S

Рис. 4а. Поверхность S⊥ — это проекция поверхности S в направлении, параллельном линиям магнитного поля
Вектор B - это проекция вектора B на направление вектора S
Рис. 4б. Вектор B⟂ — это проекция вектора B на направление вектора S

Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:

Поверхностный интеграл для вычисления магнитного потока

Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.

Источник

Добавить комментарий