Как составить упорядоченный ряд чисел – Сайт, где вы сможете решить свои вопросы

Содержание

Упорядоченные ряды данных. Таблицы распределения
Алгебра
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике

Упорядоченные ряды данных. Таблицы распределения

Ряд задач данного пункта составлен с опорой на материал главы 2 «Линейная функция» учебника и задачника.

Если в некотором измерении данных много, то лучше их как-то упорядочить. Например, если подряд записать сотню телефонных номеров и имена их владельцев, то в таком списке легко запутаться. Совсем другое дело, если расположить те же номера по алфавиту заглавных букв фамилий или имён абонентов. Тогда на каждую букву, скорее всего, придётся не более 7—8 номеров и поиск нужного номера станет простым делом.

Статистическая обработка данных, как правило, начинается с расположения данных в каком-либо разумном порядке: по алфавиту, по числовому значению, в таблице, в столбчатой или круговой диаграмме, в виде дерева возможных вариантов и т. д. Мы начнём с простейших способов упорядочивания данных.

В упражнении № 6.37 а) (см. с. 39) надо отметить на координатной плоскости 14 точек. Ряд данных, состоящий из абсцисс этих точек, выглядит так:

-1, -3, -3, -2, 3, 3, 0, 3, 3, -3, -3, 1, 1, -1.

Его можно упорядочить по возрастанию абсцисс. А именно, сначала выписать все абсциссы, принимающие наименьшее значение -3. Их будет четыре. Справа от них приписать следующую по величине абсциссу -2. Она встретилась один раз. Затем написать две абсциссы, равные -1. Потом пойдёт 0, две единицы и на правом конце ряда останутся четыре абсциссы, равные 3:

-3, -3, -3, -3, -2, -1, -1, 0, 1, 1, 3, 3, 3, 3.

Получился упорядоченный ряд данных. Сами данные в нём не изменились по сравнению с исходным рядом данных, изменился только порядок следования. Грубо говоря, мы расположили первоначальные данные «по росту».

а) Выпишите поочерёдно ординаты всех точек, указанных в № 6.37 б) на с. 39. (Сверьте свой ответ с ответом задачника.)
б) Каков объём и размах полученного ряда данных?
в) Составьте упорядоченный ряд данных.
г) Какова мода этого ряда данных? Сколько раз она встретилась?
д) Сколько всего раз встретилось число -4?
е) Сколько всего раз встретилось число -2?
ж) Сколько всего раз встретилось число 2?
з) Сколько всего раз встретилось число 7?

Вместо того чтобы в задаче № П.8 в) выписывать 0, 0, 0, 0, 0, можно сказать, что число 0 встретилось 5 раз. Так же можно поступить и с остальными числами. Собранную информацию соберём в таблице:

Получилась таблица распределения данных.

Зная упорядоченный ряд данных, нетрудно составить таблицу распределения: вместо повторений одного и того же числа записываем количество этих повторений. Верно и обратное: если известна таблица распределения, то можно восстановить упорядоченный ряд данных. Например, пусть таблица распределения данных какого-то измерения выглядит так:

Из неё получается такой упорядоченный ряд данных:

-3, -3, -3, -1, -1, -1, -1, 5, 5, 7, 8, 8, 8, 8, 8.

Приведите левые части следующих уравнений к виду ах + by + с:

1) 3x — 4y + 5 = 0;
2) 0,5(4x + 1) — у = 0;
3) у — х = 0;
4) x = 0;
5) у = 0;
6) 5у — 4 = 0;
7) 3(х + 2у) — 8 = 0;

8) 5 — 1,5(у — 2х) = 0;
9) 2(х + 2у) — 21 = 0;
10) -(2y — 3х) + 1 — 0;
11) 5-3(у-х) = 0;
12) -(x — у) + 1 = 0;
13) 0,5(3y — 2х) + 5 = 0.

а) Запишите ряд данных, состоящий из коэффициентов при переменной х.
б) Найдите объём и размах полученного ряда данных.
в) Составьте упорядоченный ряд данных.
г) Чему равна мода? Сколько раз она встретилась в ряде данных?
д) Сколько раз встретилось число -1, число 0, число 1, число 2?
е) Составьте таблицу распределения полученных данных.
ж) Сложите все числа во второй строке таблицы распределения. Объясните, почему ответ совпал с объёмом ряда данных.
з) Может ли во второй строке какой-либо таблицы распределения данных стоять число 0?

На контрольной по алгебре ученики 7 «Б» класса получили такие оценки:

Источник

Алгебра

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Понятие выборки и генеральной совокупности

Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.

В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.

В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.

В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.

Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.

Среднее арифметическое выборки

Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.

Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=

Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.

Упорядоченный ряд и таблица частот

В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Такую запись называют упорядоченным рядом данных.

Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:

При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,

С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:

(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.

Размах выборки

Следующий важная характеристика ряда данных – это размах выборки.

Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:

так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.

Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:

(8+9+9+8+9):5 = 43:5 = 8,6;

(7+10+10+6+10):5 = 43:5 = 8,6.

Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен

в то время как размах выборки второго спортсмена равен

Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.

Мода выборки

Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.

В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде

1, 2, 3, 3, 3, 4, 5, 5, 5

варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:

Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.

Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:

Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:

Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна

Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.

Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):

39, 41, 67, 36, 60, 58, 46, 44, 39, 69.

Найдем среднее арифметическое, размах, моду и медиану для этого ряда.

Решение. Сначала перепишем ряд в упорядоченном виде:

36, 39, 39, 41, 44, 46, 58, 60, 67, 69.

Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):

Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен

В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.

В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно

(44+46):2 = 90:2 = 45 кг.

Поэтому и медиана ряда будет равна 45 кг.

Ошибки в статистике

Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?

Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.

В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.

Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.

При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.

Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.

Источник

Элементы статистической обработки данных 7 класс Презентация составлена учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной

Элементы статистической обработки данных

7 класс

Презентация составлена учителем математики

МОУ «СОШ» п. Аджером Корткеросского района

Республики Коми

Мишариной Альбиной Геннадьевной

Статистика — это точная наука, изучающая методы сбора, анализа и обработки данных, которые описывают массовые действия, явления и процессы Математическая статистика – это раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений случайных массовых явлений с целью выявления существующих закономерностей.

Статистика — это точная наука, изучающая методы сбора, анализа и обработки данных, которые описывают массовые действия, явления и процессы

Математическая статистика – это раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений случайных массовых явлений с целью выявления существующих закономерностей.

Статистика изучает:

численность отдельных групп населения страны и ее регионов,
производство и потребление разнообразных видов продукции,
перевозку грузов и пассажиров различными видами транспорта,
природные ресурсы и многое другое.

Результаты статистических исследований широко используются для практических и научных выводов.

В настоящее время статистика начинает изучаться уже в средней школе, в ВУЗах это обязательный предмет, потому что связан со многими науками и отраслями.

Чтобы увеличить количество продаж в магазине, чтобы улучшить качество знаний в школе, чтобы двигать страну по экономическому росту, надо проводить статистические исследования и делать соответствующие выводы. И это должен уметь каждый.

Главные цели изучения элементов статистики

Формирование умений первичной обработки статистических данных;
изображение и анализ количественной информации, представленной в разных формах (в виде таблиц, диаграмм, графиков реальной зависимостей);
формирование представлений о важных статистических идеях, а именно: идее оценивания и идее проверки статистических гипотез;
формирование умений сравнивать вероятности наступления случайных событий с результатами конкретных экспериментов.

Содержание Ряд данных Объем ряда данных Размах ряда данных Мода ряда данных Медиана ряда Среднее арифметическое Упорядоченные ряды данных Таблица распределения данных Подведём итоги Номинативный ряд данных Частота результата Процентная частота Группировка данных Способы обработки данных Подведём итоги

Содержание

Ряд данных
Объем ряда данных
Размах ряда данных
Мода ряда данных
Медиана ряда
Среднее арифметическое
Упорядоченные ряды данных
Таблица распределения данных
Подведём итоги
Номинативный ряд данных
Частота результата
Процентная частота
Группировка данных
Способы обработки данных
Подведём итоги

Определение Ряд данных – это ряд результатов каких-либо измерений. Например: 1) измерения роста человека 2) Измерения веса человека (животного) 3)Показания счетчика (электроэнергии, воды, тепла…) 4) Результаты в беге на стометровку И т.д.

Определение

Ряд данных – это ряд результатов каких-либо измерений.

Например: 1) измерения роста человека

2) Измерения веса человека (животного)

3)Показания счетчика (электроэнергии, воды, тепла…)

4) Результаты в беге на стометровку

И т.д.

Определение Объемом ряда данных называется количество всех данных. Например: дан ряд чисел 1; 3; 6; -4; 0 объём его будет равен 5.

Определение

Объемом ряда данных называется количество всех данных.

Например: дан ряд чисел 1; 3; 6; -4; 0

объём его будет равен 5.

Выполни задание: объём Ответ: 10

Выполни задание:

объём

Ответ: 10

Определение Размах – это разность между наибольшим и наименьшим числами из ряда данных. Например: если дан ряд чисел 1; 3; 6; -4; 0; 2, то размах этого ряда данных будет равен 6 (т.к. 6 – 0 = 6)

Определение

Размах – это разность между наибольшим и наименьшим числами из ряда данных.

Например: если дан ряд чисел 1; 3; 6; -4; 0; 2,

то размах этого ряда данных будет равен 6 (т.к. 6 – 0 = 6)

Выполни задание: размах Ответ: 3

Выполни задание:

размах

Ответ: 3

Определение Модой ряда данных называется число ряда, которое встречается в этом ряду наиболее часто. Ряд данных может иметь или не иметь моду. Так, в ряду данных 47, 46, 50, 52, 47, 52, 49, 45, 43, 53 каждое из чисел 47 и 52 встречается два раза , а остальные числа - менее двух раз. В таких случаях условились считать, что ряд имеет две моды: 47 и 52.

Определение

Модой ряда данных называется число ряда, которое встречается в этом ряду наиболее часто.

Ряд данных может иметь или не иметь моду.

Так, в ряду данных 47, 46, 50, 52, 47, 52, 49, 45, 43, 53 каждое из чисел 47 и 52 встречается два раза , а остальные числа – менее двух раз.

В таких случаях условились считать, что ряд имеет две моды: 47 и 52.

Выполни задание:

В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки:

3, 5, 5, 4, 4, 4, 3, 2, 4, 5.

Определите моду данного ряда.

Ответ: 4

Так, в ряду данных

47, 46, 50, 52, 47, 52, 49, 45, 43, 53 каждое из чисел 47 и 52 встречается два раза, а остальные числа – менее двух раз. В таких случаях условились считать, что ряд имеет две моды: 47 и 52.

Медиана с нечётным числом членов – это число, записанное посередине. Медиана с чётным числом членов - это среднее арифметическое двух чисел , записанных посередине. Например: определить медиану ряда чисел 1) 6; -4; 5; -2; -3; 3; 3; -2; 3. Ответ: -3 2) -1; 0; 2; 1; -1; 0;2; -1. Ответ: 0

Медиана с нечётным числом членов – это число, записанное посередине.
Медиана с чётным числом членов – это среднее арифметическое двух чисел , записанных посередине.

Например: определить медиану ряда чисел

1) 6; -4; 5; -2; -3; 3; 3; -2; 3.

Ответ: -3

2) -1; 0; 2; 1; -1; 0;2; -1.

Ответ: 0

Выполни задание: медиану

Выполни задание:

медиану

Среднее арифметическое - ЭТО частное от деления суммы чисел ряда на их количество. Например: дан ряд чисел -1; 0; 2; 1; -1; 0; 2; -1. Тогда среднее арифметическое будет равно: (-1+0+2+1+(-1)+0+2+(-1)) : 8= =2 : 8=0,25

Среднее арифметическое – ЭТО частное от деления суммы чисел ряда на их количество.

Например: дан ряд чисел -1; 0; 2; 1; -1; 0; 2; -1.

Тогда среднее арифметическое будет равно: (-1+0+2+1+(-1)+0+2+(-1)) : 8= =2 : 8=0,25

Выполни задание: среднее арифметическое Ответ: 3,9

Выполни задание:

среднее арифметическое

Ответ: 3,9

ПРАКТИЧЕСКАЯ РАБОТА

Задание: охарактеризовать успеваемость ученика Иванова по математике за четвертую четверть.

ВЫПОЛНЕНИЕ РАБОТЫ:

1.Сбор информации:

Выписаны оценки из журнала: 5,4,5,3,3,5,4,4,4.

2.Обработка полученных данных:

объём = 9

размах = 5 – 3 = 2

мода = 4

медиана = 3

среднее арифметическое =(5+4+5+3+3+5+4+4+4) : 9 ≈ 4

Характеристика успеваемости : ученик не всегда готов к уроку.

В основном учится на «4». За четверть выходит «4».

Надо найти объём ряда, размах ряда, моду, медиану и среднее арифметическое: Карточка 1. 22,5; 23; 21,5; 22; 23. Карточка 2. 6; -4; 5; -2; -3; 3; 3; -2; 3. Карточка 3. 12,5; 12; 12; 12,5; 13; 12,5; 13. Карточка 4. -1; 0; 2; 1; -1; 0; 2; -1. Карточка 5. 125; 130; 124; 131. Карточка 6. 120; 100; 110.

Надо найти объём ряда, размах ряда, моду, медиану и среднее арифметическое:

Карточка 1. 22,5; 23; 21,5; 22; 23.

Карточка 2. 6; -4; 5; -2; -3; 3; 3; -2; 3.

Карточка 3. 12,5; 12; 12; 12,5; 13; 12,5; 13.

Карточка 4. -1; 0; 2; 1; -1; 0; 2; -1.

Карточка 5. 125; 130; 124; 131.

Карточка 6. 120; 100; 110.

Карточка 1. объём ряда = 5 размах ряда = 10 мода = 23 медиана = 21,5 среднее арифметическое = 13,3 Карточка 3. объём ряда = 7 размах ряда = 1 мода = 12,5 медиана = 12,5 среднее арифметическое = 12,5 Карточка 2. объём ряда = 9 размах ряда = 10 мода = 3 медиана = -3 среднее арифметическое = 1 Карточка 4. объём ряда = 8 размах ряда = 3 мода = -1 медиана = 0 среднее арифметическое = 0,25

Карточка 1.

объём ряда = 5

размах ряда = 10

мода = 23

медиана = 21,5

среднее арифметическое = 13,3

Карточка 3.

объём ряда = 7

размах ряда = 1

мода = 12,5

медиана = 12,5

среднее арифметическое = 12,5

Карточка 2.

объём ряда = 9

размах ряда = 10

мода = 3

медиана = -3

среднее арифметическое = 1

Карточка 4.

объём ряда = 8

размах ряда = 3

мода = -1

медиана = 0

среднее арифметическое = 0,25

Карточка 5. объём ряда = 4 размах ряда = 7 мода = нет медиана = 127 среднее арифметическое =127,5 Карточка 6. объём ряда = 3 размах ряда = 20 мода = нет медиана = 100 среднее арифметическое = 110

Карточка 5.

объём ряда = 4

размах ряда = 7

мода = нет

медиана = 127

среднее арифметическое =127,5

Карточка 6.

объём ряда = 3

размах ряда = 20

мода = нет

медиана = 100

среднее арифметическое = 110

Определение Упорядоченными рядами данных называются ряды, в которых данные расположены по какому то правилу Как упорядочить ряд чисел? Записать числа так, чтобы каждое последующее число было не меньше (не больше) предыдущего); записать некоторые названия «по алфавиту»… Причем с ами данные в ряду данных не изменяются , а изменяется только порядок их следования

Определение

Упорядоченными рядами данных называются ряды, в которых данные расположены по какому то правилу

Как упорядочить ряд чисел?

Записать числа так, чтобы каждое последующее число было не меньше (не больше) предыдущего);
записать некоторые названия «по алфавиту»…

Причем с ами данные в ряду данных не изменяются , а изменяется только порядок их следования

Выполни задание Дан ряд чисел: -1;-3;-3;-2;3;3;2;0;3;3;-3;-3;1;1;-3;-1 Упорядочить его по возрастанию чисел. Решение: -3;-3;-3;-3;-3;-2;-1;-1;0;1;1;2;3;3;3;3 Получился упорядоченный ряд. Сами данные в нем не изменились, изменился только порядок их следования .

Выполни задание

Дан ряд чисел:

-1;-3;-3;-2;3;3;2;0;3;3;-3;-3;1;1;-3;-1

Упорядочить его по возрастанию чисел.

Решение:

-3;-3;-3;-3;-3;-2;-1;-1;0;1;1;2;3;3;3;3

Получился упорядоченный ряд.

Сами данные в нем не изменились, изменился только порядок их следования .

Таблица распределения данных – это таблица упорядоченного ряда, в котором вместо повторений одного и того же числа записывается количество повторений.

И наоборот, если известна таблица распределения, то можно составить упорядоченный ряд данных.

Например:

Из нее получается такой упорядоченный ряд:

-3;-3;-3;-1;-1;-1;-1;5;5;7;8;8;8;8;8

Результат измерения

Сколько раз встречается в ряде данных

-3

-1

Выполни задание:

В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:

Цена (руб.): 500 1200 1500 1800 2000 2500

Количество: 8 9 14 15 3 1

Для данных показателей надо найти статистические характеристики:

составить упорядоченный ряд данных
объем ряда данных
размах ряда
моду ряда
медиану ряда
среднее арифметическое ряда данных

И ответить на следующие вопросы:

И ответить на следующие вопросы:

Мы познакомились с начальными понятиями того, как происходит статистическая обработка данных: данные всегда являются результатом какого-либо измерения у ряда некоторых данных можно найти: объём, размах, моду, медиану и среднее арифметическое 3) любой ряд данных можно упорядочить и составить таблицу распределения данных

Мы познакомились с начальными понятиями того, как происходит статистическая обработка данных:

данные всегда являются результатом какого-либо измерения
у ряда некоторых данных можно найти:

объём, размах, моду, медиану и

среднее арифметическое

3) любой ряд данных можно

упорядочить и составить

таблицу распределения данных

Номинативный ряд данных – это НЕ ЧИСЛОВЫЕ ДАННЫЕ, а например, имена; названия; номинации… Например: список финалистов чемпионатов мира по футболу с 1930 года: Аргентина, Чехословакия, Венгрия, Бразилия, Венгрия, Швеция, Чехословакия, ФРГ, Италия, Нидерланды, Нидерланды, ФРГ, ФРГ, Аргентина, Италия, Бразилия, Германия, Франция

Номинативный ряд данных – это НЕ ЧИСЛОВЫЕ ДАННЫЕ, а например, имена; названия; номинации…

Например: список финалистов чемпионатов мира по футболу с 1930 года: Аргентина, Чехословакия, Венгрия, Бразилия, Венгрия, Швеция, Чехословакия, ФРГ, Италия, Нидерланды, Нидерланды, ФРГ, ФРГ,

Аргентина, Италия, Бразилия, Германия, Франция

Выполни задание: Решение : объём =18; мода – немецкая команда.

Выполни задание:

Решение : объём =18; мода – немецкая команда.

Вероятность случайного события

Вероятность случайного события

Частота результата = (сколько раз результат встретился) : (объем данного ряда) Например: 19 5 частота 5:19

Частота результата = (сколько раз результат встретился) : (объем данного ряда)

Например:

19 5

частота 5:19

Процентная частота = (частота · 100% ) Например: если частота результата равна 5:19 = 0,263157…, то процентная частота будет равна : 0,263 · 100 = 26,3% Часто ответы для процентных частот могут быть не точными, а приближенными

Процентная частота = (частота · 100% )

Например:

если частота результата равна 5:19 = 0,263157…, то процентная частота будет равна : 0,263 · 100 = 26,3%

Часто ответы для процентных частот могут быть не точными, а приближенными

Группировка данных – применяется когда различных результатов измерений слишком много. Т.е их объединяют в группы. При группировке различных данных информация становится менее точной.

Группировка данных – применяется когда различных результатов измерений слишком много.

Т.е их объединяют в группы.

При группировке различных данных информация становится менее точной.

Способы обработки данных: Таблица Диаграмма круговая (каламбер) Год обучения 2007-2008 1-4 кл. 250 5-9 кл 2008-2009 2009-2010 10-11 кл 253 254 258 80 248 78 240 73

Способы обработки данных:

Таблица

Диаграмма круговая (каламбер)

Год обучения

2007-2008

1-4 кл.

250

5-9 кл

2008-2009

2009-2010

10-11 кл

253

254

258

248

240

Способы обработки данных График Гистограмма (столбчатая диаграмма)

Способы обработки данных

График
Гистограмма

(столбчатая диаграмма)

В финал конкурса «Мисс факультета» вышли 10 студенток, за которых голосовали 90 студентов.

В финал конкурса

«Мисс

факультета» вышли 10 студенток,

за которых голосовали

90 студентов.

Способы обработки данных

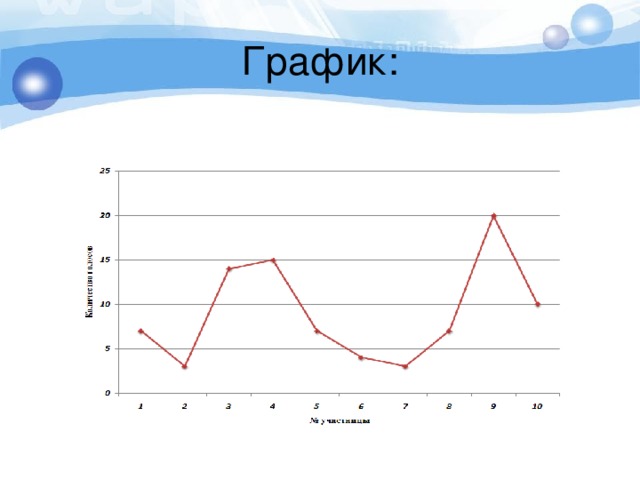
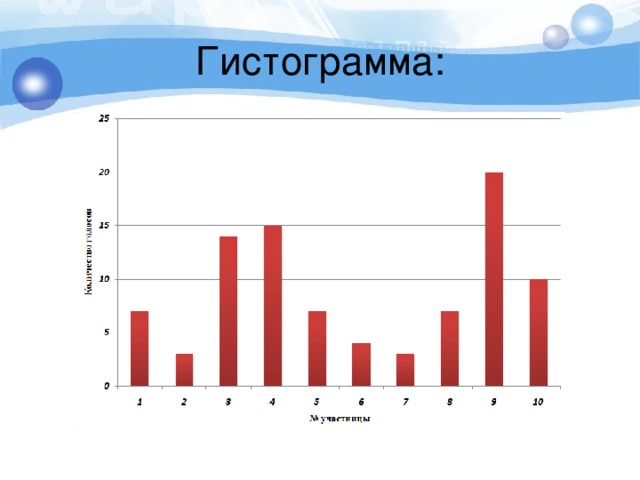
Способы обработки данных

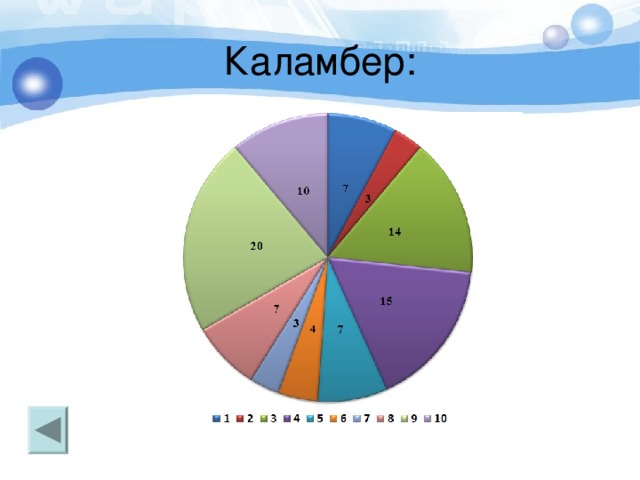
Каламбер:

Мы узнали, что….: Номинативный ряд – это…. Частота результата – это…. Группировка данных – это… Способы обработки данных : 1) таблица 2) график 3) гистограмма (или столбчатая диаграмма) 4) каламбер (или круговая диаграмма)

Мы узнали, что….:

Номинативный ряд – это….
Частота результата – это….
Группировка данных – это…
Способы обработки данных :

1) таблица

2) график

3) гистограмма (или столбчатая диаграмма)

4) каламбер (или круговая диаграмма)

Спасибо за внимание!

Спасибо за внимание!

Источник

Урок
1. Среднее арифметическое, размах, мода. Медиана, как статистическая
характеристика.

I
Актуализация и мотивация знаний

– Скажите,
пожалуйста, какие ассоциации у вас возникают при словах: мода, размах?

– Среднее арифметическое?

– Можете ли вы мне дать определение этим
понятиям?

– Как вы думаете, а какое из этих слов
относится к математике, алгебре? А ещё точнее к теории вероятности и
статистике? ВСЕ!

– Как вы думаете, что нам
поможет во всём разобраться? Учебник п. 9 стр. 36–

– Что такое упорядоченный
ряд чисел? Ряд, в котором каждое последующее число не больше(не меньше)
предыдущего.

Например:
23; 17; 35; 17; 14; 56 – произвольный ряд 14; 17; 17; 23;
35; 56 –упорядоченный ряд чисел

– Что же называется ср.
арифметическим ряда чисел? Результат частного суммы чисел к их
количеству. Если рассмотреть ряд чисел, записанный выше, попробуйте найти ср.
арифметическое данного ряда. (14+17+17+23+35+56) : 6 = 162 : 6 = 27

Размах
– это результат разности м/у наибольшим и наименьшим значениями ряда чисел.
Опять же на примере ряда, записанного ранее, определите размах

А
= 56 – 14 = 42

Мода
– это число, которое чаще других встречается в данном ряду. М = 17

– А сейчас постараемся
на практике применить полученные знания. Найдите все эти статистические характеристики
в следующих заданиях:

Медиана упорядоченного
ряда чисел с нечётным числом членов
– это число, записанное посередине, а медиана упорядоченного ряда
чисел с чётным числом членов – это среднее арифметическое двух
чисел, записанных посередине.

Медиана
произвольного ряда – медиана
соответствующего упорядоченного ряда.

– Как мы с вами можем
охарактеризовать ряд, записанный самым первым? Произвольный ряд с чётным
количеством членов ряда.

– Можете ли вы определить
значение медианы? Ме = (17+23) : 2 = 25

– Приведите пример ряда с
нечётным количеством членов и расскажите алгоритм определения медианы? 75;
64; 56; 56; 56; 48; 37; 22; 16; Ме = 56

– Какие ещё
статистические характеристики вы можете найти для данного ряда чисел?

Среднее
арифметическое, размах и моду.

II
Работа по данной теме:

В
классе: № 177, № 186, № 167 (г, а), № 168
(г, а), № 169 (г, а), № 176, № 178, № 175

Дома:
п. 9-10(выучить осн. понятия),№ 168 (б, в), № 171,№ 189. Подготовиться к С.р.

Самостоятельная
работа по теме: «Статистические характеристики».

I
вариант

1. Что
такое мода ряда? ПРИМЕР

2. Что
такое среднее арифметическое ряда чисел? ПРИМЕР

Самостоятельная
работа по теме: «Статистические характеристики».

II
вариант

1.
Что такое размах ряда? ПРИМЕР

2. Что такое
медиана ряда с чётным числом членов? ПРИМЕР

3. В таблице
приведено количество очков, набранных в чемпионате, некоторыми баскетболистами.

Источник

План урока:

Понятие выборки и генеральной совокупности

Среднее арифметическое выборки

Упорядоченный ряд и таблица частот

Размах выборки

Мода выборки

Медиана выборки

Ошибки в статистике

Понятие выборки и генеральной совокупности

1 massiv informacii

2 vyborka nabor dannyh

3 generalnaja sovokupnost

Среднее арифметическое выборки

4 srednee arifmeticheskoe vyborki

= 349:20 = 17,45.

Упорядоченный ряд и таблица частот

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Такую запись называют упорядоченным рядом данных.

5 uporjadochennyj rjad dannyh

6 kolichestvo balov

2+3+1+1+2+2+1+2+2+1+1+2 = 20.

(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =

(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.

Размах выборки

Следующий важная характеристика ряда данных – это размах выборки.

7 razmah vyborki

25 – 12 = 13,

(8+9+9+8+9):5 = 43:5 = 8,6;

(7+10+10+6+10):5 = 43:5 = 8,6.

9 – 8 = 1,

в то время как размах выборки второго спортсмена равен

10 – 6 = 4.

Мода выборки

8 moda vyborki

1, 2, 3, 3, 3, 4, 5, 5, 5

6, 6, 7, 7, 8, 8.

Медиана выборки

9 obem vyborki

10 mediana

11 nechetnoe kolichestvo

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна

(17+17):2 = 34:2 = 17.

39, 41, 67, 36, 60, 58, 46, 44, 39, 69.

Найдем среднее арифметическое, размах, моду и медиану для этого ряда.

Решение. Сначала перепишем ряд в упорядоченном виде:

36, 39, 39, 41, 44, 46, 58, 60, 67, 69.

(36+39+39+41+44+46+58+60+67+69):10 =

= 499:10 = 49,9 кг.

69 – 36 = 33 кг.

(44+46):2 = 90:2 = 45 кг.

Поэтому и медиана ряда будет равна 45 кг.

Ошибки в статистике

Источник

Ряд
распределения
– это последовательность чисел с указанием
качественного
или количественного значения признака
и частоты его встречаемости.

Виды
рядов распределения
классифицируются
по разным принципам.

По
степени упорядоченности ряды
делят на:

неупорядоченные
упорядоченные

Неупорядоченный
ряд
– это такой ряд, в котором значения
признака записаны
в порядке поступления вариантов при
исследовании.

Пример:
При исследовании роста группы студентов
были записаны его значения
в см (175,170,168,173,179).

Упорядоченный
ряд –
это ряд, полученный из неупорядоченного
в котором значения признака перезаписаны
в порядке возрастания или убывания.
Упорядоченный ряд называется
ранжированным, а процедура
ранжирования

(
упорядочивания ) называется сортировкой.

Пример:
( Рост 168,170,173,175,179 )

По
виду признака ряды распределения делятся
на:

атрибутивные
вариационные.

Атрибутивный
ряд
– это ряд, составленный на основе
качественного признака.

Вариационный
ряд
– это ряд, составленный на основе
количественного признака.

Вариационные
ряды подразделяются на дискретные,
непрерывные
и интервальные.

Вариационные
дискретные, непрерывные и интервальные
ряды названы
по соответствующему признаку, который
лежит в основе составления
ряда. Например, ряд по размеру обуви
является дискретным по
массе тела – непрерывным.

Способы
представления рядов в
практической и научной медицине делятся
на три группы:

Табличное
представление;
Аналитическое
представление (в виде формулы);
Графическое
представление.

1.
Простейшая таблица представляет собой
два столбца или две строки, в одной из
которых записаны значения признака x_i
в упорядоченном виде, а в другой –
относительная или абсолютная частота
его встречаемости n_i,
f_i.

Пример:
табличное представление оценок в группе
x_iи
числа их получивших студентов n_i.

x_i	5	4	3	2
n_i	3	8	2	–

2.
Графическое представление рядов основано
на табличных
данных. Графики строят в прямоугольной
системе координат,
где по горизонтали всегда откладывают
значения признака х_i
,
а по вертикали
абсолютную или относительную частоту
n_i
.

Основные
способы представления графиков:

Диаграмма
в отрезках.
Гистограмма
Полигон
частот.
Вариационная

( частотная
)
кривая.

Диаграмма
в отрезках
– это график представления ряда в виде
вертикальных прямых-отрезков,
положение которых на горизонтали
определяется значением признака,
а длина отрезка пропорциональна его
абсолютной или относительной частоте.

Пример:
диаграмма в отрезках для
оценок успеваемости группы.

n_i

5 4 3 2 XI

Обычно
диаграммы в отрезках строят для дискретно
заданных признаков при
небольшом числе вариантов.

Гистограмма
– это график в виде ступенчатой фигуры
из примыкающих друг
к другу прямоугольников, основаниями
которых являются интервалы значений
признаков, а высоты прямоугольников
пропорциональны частоте
или частости ( количеству объектов,
попавших в интервал ). Площади
прямоугольников соответствуют численности
групп, в данном интервале.

Гистограммы
– это графики интервальных рядов. Их
строят преимущественно
для больших объемов совокупностей.

Пример:
Гистограмма нормального распределения
эритроцитов в крови человека.
По горизонтали – диаметр
клеток х_i
(мк),
по вертикали – частота n_i
числа клеток
в интервале.

n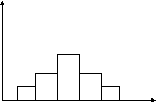_i

2
4 6 8 10 12 x_i

Полигон
(многоугольник) частот
– график ряда, представленный ломаной
линией
точки – вершины которой соответствуют
серединам интервалов, а высота точки
над горизонталью пропорциональна
частоте или частости.

Полигоны
строят для непрерывных и дискретных
вариационных рядов в тех
случаях, когда в интервалах выделены
средние значения признака. Полигоны
предпочтительнее
гистограмм при
непрерывных рядах распределения

Пример:
полигон
частот на основе гистограммы
распределения эритроцитов
в крови человека.

n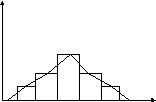_i

2
4 6 8 10 12
x_i

Вариационная
(частотная) кривая
– график ряда, полученный при условии,
что объем совокупности, стремится к
бесконечности ( N→∞
),
а длина самого
интервала стремится к нулю ( Δх→0
).

Для
практических статистических расчетов
в качестве стандартов выделено четыре
группы частотных распределений:

Прямоугольное
распределение.
Колоколообразное
унимодальное (одновершинное)
распределение.
Бимодальное
(двухвершинное) распределение.
Экспоненциальное
распределение:

нарастающее,
убывающее.

n_i

x_i

Прямоугольному
распределению подчиняются случайные
равновероятные
события.

Колоколообразному
симметричному распределению
подчиняется широкий класс
явлений ( показатели умственного
и физического развития, рост,
масса, и др ).
На практике наиболее часто встречается
симметричное унимодальное распределение,
поэтому его классическая форма называется
нормальным распределением.

Бимодальному
распределению соответствует, например
успеваемость
студентов имеющих и
не имеющих большого перерыва в учебе.

Экспоненциально
убывающему распределению
соответствует распределение
доходов в капиталистическом
обществе, ( частота
убывает при возрастании дохода
).

Соседние файлы в папке Медицинская физика

Источник

Упорядоченные ряды данных. Таблицы распределения

Алгебра

Понятие выборки и генеральной совокупности

Среднее арифметическое выборки

Упорядоченный ряд и таблица частот

Размах выборки

Мода выборки

Ошибки в статистике

Понятие выборки и генеральной совокупности

Среднее арифметическое выборки

Упорядоченный ряд и таблица частот

Размах выборки

Мода выборки

Медиана выборки

Ошибки в статистике

5 4 3 2 XI

Вам также может понравиться

Как исправить ошибку драйвера на ноутбуке

Как найти обменник с выгодным курсом

Как составить короткий бизнес план

Добавить комментарий Отменить ответ