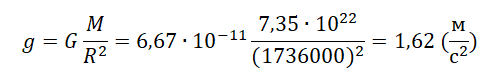Вопрос о том, как найти центростремительную силу, часто задают. Ответ на него таков: центростремительная сила — это сила, которая в основном требуется для приведения тела в движение по круговой траектории.
В этой статье мы увидим, как найти центростремительную силу, которая отвечает за круговое движение тела. Когда тело сталкивается с круговым движением, оно поддерживается центростремительной силой, которая регулируется центром оси вращения.
Допустим, мяч движется по прямолинейному пути и воспринимает нормальную силу и ускорение, необходимые для движения вперед. Когда он испытывает кривая в пути он автоматически будет иметь действие другой силы.
Нормальная сила в линейном движении эквивалентна весу объекта, который включает в себя массу и влияние гравитации. Но когда говорят, что тело движется по круговой траектории, потребуются дополнительные количества, которые способствуют этому движению.
Компания величина нормальной силы будет больше на криволинейном пути по сравнению с линейным путем. центростремительная сила будет иметь нормальную силу вместе с ней, которая имеет значение больше, чем у линейного движения.
Компания влияние гравитации при круговом движении происходит из-за наличия центростремительной силы. Эта центростремительная сила всегда действует внутрь. Когда солнце находится в движении, оно всегда направлено внутрь, к орбите и оси вращения.
Как найти формулу центростремительной силы?
Мы должны знать, что на самом деле означает сила, а затем погрузиться в тему центростремительной силы. Сила – это величина, необходимая для приведения тела в движение.
Формула общей силы фактически получена из второго закона Ньютона. То есть ф=ма. Сила — это просто произведение массы на ускорение.
Центростремительная сила не какая-то новая сила, а существующая сила в виде нескольких других сил в различных аспектах. Формула центростремительной силы имеет много факторов, которые ей помогают.
Во-первых, поскольку это круговое движение, тело совершает обороты. Теперь число оборотов называют частотой. Эта революция также рассчитывается с точки зрения периода времени.
Один оборот рассчитывается по периоду времени и равен обратной частоте. Итак, число оборотов = частота; период времени одного оборота t= 1/частота.
Когда все факторы собраны вместе, мы получаем полную формулу для центростремительной силы как fc=мв2/r, где m=масса; v= скорость; г = радиус.
Радиус на самом деле определяется окружностью кругового пути, который аналогичен расстоянию и смещению при прямолинейном движении.
Как найти центростремительную силу с массой и радиусом?
Из обычной формулы для центростремительной силы мы знаем, что масса, скорость и радиус являются факторами, влияющими на центростремительную силу.
Центростремительная сила находится в прямой зависимости от массы объекта, скорости его движения при круговом движении и радиуса кругового движения. При прямолинейном движении значение нормальной силы меньше, чем при круговом движении.
Масса в нормальной силе удерживается гравитацией и кажется меньше по сравнению с круговым движением. Когда тело привязано к веревке в центре оси масса также должна тянуться таким же образом.
Компания равнодействующая сила действуя на тело, заставит другую силу, подобную этой, действовать на тело. Когда тело тянут круговым движением, оно образует почти идеальный круг, и это только если смотреть сверху.
Когда это движение образует правильную окружность, длина окружности дает расстояние и перемещение, аналогичное линейному движению. От чего образуется диаметр, в свою очередь находится и радиус поворота.
Теперь мы можем найти центростремительную силу, используя массу и радиус с массой и радиусом, и формула будет такой же, как и обычная,
Fc= мв2/r
Давайте рассмотрим несколько задач, в которых масса и радиус играют главную роль в определении центростремительной силы.
1 задачи:
Кривая траектории имеет радиус кривизны 0.5 м при массе тела 2 кг. Приравняйте центростремительную силу всей системы, если скорость равна 5 м/с.
Решение:
Fc=мв2/r
Fc= 100 Н
2 задачи:
Мяч имеет радиус 2.5 м и весит 10 кг. Мяч вращается со скоростью 12 м/с. Найдите центростремительную силу, с которой он движется.
Решение:
Fc=мв2/r
Fc= 576 Н
Как найти центростремительную силу без массы?
Вообще существует ошибочное мнение, что центростремительная одна отдельная сила, которая приводит тело в движение по круговой траектории.
Центростремительная — это сила притяжения к центру кругового движения, которая может быть любой формой силы, скажем, силой гравитации, силой натяжения и так далее. Эта сила представляет собой всего лишь усилие, прикладываемое к объекту для того, чтобы он оставался в круговом движении.
Допустим, мяч привязан к веревке, прикрепленной к гвоздю. Когда мяч совершает круговое движение, его фактически вызывает струна, и в струне создается натяжение. Но сила направлена внутрь так сила натяжения в этом случае рассматривается центростремительная сила.
Идеология центростремительной силы состоит в том, что это просто сила, которая изображает работу другой силы, когда линейное движение. Для пример когда масса привязан к центру оси вращения, на него будет действовать сила.
Когда масса совершает круговое движение, она образует правильную окружность, и на нее действует сила, которую можно измерить. сила натяжения так как струна имеет натяжение. Тогда он будет иметь направленную вверх силу, так как его притягивает сила гравитации.
Следовательно, центростремительную силу можно найти без массы через силу натяжения. гравитационный сила, сила трения.
Как найти центростремительную силу без скорости?
Как мы уже обсуждали в предыдущей подтеме относительно определения центростремительной силы без учета массы.
Если объект совершает круговое движение, на него будет действовать сила, обеспечиваемая нормальной силой, аналогичной линейному движению. Когда объект привязан к центру вращения, его движение вызывается силой, действующей на элемент, удерживающий объект в целости.
Теперь эта сила может быть тангенциальной силой, потому что существует струна, действующая как система поддержки объекта, которая удерживает его в движении по круговой траектории. Поскольку сила натяжения действует по касательной к движущемуся объекту, она рассматривается как центростремительная сила.
На пути, по которому движется тело, совершая круговое движение, трение будет меньше или равно нулю. Таким образом, учитывая силу натяжения системы, центростремительную силу можно найти без скорости, соответственно.
Рассмотрим пример, когда центростремительная сила находится без учета скорости. Объект движется с постоянной скоростью по круговой траектории. Центростремительная сила находится через силу натяжения, и это значение должно быть найдено. Значение массы 2 кг.
Когда масса движется по кругу, она также управляется сила гравитации быть неразрывным с движением. Т=мг; Т= 2х9.8; Т= 19.6 Н. Вот как решается простая задача с использованием формулы силы натяжения для расчета центростремительной силы.
Как найти центростремительную силу с угловой скоростью?
При любом круговом движении нам нужно знать факторы или величины, которые помогают в самом круговом движении.
Угловая скорость также известна как радиальная скорость, которая приводит тело в движение. Это в основном будет определять количество оборотов в секунду, а также количество оборотов, совершаемых в секунду.
Центростремительная сила и угловая скорость идут рука об руку, когда тело движется по окружности. Отсюда мы можем легко узнать, как найти центростремительную силу с угловой силой.
Сначала нужно вывести формулу центростремительной силы, которая ФК=МВ2/r. Здесь фактор v2/r это центростремительное ускорение что аналогично формуле ж=мА; fc=m (а); ФК=МВ2/r. Расширив эту формулу, мы получим часть угловой скорости.
С v2/r это центростремительное ускорение мы можем разбить формулу дальше с точки зрения скорости. Формула для центростремительное ускорение ас=v2/r. расширяя это, мы получаем формулу угловой скорости, то есть ас=rω2, (ω=vr).
Теперь, когда мы знаем, как найти центростремительную силу через угловой скорости легче определить центростремительное ускорение также в таких случаях.
Как найти центростремительную силу по радиусу?
Формула для центростремительной силы с точки зрения радиуса дается как fc=mv2/r. В этом случае радиус определяется окружностью кругового пути.
Мы разработаем несколько примеров, где радиус находится при заданной центростремительной силе. Мы также увидим, как на центростремительную силу влияют радиус и масса объекта.
Когда радиус кругового пути мал, кривая клятвы будет острой и образует изгиб шпильки в виде кривой.
1 задачи:
Мотоцикл массой 200 кг тащит вокруг столба высотой 12 м со скоростью 10 м/с. 12 м также можно считать радиусом кругового движения, если столб согнут и ровно стоит на земле. Рассчитайте центростремительную силу по приведенным выше значениям?
Решение:
Fc=mv2/r
Fc= 1666.6 Н
2 задачи:
Шарик массой 5 кг привязан к нити, которая образует радиус 0.25 м от окружности кругового движения. Сила, действующая на мяч, вызывает его движение по окружности со скоростью 9 м/с. Определите центростремительную силу, действующую внутрь, а также действующую как сила притяжения.
Решение:
Fc=mv2/r
Fс=1620Н
Часто задаваемые вопросы
Как рассчитать центростремительную силу с радиусом и временем?
Радиус вызывает определенное количество силы, которая помогает телу двигаться. Разбивая формулу (fc=mv2/r), мы придем к периоду времени движения.
Например, скажем, что объект массой 10 кг движется со скоростью 2 м/с по круговой траектории радиусом 0.6 м, и ответом на это будет 66.6 Н. Теперь, нарушая формулу, мы приходим к центростремительное ускорение ac=v2/r, далее разбивая формулу на несколько шагов, мы окончательно приходим к формуле периода времени (t=1/f). Частота – это, по сути, мера количества оборотов, совершаемых телом при круговом движении..
Что вызывает центростремительную силу?
Компания круговое движение любого объекта вызовет центростремительное заставить действовать.
Центростремительная сила – это в основном сила притяжения, которая действует радиально внутрь окружности. Это не какая-то особая сила, а форма любых других сил, которые действуют по касательной к объекту при круговом движении.
Куда направлена центростремительная сила?
Направление центростремительной силы всегда направлено к оси вращения.
Центростремительная сила всегда направлена к оси вращения кругового движения, другими словами, она действует радиально внутрь. Эта сила также соответствует второму закону Ньютона, где сила определяется произведением массы на ускорение.
Калькулятор ниже предназначен для решения задач на центростремительную силу. Как правило, все задачи на центростремительную силу с численными данными требуют правильного применения ее формулы:
,
где
ac — центростремительное ускорение,
m — масса тела,
v — скорость,
ω — угловая скорость,
r – радиус кривизны.
В формуле участвует четыре параметра, соответственно, три параметра задаются условием задачи, иногда завуалированно, а четвертый и надо вычислить. Пример подобной задачи: Чему равна центростремительная сила, действующая на груз массой 500 г, вращающийся на веревке длиной 50 сантиметров равномерно со скоростью 5 м/с?
Хотя формула достаточно проста, ошибки в расчетах могут возникать при использовании неправильных величин, например, оборотов в секунду вместо радиан в секунду, грамм вместо килограмм, сантиметров вместо метров и тому подобное. Поэтому калькулятор ниже позволяет выбрать для каждого параметра нужные единицы измерения и сам заботится о правильном использовании стандартных единиц СИ. Формулы для вычисления каждого неизвестного параметра можно посмотреть под калькулятором.
![]()
Центростремительная сила
Скорость/Угловая скорость
Точность вычисления
Знаков после запятой: 3
Нахождение неизвестных значений в формуле центростремительной силы
Сила
Масса
Радиус кривизны
Скорость
Угловая скорость
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
По аналогии можно легко вывести основные формулы вращательного движения:
- ( omega=Delta<theta>/Delta ) , где ( omega ) — угловая скорость, ( Delta <theta>) — угол поворота, ( Delta ) — время поворота на угол ( Delta <theta>) ;
- ( alpha=Delta<omega>/Delta ) , где ( alpha ) — угловое ускорение, ( Delta <omega>) — изменение угловой скорости, ( Delta ) — время изменения угловой скорости;
- ( theta=omega_0(t_1-t_0)+<>^1!/!_2a(t_1-t_0)^2 ) , где ( omega_0 ) — это начальная скорость;
- ( omega^2_1-w^2_0=2as ) , где ( omega_1 ) — это конечная скорость.
Разбираемся с параметрами вращательного движения
В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.
Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:
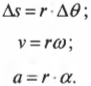
Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ) , равной 21,5 ( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.
Вычисляем линейную скорость вращательного движения
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf ) и линейной скоростью ( mathbf ) . Скорость ( mathbf ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf ) .
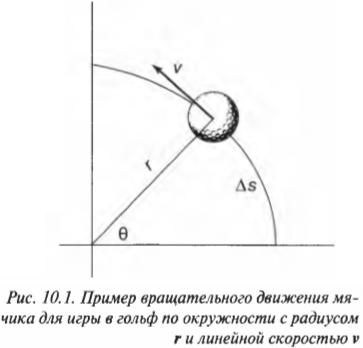
Угловая скорость связана с линейной скоростью соотношением ( v=romega ) , которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.
Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ) . Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ) , а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ) , охватывающая угол ( Deltatheta ) , равна:
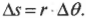
Из формулы прямолинейного движения
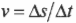
путем подстановки выражения для ( Delta s ) получим:
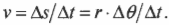
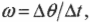
где ( omega ) — угловая скорость, ( Delta <theta>) — угол поворота, ( Delta ) — время поворота на угол ( Delta <theta>) , то:
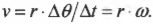
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ) , равной 21,5 ( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:
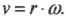
Подставляя в нее значения, получим:
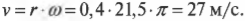
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.
Вычисляем тангенциальное ускорение
Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
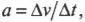
где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением
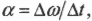
где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?
Как мы уже знаем, линейная и угловая скорости связаны равенством
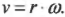
Подставим это выражение в предыдущую формулу линейного ускорения:
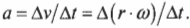
Поскольку радиус остается постоянным, то его можно вынести за скобки:
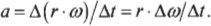
Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ) , то:
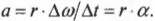
Итак, получаем следующую формулу связи между линейным и угловым ускорением:
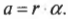
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.
Вычисляем центростремительное ускорение
Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):
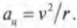
Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ) , получим:
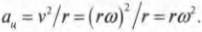
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.
Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:
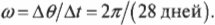
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:
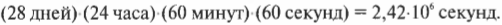
После подстановки этого значения в предыдущую формулу получим:
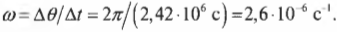
Средний радиус орбиты Луны равен 3,85·10 8 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
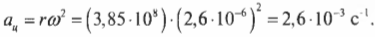
Зная это ускорение и массу Луны, которая равна 7,35·10 22 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:
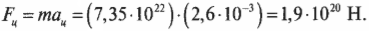
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ) , оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ) .
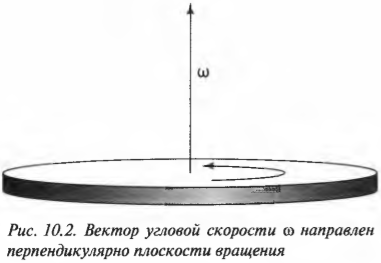
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
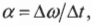
где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
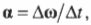
где ( mathbf <alpha>) — вектор углового ускорения, а ( Deltamathbf <omega>) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
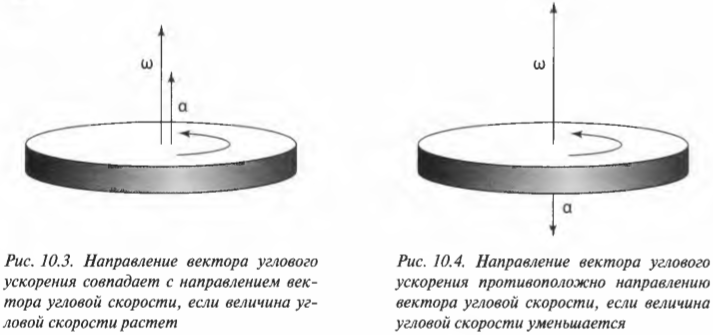
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.
Поднимаем грузы: момент силы
В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.
Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).
В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ) .
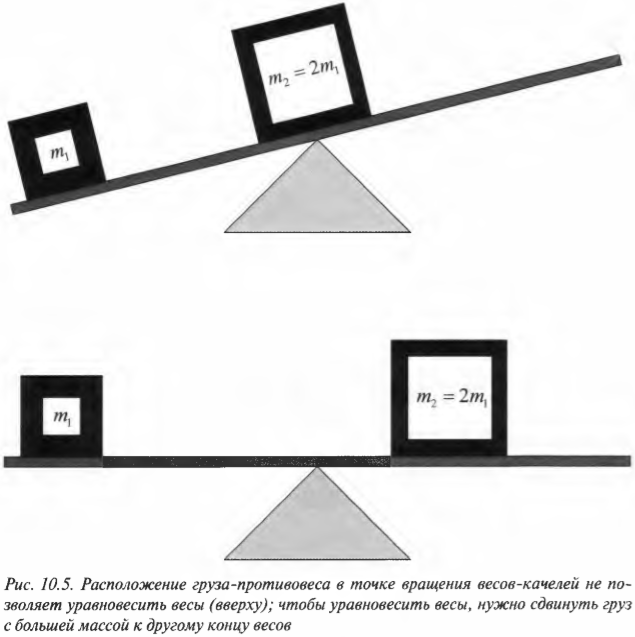
Знакомимся с формулой момента силы
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).
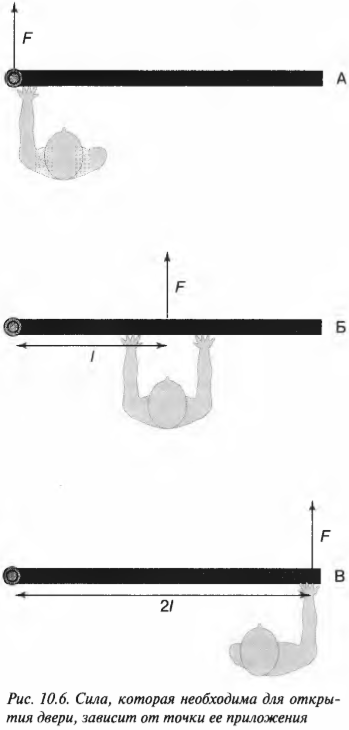
На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ) :
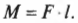
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:
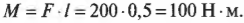
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:
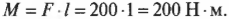
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?
Разбираемся с направлением приложенной силы и плечом силы
Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
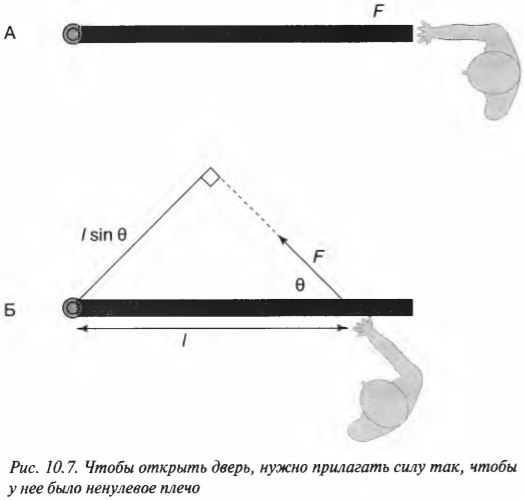
Размышляем над тем, как создается момент силы
Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.
Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ) . Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:
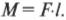
Однако в данном случае угол ( theta ) не является прямым.
В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.
Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:
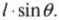
Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).
Итак, получаем для момента силы для схемы Б на рис. 10.7:
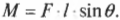
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:
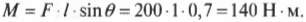
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.
Определяем направление момента силы
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
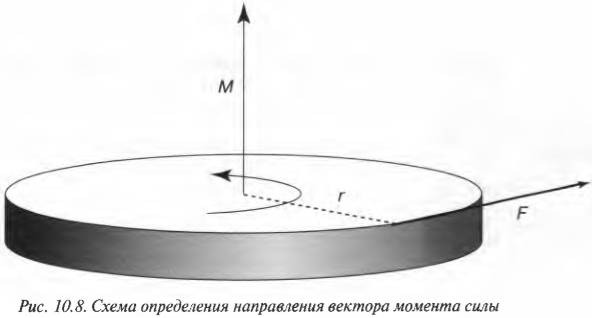
На рис. 10.8 показан пример силы ( mathbf ) с плечом ( mathbf ) и соответствующего вектора момента сил ( mathbf ) .
Уравновешиваем моменты сил
В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).
Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:
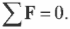
Иначе говоря, результирующая действующая сила равна нулю.
Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.
Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:
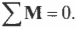
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Простой пример: вешаем рекламный плакат
Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.

Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.
Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:
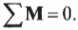
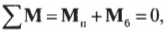
где ( mathbf ) — это момент силы со стороны плаката, а ( mathbf ) — это момент силы со стороны болта.
Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:
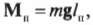
где ( m ) = 50 кг — это масса плаката, ( mathbf ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.
Подставляя значения, получим:
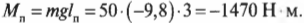
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.
Момент силы со стороны болта определяется формулой:
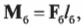
где ( mathbf ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.
Подставляя полученные выражения для моментов сил в формулу:
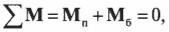
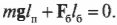
Отсюда с помощью простых алгебраических преобразований получим искомую силу:
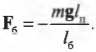
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.
Подставляя значения, получим искомый ответ:
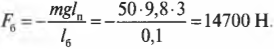
Более сложный пример: учитываем силу трения при расчете равновесия
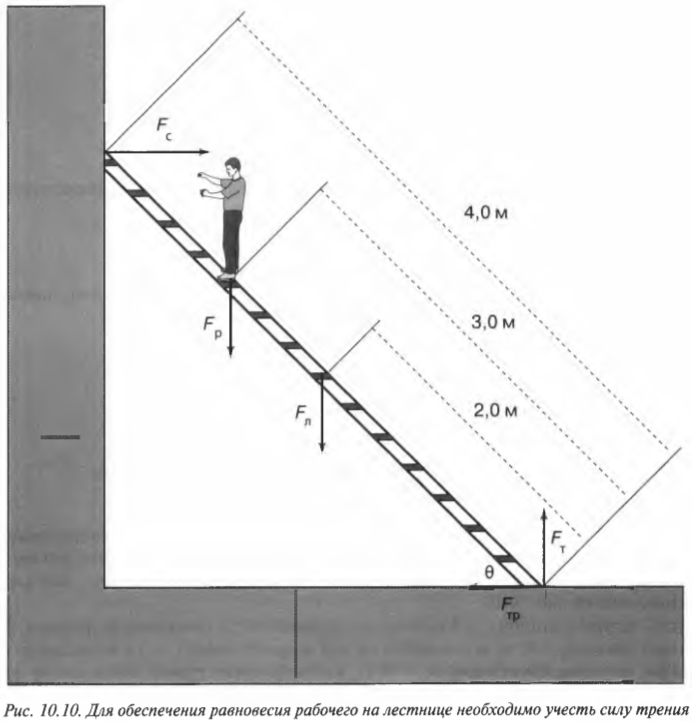
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.
Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:
- ( mathbf ) — нормальная сила со стороны стены;
- ( mathbf ) — вес рабочего;
- ( mathbf ) — вес лестницы;
- ( mathbf> ) — сила трения между поверхностью тротуара и концами лестницы;
- ( mathbf ) — нормальная сила со стороны тротуара.
Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:
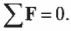
Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf> ) , должна быть равна нулю, то есть:
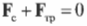
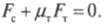
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие
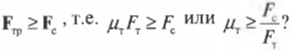
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf ) , веса лестницы ( mathbf ) и нормальной силы со стороны тротуара ( mathbf ) , должна быть равна нулю, то есть:
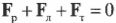
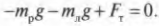
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:
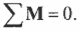
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf ) , весом лестницы ( mathbf ) и нормальной силой со стороны стены ( mathbf ) :
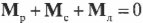
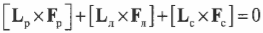
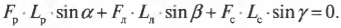
Поскольку ( L_р=l_р ) , ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ) , ( alpha=360^<circ>-theta ) , ( beta=360^<circ>-theta ) и ( gamma=theta ) , то получим:
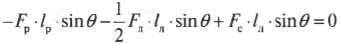
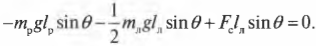
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf ) и ( mathbf ) :
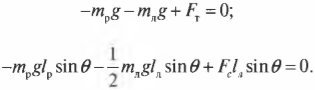
Зададимся вопросом: соблюдается ли условие
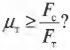
Из системы двух уравнений получим:
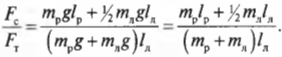
Итак, остается выяснить, соблюдается ли условие:
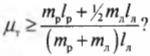
После подстановки значений получим:
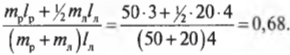
Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.
Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
4.1. Динамика поступательного движения твердого тела.
Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.
Разобьем твердое тело на элементарные массы mi , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы
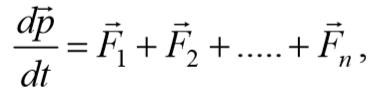
p = $$<sum_^n>$$ mi υ i=m υ C – импульс всех материальных точек твердого тела.
Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс
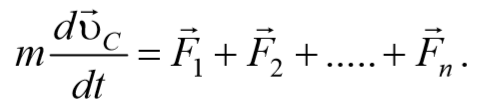
Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.
4.2. Момент импульса. Момент силы.
Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра
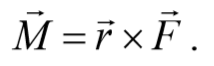
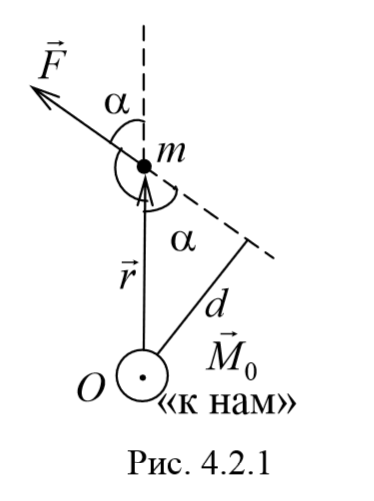
Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен
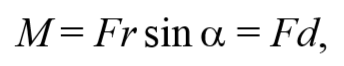
где d=r sin α − плечо силы относительно точки O .
Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.
Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.
Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:
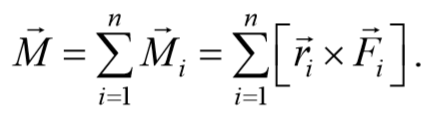
Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра
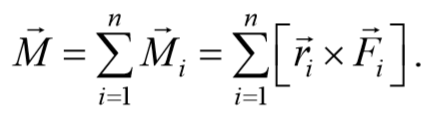
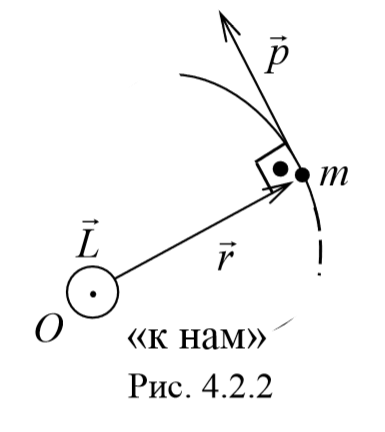
Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен
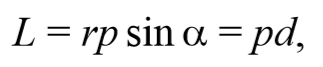
где d − плечо импульса относительно точки O .
Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.
Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.
Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы
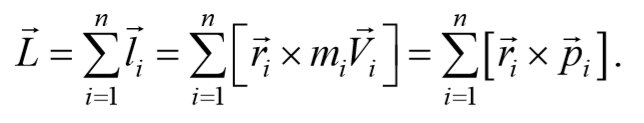
4.3. Основное уравнение динамики вращательного движения относительно точки.
Рассмотрим систему материальных точек массами m1, m2, . mn движущихся со скоростями υ 1, υ 2, . υ n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i 1, F i 2, . F i n , и равнодействующие внешних сил F e 1, F e 2, . F e n .
Запишем уравнения движения частиц:
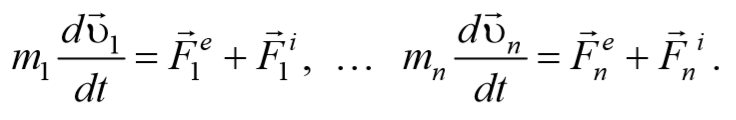
Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим
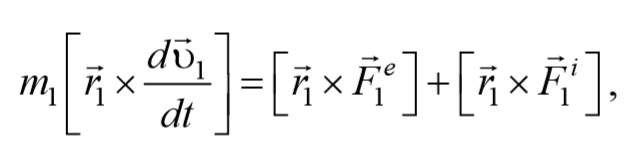
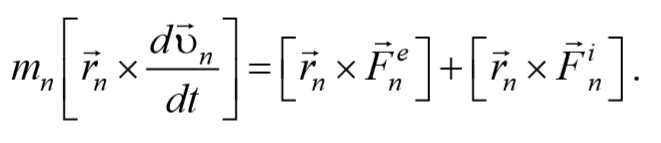
Преобразуем данные уравнения
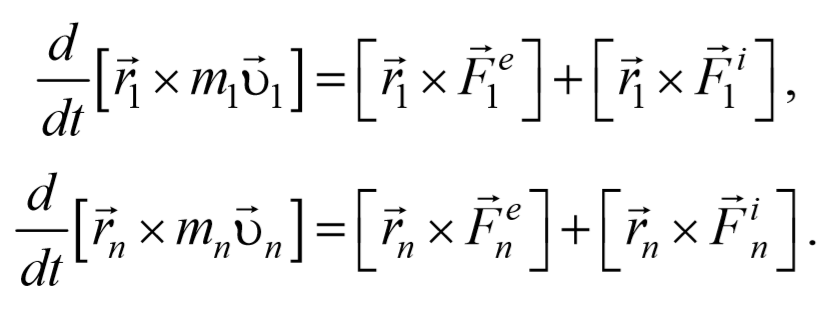
Сложим эти уравнения и получим
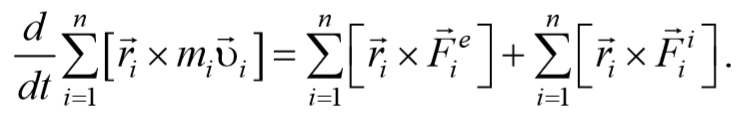
В последнем уравнении:
Таким образом, выражение (4.3.6) можно записать в виде
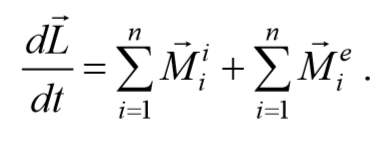
Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<sum_^n>$$ M i i=0 , получим основное уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы ).
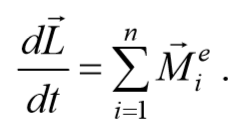
4.4. Закон сохранения момента импульса.
Если момент внешних сил $$<sum_^n>$$ M e i=0 , то получим
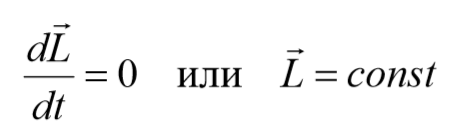
закон сохранения момента импульса.
Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.
Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.
Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.
4.5. Момент инерции.
Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:
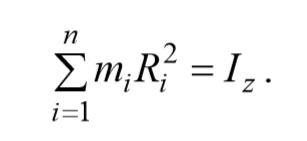
Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .
Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.
Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:
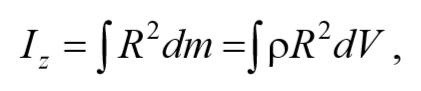
где R − расстояние от элементарной массы dm до оси вращения.
4.6. Теорема Штейнера. Правило аддитивности
Существуют два свойства момента инерции:
1) Теорема Штейнера: момент инерции тела Iz относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
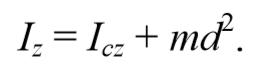
2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:
[spoiler title=”источники:”]
http://physics.belstu.by/mechanics_lk/mechanics_lk5.html
[/spoiler]
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
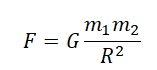
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
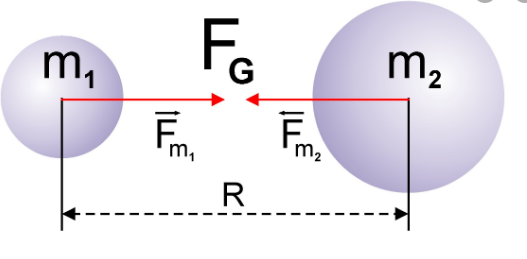
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
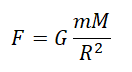
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
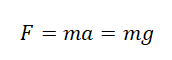
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
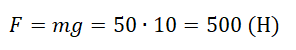
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
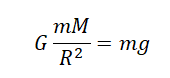
Отсюда:
Формула расчета ускорения свободного падения
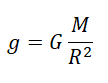
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
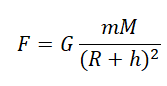
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
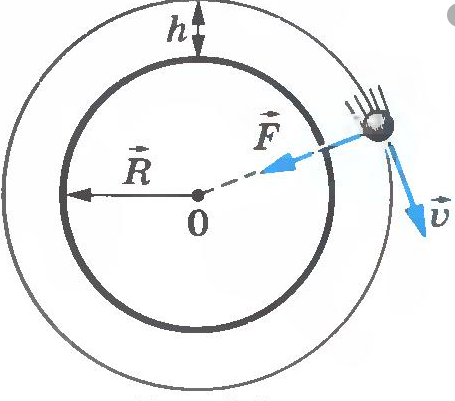
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
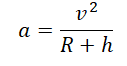
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
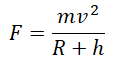
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
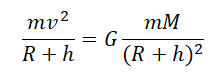
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
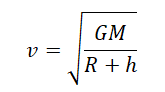
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
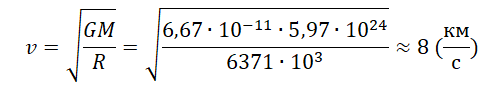
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
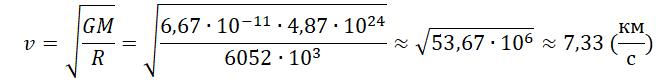
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
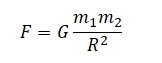
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
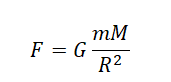
Примерим этот закон для первой и второй пары звезд:
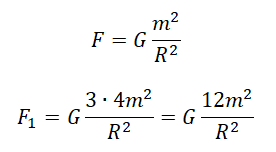
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
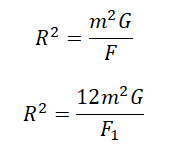
Приравняем правые части выражений и выразим силу притяжения во втором случае:
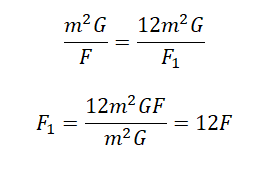
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
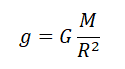
Отсюда радиус равен:
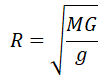
Линейная скорость и радиус орбиты связываются формулой:
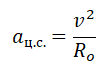
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
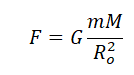
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
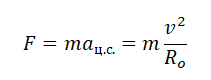
Отсюда:
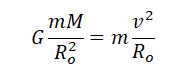
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
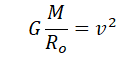
Из этой формулы выразим массу планеты:
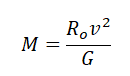
Подставим массу планеты в формулу для нахождения ее радиуса:
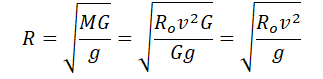
Подставляем известные данные и вычисляем:
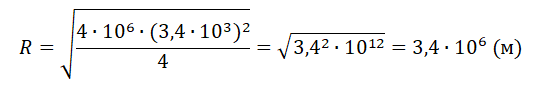
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 17.9k
Сила тяжести
Сила тяжести — сила, действующая на любое физическое тело, находящееся вблизи поверхности Земли или другого астрономического тела. Чем меньше масса планеты, тем с меньшей силой она притягивает к себе тела.
Сила тяжести на поверхности любой планеты рассчитывается по формуле:
F = G ⋅ M ⋅ mR2
Здесь G – гравитационная постоянная, равная 6.674184(78) × 10−11 м3·с-2кг-1, m – масса тела, M – масса небесного тела, R – радиус небесного тела.
Онлайн калькулятор позволяет определить силу тяжести, действующую на тело на различных планетах Солнечной системы.
Поделиться страницей в социальных сетях: