Комплексные числа в тригонометрической
и показательной формах
Тригонометрическая форма комплексного числа
Каждому комплексному числу геометрически соответствует точка
на плоскости
. Но положение точки на плоскости, кроме декартовых координат
, можно зафиксировать другой парой — ее полярных координат
в полярной системе (рис. 1.3,a).
Величина является неотрицательной и для данной точки определяется единственным образом, а угол
может принимать бесчисленное множество значений (при этом
): если точке соответствует некоторое значение
, то ей также соответствуют значения
. Например, если для точки
(см. рис. 1.1) выбрать
, то ей соответствует любое
, в частности
при
. Если же выбрать
, то
, а при
получаем
.
Используя связь декартовых и полярных координат точки (рис. 1.3,б), из алгебраической формы записи комплексного числа
получаем тригонометрическую форму:
(1.3)
Показательная форма комплексного числа
Если обозначить комплексное число , у которого
, а
, через
, то есть
, то из (1.3) получим показательную форму записи комплексного числа:
(1.4)
Равенство называется формулой Эйлера.
Заметим, что геометрически задание комплексного числа равносильно заданию вектора
, длина которого равна
, то есть
, а направление — под углом
к оси
(рис. 1.3,б).
Модуль комплексного числа
Число — длина радиуса-вектора точки
называется модулем комплексного числа
. Обозначение:
.
Из рис. 1.3,б получаем формулу для нахождения модуля числа, заданного и алгебраической форме
(1.5)
Очевидно, что и
только для числа
.
С помощью правила вычитания запишем модуль числа , где
и
А это, как известно, есть формула для расстояния между точками и
.
Таким образом, число есть расстояние между точками
и
на комплексной плоскости.
Пример 1.13. Найти модули комплексных чисел:
Решение
Аргумент комплексного числа
Полярный угол точки
называется аргументом комплексного числа
. Обозначение:
.
В дальнейшем, если нет специальных оговорок, под будем понимать значение
, удовлетворяющее условию
. Так, для точки
(см. рис. 1.1)
.
Формулу для нахождения аргумента комплексного числа , заданного в алгебраической форме, получаем, используя связь декартовых и полярных координат точки
(см. рис. 1.3,б). Для точек, не лежащих на мнимой оси, т.е. для
, у которых
, получаем
; для точек мнимой положительной полуоси, т.е. для
, у которых
, имеем
; для точек мнимой отрицательной полуоси, т.е. для
, у которых
, соответственно
.
Аргумент числа — величина неопределенная.
Нахождение аргумента при сводится к решению тригонометрического уравнения
. При
, т.е. когда
— число действительное, имеем
при
и
при
. При
решение уравнения зависит от четверти плоскости
. Четверть, в которое расположена точка
, определяется по знакам
и
. В результате получаем:
(1.6)
При решении примеров удобно пользоваться схемой, которая изображена на рис. 1.5.
Пример 1.14. Найти аргументы чисел из примера 1.13.
Решение
Пример 1.15. Найти модуль и аргумент числа .
Решение. Находим . Так как
, т.е. точка расположена в четвертой четверти, то из равенства
получаем
(рис. 1.5).
Главное значение аргумента комплексного числа
Аргумент комплексного числа определяется неоднозначно. Это следует из неоднозначности задания величины угла для данной точки, а также из тригонометрической формы записи комплексного числа и свойства периодичности функций
и
.
Всякий угол, отличающийся от на слагаемое, кратное
, обозначается
и записывается равенством:
(1.7)
где — главное значение аргумента,
.
Пример 1.16. Записать и
для чисел
.
Решение. Числа и
— действительные, расположены на действительной оси (рис. 1.6), поэтому
числа и
— чисто мнимые, расположены на мнимой оси (рис. 1.6), поэтому
Пример 1.17. Записать комплексные числа из примера 1.16:
а) в тригонометрической форме;
б) в показательной форме.
Решение
Модули всех чисел, очевидно, равны 1. Поэтому, используя решение предыдущего примера и формулы (1.3) и (1.4), получаем:
а)
б) .
Пример 1.18. Записать в тригонометрической форме числа .
Решение
Числа и
записаны в алгебраической форме (заметим, что заданная запись числа
не является тригонометрической формой записи (сравните с (1.3)). Находим модули чисел по формуле (1.5):
Далее находим аргументы. Для числа имеем
и, так как
(точка расположена в третьей четверти), получаем
(см. рис. 1.5). Для числа
имеем
, или
, и, так как
(точка расположена в четвертой четверти (см. рис. 1.5)), получаем
.
Записываем числа и
в тригонометрической форме
Заметим, что для числа решение можно найти иначе, а именно используя свойства тригонометрических функций:
.
Число является произведением двух чисел. Выполнив умножение, получим алгебраическую форму записи (найдем
и
):
. Здесь, как и для числа
, при решении удобно использовать преобразования тригонометрических выражений, а именно
.
Рассуждая, как выше, найдем . Для числа
, записанного в алгебраической форме, получаем тригонометрическую форму:
Равенство комплексных чисел в тригонометрической форме
Условия равенства комплексных чисел получаем, используя геометрический смысл модуля и аргумента комплексного числа, заданного в тригонометрической форме. Так, для чисел
из условия
. очевидно, следует:
или
(1.8)
Аргументы равных комплексных чисел либо равны (в частности равны главные значения), либо отличаются на слагаемое, кратное .
Для пары сопряженных комплексных чисел и
справедливы следующие равенства:
(1.9)
Умножение комплексных чисел в тригонометрической форме
Зададим два комплексных числа в тригонометрической форме и
и перемножим их по правилу умножения двучленов:
или
Получили новое число , записанное в тригонометрической форме:
, для которого
.
Правило умножения. При умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
(1.10)
В результате умножения чисел может получиться аргумент произведения, не являющийся главным значением.
Пример 1.19. Найти модули и аргументы чисел:
Решение
Каждое из заданных чисел записано в виде произведения. Найдем модули и аргументы сомножителей и воспользуемся правилом (1.10) умножения чисел, заданных в тригонометрической форме:
Для чисел и
находим модули и аргументы:
. Используя формулы (1.10), получаем
б) . Для числа
имеем:
; для числа
, и так как
(точка расположена в четвертой четверти), то
. Используя формулы (1.10), получаем
.
Заметим, что для решения этой задачи можно раскрыть скобки, записать каждое число в алгебраической форме, а затем найти и
, используя формулы (1.5), (1.6).
Деление комплексных чисел в тригонометрической форме
Рассмотрим частное комплексных чисел , заданных в тригонометрической форме. Из определения частного
имеем
и, применяя к произведению правило умножения (формулы (1.10)), получаем
.
Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:
(1.11)
В результате деления чисел по формуле (1.11) может получиться аргумент честного, не являющийся главным значением.
Пример 1.20. Записать в тригонометрической форме комплексное число .
Решение. Обозначим . Для чисел
и
находим модули и аргументы:
(см. пример 1.19). По формуле (1.11) получаем
и
Возведение в степень комплексного числа в тригонометрической форме
Из определения степени и правила умножения чисел, записанных в тригонометрической форме (формула (1.10)), получаем
, где
.
Правило возведения в степень. При возведении в степень комплексного числа в эту степень возводится модуль числа, а аргумент умножается на показатель степени:
(1.12)
Записывая число в тригонометрической форме
, получаем формулу возведения в степень:
(1.13)
При это равенство принимает вид и называется формула Муавра
(1.14)
Пример 1.21. Найти модуль и аргумент комплексного числа .
Решение. Обозначим . Находим модуль и аргумент числа
. Поэтому
и
. Так как по определению для главного значения аргумента выполняется условие
, то
.
Пример 1.22. Записать в тригонометрической форме число .
Решение
Пример 1.23. Используя формулу Муавра, найти выражения для и
через тригонометрические функции угла
.
Решение
Из формулы (1.14) при имеем
. Возведем левую часть в степень, учитывая, что
(см. пример 1.8):
Используя условие равенства комплексных чисел, получаем:
Извлечение корня из комплексного числа в тригонометрической форме
Рассмотрим задачу извлечения корня из комплексного числа, заданного в показательной или тригонометрической форме , или
. Искомое число
также запишем в показательной форме:
. Используя определение операции извлечения корня
и условия (1.8), получаем соотношения
или
(1.15)
Правило извлечения корня. Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент разделить на показатель корня:
(1.16)
Теперь можно записать число в показательной форме:
Если записать это соотношение в тригонометрической форме, то, учитывая периодичность тригонометрических функций, нетрудно убедиться, что выражение принимает только
различных значений. Для их записи достаточно в формуле (1.15) взять
последовательных значений
, например
. В результате получаем формулу извлечения корня из комплексного числа в тригонометрической форме, где
:
(1.17)
Замечания 1.1
1. Рассмотренная задача извлечения корня степени из комплексного числа равносильна решению уравнения вида
, где, очевидно,
.
Для решения уравнения нужно найти значений
, а для этого необходимо найти
и использовать формулу извлечения корня.
2. Исследование формулы (1.17) показывает, что все комплексные числа (значения
) имеют равные модули, т.е. геометрически расположены на окружности радиуса
. Аргументы двух последовательных чисел отличаются на
, так как
, т.е. каждое последующее значение
может быть получено из предыдущего
поворотом радиуса-вектора точки
на
.В этом заключается геометрический смысл формулы (1.17), что можно сформулировать следующим образом.
Точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой
, причем аргумент одного из значений
равен
(рис. 1.7).
Алгоритм решения комплексных уравнений вида z^n-a=0
1. Найти модуль и аргумент числа .
2. Записать формулу (1.17) при заданном значении .
3. Выписать значения корней уравнения , придавая значения
.
Пример 1.24. Решить уравнения: a) ; б)
.
Решение
Задача равносильна задаче нахождения всех значений корня из комплексного числа. Решаем в каждом случае по алгоритму.
а) Найдем .
1. Определим модуль и аргумент числа .
2. При полученных значениях и
записываем формулу (1.17):
Заметим, что справа стоит — арифметический корень, его единственное значение равно 1.
3. Придавая последовательно значения от 0 до 5, выписываем решения уравнения:
Геометрически соответствующие точки расположены в вершинах правильного шестиугольника, вписанного в окружность радиуса , одна из точек (соответствует
)
. Строим шестиугольник (рис. 1.8,в). Отметим свойства корней этого уравнения с действительными коэффициентами — его комплексные корни являются попарно сопряженными:
и
— действительные числа.
б) Найдем .
1. Определим модуль и аргумент числа .
2. По формуле (1.17) имеем
3. Выписываем корни .
Для геометрического представления решения уравнения достаточно изобразить одно значение, например (при
) — это точка окружности
, лежащая на луче
. После этого строим правильный треугольник, вписанный в окружность
(рис. 1.8,б).
Пример 1.25. Найти корень уравнения , для которого
.
Решение
Задача равносильна задаче нахождения при условие
.
1. Находим модуль и аргумент числа .
2. По формуле (1.17) имеем: .
3. Для нахождения искомого решения нет необходимости выписывать все значения корня. Нужно выбрать значение , при котором выполняется условие
(соответствующая точка — точка второй четверти). Удобно при этом использовать чертеж (рис. 1.9).
Условию поставленной задачи удовлетворяет корень (при
):
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.

Ко́мпле́ксные чи́сла (от лат. complexus — связь, сочетание[1]; о двойном ударении см. примечание[K 1]) — числа вида 









Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания[⇨], умножения[⇨] и деления[⇨]. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше[⇨]. Удобно представлять комплексные числа 
Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений, при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число[3]. Большой вклад в исследование комплексных чисел внесли такие математики как Эйлер, который ввёл общепризнанное обозначение 
Уникальные свойства комплексных чисел и функций нашли широкое применение для решения многих практических задач в различных областях математики, физики и техники: в обработке сигналов, теории управления, электромагнетизме, теории колебаний, теории упругости и многих других[5][⇨]. Преобразования комплексной плоскости оказались полезны в картографии и гидродинамике. Современная физика полагается на описание мира с помощью квантовой механики, которая опирается на систему комплексных чисел.
Известно также несколько обобщений комплексных чисел — например, кватернионы[⇨].
Комплексная арифметика[править | править код]
Связанные определения[править | править код]
Всякое комплексное число 
Противоположным для комплексного числа 



В отличие от вещественных, комплексные числа нельзя сравнивать на больше/меньше; доказано, что нет способа распространить порядок, заданный для вещественных чисел, на все комплексные так, чтобы порядок был согласован с арифметическими операциями (чтобы из 




Четыре арифметические операции для комплексных чисел (определённые ниже) имеют те же свойства, что и аналогичные операции с вещественными числами.
Сложение и вычитание[править | править код]
Определение сложения и вычитания комплексных чисел[6]:
Следующая таблица[6] показывает основные свойства сложения для любых комплексных 
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность (переместительность) | 
|
| Ассоциативность (сочетательность) | 
|
| Свойство нуля | 
|
| Свойство противоположного элемента | 
|
| Выполнение вычитания через сложение | 
|
Умножение[править | править код]
Определение произведения[6] комплексных чисел 

Следующая таблица[6] показывает основные свойства умножения для любых комплексных 
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность (переместительность) | 
|
| Ассоциативность (сочетательность) | 
|
| Свойство единицы | 
|
| Свойство нуля | 
|
| Дистрибутивность (распределительность) умножения относительно сложения | 
|
Правила для степеней мнимой единицы:
и т. д.
То есть для любого целого числа 



После определения операций с комплексными числами выражение 
Деление[править | править код]
Комплексное число 

Для каждого комплексного числа 


Определим результат деления[6] комплексного числа 

Как и для вещественных чисел, деление можно заменить умножением делимого на число, обратное к делителю.
Другие операции[править | править код]
Для комплексных чисел определены также извлечение корня, возведение в степень и логарифмирование.
Основные отличия комплексных чисел от вещественных[править | править код]
Уже упоминалось, что комплексные числа нельзя сравнивать на больше-меньше (иными словами, на множестве комплексных чисел не задано отношение порядка). Другое отличие: любой многочлен степени 

В системе вещественных чисел из отрицательного числа нельзя извлечь корень чётной степени. Для комплексных чисел возможно извлечение корня из любого числа любой степени, однако результат неоднозначен — комплексный корень 

Дополнительные отличия имеют функции комплексного переменного[⇨].
Замечания[править | править код]
Число 


Выражение 



Пример возможной ошибки при неосторожном использовании устаревшей записи:
Эта ошибка связана с тем, что квадратный корень из 
Геометрическое представление[править | править код]
Комплексная плоскость[править | править код]

Геометрическое представление комплексного числа
Комплексные числа можно представить на плоскости с прямоугольной системой координат: числу 


Модуль 

Бывает удобно рассматривать на комплексной плоскости также полярную систему координат (см. рисунок справа), в которой координатами точки являются расстояние 

В этом представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов, а вычитанию чисел соответствует вычитание радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются (последнее несложно вывести из формулы Эйлера или из тригонометрических формул суммы). Если модуль второго сомножителя равен 1, то умножение на него соответствует повороту радиус-вектора первого числа на угол, равный аргументу второго числа[16]. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза»[17].
Пример: умножение на 

Модуль[править | править код]
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же самое, расстояние от точки комплексной плоскости до начала координат). Модуль комплексного числа 



Если 

Для любых комплексных 
- 1)
, причём
только при
- 2)
(неравенство треугольника);
- 3)
- 4)
- 5) для пары комплексных чисел
и
модуль их разности
равен расстоянию между соответствующими точками комплексной плоскости;
- 6) модуль числа
связан с вещественной и мнимой частями этого числа соотношениями:
Аргумент[править | править код]
Аргументом ненулевого комплексного числа называется угол 


Для комплексного нуля значение аргумента не определено, для ненулевого числа 





Некоторые свойства аргумента[18]:
- 1) аргумент обратного числа отличается знаком от аргумента исходного:
- 2) аргумент произведения равен сумме аргументов сомножителей:
- 3) аргумент частного от деления равен разности аргументов делимого и делителя:
Сопряжённые числа[править | править код]

Геометрическое представление сопряжённых чисел
Если комплексное число 




Переход к сопряжённому числу можно рассматривать как одноместную операцию, которая сохраняет все арифметические и алгебраические свойства. Эта операция имеет следующие свойства[20]:
Произведение комплексно-сопряжённых чисел — неотрицательное вещественное число, равное нулю только для нулевого z[18]:
Сумма комплексно-сопряжённых чисел — вещественное число[18]:
Другие соотношения[18]:
Или, в общем виде: 



Пример[править | править код]
Тот факт, что произведение 
Формы представления комплексного числа[править | править код]
Алгебраическая форма[править | править код]
Выше использовалась запись комплексного числа 

Тригонометрическая форма[править | править код]

Тригонометрическое представление
Если вещественную 






Как уже сказано выше, для нуля аргумент 


Показательная форма[править | править код]
Фундаментальное значение в комплексном анализе имеет формула Эйлера[21]:
где 



Применяя эту формулу к тригонометрической форме, получим показательную форму комплексного числа[21]:
Следствия
- (1) Модуль выражения
где число
вещественно, равен 1.
- (2)
— при существенно комплексном аргументе
эти равенства могут служить определением (комплексного) косинуса и синуса.
Пример[22]. Представим в тригонометрической и показательной форме число 
(поскольку
находится в III координатной четверти).
Отсюда:
Формула Муавра и извлечение корней[править | править код]
Эта формула помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид[12]:
где 


Аналогичная формула применима также и при вычислении корней 

где k принимает все целые значения от 





![{sqrt[ {n}]{r}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10eb7386bd8efe4c5b5beafe05848fbd923e1413)
Главное значение корня[править | править код]
Если в формуле Муавра в качестве аргумента 

![{displaystyle {sqrt[{3}]{2+11i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59031aa6121d88d2f957d5ab62ba2fc3f2a2d09)

Квадратный корень[править | править код]
Для извлечения квадратного корня из комплексного числа можно преобразовать это число в тригонометрическую форму и воспользоваться формулой Муавра для 



Здесь 


Пример: для квадратного корня из 

История[править | править код]
Впервые, по-видимому, мнимые величины были упомянуты в труде Кардано «Великое искусство, или об алгебраических правилах» (1545), в рамках формального решения задачи по вычислению двух чисел, сумма которых равна 10, а произведение равно 40. Он получил для этой задачи квадратное уравнение, корни которого: 

Возможность использования мнимых величин при решении кубического уравнения впервые описал Бомбелли (1572), он же дал правила сложения, вычитания, умножения и деления комплексных чисел. Уравнение 

![{displaystyle x={sqrt[{3}]{2+11i}}+{sqrt[{3}]{2-11i}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7968a6196d49dd914966b1bf87c9fd8ab9c6bbf)
![{displaystyle {sqrt[{3}]{2pm 11i}}=2pm i,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ded79c5e4f51191bd52137c5b4103b016fffc1)
Выражения, представимые в виде 

Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам или же, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней степени 
Символ 
Геометрическое представление комплексных чисел, немало способствовавшее их легализации, предложили в конце XVIII — начале XIX веков сначала Вессель и Арган (их работы не привлекли внимания), а затем Гаусс[30]. Арифметическая (стандартная) модель комплексных чисел как пар вещественных чисел была построена Гамильтоном («Теория алгебраических пар», 1837); это доказало непротиворечивость их свойств. Термины «модуль», «аргумент» и «сопряжённое число» ввёл в начале XIX века Коши, значительно продвинувший комплексный анализ. С XIX века началось бурное и чрезвычайно плодотворное развитие исследований функций комплексного переменного[2][31].
С учётом этого успешного подхода начались поиски способа представления векторов в трёхмерном пространстве, аналогичное комплексной плоскости. В результате пятнадцатилетних поисков Гамильтон предложил в 1843 году обобщение комплексных чисел — кватернионы, которые он был вынужден сделать не трёхмерными, а четырёхмерными (трёхмерные векторы изображала мнимая часть кватернионов); также Гамильтону пришлось отказаться от коммутативности операции умножения[2].
В 1893 году Чарлз Штейнмец предложил использовать комплексные числа для расчётов электрических цепей переменного тока (см. ниже).
Комплексные функции[править | править код]
Аналитические функции[править | править код]
Комплексная функция одной переменной — это функция 


Каждая комплексная функция 




Наглядное представление комплексной функции графиком затруднительно, так как даже для функции одной комплексной переменной график требует четырёх измерений (два на область определения и ещё два для области значений). Если вместо значения функции рассматривать её модуль 
Все стандартные функции анализа — многочлен, дробно-линейная функция, степенная функция, экспонента, тригонометрические функции, обратные тригонометрические функции, логарифм — могут быть распространены на комплексную плоскость. При этом для них будут иметь место те же алгебраические, дифференциальные и другие тождества, что и для вещественного оригинала[32], например:
Для комплексных функций определяются понятия предела, непрерывности и производной так же, как в вещественном анализе, с заменой абсолютной величины на комплексный модуль[32].
Дифференцируемые комплексные функции (то есть функции, имеющие производную) обладают рядом особенностей по сравнению с вещественными[34].
- Вещественная и мнимая часть дифференцируемой функции — гармонические функции, связанные условиями Коши — Римана.
- Всякая дифференцируемая в некоторой окрестности точки
комплексная функция дифференцируема неограниченное число раз в этой точке (то есть аналитична, или голоморфна).
Определённый интеграл для функций одной комплексной переменной, вообще говоря, зависит от пути интегрирования (то есть выбора кривой от начальной до конечной точки в комплексной плоскости). Однако если интегрируемая функция аналитична в односвязной области, то её интеграл внутри этой области не зависит от пути[35].
Преобразования комплексной плоскости[править | править код]
Всякая комплексная функция может рассматриваться как преобразование комплексной плоскости (или как преобразование одной комплексной плоскости в другую). Примеры:
Поскольку любое движение на плоскости есть комбинация перечисленных трёх преобразований, функции 

Другие линейные преобразования[36]:
Важную роль в комплексном анализе играют дробно-линейные преобразования[37]:
При этом 

Среди других практически полезных функций преобразования: инверсия 
Аналитическая геометрия на комплексной плоскости[править | править код]
Исследование плоских фигур нередко облегчается, если перенести их на комплексную плоскость. Многие теоремы планиметрии допускают наглядную и компактную запись с помощью комплексных чисел, например[40]:
- Три (различные) точки
лежат на одной прямой тогда и только тогда, когда выполняется условие:
-
является вещественным числом.
- Четыре (различные) точки
лежат на одной обобщённой окружности (окружности или прямой) тогда и только тогда, когда выполняется условие:
-
- отношение
является вещественным числом.
- отношение
Параметрическое уравнение прямой на комплексной плоскости имеет вид[42]:
где
— комплексные числа,
— произвольный вещественный параметр.
Угол между двумя прямыми 







Уравнение окружности с центром 




Место в общей алгебре, топологии и теории множеств[править | править код]
Множество комплексных чисел 




Характеристика комплексного поля равна нулю, мощность 

Превратить поле комплексных чисел в упорядоченное поле невозможно, потому что в упорядоченном поле квадрат любого элемента неотрицателен, и мнимая единица в нём не может существовать.
Из свойств модуля следует, что комплексные числа образуют структуру двумерного нормированного пространства над полем 
Поле 
Поля 

Некоторые практические применения[править | править код]
Те особенности комплексных чисел и функций, которые отличают их от вещественных, оказались полезными, а часто и незаменимыми в математике, в естественных науках и технике.
Математика[править | править код]
Приложения комплексных чисел сами по себе занимают видное место в математике — в частности, понятия алгебраических чисел, нахождение корней многочленов, теория Галуа, комплексный анализ и т. д.
Перенеся геометрическую задачу с обычной плоскости на комплексную, мы нередко получаем возможность значительно упростить её решение[48][49].
Многие сложные задачи теории чисел (например, теория биквадратичных вычетов) и вещественного математического анализа (например, вычисление сложных или несобственных интегралов) удалось решить только с помощью средств комплексного анализа. Мощным инструментом для открытий в теории чисел оказались, например, гауссовы числа вида 

Нередко проблемы вещественного анализа проясняются при их комплексном обобщении. Классический пример — разложение в ряд Тейлора
Этот ряд сходится только в интервале 



При решении линейных дифференциальных уравнений важно сначала найти все комплексные корни характеристического многочлена, а затем попытаться решить систему в терминах базовых экспонент[53]. В разностных уравнениях используются для аналогичной цели комплексные корни характеристического уравнения системы разностных уравнений[54]. С помощью теории вычетов, являющейся частью комплексного анализа, вычисляются многие сложные интегралы по замкнутым контурам[55]..
Исследование функции часто связано с анализом её частотного спектра с помощью комплексного преобразования Фурье или Лапласа[56].
О представлении комплексных чисел в информатике и компьютерной поддержке комплексной арифметики изложено в статье Комплексный тип данных.
Конформное отображение[править | править код]

Как уже отмечалось выше, всякая комплексная функция может рассматриваться как преобразование одной комплексной плоскости в другую. Гладкая (аналитическая) функция обладает двумя особенностями: если в заданной точке производная не равна нулю, то коэффициент растяжения/сжатия при этом преобразовании одинаков по всем направлениям, угол поворота также постоянен (конформное отображение)[57]. С этим фактом связано широкое применение комплексных функций в картографии[58][59] и гидродинамике[60].
Квантовая механика[править | править код]
Основой квантовой механики является понятие комплексной волновой функции, Для описания динамики квантовой системы используются дифференциальные уравнения с комплексными коэффициентами типа уравнения Шрёдингера. Решения этих уравнений заданы в комплексном гильбертовом пространстве. Операторы, соответствующие наблюдаемым величинам, эрмитовы. Коммутатор операторов координаты 

Здесь 


Важную роль в квантовой механике играют матрицы Паули и матрицы Дирака, некоторые из них содержат комплексные значения[61]. Ю. Вигнер уточнял, что «…использование комплексных чисел в квантовой механике не является вычислительным трюком прикладной математики; они входят в самую суть формулировки основных законов квантовой механики.»[62].
Электротехника[править | править код]
Поскольку переменный ток есть колебательный процесс, его удобно описывать и исследовать с применением комплексных чисел. Вводятся также понятия импеданса, или комплексного сопротивления, для реактивных элементов электрической цепи, таких как ёмкость и индуктивность, — это помогает рассчитать токи в цепи[63]. Ввиду того, что традиционно символ 





Логические основания[править | править код]
Расширение поля вещественных чисел до комплексных, как и любое другое расширение алгебраической структуры, ставит множество вопросов, основные из которых — это вопросы о том, как определить операции над новым типом чисел, какие свойства будут иметь новые операции и (главный вопрос) допустимо ли такое расширение, не приведёт ли оно к неустранимым противоречиям.
Для анализа подобных вопросов в теории комплексных чисел надо сформировать набор аксиом.
Аксиоматика комплексных чисел[править | править код]
Можно определить аксиоматику множества комплексных чисел 


- С1: Для всяких комплексных чисел
определена их сумма
- С2: Сложение коммутативно:
Далее в некоторых аксиомах для краткости будем опускать оговорку «для всяких
».
- С3: Сложение ассоциативно:
- С4: Существует элемент 0 (ноль) такой, что
- С5: Для всякого комплексного числа
существует противоположный ему элемент
такой, что
- С6: Для всяких комплексных чисел
определено их произведение
- С7: Умножение коммутативно:
- С8: Умножение ассоциативно:
- С9: Умножение связано со сложением распределительным (дистрибутивным) законом:
- С10: Существует элемент 1 (единица), не равный нулю и такой, что
- С11: Для всякого ненулевого числа
существует обратное ему число
такое, что
- С12: Множество комплексных чисел
содержит подполе, изоморфное полю вещественных чисел
Для простоты далее это подполе обозначается той же буквой
- С13: Существует элемент
(мнимая единица) такой, что
- С14 (аксиома минимальности): Пусть
— подмножество
которое: содержит
и мнимую единицу и замкнуто относительно сложения и умножения. Тогда
совпадает со всем
Из этих аксиом вытекают как следствия все прочие свойства. Первые 11 аксиом означают, что 

Существуют и другие варианты аксиоматики комплексных чисел. Например, вместо того, чтобы опираться на уже построенное упорядоченное поле вещественных чисел, можно в качестве базы использовать аксиоматику теории множеств[69].
Непротиворечивость и модели[править | править код]
Стандартный способ доказать непротиворечивость новой структуры — смоделировать (интерпретировать) её аксиомы с помощью объектов другой структуры, чья непротиворечивость сомнений не вызывает. В нашем случае мы должны реализовать эти аксиомы на базе вещественных чисел[70].
Стандартная модель[править | править код]
Рассмотрим всевозможные упорядоченные пары вещественных чисел. В данной модели каждая такая пара 

Далее определим[70]:
- пары
и
считаются равными, если
и
- сложение: сумма пар
и
определяется как пара
- умножение: произведение пар
и
определяется как пара
Пояснение: сложное, на первый взгляд, определение умножения легко выводится из соотношения 
Несложно убедиться, что описанная структура пар образует поле и удовлетворяет всему приведённому перечню аксиом комплексных чисел. Вещественные числа моделируются парами 



Мнимая единица — это пара 



Описанная модель доказывает, что приведённая аксиоматика комплексных чисел непротиворечива. Потому что если бы в ней было противоречие, то это означало бы противоречие и в базовой для данной модели арифметике вещественных чисел, которую мы заранее предположили непротиворечивой[70].
Матричная модель[править | править код]
Комплексные числа можно также определить как подкольцо кольца вещественных матриц 2×2 вида
с обычным матричным сложением и умножением[2]. Вещественной единице будет соответствовать
мнимой единице —
.
Множество таких матриц является двумерным векторным пространством. Умножение на комплексное число 


Матричная модель позволяет легко продемонстрировать связь между комплексными числами и линейными преобразованиями плоскости определённого типа.
А именно, существует взаимно однозначное соответствие между комплексными числами и поворотными гомотетиями плоскости (комбинациями растяжения относительно точки и поворота): каждая поворотная гомотетия может быть представлена на комплексной плоскости как умножение на комплексное число[72].
Модель факторкольца многочленов[править | править код]
Рассмотрим кольцо многочленов ![mathbb{R}[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d1013f9dd290be70d5fe534e0d3311b0a7c6a)

![mathbb{R}[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d1013f9dd290be70d5fe534e0d3311b0a7c6a)





Множество классов эквивалентности образует кольцо с единицей. Так как многочлен 





Данный изоморфизм был обнаружен Коши в 1847 году. Этот подход может быть использован для построения обобщений комплексных чисел, таких как алгебры Клиффорда[74].
Расширенное комплексное поле как фактор-поле рациональных дробей полиномов с вещественными коэффициентами[править | править код]
Нетривиальная факторизация поля в поле невозможна, но поля, расширенные бесконечностью, могут нетривиально факторизоваться. Более того, возможны нетривиальные факторизации обычных полей в расширенные. В частности, обычное или расширенное поле рациональных дробей полиномов одной переменной с вещественными коэффициентами факторизуется в расширенное поле комплексных чисел (сферу Римана) путём отождествления полинома 


Параметризуя рациональные дроби полиномов различными числами, можно получать различные факторизации: при параметризации вещественным числом — расширенное поле вещественных, комплексным (не вещественным) — комплексных чисел. Число, используемое для параметризации, есть корень простого (над вещественным полем) полинома, отождествляемого с нулём, т. е. по модулю которого берутся числители и знаменатели (в случае вещественного числа — первой степени, комплексного — квадратный с отрицательным дискриминантом и, соответственно, двумя сопряжёнными комплексными корнями).
Алгебраическая характеризация[править | править код]
Как уже упоминалось выше, поле комплексных чисел алгебраически замкнуто и имеет характеристику ноль (из последнего свойства вытекает, что оно содержит подполе рациональных чисел 


При этом отождествлении другие структуры, вроде нормы или топологии, могут не сохраняться. Например, алгебраическое замыкание 



Вариации и обобщения[править | править код]
Ближайшее обобщение комплексных чисел было обнаружено в 1843 году. Им оказалось тело кватернионов, которое, в отличие от поля комплексных чисел, содержит три мнимые единицы, традиционно обозначаемые 
Дальнейшим применением этой процедуры образуются числа, описанные Артуром Кэли в 1845 году, до обнаружения этой процедуры, и названные «числами Кэли» (октонионы, октавы). Числа, получаемые следующим применением процедуры, названы седенионами. Несмотря на то, что эту процедуру можно повторять и далее, дальнейшие числа названий пока не имеют[78].
Другие типы расширений комплексных чисел (гиперкомплексные числа):
- Бикватернионы
- Комплексные числа гиперболического типа (двойные)
- Комплексные числа параболического типа (дуальные)
Примечания[править | править код]
- Комментарии
- ↑ Два возможных ударения указаны согласно следующим источникам.
- Большая советская энциклопедия, 3-е изд. (1973), том 12, стр. 588, статья Ко́мпле́ксные числа.
- Советский энциклопедический словарь (1982), стр. 613, статья Ко́мпле́ксное число.
- Последнее издание «Словаря трудностей русского языка» (Розенталь Д. Э., Теленкова М. А., Айрис-пресс, 2005, стр. 273) указывает оба варианта: ко́мплексные (компле́ксные) числа.
- В Большой российской энциклопедии (том 14, 2010 год) приводятся варианты: Компле́ксное число (стр. 691, автор не указан), но Ко́мплексный анализ Архивная копия от 2 июля 2019 на Wayback Machine (стр. 695, автор: член-корр. РАН Е. М. Чирка).
- Орфографический словарь русского языка (изд. 6-е, 2010), Грамматический словарь русского языка, Русский орфографический словарь Российской академии наук под ред. В. В. Лопатина (изд. 4-е, 2013) и ряд других словарей указывают варианты: ко́мплексный и компле́ксный (матем.).
- ↑ При условии непротиворечивости системы вещественных чисел.
- ↑ То есть отличается от
(поля рациональных функций для набора переменных
мощности континуум) на алгебраическое расширение
- ↑ Поскольку отображение в алгебраически замкнутое поле всегда может быть продлено на алгебраическое расширение, для установления изоморфизма между алгебраическими замкнутыми полями достаточно установить изоморфизм между их простыми подполями и биекцию между базисами трансцендентности.
- Использованная литература
- ↑ Краткий словарь иностранных слов. — 7-е изд. — М.: Русский язык, 1984. — С. 121. — 312 с.
- ↑ 1 2 3 4 5 Комплексное число // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2. — С. 1007.
- ↑ Энциклопедия элементарной математики, 1951, с. 227.
- ↑ Справочник по элементарной математике, 2006, с. 211, подстрочное примечание.
- ↑ Справочник по элементарной математике, 2006, с. 222.
- ↑ 1 2 3 4 5 6 7 Алгебра и математический анализ, 1998, с. 180—181.
- ↑ Real Part. Дата обращения: 16 января 2018. Архивировано 31 марта 2018 года.
- ↑ Мнимое число // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 708.
- ↑ Imaginary Part. Дата обращения: 16 января 2018. Архивировано 31 марта 2018 года.
- ↑ Ahlfors Lars V., 1979, с. 2.
- ↑ История математики, том III, 1972, с. 72.
- ↑ 1 2 Энциклопедия элементарной математики, 1951, с. 237—239.
- ↑ История математики, том III, 1972, с. 61—66.
- ↑ 1 2 Bunch, Bryan. Mathematical Fallacies and Paradoxes. Chapter «Eliminating paradox by definition». — Dover Publications, 1997. — 240 p. — (Dover Books on Mathematics). — ISBN 978-0486296647.
- ↑ Энциклопедия элементарной математики, 1951, с. 233—234.
- ↑ 1 2 3 4 5 Энциклопедия элементарной математики, 1951, с. 234—235, 239—240.
- ↑ ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий Архивная копия от 16 марта 2018 на Wayback Machine. Пункт 152. Комплексная амплитуда (синусоидального электрического) тока — комплексная величина, модуль и аргумент которой равны соответственно амплитуде и начальной фазе данного синусоидального электрического тока.
- ↑ 1 2 3 4 5 6 Ahlfors Lars V., 1979, с. 6—10.
- ↑ Свешников А. Г., Тихонов А. Н., 1967, с. 14—15.
- ↑ 1 2 Алгебра и математический анализ, 1998, с. 183—1851.
- ↑ 1 2 3 4 Ahlfors Lars V., 1979, с. 15—16.
- ↑ Соломенцев Е. Д., 1988, с. 7.
- ↑ Weisstein, Eric W. nth Root (англ.) на сайте Wolfram MathWorld.
- ↑ Ahlfors Lars V., 1979, с. 3—4.
- ↑ 1 2 3 Клайн Моррис. Математика. Утрата определённости. — М.: Мир, 1984. — С. 138—139.
- ↑ 1 2 Стиллвелл Д. Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — С. 258—266. — 530 с.
- ↑ История математики, том III, 1972, с. 57—61.
- ↑ Юшкевич А. П. Леонард Эйлер. Жизнь и творчество // Развитие идей Леонарда Эйлера и современная наука. Сб. статей. — М.: Наука, 1988. — ISBN 5-02-000002-7. — С. 15—47.
- ↑ Острая О. Теория функций комплексного переменного. Дата обращения: 30 ноября 2017.
- ↑ Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта. — М.—Л.: Гостехиздат, 1938. — С. 233. — 297 с. — (Классики естествознания).
- ↑ Глейзер Г. И. История математики в школе. IX—X классы. — М.: Просвещение, 1983. — С. 193. — 351 с.
- ↑ 1 2 3 4 Смирнов В. И., 2010, с. 7—15.
- ↑ Бронштейн, Семендяев, 1985, с. 360.
- ↑ Смирнов В. И., 2010, с. 15—22.
- ↑ Свешников А. Г., Тихонов А. Н., 1967, с. 44.
- ↑ 1 2 Заславский А. А. Геометрические преобразования. — 2-е изд.. — М.: МЦНМО, 2004. — С. 58. — 86 с. — ISBN 5-94057-094-1.
- ↑ 1 2 Евграфов М. А., 1968, с. 180—186.
- ↑ MAXimal :: algo :: Преобразование геометрической инверсии. e-maxx.ru. Дата обращения: 9 мая 2021. Архивировано 7 мая 2021 года.
- ↑ Е. А. Морозов, “Обобщённая задача Аполлония”, Матем. просв., сер. 3, 23, Изд-во МЦНМО, М., 2019, 80–111. www.mathnet.ru. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Привалов И. И., 1984, с. 43.
- ↑ Соломенцев Е. Д., 1988, с. 10.
- ↑ 1 2 3 Ahlfors Lars V., 1979, с. 17—18.
- ↑ Соломенцев Е. Д., 1988, с. 12.
- ↑ Числовые системы, 1975, с. 165.
- ↑ Энциклопедия элементарной математики, 1951, с. 249—251.
- ↑ Числовые системы, 1975, с. 167.
- ↑ Топологическое поле // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 386.
- ↑ Комплексные числа. 9—11 классы, 2012, Глава 5.
- ↑ Реальные применения мнимых чисел, 1988, с. 78.
- ↑ Реальные применения мнимых чисел, 1988, с. 114—124.
- ↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
- ↑ Привалов И. И., 1984, с. 14.
- ↑ Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — Эдиториал УРСС, 2004. — 240 с. — ISBN 5354004160.
- ↑ Разностное уравнение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 838. Архивировано 21 января 2022 года.
- ↑ Свешников А. Г., Тихонов А. Н., 1967, Глава 5.
- ↑ Свешников А. Г., Тихонов А. Н., 1967, Глава 8.
- ↑ Смирнов В. И., 2010, с. 22—25.
- ↑ Маркушевич А. И. Комплексные числа и конформные отображения. — М.: Гостехиздат, 1954. — 52 с. — (Популярные лекции по математике, выпуск 13). Архивировано 28 января 2018 года.
- ↑ Shao-Feng Bian, Hou-Pu Li. Mathematical Analysis in Cartography by Means of Computer Algebra System. Дата обращения: 28 января 2018. Архивировано 29 января 2018 года.
- ↑ Лаврентьев М. А., Шабат Б. В. Проблемы гидродинамики и их математические модели. — М.: Наука, 1973.
- ↑ 1 2 Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М.: Физматлит, 2004. — 800 с. — («Теоретическая физика», том III). — ISBN 5-9221-0530-2.
- ↑ Е. Вигнер. Непостижимая эффективность математики в естественных науках // УФН. — 1968. — Т. 93. — С. 535—546. — doi:10.3367/UFNr.0094.196803f.0535.
- ↑ Реальные применения мнимых чисел, 1988, с. 132—144.
- ↑ Молчанов А. П., Занадворов П. Н. Курс электротехники и радиотехники, глава «Линейные цепи». — BH V. — 608 с. — ISBN 978-5-9775-0544-4.
- ↑ Афонский А. А., Дьяконов В. П. Цифровые анализаторы спектра, сигналов и логики / Под ред. проф. В. П. Дьяконова. — М.: СОЛОН-Пресс, 2009. — С. 248. — ISBN 978-5-913-59049-7.
- ↑ Числовые системы, 1975, с. 164—165.
- ↑ Энциклопедия элементарной математики, 1951, с. 227—233.
- ↑ Числовые системы, 1975, с. 166.
- ↑ Real and Complex Numbers. Дата обращения: 13 февраля 2018. Архивировано 6 февраля 2021 года.
- ↑ 1 2 3 Числовые системы, 1975, с. 167—168.
- ↑ Энциклопедия элементарной математики, 1951, с. 230—233.
- ↑ John Stillwell. The Four Pillars of Geometry. — Springer Science & Business Media, 2005-12-30. — С. 84—86. — 240 с. — ISBN 9780387290522.
- ↑ 1 2 Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ F. Brackx, R. Delanghe, H. Serras. Clifford Algebras and their Applications in Mathematical Physics: Proceedings of the Third Conference held at Deinze, Belgium, 1993. — Springer Science & Business Media, 2012-12-06. — С. 33. — 405 с. — ISBN 9789401120067.
- ↑ David Marker. Model Theory: An Introduction, ISBN 978-0-387-22734-4. Proposition 2.2.5. Springer Science & Business Media, 2002. См. также некоторые пояснения Архивная копия от 14 мая 2018 на Wayback Machine.
- ↑ William Weiss and Cherie D’Mello. Fundamentals of Model Theory Архивная копия от 13 апреля 2018 на Wayback Machine. Lemma 7: Any two algebraically closed fields of characteristic 0 and cardinality
are isomorphic и комментарий после неё.
- ↑ 1 2 p-адическое число // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 100.: «Это расширение есть пополнение поля рациональных чисел относительно неархимедова нормирования… Поле
локально компактно».
- ↑ 1 2 Dickson, L. E. (1919), On Quaternions and Their Generalization and the History of the Eight Square Theorem, Annals of Mathematics, Second Series (Annals of Mathematics) . — Т. 20 (3): 155–171, ISSN 0003-486X, DOI 10.2307/1967865
Литература[править | править код]
- Балк М. Б., Балк Г. Д., Полухин А. А. Реальные применения мнимых чисел. — Киев: Радянська школа, 1988. — 255 с. — ISBN 5-330-00379-2.
- Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — изд. 13-е. — М.: Наука, 1985. — 544 с.
- Бурбаки, Н. Очерки по истории математики. — М., 1963.
- Виленкин Н. Я., Ивашов-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса. Учебное пособие. — Изд. 6-е. — М.: Просвещение, 1998. — 288 с. — ISBN 5-09-008036-4.
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
- Глазков Ю. А., Варшавский И. К., Гаиашвили М. Я. Комплексные числа. 9—11 классы. — М.: Экзамен, 2012. — 157 с. — ISBN 978-5-377-03467-4.
- Евграфов М. А. Аналитические функции. — 2-е изд., перераб. и дополн. — М.: Наука, 1968. — 472 с.
- Кириллов А. А. Что такое число?. — М., 1993. — 80 с. — ISBN 5-02-014942-3.
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — 4-е изд. — М.: Наука, 1972.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Нечаев В. И. Числовые системы. — М.: Просвещение, 1975. — 199 с.
- Привалов И. И. Введение в теорию функций комплексного переменного. — 13-е изд.. — М.: Физматлит, 1984. — 432 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Смирнов В. И. Курс высшей математики в трёх томах. — Изд. 10-е. — СПб.: БХВ-Петербург, 2010. — Т. 3, часть 2-я. — 816 с. — ISBN 978-5-9775-0087-6.
- Соломенцев Е. Д. Функции комплексного переменного и их применения. — М.: Высшая школа, 1988. — 167 с. — ISBN 5-06-003145-6.
- Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1951. — Т. 1. — С. 160—168. — 448 с.
- Ahlfors Lars V. Complex analysis. An introduction to the theory of analytic functions of one complex variable. — Third edition. — Harvard University: McGraw-Hill Book Company, 1979. — 317 с. — ISBN 0-07-000657-1.
Ссылки[править | править код]
Модуль и аргумент комплексного числа
Пусть задано комплексное число $ z = a+bi $.
| Формула |
| Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$ |
Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.
Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.
| Формула |
Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$:
|
Введите комплексное число
Пример 1 Пример 2 Правила ввода
| Пример 1 |
| Найти модуль и аргумент комплексного числа $ z = 3 – 4i $. |
| Решение |
|
Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$ |
| Ответ |
| $$ |z| = 5, varphi = -arctg frac{4}{3} $$ |
| Пример 2 |
| Найти модуль и аргумент комплексного числа $ z = 3i $ |
| Решение |
|
В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$ |
| Ответ |
| $$ |z| = 3, varphi = frac{pi}{2} $$ |
| Пример 3 |
| Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$ |
| Решение |
|
Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ varphi = frac{pi}{3}, |z| = 2 $$ |
| Пример 4 |
| Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$ |
| Решение |
|
Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi – arctg(sqrt{3}) = pi – frac{pi}{3} = frac{2pi}{3}. $$ |
| Ответ |
| $$ varphi = frac{2pi}{3} $$ |
Содержание:
- Комплексные числа
- Алгебраическая форма комплексного числа
- Действия над комплексными числами в алгебраической форме
- Геометрическая интерпретация комплексного числа
- Тригонометрическая форма комплексного числа
- Действия над комплексными числами в тригонометрической форме
- Показательная форма комплексного числа
- Что такое комплексное число
- Понятие о комплексном числе
- Арифметические операции над комплексными числами
- Отыскание комплексных корней уравнений
Комплексные числа
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Алгебраическая форма комплексного числа
На множестве действительных чисел ряд алгебраических задач, в частности нахождение корней квадратных уравнений с отрицательным дискриминантом, не имеет решения. Введём некоторое навое число, которое будем считать решением уравнения х2 + 1 = 0. Корень уравнения х2 + 1 = 0 или х2 = -1 называется мнимой единицей и обозначается буквой i. Таким образом i2 = -1.
В некоторых технических дисциплинах мнимую единицу обозначают буквой j. В дальнейшем будем использовать оба обозначения.
Мнимая единица позволяет ввести числа нового вида, которые называют комплексными.
Комплексным числом называют выражение вида  , где
, где  — действительные числа, i — мнимая единица.
— действительные числа, i — мнимая единица.
Число  называют действительной, а число
называют действительной, а число  — мнимой частями комплексного числа. Комплексное число, как правило, обозначают буквой
— мнимой частями комплексного числа. Комплексное число, как правило, обозначают буквой  . Два комплексных числа
. Два комплексных числа  называют равными тогда и только тогда, когда
называют равными тогда и только тогда, когда  , то есть когда равны их действительные части и коэффициенты при мнимой части.
, то есть когда равны их действительные части и коэффициенты при мнимой части.
Понятия “больше” и “меньше” для комплексных чисел не определено. Комплексное число  называется нулём и обозначается 0; комплексное число
называется нулём и обозначается 0; комплексное число  отождествляется с действительным числом
отождествляется с действительным числом  ; комплексное число
; комплексное число  называют чисто мнимым и обозначают
называют чисто мнимым и обозначают  . Число 0 является единым числом, которое одновременно и является действительным, и чисто мнимое.
. Число 0 является единым числом, которое одновременно и является действительным, и чисто мнимое.
Комплексные числа  называются сопряжёнными и обозначаются
называются сопряжёнными и обозначаются  и
и . Например, в числе
. Например, в числе  , сопряжённым к нему будет число
, сопряжённым к нему будет число  , а для числа
, а для числа  сопряжённым будет число
сопряжённым будет число  .
.
Множество комплексных чисел принято обозначать буквой С. Запись комплексного числа в виде  называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Действия над комплексными числами в алгебраической форме
Сложение, вычитание, умножение комплексных чисел в алгебраической форме по правилам соответствующих действий над многочленами.
Пример 1. Найти сумму и произведение комплексных чисел 
Решение: Сумму находим формальным сложением двучленов 

произведение находим перемножив двучлены  с последующей заменой
с последующей заменой  .
.

Ответ: 
Легко увидеть, что слагаемое двух сопряжённых чисел является действительным числом:

Воспользуемся этим свойством для введения действия деления двух комплексных чисел.
При делении комплексных чисел  , где
, где  достаточно умножить числитель и знаменатель дроби
достаточно умножить числитель и знаменатель дроби  на число сопряжённое к знаменателю, то есть на
на число сопряжённое к знаменателю, то есть на 
Пример 2. Даны комплексные числа  и
и  Найдите разность
Найдите разность  и частное
и частное 
Решение:
Находим разность вычитанием двучленов 

Чтобы найти частное  умножим числитель и знаменатель на число, сопряжённое к знаменателю:
умножим числитель и знаменатель на число, сопряжённое к знаменателю:

Ответ: 
Действия над комплексными числами имеют следующие интересные свойства:

Доказательство выходит из определения сопряжённых чисел. Действительно,

Аналогично доказываются и другие приведённые свойства.
Возведение комплексного числа в степень выполняется по формулам возведения двучлена в степень. При этом следует учитывать, что

Например:

Пример 3. Найти комплексное число 
Решение:
Выполнив в знаменателе возведение в степень, получим:

Умножив числитель и знаменатель на число, сопряжённое к знаменателю, то есть на -5-12i, получим:

Ответ: z = i.
Геометрическая интерпретация комплексного числа
Каждому комплексному числу  можно поставить в соответствие упорядоченную пару действительных чисел
можно поставить в соответствие упорядоченную пару действительных чисел  и наоборот. Такая упорядоченная пара действительных чисел определяет точку или вектор на плоскости.
и наоборот. Такая упорядоченная пара действительных чисел определяет точку или вектор на плоскости.
Следовательно, комплексное число вида  изображается на координатной плоскости точкой
изображается на координатной плоскости точкой  или вектором, начало которого совпадает с началом координат, а конец с т. М.
или вектором, начало которого совпадает с началом координат, а конец с т. М.
Сама координата плоскости называется при этом комплексной плоскости, ось абсцисс — действительной осью, ось ординат — мнимой осью.
Например, изобразим числа 


Представление комплексного числа как вектора на плоскости позволяет ввести понятие модуля и аргумента комплексного числа.
Модулем комплексного числа называют длину вектора, которая соответствует данному числу (обозначают r либо p).
Аргументом комплексного числа  называют величину угла
называют величину угла  между положительным направлением действительной оси и вектора, который соответствует данному комплексному числу.
между положительным направлением действительной оси и вектора, который соответствует данному комплексному числу.
Рассмотрим рисунок:

На основе теоремы Пифагора получаем 
Например, комплексное число  имеет модуль равный 10, так как
имеет модуль равный 10, так как

Аргумент комплексного числа  , в отличии от модуля, вычисляется неоднозначно. Так аргументом числа 5 являются следующие углы
, в отличии от модуля, вычисляется неоднозначно. Так аргументом числа 5 являются следующие углы 
 Среди бесконечного множества значений аргумента только одно принадлежит промежутку
Среди бесконечного множества значений аргумента только одно принадлежит промежутку  . Эти значения аргумента мы и будем вычислять.
. Эти значения аргумента мы и будем вычислять.
Аргумент легко вычислить, если комплексное число расположено в I четверти. Действительно, согласно тригонометрическим соотношениям в прямоугольном треугольнике (рис. 2) имеем:

Если комплексные числа размещены в других четвертях, то необходимо провести дополнительные рассуждения. Рассмотрим рис. 3. Видим, что для


Таким образом, алгоритм нахождения аргумента комплексного числа следующий:
1.Определить коэффициент  заданного комплексного числа.
заданного комплексного числа.
2. Найти 
3. Установить, в какой четверти расположено комплексное число.
4. Вычислить аргумент  согласно приведённым формулам.
согласно приведённым формулам.
Возможны и другие способы нахождения аргумента комплексного числа, например:

Пример 4. Найти аргумент комплексного числа 

Тригонометрическая форма комплексного числа
Рассмотрим рис. 2. Согласно тригонометрическим соотношениям в прямоугольном треугольнике числа  можно выразить через r и
можно выразить через r и  таким образом:
таким образом:

Тогда комплексное число запишется в виде:

Запись комплексного числа в таком виде называется тригонометрической формой комплексного числа.
Следовательно, для того, чтобы перейти от алгебраической формы записи комплексного числа  к тригонометрической, достаточно найти его модуль и аргумент.
к тригонометрической, достаточно найти его модуль и аргумент.
Пример 5. Записать число  в тригонометрической форме.
в тригонометрической форме.
Решение:
Найдём модуль 
Найдём острый угол 
Вектор, который соответствует данному комплексному числу принадлежит третьей четверти, поэтому аргумент равен  следовательно
следовательно 
Ответ:
Для того, чтобы перейти от тригонометрической формы записи комплексного числа  к алгебраической, достаточно найти действительные числа
к алгебраической, достаточно найти действительные числа  из формул
из формул 
Пример 6. Записать число  в алгебраической форме.
в алгебраической форме.
Найдём  и
и 

Ответ:
Действия над комплексными числами в тригонометрической форме
В тригонометрической форме записи комплексного числа выполняют действия умножения, деления, возведения в степень, извлечения корня n-й степени. Выведение формул, по которым выполняются действия, относительно просты и основываются на основных формулах тригонометрии.

Следовательно, при умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножают, а аргументы складывают; при делении — модули делят, а аргументы вычитают.
Правило умножения комплексных чисел автоматически распространяется на произвольное число множителей. Если взять равные множители 

Полученную формулу называют формулой Муавра.
Для извлечении корня n-й степени из комплексного числа  используют формулу:
используют формулу:

где  арифметический корень,
арифметический корень, 

Пример 8. Вычислить  Ответ записать в алгебраической форме.
Ответ записать в алгебраической форме.
Решение: Находим:

Ответ: 
Пример 9. Вычислить
Решение: Запишем число в тригонометрической форме:
в тригонометрической форме:


Пример 10. Вычислите  . Ответ запишите в алгебраической и тригонометрической формах.
. Ответ запишите в алгебраической и тригонометрической формах.
Решение: Запишем число -81 в тригонометрической форме:

Тогда:


Показательная форма комплексного числа
Рассматривая функцию  для комплексной переменной, известный математик Л. Эйлер установил соотношение
для комплексной переменной, известный математик Л. Эйлер установил соотношение 
Из заданной формулы следует, что каждое комплексное число  можно записать в виде
можно записать в виде  которое называется показательной формой записи.
которое называется показательной формой записи.
Над комплексными числами в показательной форме выполняют те же действия что и в тригонометрической форме. Выведение формул, по которым выполняют действия основывается на основных свойствах степени.
Пусть  , тогда:
, тогда:

Пример 11. Представить число  в алгебраической форме.
в алгебраической форме.
Решение: Согласно условию задачи  , поэтому
, поэтому

значит

Ответ:
Пример 12. Выполнить действия, результат записать в тригонометрической и показательной формах: 
Решение: Сначала выполним действия:

Теперь полученное число запишем в тригонометрической и показательной формах. Для этого найдём модуль и аргумент:

Тогда

Ответ: 
Что такое комплексное число
Комплексные числа — это числа вида 


Понятие о комплексном числе
Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счета предметов использовались натуральные числа. Необходимость выполнения деления привела к понятию обыкновенной (и десятичной) дроби, необходимость выполнения вычитания — к понятиям нуля и отрицательного числа, необходимость извлечения корней из положительных чисел — к понятию иррационального числа.
Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались и невыполнимые на этом множестве операции, например извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел, отличных от действительных.
Геометрически действительные числа изображаются точками на координатной прямой: каждому действительному числу соответствует одна точка прямой («образ» действительного числа) и, обратно, каждая точка координатной прямой соответствует одному действительному числу. Координатная прямая сплошь заполнена образами действительных чисел, т. е., выражаясь фигурально, «на ней нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Однако каждую точку М координатной плоскости ху можно отождествить с координатами этой точки. Поэтому естественно в качестве новых чисел ввести упорядоченные пары действительных чисел (упорядоченные в том смысле, что  — разные точки, а значит, и разные числа).
— разные точки, а значит, и разные числа).
Комплексным числом называют всякую упорядоченную пару  действительных чисел
действительных чисел 
Два комплексных числа  называют равными тогда и только тогда, когда
называют равными тогда и только тогда, когда 
Арифметические операции над комплексными числами
Суммой комплексных чисел 
 называют комплексное число
называют комплексное число 
Например, 

Комплексным нулем считают пару (0; 0). Числом, противоположным числу  считают число
считают число  обозначают его
обозначают его 
Разностью комплексных чисел  называют, как обычно, такое число
называют, как обычно, такое число  Разность всегда существует и единственна. В самом деле, пусть
Разность всегда существует и единственна. В самом деле, пусть  Тогда
Тогда 
 Это значит, что
Это значит, что  откуда находим
откуда находим 

Таким образом, получаем следующее правило вычитания комплексных чисел: 

Например, (9; 10) – (8; 12) = (9 – 8; 10 – 12) = (1;-2).
Произведением комплексных чисел 
 называют комплексное число
называют комплексное число 
Например, если  то
то

Арифметические операции над комплексными числами обладают теми же свойствами, что арифметические операции над действительными числами (см. п. 29).
Пусть  Существует, и только одно, комплексное число
Существует, и только одно, комплексное число  такое, что
такое, что  Это число и называют, как обычно, частным от деления z на w.
Это число и называют, как обычно, частным от деления z на w.
Имеем 
 Так как
Так как то должны выполняться равенства
то должны выполняться равенства

Из этой системы двух уравнений с двумя переменными находим (см. п. 164) 
 Итак,
Итак,

Получили следующее правило деления комплексных чисел: если  то
то

Например,

Алгебраическая форма комплексного числа
Используя введенные в п. 45 определения сложения и умножения комплексных чисел, легко получить следующие равенства:

Условились вместо  писать просто
писать просто  , а комплексное число (0; 1) обозначать буквой
, а комплексное число (0; 1) обозначать буквой  и называть мнимой единицей. Тогда равенство (1) принимает вид
и называть мнимой единицей. Тогда равенство (1) принимает вид  т. е.
т. е.

а равенство (2) — вид

Запись  называют алгебраической формой комплексного числа
называют алгебраической формой комплексного числа  при этом число
при этом число  называют действительной частью комплексного числа z, a bi — его мнимой частью.
называют действительной частью комплексного числа z, a bi — его мнимой частью.
Например, 

Если мнимая часть комплексного числа  отлична от нуля, то число называют мнимым, если при этом
отлична от нуля, то число называют мнимым, если при этом  = 0, т. е. число имеет вид bi, то его называют чисто мнимым, наконец, если у комплексного числа
= 0, т. е. число имеет вид bi, то его называют чисто мнимым, наконец, если у комплексного числа  мнимая часть равна нулю, то получается действительное число
мнимая часть равна нулю, то получается действительное число  .
.
Алгебраическая форма существенно облегчает выполнение арифметических операций над комплексными числами.
Сложение. Известно (см. п. 45), что

Выполнив сложение тех же чисел в алгебраической форме, считая  и с + di обычными двучленами, находим
и с + di обычными двучленами, находим

Сравнивая равенства (7) и (8), замечаем, что получился верный результат.
Вычитание. Известно (см. п. 45), что

Выполнив вычитание тех же чисел в алгебраической форме, считая  и с + di обычными двучленами, находим
и с + di обычными двучленами, находим

Сравнивая равенства (9) и (10), замечаем, что получился верный результат.
Умножение. Известно (см. п. 45), что

Выполнив умножение тех же чисел в алгебраической форме, считая  и с + di обычными двучленами, находим
и с + di обычными двучленами, находим

Воспользуемся тем, что  (см. равенство (5)); тогда
(см. равенство (5)); тогда  В результате получаем
В результате получаем

Сравнивая равенства (11) и (12), замечаем, что получился верный результат.
Деление. Известно (см. п. 45), что если  то
то

Выполним деление тех же чисел в алгебраической форме, считая  и с + di обычными двучленами, a
и с + di обычными двучленами, a  — обычной дробью. Умножив числитель и знаменатель этой дроби на с – di (предполагая, что значение дроби от этого не изменится), находим
— обычной дробью. Умножив числитель и знаменатель этой дроби на с – di (предполагая, что значение дроби от этого не изменится), находим

Итак,

Сравнивая равенства (13) и (14), замечаем, что получился верный результат.
Подводя итоги, приходим к следующему важному практическому выводу: над комплексными числами, записанными в алгебраической форме, можно осуществлять все арифметические операции как над обычными двучленами, учитывая лишь, что  Чтобы преобразовать в комплексное число дробь вида
Чтобы преобразовать в комплексное число дробь вида  нужно числитель и знаменатель дроби умножить на число с — di; числа с + di и с – di называют комплексно-сопряженными.
нужно числитель и знаменатель дроби умножить на число с — di; числа с + di и с – di называют комплексно-сопряженными.
Пример 1.
Вычислить 
Решение:
Применив формулу 
 , получим
, получим

Пример 2.
Вычислить 
Решение:


Пример 3.
Найти действительные числа х и у такие, что выполняется равенство 

Решение:
Имеем 
 Тогда заданное равенство можно переписать в виде
Тогда заданное равенство можно переписать в виде

Комплексные числа  равны тогда и только тогда, когда равны их действительные части (
равны тогда и только тогда, когда равны их действительные части ( = с) и коэффициенты при мнимых частях (Ь = d). Значит, приходим к системе уравнений
= с) и коэффициенты при мнимых частях (Ь = d). Значит, приходим к системе уравнений

из которой находим (см. п. 164) 

Пример 4.
Найти комплексные числа z, удовлетворяющие равенству 
Решение:
Будем искать комплексное число z в виде х + yi. Имеем

Из последнего равенства следует, что

Эта система имеет два решения (см. п. 164): (2; 3) и (-2; -3). Значит, 
Пример 5.
Вычислить 
Решение:
Имеем (см. п. 58) 

Значит, 

Далее, имеем 

Значит, 

Отыскание комплексных корней уравнений
Пусть  > 0. Так как
> 0. Так как 
 Тем самым мы получаем возможность извлекать квадратные корни из отрицательных действительных чисел. Это позволяет находить не только действительные, но и мнимые корни уравнений.
Тем самым мы получаем возможность извлекать квадратные корни из отрицательных действительных чисел. Это позволяет находить не только действительные, но и мнимые корни уравнений.
Пример 1.
Решить уравнение 
Решение.
Имеем (см. п. 137) 
 Итак,
Итак, 
Пример 2.
Решить уравнение 
Решение.
Имеем 
 Значит, либо х – 2 = 0, откуда находим
Значит, либо х – 2 = 0, откуда находим  либо
либо  откуда находим
откуда находим 
 Итак,
Итак, 

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету “Математика”:
Лекции:
- Производная сложной функции
- Многоугольники
- Арифметические операции над пределами
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций
- Уравнение окружности и прямой
- Область определения функции примеры решения
- Неопределенный интеграл
- Тригонометрические функции углов прямоугольного треугольника
- Решение треугольников
Содержание:
Хроника возникновения комплексных чисел:

Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b – натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
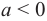
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 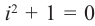 . Отсюда
. Отсюда 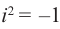 . После этого, корнями уравнения х2 + 1 = 0 являются числа
. После этого, корнями уравнения х2 + 1 = 0 являются числа 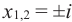 . Число
. Число 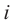 называется мнимой единицей.
называется мнимой единицей.
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 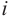 , и были справедливы все свойства сложения и умножения. Для произвольных действительных чисел а и b введём “произведение”
, и были справедливы все свойства сложения и умножения. Для произвольных действительных чисел а и b введём “произведение” 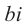 и “сумму”
и “сумму” 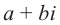 , и назовём комплексным числом следующее выражение
, и назовём комплексным числом следующее выражение 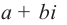 . Выражение вида
. Выражение вида 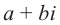 называется комплексным числом, где а и b – действительные числа,
называется комплексным числом, где а и b – действительные числа, 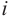 мнимая единица.Комплексные числа можно обозначать через
мнимая единица.Комплексные числа можно обозначать через 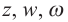 и т.д.Например,
и т.д.Например, 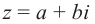 . Запись
. Запись  называется алгебраической формой комплексного числа, а является действительной частью, b – мнимой частью комплексного числа
называется алгебраической формой комплексного числа, а является действительной частью, b – мнимой частью комплексного числа 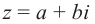 , и записывается так:
, и записывается так: 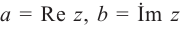 . При а = 0 получается число вида
. При а = 0 получается число вида  . Эти числа называются чисто мнимыми числами. При а = 0, b = 0 комплексное число равно нулю и наоборот, если а +
. Эти числа называются чисто мнимыми числами. При а = 0, b = 0 комплексное число равно нулю и наоборот, если а +  = 0, то а = 0 и b = 0.
= 0, то а = 0 и b = 0.
Следствие: для комплексных чисел а +  и с +
и с +  равенство
равенство
а +  = с +
= с +  справедливо тогда и только тогда, если а = с, b = d.
справедливо тогда и только тогда, если а = с, b = d.
Пример. Из равенства 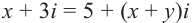 найдите х и у.
найдите х и у.
Решение: Из равенства действительных и мнимых частей получаем: х = 5
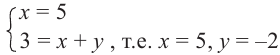 .
.
Суммой комплексных чисел  называется комплексное число
называется комплексное число 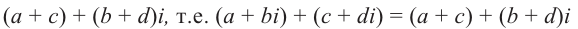
Действия над комплексными числами
Произведением комплексных чисел 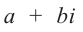 и
и 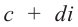 называется число
называется число 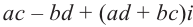 , т.е.
, т.е.
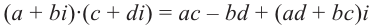
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 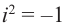 .
.
Пример №1
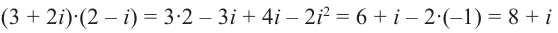
Рассмотрим частные случаи степеней мнимых единиц: 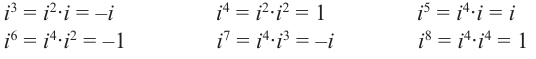
Как видно, натуральные степени мнимой единицы 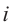 равны
равны 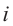 , -1, –
, -1, –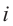 ‘, 1 и повторяются через каждые четыре шага, т.е.справедливо равенство
‘, 1 и повторяются через каждые четыре шага, т.е.справедливо равенство 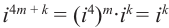
Пример №2
Вычислите: а) 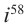 б)
б) 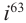
Решение: а) 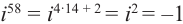 б)
б) 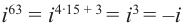
Число  называется сопряжённым для числа
называется сопряжённым для числа  и обозначается как :
и обозначается как : 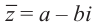 . Ясно, что если число
. Ясно, что если число  является сопряжённым для числа
является сопряжённым для числа  , то число
, то число  является сопряжённым для числа
является сопряжённым для числа  . Поэтому, числа
. Поэтому, числа 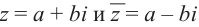 называются взаимно сопряжёнными комплексными числами. Действительные части взаимно сопряжённых чисел равны, а мнимые части являются противоположными числами.
называются взаимно сопряжёнными комплексными числами. Действительные части взаимно сопряжённых чисел равны, а мнимые части являются противоположными числами.
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 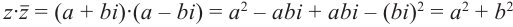 .
.
В частном случае, сопряжённым для действительного числа является само число, для мнимого – произведение числа и (-1).
Для каждого комплексного числа  существует противоположное число
существует противоположное число  и
и 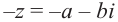 . Для каждого, отличного от нуля, комплексного числа
. Для каждого, отличного от нуля, комплексного числа 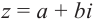 существует противоположное.
существует противоположное. 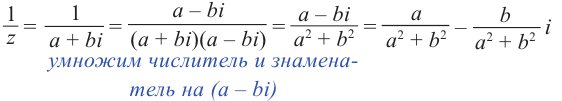
Вычитание и частное комплексных чисел определяется равенствами:
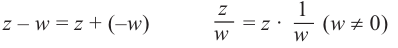
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 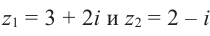 .
.
Решение: 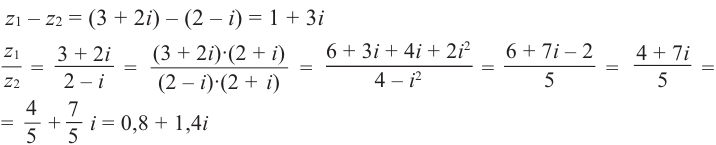
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел  и
и  справедливы тождества
справедливы тождества
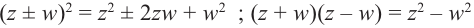
Квадратный корень комплексного числа
Число, квадрат которого равен  называется квадратным корнем комплексного числа
называется квадратным корнем комплексного числа  и обозначается как
и обозначается как  .
.
Пример №4
Найдём квадратный корень комплексного числа 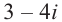
Решение: Пусть 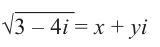 . Возведём обе части равенства в квадрат:
. Возведём обе части равенства в квадрат: 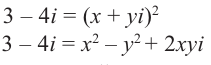
Из равенства действительных и мнимых частей имеем:
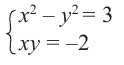
Отсюда получаем решение (2; -1) и (-2; 1). Значит, 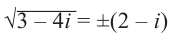
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 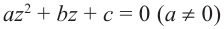 для множества комплексных чисел находится по тому же правилу, что и для действительных чисел.
для множества комплексных чисел находится по тому же правилу, что и для действительных чисел. 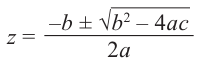
Пример №5
Решим уравнение 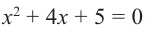 .
.
Решение:
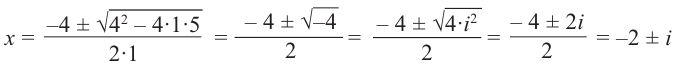 .
.

Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 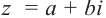 задаётся парой действительных чисел (а; b) и эта пара соответствует определённым точкам на координатной плоскости. Поставим в соответствие числу
задаётся парой действительных чисел (а; b) и эта пара соответствует определённым точкам на координатной плоскости. Поставим в соответствие числу 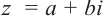 точку А (а; b) и обозначим её через
точку А (а; b) и обозначим её через  . Каждая точка на координатной плоскости изображает комплексное число и наоборот, каждое комплексное число на координатной плоскости, соответствует одной точке. Действительные числа располагаются на оси абсцисс, чисто мнимые числа на оси ординат. Поэтому ось абсцисс называется действительной осью, ось ординат – мнимой, а плоскость – комплексной плоскостью.
. Каждая точка на координатной плоскости изображает комплексное число и наоборот, каждое комплексное число на координатной плоскости, соответствует одной точке. Действительные числа располагаются на оси абсцисс, чисто мнимые числа на оси ординат. Поэтому ось абсцисс называется действительной осью, ось ординат – мнимой, а плоскость – комплексной плоскостью.
Пример:
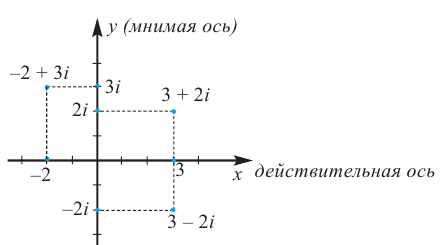
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 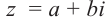 соответствует точка М(а; b). Обозначим расстояние ОМ через R, угол между лучом ОМ и положительным направлением оси абсцисс через
соответствует точка М(а; b). Обозначим расстояние ОМ через R, угол между лучом ОМ и положительным направлением оси абсцисс через  . Из
. Из  по теореме Пифагора имеем:
по теореме Пифагора имеем: 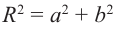
Отсюда: 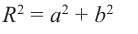
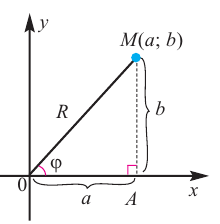
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как:  .
.
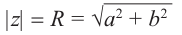
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом  комплексного числа
комплексного числа 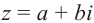 .
.
Из 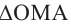 :
: 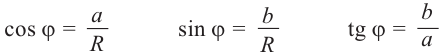
Модуль числа 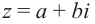 имеет единственное значение, а аргумент
имеет единственное значение, а аргумент  находится с точностью
находится с точностью 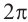 . То есть, если одно из значений аргумента равно
. То есть, если одно из значений аргумента равно  , то другое будет иметь вид
, то другое будет иметь вид  .
.
Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0;  ).
).
Пример №6
Найдём модуль и аргумент комплексного числа 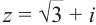
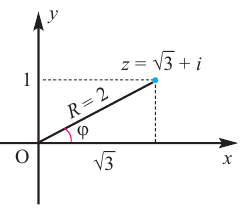
Решение: Из того, что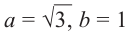 следует,что
следует,что 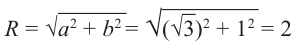
и принимая внимание, что угол  расположен в I четверти,
расположен в I четверти,
получим: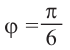
Из формул 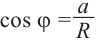 ,
, 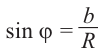 получаем:
получаем: 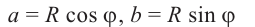
Тогда 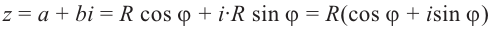
Для комплексного числа 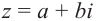 число
число 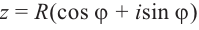 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
В частном случае для модуля и аргумента числа 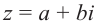 имеем:
имеем:
Пример №7
Запишем комплексное число 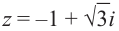
в тригонометрической форме.
Решение: 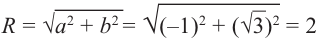
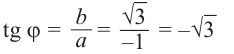
Так как угол  принадлежит II четверги, то
принадлежит II четверги, то
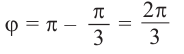
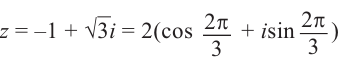
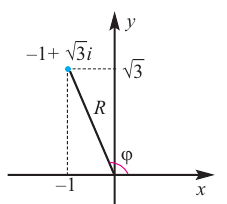
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 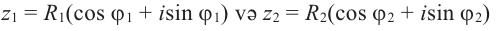 .
.
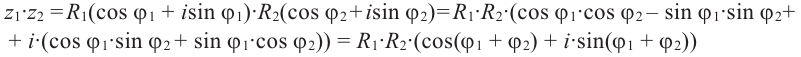
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
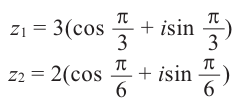
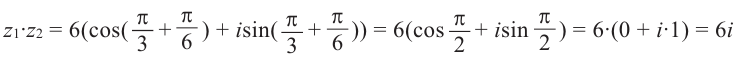
Теперь найдём отношение 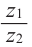
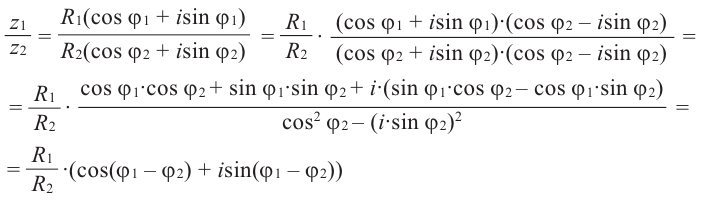
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
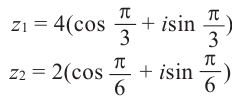
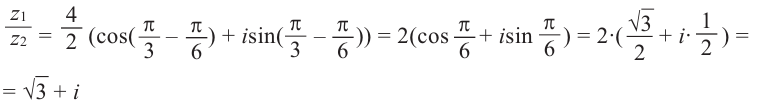
Возвести число 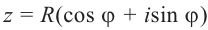 в степень с натуральным показателем n можно умножив n раз число
в степень с натуральным показателем n можно умножив n раз число 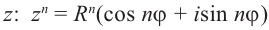
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
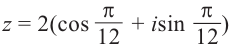
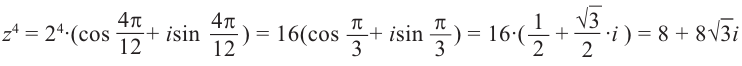
Формулу 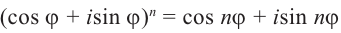 называют формулой Муавра. При помощи этой формулы можно найти синус и косинус n кратных углов через синус и косинус одинарных углов. Например, при n = 2 имеем:
называют формулой Муавра. При помощи этой формулы можно найти синус и косинус n кратных углов через синус и косинус одинарных углов. Например, при n = 2 имеем:
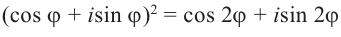
Отсюда
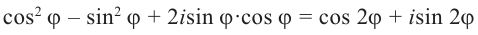
Из равенства двух комплексных чисел имеем:
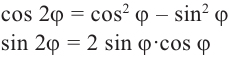
Аналогичным образом можно написать формулы для  .
.
Корень n-ой степени комплексного числа
Найдём значение выражения 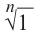 .
.
Запишем в виде 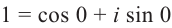 и найдём корень n – ой степени
и найдём корень n – ой степени
виде 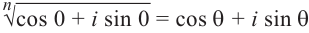 .
.
Возведём каждую из двух сторон в n-ую степень:
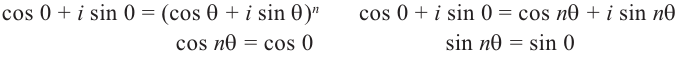
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 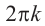 .
.
Это значит,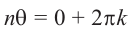
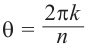
Таким образом, 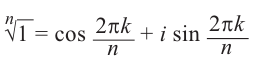
Отсюда при 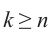 для первых
для первых 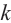 значений полученного числа равны значениям, полученным при
значений полученного числа равны значениям, полученным при  .
.
Обозначим корни  – ой степени единицы через
– ой степени единицы через 
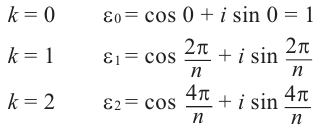
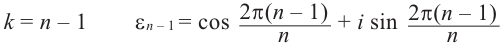
Как видно, модули корней  -ой степени равны 1, аргументы отличаются друг от друга в
-ой степени равны 1, аргументы отличаются друг от друга в 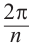 раз. То есть, эти числа расположены внутри единичной окружности, центр которой совпадает с началом координат, и соответствуют комплексным числам, являющимися вершинами правильного
раз. То есть, эти числа расположены внутри единичной окружности, центр которой совпадает с началом координат, и соответствуют комплексным числам, являющимися вершинами правильного  -угольника.
-угольника.
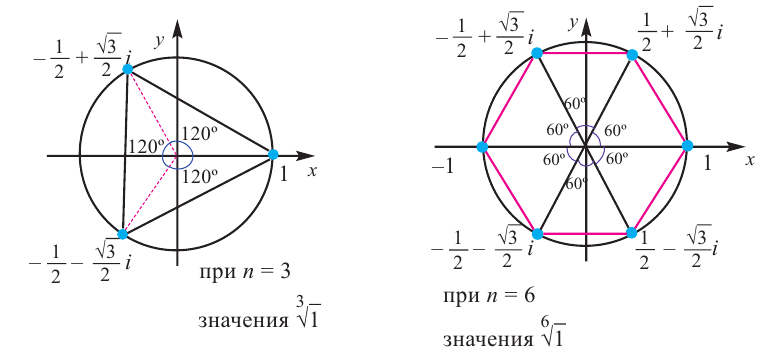
Корнем  -ой степени комплексного числа
-ой степени комплексного числа 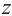 называется такое число
называется такое число  , что
, что  . Если
. Если 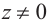 , то для корня
, то для корня  -ой степени существуют
-ой степени существуют  различных значений.
различных значений.
Запишем 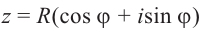 в виде
в виде
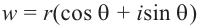 .
.
Для 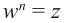 получим:
получим:
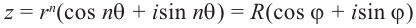
Из равенства двух комплексных чисел получим:
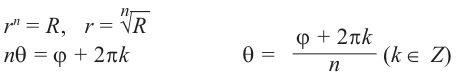
Значения при 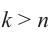 отличаются от первых
отличаются от первых  значений на
значений на 
Поэтому, должно соблюдаться следующее: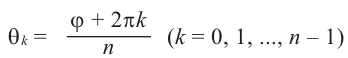
Формула корни n-ой степени комплексного числа
Если 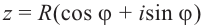 , то
, то
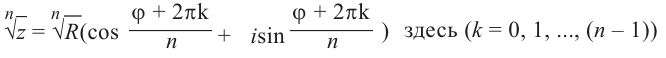
Пример №8
Найдём все значения 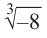
Решение: пусть 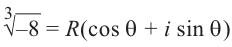
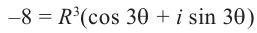
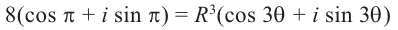
Отсюда 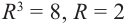
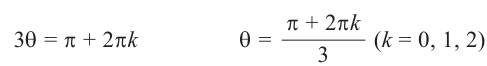
При 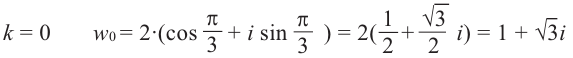
При 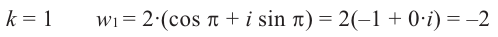
При 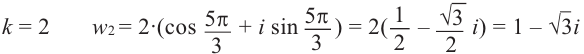
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида 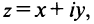 где
где  — действительные числа,
— действительные числа, 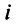 — мнимая единица.
— мнимая единица.
Число 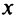 называется действительной частью числа
называется действительной частью числа 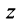 и обозначается
и обозначается 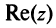 (от франц. reele — «действительный»), а число
(от франц. reele — «действительный»), а число  — мнимой частью числа
— мнимой частью числа 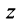 и обозначается
и обозначается 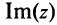 (от франц. imaginaire — «мнимый»), т.е.
(от франц. imaginaire — «мнимый»), т.е. 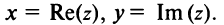
Действительное число является частным случаем комплексного
является частным случаем комплексного 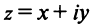 при
при 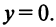 Комплексные числа вида
Комплексные числа вида 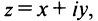 не являющиеся действительными, т.е. при
не являющиеся действительными, т.е. при  называются мнимыми, а при
называются мнимыми, а при  т.е. числа вида
т.е. числа вида 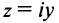 — чисто мнимыми.
— чисто мнимыми.
Числа 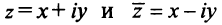 называются сопряженными.
называются сопряженными.
Два комплексных числа 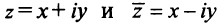 называются равными, если равны их действительные и мнимые части, т.е.
называются равными, если равны их действительные и мнимые части, т.е. 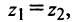 если
если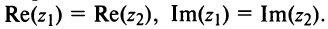 В частности,
В частности,  если
если 
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
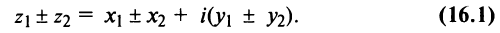
2. Умножение комплексных чисел
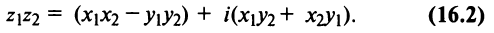
В частности,
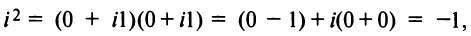
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
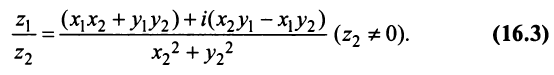
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 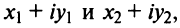 если считать
если считать 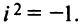 Например, произведение комплексных чисел (16.2) есть
Например, произведение комплексных чисел (16.2) есть
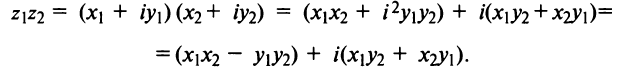
Пример №9
Даны комплексные числа 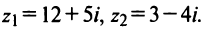
Найти 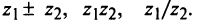
Решение:
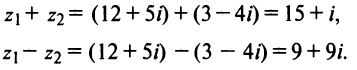
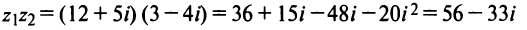 (учли, что
(учли, что 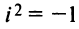 ).
).
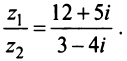 Умножая числитель и знаменатель на сопряженное делителю комплексное число
Умножая числитель и знаменатель на сопряженное делителю комплексное число 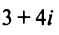 , получим
, получим
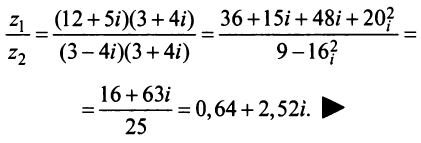
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости 
Плоскость называется комплексной, если каждому комплексному числу 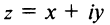 ставится в соответствие точка плоскости
ставится в соответствие точка плоскости  причем это соответствие взаимно однозначное (рис. 16.1).
причем это соответствие взаимно однозначное (рис. 16.1).
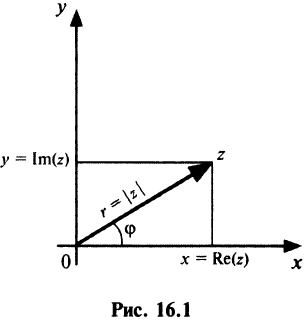
Оси  , на которых расположены действительные числа
, на которых расположены действительные числа и чисто мнимые числа
и чисто мнимые числа 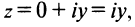 называются соответственно действительной и мнимой осями.
называются соответственно действительной и мнимой осями.
Тригонометрическая и показательная формы комплексного числа
С каждой точкой 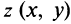 комплексной плоскости связан радиус-вектор этой точки
комплексной плоскости связан радиус-вектор этой точки  , длина которого
, длина которого  называется модулем комплексного числа
называется модулем комплексного числа 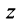 и обозначается
и обозначается 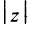 (см. рис. 16.1):
(см. рис. 16.1):

Угол 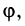 образованный радиусом-вектором
образованный радиусом-вектором 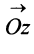 с осью
с осью 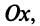 называется аргументом комплексного числа
называется аргументом комплексного числа 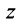 и обозначается
и обозначается 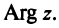 Из значений
Из значений 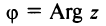 выделяется главное значение
выделяется главное значение 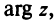 удовлетворяющее условию
удовлетворяющее условию  Например,
Например, 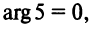
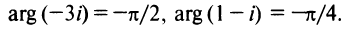
Очевидно (см. рис. 16.1), что
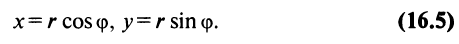
Следовательно, комплексное число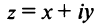 можно представить как
можно представить как

Представление комплексного числа в виде (16.6), где 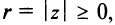
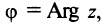 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
Сформулируем некоторые свойства арифметических операций над комплексными числами.
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел их суммы
их суммы  и разности
и разности 
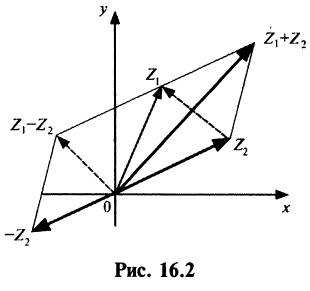
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
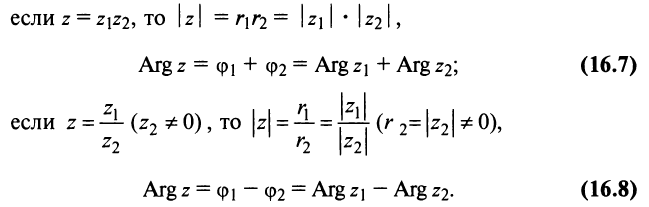
Геометрически умножение числа означает изменение длины радиуса-вектора
означает изменение длины радиуса-вектора  раз и его поворот вокруг точки
раз и его поворот вокруг точки  против часовой стрелки на угол
против часовой стрелки на угол 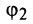
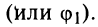
Пример №10
Комплексные числа 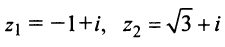 представить в тригонометрической форме и найти
представить в тригонометрической форме и найти 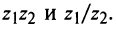
Решение:
По формуле (16.4) найдем модуль комплексного числа 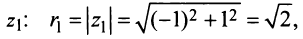 а из соотношений (16.5)
а из соотношений (16.5) 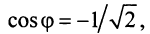
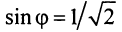 получим аргумент числа
получим аргумент числа 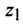 (берем его главное значение):
(берем его главное значение): 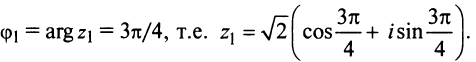
Аналогично 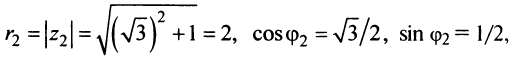 т.е.
т.е. 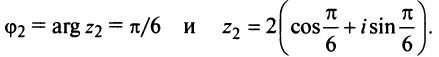
Теперь по формулам (16.7) и (16.8)
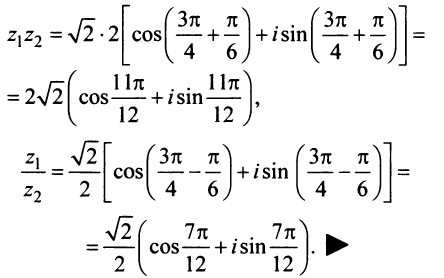
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 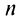 , известную как формула Муавра:
, известную как формула Муавра:
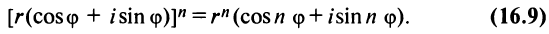
Пример №11
Найти 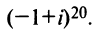
Решение:
По формуле Муавра (16.9)
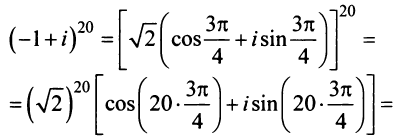
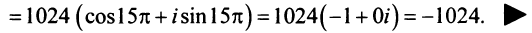 Обратимся к извлечению корня из комплексного числа.
Обратимся к извлечению корня из комплексного числа.
Пусть

Тогда, используя определение корня и формулу Муавра (16.9), получим
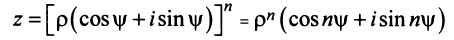
или
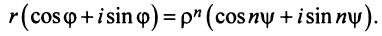
Отсюда следует, что
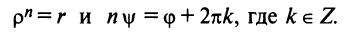
Итак,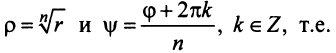
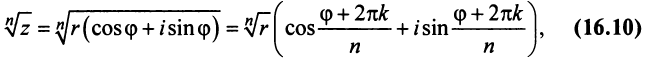
где 
При  значения корня уже будут повторяться.
значения корня уже будут повторяться.
Таким образом, корень 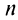 -й степени из комплексного числа (не равного нулю) имеет
-й степени из комплексного числа (не равного нулю) имеет 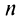 различных значений.
различных значений.
Пример №12
Найти 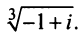
Решение:
В примере 16.2 было получено
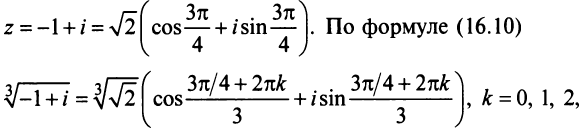
откуда получаем три значения корня
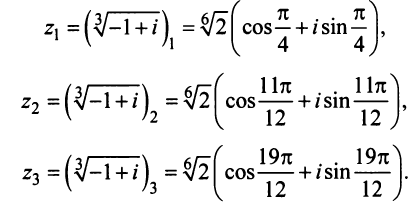
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки  расположенные на окружности радиуса
расположенные на окружности радиуса  (рис. 16.3). ►
(рис. 16.3). ►
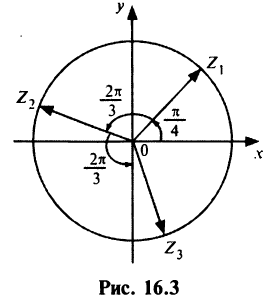
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
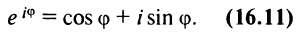
Отсюда следует показательная форма комплексного числа. 
где 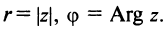
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 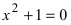 невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим
невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим 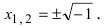
Определение: Выражение 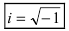 называется мнимой единицей.
называется мнимой единицей.
Определение: Комплексным числом называется выражение вида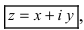 где х,у
где х,у
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 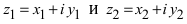 называются равными, если равны их вещественные и мнимые части, т.е.
называются равными, если равны их вещественные и мнимые части, т.е. 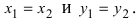
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 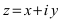 называется комплексное число
называется комплексное число 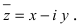
Пример №13
Записать комплексно-сопряженное число к комплексному числу 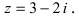
Решение:
Согласно определению комплексно-сопряженного числа получаем 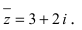
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е. 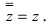
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение 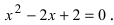
Решение:
Вычислим дискриминант уравнения 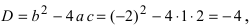 таким образом,
таким образом, 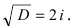 Следовательно,
Следовательно, 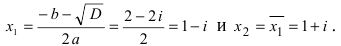
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
Комплексное число 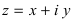 изобретается на комплексной плоскости
изобретается на комплексной плоскости  в виде вектора, соединяющего начало координат с точкой М(х; у) (Рис. 2):
в виде вектора, соединяющего начало координат с точкой М(х; у) (Рис. 2): 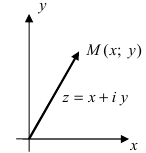
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3). 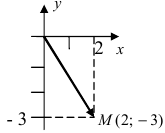
Решение:
Рис. 3. Изображение комплексного 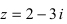 на комплексной плоскости. Если перейти от декартовой системы координат к полярной системе отсчета, т.е.
на комплексной плоскости. Если перейти от декартовой системы координат к полярной системе отсчета, т.е. 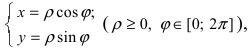 то комплексное число
то комплексное число 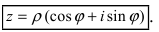
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: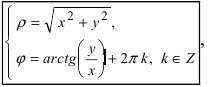 при этом
при этом 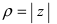 является модулем, а
является модулем, а 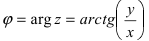 – аргументом комплексного числа z .
– аргументом комплексного числа z .
Замечание: Аргумент комплексного числа 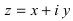 определяется в зависимости от знаков вещественной и мнимой частей:
определяется в зависимости от знаков вещественной и мнимой частей:
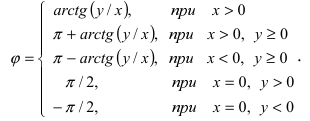
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 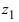
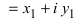 и
и 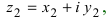 сложить (найти разность) отдельно действительные и мнимые части,
сложить (найти разность) отдельно действительные и мнимые части, 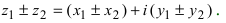
Пример №16
Найти сумму и разность чисел 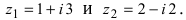 Изобразить все числа на комплексной плоскости.
Изобразить все числа на комплексной плоскости.
Решение:
Найдем сумму заданных комплексных чисел 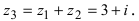 Вычислим разность данных чисел
Вычислим разность данных чисел 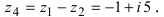 Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):
Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):
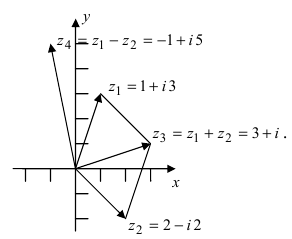
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что 
2. Для того чтобы найти произведение двух комплексных чисел 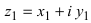 и
и 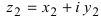 надо их перемножить, как два выражения с учетом того, что
надо их перемножить, как два выражения с учетом того, что 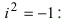
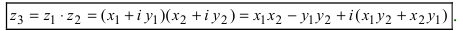
Замечание: Отметим, что 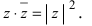
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 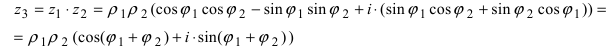 Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, n-ая степень любого комплексного числа будет иметь вид
Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, n-ая степень любого комплексного числа будет иметь вид 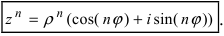 При извлечении корня п -ой степени применяют формулу Муавра
При извлечении корня п -ой степени применяют формулу Муавра 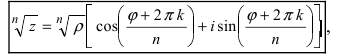 где величина
где величина 
3. Деление комплексного числа 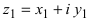 на комплексное число
на комплексное число 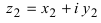 осуществляется так
осуществляется так 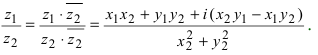
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 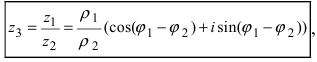 т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.
т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например, 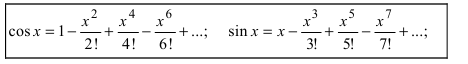
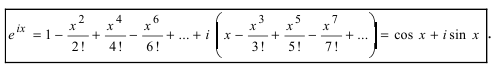
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 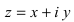 в показательной форме:
в показательной форме: 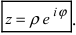 Отсюда видно, что при нахождении произведения и отношения комплексных чисел получаем
Отсюда видно, что при нахождении произведения и отношения комплексных чисел получаем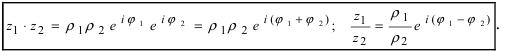
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
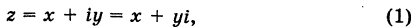
где х и у — действительные числа, a i — мнимая единица.
Числа вида 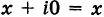 отождествляются с действительными числами; в частности,
отождествляются с действительными числами; в частности,  . Числа вида 0 + iy = iy называются чисто мнимыми.
. Числа вида 0 + iy = iy называются чисто мнимыми.
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
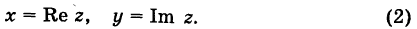
Под модулем комплексного числа z понимается неотрицательное число
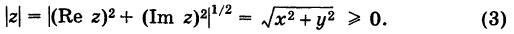
Сопряженным числом 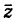 к числу (1) называется комплексное число
к числу (1) называется комплексное число
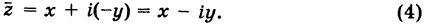
Таким образом,
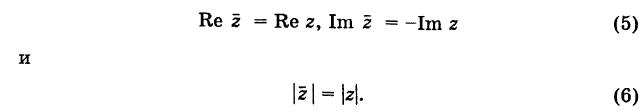
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
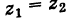
 Rez1 = Re z2, Im z1 = Im z2
Rez1 = Re z2, Im z1 = Im z2
В частности, z = 0  Re z = 0, Im z = 0.
Re z = 0, Im z = 0.
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) – Re z1 ± Re z2,
Im (z1 ± z2) – Imz1 ± 1mz2
III. z1z2 = (x1x2 – y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
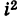 =
=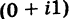
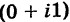 =
=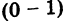 +
+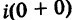 =-1
=-1
Заметим, что правило умножения III получается формально путем умножения двучленов 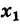 +
+ 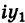 и
и 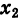 +
+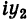 с учетом (7).
с учетом (7).
Очевидно также, что для 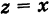
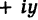
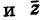
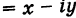 имеем
имеем
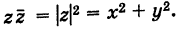
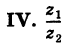 =
=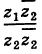 =
=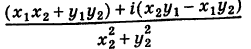
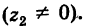
Легко проверить следующие свойства:
1)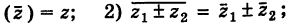
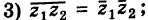
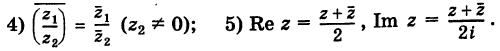
- Заказать решение задач по высшей математике
Комплексная плоскость
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
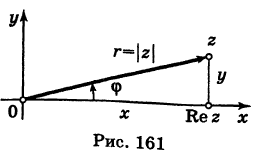
На оси Ох расположены действительные числа: z = :, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + iy = iy, она носит название мнимой оси.
:, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + iy = iy, она носит название мнимой оси.
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 
 . Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение Arg z называется главным значением его и обозначается через arg z:
. Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение Arg z называется главным значением его и обозначается через arg z:

Для аргумента ср имеем (рис. 161)
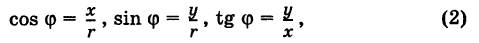
где 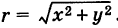
Примеры: 1) arg 2 = 0; 2) arg (-1) =  ; 3) arg i =
; 3) arg i =  .
.
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
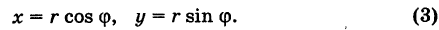
Таким образом, имеем тригонометрическую форму комплексного числа
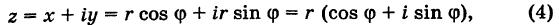
где 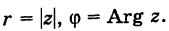
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число  соответствует точке с координатами
соответствует точке с координатами 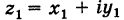 , а число
, а число 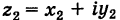 — точке с координатами
— точке с координатами  то числу
то числу 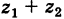 отвечает точка
отвечает точка 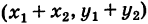 Так как (рис. 162) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами 0,
Так как (рис. 162) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами 0, 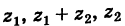 есть параллелограмм. Следовательно, радиус-вектор точки
есть параллелограмм. Следовательно, радиус-вектор точки  является суммой радиусов-векторов точек
является суммой радиусов-векторов точек  и
и 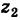 .
.
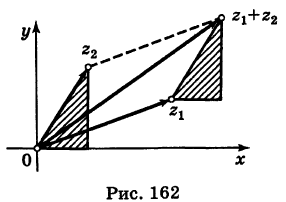
Следствие. Так как 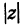 есть длина вектора
есть длина вектора 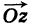 , то
, то
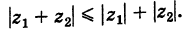
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 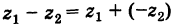 , то
, то  равен второй диагонали параллелограмма, построенного на векторах
равен второй диагонали параллелограмма, построенного на векторах  (рис. 163), т. е. равен разности радиусов-векторов точек
(рис. 163), т. е. равен разности радиусов-векторов точек  .
.
Следствие. Расстояние между двумя точками 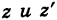 равно
равно
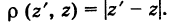
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
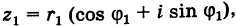
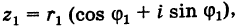
то имеем
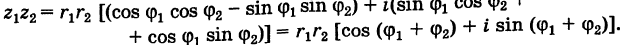
Отсюда
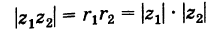
и
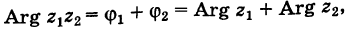
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
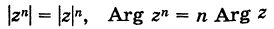
(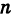 — целое положительное число).
— целое положительное число).
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
Пример №17
Построить точку 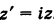 .
.
Решение:
Имеем
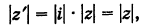
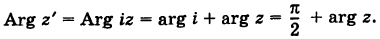
Следовательно, при умножении на i вектор 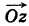 поворачивается на прямой угол против хода часовой стрелки (рис. 164).
поворачивается на прямой угол против хода часовой стрелки (рис. 164).
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
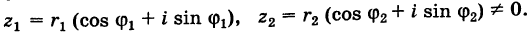
Так как
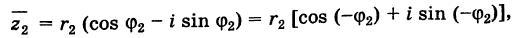
то на основании теоремы 1 имеем
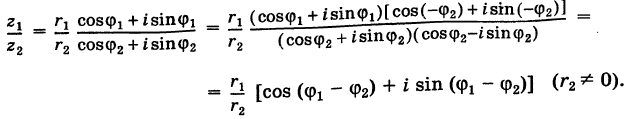
Отсюда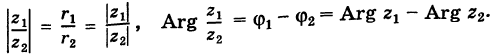
Извлечение корня из комплексного числа
Пусть
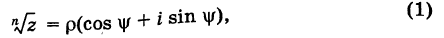
где 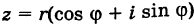 . Тогда на основании имеем
. Тогда на основании имеем
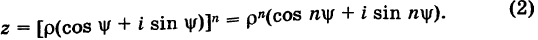
Отсюда получаем
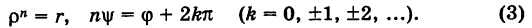
Таким образом,
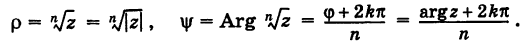
Заметим, что здесь под 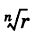 понимается арифметическое значение корня.
понимается арифметическое значение корня.
Здесь в качестве числа k достаточно брать лишь значения 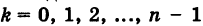 , так как при всех прочих значениях k получаются повторения уже найденных значений корня. Следовательно, окончательно имеем
, так как при всех прочих значениях k получаются повторения уже найденных значений корня. Следовательно, окончательно имеем
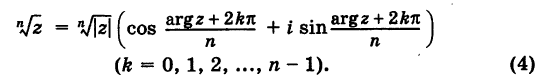
Из формулы (4) следует, что корень  -й степени из любого комплексного числа
-й степени из любого комплексного числа  =0 имеет точно л значений.
=0 имеет точно л значений.
Пример №18
Найти 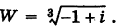
Решение:
Так как 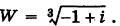 , то на основании формулы (4) имеем
, то на основании формулы (4) имеем
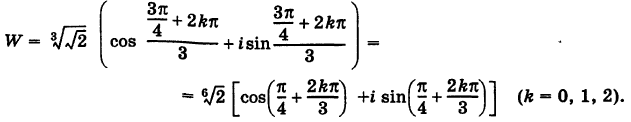
Отсюда
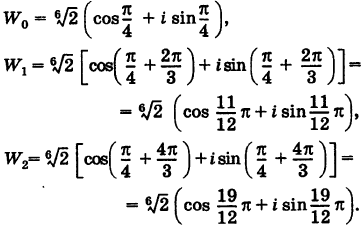
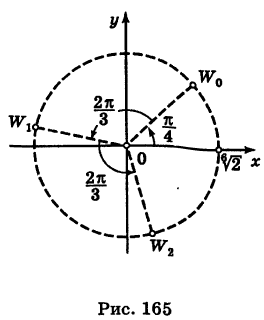
Точки  представляют собой равноотстоящие друг от друга точки, расположенные на окружности радиуса
представляют собой равноотстоящие друг от друга точки, расположенные на окружности радиуса  (рис. 165).
(рис. 165).
Понятие функции комплексной переменной
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z 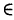 Е (Е — множество точек плоскости z) по некоторому закону f ставится в соответствие единственная точка w
Е (Е — множество точек плоскости z) по некоторому закону f ставится в соответствие единственная точка w  Е’ (Е’ — множество точек плоскости w), то говорят, что w есть функция от z (однозначная)
Е’ (Е’ — множество точек плоскости w), то говорят, что w есть функция от z (однозначная)

с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут

Множества Е и Е’ можно изображать на одной комплексной плоскости.
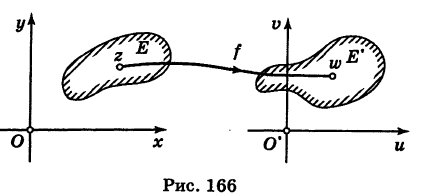
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
Пример:
Во что переходит сектор Е
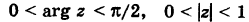
(рис. 167, а) при отображении 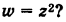
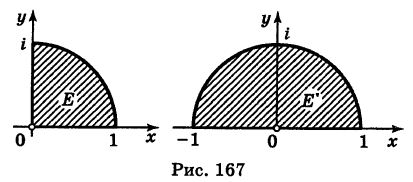
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 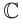 называется множество пар действительных чисел
называется множество пар действительных чисел  на котором введены операции сложения и умножения следующим образом. Если
на котором введены операции сложения и умножения следующим образом. Если 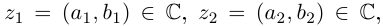 то
то 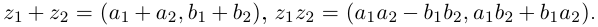 Элементы множества
Элементы множества  называются комплексными числами. Два комплексных числа
называются комплексными числами. Два комплексных числа 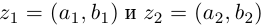 называются равными, если
называются равными, если 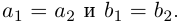
Операции сложения и умножения на множестве  обладают привычными свойствами (коммутативность сложения и умножения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения).
обладают привычными свойствами (коммутативность сложения и умножения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения).
Лемма 7.1. Для любых комплексных чисел 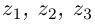 выполняются равенства
выполняются равенства
- 1)
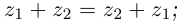
- 2)
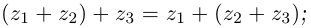
- 3)
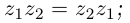
- 4)
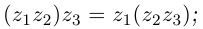
- 5)
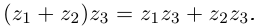
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 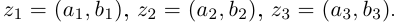 Тогда
Тогда
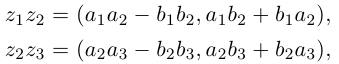
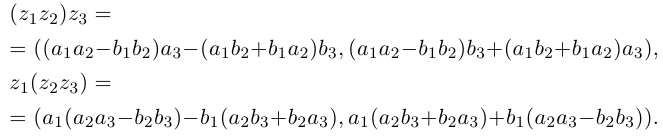
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
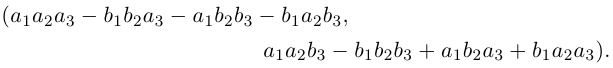 ■
■
Определение 7.2. Комплексное число 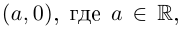 отождествляется с действительным числом а.
отождествляется с действительным числом а.
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар  и множеством действительных чисел, сохраняющее операции сложения и умножения:
и множеством действительных чисел, сохраняющее операции сложения и умножения:
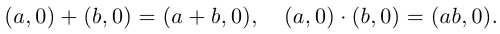
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой 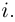
Легко видеть, что 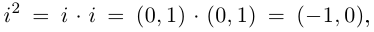 т.е.
т.е. 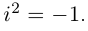
Далее, так как 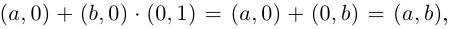 то пару
то пару 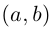 можно записать в виде
можно записать в виде 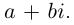 В дальнейшем комплексное число так и будем записывать:
В дальнейшем комплексное число так и будем записывать: 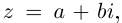 где
где  Определения операций при этом запишутся так:
Определения операций при этом запишутся так:
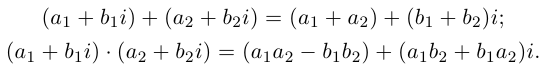
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что 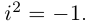
Определение 7.4. Разностью двух комплексных чисел 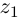 и
и 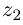 называется такое комплексное число
называется такое комплексное число 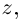 что
что 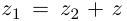 (обозначается
(обозначается 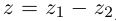 ). Частным двух комплексных чисел
). Частным двух комплексных чисел 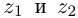 (
(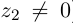 ) называется такое комплексное число z, что
) называется такое комплексное число z, что 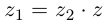 (обозначается
(обозначается 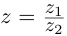 ).
).
Проверим, что эти операции однозначно определены.
□ Пусть 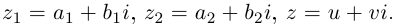 Для разности имеем:
Для разности имеем: 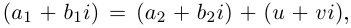 откуда
откуда 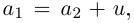
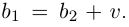 Тогда
Тогда 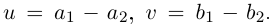 Разность двух комплексных чисел
Разность двух комплексных чисел 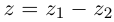 определяется однозначно:
определяется однозначно: 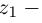
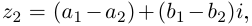 т.е. вычитание можно осуществлять непосредственно.
т.е. вычитание можно осуществлять непосредственно.
Для частного имеем: 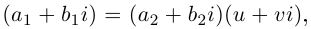 откуда
откуда 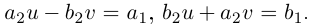 Так как
Так как 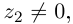 то определитель этой системы
то определитель этой системы 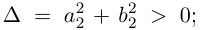 решая систему по правилу Крамера, получим:
решая систему по правилу Крамера, получим: 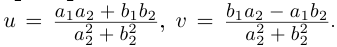 Частное двух комплексных чисел
Частное двух комплексных чисел  определено однозначно:
определено однозначно:
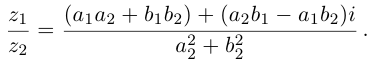
Такое деление можно осуществлять непосредственно:
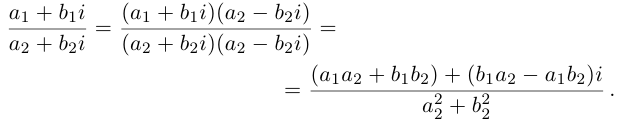
Комплексное число 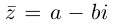 называется сопряжённым к числу
называется сопряжённым к числу  Мы воспользовались тем, что
Мы воспользовались тем, что 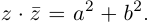 Произведённые действия аналогичны домножению числителя и знаменателя дроби со знаменателем вида
Произведённые действия аналогичны домножению числителя и знаменателя дроби со знаменателем вида 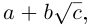 где
где 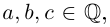
 на число
на число 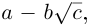 сопряжённое к знаменателю (такие действия применяются для избавления от иррациональности в знаменателе).
сопряжённое к знаменателю (такие действия применяются для избавления от иррациональности в знаменателе).
Определение 7.5. Пусть 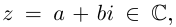 где
где 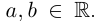 Тогда числа
Тогда числа  называются соответственно действительной и мнимой частью числа
называются соответственно действительной и мнимой частью числа  (
(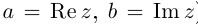 ). Комплексное число
). Комплексное число 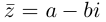 называется числом, сопряжённым к
называется числом, сопряжённым к  Действительное неотрицательное число
Действительное неотрицательное число 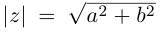 называется модулем числа
называется модулем числа 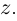
Лемма 7.2. Для любых комплексных чисел  имеют место следующие соотношения:
имеют место следующие соотношения:
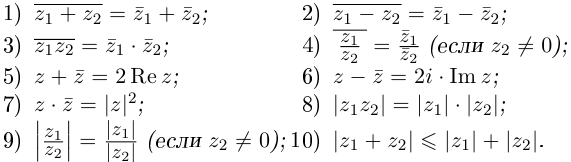
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел  геометрически интерпретируется как множество точек плоскости (комплексная плоскость
геометрически интерпретируется как множество точек плоскости (комплексная плоскость  ). Если координаты точек заданы в прямоугольной системе координат 0,
). Если координаты точек заданы в прямоугольной системе координат 0, 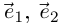 (кратчайший поворот от
(кратчайший поворот от  осуществляется против часовой стрелки), то комплексное число
осуществляется против часовой стрелки), то комплексное число 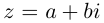 соответствует точке
соответствует точке 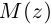 с координатами
с координатами 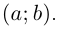 Такое соответствие является взаимно однозначным. Точка
Такое соответствие является взаимно однозначным. Точка 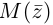 симметрична точке
симметрична точке 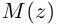 относительно оси абсцисс, которая называется действительной осью, ось ординат называется мнимой осью. Расстояние от точки
относительно оси абсцисс, которая называется действительной осью, ось ординат называется мнимой осью. Расстояние от точки  до начала координат равно
до начала координат равно  (см. рис. 7.1).
(см. рис. 7.1).
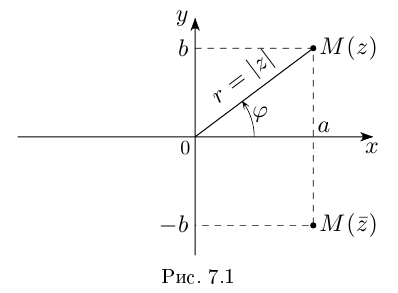
Аргументом числа  называется угол
называется угол 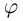 поворота от положительного луча действительной оси к лучу
поворота от положительного луча действительной оси к лучу 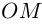 (против часовой стрелки). Этот угол определён с точностью до
(против часовой стрелки). Этот угол определён с точностью до 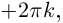
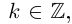 и обозначается
и обозначается 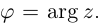 Аргумент нулевого комплексного числа не определён. Фактически мы ввели полярные координаты на комплексной плоскости:
Аргумент нулевого комплексного числа не определён. Фактически мы ввели полярные координаты на комплексной плоскости: 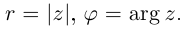 При этом
При этом 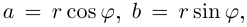 и комплексное число
и комплексное число 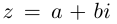 можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
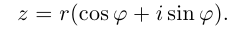
Пример:
Записать в тригонометрической форме числа 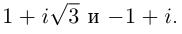
□ 1) 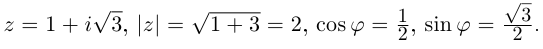
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 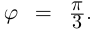 Тогда
Тогда 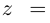
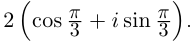
2) 
 Тогда
Тогда 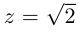 (
(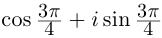 ).
).
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 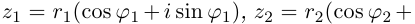
 Тогда
Тогда
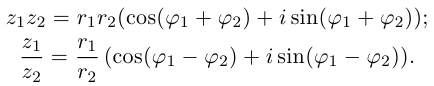
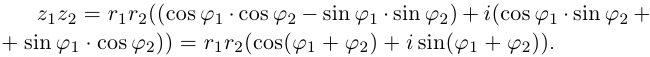
Если 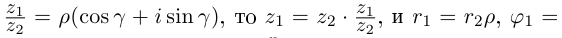
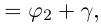 откуда следует, что
откуда следует, что 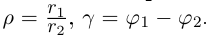
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 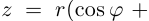
 то при любом целом
то при любом целом  имеет место равенство
имеет место равенство
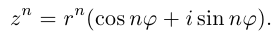
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для 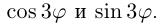
□ Имеем: 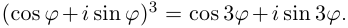 Возводя двучлен в куб, получим:
Возводя двучлен в куб, получим: 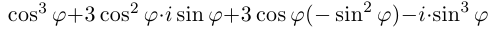 (мы воспользовались тем, что
(мы воспользовались тем, что 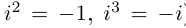 ). Приравнивая действительные и мнимые части двух равных выражений, имеем
). Приравнивая действительные и мнимые части двух равных выражений, имеем
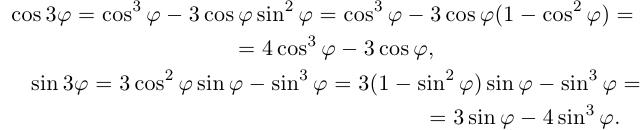
Определение 7.6. Пусть  — натуральное число,
— натуральное число,  Корнем
Корнем 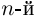 степени из комплексного числа
степени из комплексного числа 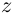 называется комплексное число
называется комплексное число 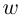 такое, что
такое, что 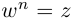 (обозначение:
(обозначение: 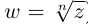 ).
).
Лемма 7.4. Если 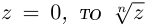 принимает единственное значение 0 при любом
принимает единственное значение 0 при любом 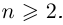 Если
Если 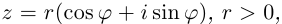 то
то 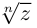 принимает ровно
принимает ровно 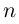 комплексных значений, имеющих одинаковый модуль
комплексных значений, имеющих одинаковый модуль 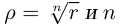 различных значений аргумента
различных значений аргумента 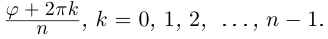
□ Правая часть леммы очевидна, так как 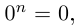 и если
и если 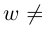
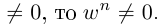 Пусть теперь
Пусть теперь 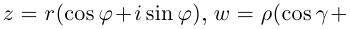
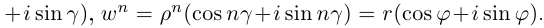 Комплексные числа, записанные в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на
Комплексные числа, записанные в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на  (пока значение
(пока значение  стояло только под знаком косинуса и синуса, неоднозначность определения
стояло только под знаком косинуса и синуса, неоднозначность определения  можно было не учитывать, если сравнивать сами углы — эту неоднозначность учитывать необходимо). Итак,
можно было не учитывать, если сравнивать сами углы — эту неоднозначность учитывать необходимо). Итак, 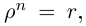
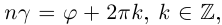 откуда
откуда 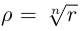 (арифметический корень
(арифметический корень  степени из положительного числа),
степени из положительного числа), 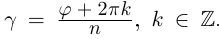
При замене  получим тот же угол, увеличенный на
получим тот же угол, увеличенный на  поэтому существенно различные значения
поэтому существенно различные значения 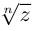 дают лишь
дают лишь 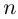 значений
значений 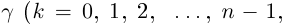 далее значения корня повторяются).
далее значения корня повторяются).
Замечание. 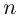 значений
значений 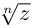 на комплексной плоскости соответствуют
на комплексной плоскости соответствуют 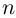 точкам, лежащим в вершинах правильного
точкам, лежащим в вершинах правильного 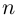 -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса 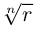 с центром в начале координат.
с центром в начале координат.
Пример №19
Найти все значения 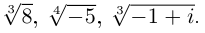
□ 1) 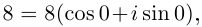 поэтому
поэтому 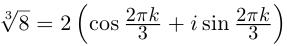
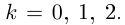 Получим 3 значения:
Получим 3 значения: 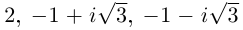 (см. рис. 7.2).
(см. рис. 7.2).
Первое из них — арифметическое значение кубического корня из положительного числа 8.
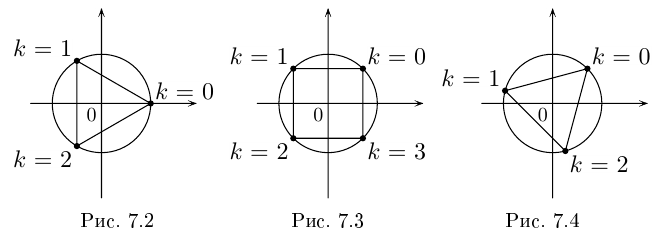
2) 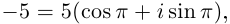 поэтому
поэтому
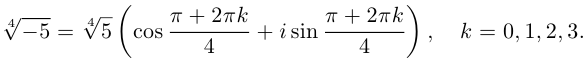
Получим 4 значения:
(см. рис. 7.3). 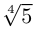 здесь — арифметическое значение корня 4-й степени из положительного числа 5.
здесь — арифметическое значение корня 4-й степени из положительного числа 5.
3) 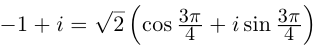 , поэтому
, поэтому
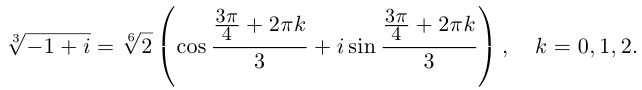
Получим 3 значения:
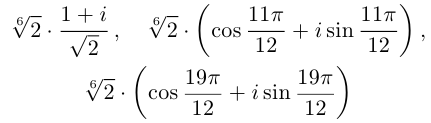
(см. рис. 7.4). ■
Определение 7.7. Пусть 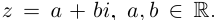 Тогда
Тогда 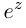 определяется как комплексное число
определяется как комплексное число 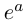
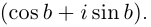
Если 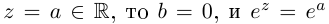 (при
(при 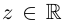 получаем обычное действительное значение
получаем обычное действительное значение 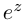 ). Отмстим, что
). Отмстим, что 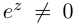 при любых
при любых 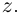
Лемма 7.5. Для любых 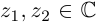 имеют место равенства
имеют место равенства 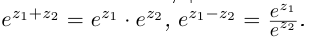
□ Пусть 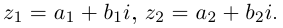 Тогда
Тогда
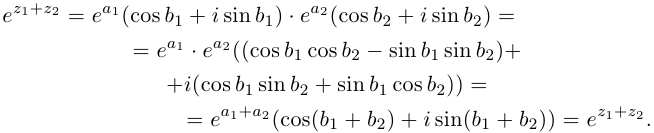
Далее, так как 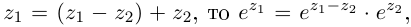 откуда следует второе утверждение леммы.
откуда следует второе утверждение леммы.
Пример №20
Вычислить 
□ Имеем: 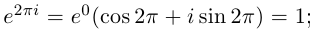
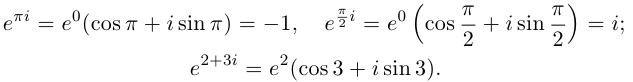
Так как при всех  выполняются равенства
выполняются равенства 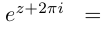
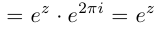 , то функция комплексной переменной
, то функция комплексной переменной 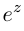 имеет мнимый период
имеет мнимый период 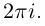 Привычной взаимной однозначности отображения при помощи функции
Привычной взаимной однозначности отображения при помощи функции 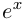 уже нет.
уже нет.
Определение 7.8. Логарифмом комплексного числа 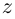 называется комплексное число
называется комплексное число 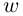 такое, что
такое, что 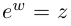 (обозначение:
(обозначение: 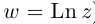 ).
).
Лемма 7.6. Если 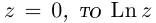 не определен. Если
не определен. Если 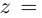
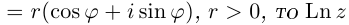 принимает бесконечно много значений, имеющих одинаковую действительную часть
принимает бесконечно много значений, имеющих одинаковую действительную часть 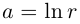 (обычный натуральный логарифм положительного числа) и бесконечное число значений мнимой части
(обычный натуральный логарифм положительного числа) и бесконечное число значений мнимой части 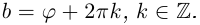
□ Первая часть леммы следует из того, что 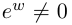 при любых
при любых  Пусть теперь
Пусть теперь 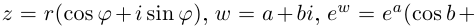
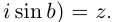 Тогда
Тогда 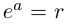 (откуда
(откуда 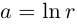 ),
), 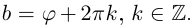
Таким образом, множество значений функции 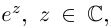 есть вся комплексная плоскость, кроме точки 0.
есть вся комплексная плоскость, кроме точки 0.
Пример №21
Найти все значения 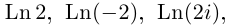
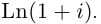
Определение 7.9. Для любых  определим
определим 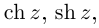
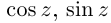 так:
так:
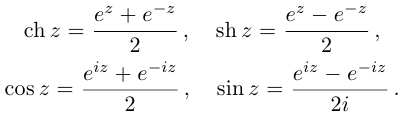
Если 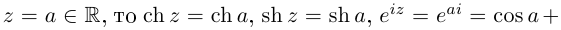
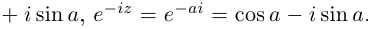 Поэтому
Поэтому
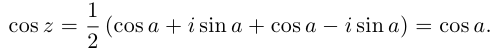
Аналогично, 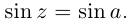
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 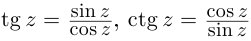 ). Например, для всех
). Например, для всех 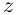
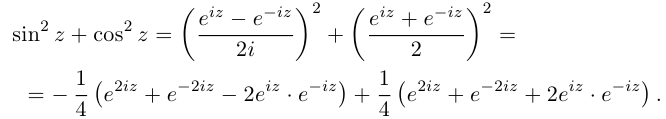
Так как 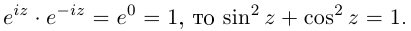
Легко видеть, что 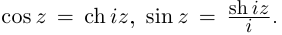 Косинус на действительной оси соответствует гиперболическому косинусу на мнимой оси и наоборот: аналогично для синусов. Поэтому формально все операции для тригонометрических и гиперболических функций проводятся одинаково с точностью до некоторых степеней числа
Косинус на действительной оси соответствует гиперболическому косинусу на мнимой оси и наоборот: аналогично для синусов. Поэтому формально все операции для тригонометрических и гиперболических функций проводятся одинаково с точностью до некоторых степеней числа 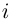 (если работать только с действительными числами, то всё будет происходить одинаково с точностью до степеней числа —1). Этим и объясняется сходство формул тригонометрии с соответствующими формулами для гиперболических функций, включая формулы для производных и разложения по формуле Тейлора.
(если работать только с действительными числами, то всё будет происходить одинаково с точностью до степеней числа —1). Этим и объясняется сходство формул тригонометрии с соответствующими формулами для гиперболических функций, включая формулы для производных и разложения по формуле Тейлора.
Комплекснозначные функции действительной переменной
Рассмотрим функцию 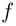 такую, что
такую, что 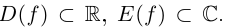 Тогда при всех
Тогда при всех 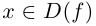 можно рассмотреть
можно рассмотреть 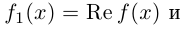
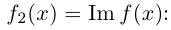
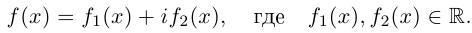
Так как  можно интерпретировать как плоскость
можно интерпретировать как плоскость  , то комплекснозначная функция действительной переменной фактически есть двумерная вектор-функция, значения которой записываются как комплексные числа.
, то комплекснозначная функция действительной переменной фактически есть двумерная вектор-функция, значения которой записываются как комплексные числа.
Определение 7.10. Комплекснозначная функция действительной переменной 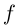 называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) в точке или на промежутке, если таковыми же являются обе функции
называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) в точке или на промежутке, если таковыми же являются обе функции 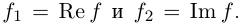 Для дифференцируемой функции по определению
Для дифференцируемой функции по определению 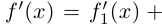
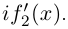
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной 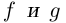 дифференцируемы в точке
дифференцируемы в точке 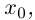 то функции
то функции 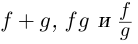 также дифференцируемы в этой точке, причем
также дифференцируемы в этой точке, причем
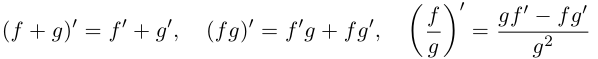
в точке  (в последнем случае нужно требовать, чтобы
(в последнем случае нужно требовать, чтобы 
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 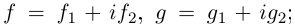 функции
функции 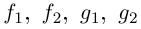 дифференцируемы в точке
дифференцируемы в точке  Тогда
Тогда
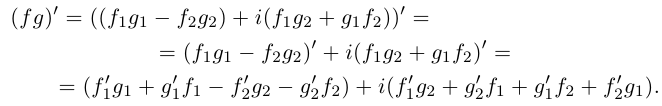
Функция 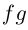 дифференцируема в точке
дифференцируема в точке 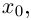 так как существуют и конечны все производные в последнем выражении. Далее,
так как существуют и конечны все производные в последнем выражении. Далее,
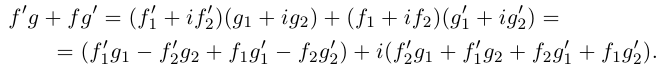
Легко видеть, что это выражение совпадает с 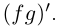
Пример №22
Доказать, что при любом 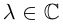 имеет место равенство
имеет место равенство
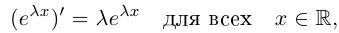
т.е. привычная для действительных  формула сохраняется и при комплексных
формула сохраняется и при комплексных 
□ Пусть 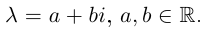
Тогда 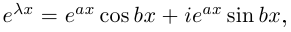
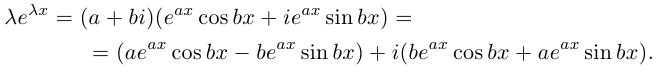
С другой стороны, 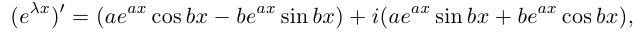
что совпадает с 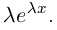
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной 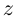
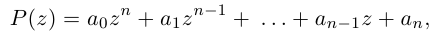
где 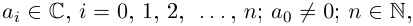 называется многочленом степени
называется многочленом степени 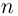 от переменной
от переменной 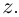 Многочлен степени 0 — это постоянная функция
Многочлен степени 0 — это постоянная функция 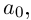 где
где 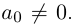 Нулевому многочлену не приписывается никакая степень (иногда удобно считать, что его степень равна
Нулевому многочлену не приписывается никакая степень (иногда удобно считать, что его степень равна 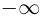 ). Если все
). Если все 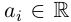 , то говорят о многочлене с действительными коэффициентами (
, то говорят о многочлене с действительными коэффициентами (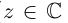 или
или 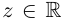 по смыслу задачи). Если все
по смыслу задачи). Если все 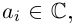 то говорят о многочлене с комплексными коэффициентами
то говорят о многочлене с комплексными коэффициентами 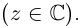
Если 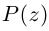 — многочлен степени
— многочлен степени 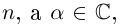 то многочлен
то многочлен 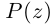 можно разделить с остатком на
можно разделить с остатком на 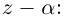
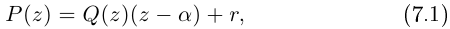
где 
Теорема 7.1 (Безу). Остаток от деления многочлена 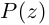 на двучлен
на двучлен 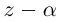 равен
равен 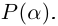
□ Из (7.1) имеем при 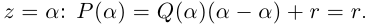
Следствие. Многочлен 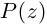 делится без остатка на
делится без остатка на  тогда и только тогда, когда число
тогда и только тогда, когда число  является корнем многочлена
является корнем многочлена 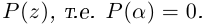
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число  является корнем многочлена
является корнем многочлена 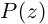 тогда и только тогда, когда
тогда и только тогда, когда 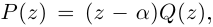 где степень многочлена
где степень многочлена  на единицу меньше степени Р.
на единицу меньше степени Р.
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени  с комплексными коэффициентами имеет комплексный корень.
с комплексными коэффициентами имеет комплексный корень.
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
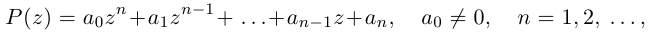
раскладывается в произведение линейных множителей
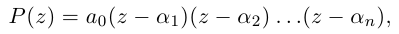
где 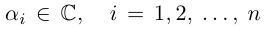 (среди чисел
(среди чисел 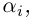 возможно, есть равные).
возможно, есть равные).
□ По основной теореме алгебры 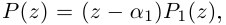 где
где 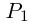 — многочлен степени
— многочлен степени 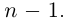 Применяя такую же процедуру к
Применяя такую же процедуру к 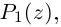 получим:
получим: 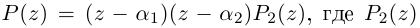 — многочлен степени
— многочлен степени  и т.д. В конце концов дойдём до многочлена степени 0.
и т.д. В конце концов дойдём до многочлена степени 0.
где  (комплексная постоянная). Здесь
(комплексная постоянная). Здесь 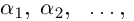
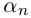 — комплексные числа, среди которых могут быть равные.
— комплексные числа, среди которых могут быть равные.
Если раскрыть скобки в правой части (7.2), то коэффициент при 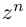 будет равен С, т.е.
будет равен С, т.е. 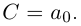
Определение 7.11. Комплексное число 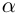 называется корнем кратности
называется корнем кратности 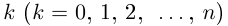 многочлена
многочлена 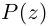 степени
степени 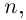 если
если 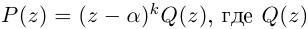 — многочлен такой, что
— многочлен такой, что 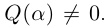 При
При 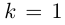 корень называется простым, при
корень называется простым, при 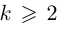 — кратным.
— кратным.
Если 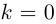 , то число
, то число 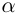 не является корнем многочлена
не является корнем многочлена 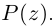
В общем случае, учитывая кратность корней, многочлен 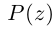 степени
степени 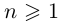 раскладывается на линейные множители:
раскладывается на линейные множители:
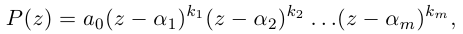
где все комплексные числа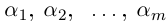 различны, корень
различны, корень 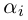 имеет кратность
имеет кратность 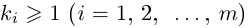 , при этом степень многочлена равна
, при этом степень многочлена равна 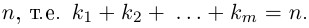
Лемма 7.8. Пусть 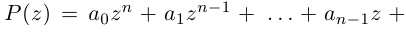
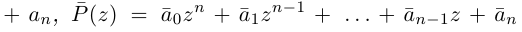 (многочлен, сопряжённый к P). Число
(многочлен, сопряжённый к P). Число 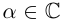 является корнем многочлена Р кратности
является корнем многочлена Р кратности 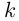 тогда и только тогда, когда число а является корнем многочлена
тогда и только тогда, когда число а является корнем многочлена 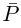 той же кратности
той же кратности 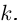
□ Так как 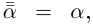 то утверждение достаточно доказать лишь в одну сторону. Пусть
то утверждение достаточно доказать лишь в одну сторону. Пусть 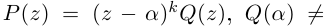
 Тогда
Тогда 
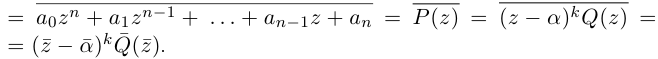
Так как  — любое комплексное число, то в последней записи можно заменить
— любое комплексное число, то в последней записи можно заменить  Получим
Получим
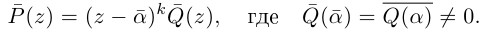
Это и означает, что 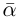 — корень многочлена
— корень многочлена 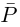 кратности
кратности 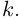
Следствие. Если 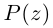 — многочлен с действительными коэффициентами, то числа
— многочлен с действительными коэффициентами, то числа 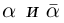 одновременно являются его корнями, причем кратности их совпадают (т.е. недействительные корни появляются «парочками» — взаимно сопряжённые корни одинаковой кратности).
одновременно являются его корнями, причем кратности их совпадают (т.е. недействительные корни появляются «парочками» — взаимно сопряжённые корни одинаковой кратности).
□ Это очевидно из леммы 7.8, так как 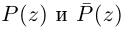 — один и тот же многочлен.
— один и тот же многочлен.
Теорема 7.4. Многочлен степени 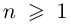 с действительными коэффициентами
с действительными коэффициентами 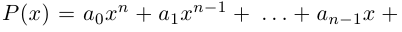
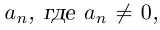 раскладывается в произведение линейных и неприводимых квадратичных множителей:
раскладывается в произведение линейных и неприводимых квадратичных множителей:
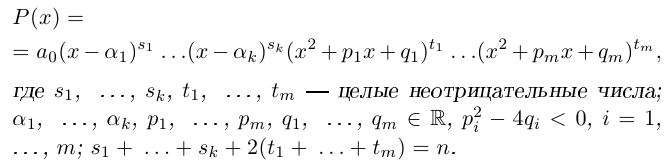
□ По теореме 7.3 и лемме 7.8
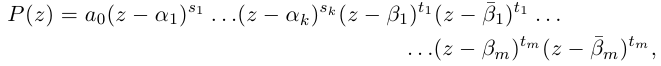
где  — действительные корни многочлена
— действительные корни многочлена  кратностей
кратностей  соответственно, a
соответственно, a  — оставшиеся корни (
— оставшиеся корни (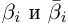 имеют одинаковую кратность
имеют одинаковую кратность 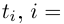
 ). Очевидно, что степень многочлена равна
). Очевидно, что степень многочлена равна 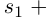
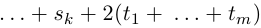 т.е. эта сумма равна
т.е. эта сумма равна 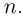
Пусть 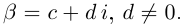 Тогда
Тогда 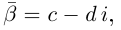
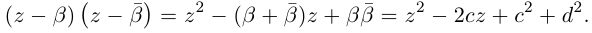
Получили квадратный трёхчлен с действительными коэффициентами 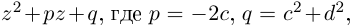 который имеет отрицательный дискриминант
который имеет отрицательный дискриминант 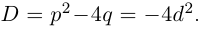 Остаётся символически заменить
Остаётся символически заменить  подчёркивая этим, что нас интересуют лишь действительные значения
подчёркивая этим, что нас интересуют лишь действительные значения  и мы получим нужное равенство.
и мы получим нужное равенство.
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
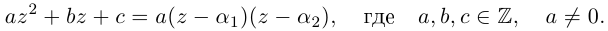
Корни 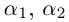 — комплексные, и они обязательно существуют. Роль дискриминанта
— комплексные, и они обязательно существуют. Роль дискриминанта 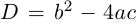 сводится только к определению того, различны ли корни
сводится только к определению того, различны ли корни 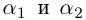 или они совпадают (т.е. квадратный трёхчлен имеет один корень
или они совпадают (т.е. квадратный трёхчлен имеет один корень 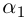 кратности 2). Если
кратности 2). Если 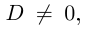 то квадратный трёхчлен имеет два различных простых корня, если
то квадратный трёхчлен имеет два различных простых корня, если 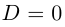 — один корень кратности 2. В самом деле, решая квадратное уравнение
— один корень кратности 2. В самом деле, решая квадратное уравнение 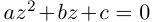 методом выделения полного квадрата, получим, как и в элементарной алгебре:
методом выделения полного квадрата, получим, как и в элементарной алгебре:
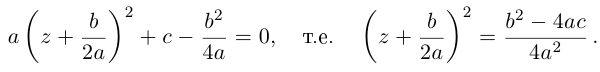
Если 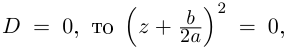 и уравнение имеет один корень
и уравнение имеет один корень 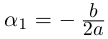 кратности 2
кратности 2 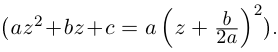 Если
Если 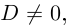 то
то 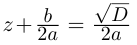 (писать ± не имеет смысла, так как
(писать ± не имеет смысла, так как 
 и под
и под 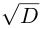 понимаются оба значения квадратного корня из ненулевого комплексного числа). Окончательно получим привычную формулу корней квадратного уравнения:
понимаются оба значения квадратного корня из ненулевого комплексного числа). Окончательно получим привычную формулу корней квадратного уравнения:
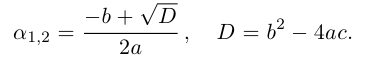
Пример №23
Решить уравнение 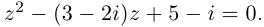
□ 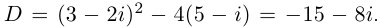 Найдём оба значения
Найдём оба значения 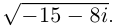 Пусть
Пусть 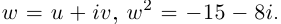 Тогда
Тогда 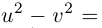
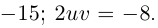 Решая эту систему, получим:
Решая эту систему, получим: 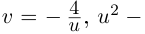
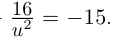 Полученное биквадратное уравнение
Полученное биквадратное уравнение 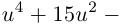
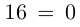 решается при помощи замены
решается при помощи замены 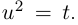 Квадратное уравнение
Квадратное уравнение 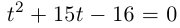 имеет корни
имеет корни 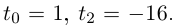 Так как
Так как 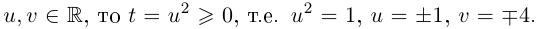 Получили два значения квадратного корня:
Получили два значения квадратного корня: 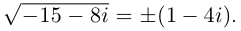 Тогда корни данного уравнения равны
Тогда корни данного уравнения равны
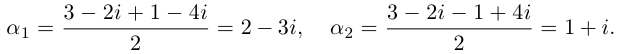
Пример №24
Найти все значения 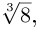 решая уравнение
решая уравнение 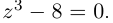
□ Левая часть раскладывается на множители:
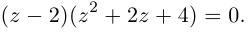
Поэтому один из корней равен 2. Квадратный трёхчлен 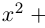
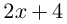 не имеет действительных корней
не имеет действительных корней 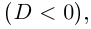 поэтому
поэтому 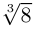 имеет всего одно действительное значение 2. Найдём оставшиеся два комплексно-сопряжённых значения. Решаем квадратное уравнение
имеет всего одно действительное значение 2. Найдём оставшиеся два комплексно-сопряжённых значения. Решаем квадратное уравнение 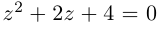 по формуле чётного коэффициента:
по формуле чётного коэффициента:
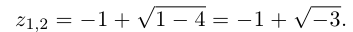
Во множестве комплексных чисел 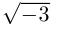 имеет два значения
имеет два значения 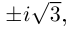 поэтому
поэтому 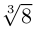 имеет 3 комплексных значения:
имеет 3 комплексных значения: 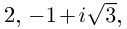
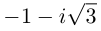 (такой же результат был получен в примере 7.3 другим способом). ■
(такой же результат был получен в примере 7.3 другим способом). ■
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 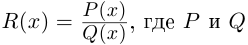 — многочлены степеней соответственно
— многочлены степеней соответственно  где
где  Дробь называется правильной, если
Дробь называется правильной, если  и неправильной, если
и неправильной, если 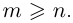
Лемма 7.9. Если 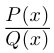 правильная дробь и
правильная дробь и  —действительный корень многочлена
—действительный корень многочлена  кратности
кратности 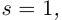 то
то
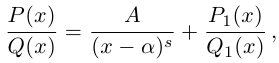
где 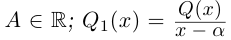 — многочлен, для которого
— многочлен, для которого 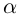 является корнем кратности
является корнем кратности 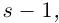 a
a 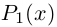 — такой многочлен, что дробь
— такой многочлен, что дробь 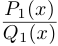 является правильной.
является правильной.
□ Так как 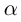 — корень
— корень 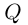 кратности
кратности 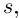 то
то 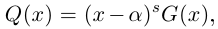 где
где 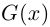 — многочлен такой, что
— многочлен такой, что 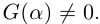 Рассмотрим число
Рассмотрим число 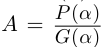 и многочлен
и многочлен 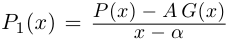 (это многочлен, так как
(это многочлен, так как 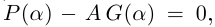 и числитель делится нацело на
и числитель делится нацело на 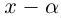 ).
).
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень 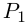 меньше степени
меньше степени 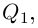 т.е. дробь
т.е. дробь 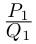 правильная. Далее,
правильная. Далее, 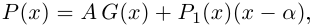 откуда
откуда 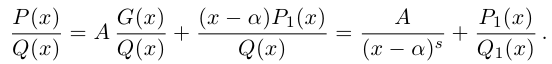
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть — неприводимый квадратный трёхчлен, входящий в разложение многочлена
— неприводимый квадратный трёхчлен, входящий в разложение многочлена  на множители в степени
на множители в степени 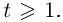 Тогда правильная дробь
Тогда правильная дробь 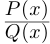 представляется в виде
представляется в виде
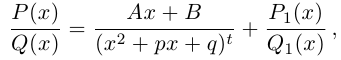
где 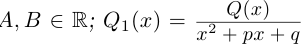 — многочлен, в разложение которого
— многочлен, в разложение которого 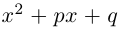 входит в степени
входит в степени 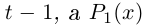 — такой многочлен, что дробь
— такой многочлен, что дробь 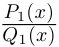 является правильной.
является правильной.
□ Пусть 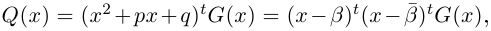 где
где 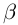 и
и 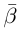 комплексно-сопряжённые корни квадратного трёхчлена
комплексно-сопряжённые корни квадратного трёхчлена 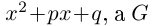 — действительный многочлен такой, что
— действительный многочлен такой, что 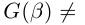
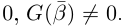 Рассмотрим действительные числа А и В такие, что
Рассмотрим действительные числа А и В такие, что
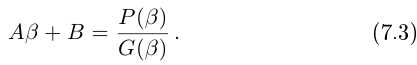
Такие числа А и В определены единственным образом, так как если 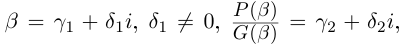 то равенство (7.3) перепишется так:
то равенство (7.3) перепишется так:
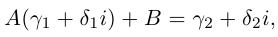
и числа А, В находятся из системы 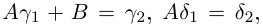 очевидно, имеющей единственное решение. Из (7.3) следует также, что
очевидно, имеющей единственное решение. Из (7.3) следует также, что 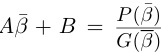 так как
так как  — многочлены с действительными коэффициентами.
— многочлены с действительными коэффициентами.
Рассмотрим многочлен 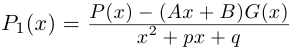 (это — многочлен, так как
(это — многочлен, так как 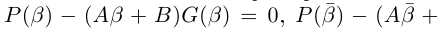
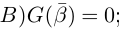 значит, числитель делится нацело на
значит, числитель делится нацело на  и на
и на  следовательно, делится на
следовательно, делится на 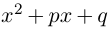 ). Пусть степень Q равна
). Пусть степень Q равна 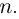 Так как степень G не превосходит
Так как степень G не превосходит 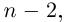 то степень многочлена
то степень многочлена 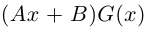 не превосходит
не превосходит 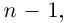 т.е. меньше степени Q. Степень Р также меньше степени Q, поэтому степень числителя последней дроби меньше степени Q.
т.е. меньше степени Q. Степень Р также меньше степени Q, поэтому степень числителя последней дроби меньше степени Q.
Значит, степень 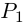 меньше, чем
меньше, чем  , т.е. меньше степени
, т.е. меньше степени  и дробь
и дробь 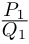 правильная. Далее,
правильная. Далее,
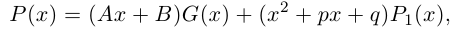
откуда
Последовательно выделяя из многочлена  линейные, а затем неприводимые квадратичные множители, и применяя соответственно леммы 7.9 и 7.10, получим разложение
линейные, а затем неприводимые квадратичные множители, и применяя соответственно леммы 7.9 и 7.10, получим разложение 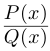 в сумму правильных дробей вида
в сумму правильных дробей вида

(здесь 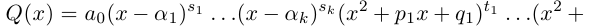
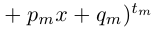 — как разложение многочлена в теореме 7.4).
— как разложение многочлена в теореме 7.4).
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом  , являются действительными числами (вообще говоря, различными). Всего их
, являются действительными числами (вообще говоря, различными). Всего их 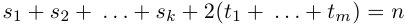 штук. Можно доказать, что они определены единственным образом. Процесс выделения слагаемых по леммам 7.9 и 7.10 прекратится, когда в знаменателе останется ровно один множитель вида
штук. Можно доказать, что они определены единственным образом. Процесс выделения слагаемых по леммам 7.9 и 7.10 прекратится, когда в знаменателе останется ровно один множитель вида 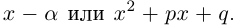 Но такая правильная дробь сама будет простейшей. Таким образом, доказана
Но такая правильная дробь сама будет простейшей. Таким образом, доказана
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
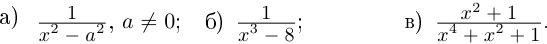
а) 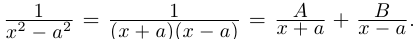 Приводя к общему знаменателю, имеем:
Приводя к общему знаменателю, имеем: 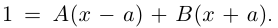 При
При 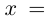
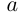 получим
получим 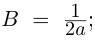 при
при 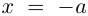 получим
получим 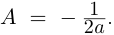 Окончательно имеем:
Окончательно имеем: 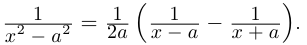
б)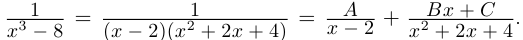 Приводя в общему знаменателю, имеем:
Приводя в общему знаменателю, имеем: 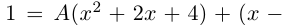
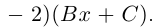 При
При 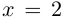 получим
получим 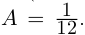 Приравнивая коэффициенты при
Приравнивая коэффициенты при 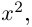 получим
получим 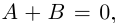 т.е.
т.е. 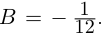 Приравнивая свободные члены, получим
Приравнивая свободные члены, получим 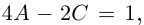 откуда
откуда 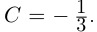 Окончательно имеем
Окончательно имеем
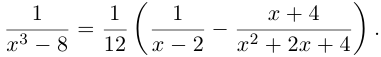
в) 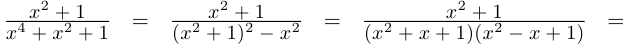
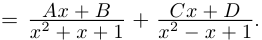 Приводя к общему знаменателю, имеем:
Приводя к общему знаменателю, имеем: 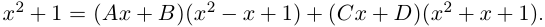 Приравнивая коэффициенты при
Приравнивая коэффициенты при 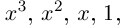 получим:
получим: 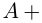
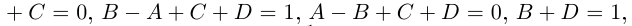 откуда
откуда 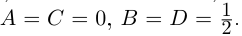 Окончательно имеем
Окончательно имеем
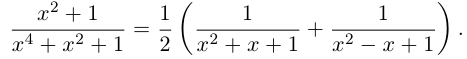
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
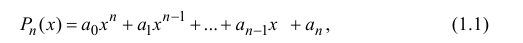
где 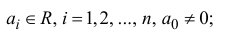
х – переменная.
Корнем многочлена (1.1) называется любое число 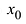 такое, что
такое, что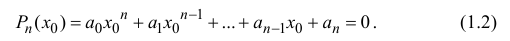
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например: 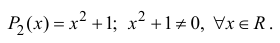
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 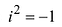 ( i называется мнимой единицей).
( i называется мнимой единицей).
Тогда ±i – два корня уравнения 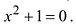
Определение 1.2. Множеством комплексных чисел называется множество
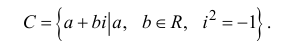
Суммой двух комплексных чисел 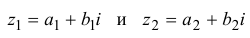 называется число
называется число
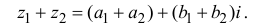 .
.
Произведением двух комплексных чисел 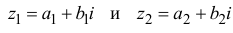 называется число
называется число
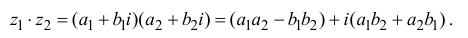
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения: 
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти 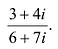
Решение:
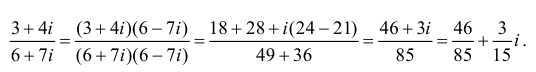
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
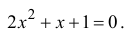
Решение:
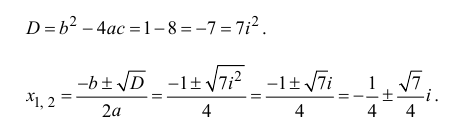
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 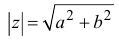 называется модулем z.
называется модулем z.
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
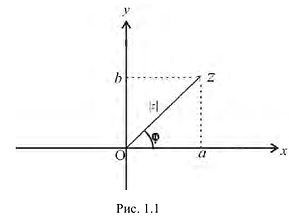
При этом 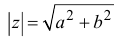 – длина радиуса-вектора точки z.
– длина радиуса-вектора точки z.
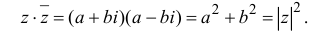
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 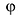 , который образует радиус-вектор точки z с положительным
, который образует радиус-вектор точки z с положительным
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 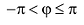 называется
называется
главным и обозначается argz.
Замечание. 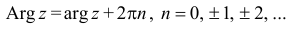
При этом
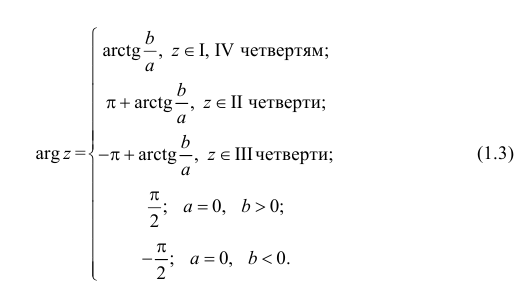
Если 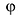 – аргумент z, то z представляется в виде
– аргумент z, то z представляется в виде 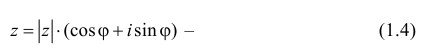
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть 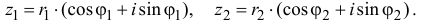
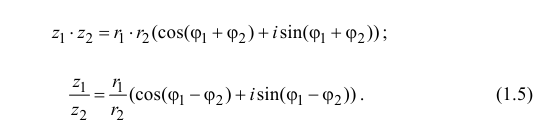
Доказательство
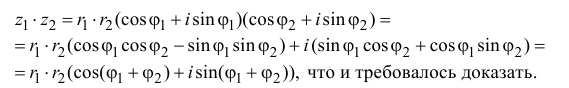
Из формул (1.5) следует, в частности, что 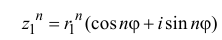 – формула Муавра. (1.6)
– формула Муавра. (1.6)
Пример №28
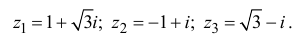 Представить числа
Представить числа  в тригонометрической форме.
в тригонометрической форме.
Решение:
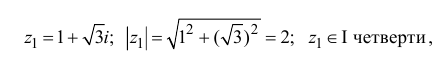
поэтому по формуле (1.3)
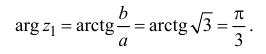
Тогда по формуле (1.4)
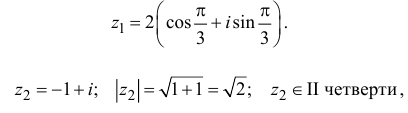
поэтому по формуле (1.3)
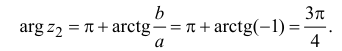
Тогда 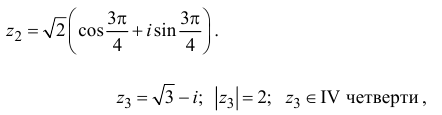
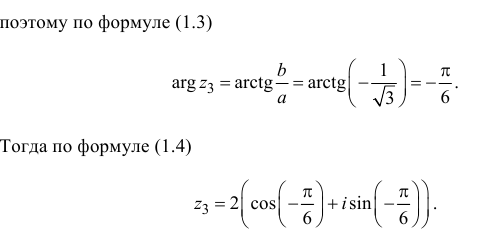
Из формул (1.5), (1.6) видно, что аргумент 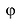 комплексного числа z при
комплексного числа z при
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 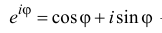 – формула Эйлера. (1.7)
– формула Эйлера. (1.7)
Тогда из теоремы 1.2 следует, что
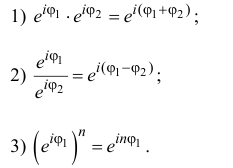
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 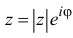 показательная форма комплексного числа.
показательная форма комплексного числа.
Пример №29
Вычислить 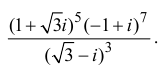
Решение:
Согласно примеру 1.3 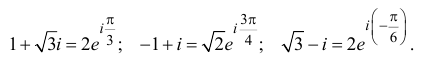
Поэтому
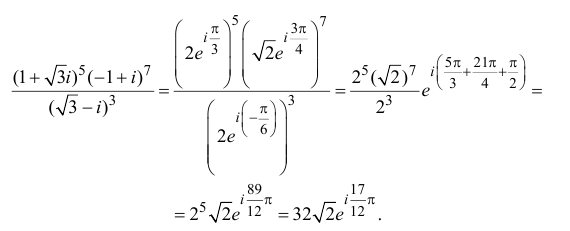
Определение 1.5. Корнем n-й степени из числа z  C называется такое
C называется такое
число 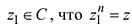 , что
, что 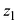 , при этом обозначается
, при этом обозначается 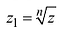 . Таким образом
. Таким образом

Из формулы (1.8) видно что 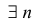 корней n-й степени из числа z, при этом,
корней n-й степени из числа z, при этом,
если 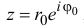 , то
, то

Пример №30
Найти 
Решение:
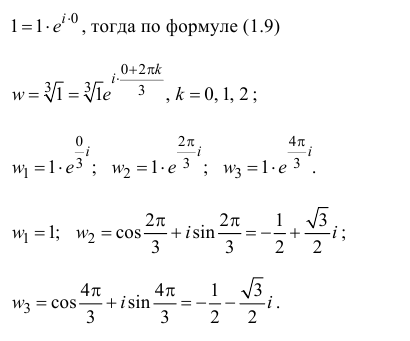
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных































![{displaystyle z^{n}=left[rleft(cos varphi +isin varphi right)right]^{n}=r^{n}left(cos nvarphi +isin nvarphi right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9210e70600dff0b9666c2b2b281250988a66473a)
![{displaystyle {begin{alignedat}{2}z^{1/n}&=left[rleft(cos left(varphi +2pi kright)+isin left(varphi +2pi kright)right)right]^{1/n}=\&={sqrt[{n}]{r}}left(cos {frac {varphi +2pi k}{n}}+isin {frac {varphi +2pi k}{n}}right),\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de027af4df44c3088e8fbf4998b3845c1f25e961)






![{displaystyle left[{hat {x}},{hat {p}}_{x}right]={hat {x}}{hat {p}}_{x}-{hat {p}}_{x}{hat {x}}=ihbar }](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c4e43ffe38509c03e051f2757ad8505dd7982f)



















