Условие задачи:
Какая установится температура воды после смешивания 39 л воды при 20° C и 21 л при 60° C?
Задача №5.1.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=39) л, (t_1=20^circ) C, (V_2=21) л, (t_2=60^circ) C, (t-?)
Решение задачи:
Понятно, что объем воды (V_2), имеющий более высокую температуру (t_2), после смешения передаст часть теплоты объему воды (V_1) c более низкой температурой (t_1), которая за счёт этой теплоты нагреется. В конце вся вода будет иметь некоторую температуру (t).
Запишем уравнение теплового баланса:
[{Q_1} = {Q_2}]
Здесь (Q_1) – количество теплоты, полученное водой объемом (V_1) при нагревании до температуры (t), а (Q_2) – количество теплоты, отданное водой объемом (V_2) при охлаждении до температуры (t).
[c{m_1}left( {t – {t_1}} right) = c{m_2}left( {{t_2} – t} right)]
Выразим массы как произведение плотности воды на объем:
[crho {V_1}left( {t – {t_1}} right) = crho {V_2}left( {{t_2} – t} right)]
[{V_1}left( {t – {t_1}} right) = {V_2}left( {{t_2} – t} right)]
Теперь раскроем скобки, в одной части равенства соберем все члены с множителем (t), вынесем его за скобки и выразим его.
[{V_1}t – {V_1}{t_1} = {V_2}{t_2} – {V_2}t]
[{V_1}t + {V_2}t = {V_2}{t_2} + {V_1}{t_1}]
[tleft( {{V_1} + {V_2}} right) = {V_2}{t_2} + {V_1}{t_1}]
[t = frac{{{V_1}{t_1} + {V_2}{t_2}}}{{{V_1} + {V_2}}}]
Переводить объемы и температуры в систему СИ нет смысла – ответ мы получим в градусах Цельсия.
[t = frac{{39 cdot 20 + 21 cdot 60}}{{39 + 21}} = 34^circ;C = 307;К]
Ответ: 307 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.1.5 Сколько тепла было передано льдинке массой 50 г, если она нагрелась на 3 К?
5.1.7 Железный стержень массой 5 кг, нагретый до 550 C, опускается в воду. Сколько теплоты
5.1.8 Сколько литров воды при 100 C нужно добавить к воде при 20 C, чтобы получить
Определить температуру воды установившуюся после смешивания 39 л при 20°С и 21 л при 60°С.
Если можно расписать решение подробно : ).
На этой странице сайта, в категории Физика размещен ответ на вопрос
Определить температуру воды установившуюся после смешивания 39 л при 20°С и 21 л при 60°С?. По уровню сложности вопрос рассчитан на учащихся
5 – 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками.
Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.
Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.
Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.
Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!
Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г
IV. Тест по русскому языку
1. В тексте про белых медведей больше всего предложений:
а) повествовательных; б) вопросительных
2. Восклицательное предложение находится:
а) в начале текста; б) в конце текста
3. Вопросительное предложение находится
а) в начале текста; б) в конце текста
4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются
а) родственными словами; б) однородными членами предложения
5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:
а) I спряжения; б) II спряжения
6. Эти глаголы стоят в форме:
а) настоящего времени; б) будущего времени; в) прошедшего времени
7. Эти глаголы стоят в форме:
а) единственного числа; б) множественного числа
8. Эти глаголы стоят в форме:
а) 1-го лица; б) 2-го лица; в) 3-го лица; г)нельзя определить лицо
9. Эти глаголы стоят в форме:
а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род
10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:
а) два слова; б) три слова
11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж:
а) Р.п.; б) В.п.
Онлайн калькулятор поможет рассчитать температуру после смешивания воды, определить изменение температуры холодной и горячей жидкости при смешивании объемов в одной емкости.
Смешивание воды разной температуры – это процесс изменения температуры воды при её объединении в общий объем.
Формула определения итоговой температуры смеси: Tобщ = (Vгоряч × Tгоряч + Vхолодн × Tхолодн) / (Vгоряч + Vхолодн)
T – температура жидкости;
V – объём жидкости.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
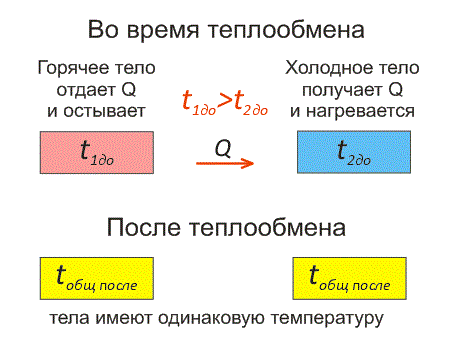
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.

Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
