In this platform, you have to learn about how to find the Perimeter and Area of irregular figures. An irregular shape will be of any size and length. We will see irregular shapes all around us, for example, a diamond shape, a kite, a leaf, a flower, etc. The Area of irregular shapes will be the space occupied by the shape which is measured in square units. The Perimeter of irregular shapes is by adding all the lengths of their sides. Any shape whose sides and angles are not of equal length is named an irregular shape.
On this page, you will learn about the definition of the area and the perimeter of irregular figures, how to find the area and perimeter of irregular figures, some solved example problems, and so on.
Read More:
- Area and Perimeter of Combined Figures
- Area of a Circular Ring
- Worksheet on Area of the Path
Irregular Figures – Definition
The Irregular Figures are defined as a figure that is not a standard geometric shape. An irregular shape is simply a shape where every single side is not the same length. But some irregular figures are made up of two or further standard geometric shapes. If the shape is irregular then it has some angles that are not all the same size. Based on the number of sides or corners we can decide that irregular figure.
How to find Perimeter and Area of Irregular Figures?
The following are the ways for finding the area and perimeter of irregular figures:
How to find Area of Irregular Shapes or Figures?
- Step 1: First, divide the compound shape into a basic regular shape.
- Step 2: Next, find each basic shape area separately.
- Step 3: Now Add all the areas of basic shapes together.
- Step 4: Now, write the final answer in square units.
How to find the Perimeter of Irregular Figures?
To find the perimeter of the irregular figure, we can simply add up each of its outer sides length of a shape. To find the perimeter of any shape like rectangle, square, and so on you have to add all the lengths of four sides. Consider ‘A’ is in this case the length of the rectangle and ‘B’ is the width of the rectangle.
See More:
- Plane Figures
- Solid Figures
- Rectilinear Figures
Perimeter and Area of Irregular Shapes Examples
Example 1:
The Irregular Figure is given below. Find the area of that figure?

Solution:
As given in the question, the irregular figure is given.
Now, we can break the given irregular figure. After separating the figure we have two rectangle blocks.
Next, we will find the area of those two rectangles. The area of the irregular figure is the sum of the areas of two rectangles.
The width of one block is 12 and the length of the block is 4.
Next, the width of the other rectangle is 2, but its length is not given. By using the upper rectangle length we can find the length of the lower rectangle. So the right side of the figure is the length of the upper rectangle block plus the length of the lower rectangle block.
Since the total length is 10 units, the right side of the upper rectangle is 4 units long. So the length of the lower rectangle will be 6 units.
So the area of the figure is,
The Area of the figure is the Area of the upper rectangle + Area of the lower rectangle
We know that the Area of the rectangle is, length x width (or) breadth.
So, the area of a figure is , lw + lw = 12(4) + 2(6).
Area of the figure is = 48 + 12 = 60sq.units.
Thus, the total area of the figure is 60 square units.
Example 2:
Find the area of the below-given irregular figure?

Solution:
As given in the question, the given figure is an irregular figure.
Now, we can break the given irregular figure. After separating the figure, we have two blocks one is a triangle block and another one is a rectangle.
Next, we will find the area of the irregular figure. The area of the irregular figure is the sum of the areas of two rectangles.
The rectangle has a length of 8 units and a width of 4 units. We need to find the base and height of the triangle.
On both sides of the rectangle 4units, the perpendicular side of the triangle is 3 units, which is 7- 4 = 3units.
Next, the length of the rectangle is 8units, so the base of the triangle is 3units, which is 8-5= 4units.
Now, we can add the areas then we get the area of the irregular figure.
So, the Area of the figure is the Area of the rectangle + the Area of the triangle.
We know the formulas, the area of the rectangle is, length x width (or) breadth.
The area of the triangle is 1/2bh.
So, the area of a figure is , lw + 1/2bh = 8(4) + 1/2(3)(3).
Area of the figure is = 32 + 4.5 = 36.5sq.units.
Hence, the total area of the given irregular figure is 36.5square units.
Example 3:
The figure is given below. Find the perimeter of the given Pentagon figure?

Solution:
As given in the question, the irregular shape figure is given.
This shape is a pentagon because it has five sides. Even though two of its sides are both 13m, it is an irregular pentagon because not all of its sides are the same length.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up the five side lengths.
We make the calculation easier by starting with the largest sides and also looking for number bonds to ten.
The two largest sides are 13m and 13m. These add together to make 26m.
The remaining three sides are 2m, 8m, and 9m. Now the value is 2m + 8m+ 9m = 19m.
Now, adding those two values are, 26m + 19m = 45m.
Thus, the perimeter of this given irregular pentagon is 45m.
Example 4:
Find the perimeter of the below-given figure?

Solution:
As given in the question, the figure is an irregular figure.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up all side lengths.
We make the mathematics easier by starting with the largest sides and also looking for number bonds to ten.
The largest sides is 10 cm. The remaining sides are 2cm, 2cm, 8cm, 8cm and 4 cm. Then the value is 2 cm + 2cm + 8 cm+ 8 cm + 4cm= 24cm.
Now, adding those two values are, 10 cm + 24 cm = 34 cm.
Thus, the perimeter of this given irregular figure is 34 cm.
FAQ’s on Perimeter and Area of Irregular Figures
1. What is meant by Irregular Figures?
An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or further standard geometric shapes.
2. Define Area of Irregular Figures?
The area of irregular shapes is defined as the quantity of space that is covered by an irregular shape. Irregular shapes are those shapes that do not have equal sides or equal angles. The unit for the area of an irregular shape is expressed in terms of square units, for representative, m2, cm2, in2, or feet2.
3. How to find the perimeter of Irregular Figures?
In order to calculate the perimeter of an irregular polygon we use the following two steps:
- Step 1: Note the length of each side of the given polygon.
- Step 2: Once the length of all the sides is acquired, then the perimeter is adding all the sides length.
Периметр, внешнее измерение замкнутой двумерной формы, зависит от количества и размеров сторон этой формы. Треугольники, квадраты, прямоугольники, многоугольники и круги – это обычные двумерные фигуры, которые используют простые методы для расчета периметра. Определение периметра помогает в идентификации формы, а меру периметра можно использовать в других расчетах.
-
Чтобы найти периметр любой формы, найдите меры всех сторон и добавьте их.
Добавьте три стороны треугольника, чтобы найти периметр. Например, если три стороны треугольника имеют размеры 2, 2 и 1, 5 дюйма, периметр равен 5, 5 дюйма.
Умножьте одну сторону квадрата на 4, чтобы найти периметр. Например, если одна сторона измеряет 2 дюйма, то 2 дюйма, умноженные на 4, равняются периметру 8 дюймов.
Умножьте длину прямоугольника на 2, умножьте ширину на 2, а затем добавьте их, чтобы найти периметр. Например, если ширина прямоугольника составляет 1 дюйм, а длина – 2 дюйма, умножение 1 дюйма на 2 приводит к 2 дюймам, умножение 2 дюймов на 2 приводит к 4 дюймам, а добавление двух чисел приводит к периметру 6 дюймов.
Умножьте длину одной стороны правильного многоугольника на количество сторон, чтобы найти его периметр. У правильных многоугольников есть стороны одинакового размера. Например, если фигура представляет собой правильный пятиугольник, который имеет 5 сторон, с длиной стороны 4 дюйма, то умножение 4 дюймов на 5 приводит к периметру 20 дюймов.
Измерьте каждую сторону неправильного многоугольника и добавьте стороны, чтобы найти периметр. Нерегулярные многоугольники имеют стороны разной длины. Нерегулярный шестиугольник имеет шесть сторон, которые в этом примере имеют размеры 3, 3, 4, 5, 2 и 2, 5 дюйма. Добавление этих сторон приводит к периметру 19, 5 дюймов.
Измерьте диаметр круга – расстояние между двумя противоположными точками по периметру круга – и умножьте это измерение на математическую константу pi, оцененную приблизительно в 3, 142, чтобы найти периметр круга, который обычно называют окружностью. Например, диаметр 10 дюймов, умноженный на пи, создает окружность приблизительно 31, 42 дюйма.
подсказки
Правила как найти периметр площадь. Калькулятор вычисления периметра и площади геометрических фигур
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Круг
Частные случаи
Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
- — пентагон;
- — гексагон;
- восемь — октагон;
- двенадцать — додекагон.
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a 2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр.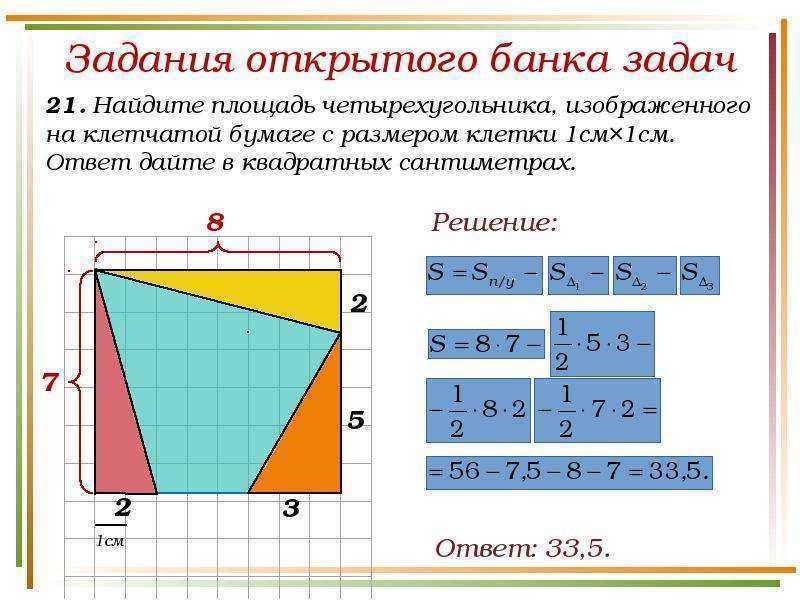 Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
Таким образом, нам понадобится 4 м бахромы для отделки платка.
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.
Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.
Определение периметра
Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Измеряем периметр
Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Круг, квадрат, равносторонний треугольник
Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).
Площадь и периметр – две численные характеристики, часто используемые в геометрии.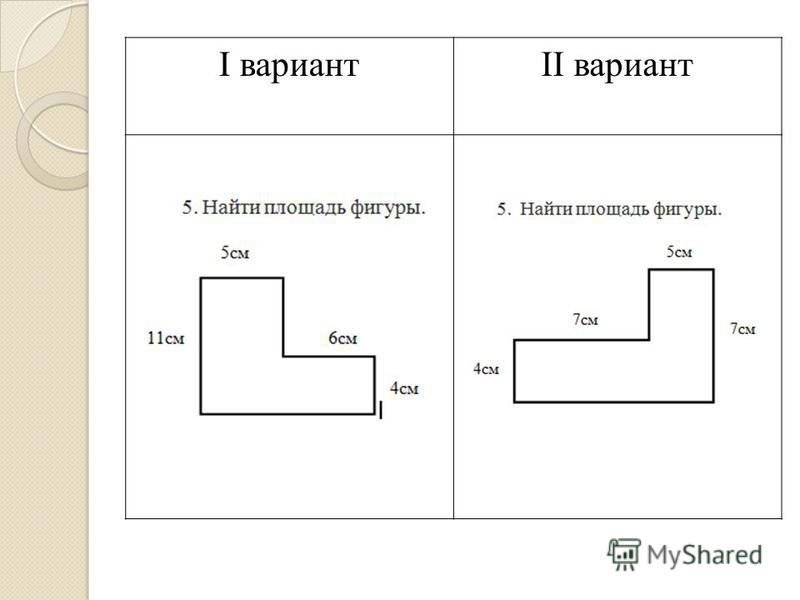 Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).
Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).
Определение
Площадь
– величина, характеризующая размер поверхности, которую занимает геометрическая фигура.
Периметр
– размер границ (контура) геометрической фигуры.
Понятия применимы для каждой геометрической фигуры и выражаются в различных единицах. Расчет периметра и площади определяется единицами измерения параметров, используемых для их вычисления: длин сторон, диаметра, высоты. В геометрии указанные параметры чаще всего измеряются в мм, см, м.
Сравнение
Периметр обозначается заглавной буквой P
, используется при измерении многоугольников и определяется как сумма длин его сторон. Площадь обозначается буквой S
и может быть использована как численная характеристика поверхности, имеющей различный контур, в том числе искривленный. Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.
Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.
Простейший случай – квадрат. Длины его сторон равны, поэтому для вычисления периметра достаточно умножить одну сторону на 4. Формула выглядит так:
Р = a + a + a + a = a х 4, где а – сторона квадрата.
Для вычисления площади квадрата используется другая формула:
S = a х a = a 2 .
Выводы сайт
- В случае с периметром речь идет о размерах контура, в случае площади – о размерах поверхности.
- Единица измерения S определяется как квадрат единицы измерения характеристик поверхности, для периметра она равна единице измерения сторон многоугольника.
- Периметр характеризует размеры многоугольника, площадь – более широкое понятие, применимое для поверхностей с различным контуром.
- Формулы для определения площадей сильно различаются, а для определения периметра достаточно просто сложить стороны многоугольника.
Не многие формулы из курса школьной математики мы применяем в повседневной жизни.
Однако, есть такие уравнения, которые имеют применение, если не на регулярной основе, то время от времени. Одна из таких формул — вычисление периметра фигуры.
Что такое периметр?
Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.
Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Прямоугольником следует называть геометрическую фигуру, которая состоит из четырех сторон разной длины и три угла у которой прямые. При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.
Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны — равнобедренного — упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Прикладное значение периметра
Вычисление периметра в повседневной жизни применяется во многих сферах, но чаще всего при выполнении строительных, геодезических, топографических, архитектурных, планировочных работах. Но перечисленным сферы применения вычисления периметра, конечно же, не ограничиваются.
Например, при выполнении геодезических и топографических работ очень часто возникает необходимость посчитать периметр границ определенного участка. Но на практике участки редко имеют правильную форму. Поэтому вычисление длины периметра происходит по формуле расчета суммы длин всех сторон участка.
Но на практике участки редко имеют правильную форму. Поэтому вычисление длины периметра происходит по формуле расчета суммы длин всех сторон участка.
Необходимость вычисления периметра участка очень часто обусловлена тем, что необходимо знать, какое количество материала потребуется для установки ограждений. Даже простой приусадебный участок нуждается в измерении периметра для того, чтобы грамотно обнести его забором.
Измерительные приборы на местности
Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант — это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр. Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.
Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.
Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника
— сумма длин всех его сторон. Формула для подсчета периметра прямоугольника
: , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется
полупериметром
. Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
Умение применять знания в нахождении периметра и площади геометрических фигур
Построение урока:
- Организация и мотивация учащихся к
деятельности на уроке. - Организация восприятия нового материала на
основе наглядного материала - Организация осмысления.
- Первичная проверка понимания нового материала.
- Организация первичного закрепления и
самостоятельный анализ учебной информации. - Применение полученных знаний на практикуме.
Цели урока:
- Обучающая. Обеспечить усвоение учащимися
нахождения площади и периметра геометрических
фигур;
визуального восприятия материала на уроке;
осмыслено понимать , что такое площадь и
периметр.
2. Развивающая. Использовать на уроке
развивающие упражнения, активизировать
мыслительную деятельность школьников.
3. Воспитательная. Обеспечить развитие
ценностно-смысловой культуры учащихся;
мотивации на умение правильно достигать
поставленной цели —
совпадение ожидания и результата.
Оборудование:
- М.И.Моро и др. “Математика” — учебник для 3
класса начальной школы, 1 часть. - Рабочая тетрадь по математике.
- Ручка, линейка, простой карандаш, треугольник,
ножницы. - Модели геометрических фигур для нахождения
площади. - Над доской плакаты с формулами нахождения
площади и периметра.
Средства обучения:
- Дидактический материал.
- Наглядные пособия.
Приемы обучения:
- Сравнение предметов.
- Сопоставления способов нахождения площади
одной и той же фигуры.
Ход урока.
1. Организационный момент и сообщение темы
урока.
Учитель: Здравствуйте, ребята. Сегодня мы
продолжим изучение большой темы под названием
“Площадь и периметр”. Тема нашего урока сегодня
:“Умение применять знания в нахождении
периметра и площади сложной фигуры”.
Сложная
фигура – это геометрическая фигура, состоящая из
нескольких простейших фигур. Сначала, повторим
то, что мы с вами изучили на прошлых уроках.
II. Устный счет.
Задачи на развитие.
Учитель: Найдите площадь данной фигуры, если
сторона квадрата 1 см.
Фигура изображена на доске.
Ученик: Если 1 квадрат имеет площадь 1 см2,
а квадратов изображено 5, то площадь этой фигуры
равна 5 см2.
Учитель: Правильно. Следующее задание.
Уберите 3 палочки, чтобы осталось 3 таких
квадрата.
Ученик выходит к доске и убирает 3 палочки.
Учитель: Уберите 4 палочки, чтобы осталось 3
таких же квадрата.
Ученик выходит к доске и убирает 4 палочки.
Решение.
III. Работа по теме урока
Учитель: Какие геометрические фигуры вы уже
знаете?
Ученик: Прямоугольник.
Ученик: Квадрат.
Учитель: Правильно. Что мы знаем о квадрате?
Ученик: У квадрата 4 стороны и 4 угла.
Учитель: Правильно. Каким свойством обладают
стороны квадрата?
Ученик: Они равны.
Учитель: Правильно. А какие углы у квадрата?
Ученик: Они прямые.
Учитель: С помощью чего мы можем построить
прямой угол?
Ученик: С помощью треугольника.
Учитель: Давайте построим квадрат со
стороной 4 см в вашей тетради. С помощью каких
инструментов мы будем чертить квадрат?
Ученик: С помощью линейки, карандаша и
треугольника.
Ученики в тетрадях строят квадрат и
раскрашивают его.
Учитель: Эта геометрическая фигура. Как найти
периметр и площадь этого квадрата?
Ученик: Периметр – это сумма всех его сторон.
Сторон у квадрата 4. Значит, 4 сложим 4 раза.
Учитель: Как это записать?
Ученики делают запись в тетради: “Найти
площадь фигуры F1”.
Ученика вызывают к доске, и он пишет: Р = 4 + 4 + 4 +
4 = 16 (см)
Ученики делают запись в тетради.
Учитель: В каких единицах еще измеряется
периметр?
Ученик: В сантиметрах, в миллиметрах, в
метрах, в дециметрах, в километрах.
Учитель: Молодец! Как еще можно записать
периметр?
Ученик: С помощью умножения.
Ученик записывает на доске: Р = 4 · 4 = 16 (см)
Ученики записывают в тетради.
Учитель: А чему равна площадь квадрата?
Ученик: Длину квадрата умножаем на его
ширину. Так как стороны у квадрата равны, то
S = 4 · 4 = 16 (см2)
Ученики делают запись в тетрадке и
записывают — “Ответ: S = 16 см2”.
Учитель: Какие еще единицы измерения площади
вы знаете?
Ученик: квадратный сантиметр, квадратный
дециметр, квадратный метр, квадратный миллиметр.
Учитель: А теперь усложним задачу. Перед вами
лежит карточка.
На этой карточке изображен квадрат такой же,
что и у вас в тетрадке. В середине этого квадрата –
еще один квадрат со стороной 2 см. Сейчас вы
возьмете ножницы и вырежете аккуратно этот
маленький квадрат.
Ученики выполняют эту работу и делают запись
в тетрадке: “Найти площадь фигуры F2”.
Учитель: У нас получилась фигура “с окошком” –
F2. Как можно найти площадь этой интересной
фигуры? Площадь квадрата уже известна и равна 16
см2.
Ученик: Нужно найти площадь маленького
квадратика со стороной 2 см.
Ученик выходит к доске и записывает – S2 = 2 · 2 =
4 (см2)
Ученики делают запись в тетрадке
Учитель: Правильно. А что можно сделать
дальше? Мы вырезали этот квадратик и из большого
квадратика, вынули его. Как найти площадь нашей
фигуры?
Ученик: Из площади большого квадратика
вычесть площадь маленького.
Учитель: Правильно.
Ученик записывает на доске – S = S1 – S2 = 16 – 4 = 12
(см2)
Ученики делают запись в тетрадке.
Учитель: Внимательно посмотрите на эту
фигурку и скажите, как еще можно измерить
площадь? Можно ли эту фигуру как-то разрезать,
чтобы получить фигуры, уже знакомые вам?
Ученики думают и говорят разные варианты.
Один из вариантов оказался очень интересным.
Ученик: Можно так разрезать , чтобы
получились прямоугольники и показывает на доске
, как это можно сделать.
Учитель: Молодец! А что дальше?
Ученик: А дальше можно найти площади этих
прямоугольников и сложить, потому, что наша
фигурка тоже сложена из этих прямоугольников.
Ученики разрезают фигуру, как показано на
доске.
Учитель: А как находится площадь
прямоугольника?
Ученик: Нужно длину умножить на ширину.
Учитель: У вас получилось четыре фигуры. Что
можно сказать про них?
Ученик: Две фигурки, как близнецы –
одинаковые, и вторые две – тоже одинаковые.
Можно найти площадь одной фигуры и умножить на
2.
Ученик решает на доске: S1 = 1 · 4 = 4 (см2)
S2 = 1 · 2 = 2 (см2)
S = 2 · S1 + 2 · S2 = 2 · 4 + 2 · 2 = 8 + 4 = 12(см2)
Учитель: Молодец! У нас получилась то же
значение площади, что и раньше.
Ученики пишут в тетрадке – “Ответ: S = 12 см2.”
Учитель: Вы, наверное, устали?
Настало время отдыхать.
Предлагаю усталость
Физкультминуткой снять.
IV. Физкультминутка.
Каждый день по утрам
Делаем зарядку (ходьба на месте).
Очень нравится нам делать по порядку:
Весело шагать (ходьба),
Руки поднимать (руки вверх),
Приседать и вставать (приседание 4-6 раз),
Прыгать и скакать (10 прыжков).
Учитель: А теперь сели за парты и
посмотрите на следующую модель. Фигура F3
Как найти площадь этой интересной фигуры?
Ученик: Треугольник, который выступает
можно отрезать и подставить в ту часть, где
треугольник “уходит” внутрь.
Учитель: Давайте возьмем ножницы, отрежем
треугольник и подставим в верхнюю часть.
Что за фигура у нас получилась?
Ученик: Прямоугольник!
Учитель: Как найти площадь этого
прямоугольника,
Если стороны нам неизвестны.
Ученик: Мы можем взять линейку и измерить
длину и ширину прямоугольника.
Ученики делают запись – “Найти площадь
фигуры F3”.
Ученики линейкой измеряют длину и ширину.
Получается длина, а = 6 см, ширина в = 2 см.
Ученик: Площадь данной фигуры равна S = 6 · 2 = 12
(см2).
Ученики делают запись в тетрадке и
записывают – “Ответ: S = 12 см2.
Учитель: Но это еще не все. Перед вами
следующая фигура. Необходимо найти ее площадь.
Что за фигура перед вами?
Ученик: Треугольник. Но площадь
треугольника
мы не умеем находить!
Учитель: Это правда. Из этого треугольника
сделаем прямоугольник. Я вам подскажу. Фигура F4
Сначала мы этот треугольник сложим пополам
Ученики: Мы поняли! Правую
сторону переворачиваем.
Получится прямоугольник.
Ученик: С помощью линейки измеряем
длину а и ширину в, и по S = а· в,
находим площадь.
Учитель: Если мы при измерении, мы
получим , что длина
будет выражена в мм, а ширина в см,
что нам делать?
Ученик: Обязательно длину и ширину перевести
в одну единицу измерения.
Ученики записывают в тетрадке: “Найти
площадь фигуры F4”.
V. Работа в парах.
Учитель: А теперь я предлагаю поработать в
паре. Вас за партой двое. Один ученик ( I вариант)
находит периметр данной фигуры, а второй ( II
вариант )- площадь.
Для этого начертим в тетради эту фигуру. После
того, как вы выполните задание, поменяетесь
тетрадями и проверите результаты друг у друга.
Ученики выполняют задание и результаты
записывают в тетрадь.
Учитель: Что у вас получилось?
Ученик: Квадрат со стороной 3 см. Р = 3 · 4 = 12(см)
S = 3 · 3 = 9 (см2) 3 см
Ученики записывают: “Ответ: P = 12 см, S = 9 см2.
Учитель: Молодцы! А теперь я вам предлагаю
поработать самостоятельно.
Найти площадь следующей фигуры. Она лежит перед
вами.
VI. Самостоятельная работа по закреплению
изученного материала.
Учитель раздает заранее заготовленные
фигуры.
Ученики самостоятельно, без помощи учителя,
разрезают эту фигуры, получают три
прямоугольника.
Ученики делают запись: “ Найти площадь
фигуры F5”.
Ученики находят S1 = 4 · 3 = 12(см2), S2 = 2 · 1 =
2(см2), потом находят площадь данной фигуры: S
= S1 + S2 + S2 = 12 + 2 + 2 = 16 (см2) и делают запись в
тетради, затем
записывают: “Ответ: S = 16 см2”.
Учитель: Понравился урок?
Ученики: Да.
Учитель: Что вы нового узнали на этом уроке?
Ученик: Мы научились находить площадь и
периметр сложных фигур. Это оказалось очень
просто. Нужно немного подумать и эту фигуру
перестроить или переделать в ту, периметр и
площадь, которой, мы уже умеем находить.
Учитель: Я очень рада, что вам понравилось.
Дома еще раз повторить формулы нахождения
периметра и площади квадрата и прямоугольника;
вспомнить, как переводить одну единицу
в другую. Сегодня хорошо отвечали следующие
ученики . . .
Учитель выставляет оценки.
VII. Домашнее задание: учебник стр. 77 № 8.
Периметр составных фигур: составные прямоугольники
- Периметр — это общее расстояние по внешней стороне фигуры.
- Два зеленых
горизонтальные Идут слева направо по этому экрану.
сторон должны быть такой же длины, как и одна длинная красная сторона.
- Два зеленых
по вертикали Идут сверху вниз на этом экране.
сторон должны быть такой же длины, как и одна более длинная красная сторона.
- Мы можем использовать этот факт, чтобы найти недостающие стороны, прежде чем мы добавим их, чтобы найти периметр.
- Отсутствующий
Вертикальный переход сверху вниз на этом экране.
сторона плюс 6 см должны равняться 9 см. Недостающая вертикальная сторона составляет 3 см.
- Отсутствующий
по горизонтали Идет слева направо по этому экрану. Сторона
плюс 4 см должны равняться 12 см. Недостающая горизонтальная сторона равна 8 см.
- Мы находим периметр, складывая внешние края нашей фигуры.
- 8 см + 12 см = 20 см и 4 см + 6 см = 10 см. Мы можем сложить эти четыре стороны, чтобы получить 30 см
- . Мы складываем оставшиеся две стороны до 30 см. 30 см + 9 см = 39 см, а затем 39 см + 3 см = 42 см.
- Периметр этой сложной формы составляет 42 см.
Периметр сложных фигур Рабочие листы и ответы
Составная фигура (или составная фигура) — это более сложная фигура, равная 9. 0045 состоит из двух или более простых фигур .
Мы рассмотрим составные фигуры, сделанные специально из двух объединенных прямоугольников.
Нас могут попросить найти периметр сложной формы, подобной приведенной выше.
Например:
Чтобы найти периметр , мы просто складываем длины каждого внешнего ребра .
При добавлении сторон может быть полезно обращать внимание на числовые связи .
Например, 7 + 3 = 10.
Сумма всех внешних сторон равна 36, поэтому периметр равен 36 см .
В некоторых вопросах периметра длины некоторых сторон могут отсутствовать .
Например:
Длина двух сторон этой прямоугольной составной формы равна , а отсутствует.
Мы можем использовать другие длины сторон, чтобы выяснить, каковы эти пропущенные значения.
Мы начнем с отсутствующей
вертикали, идущей сверху вниз на этом экране.
длина.
Чтобы найти его значение, мы рассмотрим другие длины по вертикали.
Глядя на форму, сторона длиной 9 см является такой же, как , обе стороны отсутствуют плюс сторона длиной 6 см .
9 см = ? см + 6 см
Таким образом, мы можем найти недостающую длину на вычитая 6 см из 9 см.
9 – 6 = 3
Итак, недостающая длина стороны 3 см .
Далее мы найдем недостающие
по горизонтали, двигаясь слева направо по этому экрану.
длина.
Чтобы найти недостающую горизонтальную длину, мы посмотрим на значения других горизонтальных длин.
Глядя на составную форму, сторона длиной 12 см — это , то же самое, что и , обе стороны — недостающая сторона плюс сторона длиной 4 см .
12 см = 4 см + ? см
Таким образом, мы можем найти недостающую длину, если вычтем 6 см из 9 см.
12 – 4 = 8
Итак, недостающая длина составляет 8 см .
Теперь, когда мы знаем длины всех сторон, мы можем найти периметр составной фигуры.
Опять же, может быть полезно искать число облигаций , чтобы упростить расчет периметра.
Например, 12 + 8 = 20.
Всего 42, поэтому периметр нашей составной фигуры равен 42 см .
Теперь попробуйте наш урок Вычисление площади прямоугольников и квадратов , где мы научимся находить площадь прямоугольников, включая квадраты.
5.18: Площадь и периметр составных фигур
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5002
Найдите площадь и периметр фигур, состоящих из двух или более обычных фигур.
Площадь составных фигур
Периметр — это расстояние вокруг фигуры. К периметру любой фигуры должна быть привязана единица измерения. Если не указаны конкретные единицы измерения (футы, дюймы, сантиметры и т. д.), напишите «единицы».
Площадь — это пространство внутри фигуры. Если две фигуры конгруэнтны, то они имеют одинаковую площадь ( постулат конгруэнтных площадей ).
Рисунок (PageIndex{1})
Составная фигура — это фигура, состоящая из других фигур. Чтобы найти площадь такой фигуры, просто найдите площадь каждой части и сложите их.
Постулат сложения площадей: Если фигура состоит из двух или более частей, не перекрывающих друг друга, то площадь фигуры равна сумме площадей частей.
Рассмотрим простой дом, нарисованный в виде треугольника поверх квадрата. Как найти площадь этой составной фигуры?
Пример (PageIndex{1})
Найдите площадь на рисунке ниже. 2). 92).
Обзор
Используйте картинку ниже для ответов на вопросы 1-4. Составная форма состоит из квадрата внутри квадрата.
Рисунок (PageIndex{6})
- Найдите площадь внешнего квадрата.
- Найдите площадь одного серого треугольника.
- Найдите площадь всех четырех серых треугольников.
- Найдите площадь внутреннего квадрата.
Найдите площади фигур ниже. Можно предположить, что все стороны перпендикулярны.
- Рисунок (PageIndex{7})
- Рисунок (PageIndex{8})
Найдите площади составных фигур.
- Рисунок (PageIndex{9})
- Рисунок (PageIndex{10})
- Рисунок (PageIndex{11})
- Рисунок (PageIndex{12})
- Рисунок (PageIndex{13})
- Рисунок (PageIndex{14})
Используйте рисунок, чтобы ответить на вопросы.
Рисунок (PageIndex{15})
- Какова площадь квадрата?
- Какова площадь треугольника слева?
- Какова площадь составной фигуры?
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 10.6.
Словарь
| Срок | Определение |
|---|---|
| площадь | Количество места внутри фигуры. Площадь измеряется в квадратных единицах. |
| составная форма | Фигура, состоящая из других фигур. |
| периметр | Расстояние вокруг фигуры. К периметру любой фигуры должна быть привязана единица измерения. Если не указаны конкретные единицы измерения (футы, дюймы, сантиметры и т. No related posts. |
Не совсем понятно, зачем все предыдущие ответившие упорно ищут и длину, и ширину минимального сегмента сетки, ведь периметр третьей фигуры можно найти и без этого.
По аналогии с предыдущими ответами, обозначил за Х длину и за У высоту самого маленького сегмента сетки и тогда периметры всех трёх фигур можно выразить следующим образом:
6Х + 2У = 56 – периметр фигуры А
4Х + 6У = 56 – периметр фигуры В
6У + 2Х = ? – искомый периметр фигуры С
Далее, чтобы избавиться от одной из переменных, из первого равенства выразим У ( или лучше сразу – 6У ) и найденное значение подставим во второе равенство:
6Х + 2У = 56
4Х + 6У = 56
2У = 56 – 6Х или даже ( 6У = 168 – 18Х )
4Х + ( 168 – 18Х ) = 56 из этого выражения найдём значение Х:
4Х + 168 – 18Х = 56
18Х – 4Х = 168 – 56
14Х = 112
Х = 8
Далее вернёмся ко второй формуле, периметру фигуры В и выразим из неё периметр фигуры С:
4Х + 6У = 56
6У + 2Х = 56 – 2Х и уже в правую часть этого выражения подставляем найденное выше значение Х:
6У + 2Х = 56 – 2Х = 56 – 2*8 = 56 – 16 = 40
6У + 2Х = 40 – периметр фигуры С равен 40 см, что и будет ответом на эту задачу.
Периметр сложной фигуры
Танцующая Смерть
Ученик
(93),
закрыт
4 года назад
Скажите, а как найти периметр такой фигуры? Все ведь стороны не получится сложить здесь, две стороны боковые (рядом с 4 метрами) без размера 
