Geometry is a field of study of shapes and structures. It gives a brief explanation of the different shapes and their properties. Geometry gives defined formulas for the calculation of parameters of these flat or solid shapes. These formulas are different for each shape and are derived according to their dimensions.
In the given article we have studied an eight-sided polygon viz. octagon along with its properties. The content of the article also gives the formula for the determination of the area of an octagon. Some sample numerical problems are included along with their solutions for reference.
Octagon
Octagon is a geometrical figure with 8 sides and 8 angles. The word octagon itself means “eight-sided”. An octagon is one of the plane figures or a polygon having eight sides. The interior angle of regular polygon measures to be 135 degrees each. And the exterior angles measure 45 degrees. All the midpoints of the sides of an octagon meet at its center and all the diagonals have the same length.
Octagon is a two-dimensional flat shape with eight sides and eight angles. It is a polygon made up of the joining of line segments. It has 8 sides and the sides are denoted by the letter ‘a’.

Octagon
Properties of an Octagon
- A regular polygon has eight sides.
- A polygon has eight equal angles.
- A regular polygon consists of 20 diagonals that meet at the center.
- Each interior angle measures to be 135°. And, the sum of all the interior angles equals 1080°.
- Each exterior angle measures to be 45°. And, the sum of all the exterior angles equals 360°.
Area of An Octagon
In geometry, there are set formulas for calculating the parameters of the shapes. The area of an octagon with its side length ‘a’ is given by the formula
Area of an Octagon = 2a2(1 + √2)
Where,
a is the length of the side or edge
For Example:
If an octagon with a length of 8cm is given, its area can be calculated by
Area of an Octagon = 2a2(1 + √2)
A = 2(8)2(1 + √2)
A = 309.01cm2
The formula from the calculation of the area of an octagon can be derived by four different methods. These methods are briefly derived along with their diagrams.
- Method I
A regular octagon can be seen as a collection of eight small isosceles triangles sharing a common apex point. Hence, the area of a regular octagon can be calculated by determining the area of one of the triangles and multiplying it by 8.
Mathematically the area of the octagon is given by,
Area of octagon = 8 × Area of the triangle
We have been given an octagon with eight isosceles triangles. Consider one of the triangles from the octagon and draw a line perpendicular from its base to apex to form right angles.

Here, a is the length of the side of the octagon and OZ is the height of the triangle.
Now,
tan2θ = 1 – cos2θ/1 + cos2θ [SINCE, 2sin2θ = 1 – cos2θ and 2cos2θ = 1 + cos2θ]
tan2(45/2) = 1 – cos45°/1 + cos45°
tan2(45/2) = 1 – 1/√2/1 + 1/√2
tan(45/2) = √2 – 1
ZY/OZ = √2 – 1
OZ = a/2/√2 – 1
OZ = a/2 (1 + √2)
Area of triangle XOY =1 × XY × Oz
1/2 a × a/2 (1 + √2)
a2/4 (1 + √2)
Now, Area of octagon = 8 × area of triangle
Area of octagon = 8 × a2/4 (1 + √2)
Area of octagon = 2a2(1 + √2)
- Method II
When a regular octagon is divided into non-overlapping parts then, an octagon can be subdivided into a square, four rectangles, and four isosceles right-angled triangles.

Here, a is the length of the side of the octagon.
Now, the area of the square, Asq = a2
Then, the area of the triangle = Atr = 1/2 × x
Where,
x = √(a2/2)
Since, in a right-angled triangle, b2 + h2 = square of hypotenuse = side of octagon
Area of the rectangle, Arec = x × a
Then the combined area of the given octagon will be,
Area of octagon = Asq + 4 × Arec + 4 × Atr
- Method III
An octagon can be taken as a square with four triangles attached from each corner of the square.

hence, the side of the octagon ‘a’ with be the hypotenuse of the given triangle.
A2 = 2x2
Let the length of the side of square will be 1 = a + 2x = a + 2√(a2/2)
[Since, x = √(a2/2)]
The combined area of the octagon will be,
Area = (1 × 1) – 4 (1/2 x. x)
- Method IV
A regular octagon can also be conceptualized as a composition of 4 kites.

Let the diagonals of the kites be d and w and the area will be,
Area of kite = d × w/2
Let us take the kite AHOB from the above diagram
∠HOB = 2π and HO = BO = r
And, HB = √2r
Since AO = r
Area of AHOB = AO × HB × 2
√(2r)2/2
Area of octagon = 4 × Area of kites
Area of octagon = 2 × √(2r)2
Irregular octagon
On contrary to a regular octagon an irregular octagon does not have sides and angles congruent to each other. Hence, an irregular octagon also has eight sides but is unequal with respect to each other.
The interior angles in an irregular octagon are always unequal but their sum always equals 1080°
Area formula of an irregular octagon,
Like regular octagons, irregular octagons do not have the specific derived formula for the calculation of their area. So, to calculate the area of an irregular octagon it is divided into smaller figures like triangles, squares, and rectangles. and, later these all areas are added together.
Sample Problems
Question 1: Find the area of a regular polygon with a side of 3cm.
Solution:
Given:
The side of the octagon is 3cm
Area of an Octagon = 2a2(1 + √2)
A = 2(3)2(1 + √2)
= 43.45cm2
Question 2: Find the area of a regular polygon with a side of 2.5cm.
Solution:
Given:
The side of the octagon is 2.5cm
Area of an Octagon = 2a2(1 + √2)
A = 2(2.5)2(1 + √2)
A = 30.17cm2
Question 3: Find the area of a regular polygon with a side of 7cm.
Solution:
Given:
The side of the octagon is 7cm
Area of an Octagon = 2a2(1 + √2)
A = 2(7)2(1 + √2)
A = 236.59cm2
Question 4: Find the area of a regular polygon with a side of 3.5cm.
Solution:
Given,
The side of the octagon is 3.5cm
Area of an Octagon = 2a2(1 + √2)
A = 2(3.5)2(1 + √2)
A = 59.14cm2
Question 5: Find the area of a regular polygon with a side of 6cm.
Solution:
Given,
The side of the octagon is 6cm.
Area of an Octagon = 2a2 (1 + √2)
A = 2(6)2 (1 + √2)
A = 173.82cm2
Question 6: Find the area of a regular polygon with a side of 5cm.
Solution:
Given,
The side of the octagon is 6cm.
Area of an Octagon = 2a2 (1 + √2)
A = 2(5)2(1 + √2)
A = 120.71cm2
Question 7: Find the area of a regular polygon with a side of 10cm.
Solution:
Given,
The side of the octagon is 10cm.
Area of an Octagon = 2a2 (1 + √2)
A = 2(10)2 (1 + √2)
A = 482.84cm2
|
Есть ли простая формула для определения площади восьмиугольника?
Для правильного восьмиугольника существует формула S = ( 2 + 2 sqrt(корень кв) 2) a^2. где a – длина стороны восьмиугольника. Если восьмиугольник неправильный, его стоит разбить на более простые фигуры (например, треугольники), вычислить их площади и просуммировать. Есть еще вот такой сайт-помощник автор вопроса выбрал этот ответ лучшим
Радуга-Весна 9 лет назад Для того, чтобы определить площадь правильного восьмиугольника, надо разделить его на восемь равных треугольников. После этого нам необходимо определить площадь треугольника. Далее эту площадь мы умножаем на 8. Вот и получится площадь правильного восьмиугольника. elena-kh 10 лет назад Возьмем правильный восьмиугольник.
Посмотрите внимательнее на картинку, и Вы увидите восемь одинаковых треугольников! Вспомните, что площадь треугольника =1/2* основание* высота=1/2*5*10/2=12.5 см2 Потом умножьте полученную сумму на 8. Получится 100 см2. Знаете ответ? |
Чтобы найти площадь произвольного восьмиугольника, выберите внутри него произвольную точку и проведите от нее отрезки к каждой вершине. Затем измерьте длины сторон каждого из восьми полученных треугольников. После чего, воспользовавшись формулой Герона, вычислите площадь каждого треугольника. И, наконец, сложите площади всех треугольников. Полученная сумма и будет площадью восьмиугольника. 2Чтобы воспользоваться формулой Герона, посчитайте сначала полупериметр треугольника:p = (a + b + c) / 2, где a, b, c – длины сторон треугольника; р – обозначение полупериметра.Посчитав полупериметр треугольника, подставьте полученное значение в формулу:S = √(p*(p-a)*(p-b)*(p-c)), где S – площадь треугольника. 3Если восьмиугольник выпуклый (не имеет внутренних углов, больших 180º), то в качестве внутренней точки выберите любую из вершин восьмиугольника. В этом случае, получится всего шесть треугольников, что немного упростит нахождение площади восьмиугольника. Методика расчета площадей треугольников – такая же, как описана в предыдущем пункте. 4Если восьмиугольник имеет равные стороны и углы, то это правильная геометрическая фигура – октагон. Для расчета площади такого восьмиугольника воспользуйтесь формулой:S = 2 * k * a², где а – длина стороны правильного восьмиугольника; k – коэффициент, равный (1+√2)≈2,4142135623731. 5При решении школьных задач иногда задана не длина стороны правильного восьмиугольника, а длины его наибольшей и наименьшей диагоналей. В этом случае воспользуйтесь формулой:S = d * D, где d – длина меньшей диагонали; D – длина большей диагонали.Большей диагональю октагона является отрезок, соединяющий две противоположные вершины. Меньшей диагональю правильного восьмиугольника буде отрезок, соединяющий две вершины через одну.Подробнее: http://www.kakprosto.ru/kak-78526-kak-nayti-ploshchad-vosmiugolnika#ixzz2o8I5dBW9
Содержание
- Элементы неправильного многоугольника
- Типы неправильных многоугольников
- Периметр и площадь неправильного многоугольника
- Пример неправильного многоугольника
Неправильный многоугольник – это геометрическая фигура, не удовлетворяющая условию регулярности. То есть неверно, что все его стороны имеют одинаковую длину и внутренние углы не имеют одинаковой меры.
То есть неправильный многоугольник – это не равносторонний и не равносторонний многоугольник.
Следует помнить, что многоугольник – это двухмерная геометрическая фигура, образованная несколькими неколлинеарными сегментами, образующими замкнутое пространство.
Элементы неправильного многоугольника
Элементами правильного многоугольника являются:
- Вершины: Это точки, объединение которых образует стороны фигуры. Их количество совпадает с количеством сторон. На изображении ниже шестиугольника вершинами будут A, B, C, D, E и F.
- Стороны: Это отрезки, которые соединяют вершины и образуют многоугольник. На рисунке это будут AB, BC, CD, DE, EF и AF.
- Внутренние углы: Арка, образованная объединением сторон. На нижнем изображении они будут: α, β, δ, γ, ε. ζ.
- Диагонали: Это отрезки, которые соединяют каждую вершину с противоположными вершинами. В случае с шестиугольником их девять: AC, AD, AE, BD, BE, BF, CF, CE, DF.

Типы неправильных многоугольников
Неправильные многоугольники могут быть разных типов. Вот некоторые примеры:
- Равнобедренный треугольник: У него две стороны одинаковой длины, но третья разная.

- Трапеция: Это четырехугольник с двумя параллельными сторонами (которые не пересекаются, даже если они продолжены) и двумя другими сторонами, которые не параллельны.

- Необычный Пентагон: Пятисторонний неправильный многоугольник.

- Неправильный шестиугольник: Двухмерная фигура с шестью сторонами разной длины.

Периметр и площадь неправильного многоугольника
Размеры неправильного многоугольника можно рассчитать следующим образом:
- Периметр (P): Это сумма сторон многоугольников.
- Площадь (A): Площадь многоугольника можно рассчитать по-разному. В случае треугольника мы следуем, например, формуле Герона, которая s полупериметр, который представляет собой периметр, разделенный пополам. Кроме того, a, b и c – длины сторон треугольника.

Точно так же в случае неправильного восьмиугольника, такого как тот, который мы видим ниже, например, мы можем разделить фигуру на треугольники, вычислить площадь каждого из них, а затем выполнить соответствующее суммирование. Конечно, это будет возможно, если мы будем иметь данные об измерении соответствующих диагоналей.

Пример неправильного многоугольника
Предположим, у нас есть прямоугольник со сторонами 20 и 30 метров. Каков периметр и площадь фигуры?
P = (2 * 20) + (2 * 30) = 40 + 60 = 100 м
Следовательно, периметр 100 метров.
Затем мы вспоминаем, что площадь прямоугольника вычисляется путем умножения длины двух разных сторон:
A = 20 * 30 = 600 м2
Таким образом, можно сделать вывод, что площадь составляет 600 квадратных метров.
Вы поможете развитию сайта, поделившись страницей с друзьями
Как рассчитать периметр и площадь восьмиугольника

Геометрическая фигура восьми сторон, называемая восьмиугольником или восьмиугольником, обычно представляется в двух измерениях в виде чертежа или плоского объекта, распространенным примером которого является сигнал светофора. Площадь восьмиугольной фигуры легко рассчитывается с помощью базовой математики. Вычисление стороны, сторон или периметра восьмиугольника, это простой вопрос сложения длин сторон. Хотя это редко, трехмерные объекты также могут быть сформированы с восемью сторонами, и боковая площадь вычисляется по той же формуле, что и квадрат или прямоугольник. Мы хотим облегчить вам задачу и объясним, как рассчитать периметр и площадь восьмиугольника.
Вам понадобится:
- правило
- калькулятор
Шаги, чтобы следовать:
1
Первое, что вам нужно сделать, это измерить длину каждой стороны восьмиугольника ; Следует отметить, что этот многоугольник может быть регулярным, то есть все его стороны идентичны и иметь одинаковые размеры, или нерегулярными в случае, если стороны разные.
2
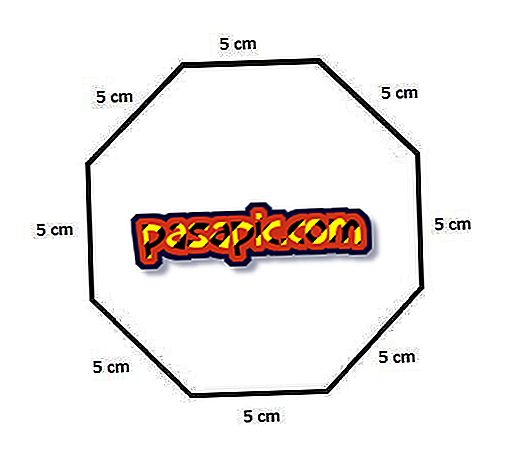
Чтобы узнать периметр правильного восьмиугольника, подобного тому, который вы видите на рисунке ниже, вы должны умножить длину одной стороны восьмиугольника на количество сторон в восьмиугольнике, равное 8. Таким образом, математическая формула говорит, что P = l · 8
Например, если восемь сторон восьмиугольника имеют одинаковую длину в пять сантиметров, периметр восьмиугольника рассчитывается:
5 см х 8 сторон = 40 см по периметру
3
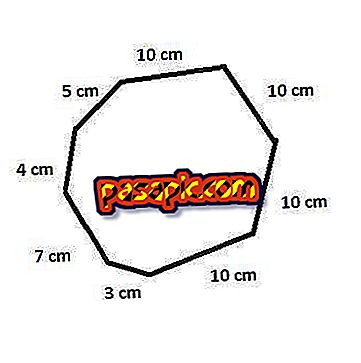
В случае неправильных восьмиугольников вы должны определить периметр, рассчитав каждую сторону отдельно и сумму этих цифр .
Например: если первая сторона 5 сантиметров, вторая сторона 4 сантиметра, третья сторона 7 сантиметров, четвертая сторона 3 сантиметра, а стороны пять, шесть, семь и восемь равны 10 сантиметрам, периметр восьмиугольник будет равен 60 сантиметрам
Периметр = 5 + 4 + 7 + 3 + 10 + 10 + 10 + 10 = 60 см.
4
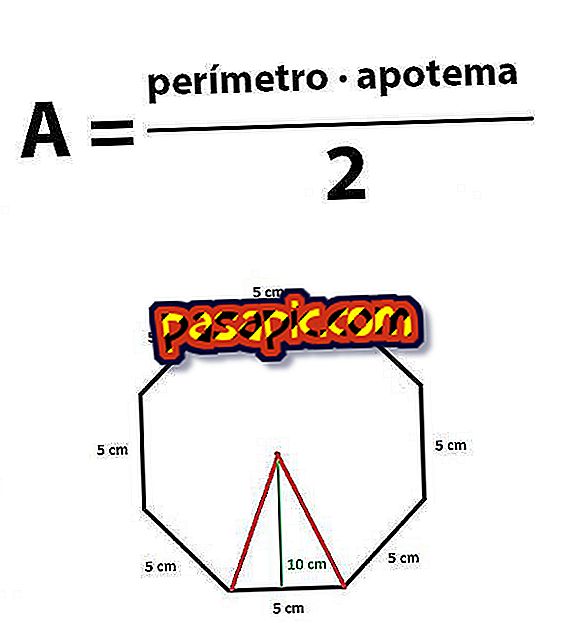
Если мы хотим вычислить поверхность или площадь правильного восьмиугольника, мы должны применить математическую формулу, которая гласит, что площадь равна умножению периметра на апотем, деленный на два.
Итак, мы уже знаем, как рассчитать периметр восьмиугольника, но что такое апофем ? Это расстояние, которое отделяет центр многоугольника от центральной точки каждой стороны восьмиугольника; Если вы посмотрите на изображение, мы указали его зеленым цветом.
Следуя примеру, если каждая сторона равна 5 см, а апотема равна 10 см, мы вычисляем поверхность восьмиугольника, умножая сторону на 8 и на апотему и деля результат на два:
S = (5 см · 8 см) · 10/2 = 40 · 10/2 = 200 см²
5
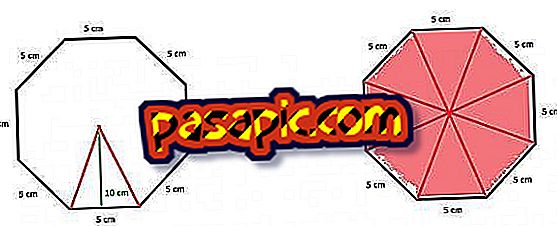
Другой не менее действительный вариант для вычисления поверхности правильного восьмиугольника – это разделить многоугольник на восемь равных треугольников, вычислить его площадь и затем умножить на восемь. Таким образом, апофема правильного восьмиугольника будет равна высоте каждого из этих треугольников и стороне, равной основанию, которые являются двумя элементами, которые нам нужны для вычисления площади треугольника.
Таким образом, поверхность треугольника получается путем применения формулы, которая говорит, что она равна умножению основания на высоту и делению его результата на два:
S = (5 · 10) / 2 = 50/2 = 25 см²
Как только это будет сделано, нам нужно будет только умножить поверхность или площадь треугольника на 8, то есть количество правильных треугольников, составляющих многоугольник с восемью сторонами:
S = 25 · 8 = = 200 см²
Как видим, результат один и тот же, несмотря на применение двух разных методов.
6
Эти другие статьи:
- Как найти периметр четырехугольника
- Как найти периметр квадрата
- Как определить площадь овала
- Как найти высоту косого треугольника с площадью
чаевые
- Помните, что всякий раз, когда вы вычисляете расстояния, поверхности, углы и т. Д., Вы должны указывать единицы измерения в результате.

