Как найти синус угла зная углы треугольника

• Прямоугольный треугольник заключает в себе великое множество различных отношений между всеми своими составляющими. Один из углов в таком треугольнике имеет величину 90°, за счет чего и появляются его особенные свойства. Стороны, прилегающие к прямому углу, называются катетами прямоугольного треугольника, а сторона, лежащая напротив него – гипотенузой. Прямой угол в основе треугольника регулирует отношение сторон таким образом, что зная их можно рассчитать любой острый угол. Отношение противолежащего углу α катета a к гипотенузе c называется синусом угла α и записывается следующим образом:
  

  Разделив катет на гипотенузу, мы получим значение синуса, соответствующее определенной градусной мере, найти которую можно в таблице синусов. Таблица основных значений синусов приведена ниже, а полную версию можно найти по ссылке.

  

  Свойства

  Синус угла sin(α) — есть отношение противолежащего катета a к гипотенузе c.

  

  Таблица синусов

  Синус угла 0° градусов	0	0.000
  Синус угла 30° градусов	1/2	0.500
  Синус угла 45° градусов	√2/2	0.707
  Синус угла 60° градусов	√3/2	0.866
  Синус угла 90° градусов	1	1

Синус в треугольнике

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Синус угла. Таблица синусов.

Синус угла через градусы, минуты и секунды

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция – arcsin(y)=x

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Определение синуса

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° – α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° – α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° – α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° – 60°) = sin60° = 3/√2;
• sin150° = sin(180° – 30°) = sin30° = 1/2;
• sin135° = sin(180° – 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° – α)

Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° – 45° – 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

[spoiler title=”источники:”]

http://calc-best.ru/matematicheskie/trigonometriya/sinus-ugla?n1=3

http://skysmart.ru/articles/mathematic/teorema-sinusov

[/spoiler]

Определение синуса угла

Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.

Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.

Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.

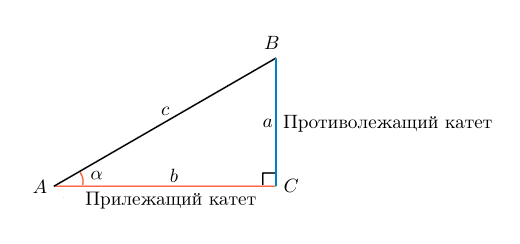
В случае с рисунком, описанным выше: sin⁡α=acsinalpha=frac{a}{c}

Задача 1

В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.

Решение

Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:

3⋅x=123cdot x=12

x=123=4x=frac{12}{3}=4

a=x=4a=x=4

По теореме Пифагора найдем гипотенузу:

a2+b2=c2a^2+b^2=c^2

42+32=c24^2+3^2=c^2

25=c225=c^2

c=5c=5

sin⁡α=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8

Ответ

0.80.8

Задача 2

Вычислите синус 45 градусов.

Решение

Для этого воспользуемся тригонометрической таблицей углов. Находим, что:

sin⁡45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785

Ответ

0.7850.785

Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:

Основное тригонометрическое тождество

sin⁡2α+cos⁡2α=1sin^2alpha+cos^2alpha=1

αalpha — любой угол.

Задача 3

Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.

Решение

Воспользуемся основным тригонометрическим тождеством:

sin⁡2α+cos⁡2α=1sin^2alpha+cos^2alpha=1

sin⁡2α+0.8=1sin^2alpha+0.8=1

sin⁡2α=0.2sin^2alpha=0.2

sin⁡α=0.2sinalpha=sqrt{0.2}

sin⁡α≈0.447sinalphaapprox0.447

Ответ

0.4470.447

Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!

Тест по теме «Вычисление синуса»

Как найти синус, зная угол

Одной из фундаментальных основ точных наук является понятие о тригонометрических функциях. Они определяют простые отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Найти его, зная угол, можно большим количеством способов, включающих экспериментальные, вычислительные методы, а также использование справочной информации.

Вам понадобится

• – калькулятор;
• – компьютер;
• – электронные таблицы;
• – таблицы брадиса;
• – бумага;
• – карандаш.

Инструкция

Используйте калькулятор с функцией вычисления синуса для получения нужных значений на основании знания угла. Подобный функционал сегодня имеют даже самые простые устройства. При этом вычисления производятся с очень высокой степенью точности (как правило, до восьми и более знаков после запятой).

Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами подобных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в любую ячейку формулу, состоящую из вызова функции вычисления синуса с нужным аргументом. Нажмите Enter. В ячейке отобразится искомая величина. Преимуществом электронных таблиц является возможность быстрого расчета значений функций для большого набора аргументов.

Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками после запятой.

Найдите приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого необходимо найти. Начертите еще один отрезок, пересекающий первый в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два уже существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Разделите второе значение на первое. Это и будет искомая величина.

Рассчитайте синус угла, используя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х – (х^3)/3! + (х^5)/5! – (х^7)/7! + (х^9)/9! – … Для повышения скорости расчетов записывайте текущее значение числителя и знаменателя последнего члена ряда, производя вычисление следующего значения на основе предыдущего. Увеличивайте длину ряда для получения более точной величины.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?