Серiя: Техшчш науки ISSN 2225-6733
8. Samotugin S.S., Gagarin V.A., Mazur V.A. Plazmotron dliapoverkhnevoho zmitsnennia [Plasmo-tron for the superficial strengthening]. Patent of UA, no.108154, 2016. (Ukr.)
9. Samotugin S.S., Gagarin V.A. Printsipyi usovershenstvovaniya konstruktsii plazmotrona dlya po-verhnostnoy uprochnyayuschey obrabotki napravlyayuschih stankov [The principles of improvement plasmatron design for the surfaces of strengthening treatment of machine tools guides/ Visnik Pria-zovs’kogo derzhavnogo tehnichnogo universitetu. Seriia: Tekhnichni nauki – Reporter of the Pria-zovskyi State Technical University. Section: Technical Sciences, 2013, iss. 26, pp. 168-174. (Rus.)
Рецензент: В.В. Суглобов
д-р техн. наук, проф., ГВУЗ «ПГТУ»
Статья поступила 07.09.2017
УДК 621.838.225
© Коноваленко В.В.1, Пополов Д.В.2, Зайцев Г.Л.3,
Засельский И.В.4
К РАСЧЕТУ ГОРИЗОНТАЛЬНОЙ ЖЕСТКОСТИ ВИНТОВЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
В работе получена аналитическая зависимость, связывающая горизонтальную и вертикальную жесткости винтовой цилиндрической пружины с круглым и прямоугольным сечением витка, позволяющая определить рациональные параметры виброизолирующих опор вибрационных грохотов. На основании полученных зависимостей установлено, что получение ровной горизонтальной и вертикальной жесткости в виброизолирующих опорах, состоящих из винтовых цилиндрических пружин, невозможно.
Ключевые слова: грохот, винтовая цилиндрическая пружина, жесткость.
Коноваленко В.В., Пополов Д.В., Зайцев Г.Л., Засельський 1.В. До розрахунку горизонтальноi жорсткост1 гвинтових цилтдричних пружин. У роботi отрима-на аналтична залежтсть, що зв’язуе горизонтальну та вертикальну жорсткостi гвинтовог цилтдричног пружини з круглим i прямокутним перетином витка, яка дозволяе визначити ращональт параметри вiброiзолюючих опор вiбрацiйних гро-хотiв. На пiдставi отриманих залежностей встановлено, що отримання рiвноi горизонтальноi i вертикальног жорсткостi у вiброiзолюючих опорах, що складають-ся з гвинтових цилiндричних пружин, неможливо. Ключов1 слова: грохот, гвинтова цилтдрична пружина, жорстюсть.
V. V. Konovalenko, D. V. Popolov, G.L. Zaytsev, I. V. Zaselskiy. To the calculation of horizontal rigidity of coiled springs. The article reveals the problems of the design of elastic vibration isolating elements of vibrating screens. Particular attention is paid to ensuring the equality of horizontal and vertical rigidity. Based on the calculation methods study of the coiled cylindrical springs stiffness, it has been established that the formulas used to calculate the horizontal stiffness give incorrect results. Thus, the goal of sci-
1 канд. техн. наук, доцент, Криворожский металлургический институт Национальной металлургической академии Украины, г. Кривой Рог
2 канд. техн. наук, доцент, Криворожский металлургический институт Национальной металлургической академии Украины, г. Кривой Рог, dmitrykr@ukr. net
3 канд. техн. наук, доцент, Криворожский металлургический институт Национальной металлургической академии Украины, г. Кривой Рог, zajtsev gennady@ukr.net
4 канд. техн. наук, доцент, Криворожский металлургический институт Национальной металлургической академии Украины, г. Кривой Рог, zasicom82@gmail. com
Серiя: Техшчш науки ISSN 2225-6733
entific research was to obtain a new relationship to determine the horizontal stiffness of a helical coil spring, that would make it possible to establish the rational parameters of the vibration isolating supports of the vibrating screens. On the analytical studies basis, the authors managed to obtain a relation between the horizontal and vertical stiffness of a coiled spring with a circular cross section of the coil. The analysis, which substantiates the hypothesis that it’s impossible to produce a coiled spring with equal horizontal and vertical stiffnesses. Analytical relations for determination of the horizontal rigidityof the springs of round and rectangular cross sections of the coils have been received. Analytical relations provide the results with an error not exceeding 0,5%. On the basis of that, the authors give recommendations as to the promising directions in the development of the design of elastic vibration isolating elements of vibrating screens. Keywords: vibrating screen, coiled spring, rigidity.
Постановка проблемы. Одной из основных задач при проектировании вибрационных грохотов является выбор параметров упругих виброизолирующих элементов, которые обеспечивают заданные режимы колебаний рабочего органа и эффективное снижение динамических усилий, передаваемых на фундамент или несущие конструкции. Необходимым условием для этого является обеспечение несвязанных свободных или ударных колебаний при выбеге вибрационной машины. Это достигается при соблюдении ряда правил, одним из них является равенство вертикальной и горизонтальной жесткостей упругих элементов [1], в качестве которых широко применяют винтовые цилиндрические пружины. Если формула определения вертикальной жесткости винтовой цилиндрической пружины широко известна и четко определена [1-3], то с определением горизонтальной жесткости вопрос однозначно не решен.
Анализ последних исследований и публикаций. Так в работе [4] для пружин с витками круглого поперечного сечения жесткость при сдвиге определяется зависимостью
E • d 4 • H
Cx = , (1)
8 • D3 • i
где E – модуль упругости материала, Па; d – диаметр проволоки, м; H – рабочая высота пружины, м; D – средний диаметр витка, м; i – число рабочих витков.
Использовав для анализа выражения (1) правило размерностей, получим значение жесткости в ньютонах, что противоречит принятой единице измерения.
Наибольшее распространение для определения горизонтальной жесткости пружины с круглым сечением витка получила зависимость, предложенная в работах [5, 6]
Cx =-
6 • E • I
—р (2)
п-D• И°2 • г (2 +
где I – экваториальный момент инерции сечения витка, м4; И° – высота пружины в свободном состоянии, м; ц – коэффициент Пуассона; ^ – расчетный коэффициент, определяемый из выражения
„=_(1 – °-625 • {‘И°)2_2+0,331-(о / И, )2, (3)
1 -1,4341-/-И°/ О 2 + 0,88 •(/ / О)2
где / – статический прогиб пружины, м.
Для оценки возможности применимости выражения (2) был выполнен его численный анализ относительно различных номеров позиций витка пружины по ГОСТ 13769-86 при условии постоянной нагрузки, равной 25 кН. Полученные результаты сведены в табл. 1. Из анализа полученных данных видно, что у рассматриваемых пружин, практически с одинаковой вертикальной жесткостью, горизонтальная меняется в 13 раз, при этом ее значение может быть меньше вертикальной, что не соответствует результатам экспериментальных замеров.
Целью данной работы является получение новой аналитической зависимости для определения горизонтальной жесткости винтовой цилиндрической пружины с круглым сечением витка.
Изложение основного материала. Используя расчетную схему, приведенную на рис. 1, рассмотрим работу одного рабочего витка пружины, нагруженного вертикальной Рв и горизонтальной Рг силами, которые будут равны
Серiя: TexHÍ4HÍ науки ISSN 2225-6733
Рв = mg ± Ра, (4)
Рг =±Ра, (5)
где т – масса машины, приходящаяся на одну пружину, кг; g – ускорение свободного падения, м/с2; Ра – активная возмущающая сила, действующая по периодическому закону, Н.
Таблица 1
Результаты численного анализа
Параметр Значение
Номер позиции витка пружины по ГОСТ 13769-86 203 207 210
Диаметр проволоки d, мм 56 50 45
Средний диаметр витка D, мм 504 350 235
Индекс пружины к = D / d 9 7 5,22
Вертикальная жесткость витка C’y, Н/мм 753,6 1430 3104
Число рабочих витков i 2 4 8
Полное число витков iH 3,5 5,5 9,5
Вертикальная жесткость пружины Cy, Н/мм 376,8 357,5 388
Статический прогиб пружины f , мм 39,05 41,16 37,92
Высота пружины в свободном состоянии H0 , мм 248 334 485
Угол наклона витка к горизонту при статической деформации а, град. 2,765 3,16 3,89
Расчетный коэффициент ^ 2,2251 1,3669 1,7397
Горизонтальная жесткость пружины по Cx, Н/мм 610,2 250,6 45,6
Рис. 1 – Расчетная схема витка
В результате этого верхняя опорная плоскость пружины совершает колебания по вертикали ± Y и горизонтали ± X (см. рис. 1).
По оси витка действует деформирующая сила
P = Рг ■ cos а , (6)
а перпендикулярно силе P в плоскости, проходящей через вертикальную ось витка и линию действия силы Рг , действует сила
Р0 = Рг ■ sin а, (7)
где а – угол наклона витка при статической деформации (под действием массы машины, приходящейся на одну пружину) к опорной плоскости.
Серiя: TexHÍ4HÍ науки ISSN 2225-6733
Сила Р, стремится повернуть сечение А против часовой стрелки относительно сечения Б, но такая возможность, учитывая условия закрепления опорных торцов и то, что Р, < mg, исключена. Верхняя опорная плоскость все время параллельна нижней, поэтому в дальнейшем силу Ро, которая перпендикулярна силе, действующей вдоль оси витка, не учитываем, так как она не влияет на горизонтальную деформацию пружины. Сила Р стремится сместить сечение А в сторону сечения Б, а сечение Б – удалить от опорного сечения В.
Определим горизонтальное перемещение верхнего торца пружины ^ под действием горизонтальной силы Рг, которая формирует действующую по оси витка силу Р (см. рис. 2, а),
(р
/рк^д/5
связанные между собой зависимостью (6).
Рис. 2 – Виток пружины: а – в горизонтальной плоскости; б – расчетная схема
Из опыта проектирования и использования пружин в вибротехнике угол а не превышает 4° (см. табл. 1), поэтому будем считать, что виток расположен чисто в горизонтальной плоскости, тогда а = 0.
Рассмотрим расчетную схему витка пружины, приведенную на рис. 2, б и определим перемещение f торца А по отношению к неподвижному торцу В в горизонтальной плоскости под действием силы Р по алгоритму [7]
f =
J M-M 0 dS + J N-N 0 dS
E-I
E-F’
(8)
где М – момент в текущем сечении витка (на рис. 2, б – сечение D) от силы Р, Н-м; N -нормальное усилие в текущем сечении витка от силы Р, Н; М0 – момент в текущем сечении витка от единичной силы по линии действия силы Р, Н-м; N0 – нормальное усилие в текущем сечении витка от единичной силы по линии действия силы Р, Н; F’ – площадь поперечного сечения витка, м2; £ – длина дуги АО.
Вычислим М, N , M0 , N0 и dS :
M = P-R – sin ф; N = – P sin ф;
M 0 = R sin ф;
N =- sin ф; dS = Rdф.
Подставим приведенные значения в (8) 2л 3 2л 2
f J P-R – sin фdф + J P-R – sin фdф
(9) (10) (11)
(12) (13)
0
E-I
0
E-F’
P R 3 P R
+ –
E-I E-F’
2л
J sin 2 фdф =
0
P-R” P-R
+ –
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
E-I E-F’
ф
sin ф
2л
л-P-R
E I 113
1 + –
F’- R2
л-P-R
E I
‘ /2 ^
1+””2т R2
б
а
1
1
2
4
Серiя: TexHÍ4HÍ науки ISSN 2225-6733
где ip – радиус инерции сечения витка, м.
Учитывая (6) и то, что f – деформация витка вдоль его продольной оси, горизонтальное перемещение опорного торца А может быть определено как
fx = f • cos а ,
fx
я-Рг ■ R3 ■ cos2а
E ■ I
1 +
R2
л-Рг ■ R ■ cos2 а-(R 2 + ip 2)
E ■ I
Тогда податливость витка по горизонтали будет
Х =
я^R■ cos2а■ (R2 + i 2)
E ■ I
откуда жесткость витка в горизонтальной плоскости
1
С’ = —=
^г –
E ■ I
^ я ■ R ■ cos2 а(R2 + ip2)
(15)
(16)
(17)
(18)
Проверим возможность смещения торца А по линии действия единичной силы 1(Р), как показано на рис. 3.
Рис. 3 – Нагружение витка пружины единичной силой, перпендикулярной линии действия силы Р
Из рисунка видно, что
M 0 = -R ■(! – cos ф);
N =- cos ф.
Подставив (9), (10), (13), (19), (20) в (8), получим
2я 2я
f L =-J – Р ■ R3 ■ sin ф ■ (1 – cos ф)аф +— J Р ■ R ■ sin ф ■ cos фйф =
E ■ I
E ■ F’
Р ■ RJ
2я
2я
J [- sin ф + sin ф ■ cos ф]úfy + Р R J sin ф ■ cos ф dф –
E ■ I 0 E ■ F’ 0
Р ■ RJ
E ■ I
2я
Р ■ R 1 . 2 +–;—sin ф
2я
E ■ F’ 2
= 0.
(19)
(20)
(21)
1 • 2 cos ф +—sin ф
2 0 ~ ” 0 Перемещение верхнего торца в направлении, перпендикулярном линии действия горизонтальной силы, отсутствует.
Применим полученный результат к винтовым цилиндрическим пружинам, изготовленным из стали круглого сечения. Тогда жесткость витка пружины в горизонтальной плоскости определится как
E ■ d
E d (22)
С’ =
2 ■ k ■ cos2 а ■ (4 ■ k2 +1)
2
Серiя: Техшчш науки ISSN 2225-6733
Учитывая, что вертикальная жесткость витка круглого сечения [1-3]
где G – модуль сдвига Н/м
2
с; = , (23)
y 8 • D
E
G = —,-ч , (24)
2 •(l +
то с учетом зависимостей (23, 24) зависимость (22) примет вид
с, = с, 8 •ft + М>k 2 (25)
^х-^; , / , • cos2 а • (4• k2 +1)
Для того чтобы горизонтальная и вертикальная жесткости были равны, необходимо выполнение условия
8 •(l + д)-k 2
cos2 а • (4• k2 +1)
=1. (26)
Выполнение этого условия возможно только при к < 1, т. е. D < d – пружин с таким индексом не существует, и горизонтальная жесткость всегда больше вертикальной — для пружин, у которых торцы всегда параллельны, и выполняется соотношение
^ < 3. (27)
D
Условие (27) – условие устойчивости пружины от выпучивания [4].
Проверим возможность изготовления винтовой цилиндрической пружины с витками прямоугольного сечения высотой h и шириной а, при h > а, обеспечивающей равенство горизонтальной и вертикальной жесткости.
Для прямоугольного сечения витка уравнение (18) примет вид
2 • E • h
СХ =-2-E-h-Г”, (28)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
л • к1 • (3 • к1 +1) • cos а
где k – индекс витка пружины с прямоугольным сечением, k = D / a . Вертикальная жесткость витка прямоугольного сечения [4, 5]
G • a 4
С; = G-aJ, (29)
; Д • D 3
где Д – коэффициент, который выбирается по таблице [4, 5] в зависимости от значения
h
Р = h. (30)
a
С учетом (24) уравнение (29) примет вид
с; = ,E;a 2. (31)
2 •(! + kj2
Приравняв (28) и (31), получим
р.А=^-(3• *? +1)-ео^2а . (32)
4 .(1 + ц). £2
Для равенства горизонтальной и вертикальной жесткостей необходимо выполнение условия (32). Минимальное значение левой части (32) по [4] при р = 10 составляет 2,52. Максимальное значение правой части (32) при а = 0, ц = 0 и минимально рекомендуемом £1 = 4 не превышает
л^ • k2 +1)
4 • kj2
= 2,405 . (33)
Следовательно, изготовление винтовой цилиндрической пружины с равными вертикальной и горизонтальной жесткостями невозможно. Это объясняется тем, что при вертикальной
В1СНИК ПРИАЗОВСЬКОГО ДЕРЖАВНОГО ТЕХШЧНОГО УН1ВЕРСИТЕТУ 2017р. Серiя: Техшчш науки Вип. 35
ISSN 2225-6733
деформации витки пружины работают на срез, при этом величина деформации зависит от модуля G, а при горизонтальной деформации витки пружины работают на изгиб, и величина деформации зависит от модуля Е.
Горизонтальные жесткости пружин Cx = C’x /i в соответствии с расчетной формулой (22) для параметров, представленных в табл. 1, приведены в табл. 2.
Таблица 2
Значения горизонтальной жесткости пружины
Параметр Значение
Номер витка пружины 203 207 210
Горизонтальная жесткость, Н/мм 1007,5 954,7 1033,4
Из анализа полученных результатов видно, что отношение горизонтальной жесткости к вертикальной для всех трех пружин с параметрами, приведенными в таблице 1, близко к численному значению отношения
с
Сх = 2 .(1 + ц). (34)
Су
Численный анализ (22), (28) показал, что при а = 0 погрешность не превышает 0,5%, поэтому для практического применения определять горизонтальную жесткость цилиндрических витков круглого и прямоугольного сечения можно из следующих зависимостей, соответственно:
с; =-Е ( , . (35)
2• к .(4• к2 +1)
2 • E • h л-k1 • (3• k2 +1)
с;=-^—. (36)
2
Выводы
В результате анализа существующих формул для определения горизонтальной жесткости винтовых цилиндрических пружин установлено, что они дают некорректные результаты и приводят к существенным ошибкам при выборе виброизолирующих опор вибрационных машин. Для устранения существующих недостатков были получены новые аналитические зависимости по определению горизонтальной жесткости винтовых цилиндрических пружин с витками круглого и прямоугольного сечения. Анализ полученных зависимостей показал, что изготовить винтовую цилиндрическую пружину с равной горизонтальной и вертикальной жесткостями невозможно. Перспективным представляется применение упругих элементов, работающих в вертикальной плоскости на сдвиг, или изготовление комбинированных амортизаторов из различных материалов, обеспечивающих равенство жесткостей.
Список использованных источников:
1. Вайсберг Л.А. Проектирование и расчет вибрационных грохотов / Л.А. Вайсберг. – М. : Недра. – 1986. – 144 с.
2. Analysis of dynamic stiffness effect of primary suspension helical springs on railway vehicle vibration / W. Sun, D.J. Thompson, J. Zhou, D. Gong // Journal of Physics. – 2016. – № 744. -Pp. 1-8. – Mode of access : DOI:10.1088/1742-6596/744/1/012149.
3. Dym C.L. Consistent derivations of spring rates for helical springs / Dym C.L. // Journal of Mechanical Design. – 2009. – Vol. 131. – Pp. 1-5. – Mode of access : DOI: 10.1115/1.3125888.
4. Пономарев С.Д. Расчет упругих элементов машин и приборов / С.Д. Пономарев, Л.Е. Андреева. – М. : Машиностроение. – 1980. – 326 с.
5. Курендаш Р.С. Конструирование пружин / Р.С. Курендаш. – К. : Машгиз. – 1958. – 109 с.
6. Вибрационные процессы и машины / Г.Г. Азбель [и др.]; под ред. Э.Э. Лавендела. – М. : Машиностроение, 1981. – 509 с. – (Вибрации в технике : справочник : в 6-ти т.; Т. 4).
7. Беляев Н.М. Сопротивление материалов / Н.М. Беляев. – М. : Наука. – 1965. – 856 с.
Серiя: TexHÏ4HÏ науки ISSN 2225-6733
References:
1. Vaysberg L.A. Proektirovanie i raschet vibratsionnykh grokhotov [Engineering design and calculation of vibrating screens]. Moscow, Nedra Publ., 1986. 144 p. (Rus.)
2. Sun W., Thompson D.J., Zhou J., Gong D. Analysis of dynamic stiffness effect of primary suspension helical springs on railway vehicle vibration. Journal of Physics, 2016, no.744, pp. 1-8. doi: 10.1088/1742-6596/744/1/012149.
3. Dym C.L. Consistent derivations of spring rates for helical springs. Journal of Mechanical Design, 2009, vol. 131, pp. 1-5. doi: 10.1115/1.3125888.
4. Ponomarev S.D., Andreeva L.E. Raschet uprugikh elementov mashin i priborov [Calculation of elastic elements of machines and indicators]. Moscow, Mashinostroenie Publ., 1980. 326 p. (Rus.)
5. Kurendash R.S. Konstruirovanie pruzhin [Design engineering of springs]. Kiev, Mashgiz Publ., 1958. 109 p. (Rus.)
6. Azbel’ G.G. Vibratsii v tekhnike. Tom 4: Vibratsionnye protsessy i mashiny [Vibrations in the equipment. Vol. 4: Vibration processes and machines]. Moscow, Mashinostroenie Publ., 1981. 509 p. (Rus.)
7. Belyaev N.M. Soprotivlenie materialov [Structural resistance]. Moscow, Nauka Publ., 1965. 856 p. (Rus.)
Рецензент: А.Д. Учитель
д-р техн. наук, проф., КМИ НМетАУ
Статья поступила 23.10.2017
УДК 621.643.053
© Мазур С.В.1, Стршець В.М.2, Стршець О.Р.3, Степанюк А.А.4
РУХ Р1ДИНИ ПО КАНАВЦ1 У ВИГЛЯД1 СП1РАЛ1 АРХ1МЕДА ОБЕРТОВОГО К1ЛЬЦЯ ТОРЦЕВОГО УЩЫЬНЕННЯ ПIДВИЩЕНОÏ
ГЕРМЕТИЧНОСТ1
Описана будова торцевого ущыьнення тдвищеног’ герметичност1 з канавкою на торц обертового кыьця у вигляд1 страл1 Арх1меда i принцип його роботи. Розгля-нутий рух рiдини, яка хоче проникнути через стик обертового та необертового ю-лець торцевого ущыьнення i3 герметичноï камери назовт, i повернення ïï назад у герметичну камеру. На основi аналтичних i графiчних залежностей, отриманих за допомогою комп’ютерного моделювання, зроблений висновок про умови робото-здатностi запропонованого торцевого ущыьнення.
Ключовi слова: торцеве ущыьнення, тдвищена герметичтсть, страль Архiмеда, канавка, рух рiдини, обертове кыьце.
Мазур С.В., Стрелец В.Н., Стрилец О.Р., Степанюк А.А. Движение жидкости по канавке в виде спирали Архимеда вращающегося кольца торцевого уплотнения повышенной герметичности. Описано строение торцевого уплотнения повышенной герметичности с канавкой на торце вращающегося кольца в виде спирали Архимеда и принцип его работы. Рассмотрено движение жидкости, которая
1 студент, Нацюналъний ушверситет водного господарства та природокористування, м. Рiвне, mazur01 m15@nuwm.edu.ua
2 канд. техн. наук, доцент, професор, Нацюналъний ушверситет водного господарства та природокористування, м. Рiвне, V. т. strilets@nuwm. edu.ua
3 канд. техн. наук, доцент, Нацюналъний ушверситет водного господарства та природокористування, м. Рiвне, ua oleg@hotmail.com
4 канд. техн. наук, асистент, Нацюналъний ушверситет водного господарства та природокористування, м. Рiвне, а. а. stepaniuk@nuwm. edu.ua
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).

Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
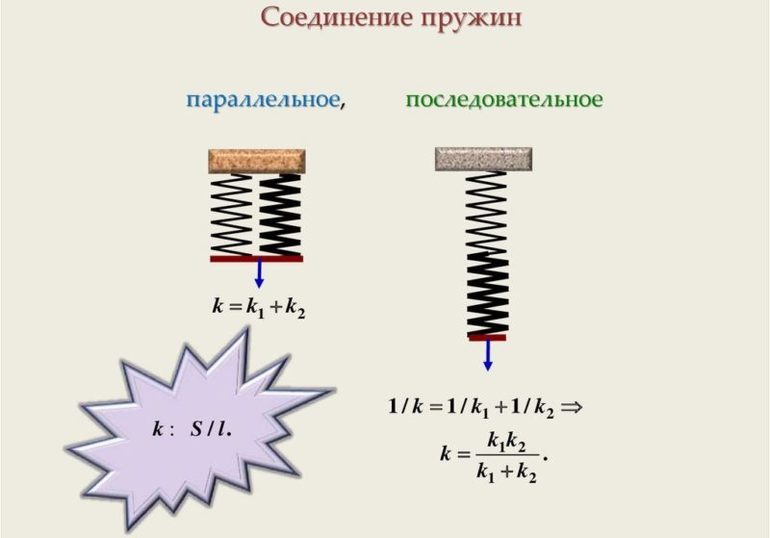
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие.
Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Определение и формула жесткости пружины
При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
- Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
- При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
- Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
- При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
- Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.

Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd4/8D3n. В этой формуле указываются нижеприведенные обозначения:
- G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
- d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
- D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
- n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
Формула жесткости соединений пружин
Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:
- Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
- Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.

В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.
При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k1+1/k2+…+1/kn. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k1+k2+…kn.
Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.
Коэффициент жесткости соединений пружин
Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
- При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
- Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
- Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.

Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Коэффициент жесткости цилиндрической пружины
На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
- При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
- При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
- Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
- Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
- Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
- Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
- Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.
Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
- Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
- Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
- Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
- Модуля сдвига, который зависит от типа применяемого материала.

Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
Единицы измерения
При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.
Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.
Разделение пружины по цветам проводится в сфере автомобилестроения.
Среди особенностей подобной маркировки отметим следующее:
- Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
- Класса В представлен синим, голубым, черным и желтым цветом.
Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.
Особенности расчета жесткости соединений пружин
Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
- Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
- Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
- Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
Пружиной называют объект, способный с помощью деформации, вызванной внешними силами, накапливать и сохранять упругую потенциальную энергию, а после прекращения их воздействия восстанавливаться до прежнего состояния. Реально существующие пружины абсолютно точно восстановить свою прежнюю форму не в состоянии т.к. при внешнем воздействии в той или иной степени нарушается структура их материала, в результате чего возникают так называемые пластичные деформации. Чем они меньшее, тем более качественным считается изделие.

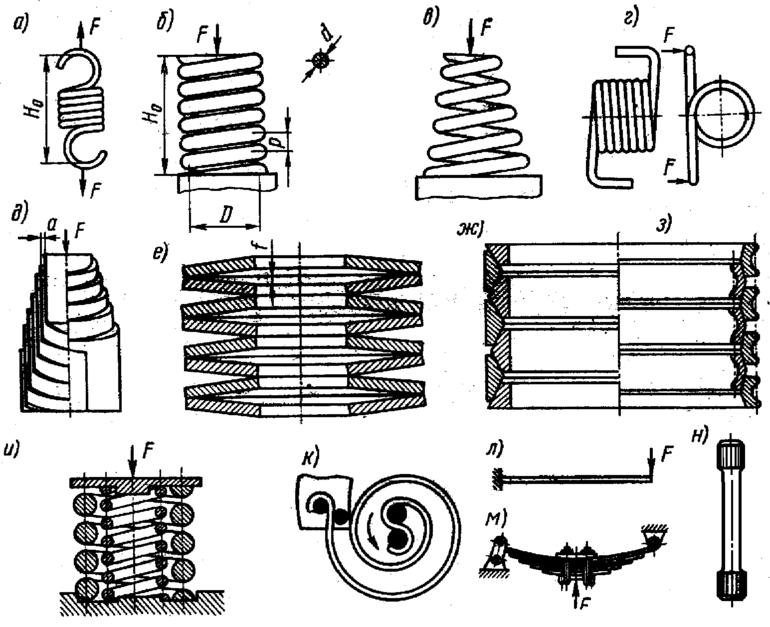
Какие бывают типы пружин
В первую очередь их принято делить на предназначенные для работы в режиме растягивания и предназначенные для работы в режиме сжатия.
Пружины растяжения при действии на них полезной нагрузки растягиваются. Они не нуждаются в жёстком захвате и, как правило, имеют нулевой шаг, т. е. витки у них прилегают вплотную друг к другу. В обычной жизни подобные изделия большинство людей может заметить, проходя через двери с механическим механизмом закрытия или при пользовании пружинными весами. В технике пружины растяжения используются для соединения элементов, положение которых меняется при их работе. В качестве примера можно привести завес рычагов.
Пружины сжатия под нагрузкой по длине уменьшаются. Для правильной работы их концы должны быть жёстко зафиксированы. Витки проволоки в свободном состоянии не касаются друг друга, т.к. им необходим некоторый промежуток, чтобы под внешней нагрузкой было куда перемещаться. В качестве примера использования таких изделий можно привести пружину в шариковой ручке или автомобильную подвеску.
В технике широкое применение находят и другие типы пружин: пружины кручения (в точных весах), плоские спиральные (как заводные в часах), плоские (в автомобильных рессорах), тарельчатые (в грузовых весах). В некотором роде пружинами можно назвать некоторые изделия из резины и из других полимерных эластичных материалов. Все они работают по одной и той же схеме – запасают кинетическую энергию в виде энергии упругости, а затем, когда нагрузка ослабнет или вовсе перестанет действовать, её возвращают.
Основные характеристики пружин
Зная материал и диаметр проволоки, форму её сечения, длину и диаметр пружины, как единого целого, можно с очень высокой достоверностью судить, насколько пружина может сопротивляться попыткам деформировать себя. Существуют также другие характеристики, от которых работоспособность пружины может зависеть очень серьёзно. К таковым относятся усталость материала проволоки, шаг витка, индекс пружины и т. д.
Материал и сила жесткости пружины
Зависимость между этими характеристиками пружин индивидуальная и вычисляется опытным путём. Чаще всего для изготовления металлических пружин используют высокоуглеродистые стали, легированные ванадием, кремнием и марганцем. Для изделий, предназначенных для длительной работы в агрессивных средах используют нержавеющую сталь, оловянносвинцовую, бериллиевую и кремнемарганцевую бронзу, различные чугуны, а также некоторые из титановых сплавов.
Небольшие пружины изготавливают из уже закалённой проволоки. Крупные изделия делают из отожжённой стали, а закалку проводят уже после формовки.
Как связана жесткость пружины с диаметром и формой сечения проволоки, из которой она сделана
Чем он меньше, тем пружина более эластична. Способность запасать энергию с уменьшением диаметра тоже становится меньше. Пружины сжатия, как правило, делают из более толстой проволоки.
Следует отметить, что не всегда сечение проволоки для пружин бывает круглым, в пружинах сжатия оно иногда бывает уплощённым. Это обеспечивает лучшую посадку одного витка на другой и делает конструкцию более устойчивой.
Длина и диаметр
Определение
Под длиной пружины понимают её длину в свободном, недеформированном состоянии.
Также следует различать длину собственно изделия и длину проволоки, из которой оно сделано. Это две совершенно разные величины. Не малое значение имеет число витков. В пружинах сжатия, чем их больше, тем выше вероятность соскальзывания изделия с опоры и, как следствие, выхода детали из строя.
О понятии жесткости. Жесткость пружины: формула
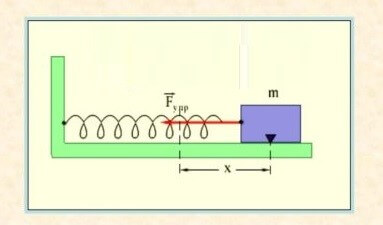
Определение
Жёсткостью пружины называют коэффициент, который связывает силу прилагаемую к ней с удлинением или сжатием.
Посмотрите на закон Гука.
Формула
Fупр = –kx
Зако́н Гу́ка — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе.
k – это и есть жёсткость пружины.
Fупр — сила жесткости или упругости пружины.
x — расстояние, на которое изменилась длина изделия после того как та была уравновешена.
Минус в формуле свидетельствует о том, что сила F имеет по сравнению с нагрузкой противоположное направление.
Закон Гука является одним из основных законов физики.
Как найти жесткость пружины? Формулу из выше приведённого уравнения понять достаточно легко:
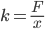
Коэффициент жесткости пружины можно вычислить и экспериментальным путём. Для этого нужно подвесить на вертикально закреплённую пружину груз с известной массой.
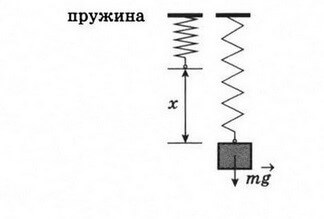
Имеем два уравнения:
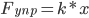
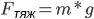
Т. к. Fупр =Fтяж, получаем
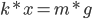
Отсюда разделив обе части уравнения на x, найдём, что жёсткость равна
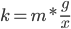
Массу самой пружины считаем равной нулю. Для исключения случайных ошибок проводим несколько измерений с грузами разной массы.
Нет времени решать самому?
Наши эксперты помогут!
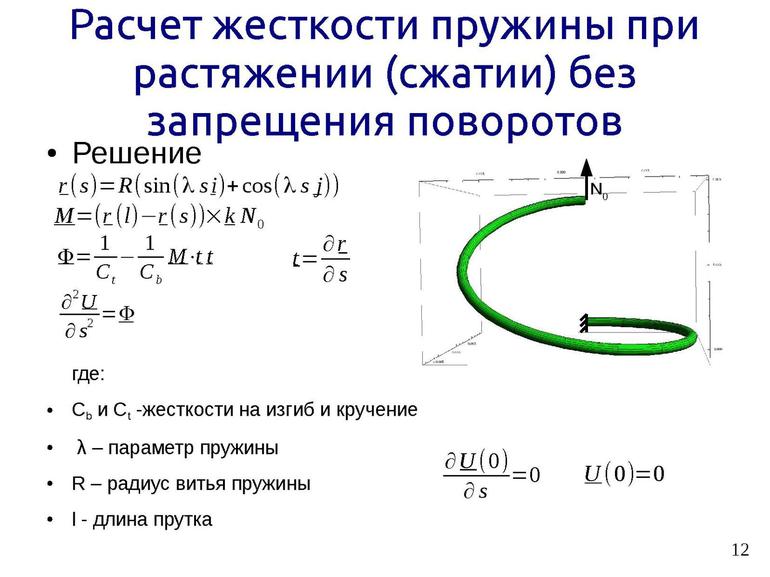
Как рассчитать жесткость цилиндрической пружины
В плоской пружине в момент её изгиба расстояния между молекулами, находящимися в одном месте уменьшаются, а в другом увеличиваются. Сила электромагнитных межмолекулярных связей стремится вернуть изделие в прежнее положение.
С цилиндрической пружиной всё несколько иначе. В ней энергия запасается не из-за деформации изгиба, а благодаря скручиванию проволоки вдоль своей оси навивания.
Давайте мысленно увеличим выполненное перпендикулярно её оси плоскостью сечение проволоки. Это нам позволит не учитывать спиральную форму изделия. Разобьём весь объём проволоки на очень много касающихся друг друга своими торцами цилиндров. Их диаметр совпадает с диаметром проволоки, а высота бесконечно мала. Торцам не дают разъединится действующие между ними межмолекулярные силы. Именно они препятствуют деформации.
Когда пружина растягивается или сжимается, цилиндры вынуждены вращаться друг относительно друга в противоположных направлениях вокруг общей оси. В каждом из сечений запасается некоторая энергия. Отсюда легко сделать вывод, что чем проволока длиннее, тем больше энергии такая пружина способна запасти. Увеличение проволоки по диаметру тоже способствует возрастанию её энергоёмкости.
Окончательная формула для жёсткости цилиндрической пружины такова:
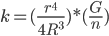
Буквой R у нас обозначен радиус цилиндра пружины, n – количество витков проволоки, r—её радиус, G – коэффициент, индивидуальный для материала проволоки.
Чтобы по данной формуле сделать расчёт жёсткости, достаточно просто подставить вместо букв, обозначающих величины, их числовые значения.
Трактовка понятий
В физике упругая деформация возникает из-за силы, равной по модулю оказываемому воздействию. Сила упругости для пружины (F) пропорциональна её удлинению. Для определения жесткости пружины зависимость записывается математически с помощью следующей формулы: F = k·x; где х — длина предмета после его растяжения, а k — коэффициент жесткости.
Формула считается частным случаем закона Гука, который используется для растяжимого тонкого стержня. Чрезмерное воздействие приводит к появлению разных дефектов. Для процесса характерны некоторые особенности, от чего зависит жесткость пружины:
- геометрические параметры детали;
- срок эксплуатации;
- значение коэффициента k, который при определённых условиях способствует снижению сжатия и сохранению силы на одинаковом уровне;
- тип используемого материала (сталь, сплав) в процессе изготовления пружины.
На практических занятиях по физике в 7 классе применяются изделия разных типов. В автомобилестроении используется цветовое обозначение. Для расчета коэффициента жесткости пружины специалисты ориентируются на формулу k=Gd 4 /8D 3 n, где:

- G — определяет модуль сдвига (свойство зависит, к примеру, от используемого сырья);
- d — диаметр куска проволоки (величина определяется в период производства путём проката, а результат записывается в технической документации);
- D — диаметр витков, которые получаются в результате намотки на проволоку (расчет осуществляется с учетом поставленных задач и зависит от нагрузки, оказываемой для сжатия объекта);
- n — количество витков в системе (показатель варьируется в значительном диапазоне, от чего зависят эксплуатационные характеристики предмета).
С помощью формулы может измеряться жёсткость цилиндрической пружины, используемой в разных механизмах. Показатель измеряется в Ньютонах и обозначается Н.
Практические занятия
Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.
Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.
На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:
- k — суммарная жёсткость соединений;
- k1 …ki — жёсткость каждого элемента системы;
- i — число пружин в цепи.
Если невесомые (расположены горизонтально) предметы соединены параллельно, значение общего k будет увеличиваться. Величина вычисляется по следующей формуле: k = k1 + k2 + … + ki.
Основная методика для вычислений
На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:
- Пружина фиксируется вертикально. Для этого используется любая удобная опора со свободной нижней частью.
- Линейкой измеряется длина предмета. Результат записывается как х1.
- На свободный конец подвешивается груз с известной массой m.
- Измеряется длина изделия под воздействием амплитуды. Вывод записывается как х2.
- Производит подсчёт абсолютного удлинения: x = x2-x1. Для определения энергии (силы) и k в международной системе СИ осуществляется перевод длины из разных единиц измерения в метры.
- Сила, спровоцировавшая деформацию, считается силой тяжести тела. Она рассчитывается по формуле: F = mg, где м является массой используемого груза (вес переводится в килограммы), а g (равен 9,8) — постоянная величина, с помощью которой отмечается ускорение свободного падения.
Если вышеописанные вычисления произведены, необходимо найти значение коэффициента жёсткости. Используется закон Гука, из которого следует, что k=F/x.
Решение задач
Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.
Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.
Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.
Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.
Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.
Применение цилиндрических пружин
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.
Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.
Главными параметрами изделия считаются:
- малый, средний и большой диаметр витков и самой проволоки;
- шаг размещения отдельный колец.
В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:
- Исполнение, рассчитанное на сжатие, характеризуется дальним размещением витков. Расстояние, образуемое между ними, появляется возможность на сжатие.
- Модель, связанная с растяжением, имеет кольца, расположенные плотно между собой. Такая форма определяет то, что при максимальной силе растяжение минимальное.
Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.
Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.

