Найти производную: алгоритм и примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
.
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
.
Пример 2. Найти производную функции
.
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200. ), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций”.
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u‘v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями”.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
.
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями”.
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций”.
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Найти производные самостоятельно, а затем посмотреть решения
Пример 7. Найти производную функции
.
Пример 8. Найти производную функции
.
Пример 9. Найти производную функции
, где a и b – константы.
Пример 10. Найти производную функции
.
Пример 11. Найти производную функции
.
Ещё больше домашних заданий на нахождение производных
Продолжаем искать производные вместе
Пример 12. Найти производную функции
.
Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных – под номером 3), получим
.
Пример 13. Найти производную функции
Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
Пример 14. Найти производную функции
Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:
Теперь вычислим производные в числителе и перед нами уже требуемый результат:
Пример 15.Найти производную функции
Шаг1. Применяем правило дифференцирования суммы:
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных – номер 5):
Шаг3. В частном знаменатель – также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя – это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
,
а производная, требуемая в условии задачи:
Ещё больше домашних заданий на нахождение производных
Напоминаем, что чуть более сложные примеры на производную произведения и частного – в статьях “Производная произведения и частного функций” и “Производная суммы дробей со степенями и корнями”.
Также настоятельно рекомендуем изучить производную сложной функции.
Пошаговый калькулятор производных онлайн
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Примеры решения производных с ответами
Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения производных
Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.
Процесс нахождения производный называется дифференцированием.
- 0, c neq 1″ title=”Rendered by QuickLaTeX.com” height=”20″ width=”219″ style=”vertical-align: -5px;” />
- 0, c neq 1″ title=”Rendered by QuickLaTeX.com” height=”20″ width=”180″ style=”vertical-align: -5px;” />
– производная суммы (разницы).
– производная произведения.
– производная частного.
Нужна помощь в написании работы?
Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Примеры решений производных
Задача
Найти производную функции
Решение
Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:
Ответ
Задание
Найти производную функции
Решение
Обозначим , где . Тогда, согласно правила вычисления производной сложной функции, получим:
Ответ
Задача
Найти производную функции при .
Решение
.
.
Ответ
.
Задача
Найти производную функции .
Решение
.
После приведения подобных членов получаем:
.
Ответ
Задача
Найти производную функции .
Решение
В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.
Ответ
.
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Применяя правила дифференцирования котангенса, получаем:
.
Учитывая, что и , после упрощения получим:
.
Ответ
.
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Ответ
.
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Ответ
.
Задача
Найти производную функции .
Решение
Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты:
.
Ответ
.
Задача
Найти производную функции .
Решение
По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.
Ответ
.
[spoiler title=”источники:”]
http://mathdf.com/der/ru/
http://nauchniestati.ru/spravka/primery-resheniya-proizvodnyh/
[/spoiler]
Дифференциальные уравнения. Что это?
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Вы уже имеете находить производные и интегралы? Тогда настало самое время, чтобы перейти к более сложной теме, а именно, решению дифференциальных уравнений (ДУ, в простонародье диффуров). Но не все так страшно, как кажется на первый взгляд.
Дифференциальное уравнение: что это такое?
Дифференциальное уравнение (ДУ) – это уравнение, которое вместе с самой функцией (и ее аргументами), содержит еще и ее производную или несколько производных.
Дифференциальное уравнение: что нужно знать еще?
Первое (и главное), что понадобится, это умение правильно определять тип дифференциального уравнения. Второе, но не менее важное, это умение хорошо интегрировать и дифференцировать.
Не секрет, что дифференциальные уравнения бывают разных типов. Но… для начала отметим, что ДУ бывают разных порядков. Порядок ДУ — это порядок высшей производной, входящей в дифференциальное уравнение. Классификацию ДУ согласно порядку уравнения можно посмотреть в следующей таблице:
| Порядок уравнения | Вид уравнения | Пример |
|---|---|---|
| I | 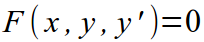 |
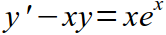 |
| II | 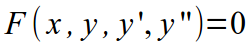 |
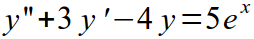 |
| … | … | … |
| n | 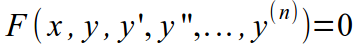 |
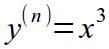 |
Наиболее часто приходится иметь дело с ДУ первого и второго порядка, реже третьего. В 99% случаев в задачах встречаются три типа ДУ первого порядка: уравнения с разделяющимися переменными, однородные уравнения и линейные неоднородные уравнения. Иногда еще встречаются более редкие типы ДУ: уравнения в полных дифференциалах, уравнения Бернулли и др. Среди ДУ второго порядка часто встречаются уравнения, приводящиеся к ДУ первого порядка, линейные однородные и неоднородные уравнения с постоянными коэффициентами.
Дифференциальное уравнение: решение – что это значит и как его найти?
При решении ДУ нам предлагается найти либо общее решение (общий интеграл), либо частное решение. Общее решение y = f(x, C) зависит от некоторой постоянной ( С — const), а частное решение не зависит: y = f(x, C0).
С геометрической точки зрения общее решение – это семейство кривых на координатной плоскости, а частное решение – это одна прямая этого семейства, проходящая через некоторую точку. 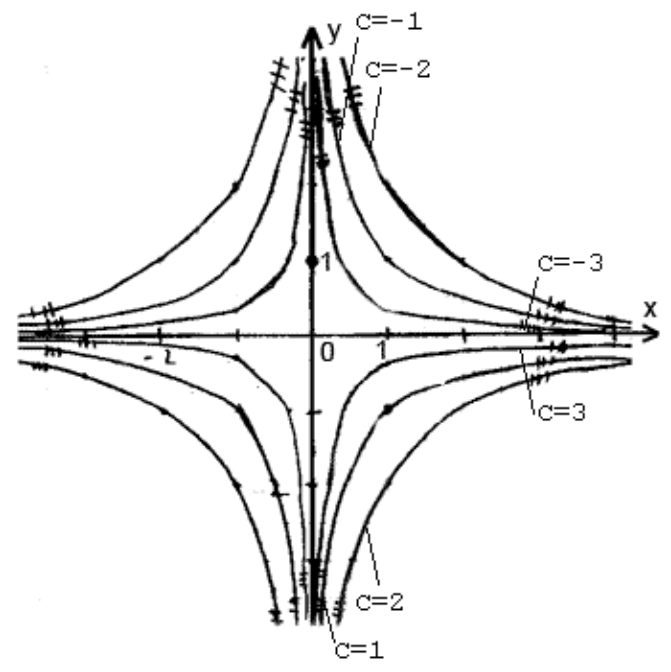
Давайте рассмотрим примеры решения некоторых ДУ. Начнем с ДУ первого порядка с разделяющимися переменными:
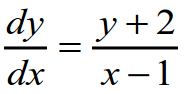
Здесь все очень просто как на уроке физкультуры, когда ученики класса делятся на две команды, в одну из которых входят только мальчики, а в другую – только девочки. Применительно к уравнению делаем следующее: в левую часть от знака равенства переносим все то, что содержит переменную y, а в правую часть – переменную x.
Получаем:
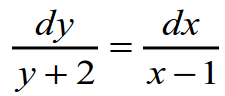
Далее интегрируем обе части:
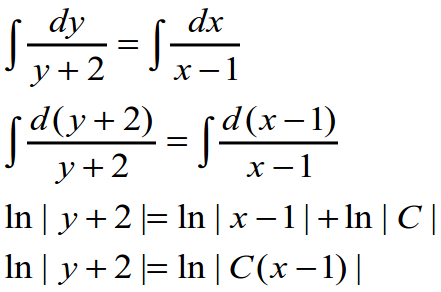
Итоговое общее решение выглядит следующим образом: y = C(x-1) — 2. Все оказалось очень просто, не правда ли?
Не сложнее и решение однородных ДУ второго порядка с постоянными коэффициентами. Здесь всего-то и нужно знать из курса школьной алгебры, как решаются квадратные уравнения, а из курса по ДУ, как правильно записать общее решение.
Для наглядности рассмотрим пример:
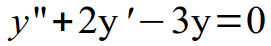
Составляем характеристическое уравнение, заменяя переменную y на переменную k, а количество штрихов соответствующей степенью (два штриха – степень 2, один штрих – степень 1, нет штрихов – степень 0). Получаем квадратное уравнение, решить которое можно с помощью дискриминанта или теоремы Виета:
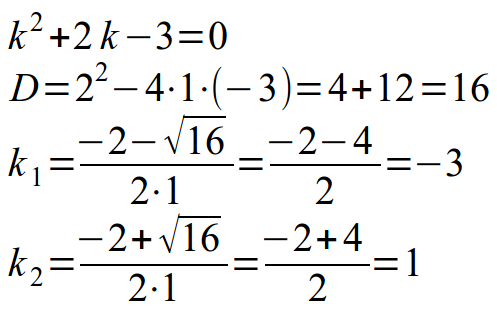
После того, как корни характеристического уравнения найдены, вспоминаем правила записи общего решения однородного ДУ:
- Корни характеристического уравнения являются действительными и различными. Общее решение записывается в виде:
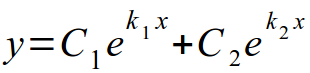
- Корни характеристического уравнения являются комплексными. Общее решение записывается в виде:
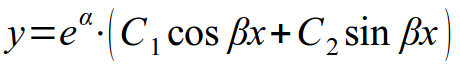
- Корни характеристического уравнения являются действительными и равными. Общее решение записывается в виде:
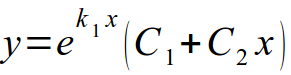
Вспоминаем, что наше уравнение имеет два различных действительных корня. Следовательно, общее решение запишем в виде:
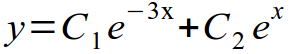
Решение линейных неоднородных ДУ с постоянными коэффициентами выполняется в два этапа:
- нахождение общего решения линейного однородного ДУ;
- нахождение и частного решения линейного неоднородного ДУ.
Выполнение первого этапа рассмотрено на примере чуть раньше. То, в каком виде мы будем искать частное решение неоднородного ДУ, зависит от того, что стоит в уравнении справа от знака равенства. Все возможные случаи подробно рассматривают в учебной литературе.
Итак, тема «Решение задач по дифференциальным уравнениям» изучается в ВУЗах, но, как было показано выше, решить некоторые ДУ может и школьник.
Дифференциальные уравнения и методы их решения рассматриваются практически в каждом учебнике по высшей математике и математическому анализу. Особенно хорошо данная тема рассмотрена в учебнике автора Пискунов Н.С., а называется он «Дифференциальное и интегральное исчисления: Учеб. Для втузов. В 2-х т. Т. II». С помощью данного учебника можно самостоятельно изучить методы решения тех типов ДУ, которые не были рассмотрены в данной статье.
Решение дифференциальных уравнений на заказ
У нас вы можете выгодно заказать решение задач с дифференциальными уравнениями. Нами накоплен большой опыт решения заданий по данной дисциплине, которым мы готовы поделиться с вами. Работа будет оформлена очень подробно. При заказе большого количества задач действует скидка. Купить решение можно, сделав заказ у нас на сайте.
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Линейные дифференциальные уравнения в частных производных первого порядка
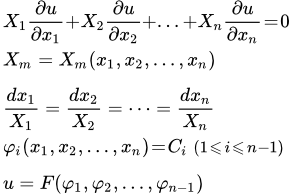
Линейные однородные уравнения в частных производных первого порядка
Пусть X 1 , X 2 , . Xn – заданные функции переменных x 1 , x 2 , . xn .
Чтобы решить линейное однородное уравнение в частных производных первого порядка:
необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ 1( x 1 , x 2 , . xn ) = C 1 ,
φ 2( x 1 , x 2 , . xn ) = C 2 ,
.
φn- 1 ( x 1 , x 2 , . xn ) = Cn- 1 ,
где Ck – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.
Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .
Линейные неоднородные уравнения в частных производных первого порядка
Пусть X 1 , X 2 , . Xn+ 1 – заданные функции от переменных x 1 , x 2 , . xn и z .
Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ 1( x 1 , x 2 , . xn , z ) = C 1 ,
φ 2( x 1 , x 2 , . xn , z ) = C 2 ,
.
φn ( x 1 , x 2 , . xn , z ) = Cn .
После чего сразу получаем общий интеграл в неявном виде:
где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ 1 = F ( φ 2 , φ 3 , . φn ) ,
φ 2 = F ( φ 1 , φ 3 , . φn ) ,
и т. д.
Примеры решений линейных уравнений в частных производных первого порядка
Однородное уравнение
Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .
Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.
Выбираем и решаем первое уравнение:
Здесь переменные уже разделены, интегрируем:
Интегралы табличные,
Потенцируем:
Отсюда
Подставим во второе уравнение:
Или:
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:
Интегрируем:
Подставим полученное ранее выражение C1 = x y 2 :
Итак, мы нашли два интеграла уравнения характеристик:
Общее решение исходного уравнения в частных производных имеет вид:
где F — произвольная функция от двух аргументов F(φ1, φ2) . Найдем ее вид из граничного условия
при .
Рассматриваем решение на границе.
Положим x y = –1 :
Отсюда
На границе
.
Итак, мы нашли, что на границе функция F имеет вид:
F ( φ 1 , φ 2 ) = φ 1 φ 2 .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:
Общее решение:
где F — произвольная функция от двух аргументов F ( φ 1 , φ 2 ) .
Неоднородное уравнение
Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .
Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.
Решаем уравнение:
Умножаем на 2 z и интегрируем:
Интегралы табличные,
Потенцируем:
Отсюда
x = C 1 y
Подставим во второе уравнение:
Или:
Замечаем, что , тогда
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:
Интегрируем:
Подставим полученное ранее выражение и преобразуем:
Итак, мы нашли два интеграла уравнения характеристик:
Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:
Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ 1 , φ 2) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ 1 = F ( φ 2) ,
где F — произвольная функция от одного аргумента.
Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем
Итак, мы нашли, что на границе:
.
Подставим в выражение общего интеграла:
φ 1 = F ( φ 2)
.
Сделаем подстановку
:
.
Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ1 и φ2 :
.
Умножим на a 2 y 2 .
Автор: Олег Одинцов . Опубликовано: 23-09-2014
источники:
http://mathdf.com/dif/ru/
http://1cov-edu.ru/differentsialnye-uravneniya/chastnie_proizvodnie/
Правила вычисления производных
7 апреля 2011
- Скачать все правила
Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:
![]()
Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x
2 + (2x + 3) · e
x
· sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.
Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.
Производные элементарных функций
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
| Название | Функция | Производная |
| Константа | f(x) = C, C ∈ R | 0 (да-да, ноль!) |
| Степень с рациональным показателем |
f(x) = x n |
n · x n − 1 |
| Синус | f(x) = sin x | cos x |
| Косинус | f(x) = cos x | − sin x (минус синус) |
| Тангенс | f(x) = tg x | 1/cos2 x |
| Котангенс | f(x) = ctg x | − 1/sin2 x |
| Натуральный логарифм | f(x) = ln x | 1/x |
| Произвольный логарифм |
f(x) = log a x |
1/(x · ln a) |
| Показательная функция |
f(x) = e x |
e x (ничего не изменилось) |
Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:
(C · f)’ = C · f ’.
В общем, константы можно выносить за знак производной. Например:
(2x
3)’ = 2 · (x
3)’ = 2 · 3x
2 = 6x
2.
Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.
Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
Задача. Найти производные функций: f(x) = x
2 + sin x; g(x) = x
4 + 2x
2 − 3.
Функция f(x) — это сумма двух элементарных функций, поэтому:
f ’(x) = (x
2 + sin x)’ = (x
2)’ + (sin x)’ = 2x + cos x;
Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x) = (x
4 + 2x
2 − 3)’ = (x
4 + 2x
2 + (−3))’ = (x
4)’ + (2x
2)’ + (−3)’ = 4x
3 + 4x + 0 = 4x · (x
2 + 1).
Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x
2 + 1).
Производная произведения
Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike“>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Задача. Найти производные функций: f(x) = x
3 · cos x; g(x) = (x
2 + 7x − 7) · e
x
.
Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x
3 · cos x)’ = (x
3)’ · cos x + x
3 · (cos x)’ = 3x
2 · cos x + x
3 · (− sin x) = x
2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x
2 + 7x − 7) · e
x
)’ = (x
2 + 7x − 7)’ · e
x
+ (x
2 + 7x − 7) · (e
x
)’ = (2x + 7) · e
x
+ (x
2 + 7x − 7) · e
x
= e
x
· (2x + 7 + x
2 + 7x −7) = (x
2 + 9x) · e
x
= x(x + 9) · e
x
.
Ответ:
f ’(x) = x
2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e
x
.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Производная частного
Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:
![]()
Неслабо, да? Откуда взялся минус? Почему g
2? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.
Задача. Найти производные функций:
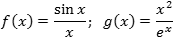
В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:
![]()
![]()
По традиции, разложим числитель на множители — это значительно упростит ответ:
![]()
Ответ:
![]()
Производная сложной функции
Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x
2 + ln x. Получится f(x) = sin (x
2 + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.
Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:
f ’(x) = f ’(t) · t ’, если x заменяется на t(x).
Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.
Задача. Найти производные функций: f(x) = e
2x + 3; g(x) = sin (x
2 + ln x)
Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e
x
. Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e
t
. Ищем производную сложной функции по формуле:
f ’(x) = f ’(t) · t ’ = (e
t
)’ · t ’ = e
t
· t ’
А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:
f ’(x) = e
t
· t ’ = e
2x + 3 · (2x + 3)’ = e
2x + 3 · 2 = 2 · e
2x + 3
Теперь разберемся с функцией g(x). Очевидно, надо заменить x
2 + ln x = t. Имеем:
g ’(x) = g ’(t) · t ’ = (sin t)’ · t ’ = cos t · t ’
Обратная замена: t = x
2 + ln x. Тогда:
g ’(x) = cos (x
2 + ln x) · (x
2 + ln x)’ = cos (x
2 + ln x) · (2x + 1/x).
Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.
Ответ:
f ’(x) = 2 · e
2x + 3;
g ’(x) = (2x + 1/x) · cos (x
2 + ln x).
Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.
Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:
(x
n
)’ = n · x
n − 1
Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x
0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.
Задача. Найти производную функции:
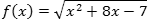
Для начала перепишем корень в виде степени с рациональным показателем:
f(x) = (x
2 + 8x − 7)0,5.
Теперь делаем замену: пусть x
2 + 8x − 7 = t. Находим производную по формуле:
f ’(x) = f ’(t) · t ’ = (t
0,5)’ · t ’ = 0,5 · t
−0,5 · t ’.
Делаем обратную замену: t = x
2 + 8x − 7. Имеем:
f ’(x) = 0,5 · (x
2 + 8x − 7)−0,5 · (x
2 + 8x − 7)’ = 0,5 · (2x + 8) · (x
2 + 8x − 7)−0,5.
Наконец, возвращаемся к корням:
![]()
Ответ:
![]()
Смотрите также:
- Вводный урок по вычислению производных степенной функции

- Уравнение касательной к графику функции

- Тест к параграфу «Что такое логарифм» (легкий)

- Комбинаторика в задаче B6: легкий тест

- Задача B2: лекарство и таблетки

- Задача B4 про шерсть и свитер

Содержание
- Что такое производная?
- Таблица производных.
- Термины и обозначения.
- Таблица производных.
- Малоизвестные факты о штрихкодах — загадочные цифры под штрихкодом
- Загадочные цифры под штрихкодом
- Кассовый штрихкод
- GS1 DataMatrix
Что такое производная?
Таблица производных.
Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.
Это знакомство позволит:
— понимать суть несложных заданий с производной;
— успешно решать эти самые несложные задания;
— подготовиться к более серьёзным урокам по производной.
Сначала — приятный сюрприз.)
Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!
Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует.
Приступим к знакомству?)
Термины и обозначения.
В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.
Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.
Дифференцирование — действие над функцией.
Производная — результат этого действия.
Так же, как, например, сумма — результат сложения. Или частное — результат деления.
Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т.п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y’ или f'(x) или S'(t) и так далее.
Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли. )
Штрих также может обозначать производную конкретной функции, например: (2х+3)’, (x 3 )’, (sinx)’ и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.
Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.
Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:
1. Таблица производных (формулы дифференцирования).
3. Производная сложной функции.
Начнём по порядку. В этом уроке рассмотрим таблицу производных.
Таблица производных.
В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.
Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)
Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
| Функция y |
Производная функции y y’ |
|
| 1 | C (постоянная величина) | C’ = 0 |
| 2 | x | x’ = 1 |
| 3 | x n (n — любое число) | (x n )’ = nx n-1 |
| x 2 (n = 2) | (x 2 )’ = 2x | |
 |
 |
|
 |
 |
|
| 4 | sin x | (sin x)’ = cosx |
| cos x | (cos x)’ = — sin x | |
| tg x |  |
|
| ctg x |  |
|
| 5 | arcsin x |  |
| arccos x |  |
|
| arctg x |  |
|
| arcctg x |  |
|
| 4 | a x |  |
| e x |  |
|
| 5 | loga x |  |
| ln x (a = e) |  |
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету.
Рассмотрим несколько примеров:
1. Найти производную функции y = x 3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x 3 )‘ = 3·x 3-1 = 3x 2
Ответ: y’ = 3x 2
2. Найти значение производной функции y = sinx в точке х = 0.
Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию. Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.
По табличке находим синус и соответствующую производную:
Подставляем ноль в производную:
Это и будет ответ.
3. Продифференцировать функцию:
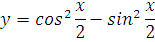
Что, внушает? ) Такой функции в таблице производных и близко нет.
Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает.
Но если увидеть, что наша функция — это косинус двойного угла, то всё сразу налаживается!
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
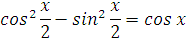
Т.е. наша хитрая функция есть не что иное, как y = cosx. А это — табличная функция. Сразу получаем:
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
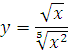
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями. То вполне можно упростить эту функцию. Вот так:

А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:

Вот и всё. Это будет ответ.
Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.
Источник
Малоизвестные факты о штрихкодах — загадочные цифры под штрихкодом
Число зверя, штрихи смерти — насколько все это реально? Можно ли зашить в штрихкод видеоролик или фото голой Эммы Уотсон? Бывают ли “неправильные штрихкоды”, и что вообще значит “неправильный штрихкод”?
В “Клеверенсе” мы разрабатываем платформу Mobile SMARTS для создания мобильных решений по учету маркированного товара и постоянно сталкиваемся с детскими ошибками в маркировке. Обычно они вызваны простым нежеланием людей хоть немного разбираться в теме.
Наша платформа тоже не идеальна, но кое-что в своём деле мы понимаем. Статья не к тому, что типа мы крутые и разбираемся, а все вокруг не крутые и не разбираются, нет. У каждого свои задачи, мы тоже часто лажаем. Просто тема набирает популярность и выходит в массы, а любые ошибки стоят денег.
Сначала для затравки расскажем про кассовый штрихкод, а затем про загадочный GS1 DataMatrix, который используется в проекте тотальной маркировки товаров.
Сама статья больше развлекательная, всё изложенное при желании легко гуглится, но может и побудить кого-то изучить тему глубже.
Загадочные цифры под штрихкодом
Цифры под штрихкодом — что это такое? Знающие люди говорят, что тут всё просто: именно эти цифры “зашиты” в штрихкод. Девушка на кассе вбивает в программу цифры под штрихкодом — и вуаля — товар найден.
К сожалению, это заблуждение. Цифры под штрихкодом не “зашиты” в штрихкод. Для разговоров у камина сойдет, а для айтишника беда.
Это распространенное заблуждение приводит к тому, что когда встает задача распечатать штрихкод, человек гуглит бесплатный онлайн генератор штрихкода, пихает в поле эти самые цифры, и… получает проблему на ровном месте.
Надписи под штрихкодом называются Human readable interpretation (HRI). Одно только название уже должно наводить на мысль, что тут не всё в порядке.
В самом мягком варианте вера в то, что цифры под штрихкодом повторяют содержимое штрихкода — это примерно как верить в то, что название файла определяет его содержимое. Типа: “Переименовала ваш файл в .doc, но он всё равно не открывается”.
Рассмотрим подробнее, где тут собака зарыта.
Кассовый штрихкод
Пример про кассовый штрихкод — для затравки. Он на самом деле не вызывает никаких проблем, потому что за 50 лет использования в софте и оборудовании были вставлены 1000 костылей, чтобы обойти все проблемы (ну почти). Зато он хорошо иллюстрирует вопрос.
Вот в этих двух штрихкодах (EAN-13) ниже, под которыми написано “4601200000003” и “0123456789128”, в обоих нет штрихов для первой цифры. В первом штрихкоде нет штрихов для “4” (она закодирована другим способом), а во втором штрихкоде вообще в принципе нет лидирующего нуля, хотя он и напечатан под штрихкодом.
Да-да, именно первой цифры, а не последней (чексуммы) как можно было бы подумать. Последняя цифра (чексумма) в полосках этих штрихкодов как раз-таки есть, иначе затея с чексуммой не будет работать.
Рассмотрим поближе, что тут происходит.
В первом приведенном штрихкоде (“4601200000003”) в начале идут две длинные полосочки, они кодируют “начало штрихкода”, далее идут штрихи и пропуски для цифры “6”, затем про цифры “0”, “1”, “2”, “0” и “0”, две длинные полосочки в центре говорят про середину, затем пять одинаковых групп штрихов и пропусков кодируют “00000”, далее идут штрихи и пропуски для цифры “3” и завершающие две длинные полоски про конец штрихкода. Итого, в штрихкоде есть штрихи только про “601200000003”. Цифра “3” (последняя) в полосках штрихкода есть, а первой “4” нет! Откуда же взялась “4”?
Дело в том, что “4” закодирована грязным хаком. Для неё не хватает места, и вообще всё это большой исторический казус.
Изначально такие кассовые штрихкоды появились в США, там они состоят из 12 цифр и называются UPC (Universal Product Code). Для переноса технологии в Европу и адаптации стандарта Европе нужны были дополнительные цифры, потому что американские 12 все уже были заняты.
Первым товаром, приобретенным по штрих-коду на этикетке, стал блок из 10 жевательных резинок Wrigley Juicy Fruit. Это произошло в супермаркете Marsh города Трой (Огайо) в четверг, 26 июня 1974 года в 8.01 утра. В историю вошли и имя покупателя, и имя кассира, открывших новую страницу розничной торговли. Теперь упаковка жвачки, которая тогда обошлась в 67 центов, вместе с чеком хранятся в музее американской истории Смитсоновского института.
Чтобы расширить емкость, можно было бы просто добавить еще немного штрихов и пропусков, но в те времена это серьезно ухудшало считываемость. Поэтому вместо того, чтобы просто увеличить штрихкод в ширину, был применен “хак”.
По американскому стандарту любая из цифр штрихкода может быть записана: а) обычными штрихами и пропусками; б) их зеркальным отражением; в) инверсией черного и белого; г) зеркальной инверсией. Всё это нужно для того, чтобы можно было печатать инверсные штрихкоды (белым по черному) и сканировать штрихкод вверх ногами (зеркальное отражение в случае штрихкода — то же самое, что и поворот на 180°).
В “американском” штрихкоде (который на 12 цифр) первые 6 цифр кодируются обычными штрихами, а вторые 6 цифр инвертированными штрихами (где черные штрихи заменены на белые полоски и наоборот). Это сделано для того, чтобы понимать, перевернут штрихкод или нет, нормально я его сканирую или вверх ногами (и затем декодировать цифры в правильном порядке, а не задом наперед).
В новом “европейском” штрихкоде (который на 13 цифр), первая цифра (например, “4”) кодируется не штрихами, а путем «перетасовывания» способов кодирования следующих за ней 6 цифр из первого блока (второй блок из 6 оставили в покое).
Например, следующая за четверкой “6” выводится как обычно, штрихи следующего за ней “0” выводятся в обратном порядке (зеркально), следующие за ней “1” и “2” выводится снова в обычном виде, следующие два “0” снова зеркально. Общая длина штрихкода и число штрихов в результате этого трюка не меняется.
Для “американского сканера” такая белиберда не имеет смысла, а для Европы это тайный знак того, что в штрихкоде закодирована еще одна цифра! (да, мы всегда знали, что европейцы извращенцы).
Для всех цифр от “1” до “9” были придуманы такие правила тасовки способов кодирования. Для “0” ничего нет, т.е. 13-значный штрихкод с лидирующим нулем визуально ничем не отличается от 12-значного штрихкода без этого лишнего ноля (EAN-13 с лидирующим нулем эквивалентен UPC-А).
Из этого получается первый прикол, что если перед нами “американский” штрихкод (в котором варианты кодирования не “перетасованы”), то “американский сканер” читает 12 цифр, а условный “европейский сканер” может считать, что в нем есть лидирующий «0», и считывать лишний ноль (т.к. для кодирования ноля не предусмотрено никакой “перетасовки”, этого “лидирующего нуля” очевидно в принципе нигде нет в штрихкоде).
Конечно, мир давно глобализован, поэтому “американский” сканер и “европейский” сканер — это просто условности. Сканер один и тот же, но у него есть настройка: нужно ли ему в принципе считывать EAN-13 (Европа) или читать только UPC-А (США), а если считывать EAN-13, то надо ли добавлять лишний ноль к американским штрихкодам UPC-А.
С этим связана одна распространенная проблема при внедрении штрихкодирования: когда в базе данных у компании либо нет нолей в начале штрихкодов, а сканер считывает с “лишним” нолем, либо наоборот, в базе данных есть ноль в начале, а сканер его “не считывает” (хотя, что там считывать, — этого ноля в принципе в штрихкоде нет).
Казалось бы, сложно накосячить в использовании EAN-13/UPC. Тем не менее, люди делают следующие ошибки:
- Сохраняют штрихкод в учетной системе без чексуммы (последнего знака).
- Забывают обрабатывать присутствие/отсутствие лидирующего нуля при разработке алгоритма поиска по штрихкоду.
- Требуют ввода 13 символов, а потом приходят сигареты с EAN-8 (с вводом маркировки табака станет неактуально, но пока так).
- Не оставляют положенных широких белых полей справа и слева от штрихкода.
В наших программных продуктах, таких как “Магазин 15” или “Склад 15”, построенных на платформе Mobile SMARTS, мы решаем эту проблему очень просто: сканер устройства всегда автоматически настраивается на возврат ноля, а поиск товара по базе данных производится два раза: и с нолем, и без ноля (чтобы уж точно найти товар).
Сканер мы стараемся настраивать программно, без участия человека. Если сканер нельзя настроить программно — то это всегда проблема, потому что по умолчанию сканером может обрезаться не только 0 (который в начале), но еще и чексумма (которая в конце), тогда в программу придут не 13, а уже 11 символов, зачастую даже без указания типа штрихкода (такие замечательные сканеры тоже бывают).
В этом случае мы бессильны улучшить результат. 11 символов могли прийти от сканирования любого другого типа штрихкода, мы не можем считать все штрихкоды как EAN-13. Чтобы настроить сканер, человеку придется сканировать с листа настроечные штрихкоды или заходить в какие-нибудь меню, а всё это — источники ошибок.
GS1 DataMatrix
Этот пример стал популярным благодаря введению обязательной маркировки товаров. История полна граблей, велосипедов и трупиков мелких животных, как сарай вашей бабушки.
Ну ладно, допустим с EAN-13 можно придраться и сказать, что первая цифра всё-таки есть в штрихкоде, просто она закодирована не совсем штрихами (хотя для лидирующего “0” это и не так).
Возьмем тогда другой пример, штрихкод GS1 DataMatrix «(21)abba01(01)04601200000003»:
В этом штрихкоде “внутри” нет ни скобок, ни символа «0», ни буквы «a», ни переноса строки.
Что тут происходит?
Во-первых, никакие скобки в штрихкод не кодируются, они печатаются только для удобства прочтения человеком. Это снова называется Human readable interpretation (HRI), привет, кожаный мешок.
Во-вторых, в штрихкоде есть специальные управляющие символы, которые должна расставить та программа, которая формирует данные для штрихкода. Не какая-то бесплатная opensource программа, написанная умными очкариками, а ваша программа, та самая, которую пишете Вы, мой друг. В этот раз символы, которые нужно вставить, не имеют отношения к “коррекции” и т.п., а размечают данные, которые нужно закодировать в штрихкод.
В самом начале в штрихкод вставляется управляющий символ, который называется FNC1 и имеет код 232, что соответствует либо странному печатаемому символу «Þ» (ANSI), либо русской букве “и” (Windows-1251), смотря какую кодировку использовать. Этот символ говорит, что у нас не просто абы какой DataMatrix, а именно GS1 DataMatrix, данные в котором имеют определенный формат: массив данных из пар (“код поля”, “значение поля”).
Этот управляющий символ FNC1 попадает в самое начало штрихкода, но его нельзя “передать” в штрихкод в составе данных.
Кроме того, непечатаемые символы, вполне очевидно, нельзя копипастить в составе строки, хаха! Страдай, кожаный мешок!
Указание, нужен префикс или не нужен, обычно передают как отдельную настройку (галочку) в программу формирования штрихкода. Если передать префикс как часть данных, то получим либо ошибку, либо два префикса в штрихкоде (в зависимости от используемой программы).
Далее, поскольку в штрихкоде внутри нет скобок, то уже непонятно, где кончается одно поле и начинается другое, где тут номера полей. Без скобок получается “21abba010104601200000003” (тут “01” встречается три раза, ха-ха).
Где заканчивается “01” из значения поля (21) и начинается настоящее (01)?
Это решается следующим способом:
По стандарту GS1 поля имеют формат. Не абы что, а формат значения. Например, значение для (01) должно состоять из 14 цифр и баста (нельзя 13 цифр, нельзя 12 цифр, нельзя не цифры). А поле (21), наоборот, имеет переменную длину, разрешены цифры, латинские буквы обоих регистров, знаки препинания и даже (опачки!) скобки.
Если после значения для (21) штрихкод не закончился, и там еще что-то есть, то в данные вставляется разделитель (это может быть снова или FNC1, или непечатаемый символ GS с кодом 29).
А общее правило звучит так: спецсимвол GS не вставляется, только в случае если AI начинается с пары цифр из этой вот таблицы:
Для всех остальных полей GS1 (не из этой таблицы) в конце значения нужно вставлять GS.
Т.е., мы получим “FNC121abba01GS0104601200000003” (только помним, что первый FNC1 мы не будем передавать в программу формирования штрихкода, а второй GS — это не строка “GS”, а один символ с кодом 29).
Эти требования — именно про данные, а не про штрихкод DataMatrix, потому что в штрихкод DataMatrix можно положить любые данные, они прекрасно закодируются и прочитаются. Тут речь о GS1 DataMatrix, который имеет определенный формат, и ваша программа должна соблюсти этот формат, прежде чем подавать данные в штрихкод.
Вообще говоря, в мире существуют программы печати штрихкодов, которым можно скармливать данные со скобками и они сами всё разрулят. Но это специализированный софт, который стоит денег, а не тот бестолковый и бесплатный онлайн-генератор штрихкодов, которым вы пользуетесь.
И наконец. То, как это будет напечатано и то, как это будет отсканировано, — две большие разницы. То, как данные печатаются под штрихкодом, и как они передаются сканером — это в чистом виде настройки принтера и сканера.
В нашем примере мы закодировали в штрихкод поля порядке: сначала (21), потом (01), а на изображении под штрихкодом распечаталось сначала (01), потом (21). Это снова называется Human readable interpretation (HRI), и порядок вывода в подписи соответствует правилу “потому что так принято”.
Сканер штрихкодов тоже имеет свои настройки, которые заставляют его переставлять поля, вставлять скобки и другие символы, переносить строки и т.п.
В большинстве случаев сканер прочитает наш штрихкод как “21abba01GS0104601200000003”. Никакого лидирующего FNC1, никаких скобок, GS не печатаемый и не виден в “Блокноте” (нужно использовать хотя бы Notepad+).
И принтер, и сканер могут делать со штрихкодами что хотят: добавлять и убирать символы, менять их местами — ради соответствия гайдлайну или для совместимости со сторонней программой.
Что еще интересно: в этом штрихкоде только 16 байт данных (на 24 символа без скобок).
Вот что тут происходит:
- пары подряд идущих цифр кодируются одним байтом;
- все отдельно стоящие цифры, не парные, а также все символы из таблицы ASCII (а это символы с кодами с 0 по 127, без русских букв, и печатаемые, и непечатаемые) кодируются в штрихкод как (значение байта символа)+1.
Т.е. чтобы закодировать “a”, нужно записать в штрихкод “b”, чтобы закодировать “1”, нужно записать “2” и т.д., именно поэтому прямо в самом штрихкоде нет байта 97 (значение буквы “a” в ASCII).
Итого, в приведенном штрихкоде “закодировано” в байтах 232, 151, 98, 99, 99, 98, 131, 232, 131, 134, 190, 142, 130, 130, 130, 133. И это еще до кодов коррекции и паддинга!
Непонимание процесса кодирования приводит к тому, что, например, для начавшейся обязательной маркировки обуви люди печатают на принтер неправильно сформированные данные и получают неправильные штрихкоды, которые выглядят вполне нормально, читаются приложением “Честный знак”, но данные в них неверные, как минимум это не GS1 DataMatrix.
Штрихкоды неправильно напечатаны, неправильно читаются, и такая обувь не считается правильно промаркированной.
В своем софте “Кировка” мы боремся с этим следующим образом: для печати принимаем в качестве исходных данных любой мусор, пытаемся распарсить его как GS1 DataMatrix, разбираем на косточки. Если всё прошло удачно, то конвертируем в правильный формат, чтобы принтер это понял; а при сканировании перепроверяем данные от сканера, делая таким образом вывод о правильности печати.
Для этого нам, конечно, приходится работать на нативном уровне и со сканером мобильных устройств, и с принтерами, чтобы всё это было правильно ими интерпретировано, а мы собирали максимально полную информацию.
Выполним еще одно упражнение: посмотрим, какого размера должен быть штрихкод GS1 DataMatrix для хранения кода маркировки обуви и легпрома.
На сайте «Честного знака» написано, что код маркировки обуви должен содержать следующие поля (для легпрома те же требования):
- Кода товара, 14 цифровых символов (GTIN).
- Индивидуального серийного номера единицы товара, который генерируется оператором системы или участником оборота товаров, 13 символов (s/n).
- Ключ проверки, предоставляемый оператором системы, 4 символа.
- Код проверки, предоставляемый оператором системы, 88 символов.
Для каждого из этих полей в данных для штрихкода должен быть указан идентификатор применения GS1 (AI, application identifier).

Таблица codeword для DataMatrix
Таблица, объясняющая кодирование КМ обуви в DataMatrix:
| Что | Формат | Codewords | Сколько байт | Всего байт, минимум | Всего байт, максимум |
|---|---|---|---|---|---|
| — | Codeword [232] | 1 | 1 | 1 | |
| AI (00) | — | Codeword [130] | 1 | 2 | 2 |
| GTIN | 14 цифр | Codeword со [130] по [229] | 7 | 9 | 9 |
| AI (21) | — | Codeword [141] | 1 | 10 | 10 |
| s/n | 13 знаков ASCII | Codewords с [1] по [128] и со [130] по [229] | от 7 до 13* | 17 | 23 |
| — | Codeword 30 | 1 | 18 | 24 | |
| AI (91) | — | Codeword 221 | 1 | 19 | 25 |
| Ключ проверки | 4 цифры | Codeword с 130 по 229 | 4 | 23 | 29 |
| AI (92) | — | Codeword 222 | 1 | 24 | 30 |
| Код проверки | 88 знаков ASCII | Codewords с [1] по [128] и со [130] по [229] | от 44 до 88* | 28 | 118 |
* если в данных для штрихкода есть пары подряд идущих цифр, то они будут кодироваться одним байтом, а не двумя (Codewords со [130] по [229]), и это экономит байты.
Как видно, размер данных в теории может меняться в широких пределах от 68 до 118 байт. На практике разброс меньше, длина ближе к 118, потому что в серийном номере и в криптокоде мало цифр и много знаков препинания, включая скобки.
Согласно GS1 DataMatrix Guideline, такие данные укладываются в штрихкоды размером от 36х36 до 44х44 (колонок и строк битов, не миллиметров). В миллиметрах размер будет зависеть от разрешающей способности принтера (обычно это 203-600 dpi).

Таблица из GS1 DataMatrix Guideline
А как же голая Эмма Уотсон? Рассмотрим в следующей статье.
Источник
Как определять цену деления приборов
Измерительные приборы, как правило, имеют шкалу. Это значит, что на нем нанесены штриховые деления, а рядом написаны числовые значения величин, соответствующие делениям. Расстояния между двумя штрихами, возле которых написаны значения физической величины, могут быть дополнительно разделены еще на несколько делений, не подписанных числами. Расстояние между двумя ближайшими штрихами называется ценой деления шкалы прибора, которую необходимо определить перед использованием самого оборудования.

Инструкция
Перед тем, как находить цену деления, внимательно рассмотрите сам прибор: что он измеряет, в каких единицах, его исправность. Это позволит нарисовать полную картину проводимого опыта по определению той или иной величины. Найдите на шкале два ближайших штриха, возле которых написаны числовые значения величины. Посчитайте сколько между ними делений (но не штрихов).
Пример. Пусть нужно определить цену деления бытового термометра. Соседние подписанные штрихи 10 и 20 градусов Цельсия. Между ними помещается десять делений.Найдите положительную разность между выбранными числовыми значениями величины, для этого отнимите от большего числа меньшее число. Полученную разницу разделите на количество делений, находящихся между ними. Полученное частное является ценой деления, без знания которой не определить показания измерительного прибора.
Пример. 20-10=10 градусов Цельсия. Разность, равная десяти градусам Цельсия, делится на десять делений между штрихами: 10/10=1 градус Цельсия. Значит, цена деления выбранного термометра равна один градус Цельсия.
Видео по теме
Обратите внимание
У разных приборов, называющихся одинаково, может быть разная шкала, следовательно, и цена деления может отличаться.
Источники:
- Опыт работы учителем физики.
- цена деления термометра
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
