Как найти дополнительные плоские углы

Содержание:

• Определение плоского угла
• Плоские углы бывают следующих типов:
• Виды плоских углоов, в зависимости от меры

Определение плоского угла

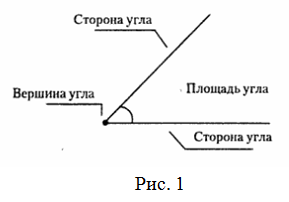
Плоские углы бывают следующих типов:

Виды плоских углоов, в зависимости от меры

Читать дальше: что такое прямой угол.

Содержание

• Примеры
• Пример А
• Пример Б
• Пример C
• Пример D
• Пример E
• Пример F
• Упражнения
• – Упражнение I
• Решение
• – Упражнение II.
• Решение
• – Упражнение III.
• Решение
• Дополнительные углы в двух параллелях, разрезанных секущей
• – Упражнение IV.
• Решение
• Ссылки

Два или более дополнительные углы если сумма его мер соответствует мере прямого угла. Мера прямого угла, также называемого плоским углом, в градусах равна 180º, а в радианах – π.

Например, мы обнаруживаем, что три внутренних угла треугольника являются дополнительными, поскольку сумма их мер равна 180 °. На рисунке 1 показаны три угла. Из вышесказанного следует, что α и β являются дополнительными, так как они смежны и их сумма составляет прямой угол.

Также на том же рисунке у нас есть углы α и γ, которые также являются дополнительными, потому что сумма их мер равна мере плоского угла, то есть 180º. Нельзя сказать, что углы β и γ являются дополнительными, потому что, поскольку оба угла тупые, их размеры больше 90 °, и поэтому их сумма превышает 180 °.

Вместо этого можно сказать, что мера угла β равна мере угла γ, поскольку, если β является дополнительным к α, а γ является дополнительным к α, тогда β = γ = 135º.

Примеры

В следующих примерах предлагается найти неизвестные углы, обозначенные вопросительными знаками на рисунке 2. Они варьируются от самых простых примеров до более сложных, и читателю следует быть более внимательным.

Пример А

На рисунке мы видим, что смежные углы α и 35º в сумме составляют плоский угол. То есть α + 35º = 180º и, следовательно, верно, что: α = 180º- 35º = 145º.

Пример Б

Поскольку β является дополнительным к углу 50º, то отсюда следует, что β = 180º – 50º = 130º.

Пример C

Из рисунка 2C можно увидеть следующую сумму: γ + 90º + 15º = 180º. То есть γ является дополнительным с углом 105º = 90º + 15º. Отсюда делается вывод, что:

γ  = 180º- 105º = 75º

Пример D

Поскольку X является дополнительным к 72º, отсюда следует, что X = 180º – 72º = 108º. Кроме того, Y дополняет X, поэтому Y = 180º – 108º = 72º.

И, наконец, Z дополняет 72º, поэтому Z = 180º – 72º = 108º.

Пример E

Углы δ и 2δ являются дополнительными, поэтому δ + 2δ = 180º. Это означает, что 3δ = 180º, а это, в свою очередь, позволяет нам написать: δ = 180º / 3 = 60º.

Пример F

Если мы назовем угол между 100º и 50º U, то U будет дополнительным для них обоих, потому что наблюдается, что их сумма завершает плоский угол.

Отсюда сразу следует, что U = 150º. Так как U по вершине противоположно W, то W = U = 150º.

Упражнения

Ниже предлагаются три упражнения, во всех которых значение углов A и B должно быть найдено в градусах, чтобы выполнялись соотношения, показанные на рисунке 3. При решении всех из них используется концепция дополнительных углов.

– Упражнение I

Определите значения углов A и B из части I) рисунка 3.

Решение

A и B являются дополнительными, из чего мы получаем, что A + B = 180 градусов, тогда выражение A и B подставляется как функция от x, как показано на изображении:

(х + 15) + (5x + 45) = 180

Получено линейное уравнение первого порядка. Для ее решения термины сгруппированы ниже:

6 х + 60 = 180

Разделив оба члена на 6, мы получим:

х + 10 = 30

И, наконец, решая, следует, что x стоит 20º.

Теперь мы должны подставить значение x, чтобы найти требуемые углы. Следовательно, угол A равен: A = 20 +15 = 35º.

В свою очередь, угол B равен B = 5 * 20 + 45 = 145º.

– Упражнение II.

Найдите значения углов A и B из части II) рисунка 3.

Решение

Поскольку A и B – дополнительные углы, мы имеем A + B = 180 градусов. Подставляя выражение для A и B как функцию от x, приведенное в части II) рисунка 3, мы имеем:

(-2x + 90) + (8x – 30) = 180

Снова получается уравнение первой степени, для которого необходимо удобно сгруппировать члены:

6 х + 60 = 180

Разделив оба члена на 6, мы получим:

х + 10 = 30

Отсюда следует, что x стоит 20º.

Другими словами, угол A = -2 * 20 + 90 = 50º. При этом угол B = 8 * 20 – 30 = 130º.

– Упражнение III.

Определите значения углов A и B из части III) рисунка 3 (зеленого цвета).

Решение

Поскольку A и B – дополнительные углы, мы имеем A + B = 180 градусов. Мы должны подставить выражение для A и B как функцию от x, приведенное на рисунке 3, из которого мы имеем:

(5x – 20) + (7x + 80) = 180

12 х + 60 = 180

Разделив оба члена на 12, чтобы найти значение x, мы имеем:

х + 5 = 15

Наконец, оказывается, что x стоит 10 градусов.

Теперь переходим к замене, чтобы найти угол A: A = 5 * 10 -20 = 30º. А для угла B: B = 7 * 10 + 80 = 150º.

Дополнительные углы в двух параллелях, разрезанных секущей

Две параллельные прямые, пересекаемые секущей, – обычная геометрическая конструкция в некоторых задачах. Между такими линиями образовано 8 углов, как показано на рисунке 4.

Из этих 8 углов некоторые пары углов являются дополнительными, которые мы перечисляем ниже:

1. Внешние углы A и B, а также внешние углы G и H
2. Внутренние углы D и C, а также внутренние углы E и F
3. Внешние углы A и G, а также внешние углы B и H
4. Внутренние углы D и E, а внутренние C и F

Для полноты картины равные друг другу углы также называются:

1. Внутренние альтернативы: D = F и C = E
2. Внешние альтернативы: A = H и B = G
3. Соответствующие: A = E и C = H
4. Противоположности по вершине A = C и E = H
5. Соответствующие: B = F и D = G
6. Противоположности вершин B = D и F = G

– Упражнение IV.

Ссылаясь на рисунок 4, на котором показаны углы между двумя параллельными линиями, пересеченными секущей, определите значение всех углов в радианах, зная, что угол A = π / 6 радиан.

Решение

A и B – дополнительные внешние углы, поэтому B = π – A = π – π / 6 = 5π / 6

А = Е = С = Н = π / 6

B = F = D = G = 5π / 6

Ссылки

1. Балдор, Дж. А. 1973. Плоская и космическая геометрия. Центральноамериканская культура.
2. Математические законы и формулы. Системы измерения углов. Получено с: ingemecanica.com.
3. Вентворт, Г. Плоская геометрия. Получено с: gutenberg.org.
4. Википедия. Дополнительные углы. Получено с: es.wikipedia.com
5. Википедия. Конвейер. Получено с: es.wikipedia.com
6. Сапата Ф. Гониометро: история, детали, работа. Получено с: lifeder.com

 Дата:              
Тема: «Свойство плоских углов». Каломыцов Т.В

Цель
Научиться находить меры плоских углов используя свойства линейных углов.
Применение теоремы о сумме плоских углов

«∠», обозначение угла в математике

Плоский у́гол — неограниченная геометрическая фигура, 

образованная двумя лучами (сторонами угла), выходящими из одной

 точки (вершины угла).

Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.

Иногда, для краткости, углом называют угловую меру.

Угловая мера

Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — 

отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.

1 оборот = 2π радианам = 360°
= 400 градам.

В системе СИ принято использовать радианы.

В морской терминологии углы обозначаются румбами.

Углы на тригонометрической окружности

В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.

В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.

Типы углов

Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.

Центральные и вписанные углы окружности.

В зависимости от величины углы разделяются на:

Невыпуклый угол

Прямой угол

• Острые (от 0 до 90°)
• Прямые (90°)
• Тупые (от 90° до 180°)
• Развернутые (180°)
• Невыпуклые (от 180° до 360°)
• Полные (360°)

Теорема
: Сумма величин всех
плоских углов выпуклого многогранного угла меньше 360 ⁰

Вариации и обобщения

Величиной ориентированного угла между прямыми AB и CD (обозначение:  называют величину угла, на который нужно 

повернуть против часовой стрелки прямую AB так, чтобы она стала 

параллельна прямой CD. При этом углы, отличающиеся на 

 считаются равными. Следует отметить, что ориентированный угол

 между прямыми CD и AB не равен ориентированному углу между

 прямыми AB и CD (они составляют в сумме  или, что по нашему соглашению то же самое,  Ориентированные углы обладает следующими свойствами: а) б) в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда .

Ряд практических задач приводит к целесообразности рассматривать

 угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы,

 большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный     угол

Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.

Образцы
решения задач

Задача
1

Все
плоские углы трёхгранного угла равны 90^o . Найдите
углы между биссектрисами плоских углов.

Решение

Рассмотрим
куб ABCDA1B1C1D1 . Плоские углы трёхгранного
угла ABDA1 с вершиной A равны 90^o .
Найдём угол между биссектрисой AC плоского угла BAD и
биссектрисой AD₁ плоского угла DAA₁ .
Для этого рассмотрим треугольник CAD₁ . Его
стороны – диагонали равных квадратов. Значит, этот треугольник равносторонний.
Следовательно,  CAD1 = 60^o .

Ответ

60^o .

Задача
2

Дан
трёхгранный угол. Рассмотрим три плоскости, содержащие его грани. Эти плоскости
разбивают пространство на восемь трёхгранных углов.

. а)
Найдите плоские углы всех образовавшихся трёхгранных углов, если плоские углы
исходного трёхгранного угла равны x , y и z .

 б)
Найдите двугранные углы всех образовавшихся трёхгранных углов, если двугранные
углы исходного трёхгранного угла равны α , β и γ .

Ответ

а) 180^o –
x , 180^o – y , z ; x , 180^o –
y , 180^o – z ; 180^o –
x , y , 180^o – z ; x , y , z ; 180^o –
x , 180^o – y , z ; x , 180^o –
y , 180^o – z ; 180^o –
x , y , 180^o – z ;

 б) 180^o –
α , 180^o – β , γ ; α , β , 180^o –
γ ; 180^o – α , β , 180^o-γ ; α , β , γ ; 180^o –
α , 180^o – β , γ ; α , β , 180^o –
γ ; 180^o – α , β , 180^o –
γ .

Задача
3

Все
плоские углы трёхгранного угла равны по 60^o .
Найдите углы, образованные рёбрами этого трёхгранного угла с плоскостями
противоположных граней.

Решение

Пусть O –
вершина данного трёхгранного угла. Отложим на его рёбрах отрезки OA , OB и OC ,
причём OA = OB = OC = a . Тогда треугольники OAB , OAC и OBC –
равносторонние. Поэтому AB = BC = AC = a . Таким образом все
грани пирамиды OABC – равные равносторонние треугольники со стороной a .
Пусть M – ортогональная проекция точки A на
плоскость OBC . Тогда AOM – угол между
ребром OA и противоположной ему гранью BOC данного
трёхгранного угла. Так как AB = AC = AO , то M –
центр равностороннего треугольника BOC . Из прямоугольного треугольника AMO находим,
что

cos  AOM
=  =  = .

Поэтому  AOM =
arccos  . Ясно, что
остальные углы также равны arccos  .

Ответ

arccos  .

Задача
4. Найдите дополнительные плоские углы,
зная, что: 1) один из них в 5 раз больше другого; 2) один из них на 100° больше
другого; 3) разность их равна 20°.

1) Пусть
1-й угол равен x°, тогда 2-й будет 5x°, а т.к. сумма двух плоских углов равна
360°, то:

x + 5x =
360°, 6x = 360°, x = 60°.

Значит,
1-й угол — 60°, а 2-й — 300°.

2) Пусть
1 -й угол равен x°, тогда 2-й будет (x + 100°), а их сумма 360°, т.е.:

x + x +
100° = 360°, 2x = 260°, x = 130°,

100° + x =
230°.

Значит,
1-й угол— 130°, а 2-й — 230°.

3) Пусть
1-й угол равен x°, тогда 2-й будет x + 20°, а их сумма 360°, т.е.:

x + х +
20° = 360°, 2x = 340°, x = 170°,

20° + x =
190°.

Значит,
1-й угол — 170°, а 2-й — 190°. Ответ: 1) 60°, 300°; 2) 130°, 230°; 3) 170°,
190°.

Домашнее
задание Решить задачи  ( 7 ,13)

№7
Сущетвует ли трёхгранный угол, плоские углы которого равны:  1)90 65 45 2) 33
45 78

№13
нарисуйте многогранник имеющий 5 граней и 5 вершин . Сколько ребер он имеет.