Ряды с комплексными членами.
19.3.1. Числовые ряды с комплексными членами. Все основные определения сходимости, свойства сходящихся рядов, признаки сходимости для комплексных рядов ничем не отличаются от действительного случая.
19.3.1.1. Основные определения. Пусть дана бесконечная последовательность комплексных чисел  . Действительную часть числа
. Действительную часть числа  будем обозначать
будем обозначать  , мнимую –
, мнимую –  (т.е.
(т.е.  .
.
Числовой ряд – запись вида  .
.
Частичные суммы ряда: 
Определение. Если существует предел S последовательности частичных сумм ряда при  , являющийся собственным комплексным числом, то говорят, что ряд сходится; число S называют суммой ряда и пишут
, являющийся собственным комплексным числом, то говорят, что ряд сходится; число S называют суммой ряда и пишут  или
или  .
.
Найдём действительные и мнимые части частичных сумм: 
 , где символами
, где символами  и
и  обозначены действительная и мнимая части частичной суммы. Числовая последовательность сходится тогда и только тогда, когда сходятся последовательности, составленные из её действительной и мнимой частей. Таким образом, ряд с комплексными членами сходится тогда и только тогда, когда сходятся ряды, образованные его действительной и мнимой частями.
обозначены действительная и мнимая части частичной суммы. Числовая последовательность сходится тогда и только тогда, когда сходятся последовательности, составленные из её действительной и мнимой частей. Таким образом, ряд с комплексными членами сходится тогда и только тогда, когда сходятся ряды, образованные его действительной и мнимой частями.
Пример. Исследовать на сходимость ряд  .
.
Выпишем несколько значений выражения  :
:  дальше значения периодически повторяются. Ряд из действительных частей:
дальше значения периодически повторяются. Ряд из действительных частей:  ; ряд из мнимых частей
; ряд из мнимых частей  ; оба ряда сходятся (условно), поэтому исходный ряд сходится.
; оба ряда сходятся (условно), поэтому исходный ряд сходится.
Рекомендуемые материалы
19.3.1.2. Абсолютная сходимость.
Определение. Ряд  называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд  , составленный из абсолютных величин его членов.
, составленный из абсолютных величин его членов.
Так же, как и для числовых действительных рядов с произвольными членами, можно доказать, что если сходится ряд  , то обязательно сходится ряд
, то обязательно сходится ряд  . Если ряд
. Если ряд  сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  называется условно сходящимся.
называется условно сходящимся.
Ряд  – ряд с неотрицательными членами, поэтому для исследования его сходимости можно применять все известные признаки ( от теорем сравнения до интегрального признака Коши).
– ряд с неотрицательными членами, поэтому для исследования его сходимости можно применять все известные признаки ( от теорем сравнения до интегрального признака Коши).
Пример. Исследовать на сходимость ряд  .
.
Составим ряд из модулей ( ):
):  . Этот ряд сходится (признак Коши
. Этот ряд сходится (признак Коши  ), поэтому исходный ряд сходится абсолютно.
), поэтому исходный ряд сходится абсолютно.
19.1.3.4. Свойства сходящихся рядов. Для сходящихся рядов c комплексными членами справедливы все свойства рядов с действительными членами:
Необходимый признак сходимости ряда. Общий член сходящегося ряда стремится к нулю при  .
.
Если сходится ряд  , то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при  .
.
Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
Сходящиеся ряды (А) и (В) можно почленно складывать и вычитать; полученный ряд тоже будет сходиться, и его сумма равна  .
.
Если члены сходящегося ряда сгруппировать произвольным образом и составить новый ряд из сумм членов в каждой паре круглых скобок, то этот новый ряд тоже будет сходиться, и его сумма будет равна сумме исходного ряда.
Если ряд сходится абсолютно, то при любой перестановке его членов сходимость сохраняется и сумма не изменяется.
Если ряды (А) и (В) сходятся абсолютно к своим сумма  и
и  , то их произведение при произвольном порядке членов тоже сходится абсолютно, и его сумма равна
, то их произведение при произвольном порядке членов тоже сходится абсолютно, и его сумма равна  .
.
19.3.2. Степенные комплексные ряды.
Определение. Степенным рядом с комплексными членами называется ряд вида

 ,
,
где  – постоянные комплексные числа (коэффициенты ряда),
– постоянные комплексные числа (коэффициенты ряда),  – фиксированное комплексное число (центр круга сходимости). Для любого численного значения z ряд превращается в числовой ряд с комплексными членами, сходящийся или расходящийся. Если ряд сходится в точке z, то эта точка называется точкой сходимости ряда. Степенной ряд имеет по меньшей мере одну точку сходимости – точку
– фиксированное комплексное число (центр круга сходимости). Для любого численного значения z ряд превращается в числовой ряд с комплексными членами, сходящийся или расходящийся. Если ряд сходится в точке z, то эта точка называется точкой сходимости ряда. Степенной ряд имеет по меньшей мере одну точку сходимости – точку  . Совокупность точек сходимости называется областью сходимости ряда.
. Совокупность точек сходимости называется областью сходимости ряда.
Как и для степенного ряда с действительными членами, все содержательные сведения о степенном ряде содержатся в теореме Абеля.
Теорема Абеля. Если степенной ряд сходится в точке  , то
, то
1. он абсолютно сходится в любой точке круга  ;
;
2. Если этот ряд расходится в точке  , то он расходится в любой точке z, удовлетворяющей неравенству
, то он расходится в любой точке z, удовлетворяющей неравенству  (т.е. находящейся дальше от точки
(т.е. находящейся дальше от точки  , чем
, чем  ).
).
Доказательство дословно повторяет доказательство раздела 18.2.4.2. Теорема Абеля для ряда с действительными членами.
Из теоремы Абеля следует существование такого неотрицательного действительного числа R, что ряд абсолютно сходится в любой внутренней точке круга радиуса R с центром в точке  , и расходится в любой точке вне этого круга. Число R называется радиусом сходимости, круг – кругом сходимости. В точках границы этого круга – окружности
, и расходится в любой точке вне этого круга. Число R называется радиусом сходимости, круг – кругом сходимости. В точках границы этого круга – окружности  радиуса R с центром в точке
радиуса R с центром в точке  – ряд может и сходиться, и расходиться. В этих точках ряд из модулей имеет вид
– ряд может и сходиться, и расходиться. В этих точках ряд из модулей имеет вид  . Возможны такие случаи:
. Возможны такие случаи:
1. Ряд  сходится. В этом случае в любой точке окружности
сходится. В этом случае в любой точке окружности  ряд сходится абсолютно.
ряд сходится абсолютно.
2. Ряд  расходится, но его общий член
расходится, но его общий член  . В этом случае в некоторых точках окружности ряд может сходиться условно, в других – расходиться, т.е. каждая точка требует индивидуального исследования.
. В этом случае в некоторых точках окружности ряд может сходиться условно, в других – расходиться, т.е. каждая точка требует индивидуального исследования.
Вместе с этой лекцией читают “7.1 Кочевники Южной Сибири в средние века”.
3. Ряд  расходится, и его общий член
расходится, и его общий член  не стремится к нулю при
не стремится к нулю при  . В этом случае ряд расходится в любой точке граничной окружности.
. В этом случае ряд расходится в любой точке граничной окружности.
Примеры.
1.  . Ряд из модулей:
. Ряд из модулей:  . Признак Даламбера:
. Признак Даламбера:  . Радиус и круг сходимости определены. На границе круга сходимости – окружности
. Радиус и круг сходимости определены. На границе круга сходимости – окружности  – ряд из модулей
– ряд из модулей  сходится, следовательно, исходный ряд абсолютно сходится в любой точке этой окружности.
сходится, следовательно, исходный ряд абсолютно сходится в любой точке этой окружности.
2.  . Ряд из модулей:
. Ряд из модулей:  . Признак Коши:
. Признак Коши:  .
.
На границе круга ряд из модулей имеет вид 
 . Предел общего члена
. Предел общего члена  , поэтому ряд расходится в любой точке граничной окружности.
, поэтому ряд расходится в любой точке граничной окружности.
3.  . Ряд из модулей:
. Ряд из модулей:  . Признак Даламбера:
. Признак Даламбера:  . На границе круга сходимости ряд из модулей
. На границе круга сходимости ряд из модулей  расходится (интегральный признак Коши), однако общий член
расходится (интегральный признак Коши), однако общий член  , поэтому в различных точках ряд может и сходиться, и расходится. Так, в точке
, поэтому в различных точках ряд может и сходиться, и расходится. Так, в точке 
 ряд имеет вид
ряд имеет вид  и, как ряд Лейбница, сходится условно; в точке
и, как ряд Лейбница, сходится условно; в точке  ряд имеет вид
ряд имеет вид  , следовательно, расходится.
, следовательно, расходится.
19.4.1.
Числовые ряды с комплексными членами.
Все основные определения сходимости,
свойства сходящихся рядов, признаки
сходимости для комплексных рядов ничем
не отличаются от действительного случая.
19.4.1.1. Основные
определения.
Пусть дана бесконечная последовательность
комплексных чисел z1,
z2,
z3,
…, zn,
… .Действительную часть числа zn
будем обозначать an,
мнимую – bn
(т.е.
zn
= an
+ i
bn,
n
= 1, 2, 3, …).
Числовой ряд
– запись вида ![]() .
.
Частичные
суммы
ряда:
S1
= z1,
S2
= z1
+ z2,
S3
= z1
+ z2
+ z3,
S4
= z1
+ z2
+ z3
+ z4,
…,
Sn
= z1
+ z2
+ z3
+ … + zn,
…
Определение.
Если существует предел S
последовательности частичных сумм
ряда при ![]() ,
,
являющийся собственным комплексным
числом, то говорят, что ряд сходится;
число S
называют суммой ряда и пишут S
= z1
+ z2
+ z3
+ … +
zn
+ …
или ![]() .
.
Найдём действительные
и мнимые части частичных сумм:
Sn
= z1
+ z2
+ z3
+ … + zn
= (a1
+
i
b1)
+ (a2
+ i
b2)
+ (a3
+
i
b3)
+ … + (an
+ i
bn)
= (a1
+
a2
+
a3
+…+
an)
+
![]() ,
,
где символами ![]()
и ![]()
обозначены действительная и мнимая
части частичной суммы. Числовая
последовательность сходится тогда и
только тогда, когда сходятся
последовательности, составленные из
её действительной и мнимой частей. Таким
образом, ряд с комплексными членами
сходится тогда и только тогда, когда
сходятся ряды, образованные его
действительной и мнимой частями. На
этом утверждении основан один из способов
исследования сходимости рядов с
комплексными членами.
Пример.
Исследовать на сходимость ряд
 .
.
Выпишем несколько
значений выражения
![]() :
:![]()
дальше значения периодически повторяются.
Ряд из действительных частей: ![]() ;
;
ряд из мнимых частей ![]() ;
;
оба ряда сходятся (условно), поэтому
исходный ряд сходится.
19.4.1.2. Абсолютная сходимость.
Определение.
Ряд ![]()
называется абсолютно
сходящимся,
если сходится ряд ![]() ,
,
составленный из абсолютных величин его
членов.
Так же, как и для
числовых действительных рядов с
произвольными членами, легко доказать,
что если сходится ряд ![]() ,
,
то обязательно сходится ряд ![]()
(![]() ,
,
поэтому ряды, образованные действительной
и мнимой частями ряда![]() ,
,
сходятся абсолютно). Если ряд ![]()
сходится, а ряд ![]()
расходится, то ряд ![]()
называется условно сходящимся.
Ряд ![]()
– ряд с неотрицательными членами, поэтому
для исследования его сходимости можно
применять все известные признаки ( от
теорем сравнения до интегрального
признака Коши).
Пример.
Исследовать на сходимость ряд ![]() .
.
Составим ряд из
модулей (![]() ):
):
![]() .
.
Этот ряд сходится (признак Коши ![]() ),
),
поэтому исходный ряд сходится абсолютно.
19.4.1.3.
Свойства сходящихся рядов. Для
сходящихся рядов c
комплексными членами справедливы все
свойства рядов с действительными
членами:
Необходимый
признак сходимости ряда.
Общий член
сходящегося ряда стремится к нулю при
![]() .
.
Если
сходится ряд
![]() ,
,
то сходится любой его остаток, Обратно,
если сходится какой-нибудь остаток
ряда, то сходится и сам ряд.
Если
ряд сходится, то сумма его остатка после
n-го
члена стремится к нулю при
![]() .
.
Если
все члены сходящегося ряда умножить на
одно и то же число с,
то сходимость ряда сохранится, а сумма
умножится на с.
Сходящиеся
ряды (А)
и (В)
можно почленно складывать и вычитать;
полученный ряд тоже будет сходиться, и
его сумма равна
![]() .
.
Если
члены сходящегося ряда сгруппировать
произвольным образом и составить новый
ряд из сумм членов в каждой паре круглых
скобок, то этот новый ряд тоже будет
сходиться, и его сумма будет равна сумме
исходного ряда.
Если
ряд сходится абсолютно, то при любой
перестановке его членов сходимость
сохраняется и сумма не изменяется.
Если ряды (А)
и (В)
сходятся абсолютно к своим суммам
![]()
и
![]() ,
,
то их произведение при произвольном
порядке членов тоже сходится абсолютно,
и его сумма равна
![]() .
.
Соседние файлы в папке tfcv
- #
- #
- #
- #
Числовые последовательности и ряды с комплексными членами
Последовательности комплексных чисел
Основные понятия, связанные с последовательностями комплексных чисел, вводятся так же, как в действительной области.
1. Если каждому натуральному числу поставлено в соответствие комплексное число
, то говорят, что задана последовательность комплексных чисел (последовательность с комплексными членами):
.
2. Последовательность называется ограниченной, если существует число
, такое, что для любого
выполняется неравенство
. Последовательность, не являющаяся ограниченной, называется неограниченной: для
, что
.
3. Последовательность называется бесконечно малой, если для любого числа
найдется номер
, такой, что для всех
, удовлетворяющих условию
, выполняется неравенство
— бесконечно малая
.
Правило 1.1. Чтобы по определению доказать, что данная последовательность является бесконечно малой, следует:
1) записать неравенство , где
— любое,
;
2) решить это неравенство относительно ;
3) из полученного решения , определить
.
4. Последовательность называется бесконечно большой, если для любого числа
найдется номер
, такой, что для всех
, удовлетворяющих условию
, выполняется неравенство
. Геометрически это означает, что члены последовательности
для
расположены в окрестности бесконечно удаленной точки, в области
.
Из определений бесконечно малой и бесконечно большой последовательностей легко установить связь между ними. Если — бесконечно малая последовательность, то
— бесконечно большая, и наоборот, если
— бесконечно большая последовательность, то
— бесконечно малая.
5. Число называется пределом последовательности
, если последовательность
является бесконечно малой (обозначается
):
для
.
Из определения получаем правило.
Правило 1.2.Чтобы доказать, что заданное число является пределом данной последовательности
, следует:
1) составить последовательность ;
2) доказать, что — бесконечно малая последовательность (см. правило 1.1).
6. Последовательность, имеющая предел, называется сходящейся, а последовательность, не имеющая предела, — расходящейся.
Расходящейся последовательностью является любая неограниченная последовательность, в частности бесконечно большая. Для бесконечно большой последовательности принято обозначение .
Интерпретация комплексных чисел точками сферы Римана придает этому равенству большую наглядность. Действительно, образами точек последовательности на сфере Римана являются точки
с координатами
, где
.
Эти соотношения получаются из равенств и уравнения сферы
(см. замечание 1.2). Поскольку
, то условие
означает, что последовательность точек
сходится к точке
сферы Римана, так как при этом
Пример 1.36. Записать пять первых членов последовательностей: а) ; б)
.
Решение
Подставляя последовательно значения , получаем:
а) ;
б)
Пример 1.37. Исследовать на ограниченность последовательности: .
Решение. Так как , то для любого
выполняется, например, неравенство
. По определению последовательность
— ограниченная.
Для второй последовательности, используя свойство модуля, находим
Далее рассматриваем неравенство при любом
и решаем его относительно
. В качестве
можно взять любое
. По определению последовательность неограниченная.
Пример 1.38. Доказать, что последовательность вида
является бесконечно малой, если
, и бесконечно большой, если
.
Решение
Пример 1.39. Применяя определение, доказать, что .
Решение
Используем правило 1.2:
1) составляем последовательность ;
2) доказываем, что — бесконечно малая. Находим
. Так как
, то
и, следовательно,
— бесконечно малая.
Исследование сходимости последовательности комплексных чисел и нахождение ее предела (в случае сходимости) можно свести к соответствующей задаче дли последовательностей с действительными членами. А именно имеет место следующее утверждение.
Утверждение 1.2. Для сходимости последовательности z„ необходимо и достаточно, чтобы сходились две последовательности и
, причем
, иначе
Из утверждения 1.2 и свойств сходящихся последовательностей действительных чисел вытекают следующие свойства последовательностей с комплексными членами. Эти свойства приведем в виде утверждения.
Утверждение 1.3. Если , то
Пример 1.40. Вычислить предел последовательности с комплексными членами .
Решение
Первый способ. Используем утверждение 1.2. Обозначим и найдем
, выполняя операцию деления комплексных чисел:
Получаем . Найдем пределы последовательностей действительных чисел:
, то есть
.
Следовательно, .
Второй способ. Используем утверждение 1.3, применяя соответствующие методы, как в действительном анализе. Находим
, так как здесь
и
бесконечно малые.
Ряды с комплексными членами
Основные понятия, связанные с рядами в комплексной области, вводятся так же, как в действительной области.
1. Выражение вида , где
— последовательность комплексных чисел, называется числовым рядом с комплексными членами (обозначается
).
2. Сумма называется n-й частичной суммой ряда, обозначается
последовательность
— последовательность частичных сумм ряда.
3. Ряд называется сходящимся, если сходится последовательность его частичных сумм, т.е. существует
. Этот предел называется суммой ряда:
— сумма ряда;
— остаток ряда.
4. Ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов, т.е. ряд
. Заметим, что ряд
— ряд с действительными положительными членами.
Признаки сходимости рядов с комплексными членами
Критерий Коши. Дня сходимости ряда необходимо и достаточно, чтобы для любого
можно было найти
, такое, что для любого
и любого
(натурального) выполнялось неравенство
.
Необходимый признак сходимости ряда. Если ряд сходится, то
.
Отсюда следует, что условие является достаточным условием расходимости ряда
.
Исследование сходимости ряда с комплексными членами можно свести к соответствующей задаче для рядов с действительными членами.
Утверждение 1.4. Дня сходимости ряда с комплексными членами необходимо и достаточно, чтобы сходились два ряда с действительными членами:
и
,
причем
Правило 1.3. Чтобы исследовать ряд с комплексными членами на сходимость, необходимо:
1) для данного ряда найти
и
;
2) составить ряды и
и исследовать их на сходимость, как ряды с действительными членами. Если оба ряда сходятся, то ряд
, сходящийся, если хотя бы один из рядов
или
расходится, то ряд
, расходящийся.
Правило 1.4. Чтобы исследовать комплексный ряд на абсолютную сходимость, необходимо:
1) составить ряд , членами которого являются модули членов данного ряда
;
2) исследовать полученный ряд на сходимость, как ряд с действительными положительными членами. Для этого могут быть использованы признаки сходимости таких рядов: признак Даламбера, Коши, признаки сравнения, интегральный признак.
Если ряд сходится, то ряд
сходится абсолютно.
Если расходится, то
может быть либо расходящимся, либо сходящимся; в последнем случае он называется условно сходящимся.
Признаки абсолютной сходимости рядов с комплексными членами
А. Признак Даламбера. Если , то ряд
сходится абсолютно.
Б. Признак Коши. Если , то ряд
сходится абсолютно.
В. Признак сравнения. Если и
сходится, то ряд
, сходится абсолютно.
Замечание 1.3. При исследовании на сходимость рядов , где
— дробно-рациональное, или дробно-иррациональное выражение от
, используется признак сравнения; при этом в качестве ряда
выбирается ряд вида
, который, как доказывается в действительном анализе, сходится при
и расходится при
.
Пример 1.41. Исследовать на сходимость ряды; в случае сходимости найти суммы рядов:
Решение
Пример 1.42. Исследовать на сходимость ряды:
Решение
Для этих рядов нахождение и
затруднительно, поэтому будем пользоваться другими признаками:
1) здесь , ряд расходится, так как не выполняется необходимый признак сходимости;
2) для этого ряда , необходимый признак выполняется, но в силу его недостаточности требуется дальнейшее исследование. Воспользуемся замечанием 1.3. Применим признак сравнения с рядом
Итак, по признаку сравнения ряд сходится абсолютно.
Пример 1.43. Доказать, что сходится абсолютно ряд
Решение
Используя признак Даламбера, рассмотрим
Так как , то ряд сходится абсолютно.
Заметим, что сходится абсолютно любой ряд вида , где
— любое комплексное число.
Свойства абсолютно сходящихся рядов с комплексными членами
Как и в действительной области, для абсолютно сходящихся рядов с комплексными членами справедливы те же правила действий, что и с конечными суммами.
1. В абсолютно сходящихся рядах допустима любая перестановка и группировка членов (даже бесконечного их числа).
Например, если ряд сходится абсолютно, то сходятся и ряды, полученные группировкой членов этого ряда, например
и
— ряды членов с четными и нечетными номерами, причем
.
2. Абсолютно сходящиеся ряды можно перемножать по правилу перемножения многочленов.
Пример 1.44. Найти произведение рядов и
Решение
Как отмечено в примере 1.43, ряды вида — абсолютно сходятся при любом фиксированном
. Поэтому сомножителями являются абсолютно сходящиеся ряды. Перемножим их по правилу перемножения многочленов:
Перепишем последнее выражение следующим образом:
Общий член этого ряда имеет вид , или, согласно формуле бинома Ньютона,
. Таким образом, окончательно получаем
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Числовые ряды
Ряд
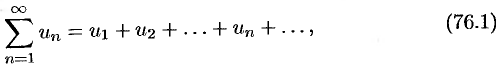
членами которого являются комплексные числа, называется числовым рядом (в комплексной области). Ряд (76.1) с комплексными членами 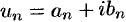 можно записать в виде
можно записать в виде
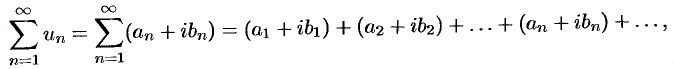
где 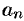 и
и 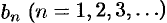 — действительные числа.
— действительные числа.
Сумма 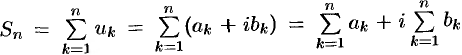 первых
первых  членов ряда (76.1) называется
членов ряда (76.1) называется  -й частичной суммой ряда.
-й частичной суммой ряда.
Если существует конечный предел  последовательности частичных сумм
последовательности частичных сумм 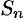 ряда:
ряда: 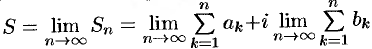 , то ряд (76.1) называется сходящимся, a
, то ряд (76.1) называется сходящимся, a  — суммой ряда; если
— суммой ряда; если 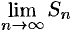 не существует, то ряд (76.1) называется расходящимся.
не существует, то ряд (76.1) называется расходящимся.
Очевидно, что ряд (76.1) сходится тогда и только тогда, когда сходится каждый из рядов
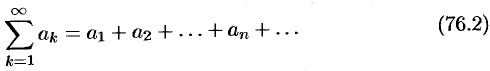
и
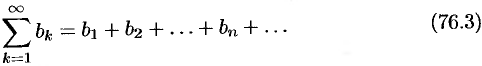
При этом 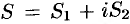 , где
, где 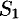 — сумма ряда (76.2), a
— сумма ряда (76.2), a 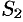 — сумма ряда (76.3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (76.2) и (76.3) с действительными членами.
— сумма ряда (76.3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (76.2) и (76.3) с действительными членами.
В теории рядов с комплексными членами основные определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами.
Приведем некоторые из них.
Остатком ряда (76.1) называется разность
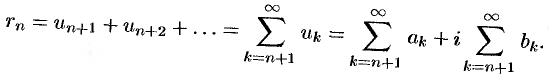
Теорема 76.1 (необходимый признак сходимости ряда). Если ряд (76.1) сходится, то его общий член 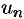 при
при 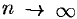 стремится к нулю:
стремится к нулю: 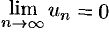 .
.
Ряд (76.1) называется абсолютно сходящимся, если сходится ряд
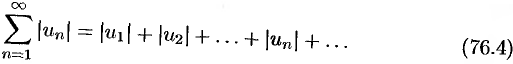
Теорема 76.2. Если сходится ряд (76.4), то абсолютно сходится ряд (76.1).
По условию ряд с общим членом 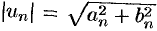 сходится. Тогда в силу очевидных неравенств
сходится. Тогда в силу очевидных неравенств 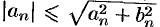 и
и 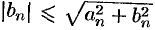 и на основании признака сравнения (теорема 60.1) сходятся ряды
и на основании признака сравнения (теорема 60.1) сходятся ряды 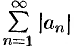 и
и 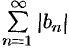 . Отсюда, следует сходимость рядов (76.2) и (76.3), а значит, и абсолютная сходимость ряда (76.1).
. Отсюда, следует сходимость рядов (76.2) и (76.3), а значит, и абсолютная сходимость ряда (76.1).
Если ряд абсолютно сходится и имеет сумму  , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму
, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму  , что и исходный ряд.
, что и исходный ряд.
Абсолютно сходящиеся ряды можно почленно складывать и перемножать.
При исследовании на сходимость рядов с комплексными членами применимы все известные из действительного анализа признаки сходимости знакопостоянных рядов, в частности признак Даламбера: если существует 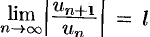 , то при
, то при 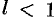 ряд (76.4) абсолютно сходится, а при
ряд (76.4) абсолютно сходится, а при 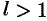 — расходится.
— расходится.
Степенные ряды
Степенным рядом в комплексной области называют ряд вида
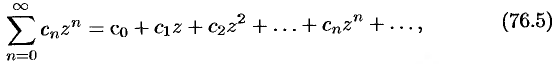
где 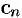 — комплексные числа (коэффициенты ряда),
— комплексные числа (коэффициенты ряда), 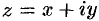 — комплексная переменная.
— комплексная переменная.
Рассматривают также и степенной ряд вида

который называют рядом по степеням разности 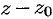 ,
, 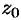 — комплексное число. Подстановкой
— комплексное число. Подстановкой 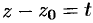 ряд (76.6) сводится к ряду (76.5).
ряд (76.6) сводится к ряду (76.5).
Ряд (76.5) при одних значениях аргумента  может сходиться, при
может сходиться, при
других — расходиться.
Совокупность всех значений  , при которых ряд (76.5) сходится, называется областью сходимости этого ряда.
, при которых ряд (76.5) сходится, называется областью сходимости этого ряда.
Основной теоремой теории степенных рядов является теорема Абеля, устанавливающая область сходимости степенного ряда.
Теорема 76.3 (Абель). Если степенной ряд (76.5) сходится при 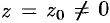 (в точке
(в точке 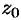 ), то он абсолютно сходится при всех значениях
), то он абсолютно сходится при всех значениях  , удовлетворяющих условию
, удовлетворяющих условию 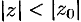 .
.
Доказательство теоремы аналогично доказательству теоремы Абеля в действительном анализе (теорема 63.1).
Следствие 76.1. Если ряд (76.5) расходится при 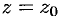 , то он расходится при всех значениях
, то он расходится при всех значениях  , удовлетворяющих условию
, удовлетворяющих условию 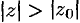 (т. е. вне круга радиуса
(т. е. вне круга радиуса 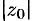 с центром в начале координат).
с центром в начале координат).
Из теоремы Абеля следует существование числа 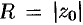 такого, что при всех значениях
такого, что при всех значениях  , удовлетворяющих неравенству
, удовлетворяющих неравенству 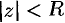 , степенной ряд (76.5) абсолютно сходится. Неравенству
, степенной ряд (76.5) абсолютно сходится. Неравенству 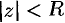 удовлетворяют точки комплексной области, лежащие внутри круга радиуса
удовлетворяют точки комплексной области, лежащие внутри круга радиуса 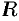 с центром в точке
с центром в точке 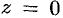 .
.
Величина 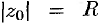 называется радиусом сходимости ряда (76.5), а круг
называется радиусом сходимости ряда (76.5), а круг 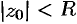 — кругом сходимости ряда. В круге
— кругом сходимости ряда. В круге 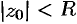 ряд (76.5) сходится, вне этого круга — расходится; на окружности
ряд (76.5) сходится, вне этого круга — расходится; на окружности 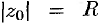 могут располагаться как точки сходимости, так и точки расходимости ряда.
могут располагаться как точки сходимости, так и точки расходимости ряда.
Принято считать, что 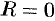 , когда ряд (76.5) сходится в одной точке
, когда ряд (76.5) сходится в одной точке 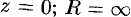 , когда ряд сходится на всей комплексной плоскости. Кругом сходимости ряда (76.6) является круг
, когда ряд сходится на всей комплексной плоскости. Кругом сходимости ряда (76.6) является круг 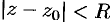 с центром в точке
с центром в точке 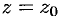 .
.
Радиус сходимости ряда (76.5) можно вычислить по формуле 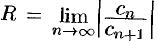 (или
(или 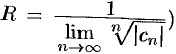 ), получаемой после применения признака Даламбера (или Коши) к ряду из модулей его членов исходного ряда.
), получаемой после применения признака Даламбера (или Коши) к ряду из модулей его членов исходного ряда.
Приведем (без доказательств) некоторые свойства степенного ряда.
- Сумма степенного ряда внутри круга его сходимости есть аналитическая функция.
- Степенной ряд внутри круга сходимости можно почленно дифференцировать и почленно интегрировать любое число раз. Полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд.
Пример №76.1.
Найти область сходимости ряда 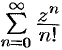 .
.
Решение: Здесь 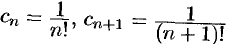 ,
,
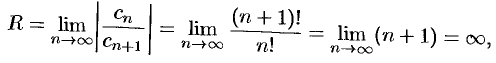
т. е. 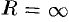 . Следовательно, областью сходимости является вся плоскость
. Следовательно, областью сходимости является вся плоскость  .
.
Пример №76.2.
Найти область сходимости ряда 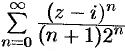 .
.
Решение:
Здесь 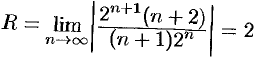 . Данный ряд сходится в области
. Данный ряд сходится в области 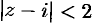 .
.
Дополнительный пример №76.3.
Ряд Тейлора
Теорема 76.4. Всякая аналитическая в круге 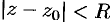 функция
функция  может быть единственным образом разложена в этом круге в степенной ряд
может быть единственным образом разложена в этом круге в степенной ряд
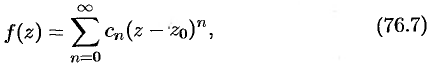
коэффициенты которого определяются формулами
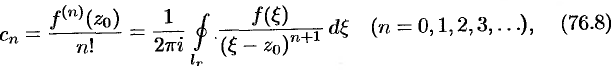
где 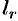 — произвольная окружность с центром в точке
— произвольная окружность с центром в точке 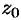 , лежащая внутри круга.
, лежащая внутри круга.
Степенной ряд (76.7) называется рядом Тейлора для функции  в рассматриваемом круге.
в рассматриваемом круге.
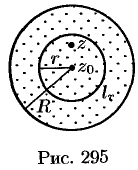
Возьмем произвольную точку  внутри данного круга и проведем окружность с центром в точке
внутри данного круга и проведем окружность с центром в точке 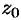 и радиусом
и радиусом 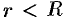 так, чтобы точка
так, чтобы точка  находилась внутри круга
находилась внутри круга 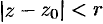 (см. рис. 295).
(см. рис. 295).
Так как функция  аналитична в круге
аналитична в круге 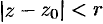 и на его границе
и на его границе 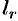 , то ее значение в точке
, то ее значение в точке  можно найти по формуле Коши (75.9):
можно найти по формуле Коши (75.9): 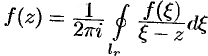 , где
, где 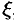 — точка на окружности
— точка на окружности 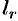 . Имеем:
. Имеем:
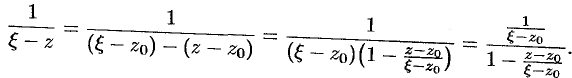
Так как 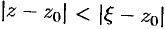 , то
, то 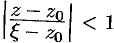 , следовательно, выражение
, следовательно, выражение 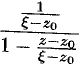 можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии с первым членом
можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии с первым членом 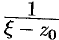 и знаменателем
и знаменателем 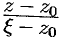 . Таким образом,
. Таким образом,
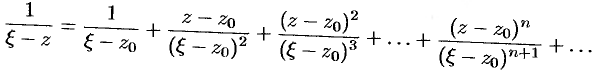
Умножим обе части этого равенства на величину 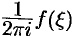 и проинтегрируем его почленно по контуру
и проинтегрируем его почленно по контуру 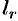 . Получим:
. Получим:
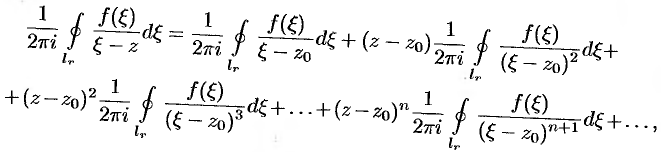
т. e. 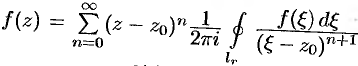 , или
, или 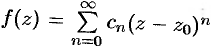 , где
, где 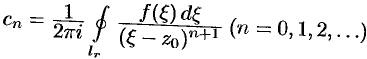 . Используя формулу (75.10), получим представление коэффициентов ряда через
. Используя формулу (75.10), получим представление коэффициентов ряда через  -е производные функции
-е производные функции  в точке
в точке 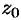 :
: 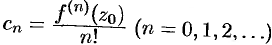 .
.
Таким образом, мы получили разложение функции  в степенной ряд (76.7), коэффициенты которого определяются по формулам (76.8).
в степенной ряд (76.7), коэффициенты которого определяются по формулам (76.8).
Докажем единственность этого разложения.
Допустим, что функция  в круге
в круге 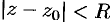 представлена другим степенным рядом
представлена другим степенным рядом
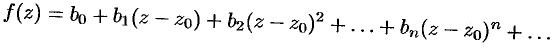
Последовательно дифференцируя почленно этот ряд бесконечное число раз, будем иметь:
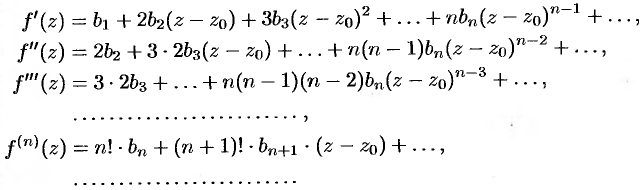
Полагая в этих равенствах, а также в исходном ряде 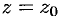 , получаем:
, получаем: 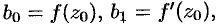
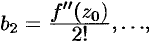
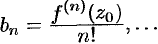 Сравнивая найденные коэффициенты
Сравнивая найденные коэффициенты 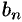 ряда с коэффициентами ряда (76.7), устанавливаем, что
ряда с коэффициентами ряда (76.7), устанавливаем, что  , а это означает, что указанные ряды совпадают.
, а это означает, что указанные ряды совпадают.
Функция  разлагается в степенной ряд единственным образом.
разлагается в степенной ряд единственным образом.
Приведем разложения некоторых элементарных функций в ряд Тейлора (Маклорена):
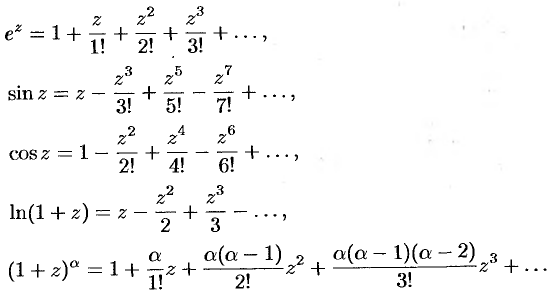
Первые три разложения справедливы во всех точках комплексной плоскости, последние два — в круге  .
.
Заменив  на
на 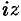 в разложении функции
в разложении функции 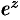 , получим:
, получим:
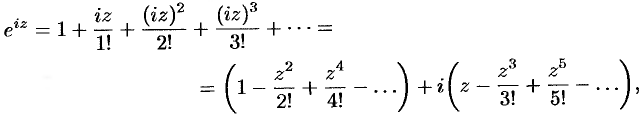
т. е. формулу Эйлера 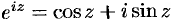 .
.
Дополнительная лекция: Нули аналитической функции
Ряд Лорана
Теорема 76.5. Всякая аналитическая в кольце 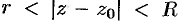
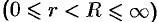 функция
функция  может быть разложена в этом кольце в ряд
может быть разложена в этом кольце в ряд
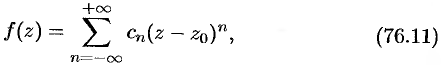
коэффициенты которого определяются формулой
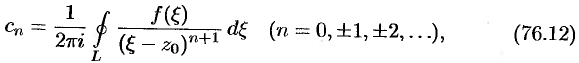
где  — произвольная окружность с центром в точке
— произвольная окружность с центром в точке 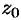 , лежащая внутри данного кольца.
, лежащая внутри данного кольца.
Рад (76.11) называется рядом Лорана для функции  в рассматриваемом кольце.
в рассматриваемом кольце.
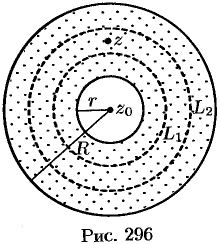
Возьмем произвольную точку  внутри кольца
внутри кольца 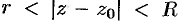 и проведем две окружности
и проведем две окружности 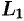 и
и 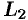 с центрами в точке
с центрами в точке 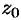 так, чтобы точка
так, чтобы точка  была между ними и каждая окружность находилась внутри данного кольца (см. рис. 296).
была между ними и каждая окружность находилась внутри данного кольца (см. рис. 296).
Функция  аналитична в кольце между окружностями
аналитична в кольце между окружностями 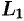 и
и 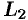 и на самих окружностях. Поэтому по формуле Коши для многосвязной области имеем:
и на самих окружностях. Поэтому по формуле Коши для многосвязной области имеем:
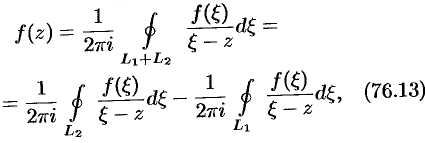
где обе окружности 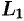 и
и 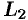 обходятся против часовой стрелки.
обходятся против часовой стрелки.
Преобразуем слагаемые, стоящие в правой части равенства (76.13), рассуждая, как и при выводе формулы Тейлора.
На окружности 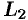 выполняется неравенство
выполняется неравенство 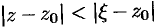 , или
, или 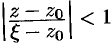 . Поэтому дробь
. Поэтому дробь 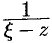 можно представить в виде
можно представить в виде
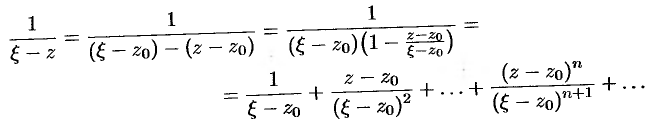
Тогда
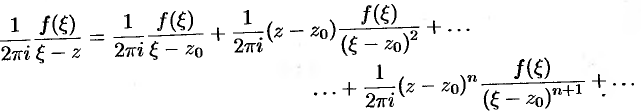
Проинтегрируем это равенство по контуру 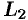 :
:
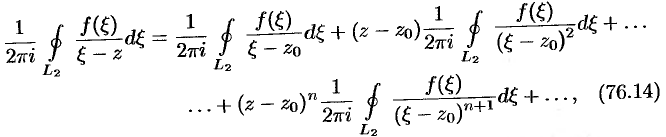
т.е. 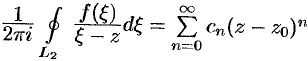 , где
, где
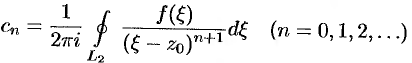
(здесь 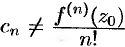 , так как функция
, так как функция  , возможно, не аналитична в точке
, возможно, не аналитична в точке 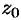 ).
).
На окружности 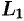 имеем
имеем 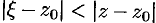 , т. е.
, т. е. 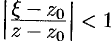 . Тогда
. Тогда
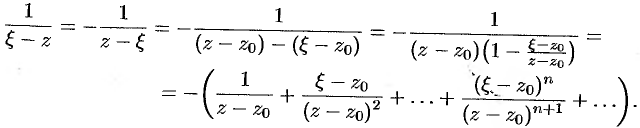
Значит,
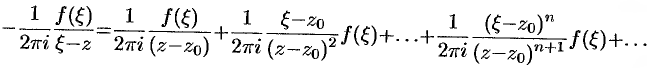
Проинтегрируем это равенство почленно по контуру 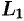 :
:
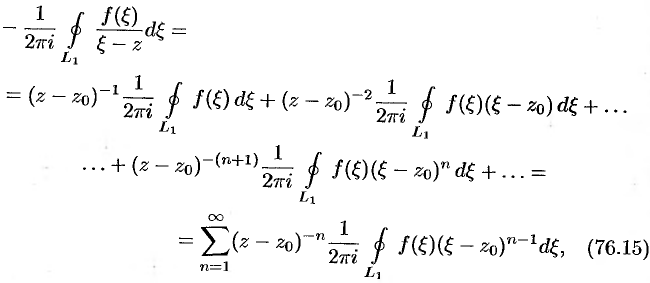
т.е. 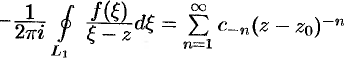 , где
, где
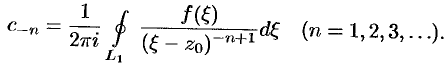
Подставив разложения (76.14) и (76.15) в равенство (76.13), получим
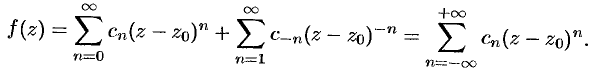
Формулы для коэффициентов 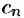 и
и 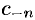 можно объединить, взяв вместо контура
можно объединить, взяв вместо контура 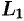 и
и 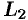 любую окружность
любую окружность  с центром в точке
с центром в точке 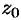 , лежащую в кольце между
, лежащую в кольце между 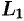 и
и 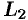 (следует из теоремы Коши для многосвязной области):
(следует из теоремы Коши для многосвязной области): 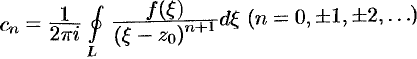 .
.
Можно доказать, что функция  , аналитическая в данном кольце
, аналитическая в данном кольце 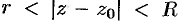 , разлагается в ряд Лорана (76.11) единственным образом.
, разлагается в ряд Лорана (76.11) единственным образом.
Ряд Лорана для функции
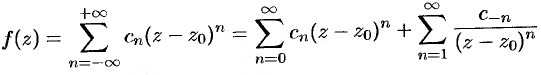
состоит из двух частей. Первая часть ряда Лорана, т. е. ряд
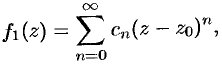
называется правильной частью ряда Лорана, этот ряд сходится к аналитической функции 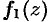 внутри круга
внутри круга 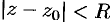 . Вторая часть ряда Лорана, т. е. ряд
. Вторая часть ряда Лорана, т. е. ряд
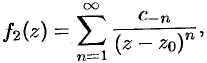
называется главной частью ряда Лорана; этот ряд сходится к аналитической функции 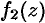 вне круга
вне круга 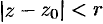 .
.
Внутри кольца 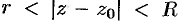 ряд
ряд 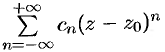 сходится к аналитической функции
сходится к аналитической функции 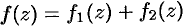 .
.
В частности, если функция  не имеет особых точек внутри круга
не имеет особых точек внутри круга 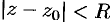 , то ее разложение в ряд Лорана обращается в ряд Тейлора.
, то ее разложение в ряд Лорана обращается в ряд Тейлора.
Замечание. На практике при разложении функции в ряд Лорана используют известные разложения основных элементарных функций; дробь вида 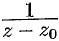 разлагается в ряд, являющийся рядом геометрической прогрессии; дробь вида
разлагается в ряд, являющийся рядом геометрической прогрессии; дробь вида 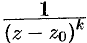 , где
, где 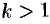 — целое, разлагается в ряд, который получается из ряда геометрической прогрессии последовательным дифференцированием
— целое, разлагается в ряд, который получается из ряда геометрической прогрессии последовательным дифференцированием 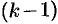 раз; сложная дробь представляется в виде суммы простейших дробей.
раз; сложная дробь представляется в виде суммы простейших дробей.
Пример №76.4.
Разложить в ряд Лорана функцию 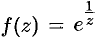 в окрестности точки
в окрестности точки 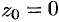 .
.
Решение:
Воспользуемся известным разложением
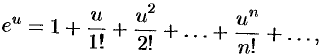
справедливым на всей комплексной плоскости. Положив 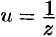 , получим
, получим
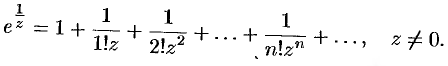
Дополнительный пример №76.5.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:

