Поскольку
для операторных токов, напряжений и
сопротивлений справедливы законы Ома
и Кирхгофа, то расчет операторных токов
и напряжений будет аналогичным расчету
постоянных токов и напряжений в
резистивных цепях постоянного тока. В
частности, могут быть использованы все
известные методы расчета (метод
эквивалентных преобразований, метод
узловых напряжений и т.д.), которые
основаны на законах Ома и Кирхгофа.
Учитывая изложенное, приведем методику
решения задач операторным методом.
-
Определяются
начальные условия и
и  обычным
обычным
путем на основании законов коммутации. -
Для
цепи после коммутации составляется
операторная схема замещения, в которой
элементы представляются их операторными
схемами замещения, реальные токи и
напряжения заменяются операторными.
Такой замене подвергаются как искомые
токи и напряжения, так и известные токи
и напряжения источников. -
Для
операторной схемы замещения определяются
искомые операторные токи и напряжения
с использованием законов Ома, Кирхгофа
и всех методов расчета (эквивалентных
преобразований, эквивалентного
генератора, узловых напряжений и т.д.). -
По
найденным операторным токам и напряжениям
определяются реальные токи и напряжения
по таблицам или по формуле разложения,
которая будет рассмотрена ниже.
Необходимо
отметить, что при расчете переходных
процессов операторным методом мы будем
иметь дело с алгебраическими операциями
над простейшими функциями переменного
“р”
каковыми являются операторные
сопротивления и операторные функции
источников (см. таблицу 3.1).
3.6. Примеры решения задач операторным методом.
Пример
1.
Для цепи на рис. 3.3 определить ток ![]() после
после
коммутации.

Начальные
условия задачи нулевые ![]() .
.
Поэтому в операторной схеме замещения
не будет дополнительных источников.
Операторная схема замещения показана
на рис. 3.4. В ней представлены операторные
сопротивления элементов и операторный
искомый ток I1(p)
. Задающий ток I0 источника
постоянного тока преобразуется в
задающий операторный ток ![]() согласно
согласно
преобразованию Лапласа от постоянной
величины (см. таблицу 3.1 соответствие
2).
Для
определения тока ![]() в
в
операторной схеме замещения можно
использовать метод эквивалентных
преобразований: определить эквивалентное
сопротивление относительно зажимов
источника, затем напряжение ![]() на
на
зажимах источника (оно же действует и
на резисторе R1)
и наконец ток ![]() .
.
Операторное
сопротивление последовательной
цепи R2L – ![]() ;
;
эквивалентное операторное сопротивление
соответствует параллельному соединению
ветвей R1 иZRL(p) и
равно
![]() .
.
Операторное
напряжение на резисторе R1
![]()
Искомый
операторный ток:
![]()
Приводим
его к табличному виду:

К
оригиналу переходим по таблице 3.1, от
каждого слагаемого по отдельности,
используя соответствия 4 и 3:
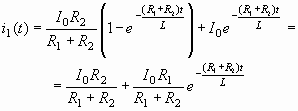
График i1(t) приведен
на рис. 3.5.
Пример
2.
В схеме на рис. 3.6 определить ток ic(t) и
напряжение uc(t) на
емкостном элементе после коммутации.
Начальные
условия определяются из схемы до
коммутации для режима постоянного тока,
в которой емкость заменена обрывом. При
этом ![]() .
.
В операторной схеме замещения (рис. 3.7)
будет дополнительный источник операторного
напряжения, обусловленный ненулевыми
начальными условиями согласно рис. 3.2.
Уравнение по второму Закону Кирхгофа
для операторной схемы:
 ,
,
откуда
при подстановке найденного выше
значения uC(0)
получим изображение
 и
и
оригинал по таблице 3.1:

Изображение
напряжения на емкости определим с
помощью найденного выше изображения
тока по формуле

Реальное
напряжение, согласно таблице 3.1:

Соседние файлы в папке шпоры
- #
- #
- #
- #
- #
- #
- #
Содержание:
Операторный метод расчета переходных процессов:
Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.
Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного 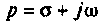
Переход от функции вещественного переменного t к функции комплексного переменного p осуществляется с помощью прямого преобразования Лапласа
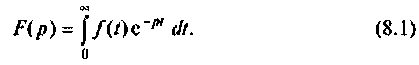
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа
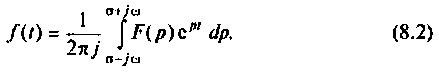
Функцию 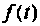 называют оригиналом, а функцию
называют оригиналом, а функцию 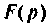 — изображением оригинала по Лапласу или просто изображением.
— изображением оригинала по Лапласу или просто изображением.
Напомним, что для того чтобы функция 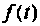 имела изображение (8.1), необходимо, чтобы она:
имела изображение (8.1), необходимо, чтобы она:
- удовлетворяла условиям Дирихле;
- была равна нулю для отрицательных значений t, т. е. при
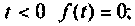
- в интервале
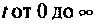 не возрастала быстрее, чем некоторая показательная функция
не возрастала быстрее, чем некоторая показательная функция
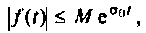
где 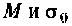 – произвольные положительные числа, т.е. здесь не требуется абсолютная интегрируемость функции
– произвольные положительные числа, т.е. здесь не требуется абсолютная интегрируемость функции 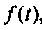 как это требуется в интегралах Фурье. Поэтому преобразования Лапласа возможны для более широкого класса функций, чем преобразования Фурье.
как это требуется в интегралах Фурье. Поэтому преобразования Лапласа возможны для более широкого класса функций, чем преобразования Фурье.
Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.
Особенностью метода является необходимость выполнения трех этапов:
Эквивалентные операторные схемы замещения элементов
Активное сопротивление:
На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде 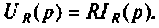
Индуктивность:
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.
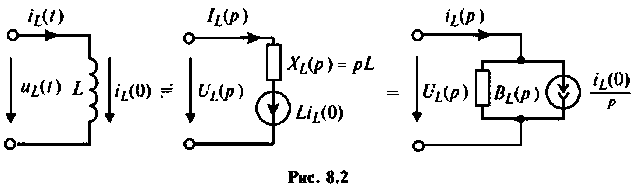
Связь между операторным напряжением и током записывается в виде 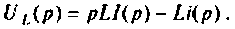
Емкость:
Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.
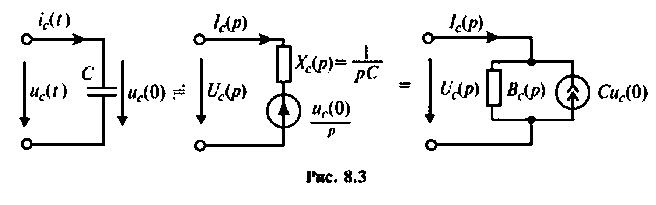
Связь между напряжением и током устанавливает соотношение
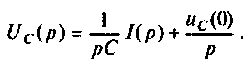
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 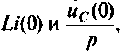 которые называются внутренними. Они указывают на то, что в магнитном поле катушки и в электрическом поле конденсатора в момент коммутации была запасена энергия. Таким образом, начальные условия автоматически учитываются при переходе от интегрально-дифференциальных уравнений к алгебраическим (постоянную интегрирования вычислять не нужно).
которые называются внутренними. Они указывают на то, что в магнитном поле катушки и в электрическом поле конденсатора в момент коммутации была запасена энергия. Таким образом, начальные условия автоматически учитываются при переходе от интегрально-дифференциальных уравнений к алгебраическим (постоянную интегрирования вычислять не нужно).
Порядок расчета:
- определяют независимые начальные условия;
- составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
- составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
- для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.
Операторные функции электрических цепей
Основные операторные функции:
Операторной функцией цепи называется отношение изображения по Лапласу выходной величины 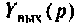 к изображению входной
к изображению входной 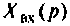 при нулевых начальных условиях, т. е,
при нулевых начальных условиях, т. е,
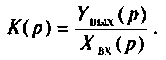
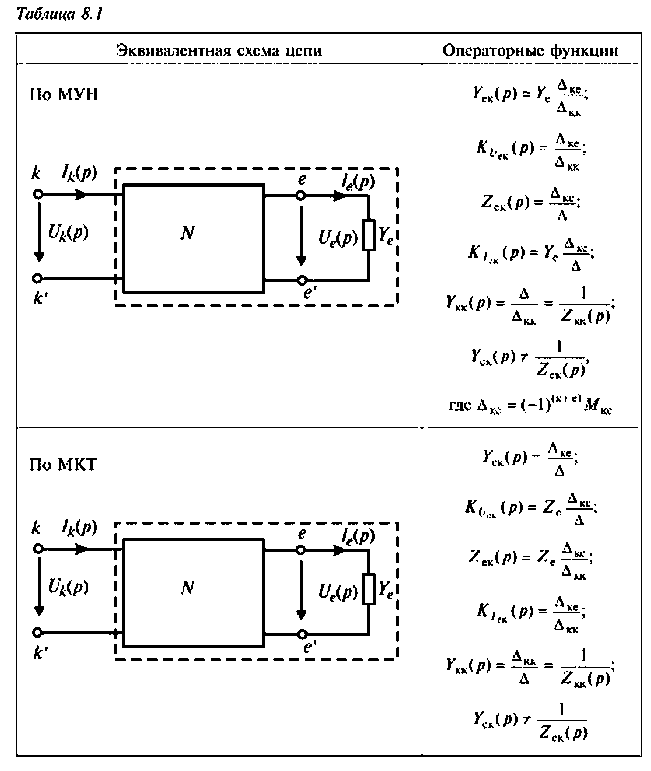
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.
Для расчета операторных функции можно применять все методы расчета комплексных функций
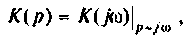
т. е. комплексная функция является частным случаем операторной при замене оператора 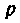 на переменную
на переменную 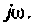
Анализ переходных процессов в цепях с помощью операторных функций
По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие
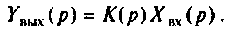
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.

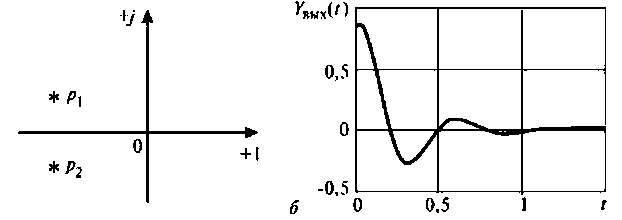
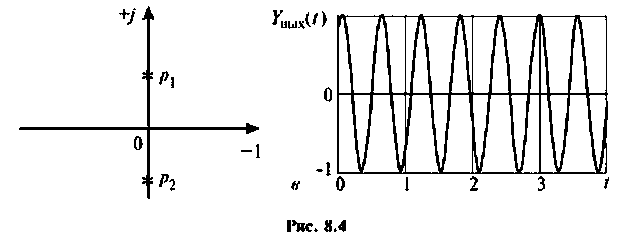
По расположению полюсов операторной функции можно судить о характере переходное процесса:
- если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
- если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
- если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.
Примеры решения задач
Пример 8.4.1.
В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение  построить его график, если
построить его график, если
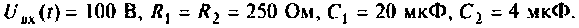
Решение
Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало: 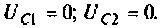
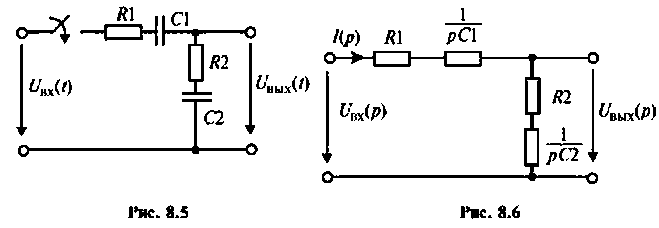
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).
Находят изображение напряжения 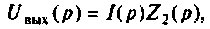 где
где
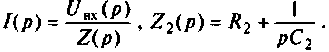
Сопротивление всей цепи определяется выражением
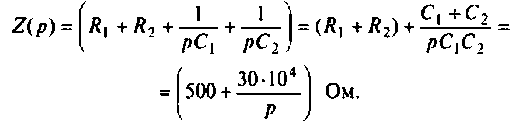
Тогда:
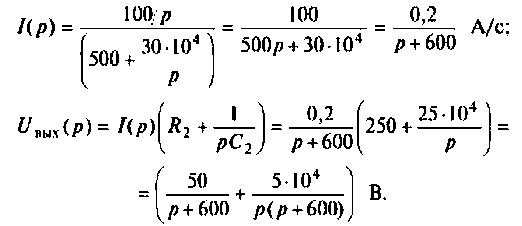
По данному изображению находят оригинал (рис. 8.7) напряжения  для этого пользуются таблицей преобразования Лапласа (см. табл. 8.2, п. 3.5) или преобразованиями в среде Mathcad (рис. 8.7).
для этого пользуются таблицей преобразования Лапласа (см. табл. 8.2, п. 3.5) или преобразованиями в среде Mathcad (рис. 8.7).
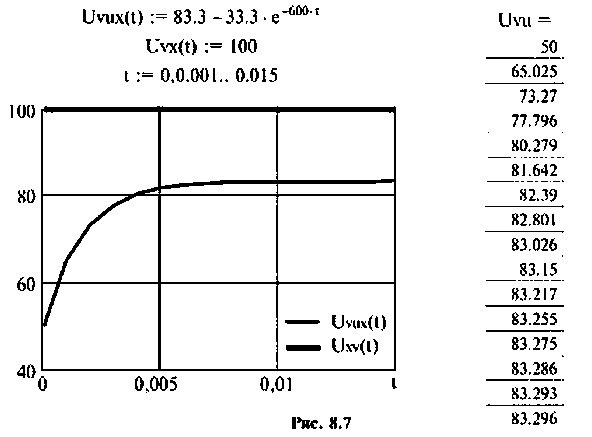
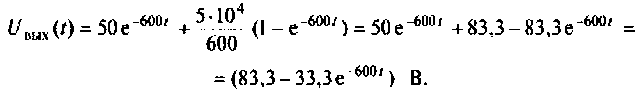
Пример 8.4.2.
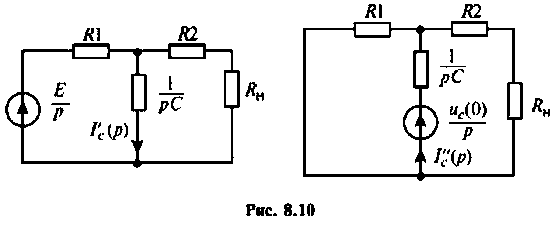
К пассивному RС-фильтру нижних частот подключается нагрузка  (рис. 8.8). Рассчитать и построить график, изменения
(рис. 8.8). Рассчитать и построить график, изменения 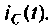
Дано: 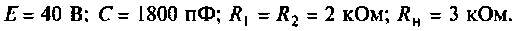
Решение
Определяют независимые начальные условия – напряжение на емкости
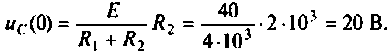
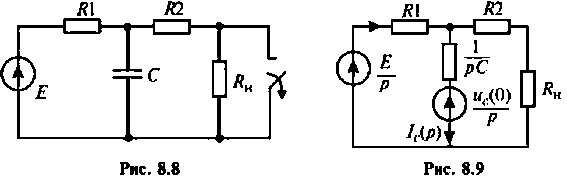
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).
Операторный ток 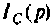 определяют методом наложения, т.е. как алгебраическую сумму двух частичных токов
определяют методом наложения, т.е. как алгебраическую сумму двух частичных токов 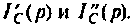
Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.
Искомый ток 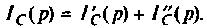
Определяют частичный ток
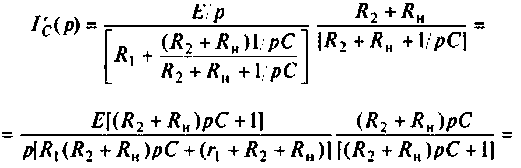
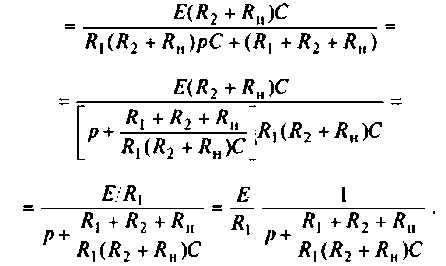
Аналогично определяют частичный ток
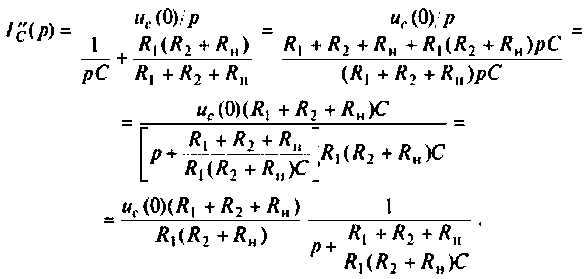
Искомый ток
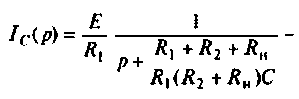
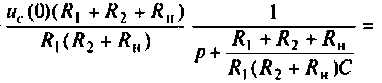
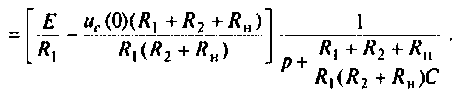
По данному изображению 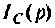 находят оригинал
находят оригинал
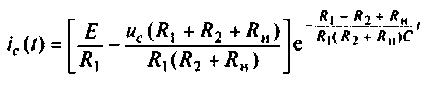
Подставляя числовые значения величин, получают
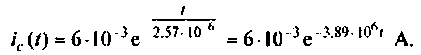
Строят график тока  в компьютерной программной среде (рис. 8.11).
в компьютерной программной среде (рис. 8.11).
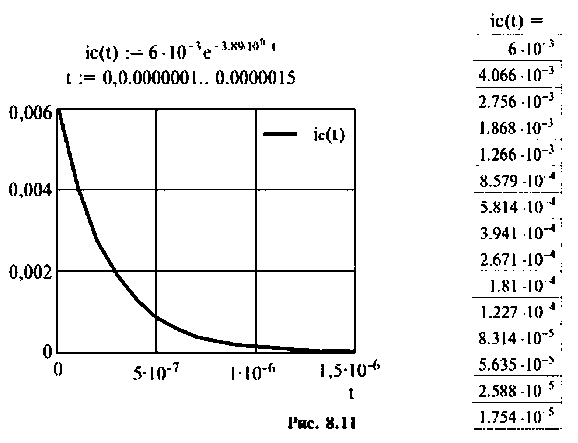
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 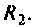 Ток, проходящий через емкость, был равен нулю. После коммутации произошло перераспределение напряжения между сопротивлениями
Ток, проходящий через емкость, был равен нулю. После коммутации произошло перераспределение напряжения между сопротивлениями 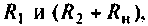 вследствие чего напряжение на емкости повысилось и образовался зарядный ток. Когда конденсатор зарядится до напряжения, определяемого на сопротивлениях
вследствие чего напряжение на емкости повысилось и образовался зарядный ток. Когда конденсатор зарядится до напряжения, определяемого на сопротивлениях 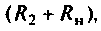 прохождение тока через емкость прекратится.
прохождение тока через емкость прекратится.
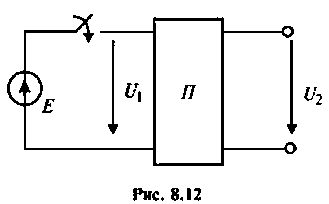
Пример 8.4.3.
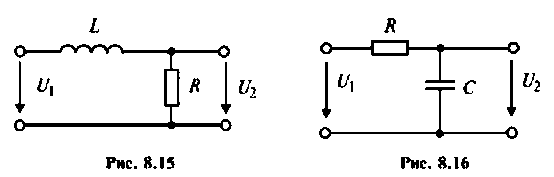
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 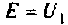 получить на выходе напряжение вида:
получить на выходе напряжение вида:
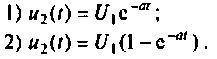
Решение
Применяя преобразования Лапласа, находят изображения 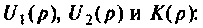
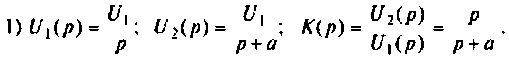
Из прямых преобразований Лапласа и Фурье следует, что
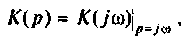
тогда
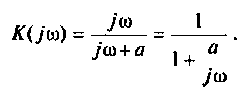
Если принять 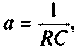 тогда
тогда 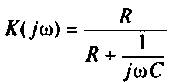 и схему можно составить из
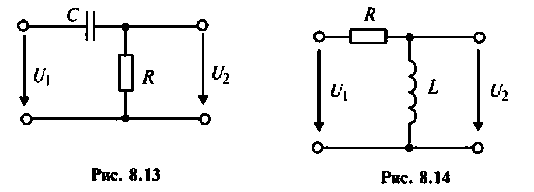
и схему можно составить из 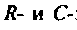 элементов (рис. 8.13).
элементов (рис. 8.13).
Если принять 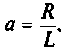 тогда
тогда 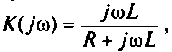 и схему можно составить из
и схему можно составить из  элементов (рис. 8.14).
элементов (рис. 8.14).
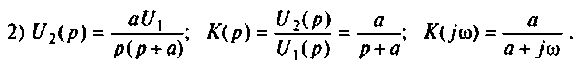
Если принять 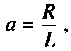 тогда
тогда 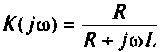 и схема будет иметь вид, изображенный на рис. 8.15.
и схема будет иметь вид, изображенный на рис. 8.15.
Если принять 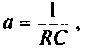 тогда
тогда 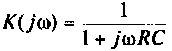 и схема будет иметь вид, изображенный на рис. 8.16.
и схема будет иметь вид, изображенный на рис. 8.16.
Пример 8.4.4.
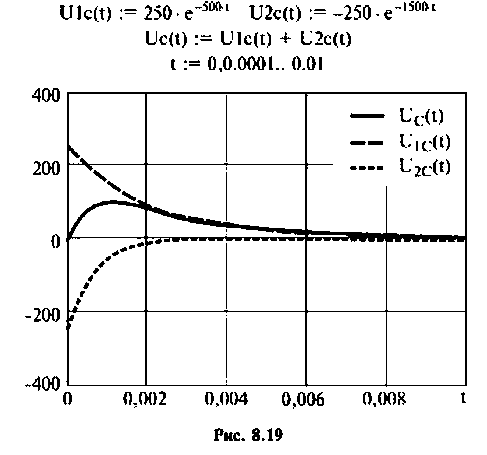
Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение 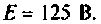
Определить напряжение на конденсаторе и построить его опюру, если:
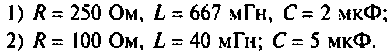
Решение
Определяют независимые начальные условия: напряжение на конденсаторе 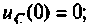 ток в катушке индуктивности
ток в катушке индуктивности 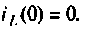
Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).
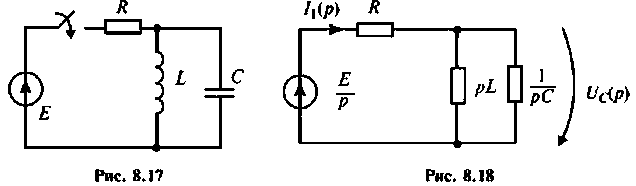
Находят изображение напряжения на конденсаторе
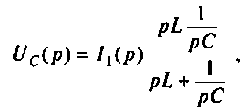
где
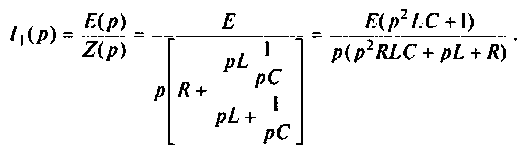
Тогда
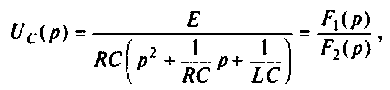
где
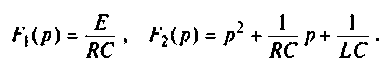
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции
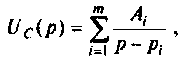
где 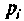 — некратные полюсы изображения напряжения
— некратные полюсы изображения напряжения 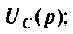
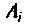 — начальные значения компонент изображения
— начальные значения компонент изображения 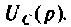
При простых (некратных) полюсах 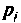 начальные значения компонент определяются но выражению [4]
начальные значения компонент определяются но выражению [4]
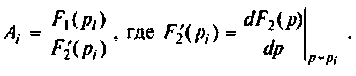
а) Для первого варианта значений:
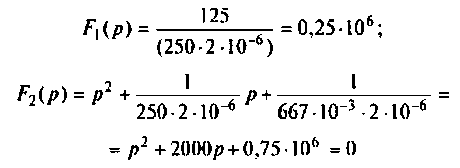
Полюсы изображения 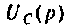 после вычислений имеют значения:
после вычислений имеют значения:
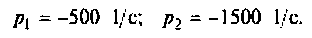
Вычисляют производную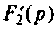 и ее значение при
и ее значение при 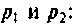 .
.
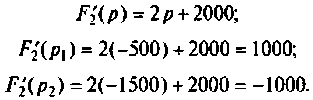
Вычисляют начальные значения компонент 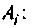
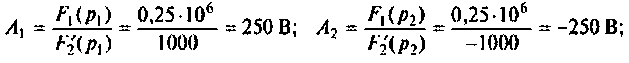
Следовательно,
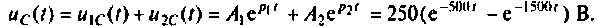
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.
Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде
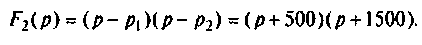


б) Для второго варианта числовых значений:
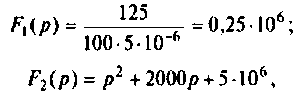
а полюсы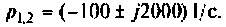
Находят производную от 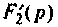 и вычисляют ее значения при
и вычисляют ее значения при 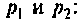
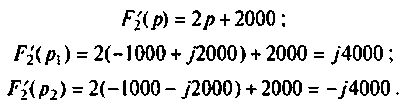
Следовательно,
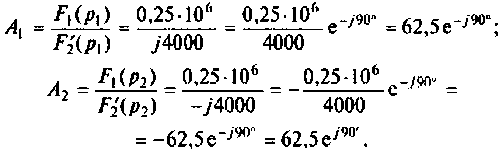
По теореме разложения определяют
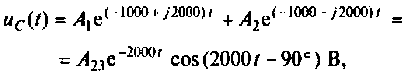
где 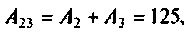
или 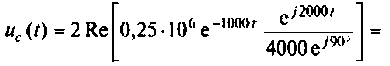
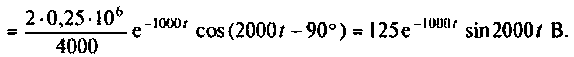
График изменения напряжения 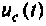 представлен на рис. 8.20.
представлен на рис. 8.20.
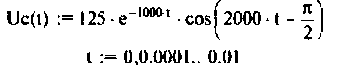
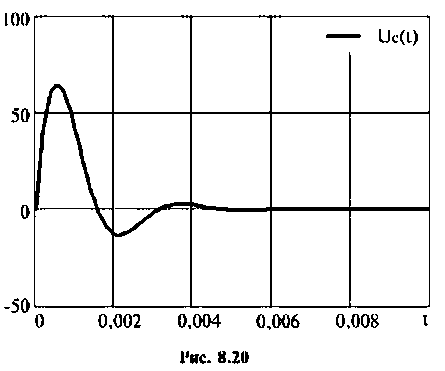
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель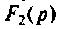 представить в виде
представить в виде
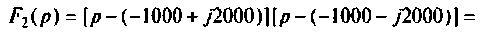
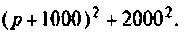
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.
Пример 8.4.5.
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте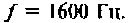
Определить:
а) коэффициент передачи по напряжению 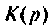 в режиме холостого хода и при активной нагрузке
в режиме холостого хода и при активной нагрузке 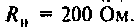
б) характер переходного процесса по кривой переходного процесса.
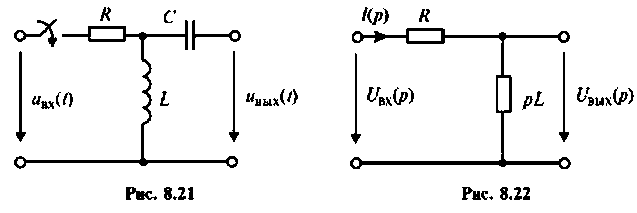
Дано: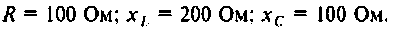
Решение
В режиме холостого хода
Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.
Находят изображение напряжения на выходе
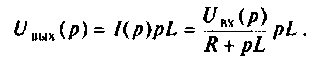
Откуда
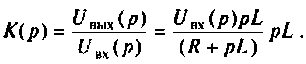
Определяют полюсы операторной функции из уравнения 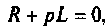 тогда
тогда
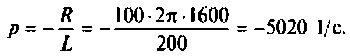
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).
В режиме нагрузки
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).
Определяют операторную функцию 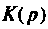 по методу контурных токов, используя соотношение (см. табл. 8.1):
по методу контурных токов, используя соотношение (см. табл. 8.1):
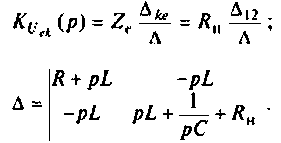
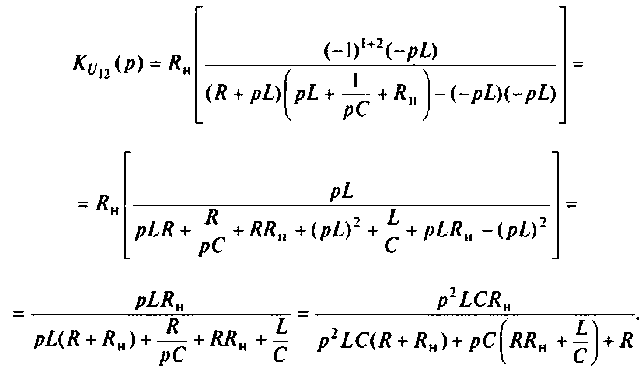
Определяют полюсы операторной функции из уравнения
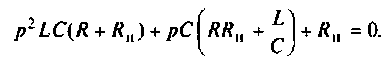
Для этога вначале вычисляют L и С.
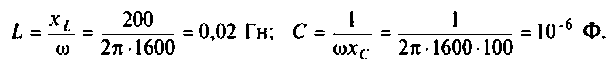
Находят корни уравнения:
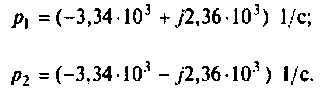
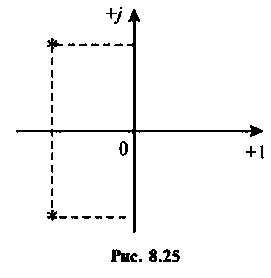
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
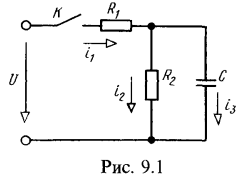
1. Для схемы рис. 9.1 операторным методом найти выражения мгновенных значений тока в неразветвленной части цепи и напряжения на обкладках конденсатора при замыкании контакта К. Дано:![]()
Решение:
Находим изображение тока в неразветвленной части цепи по закону Ома: ![]() , где изображение постоянного напряжения (см. по табл. 0.9.1, № 2)
, где изображение постоянного напряжения (см. по табл. 0.9.1, № 2) ![]() , а операторное сопротивление
, а операторное сопротивление

Итак,
![]()
Оригинал этого тока определим двумя способами.
Способ 1. Используя таблицу 0.9.1 (смотри внизу), связывающую оригинал и его изображение, преобразуем ![]() так, чтобы получить табличные изображения.
так, чтобы получить табличные изображения.![]() представим в виде суммы двух функций, которые после преобразования примут вид формул, данных в табл. 0.9.1, № 5 и 11:
представим в виде суммы двух функций, которые после преобразования примут вид формул, данных в табл. 0.9.1, № 5 и 11:
Способ 2. Решим задачу с помощью теоремы разложения [см. формулу (0.9.11), представлена ниже]
В данном случае: ![]()
Вычисляем корень уравнения: ![]()
Определяем

Подставляя найденные значения в формулу, получим
![]()
Проверка. При ![]() , ток
, ток ![]() . Действительно, в момент начала переходного процесса напряжение на конденсаторе равно нулю. Это соответствует тому, что конденсатор ведет себя так, будто он закорочен, и тем самым шунтирует сопротивление
. Действительно, в момент начала переходного процесса напряжение на конденсаторе равно нулю. Это соответствует тому, что конденсатор ведет себя так, будто он закорочен, и тем самым шунтирует сопротивление ![]() , поэтому ток
, поэтому ток ![]() определяется только сопротивлением
определяется только сопротивлением ![]() .
.
Определим напряжение на конденсаторе в операторной форме

Применяя один из указанных способов, найдем
![]()
Проверка. При ![]() напряжение
напряжение ![]() , что соответствует начальному условию.
, что соответствует начальному условию.
2. Решить задачу №1 предыдущего раздела операторным методом.
Решение:
Прежде всего найдем операторное сопротивление цепи

Далее определим изображение тока ![]() через изображение входного напряжения
через изображение входного напряжения ![]() :
:
![]()
Изображение напряжения на конденсаторе получим, умножая изображение тока на операторное сопротивление параллельных ветвей:

где числитель
![]()
а знаменатель
![]()
причем корни уравнения ![]()

1. Решим задачу для первого варианта числовых значений по формуле разложения (0.9.10). По формулам (9.2) — (9.4) определяем
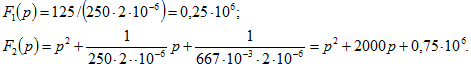
Найдем корни уравнения:

Вычислим производную ![]() и ее значения при
и ее значения при ![]() и
и ![]() :
:
![]()
По формуле (9.1) определяем
![]()
По формуле разложения,
![]()
Те же результаты можно получить по формуле табл. 0.9.1, № 13, если знаменатель изображения напряжения на конденсаторе представить в виде ![]() .
.
2. Решим задачу, подставляя числовые значения второго варианта. По формулам (9.2) — (9.4) определим
![]()
Изображение напряжения на конденсаторе [см. формулу 9.1)] имеет вид
![]()
В связи с тем, что имеются кратные корни (порядок кратности m=2), оригинал находим по формуле (0.9.12), в которой

Таким образом,

Можно также определить оригинал по формуле табл. 0.9.1, № 9.
3. Рассмотрим третий вариант числовых значений. По формулам (9.2) — (9.4) находим
![]()
Производная от ![]() и ее значения при
и ее значения при ![]() и
и ![]() равны:
равны:
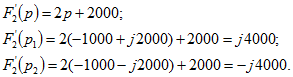
Искомый оригинал имеет вид [см. формулу 0.9.10]:

Те же результаты можно получить по формуле табл. 0.9.1, № 18, если знаменатель ![]() представить в виде
представить в виде
![]()
3. Решить задачу №3 предыдущего раздела операторным методом.
Решение:
Это пример задачи с ненулевым начальным условием для тока ![]() , проходящего через индуктивную катушку. Операторная схема замещения изображена на рис. 9.10, а. Составляем для нее уравнения Кирхгофа:
, проходящего через индуктивную катушку. Операторная схема замещения изображена на рис. 9.10, а. Составляем для нее уравнения Кирхгофа:

В этих уравнениях ![]() — начальное значение тока, проходящего через индуктивную катушку
— начальное значение тока, проходящего через индуктивную катушку ![]() — изображение постоянной ЭДС.
— изображение постоянной ЭДС.
Уравнения (9.1) — (9.3) решим совместно относительно тока ![]() :
:

По формуле разложения (0.9.11) оригинал функции имеет вид
![]()
Для упражнения эту же задачу решим методом сведения к нулевым начальным условиям. Для этого вычислим напряжение на разомкнутом контакте (см. рис. 8.9, а):
![]()
Добавим в ветвь ![]() два встречно включенных источника с ЭДС
два встречно включенных источника с ЭДС ![]() , как показано на рис. 9.10, б.
, как показано на рис. 9.10, б.
Расчет схемы после коммутации проведем по методу наложения. Составляющая тока ![]() (от системы
(от системы ![]() ) совпадает со своим значением
) совпадает со своим значением ![]() до коммутации, так как подключение ЭДС
до коммутации, так как подключение ЭДС ![]() (рис. 9.10, в) не вызовет каких-либо изменений в исходной схеме с выключенным контактом К. Таким образом,
(рис. 9.10, в) не вызовет каких-либо изменений в исходной схеме с выключенным контактом К. Таким образом, ![]() .
.
Вызываемую действием ЭДС ![]() подключаемой к обесточенной схеме (рис. 9.10, г), составляющую тока
подключаемой к обесточенной схеме (рис. 9.10, г), составляющую тока ![]() можно записать в операторной форме:
можно записать в операторной форме:

Подставляя числовые значения и переходя к оригиналу для искомого тока, получим
![]()

4. Определить операторным методом напряжение на конденсаторе и токи при замыкании контакта К (рис. 8.20). Дано: Е=24 В, R=20 Ом, ![]() С=3 мкФ.
С=3 мкФ.
Решение:
Эта задача имеет ненулевое начальное условие для напряжения на конденсаторе ![]() . Операторная схема замещения изображена на рис. 9.12.
. Операторная схема замещения изображена на рис. 9.12.
Для этой схемы по методу контурных токов имеем

Решая эти уравнения относительно ![]() и учитывая, что
и учитывая, что ![]() , найдем
, найдем
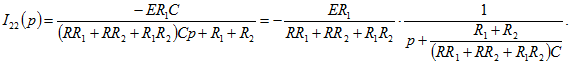
Подставив числовые значения, получим
![]()
На основании (0.9.10) или по табл. 0.9.1, № 5 определим оригинал:
![]()
Аналогично из уравнений (9.1) и (9.2) можно наши другие токи и напряжение на конденсаторе.


5. В схеме (рис. 9.14, а) при разомкнутом контакте имеется установившийся процесс. В момент t=0 контакт замыкается и накоротко шунтирует сопротивление ![]() .
.
Найти выражения для токов и напряжение на конденсаторе при переходном процессе. Дано:![]()
Решение:
Это пример задачи с ненулевыми начальными условиями. Определим их. Через индуктивную катушку до замыкания контакта проходит постоянный ток
![]()
Напряжение на конденсаторе до коммутации: ![]()
Для схемы, образующейся после коммутации, начертим операторную схему замещения (рис. 9.14, б). Найдем, например, ток ![]() методом эквивалентного источника ЭДС. Для этого отключаем первую ветвь (рис. 9.14, в) и найдем операторную ЭДС эквивалентного источника
методом эквивалентного источника ЭДС. Для этого отключаем первую ветвь (рис. 9.14, в) и найдем операторную ЭДС эквивалентного источника ![]() и его сопротивление
и его сопротивление ![]() . Из рис. 9.14, в следует, что
. Из рис. 9.14, в следует, что
а из рис. 9.14, г
Ток в первой ветви (рис. 9.14, д)
Подставим сюда ![]() из (9.1) и (9.2), получим
из (9.1) и (9.2), получим
![]()
Подставляя числовые значения, имеем:

По изображению (9.14) найдем оригинал тока ![]() с помощью теоремы разложения. Для этого определим значения функции
с помощью теоремы разложения. Для этого определим значения функции ![]() при р=0.
при р=0.
![]()
Зачем находим корни уравнения

Далее вычислим производную и ее значения при ![]()

Определим ![]() при
при ![]()
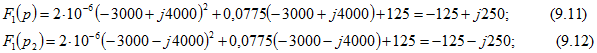
Наконец, подставим полученные в уравнениях (9.7)-(9.12) значения в формулу (0.9.11) и, учитывая замечание теоремы разложения, определяем

Проверка. При ![]() , что удовлетворяет начальному условию.
, что удовлетворяет начальному условию.
Остальные два тока могут быть найдены следующим образом. Если из U вычесть падение напряжения на ветви ![]() , то можно найти мгновенное значение напряжения на параллельных ветвях:
, то можно найти мгновенное значение напряжения на параллельных ветвях:
![]()
Затем определим токи: ![]()

6. К зажимам цепи (рис. 9.18, а) приложено напряжение ![]() . Параметры цепи:
. Параметры цепи: ![]() .
.
В момент прохождения тока через положительный максимум замыкается контакт К. Найти токи ![]() .
.
Решение:
До замыкания контакта ток в цепи
![]()
где

По условию задачи в момент включения этот ток максимален, т. е.

Отсюда можно рассчитать угол включения y:![]()
Так как изображение синусоидальной функции определяется сравнительно сложной формулой, в данной задаче операторным методом вычислим только свободную составляющую тока ![]() , а установившуюся составляющую тока
, а установившуюся составляющую тока ![]() найдем, рассчитав схему задачи (см. рис. 9.18, а) после коммутации символическим методом
найдем, рассчитав схему задачи (см. рис. 9.18, а) после коммутации символическим методом

Начальное значение свободного тока: ![]()
Операторная схема замещения для расчета свободной составляющей переходного процесса с учетом ненулевых начальных значений свободных токов показана на рис. 9.18, б.
По второму закону Кирхгофа для первого контура имеем: ![]() и, подставляя числовые значения и вычисляя изображение свободного тока, находим
и, подставляя числовые значения и вычисляя изображение свободного тока, находим
![]()
По формуле разложения: ![]() . Суммирование установившегося и свободного токов определяет искомый ток:
. Суммирование установившегося и свободного токов определяет искомый ток: ![]() .
.
Аналогично вычисляем ток ![]() . Отличие заключается в том, что установившийся ток равен нулю:
. Отличие заключается в том, что установившийся ток равен нулю: ![]()
Поэтому ![]() . По второму закону Кирхгофа, для второго контура (рис. 9.18, б)
. По второму закону Кирхгофа, для второго контура (рис. 9.18, б)
![]()
По формуле разложения: ![]()

7. Цепь, состоящая из источника постоянного тока ![]() , нагруженная на
, нагруженная на ![]() — ветвь, находится в установившемся режиме (рис. 9.24, а). В момент t=0 замыканием контакта К осуществляется коммутация, включающая резистор сопротивлением
— ветвь, находится в установившемся режиме (рис. 9.24, а). В момент t=0 замыканием контакта К осуществляется коммутация, включающая резистор сопротивлением ![]() . Найти закон изменения тока
. Найти закон изменения тока ![]() , протекающего через ветвь
, протекающего через ветвь ![]() после замыкания.
после замыкания.
Решение:
До коммутации по ветви ![]() проходил постоянный ток:
проходил постоянный ток: ![]() .
.
Начертим эквивалентную операторную схему замещения после коммутации (рис. 9.24, б) и заменим ее схемой рис. 9.24, в, в которой параллельно соединенные сопротивления ![]() заменим эквивалентным:
заменим эквивалентным: ![]() . По методу контурных токов имеем
. По методу контурных токов имеем ![]() . Отсюда, учитывая, что
. Отсюда, учитывая, что ![]() найдем
найдем

Используя таблицу 0.9.1, № 5 и 11, найдем оригинал каждого из этих изображений. В результате получим

где ![]()

ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Преобразование Лапласа. В основу операторного метода положено следующее. Функция ![]() [обычно ток
[обычно ток ![]() или напряжение
или напряжение ![]() ] вещественного переменного
] вещественного переменного ![]() (время), называемая оригиналом, заменяется соответствующей ей функцией
(время), называемая оригиналом, заменяется соответствующей ей функцией ![]() комплексного переменного
комплексного переменного ![]() , называемой изображением.
, называемой изображением.
Эти функции связаны соотношением

называемым прямым преобразованием Лапласа. Сокращенно эту связь записывают в таком виде: ![]() .
.
В табл. 0.9.1 приводятся оригиналы простейших функций и их изображения, полученные по формуле (0.9.1) и используемые при решении задач на переходные процессы.
Таблица 0.9.1
|
№ п/п |
Оригинал |
Изображение |
№ п/п |
Оригинал |
Изображение |
|
1 |
|
|
12 |
|
|
|
2 |
|
|
13 |
|
|
|
3 |
|
|
14 |
|
|
|
4 |
|
|
15 |
|
|
|
5 |
|
|
16 |
|
|
|
6 |
|
|
17 |
|
|
|
7 |
|
|
18 |
|
|
|
8 |
|
|
19 |
|
|
|
9 |
|
|
20 |
|
|
|
10 |
|
|
21 |
|
|
|
11 |
|
|
22 |
|
|
|
n — целое положительное число |
2. Теорема разложения. Если изображение искомого тока или напряжения имеет вид рациональной дроби
![]()
причем многочлены (относительно ![]() )
) ![]() удовлетворяют следующим условиям: степень
удовлетворяют следующим условиям: степень ![]() ниже степени
ниже степени ![]() — вещественные числа, а корни
— вещественные числа, а корни ![]() уравнения
уравнения ![]() различны, то оригинал определяется выражением
различны, то оригинал определяется выражением

Если знаменатель уравнения ![]() имеет один корень, равный нулю, т. е.
имеет один корень, равный нулю, т. е. ![]() , то оригинал находят по формуле
, то оригинал находят по формуле

Замечание. Если среди корней уравнения ![]() имеются комплексно-сопряженные корни
имеются комплексно-сопряженные корни ![]() , то при вычислении соответствующих им слагаемых, стоящих в правой части суммы уравнений (0.9.10) и (0.9.11), достаточно определить слагаемое для одного из этих корней, например
, то при вычислении соответствующих им слагаемых, стоящих в правой части суммы уравнений (0.9.10) и (0.9.11), достаточно определить слагаемое для одного из этих корней, например ![]() для сопряженного корня
для сопряженного корня ![]() следует взять сопряженное значение этого слагаемого. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней.
следует взять сопряженное значение этого слагаемого. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней.
Если в уравнении (0.9.11) ![]() имеет
имеет ![]() различных корней
различных корней ![]() и из них корень
и из них корень ![]() кратностью
кратностью ![]() , корень
, корень ![]() кратностью т2, корень рп кратностью
кратностью т2, корень рп кратностью ![]() , то по изображению
, то по изображению ![]() оригинал вычисляют по формуле
оригинал вычисляют по формуле

Здесь выражение, стоящее в знаменателе квадратной скобки, надо сначала сократить на ![]() и лишь после этого дифференцировать.
и лишь после этого дифференцировать.
Если уравнение ![]() содержит одновременно и простые, и кратные корни, то для определения слагаемых, соответствующих простым корням, используется формула (0.9.10) или (0.9.11), если имеется простой корень
содержит одновременно и простые, и кратные корни, то для определения слагаемых, соответствующих простым корням, используется формула (0.9.10) или (0.9.11), если имеется простой корень ![]() , а для кратных — формула (0.9.12).
, а для кратных — формула (0.9.12).
Сущность операторного метода заключается в том, что функции ![]() вещественной переменной t, которую
вещественной переменной t, которую
называют оригиналом, ставится в соответствие функция ![]() комплексной переменной
комплексной переменной ![]() , которую называют изображением.
, которую называют изображением.
В результате этого производные и интегралы от оригиналов заменяются алгебраическими
функциями от соответствующих изображений (дифференцирование заменяется умножением
на оператор р, а интегрирование – делением на него), что в свою очередь определяет
переход от системы интегро-дифференциальных уравнений к системе алгебраических
уравнений относительно изображений искомых переменных. При решении этих уравнений
находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим
моментом при этом в практическом плане является необходимость определения только
независимых начальных условий, что существенно облегчает расчет переходных процессов
в цепях высокого порядка по сравнению с классическим методом.
Изображение ![]() заданной функции
заданной функции ![]() определяется в соответствии с
определяется в соответствии с
прямым преобразованием Лапласа:
 . . |
(1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается,
как:
 или
или 
Следует отметить, что если оригинал ![]() увеличивается с ростом t,
увеличивается с ростом t,
то для сходимости интеграла (1) необходимо более быстрое убывание модуля ![]() . Функции, с которыми встречаются
. Функции, с которыми встречаются
на практике при расчете переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций,
часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал  |
Изображение  |
| A |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:
- При умножении оригинала на коэффициент на тот же коэффициент умножается
изображение:
 .
.
![]() .
.
С использованием этих свойств и данных табл. 1, можно показать, например,
что
 .
.
Изображения производной и интеграла
В курсе математики доказывается, что если ![]() , то
, то ![]() , где
, где ![]() – начальное значение функции
– начальное значение функции
![]() .
.
Таким образом, для напряжения на индуктивном элементе можно записать
![]()
или при нулевых начальных условиях
![]() .
.
Отсюда операторное сопротивление катушки индуктивности
![]() .
.
Аналогично для интеграла: если ![]() , то
, то  .
.
С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:
 .
.
Тогда

или при нулевых начальных условиях
 ,
,
откуда операторное сопротивление конденсатора
 .
.
Закон Ома в операторной форме
Пусть имеем некоторую ветвь ![]() (см. рис. 1), выделенную
(см. рис. 1), выделенную
из некоторой

сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу,
при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем
случае ненулевые.
Для мгновенных значений переменных можно записать:
 .
.
Тогда на основании приведенных выше соотношений получим:
 .
.
Отсюда
 , , |
(2) |
где  – операторное сопротивление рассматриваемого
– операторное сопротивление рассматриваемого
участка цепи.
Следует обратить внимание, что операторное сопротивление ![]() соответствует комплексному сопротивлению
соответствует комплексному сопротивлению
![]() ветви в цепи синусоидального
ветви в цепи синусоидального
тока при замене оператора р на ![]() .
.
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником
ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать
операторную схему замещения, представленную на рис. 2.

Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов,
сходящихся в узле, равна нулю
 .
.
Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
 .
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости
учета ненулевых начальных условий (если они имеют место). С их учетом последнее
соотношение может быть переписано в развернутом виде
 .
.

В качестве примера запишем
выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 –
![]() ; 2 –
; 2 – ![]() .
.
В первом случае в соответствии с законом Ома  .
.
Тогда

и


Во втором случае, т.е. при
![]() , для цепи на рис. 3 следует составить
, для цепи на рис. 3 следует составить
операторную схему замещения, которая приведена на рис. 4. Изображения токов
в ней могут быть определены любым методом расчета линейных цепей, например,
методом контурных токов:

откуда ![]() ;
; ![]() и
и ![]() .
.
Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен
следующими способами:
1. Посредством обратного преобразования Лапласа
 ,
,
которое представляет собой решение интегрального уравнения (1) и сокращенно
записывается, как:
![]() .
.
На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия,
охватывающих практически все задачи электротехники. Согласно данному способу
необходимо получить изображение искомой величины в виде, соответствующем табличному,
после чего выписать из таблицы выражение оригинала.

Например,
для изображения тока в цепи на рис. 5 можно записать
 .
.
Тогда в соответствии с данными табл. 1
 ,
,
что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение ![]() искомой переменной определяется
искомой переменной определяется
отношением двух полиномов
 ,
,
где ![]() .
.
Это выражение может быть представлено в виде суммы простых дробей
 , , |
(3) |
где ![]() – к-й корень уравнения
– к-й корень уравнения ![]() .
.
Для определения коэффициентов ![]() умножим левую и правую части
умножим левую и правую части
соотношения (3) на ( ![]() ):
):
 .
.
При ![]()
 .
.
Рассматривая полученную неопределенность типа ![]() по правилу Лопиталя, запишем
по правилу Лопиталя, запишем
 .
.
Таким образом,
 .
.
Поскольку отношение  есть постоянный коэффициент,
есть постоянный коэффициент,
то учитывая, что  , окончательно получаем
, окончательно получаем
 . . |
(4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней
уравнения ![]() равен нулю, т.е.
равен нулю, т.е. ![]() , то уравнение (4) сводится к
, то уравнение (4) сводится к
виду
 .
.
В заключение раздела отметим, что для нахождения начального ![]() и конечного
и конечного ![]() значений оригинала можно использовать
значений оригинала можно использовать
предельные соотношения

которые также могут служить для оценки правильности полученного изображения.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные
условия? - Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты
ее написания? -
С использованием теоремы об
активном двухполюснике записать операторное изображение для тока через катушку
индуктивности в цепи на рис. 6.
- С использованием предельных соотношений и решения предыдущей задачи найти
начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ:  .
.
Ответ: ![]() .
.

