Порядок выполнения работы
-
Не включая
установки, знакомятся с приборами на
стенде, определяют пределы их измерения
и цену деления каждого прибора. -
Заранее составляют
таблицу, в которую будут заносить
результаты, так как образец быстро
нагревается, а остывает медленно, и
повторить опыт с целью исправления
ошибки можно только через продолжительное
время. -
Включают установку.
С помощью автотрансформатора подают
на первичную обмотку максимальное
напряжение. Через равные промежутки
времени записывают показания
микроамперметра и милливольтметра в
один и тот же момент. Сначала интервалы
времени можно брать около 30 с. Как только
будет отмечено падение показаний
микроамперметра, интервалы следует
сократить примерно до 10 с. Полученные
данные записывают в таблицу:
|
|
||||
|
|
Начальное показание
милливольтметра может оказаться не
нулевым, если работа выполнялась на
предыдущем занятии и температура образца
не успела снизиться до комнатной.
-
По полученным
данным строят график, причем по
горизонтальной оси откладывают показания
милливольтметра, а по вертикальной –
показания микроамперметра. График
имеет вид, схематически изображенный
на рис. 9. Для определения точки Кюри
экстраполируют на графике кривую
падения тока до нуля по вертикали, чтобы
она достигла горизонтальной оси. По
делениям горизонтальной оси определяют
показания милливольтметра как момент
наиболее резкого падения тока во
вторичной цепи и ему соответствующую
температуру.

рис. 9
Температуру Кюри
определяют по градуировочному графику
термопары, расположенному на стенде.
Градуировочный график – это график
зависимости показаний милливольтметра
от температуры горячего спая термопары.
По оси показаний милливольтметра находят
показание, соответствующее точке Кюри
на построенном графике, проводят мысленно
перпендикуляр до пересечения с
градуировочным графиком и найденную
точку сносят на ось температур. Никакие
пометки на градуировочном графике
недопустимы.
Найденную точку
Кюри записывают в ответ. Так как измерение
прямое, и оно проводится один раз, оценить
погрешность результата затруднительно,
и эта оценка не производится в работе.
Отчет по работе
должен содержать:
1. Название и
цель работы.
2. Определение
магнитной проницаемости и классификацию
магнетиков по величине магнитной
проницаемости.
3. Определение
точки Кюри.
4. Схематическое
изображение установки с пояснениями.
-
Таблицу результатов.
-
График зависимости
I
от показаний милливольтметра

. -
Найденную точку
Кюри в градусах Цельсия.
Вопросы для самопроверки
-
Что такое магнитная
проницаемость магнетика и как магнетик
классифицируется по величине магнитной
проницаемости? -
Что такое магнитный
момент? Какими магнитными моментами
обладают атомы и молекулы? -
Чем определяются
магнитные свойства ферромагнетиков? -
Что такое точка
Кюри? -
Опишите принцип
действия установки? -
докажите, что ток
во вторичной обмотке зависит от магнитной
проницаемости образца. -
Что такое
градуировочный график термопары? -
Придумайте способ
хотя бы грубой оценки погрешности
измерения точки Кюри.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Что такое сегнетоэлектрики
Определение
Сегнетоэлектрики это диэлектрики, которые обладают рядом специфических свойств, которые реализуются благодаря тому, что обладают доменной структурой и в некоторой области температур могут спонтанно поляризоваться, причем направление этой поляризации можно изменить с помощью электрического поля.
В некоторых твердых и жидких веществах при определенных внешних воздействиях происходят фазовые превращения без изменения их агрегатных состояний. Например, сегнетоэлектрик может превращаться в параэлектрик.
Что такое точка Кюри
Если повышать температуру сегнетоэлектрика до некоторой температуры ($T_k$), которая своя для каждого вещества, то сегнетоэлектрические свойства диэлектрика исчезают, и он становится обычным диэлектриком. Такая точка фазового перехода из состояния сегнетоэлектрика в состояние полярного диэлектрика называется точкой Кюри, а соответствующая температура ($T_k$) – температурой Кюри. Существуют сегнетоэлектрики, у которых две точки Кюри, верхняя и нижняя. Такие вещества сохраняют свои сегнетоэлектрические свойства в интервале температур, которые заданы верхней и нижней границами. Таких сегнетоэлектриков сравнительно не много. У большинства сегнетоэлектриков только верхняя точка Кюри.
График зависимости спонтанной поляризации сегнетоэлектрика ($P_S$) от температуры вблизи точки Кюри приведен на рис.1.
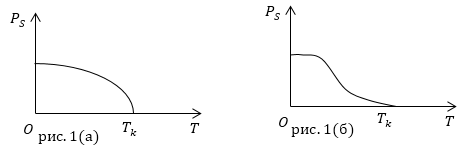
В окрестности фазового превращения (в точке Кюри) структура вещества сегнетоэлектрика оказывается податлива к внешним воздействиям. Даже небольшие изменения напряженности поля вблизи фазового перехода вызывают существенные изменения электрических свойств диэлектрика.
Вблизи точки Кюри у сегнетоэлектриков, находящихся в полярной фазе, значения диэлектрической проницаемости достигают очень больших значений, (вплоть до ${10}^4- {10}^5)$. Например, у титаната бария $(BaTiO_3)$ точка Кюри лежит около температуры $120^oC$, а диэлектрическая проницаемость достигает в максимуме $6000-7000$. Надо отметить, что существуют сегнетоэлектрики и с не очень большой диэлектрической проницаемостью, например, некоторые водорастворимые сегнетоэлектрики имеют проницаемость $varepsilon =5-6$.
Причем максимум диэлектрической проницаемости достигается в точке Кюри (рис.2).
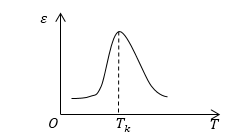
Рис. 2
Закон изменения диэлектрической восприимчивости
Закон изменения диэлектрической восприимчивости в неполярной фазе сегнетоэлектрика около точки Кюри можно записать как:
[varkappa =frac{A}{T-T_0}left(1right),]
где $A$ — постоянная. $T_0$ — температура Кюри — Вейсса, близкая к температуре точки Кюри ($T_k$). Очень часто в формуле (1) вместо $T_0$ используют $T_k$. В том случае, если у сегнетоэлектрика есть две точки Кюри, то вблизи второй точки закон Кюри-Вейсса запишется как:
[varkappa =frac{A’}{{T’}_0-T}left(2right).]
В случае неизотропных диэлектриков скалярная величина $varkappa $ в формулах (1) и (2) должна быть заменена на тензор ${varkappa }_{ij}.$ Температурная зависимость при этом не изменится.
На практике для сегнетоэлектриков закон Кюри-Вейсса можно записать для нахождения диэлектрической проницаемости в виде:
[varepsilon =frac{С}{T-T_k}left(3right),]
где $С=frac{1}{alpha T_k}$ — постоянная Кюри-Вейсса, $T_k$ — температура Кюри, при которой происходит фазовый переход, а $alpha $ изменяет знак. Если $Сsim {10}^3$, то фазовый переход происходит с упорядочением некоторых структурных элементов, ионов, протонов или групп атомов. Такой переход иногда называют: порядок — беспорядок. Если $Сsim {10}^5$, то переход типа смещения относительно положения равновесия. Постоянную Кюри — Вейсса часто определяют из графика зависимости $frac{1}{varepsilon }=frac{1}{varepsilon }left(Tright).$
Надо сказать, что разные сегнетоэлектрики могут обладать фазовыми переходами, как первого, так и второго рода. К сегнетоэлектрикам с фазовым переходом первого рода (рис. 1(а)) относят такие, которые испытывают скачки поляризации при постоянных температуре и давлении:
[P_i=-{left(frac{partial Ф}{partial E_i}right)}_{T,p}left(4right),]
где $Ф$ — термодинамический потенциал, равный:
[Ф=U-TS+pV-PE left(5right).]
К сегнетоэлектрикам с фазовым переходом второго рода (рис.2(а)) относят диэлектрики, у которых скачком изменяется диэлектрическая восприимчивость (?) при постоянных давлении и температуре:
[varkappa =-{left(frac{{partial }^2Ф}{partial {E_i}^2}right)}_{p,T}left(6right).]
Наличие точки Кюри является характерным свойством всех сегнетоэлектриков.
«Точка Кюри сегнетоэлектриков» 👇
Пример 1
Задание: Для гидрофосфата калия ($KH_2PO_4$) который является сегнетоэлектриком, поляризация в котором обусловлена смещением ионов водорода при температурах неблизких к точке Кюри, опыт дает:
[varepsilon =4,5+frac{3100}{T-121}(1.1).]
Определите, значения каких величин, представлены в выражении (1.1)? Найдите коэффициент внутреннего поля $beta ,$ используя формулу (1.2):
[beta =frac{4pi T_k}{C-T_kleft({varepsilon }_0-1right)}left(1.2right).]
Решение:
За основу решения задачи примем формулу, которая определяет связь диэлектрической проницаемости сегнетоэлектрика с температурой:
[varepsilon ={varepsilon }_0+frac{С}{T-T_k}left(1.3right).]
Тогда, сравнивая выражения (1.3) и (1.1) получаем:
[{varepsilon }_0=4,5; С=3100; T_k=121К.]
В таком случае коэффициент $beta $ легко вычислить, используя (1.2). Получим:
[beta =frac{4cdot 3,14cdot 121}{3100-121left(4,5-1right)}=0,567]
Ответ: $beta =0,567$.
Пример 2
Задание: Даны два графика зависимости $varepsilon $(T) и $frac{1}{varepsilon }left(T right)$ рис.3 (а,б). Определите, к какой фазе сегнетоэлектрика относятся части графиков I и II.
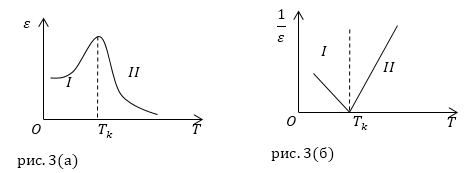
Рис. 3
Решение:
Рассмотрим график рис. 3(а). Отрезок кривой, обозначенный цифрой I, соответствует сегнетоэлектрической фазе диэлектрика, в точке Кюри ( $T_k$) поляризация достигает максимума, отрезок с цифрой II соответствует пароэлектрической фазе диэлектрика. Диэлектрическая проницаемость резко падает, с ростом температуры разрушается доменная структура вещества.
Рассмотрим график рис. 3(б). В соответствии с законом Кюри-Вейсса:
[varepsilon =frac{С}{T-T_k}left(2.1right),]
следовательно:
[frac{1}{varepsilon }=frac{T-T_k}{С}left(2.2right).]
Отрезок I, относится к фазе — сегнетоэлектрик. Величина, обратная к диэлектрической проницаемости, линейно уменьшается с ростом температуры, вплоть до $T>T_k$, при $T=T_k$ $frac{1}{varepsilon }=0$. Далее отрезок II – параэлектрик при температуре выше, чем точка Кюри.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Точка Кюри — это температура, при которой изменяется фазовое состояние вещества. В данной работе изучается фазовый переход из ферромагнитного состояния в парамагнитное на примере изменения магнитной восприимчивости $chi $ от температуры.

На рис. 1 приведен теоретический вид зависимости спонтанной намагниченности $M_s$ ниже точки Кюри и магнитной восприимчивости $chi $ выше точки Кюри. При абсолютном нуле температуры спонтанная намагниченность ферромагнетика $M_s$ имеет максимальное значение. При повышении температуры возрастает дезориентирующая роль теплового движения, что приводит к монотонному уменьшению спонтанной намагниченности, и при достижении температуры Кюри $T_c,$ $M_s$ должна обратиться в нуль.
Из классической теории фазовых переходов [1. Гл. 16 и 3. Гл. 3] следует, что в области температур выше точки Кюри ферромагнетики должны подчиняться закону Кюри — Вейсса
$$ label{GrindEQ__33_}
chi =frac{C}{T-T_{c} } .
$$
Эта зависимость несколько напоминает закон Кюри для парамагнетиков $chi =frac{C}{T} $, но магнитная восприимчивость $chi $ в формуле обратно пропорциональна не абсолютной температуре $T,$ а разности температур $(T-T_{c}).$
Опыт показал, что в области высоких температур, при $T>T_{c} $ (в парамагнитной области), линейная зависимость обратной восприимчивости $frac{1}{chi }$ от температуры $T$ достаточно хорошо выполняется (см. рис. 2).

Но в непосредственной близости к точке Кюри, при приближении к ней со стороны высоких температур, имеется значительное отклонение от линейной зависимости (вблизи точки Кюри имеется изгиб). Оказалось, что переход из ферромагнитного состояния в парамагнитное происходит не сразу, а постепенно. Вещество находится в промежуточном состоянии между ферромагнетным и парамагнетным в некотором интервале температур выше точки Кюри (так называемой переходной области). Для чистых ферромагнитных материалов этот интервал температур небольшой, для сплавов же он значительно шире.
Вероятная схема, объясняющая это явление состоит в том, что вблизи точки Кюри при $Tge T_{c} $ ещё существуют «группы» параллельных спинов (аналог капелек жидкости в паре), которые и приводят к бoльшему значению магнитной восприимчивости. Из-за наличия теплового движения «группы» спинов очень подвижны, т.е. в одних местах они исчезают — в других появляются. При температурах выше точки Кюри время жизни ориентированных спинов очень мало. Предполагаемые причины существования «групп» спинов:
-
флуктуации концентрации примесей по объему образца;
-
неоднородные механические деформации, приводящие к искажениям решетки.
Для определения границ переходной области, помимо ферромагнитной точки Кюри $T_{c}^{ф},$ вводится парамагнитная точка Кюри $T_{c}^{n},$ которая устанавливает верхнюю границу переходной области. Парамагнитная точка Кюри определяется экстраполяцией линейного участка кривой $frac{1}{chi }=f(T)$ до пересечения с осью температуры (рис. 2).
Температурные зависимости спонтанной намагниченности $M_s$ и магнитной восприимчивости $chi $ описываются следующими выражениями:
$$
M_s=A(T_c-T)^{beta }, T< T_c,
$$
$$
frac{1}{chi } =B(T-T_{c} )^{gamma } , T > T_c,
$$
где $A$ и $B$ — константы; $beta $ и $gamma $} — критические индексы магнитного перехода, которые в парамагнитной области равны: $beta = frac 12,$ $gamma =1.$ Вблизи точки Кюри $T_c $ значения критических индексов существенно отличаются от теоретических (см. табл. 1).
Таблица 1
Критические значения показателей степени в законе Кюри–Вейсса для некоторых ферромагнетиков [1, с. 546]
| Вещество | $gamma $ | $beta $ | $Т_к$ |
|---|---|---|---|
| Fe | 1.33 | 0.34 | 1 043 |
| Co | 1.21 | — | 1 388 |
| Ni | 1.35 | 0.42 | 627 |
| Gd | 1.3 | — | 292 |
| CrO$_{2}$ | 1.63 | — | 387 |
| CrBr$_{3}$ | 1.215 | 0.368 | 32.56 |
| EuS | — | 0.33 | 16.5 |
В соответствии с выражением $
frac{1}{chi } =B(T-T_{c} )^{gamma } , T > T_c,
$ магнитная восприимчивость в точке Кюри должна быть бесконечной. В действительности для реальных образцов она принимает конечное значение $chi _0$, поэтому величину $gamma $ определяют из соотношения
$$ label{GrindEQ__36_}
frac{1}{chi } -frac{1}{chi _{0} } =B(T-T_{c} )^{gamma } .
$$
Для определения величины критического индекса магнитной восприимчивости $gamma$ необходимо:
-
получить экспериментальную зависимость магнитной восприимчивости от температуры (см. рис. 4), после обработки которой найти температуру Кюри $T_c$ и соответствующее значение $chi _0$;

-
зная значения $T_c$ и $chi _0$, построить график зависимости $lg left(frac{1}{chi } – frac{1}{chi _0}right)$ от $lg left(T-T_{c} right)$ и по угловому коэффициенту прямой определить значение $gamma $.
Назад к описанию лабораторных работ «Электрические и магнитные свойства твердых тел» или далее
к описанию установки
Определение точки Кюри ферромагнетика методом Зилова-Ренкина
Подобный материал:
- Физика магнитных явлений, часть, 19.63kb.
- Пьер Кюри и Мария Склодовская-Кюри, 46.42kb.
- Н. Э. Баумана кафедра химии овчаренко Л. П., Татьянина И. В., Горячева В. Н. Определение, 217.5kb.
- №2: «Мария Склодовская – Кюри», 214.49kb.
- Химический анализ водорастворимых солей, 388.64kb.
- Жизнь Марии Кюри вдохновила многих кинематографистов решение, 838.31kb.
- Лабораторная работа э-10 изучение зависимости магнитной проницаемости ферромагнетика, 76.57kb.
- Темы курсовых работ для студентов 2-го курса (кафедра физики низких температур и сверхпроводимости), 29.79kb.
- Сибирский независимый университет, 57.5kb.
- Определение удельной поверхности материалов (твердых тел) газохроматографическим методом, 114.43kb.
Определение точки Кюри ферромагнетика методом Зилова-Ренкина.
ОБОРУДОВАНИЕ
- весы аналитические АДВ 200М с магнитными подвесами и компенсационным устройством,
- держатель образца с нагревателем,
- цифровой вольтамперметр Щ301 1,
- цифровой вольтметр Щ1516,
- источник постоянного напряжения ВС 24М,
- источник питания постоянного тока Б5 46,
- магазин сопротивлений.
ФИЗИЧЕСКОЕ ВВЕДЕНИЕ
Способность пара- и ферромагнетиков намагничиваться различна при разных температурах, т.е. их магнитная восприимчивость зависит от температуры. Напротив, магнитная восприимчивость диамагнетиков практически не зависит от температуры. Для многих парамагнитных веществ изменение удельной (т.е. отнесенной к единице массы) магнитной восприимчивости с температурой подчиняется закону, установленному Кюри:
| =С/Т | |
где С – константа, зависящая от исследуемого вещества.
Зависимость магнитной восприимчивости от температуры для ферромагнетиков имеет более сложный характер. При повышении температуры способность ферромагнетиков намагничиваться уменьшается. При некоторой температуре ТС , называемой температурой Кюри, спонтанный магнитный момент М становиться равным нулю, и ферромагнитные свойства исчезают вовсе. При Т>ТK ферромагнетик превращается в парамагнетик. Зависимость магнитной восприимчивости от температуры для таких парамагнетиков подчиняется закону Кюри-Вейсса:
| =С/(Т– ТK ) | (2) |
Температуру Кюри ферромагнитного образца можно определить с помощью магнитных весов. Принцип действия которых основан на измерении механической силы F , которая возникает при помещении образца в неоднородное магнитное поле dH/dx, создаваемое магнитом.
| F =(M+mH)*dH/dx | (3) |
где m – масса образца.
В методе Фарадея измеряется сила действующая на исследуемый образец, а в методе Зилова-Ренкина, используемого в данной работе, измеряется сила действующая на магнит. Метод Зилова-Ренкина, по сравнению с другими методами, дает большую возможность производить измерения в широком интервале полей и температур.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
 |
Рис.1. Магнитные весы Зилова-Ренкина.
Цифрами обозначены: 1 – аналитические весы, 2 и 3 – постоянные магниты, 4 исследуемый образец, 5 – нагреватель, 6 – катушка компенсационного устройства, 7 – термопара, 8 – сосуд с таящим льдом для термостатирования холодного спая термопары. Нагреватель образца питается от источника ВС–24М, катушка компенсационного устройства питается от стабилизированного источника питания постоянного тока Б5 46. Ток в катушке регулируется магазином сопротивлений и измеряется цифровым вольтамперметром Щ301 1. |
ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ТОЧКИ КЮРИ
В данной работе используется нулевой способ измерений, в котором компенсация изменения силы F осуществляется изменением силы взаимодействия постоянного магнита – 3 и электромагнита –6 посредством уменьшения или увеличения тока i через катушку электромагнита. В области малых магнитных полей и Н*dН/dх=const (что обеспечивается фиксацией нулевой отметки шкалы весов):
| i=А*F | (4) |
где А=const.
Согласно (3) и (4) в точке Кюри изменения i с температурой максимальны. Поэтому точка Кюри экспериментально определяется как максимум на графике зависимости i/Т от температуры.ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЕ ТОЧКИ КЮРИ
В данной работе используется нулевой способ измерений, в котором компенсация изменения силы F осуществляется изменением силы взаимодействия постоянного магнита – 3 и электромагнита –6 посредством уменьшения или увеличения тока i через катушку электромагнита. В области малых магнитных полей и Н*dН/dх=const (что обеспечивается фиксацией нулевой отметки шкалы весов):
| i=А*F | (4) |
где А=const.
Согласно (3) и (4) в точке Кюри изменения i с температурой максимальны. Поэтому точка Кюри экспериментально определяется как максимум на графике зависимости i/Т от температуры.
ХОД РАБОТЫ
Для определения точки Кюри исследуемого образца La0.7Sr0.3MnO3 необходимо провести измерения в интервале температур от комнатной до 130С. Измерения производятся при непрерывном нагреве образца, при этом стрелку весов надо удерживать на нулевой отметке, регулируя ток компенсации i магазином сопротивлений. В каждой точке необходимо записывать ЭДС термопары и величину тока компенсации. Измерения следует проводить при скорости изменения температуры около ~100 С в час так, что одна точка измерений приходиться на 2–4 С. По полученным данным построить два графика: i(Т) и di/dТ (T) и по максимуму на втором графике определить точку Кюри.
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Справедлив ли закон Кюри-Вейсса для исследуемого образца?
- Что определяет основную ошибку определения точки Кюри?
- Как размагнитить постоянный магнит? В какие виды превращается при этом энергия магнитного поля?
ЛИТЕРАТУРА
- И.Е.Тамм, ОСНОВЫ ТЕОРИИ ЭЛЕКТРИЧЕСТВА. — М., Наука, 1966. §72 Ферромагнетизм. Молекулярное поле Вейсса.
- И.В.Савельев, КУРС ОБЩЕЙ ФИЗИКИ, том: Электричество и магнетизм. — М., Наука, 1982. §59 Ферромагнетизм.
- С.Г.Калашников. ЭЛЕКТРИЧЕСТВО. – М., Наука, 1970. Глава ХI. Магнетики.
- В.И.Чечерников. МАГНИТНЫЕ ИЗМЕРЕНИЯ. – М., МГУ, 1969. Глава VII. Методы исследования слабомагнитных веществ.
