Как найти арктангенс единицы

Как найти арктангенс единицы

Арктангенс — обратная тригонометрическая функция. Общепринятое обозначение арктангенса — arctg x. При этом довольно часто, особенно в зарубежной литературе можно встретить иное обозначение — arctan x.

Арктангенс калькулятор

Калькулятор арктангенса

Калькулятор арктангенса

Как пользоваться калькулятором арктангенса

Введите значение тангенса угла и нажмите кнопку посчитать. В результате вы получите значение арктангенса выраженное в градусах и радианах.

Что такое арктангенс

Арктангенс числа x — это значение угла в радианах, для которого справедливо равенство tg a = m. 

К примеру, что такое arctg 1? Это угол в радианах, тангенс которого равен 1.

Ваша оценка

[Оценок: 9104 Средняя: 3.8]

Арктангенс Автор admin средний рейтинг 3.8/5 – 9104 рейтинги пользователей

Источник
  • Определение

  • График арктангенса

  • Свойства арктангенса

  • Таблица арктангенсов

Определение

Арктангенс (arctg или arctan) – это обратная тригонометрическая функция.

Арктангенс x определяется как функция, обратная к тангенсу x, где x – любое число (x∈ℝ).

Если тангенс угла у равен х (tg y = x), значит арктангенс x равняется y:

arctg x = tg-1 x = y, причем -π/2<y<π/2

Примечание: tg-1x означает обратный тангенс, а не тангенс в степени -1.

Например:

arctg 1 = tg-1 1 = 45° = π/4 рад

График арктангенса

Функция арктангенса пишется как y = arctg (x). График в общем виде выглядит следующим образом:

График арктангенса

Свойства арктангенса

Ниже в табличном виде представлены основные свойства арктангенса с формулами.

Таблица арктангенсов
arctg x (°) arctg x (рад) x
-90° -π/2 -∞
-71.565° -1.2490 -3
-63.435° -1.1071 -2
-60° -π/3 -√3
-45° -π/4 -1
-30° -π/6 -1/√3
-26.565° -0.4636 -0.5
0° 0 0
26.565° 0.4636 0.5
30° π/6 1/√3
45° π/4 1
60° π/3 √3
63.435° 1.1071 2
71.565° 1.2490 3
90° π/2 ∞

microexcel.ru

Источник

Арксинус, арккосинус, арктангенс и арккотангенс – начальные сведения

Задача, обратная нахождению значения синуса, косинуса, тангенса и котангенса данного угла (числа), подразумевает нахождение угла (числа) по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.

В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение упомянем про аркфункции и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.

Навигация по странице.

Определения, обозначения, примеры

Арксинус, арккосинус, арктангенс и арккотангенс можно определить как угол и как число. Это связано с тем, что мы определили синус, косинус, тангенс и котангенс как угла, так и числа (смотрите синус, косинус, тангенс и котангенс в тригонометрии). Остановимся на обоих подходах к определению арксинуса, арккосинуса, арктангенса и арккотангенса.

Арксинус, арккосинус, арктангенс и арккотангенс как угол

Пусть про угол альфа α известно лишь то, что его синус равен числу 1/2 , то есть, sinα=1/2 . Последнее равенство определяет угол α неоднозначно, так как ему удовлетворяет бесконечное множество углов α=(−1) k ·30°+180°·k ( α=(−1) k ·π/6+π·k ), где k∈Z . Однако, если потребовать, чтобы величина угла α в градусах принадлежала отрезку [−90, 90] (в радианах – отрезку [−π/2, π/2] ), то равенство sinα=1/2 будет определять угол альфа однозначно. При этом условии равенству удовлетворяет единственный угол в 30 градусов ( π/6 радианов).

Вообще, равенство sinα=a (не путайте a и альфа: a и α ) при любом числе a∈[−1, 1] и условии −90°≤α≤90° ( −π/2≤α≤π/2 ) определяет единственный угол α . Этот угол называют арксинусом числа a .

Арксинус числа a∈[−1, 1] – это угол −90°≤α≤90° ( −π/2≤α≤π/2 ), синус которого равен a .

Аналогично определяются арккосинус, арктангенс и арккотангенс.

Арккосинус числа a∈[−1, 1] – это угол 0°≤α≤180° ( 0≤α≤π ), косинус которого равен a .

Арктангенс числа a∈(−∞, +∞) – это угол −90° ( −π/2 ), тангенс которого равен a .

Арккотангенс числа a∈(−∞, +∞) – это угол 0° ( 0 ), котангенс которого равен a .

Для записи арксинуса, арккосинуса, арктангенса и арккотангенса приняты следующие обозначения: arcsin , arccos , arctg и arcctg . То есть, арксинус числа a можно записать как arcsin a , арккосинус, арктангенс и арккотангенс числа a запишутся соответственно как arccos a , arctg a и arcctg a .

Также можно встретить обозначения arctan и arccot , они являются другой формой обозначения арктангенса и арккотангенса, которая принята в англоязычной литературе. Мы же арктангенс и арккотангенс будем обозначать как arctg и arcctg .

В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа можно записать более формально:

arcsin a , a∈[−1, 1] , есть такой угол α , что −90°≤α≤90° ( −π/2≤α≤π/2 ) и sinα=a ;

arccos a , a∈[−1, 1] , есть такой угол α , что 0°≤α≤180° ( 0≤α≤π ) и cosα=a ;

arctg a , a∈(−∞, +∞) , есть такой угол α , что −90° ( −π/2 ) и tgα=a ;

arcctg a , a∈(−∞, +∞) , есть такой угол α , что 0° ( 0 ) и ctgα=a .

Подчеркнем, что арксинус и арккосинус числа определен для чисел, принадлежащих отрезку [−1, 1] , для остальных чисел арксинус и арккосинус не определен. Например, не имеет смысла запись arcsin2 . Аналогично не определен арксинус пяти, арксинус минус корня из трех, арккосинус семи целых двух третьих и арккосинус минус пи, так как числа 2 , 5 , , −π выходят за пределы числового отрезка от −1 до 1 . В свою очередь записи arctg a и arcctg a имеют смысл для любого действительного числа a , например, имеют смысл записи arctg0 , arctg(−500,2) , arcctg(6·π+1) и т.п.

Теперь можно привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.

Начнем с примеров арксинуса. Определение арксинуса позволяет утверждать, что угол π/3 является арксинусом числа , то есть, (здесь и α=π/3 ). Действительно, число принадлежит отрезку [−1, 1] , угол π/3 лежит в пределах от −π/2 до π/2 и . Приведем еще несколько примеров арксинуса числа: arcsin(−1)=−90° , arcsin(0,5)=π/6 , .

А вот π/10 не является арксинусом 1/2 , так как sin(π/10)≠1/2 . Еще пример: несмотря на то, что синус 270 градусов равен −1 , угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270 градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.

Для полноты картины приведем примеры арккосинуса, арктангенса и арккотангенса числа. Например, угол 0 радианов является арккосинусом единицы, то есть, arccos1=0 (так как выполняются все условия из определения арккосинуса: число 1 принадлежит отрезку от −1 до 1 , угол нуль радианов лежит в пределах от нуля до пи включительно и cos0=1 ). Аналогично, угол π/2 есть арккосинус нуля: arccos0=π/2 . По определению арктангенса числа arctg(−1)=−π/4 или arctg(−1)=−45° . Арктангенс корня из трех равен 60 градусам ( π/3 рад). А из определения арккотангенса можно заключить, что arcctg0=π/2 , так как угол π/2 лежит в рамках от 0 до пи и ctg(π/2)=0 .

Подобный подход к определению арксинуса, арккосинуса, арктангенса и арккотангенса описан в учебнике Кочеткова [1, с. 260-278] .

Арксинус, арккосинус, арктангенс и арккотангенс как число

Когда мы имеем дело с синусом, косинусом, тангенсом и котангенсом угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять как угол. Если же мы начинаем говорить про синус, косинус, тангенс и котангенс числа, а не угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять уже как число.

Арксинусом числа a∈[−1, 1] называется такое число t∈[−π/2, π/2] , синус которого равен a .

Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса

В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».

Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.

Для четкого понимания рассмотрим пример.

Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .

Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °

Основные значения arcsin, arccos, arctg и arctg

Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.

Таблица синусов основных углов предлагает такие результаты значений углов:

sin ( – π 2 ) = – 1 , sin ( – π 3 ) = – 3 2 , sin ( – π 4 ) = – 2 2 , sin ( – π 6 ) = – 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1

Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от – 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.

Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.

в р а д и а н а х

α – 1 – 3 2 – 2 2 – 1 2 0 1 2 2 2 3 2
a r c sin α к а к у г о л – π 2 – π 3 – π 4 – π 6 0 π 6 π 4 π 3
в г р а д у с а х – 90 ° – 60 ° – 45 ° – 30 ° 0 ° 30 ° 45 ° 60 °
a r c sin α к а к ч и с л о – π 2 – π 3 – π 4 – π 6 0 π 6 π 4 π 3

Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:

cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = – 1 2 , cos 3 π 4 = – 2 2 , cos 5 π 6 = – 3 2 , cos π = – 1

Следуя из таблицы, находим значения арккосинуса:

a r c cos ( – 1 ) = π , arccos ( – 3 2 ) = 5 π 6 , arcocos ( – 2 2 ) = 3 π 4 , arccos – 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0

в р а д и а н а х

α – 1 – 3 2 – 2 2 – 1 2 0 1 2 2 2 3 2 1
a r c cos α к а к у г о л π 5 π 6 3 π 4 2 π 3 π 2 π 3 π 4 π 6 0
в г р а д у с а х 180 ° 150 ° 135 ° 120 ° 90 ° 60 ° 45 ° 30 ° 0 °
a r c cos α к а к ч и с л о π 5 π 6 3 π 4 2 π 3 π 2 π 3 π 4 π 6 0

Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.

α – 3 – 1 – 3 3 0 3 3 1 3
a r c t g a к а к у г о л в р а д и а н а х – π 3 – π 4 – π 6 0 π 6 π 4 π 3
в г р а д у с а х – 60 ° – 45 ° – 30 ° 0 ° 30 ° 45 ° 60 °
a r c t g a к а к ч и с л о – π 3 – π 4 – π 6 0 π 6 π 4 π 3

Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса

a r c sin , a r c cos , a r c t g и a r c c t g

Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.

Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( – α ) = – a r c sin α , a r c cos ( – α ) = π – a r c cos α , a r c t g ( – α ) = – a r c t g α , a r c c t g ( – α ) = π – a r c c t g α .

Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.

Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.

Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.

Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.

Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .

Нахождение значения arcsin, arccos, arctg и arcctg

Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).

При известном a r c sin α = – π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:

a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .

Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.

Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.

При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.

Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.

Арктангенс и арккотангенс. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Арктангенс и арккотангенс − теория, примеры и решения

Функция арктангенс и ее график

Функция тангенс определена в интервале [−∞;+∞] кроме точек , . и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции тангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арктангенс.

  1. Область определения функции: .
  2. Область значений функции: .
  3. Функция является нечетной: .
  4. Функция возрастает.
  5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение

Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.

Решение уравнения (2) представлен на Рис.3:

Так как tg t − это ординат точки пересечения прямой OMt1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OTt пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Используя онлайн калькулятор получим:

Функция арккотангенс и ее график

Как известно, функция котангенс определена в интервале [−∞;+∞] кроме точек -2π, –π 0, π, 2π. и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:

Функция (4) − это функция, обратная к функции

График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арккотангенс.

  1. Область определения функции: .
  2. Область значений функции: .
  3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
  4. Функция убывает.
  5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:

Решения уравнения (5) можно представить на единичной окружности (Рис.6):

ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (6):

Так как в интервале (0; π), то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (6), имеем

С помощью онлайн калькулятора вычисляем . Тогда

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/trigonometrija/nahozhdenie-znachenij-arksinusa-arkkosinusa-arktan/

http://matworld.ru/trigonometry/arktangens-i-arkkotangens.php

[/spoiler]

Источник

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика XVIII века Карла Шерфера и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: {displaystyle sin ^{-1},{frac {1}{sin }},} но они не прижились[1].
Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin−1, cos−1 для арксинуса, арккосинуса и т. п.[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.

Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, arcsin 1/2 означает множество углов left ( frac{pi}{6}, frac{5 pi}{6}, frac{13 pi}{6}, frac{17 pi}{6} dots ~ (30^circ, 150^circ, 390^circ, 510^circ dots) right ), синус которых равен 1/2. Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.

В общем случае при условии -1leqslant alpha leqslant 1 все решения уравнения sin x=alpha можно представить в виде x=(-1)^{n}arcsin alpha +pi n,~n=0,pm 1,pm 2,dots ~.[3]

Основное соотношение[править | править код]

arcsin x+arccos x={frac {pi }{2}}
operatorname {arctg},x+operatorname {arcctg},x={frac {pi }{2}}

Функция arcsin[править | править код]

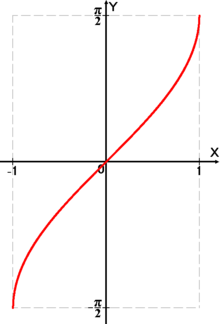
График функции y=arcsin x

Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого {displaystyle sin y=x,quad -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},quad |x|leqslant 1.}

Функция y=arcsin x непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.

Свойства функции arcsin[править | править код]

Получение функции arcsin[править | править код]

Дана функция y=sin x. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие y=arcsin x функцией не является. Поэтому рассмотрим отрезок {displaystyle [-pi /2;pi /2]}, на котором функция y=sin x строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на отрезке {displaystyle [-pi /2;pi /2]} существует обратная функция y=arcsin x, график которой симметричен графику функции y=sin x относительно прямой y=x.

Функция arccos[править | править код]

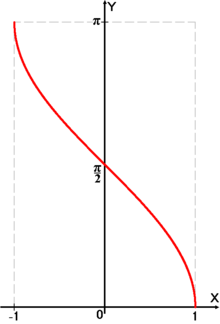
График функции y=arccos x

Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого {displaystyle cos y=x,qquad 0leqslant yleqslant pi ,quad |x|leqslant 1.}

Функция y=arccos x непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.

Свойства функции arccos[править | править код]

Получение функции arccos[править | править код]

Дана функция y=cos x. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие y=arccos x функцией не является. Поэтому рассмотрим отрезок [0;pi ], на котором функция y=cos x строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на отрезке [0;pi ] существует обратная функция {displaystyle y=arccos x}, график которой симметричен графику функции y=cos x относительно прямой y=x.

Функция arctg[править | править код]

График функции y=operatorname {arctg},x

Аркта́нгенсом числа x называется такое значение угла {displaystyle y,} выраженное в радианах, для которого {displaystyle operatorname {tg} y=x,quad -{frac {pi }{2}}<y<{frac {pi }{2}}.}

Функция y=operatorname {arctg}x определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.

Свойства функции arctg[править | править код]

Получение функции arctg[править | править код]

Дана функция y=operatorname {tg},x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=operatorname {arctg},x функцией не является. Поэтому рассмотрим интервал {displaystyle (-pi /2;pi /2)}, на котором функция y=operatorname {tg},x строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на интервале {displaystyle (-pi /2;pi /2)} существует обратная функция y=operatorname {arctg},x, график которой симметричен графику функции y=operatorname {tg},x относительно прямой y=x.

Функция arcctg[править | править код]

График функции {displaystyle y=operatorname {arcctg} x}

Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого {displaystyle operatorname {ctg} ,y=x,quad 0<y<pi .}

Функция y=operatorname {arcctg},x определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.

Свойства функции arcctg[править | править код]

Получение функции arcctg[править | править код]

Дана функция y=operatorname {ctg},x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=operatorname {arcctg},x функцией не является. Поэтому рассмотрим интервал (0;pi ), на котором функция y=operatorname {ctg},x строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на интервале (0;pi ) существует обратная функция y=operatorname {arcctg},x, график которой симметричен графику функции y=operatorname {ctg},x относительно прямой y=x.

График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, xrightarrow -x) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы operatorname {arcctg}x=operatorname {arctg}(-x)+pi /2.

Функция arcsec[править | править код]

График функции {displaystyle y=operatorname {arcsec} x}

Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого {displaystyle sec y=x,qquad |x|geqslant 1,quad 0leqslant yleqslant pi .}

Функция {displaystyle y=operatorname {arcsec} x} непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.

Свойства функции arcsec[править | править код]

Функция arccosec[править | править код]

График функции {displaystyle y=operatorname {arccosec} x}

Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого {displaystyle operatorname {cosec} y=x,qquad |x|geqslant 1,quad -pi /2leqslant yleqslant pi /2.}

Функция {displaystyle y=operatorname {arccosec} x} непрерывна и ограничена на всей своей области определения. Она является строго убывающей.

Свойства функции arccosec[править | править код]

Разложение в ряды[править | править код]

Производные от обратных тригонометрических функций[править | править код]

Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:

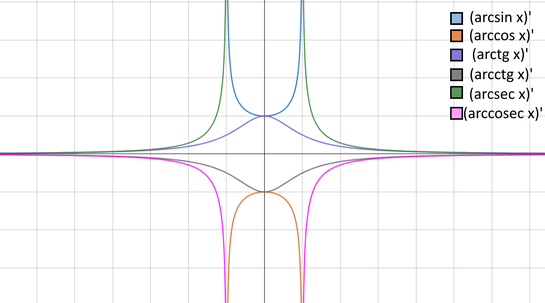
производные обратных тригонометрических функций

Функция f(x) Производная f'(x) Примечание
{displaystyle arcsin {x}} {frac {1}{{sqrt {1-x^{2}}}}}

Доказательство                                 

Найти производную арксинуса можно при помощи взаимно обратных функций.
{displaystyle sin(arcsin((x))=x}
После чего мы должны взять производную этих обеих функций.
{displaystyle [sin(arcsin((x))]'=x'}
{displaystyle cos(arcsin(x))cdot (arcsin(x))'=1}
Теперь мы должны выразить производную арксинуса.
{displaystyle (arcsin(x))'={frac {1}{cos(arcsin(x))}}}
Исходя из тригонометрического тождества({displaystyle sin^{2}x+cos^{2}x=1}) — получаем.
{displaystyle (arcsin(x))'={frac {1}{pm {sqrt {1-sin^{2}(arcsin(x))}}}}}
Для того, чтобы понять плюс должен стоять или минус взглянем какие значения.
{displaystyle D(cos(x))=[{frac {pi }{2}};-{frac {pi }{2}}]}
Так как косинус находится в 2-й и 4-й четвертях то, получается что косинус положительный.
{displaystyle (arcsin(x))'={frac {1}{sqrt {1-sin^{2}(arcsin(x))}}}}
Получается.
{displaystyle (arcsin(x))'={frac {1}{sqrt {1-x^{2}}}}}

{displaystyle arccos {x}} -{frac {1}{{sqrt {1-x^{2}}}}}

Доказательство                                 

Найти производную арккосинуса можно при помощи данного тождества:
{displaystyle arcsin(x)+arccos(x)={frac {pi }{2}}}
Теперь находим производную обеих частей этого тождества.
{displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}
{displaystyle (arcsin(x))'+(arccos(x))'=0}
Теперь выражаем производную арккосинуса.
{displaystyle (arccos(x))'=-(arcsin(x))'}
Получается.
{displaystyle (arccos(x))'=-{frac {1}{sqrt {1-x^{2}}}}}

{displaystyle mathrm {arctg} x} {displaystyle {frac {1}{1+x^{2}}}}

Доказательство                                 

Найти производную арктангенса можно при помощи взаимнообратной функции:
{displaystyle tg(arctg(x))=x}
Теперь находим производную обеих частей этого тождества.
{displaystyle [tg(arctg(x))]'=1}
{displaystyle {frac {1}{cos^{2}(arctg(x))}}cdot (arctg(x))'=1}
Теперь мы должны выразить производную арктангенса:
{displaystyle (arctg(x))'=cos^{2}(arctg(x))}
Теперь на помощь нам придет на помощь тождество({displaystyle cos(x)={frac {1}{sqrt {1+tg^{2}(x)}}}}):
{displaystyle (arctg(x))'=({frac {1}{sqrt {1+tg^{2}(arctg(x))}}})^{2}}
Получается.
{displaystyle (arctg(x))'={frac {1}{1+x^{2}}}}

{displaystyle mathrm {arcctg} x} {displaystyle -{frac {1}{1+x^{2}}}}

Доказательство                                 

Найти производную арккотангенса можно при помощи данного тождества:
{displaystyle arctg(x)+arcctg(x)={frac {pi }{2}}}
Теперь находим производную обеих частей этого тождества.
{displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}
{displaystyle (arctg(x))'+(arcctg(x))'=0}
Теперь выражаем производную арккотангенса.
{displaystyle (arcctg(x))'=-(arctg(x))'}
Получается.
{displaystyle (arcctg(x))'=-{frac {1}{1+x^{2}}}}

{displaystyle mathrm {arcsec} x} {displaystyle {frac {1}{|x|{sqrt {x^{2}-1}}}}}

Доказательство                                 

Найти производную арксеканса можно при помощи тождества:

{displaystyle arcsec(x)=arccos({frac {1}{x}})}

Теперь находим производную обеих частей этого тождества.

{displaystyle (arcsec(x))'=(arccos({frac {1}{x}}))'}

{displaystyle (arcsec(x))'=-{frac {1}{sqrt {1-{frac {1}{x^{2}}}}}}cdot (-{frac {1}{x^{2}}})}

{displaystyle (arcsec(x))'={frac {1}{x^{2}{sqrt {frac {x^{2}-1}{x^{2}}}}}}}

{displaystyle (arcsec(x))'={frac {1}{x^{2}{frac {sqrt {x^{2}-1}}{|x|}}}}}

Получается.

{displaystyle (arcsec(x))'={frac {1}{|x|{sqrt {x^{2}-1}}}}}

{displaystyle mathrm {arccosec} x} {displaystyle -{frac {1}{|x|{sqrt {x^{2}-1}}}}}

Доказательство                                 

Найти производную арккосеканса можно при помощи данного тождества:
{displaystyle arccosec(x)+arcsec(x)={frac {pi }{2}}}
Теперь находим производную обеих частей этого тождества.
{displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}
{displaystyle (arccosec(x))'+(arcsec(x))'=0}
Теперь выражаем производную арккосинуса.
{displaystyle (arccosec(x))'=-(arcsec(x))'}
Получается.
{displaystyle (arccosec(x))'=-{frac {1}{|x|{sqrt {x^{2}-1}}}}}

Интегралы от обратных тригонометрических функций[править | править код]

Неопределённые интегралы[править | править код]

Для действительных и комплексных x:

{begin{aligned}int arcsin x,dx&{}=x,arcsin x+{sqrt {1-x^{2}}}+C,\int arccos x,dx&{}=x,arccos x-{sqrt {1-x^{2}}}+C,\int operatorname {arctg},x,dx&{}=x,operatorname {arctg},x-{frac {1}{2}}ln left(1+x^{2}right)+C,\int operatorname {arcctg},x,dx&{}=x,operatorname {arcctg},x+{frac {1}{2}}ln left(1+x^{2}right)+C,\int operatorname{arcsec} x,dx&{}=x,operatorname{arcsec} x-ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C,\int operatorname {arccosec},x,dx&{}=x,operatorname {arccosec},x+ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C.end{aligned}}

Для действительных x ≥ 1:

{begin{aligned}int operatorname{arcsec} x,dx&{}=x,operatorname{arcsec} x-ln left(x+{sqrt {x^{2}-1}}right)+C,\int operatorname {arccosec},x,dx&{}=x,operatorname {arccosec},x+ln left(x+{sqrt {x^{2}-1}}right)+C.end{aligned}}
См. также Список интегралов от обратных тригонометрических функций

Использование в геометрии[править | править код]

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.

В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.
Так, если катет длины a является противолежащим для угла alpha , то

{displaystyle alpha =arcsin(a/c)=arccos(b/c)=operatorname {arctg} (a/b)=operatorname {arccosec} (c/a)=operatorname {arcsec}(c/b)=operatorname {arcctg} (b/a).}

Связь с натуральным логарифмом[править | править код]

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

{displaystyle {begin{aligned}arcsin z&{}=-iln(iz+{sqrt {1-z^{2}}})={frac {pi }{2}}-iln(z+{sqrt {z^{2}-1}})=-ioperatorname {arsh} ,iz,end{aligned}}}
{displaystyle arccos(z)={dfrac {pi }{2}}+iln(iz+{sqrt {1-z^{2}}})=-ioperatorname {arch} (iz)}
{displaystyle operatorname {arctg} (z)={dfrac {i}{2}}(ln(1-iz)-ln(1+iz))=-ioperatorname {arth} (iz)}
{displaystyle operatorname {arcctg} (z)={dfrac {i}{2}}left(ln left({dfrac {z-i}{z}}right)-ln left({dfrac {z+i}{z}}right)right)=ioperatorname {arcth} (iz)}
{displaystyle operatorname {arcsec}(z)=arccos left(z^{-1}right)={dfrac {pi }{2}}+iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right),}
{displaystyle operatorname {arccosec} ,(z)=arcsin left(z^{-1}right)=-iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right).}

См. также[править | править код]

  • Обратные гиперболические функции
  • Теорема Данжуа — Лузина

Примечания[править | править код]

Ссылки[править | править код]

  • Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
  • Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1982. — [dic.academic.ru/dic.nsf/enc_mathematics/3612/%D0%9E%D0%91%D0%A0%D0%90%D0%A2%D0%9D%D0%AB%D0%95 Т. 3. — с. 1135].
  • Обратные тригонометрические функции — статья из Большой советской энциклопедии.  — М.: «Советская Энциклопедия», 1974. — Т. 18. — с. 225.
  • Обратные тригонометрические функции // Энциклопедический словарь юного математика / Савин А.П. — М.: Педагогика, 1985. — С. 220—221. — 352 с.
  • Построение графиков обратных тригонометрических функций онлайн
  • Онлайн калькулятор: обратные тригонометрические функции

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым).

Список проблемных доменов

  • dic.academic.ru
Источник

Арктангенс(y = arctg(x)) – это обратная тригонометрическая функция к тангенсу x = tg(y). Область определения -∞ ≤ x ≤ +∞ и множество значений -π/2 ≤ y ≤ +π/2.

arctg(0) = 0° arctg(-1.732050808) = 120° arctg(1.732050808) = 240°
arctg(0.01745506493) = 1° arctg(-1.664279482) = 121° arctg(1.804047755) = 241°
arctg(0.03492076949) = 2° arctg(-1.600334529) = 122° arctg(1.880726465) = 242°
arctg(0.05240777928) = 3° arctg(-1.539864964) = 123° arctg(1.962610506) = 243°
arctg(0.06992681194) = 4° arctg(-1.482560969) = 124° arctg(2.050303842) = 244°
arctg(0.08748866353) = 5° arctg(-1.428148007) = 125° arctg(2.144506921) = 245°
arctg(0.1051042353) = 6° arctg(-1.37638192) = 126° arctg(2.246036774) = 246°
arctg(0.1227845609) = 7° arctg(-1.327044822) = 127° arctg(2.355852366) = 247°
arctg(0.1405408347) = 8° arctg(-1.279941632) = 128° arctg(2.475086853) = 248°
arctg(0.1583844403) = 9° arctg(-1.234897157) = 129° arctg(2.605089065) = 249°
arctg(0.1763269807) = 10° arctg(-1.191753593) = 130° arctg(2.747477419) = 250°
arctg(0.1943803091) = 11° arctg(-1.150368407) = 131° arctg(2.904210878) = 251°
arctg(0.2125565617) = 12° arctg(-1.110612515) = 132° arctg(3.077683537) = 252°
arctg(0.2308681911) = 13° arctg(-1.07236871) = 133° arctg(3.270852618) = 253°
arctg(0.2493280028) = 14° arctg(-1.035530314) = 134° arctg(3.487414444) = 254°
arctg(0.2679491924) = 15° arctg(-1) = 135° arctg(3.732050808) = 255°
arctg(0.2867453858) = 16° arctg(-0.9656887748) = 136° arctg(4.010780934) = 256°
arctg(0.3057306815) = 17° arctg(-0.9325150861) = 137° arctg(4.331475874) = 257°
arctg(0.3249196962) = 18° arctg(-0.9004040443) = 138° arctg(4.704630109) = 258°
arctg(0.3443276133) = 19° arctg(-0.8692867378) = 139° arctg(5.144554016) = 259°
arctg(0.3639702343) = 20° arctg(-0.8390996312) = 140° arctg(5.67128182) = 260°
arctg(0.383864035) = 21° arctg(-0.8097840332) = 141° arctg(6.313751515) = 261°
arctg(0.4040262258) = 22° arctg(-0.7812856265) = 142° arctg(7.115369722) = 262°
arctg(0.4244748162) = 23° arctg(-0.7535540501) = 143° arctg(8.144346428) = 263°
arctg(0.4452286853) = 24° arctg(-0.726542528) = 144° arctg(9.514364454) = 264°
arctg(0.4663076582) = 25° arctg(-0.7002075382) = 145° arctg(11.4300523) = 265°
arctg(0.4877325886) = 26° arctg(-0.6745085168) = 146° arctg(14.30066626) = 266°
arctg(0.5095254495) = 27° arctg(-0.6494075932) = 147° arctg(19.08113669) = 267°
arctg(0.5317094317) = 28° arctg(-0.6248693519) = 148° arctg(28.63625328) = 268°
arctg(0.5543090515) = 29° arctg(-0.600860619) = 149° arctg(57.28996163) = 269°
arctg(0.5773502692) = 30° arctg(-0.5773502692) = 150° arctg(∞) = 270°
arctg(0.600860619) = 31° arctg(-0.5543090515) = 151° arctg(-57.28996163) = 271°
arctg(0.6248693519) = 32° arctg(-0.5317094317) = 152° arctg(-28.63625328) = 272°
arctg(0.6494075932) = 33° arctg(-0.5095254495) = 153° arctg(-19.08113669) = 273°
arctg(0.6745085168) = 34° arctg(-0.4877325886) = 154° arctg(-14.30066626) = 274°
arctg(0.7002075382) = 35° arctg(-0.4663076582) = 155° arctg(-11.4300523) = 275°
arctg(0.726542528) = 36° arctg(-0.4452286853) = 156° arctg(-9.514364454) = 276°
arctg(0.7535540501) = 37° arctg(-0.4244748162) = 157° arctg(-8.144346428) = 277°
arctg(0.7812856265) = 38° arctg(-0.4040262258) = 158° arctg(-7.115369722) = 278°
arctg(0.8097840332) = 39° arctg(-0.383864035) = 159° arctg(-6.313751515) = 279°
arctg(0.8390996312) = 40° arctg(-0.3639702343) = 160° arctg(-5.67128182) = 280°
arctg(0.8692867378) = 41° arctg(-0.3443276133) = 161° arctg(-5.144554016) = 281°
arctg(0.9004040443) = 42° arctg(-0.3249196962) = 162° arctg(-4.704630109) = 282°
arctg(0.9325150861) = 43° arctg(-0.3057306815) = 163° arctg(-4.331475874) = 283°
arctg(0.9656887748) = 44° arctg(-0.2867453858) = 164° arctg(-4.010780934) = 284°
arctg(1) = 45° arctg(-0.2679491924) = 165° arctg(-3.732050808) = 285°
arctg(1.035530314) = 46° arctg(-0.2493280028) = 166° arctg(-3.487414444) = 286°
arctg(1.07236871) = 47° arctg(-0.2308681911) = 167° arctg(-3.270852618) = 287°
arctg(1.110612515) = 48° arctg(-0.2125565617) = 168° arctg(-3.077683537) = 288°
arctg(1.150368407) = 49° arctg(-0.1943803091) = 169° arctg(-2.904210878) = 289°
arctg(1.191753593) = 50° arctg(-0.1763269807) = 170° arctg(-2.747477419) = 290°
arctg(1.234897157) = 51° arctg(-0.1583844403) = 171° arctg(-2.605089065) = 291°
arctg(1.279941632) = 52° arctg(-0.1405408347) = 172° arctg(-2.475086853) = 292°
arctg(1.327044822) = 53° arctg(-0.1227845609) = 173° arctg(-2.355852366) = 293°
arctg(1.37638192) = 54° arctg(-0.1051042353) = 174° arctg(-2.246036774) = 294°
arctg(1.428148007) = 55° arctg(-0.08748866353) = 175° arctg(-2.144506921) = 295°
arctg(1.482560969) = 56° arctg(-0.06992681194) = 176° arctg(-2.050303842) = 296°
arctg(1.539864964) = 57° arctg(-0.05240777928) = 177° arctg(-1.962610506) = 297°
arctg(1.600334529) = 58° arctg(-0.03492076949) = 178° arctg(-1.880726465) = 298°
arctg(1.664279482) = 59° arctg(-0.01745506493) = 179° arctg(-1.804047755) = 299°
arctg(1.732050808) = 60° arctg(0) = 180° arctg(-1.732050808) = 300°
arctg(1.804047755) = 61° arctg(0.01745506493) = 181° arctg(-1.664279482) = 301°
arctg(1.880726465) = 62° arctg(0.03492076949) = 182° arctg(-1.600334529) = 302°
arctg(1.962610506) = 63° arctg(0.05240777928) = 183° arctg(-1.539864964) = 303°
arctg(2.050303842) = 64° arctg(0.06992681194) = 184° arctg(-1.482560969) = 304°
arctg(2.144506921) = 65° arctg(0.08748866353) = 185° arctg(-1.428148007) = 305°
arctg(2.246036774) = 66° arctg(0.1051042353) = 186° arctg(-1.37638192) = 306°
arctg(2.355852366) = 67° arctg(0.1227845609) = 187° arctg(-1.327044822) = 307°
arctg(2.475086853) = 68° arctg(0.1405408347) = 188° arctg(-1.279941632) = 308°
arctg(2.605089065) = 69° arctg(0.1583844403) = 189° arctg(-1.234897157) = 309°
arctg(2.747477419) = 70° arctg(0.1763269807) = 190° arctg(-1.191753593) = 310°
arctg(2.904210878) = 71° arctg(0.1943803091) = 191° arctg(-1.150368407) = 311°
arctg(3.077683537) = 72° arctg(0.2125565617) = 192° arctg(-1.110612515) = 312°
arctg(3.270852618) = 73° arctg(0.2308681911) = 193° arctg(-1.07236871) = 313°
arctg(3.487414444) = 74° arctg(0.2493280028) = 194° arctg(-1.035530314) = 314°
arctg(3.732050808) = 75° arctg(0.2679491924) = 195° arctg(-1) = 315°
arctg(4.010780934) = 76° arctg(0.2867453858) = 196° arctg(-0.9656887748) = 316°
arctg(4.331475874) = 77° arctg(0.3057306815) = 197° arctg(-0.9325150861) = 317°
arctg(4.704630109) = 78° arctg(0.3249196962) = 198° arctg(-0.9004040443) = 318°
arctg(5.144554016) = 79° arctg(0.3443276133) = 199° arctg(-0.8692867378) = 319°
arctg(5.67128182) = 80° arctg(0.3639702343) = 200° arctg(-0.8390996312) = 320°
arctg(6.313751515) = 81° arctg(0.383864035) = 201° arctg(-0.8097840332) = 321°
arctg(7.115369722) = 82° arctg(0.4040262258) = 202° arctg(-0.7812856265) = 322°
arctg(8.144346428) = 83° arctg(0.4244748162) = 203° arctg(-0.7535540501) = 323°
arctg(9.514364454) = 84° arctg(0.4452286853) = 204° arctg(-0.726542528) = 324°
arctg(11.4300523) = 85° arctg(0.4663076582) = 205° arctg(-0.7002075382) = 325°
arctg(14.30066626) = 86° arctg(0.4877325886) = 206° arctg(-0.6745085168) = 326°
arctg(19.08113669) = 87° arctg(0.5095254495) = 207° arctg(-0.6494075932) = 327°
arctg(28.63625328) = 88° arctg(0.5317094317) = 208° arctg(-0.6248693519) = 328°
arctg(57.28996163) = 89° arctg(0.5543090515) = 209° arctg(-0.600860619) = 329°
arctg(∞) = 90° arctg(0.5773502692) = 210° arctg(-0.5773502692) = 330°
arctg(-57.28996163) = 91° arctg(0.600860619) = 211° arctg(-0.5543090515) = 331°
arctg(-28.63625328) = 92° arctg(0.6248693519) = 212° arctg(-0.5317094317) = 332°
arctg(-19.08113669) = 93° arctg(0.6494075932) = 213° arctg(-0.5095254495) = 333°
arctg(-14.30066626) = 94° arctg(0.6745085168) = 214° arctg(-0.4877325886) = 334°
arctg(-11.4300523) = 95° arctg(0.7002075382) = 215° arctg(-0.4663076582) = 335°
arctg(-9.514364454) = 96° arctg(0.726542528) = 216° arctg(-0.4452286853) = 336°
arctg(-8.144346428) = 97° arctg(0.7535540501) = 217° arctg(-0.4244748162) = 337°
arctg(-7.115369722) = 98° arctg(0.7812856265) = 218° arctg(-0.4040262258) = 338°
arctg(-6.313751515) = 99° arctg(0.8097840332) = 219° arctg(-0.383864035) = 339°
arctg(-5.67128182) = 100° arctg(0.8390996312) = 220° arctg(-0.3639702343) = 340°
arctg(-5.144554016) = 101° arctg(0.8692867378) = 221° arctg(-0.3443276133) = 341°
arctg(-4.704630109) = 102° arctg(0.9004040443) = 222° arctg(-0.3249196962) = 342°
arctg(-4.331475874) = 103° arctg(0.9325150861) = 223° arctg(-0.3057306815) = 343°
arctg(-4.010780934) = 104° arctg(0.9656887748) = 224° arctg(-0.2867453858) = 344°
arctg(-3.732050808) = 105° arctg(1) = 225° arctg(-0.2679491924) = 345°
arctg(-3.487414444) = 106° arctg(1.035530314) = 226° arctg(-0.2493280028) = 346°
arctg(-3.270852618) = 107° arctg(1.07236871) = 227° arctg(-0.2308681911) = 347°
arctg(-3.077683537) = 108° arctg(1.110612515) = 228° arctg(-0.2125565617) = 348°
arctg(-2.904210878) = 109° arctg(1.150368407) = 229° arctg(-0.1943803091) = 349°
arctg(-2.747477419) = 110° arctg(1.191753593) = 230° arctg(-0.1763269807) = 350°
arctg(-2.605089065) = 111° arctg(1.234897157) = 231° arctg(-0.1583844403) = 351°
arctg(-2.475086853) = 112° arctg(1.279941632) = 232° arctg(-0.1405408347) = 352°
arctg(-2.355852366) = 113° arctg(1.327044822) = 233° arctg(-0.1227845609) = 353°
arctg(-2.246036774) = 114° arctg(1.37638192) = 234° arctg(-0.1051042353) = 354°
arctg(-2.144506921) = 115° arctg(1.428148007) = 235° arctg(-0.08748866353) = 355°
arctg(-2.050303842) = 116° arctg(1.482560969) = 236° arctg(-0.06992681194) = 356°
arctg(-1.962610506) = 117° arctg(1.539864964) = 237° arctg(-0.05240777928) = 357°
arctg(-1.880726465) = 118° arctg(1.600334529) = 238° arctg(-0.03492076949) = 358°
arctg(-1.804047755) = 119° arctg(1.664279482) = 239° arctg(-0.01745506493) = 359°
Источник

Добавить комментарий