Перпендикулярные прямые


4.6
Средняя оценка: 4.6
Всего получено оценок: 1045.
4.6
Средняя оценка: 4.6
Всего получено оценок: 1045.
Перпендикулярные прямые образуют собой целый пласт фигур, построений и вычислений в геометрии. Без понимания перпендикулярных прямых не получится решать такие фигуры, как прямоугольный треугольник, прямоугольник, квадрат или прямоугольная трапеция. Поэтому стоит особенное внимание уделить этим понятиям.

Опыт работы учителем математики – более 33 лет.
Что такое перпендикулярные прямые
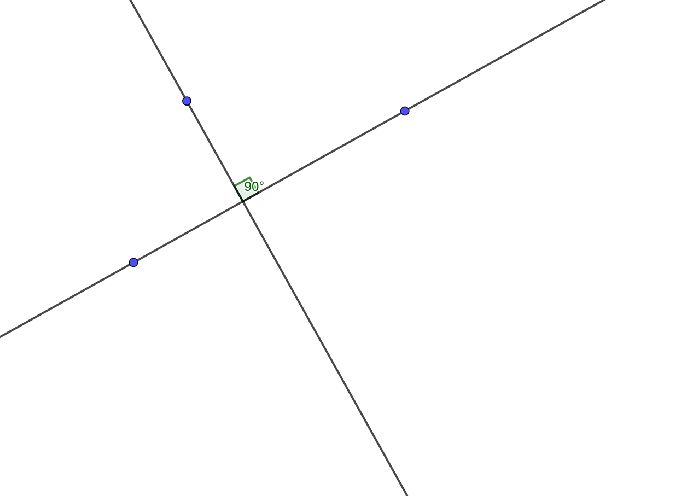
При пересечении двух прямых образуется 4 угла. Определение перпендикулярных прямых звучит так: это прямые, угол между которыми равен 90 градусам. Углов всего 4, полный угол это 360 градусов. Если один из углов равен 90 градусам, то и 3 других будут по 90.
Чтобы отрезки назывались перпендикулярными, должно выполняться условие: отрезки могут пересекаться или не пересекаться, но угол пересечения между прямыми, на которых они лежат, должен равняться 90 градусам.
Свойства
У перпендикулярных прямых не так много свойств. Все они не требуют доказательств, так как исходят из определения перпендикулярности.
- Если каждая из двух прямых перпендикулярна третьей, то эти прямые параллельны. А параллельны они в силу того, что получившиеся односторонние углы будут в сумме давать 180 градусов. А значит, прямые параллельны по 3 признаку параллельности. Это свойство можно доказать по любому из трех признаков параллельности.
- Перпендикулярный отрезок от точки до прямой (или отрезка) будет называться расстоянием от точки до прямой (или отрезка).
- Расстояние от прямой до прямой так же является общим перпендикуляром, опущенным из точки одной прямой на другую прямую. (это понятие относится к параллельным и скрещивающимся прямым).
- Если на протяжении всей длины двух прямых расстояние между ними не меняется, то прямые будут параллельными.
Фигуры с перпендикулярными прямыми
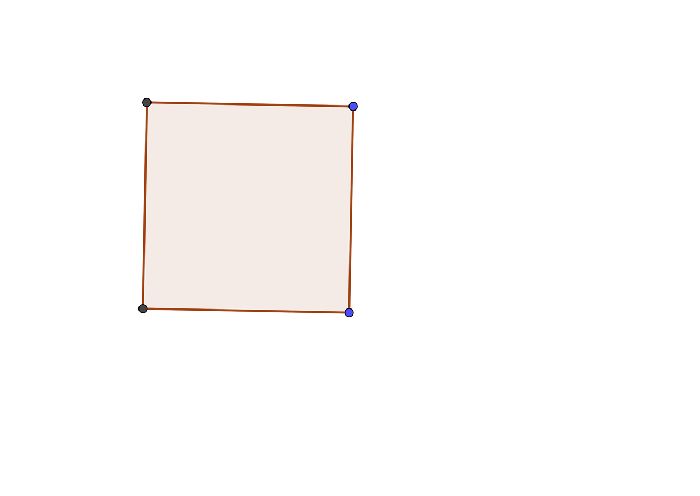
Одной из первых фигур, с которыми знакомится человек, являются квадрат и прямоугольник.
Прямые углы приятны человеческому взгляду, поэтому очень часто квадрат или прямоугольник используют как форму для столешниц, стульев, тумбочек и других предметов. Весь окружающий человека мир составлен из параллельных и перпендикулярных линий.
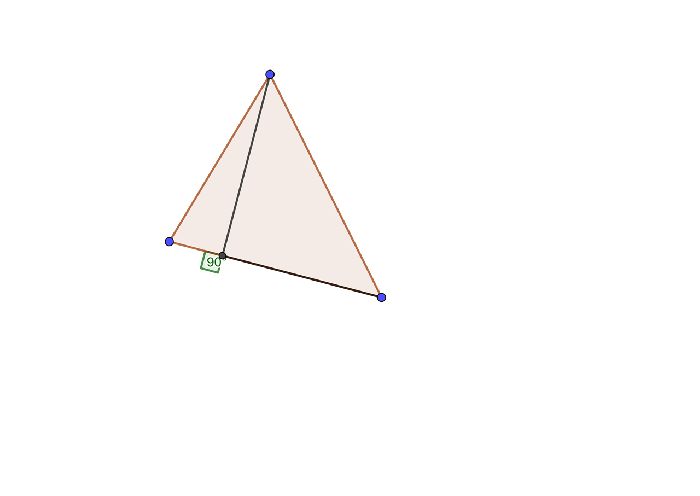
Еще со времен Древней Греции известен прямоугольный треугольник. Форму прямоугольного треугольника принимали различные приборы для навигации, кроме того, много времени изучению свойств прямоугольного треугольника уделил Пифагор. Именно его авторству принадлежит Теорема Пифагора, которая часто востребована в решениях задач.
Существует прямоугольная трапеция, у которой одна из сторон перпендикулярна обоим основанием. А стереометрия и вовсе пестрит перпендикулярами в пространстве: правильная призма, прямоугольная пирамида и самый обычный куб.
К тому же, в любом треугольнике можно провести высоту, что необходимо для нахождения площади фигуры. Перпендикуляр для нахождения площади пригодится и в параллелограмме, а прямоугольный треугольник и квадрат имеют высоту в составе своих сторон, из-за чего площадь этих фигур гораздо проще найти.

Что мы узнали?
Мы разобрали, что такое перпендикулярные прямые, поговорили о свойствах перпендикуляров и описали фигуры, для построения которых необходимы перпендикулярные прямые. Разобрались в теме для полного понимания при первой встрече с данным вопросом в 6 классе.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Гасан Тагиев
5/5
-

Даниил Переверзев
5/5
-

Никита Червоненко
3/5
-

Arsen Krutof
3/5
-

Андрей Ревякин
5/5
-

Денис Карпов
5/5
-

Алекс Горбунов
4/5
-

Серёжа Манцеров
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 1045.
А какая ваша оценка?
Представим
себе такую историю…
–
Саша, ты меня звал? – спросил у друга Паша.
–
Да, звал, – ответил Саша. – Помоги мне, пожалуйста, разобраться. Я собрался
ехать на велосипеде в книжный магазин и спросил у старшего брата, как туда
проехать. Он мне объяснил, что сначала надо проехать км
по дороге в сторону школы, а затем свернуть на дорогу, перпендикулярную той, по
которой я ехал. Это как?
–
Давай представим, что дороги – это у нас прямые. И твой брат сказал, что они
перпендикулярны, – начал рассуждать Паша.
–
А что это за перпендикулярные прямые? – перебил его Саша.
–
Даже не знаю, – задумчиво ответил Паша и предложил, – а давай спросим у
Мудряша.
–
Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним
устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу и выясним, какие же прямые называют
перпендикулярными, – начал Мудряш. – Ребята, давайте вспомним, какой угол
называют развёрнутым.
–
Развёрнутым углом называют угол, равный ,
– напомнили мальчишки.
–
Построим развёрнутый ,
– продолжил Мудряш. – Обратите внимание, что его стороны и
образуют
прямую. Теперь проведём биссектрису .
–
Биссектриса делит угол на два равных угла, – вспомнил Паша.
–
Верно! – отметил Мудряш.
–
А значит, ,
– сказал Саша.
–
Развёрнутый ,
тогда можем записать, что ,
– продолжил объяснять Мудряш. – А так как углы ,
то запишем: .
Если
мы с вами достроим луч до
прямой ,
то получим развёрнутый .
И эта сумма равна .
Выше мы выяснили, что .
Выразим из предпоследнего равенства :
.
Подставим значение :
.
Выполним вычитание и получим, что .
Таким
же образом мы можем показать, что и .
Итак,
при пересечении прямых и
образовалось
четыре прямых угла.
–
И эти прямые называются перпендикулярными, – догадались Саша и Паша.
–
Молодцы! – похвалил ребят Мудряш. – Запомните! Две прямые, образующие
при пересечении четыре прямых угла, называют перпендикулярными
прямыми.
Обозначают
перпендикулярные прямые вот так: .
Прямые
можно обозначать и одной маленькой латинской буквой. Например, .
–
А можно проверить, являются ли прямые перпендикулярными? – спросили у Мудряша
мальчишки.
–
Конечно. Проверить, перпендикулярны прямые или нет, можно, например, с помощью угольника,
– начал объяснять Мудряш. – Для этого нам надо совместить точку пересечения
прямых с вершиной прямого угла угольника и расположить его так, чтобы одна из прямых
совпала со стороной прямого угла угольника.
–
Тогда если вторая прямая совпадёт со второй стороной прямого угла угольника, то,
значит, прямые пересекаются под прямым углом, – догадался Саша.
–
Верно! – сказал Мудряш. – Следовательно, прямые перпендикулярны.
–
А есть ещё какой-нибудь способ проверить, перпендикулярны ли прямые? – спросил
Паша.
–
Есть, – ответил Мудряш. – Это можно сделать с помощью транспортира.
Для этого нам надо совместить точку пересечения прямых с центром транспортира и
расположить транспортир так, чтобы одна из прямых прошла по линейке.
–
Тогда если вторая прямая проходит через штрих «»,
то данные прямые пересекаются под прямым углом, – помог Мудряшу Саша.
–
А значит, эти прямые перпендикулярны, – добавил Паша.
–
Молодцы! – похвалил ребят Мудряш. – Отметим, что совсем не обязательно измерять
все четыре угла. Если один угол прямой, то и остальные три тоже будут прямыми.
–
Давайте попробуем построить перпендикулярные прямые, – предложили мальчишки
Мудряшу.
–
Построить перпендикулярные прямые также можно с помощью угольника или
транспортира, – начал Мудряш. – Чтобы построить перпендикулярные прямые с
помощью угольника, мы сначала проведём произвольную прямую .
Возьмём угольник и совместим сторону его прямого угла с этой прямой. Затем
вдоль второй стороны прямого угла угольника проведём прямую Таким
образом, мы получим перпендикулярные прямые и
.
–
Построить перпендикулярные прямые с помощью транспортира, наверное, будет
сложнее, – задумались мальчишки.
–
Совсем нет, – успокоил ребят Мудряш. – Давайте снова проведём произвольную
прямую
.
Приложим к этой прямой транспортир так, чтобы она прошла по линейке. Затем
найдём на шкале штрих, который соответствует .
–
И проведём через него прямую, которая и будет перпендикулярна прямой ,
– догадался Паша.
–
И назовём эту прямую ,
– добавил Саша.
–
Всё верно! – отметил Мудряш и продолжил, – отметим, что с помощью угольника мы
можем провести прямую, которая перпендикулярна данной, через некоторую точку.
Причём эта точка может лежать на данной прямой, а может и не лежать.
Давайте
построим произвольную прямую и
отметим на ней произвольную точку .
Возьмём
угольник и совместим сторону прямого угла угольника с нашей прямой ,
а вершину прямого угла угольника совместим с точкой .
Затем
проведём прямую вдоль
второй стороны прямого угла угольника.
Вот
так мы с вами провели прямую ,
перпендикулярную прямой ,
через точку ,
лежащую на прямой .
Ребята,
а сейчас давайте построим произвольную прямую и
отметим произвольную точку ,
которая не лежит на этой прямой.
–
И проведём через эту точку прямую, перпендикулярную прямой ?
– заинтересованно спросили у Мудряша мальчики.
–
Да, – ответил Мудряш. – Для этого мы приложим угольник так, чтобы одна сторона
его прямого угла совпала с нашей прямой ,
а вторая проходила через точку .
–
Затем проведём прямую вдоль второй стороны прямого угла угольника, – продолжил
построение Паша. – Можем назвать её, например, .
–
Получается, что мы провели прямую ,
перпендикулярную прямой ,
через точку ,
которая не лежит на прямой ,
– сделали вывод Саша и Паша.
–
Молодцы, ребята! – похвалил Пашу и Сашу Мудряш. – А теперь посмотрите на
следующие рисунки. На них изображены перпендикулярные прямые, на которых лежат
пары отрезков. Такие отрезки называют перпендикулярными.
Так,
на первом рисунке на перпендикулярных прямых 𝑎
и лежат
перпендикулярные отрезки и
.
На втором рисунке на перпендикулярных прямых и
также
лежат перпендикулярные отрезки и
.
Перпендикулярными
также могут быть два луча, луч и отрезок, отрезок и прямая, луч и прямая.
Посмотрите на следующие рисунки.
–
На первом рисунке на перпендикулярных прямых и
изображены
лучи и
.
Они перпендикулярны, – сказали Саша и Паша.
–
Верно! – отметил Мудряш.
–
На втором рисунке на перпендикулярных прямых и
𝑏 изображены луч и
отрезок .
Они тоже перпендикулярны, – продолжили ребята, и у них возник вопрос, – а что
на третьем рисунке?
–
На следующем рисунке у нас изображены перпендикулярные прямые 𝑎
и .
На прямой лежит
отрезок ,
– начал объяснять Мудряш.
–
А значит, отрезок перпендикулярен
прямой ,
– догадался Паша и продолжил, – тогда на последнем рисунке, так как прямые и
перпендикулярны,
луч перпендикулярен
прямой .
–
Правильно, – сказал Мудряш и задал вопрос, – Саша, Паша, а какие геометрические
фигуры, элементы которых перпендикулярны, вы знаете?
–
Прямоугольник, – сразу же ответил Саша.
–
Да, любые его две соседние стороны перпендикулярны, – добавил Мудряш.
–
Прямоугольный треугольник, – привёл пример Паша, – так как один из его углов
равен девяноста градусам.
–
А ещё примером является прямоугольный параллелепипед, ведь он состоит из шести
прямоугольников, а мы выше сказали, что у прямоугольника любые две соседние
стороны перпендикулярны.
–
Ребята, а сейчас давайте выполним задание, чтобы закрепить навыки построения
перпендикулярных прямых, – сказал Мудряш.
Задание:
Начертите
угол ,
градусная мера которого равна .
Отметьте на луче точку
и
проведите через неё прямые, перпендикулярные прямым и
.
Решение: в
первую очередь мы с вами построим угол, равный .
Для этого отметим произвольную точку .
Затем начертим луч с
началом в этой точке .
Теперь приложим к этому лучу транспортир так, чтобы его центр совпал с точкой ,
а сам луч прошёл через начало отсчёта на шкале. Найдём на шкале транспортира
штрих, который соответствует ,
и проведём через него луч .
Таким образом, мы построили угол ,
который равен .
Отметим
на луче точку
.
Проведём через неё сначала прямую, перпендикулярную прямой .
Для этого воспользуемся угольником. Совместим сторону его прямого угла с прямой
,
а вершину прямого угла – с точкой .
И проведём прямую вдоль
второй стороны прямого угла нашего угольника.
Теперь
проведём через точку прямую,
перпендикулярную прямой .
Приложим
угольник так, чтобы одна сторона его прямого угла совпала с нашей прямой ,
а вторая проходила через точку .
Теперь проведём прямую вдоль второй стороны прямого угла угольника и назовём её
.
Итак,
мы провели прямые и
,
которые перпендикулярны соответственно прямым и
.
До этого на уроках математики мы работали с числами, буквами, выражениями.
Иногда не только писали, но и рисовали схемы, координатные прямые и рисунки, чтобы лучше разбираться в изучаемом вопросе.
Сегодня мы будем изучать геометрические понятия, а именно, что является прямой, а что нет, какие прямые называются перпендикулярными.
Также узнаем, как строить перпендикулярные прямые разными способами.
Эта информация доступна зарегистрированным пользователям
В геометрии есть два понятия, которые не имеют определения, их мы принимаем как аксиомы.
Это понятия точки и прямой.
Все остальные определения будут так или иначе выражаться через эти два понятия.
Определение: луч или полупрямая – это часть прямой, состоящая из данной точки и всех точек, лежащих по одну сторону от нее.
Заметим, что любая точка, лежащая на прямой, разделяет эту прямую на два луча.
Разделяющую точку также называют началом луча.
Определение: отрезок – часть прямой, ограниченная двумя точками.
И еще немного формализма.
Определение: угол – геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Эти лучи называют сторонами угла, а их общее начало вершиной угла.
Эта информация доступна зарегистрированным пользователям
Есть величины для измерения длины: метр, сантиметр, километр и прочие производные метра.
Для измерения угла используются другие величины: градусы, минуты, секунды, радианы.
Одним из наиболее простых приборов для измерения углов является транспортир. Достаточно приложить его прямую часть к одной стороне угла и посмотреть, какое деление совпадет со второй стороной угла.
Главное, быть внимательным и смотреть, с какой стороны находится внутренняя часть угла.
Допустим, имеется такая конфигурация:
Эта информация доступна зарегистрированным пользователям
Приложим транспортир:
Эта информация доступна зарегистрированным пользователям
Углы обычно обозначаются тремя буквами, где буква посередине обозначает вершину угла.
Величина угла AOB будет равняться 45-ти градусам, можно записать как (mathbf{45^circ}).
Если необходимо измерить угол BOC, то нужно из 180-ти градусов вычесть 45 градусов, так как метки на транспортире соответствуют величинам углов, если считать от нуля, а в данном случае луч ОС лежит на отметке 180.
Также часто перед буквенным обозначением угла ставят следующий знак: (mathbf{angle}), получаются такие записи: (mathbf{angle AOB}), (mathbf{angle BOC}).
Иногда, когда нет неоднозначности, угол могут обозначать и одной буквой, например (mathbf{angle A})
Определение: прямой угол – угол в (mathbf{90^circ}).
На транспортире данная отметка находится посередине.
Эта информация доступна зарегистрированным пользователям
Если обычный угол часто обозначают маленькой дугой, то прямые углы принято обозначать таким квадратиком.
Прямой угол один из самых распространенных в мире: с большой вероятностью вы сейчас сидите в комнате с такиими углами, у вашего стола прямые углы, а также у окна и так далее.
Теперь мы подготовили все определения, чтобы определить термин из заголовка урока.
Определение: две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
Эта информация доступна зарегистрированным пользователям
Прямые часто обозначают одной строчной латинской буквой. В данном случае прямые a и b перпендикулярные по определению, потому что образуют прямые углы.
Эта информация доступна зарегистрированным пользователям
Если бы они пересекались под другим углом или не пересекались бы, то они не были бы перпендикулярными. В данном случае прямые a и b не являются перпендикулярными.
Эта информация доступна зарегистрированным пользователям
Перечислим основные способы в порядке возрастания сложности.
Самый простой способ взять предмет с прямым углом- чертежный треугольник, линейку, банковскую или проездную карту (придется только дорисовать скошенный угол от руки), и обвести его.
Эта информация доступна зарегистрированным пользователям
Правда, мы не можем гарантированно полагаться на перечисленные кроме треугольника предметы, так как они не предназначены для черчения, и угол может быть не совсем прямым.
Лучи, являющиеся сторонами угла, будут перпендикулярны, а значит, будут частями перпендикулярных прямых.
Также можно построить любой угол, в том числе прямой, с помощью транспортира.
1) Вершину угла мы ставим в центре прямой части транспортира.
2) Одни сторону проводим по прямой части транспортира в сторону нуля.
3) Ставим метку напротив риски с соответствующей величиной угла.
4) Соединяем вершину угла с меткой.
Эта информация доступна зарегистрированным пользователям
Аналогичным образом строится прямой угол.
В таком случае его стороны опять же будут перпендикулярными лучами, следовательно, частями перпендикулярных прямых.
Прежде чем перейти к более сложному и интересному способу, надо упомянуть, что клетки в тетради начерчены перпендикулярными прямыми, поэтому можно от руки обвести одну вертикальную линию и одну горизонтальную.
Эта информация доступна зарегистрированным пользователям
Скорее всего линии получатся не совсем прямыми, но если это нужно для какой-то схемы в черновике, то почему бы и нет.
Хотя конечно же во всех работах лучше использовать приборы и линейку чтобы рисунок был максимально красивым.
Интересно, что перпендикулярные прямые можно построить с помощью циркуля и линейки без разметки (ну и карандаша/ручки, конечно же).
Подробнее, почему алгоритм является корректным, вы узнаете в курсе геометрии за 7-й класс, но пока что посмотрим на сам алгоритм.
1) Чертим прямую и отмечаем на ней точку (назовем ее О).
2) Ставим в эту точку циркуль и с помощью него делаем две пометки, получаем две точки, равноудаленные от первой точки (назовем из А и В).
3) Проводим из каждой из точек А и В окружности одинакового радиуса, или лучше только нужные их части, так чтобы получить хотя бы одно пересечение (назовем его точной С).
4) Соединяем точку С с исходной точкой О, готово, мы получили перпендикулярную прямую, причем проходящую через точку, которую мы сами выбрали.
Эта информация доступна зарегистрированным пользователям
В этом алгоритме важна аккуратность: если точки А и В будут на разном расстоянии от центра или окружности из точек А и В будут разного радиуса, прямая может получится не перпендикулярной.
Эта информация доступна зарегистрированным пользователям
В данном уроке нам необходимо было пользоваться простейшим прибором для черчения: линейкой.
Оказывается, самые старые линейки появились еще в Древней Греции для построения чертежей.
Важно, что, в первую очередь, линейка была способом построения прямой линии, измерять по ней длины достаточно грубо из-за разных погрешностей.
В древности линейки представляли из себя аккуратно обструганные дощечки.
Позже развились технологии, и уже европейские монахи для разметки листов бумаги использовали свинцовые пластины.
Свинец считается не самым полезным металлом, но его проще обрабатывать, поэтому его и использовали.
Также иногда использовались металлические прутья под названиями «шильцы».
У русских писцов также были похожие приборы, и они назывались «правильца».
Современная метрическая система измерения длины сложилась во Франции в начале XIX века.
За основу взяли длину географического меридиана, проходящего через Париж, и поделили его на 40 миллионов, так получился метр.
Тогда изготовили две линейки из платины, каждая длинной в один метр.
Массовое производство линеек пошло уже в конце XIX века, и в XX веке линейка стала обыденным предметом.
Также появлялись линейки под специальные нужды, например, артиллерийская линейка:
Эта информация доступна зарегистрированным пользователям
Или штурманская линейка:
Эта информация доступна зарегистрированным пользователям
В современном мире на производстве чертят уже с помощью компьютерных программ, и там построение прямых линий идет программными средствами.
В образовательных целях или же при разметке какого-либо материала, линейки и их аналоги используются по сей день.
Читайте также
Перпендикулярные прямые
29 июня 2022
Перпендикулярные прямые — это просто две прямые, которые пересекаются под углом 90°:
Перпендикулярные прямые встречаются в огромном количестве задач. Прямоугольные треугольники, координаты и даже клеточки в вашей тетради — это всё перпендикулярные прямые. Поэтому разберёмся с ними.
Урок состоит из пяти частей:
- Краткая вводная.
- Определение перпендикулярных прямых.
- Свойства перпендикулярных прямых.
- Простые задачи.
- Злые задачи.:)
Начнём с краткой вводной: что уже нужно знать про прямые и углы в данному моменту.
1. Кратная вводная
Для работы с перпендикулярными прямыми нам потребуются два вида углов: смежные и вертикальные.
1.1.Смежные углы
Определение. Два угла называются смежными, если одна сторона у них общая, а две другие являются продолжением друг друга.
Вот пример смежных углов с общей стороной $MN$:
Основное свойство таких углов: их сумма всегда равна 180°:
[angle 1+angle 2={180}^circ ]
Таким образом, зная один смежный угол, мы тут же найдём другой.
1.2. Вертикальные углы
Определение. Углы, которые образуются при пересечении двух прямых и лежат напротив друг друга, называются вертикальными.
На самом деле на пересечении двух прямых возникает сразу две пары таких углов:
Вертикальные углы всегда равны — и это их главное свойство. На рисунке мы видим, что $angle 1=angle 3$ и $angle 2=angle 4$.
1.3. Какие бывают углы
И вообще, нам пока известны четыре типа углов: острый, прямой, тупой и развёрнутый.
Интересное свойство прямого угла: если при пересечении двух прямых возник прямой угол, то все остальные углы (вертикальные, смежные с ним) тоже будут прямыми. И вот тут мы переходим к основной теме урока.
2. Определение перпендикулярных прямых
Определение. Если при пересечении двух прямых возникло четыре прямых угла, такие прямые называются перпендикулярными.
Мы уже знаем, что достаточно найти на таком пересечении всего один угол в 90 градусов — остальные три угла станут прямыми автоматически:
Перпендикулярные прямые обозначают значком «$bot $»: $ABbot CD$, $abot b$ и т.д.
Часто в задачах рассматриваются не все прямые, а лишь отрезки, лежащие на этих прямых
3. Свойства перпендикулярных прямых
Сначала разберём два «стандартных» свойства, которые вы найдёте в любом учебнике геометрии 7-го класса. А затем — одно «нестандартное», но именно оно чаще всего и встречается в настоящих задачах.
3.1. Теорема о двух прямых, перпендикулярных третьей
Теорема 1. Две прямые, перпендикулярные к третьей, не пересекаются.
Прямая $ABbot EF$ и прямая $MNbot EF$. Следовательно, прямые $AB$ и $MN$ не пересекаются. Проще говоря, они параллельны (см. урок «Параллельные прямые»).
3.2. Теорема о прямой, перпендикулярной данной
Теорема 2. Через каждую точку прямой можно провести прямую, перпендикулярную данной, и притом только одну.
Доказательство этой теоремы состоит из двух частей: сначала докажем, что такую прямую провести можно, а затем — что она единственная.
Прямая, перпендикулярная данной, строится очень просто. Рассмотрим прямую $a$, на которой отмечена точка $M$:
Отложим от луча $MK$ угол, равный 90°. В любую сторону: в верхнюю полуплоскость или нижнюю — не имеет значения. Получим луч $MN$:
Наконец, продолжим луч $MN$ в противоположную другую сторону (т.е. построим дополнительный луч). Получим искомую прямую $MNbot a$:
Единственность такого построения следует либо из аксиомы о том, что нужный угол можно отложить в нужном направлении одним и только одним способом, либо из предыдущей теоремы о двух прямых, перпендикулярных данной. В самом деле, пусть есть ещё одна прямая $ML$, которая, как и $MN$, перпендикулярна прямой $a$:
Поскольку $MNbot a$ и $MLbot a$, по предыдущей теореме эти прямые не пересекаются. Что противоречит нашему построению, в котором у прямых $MN$ и $ML$ есть общая точка $M$. Следовательно, прямые $MN$ и $ML$ совпадают, что и требовалось доказать.
3.3. Важное свойство прямого угла
Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:
Теорема 3. Если прямой угол разделить на две части, то сумма этих новых углов равна 90°. Другими словами, если один угол равен $alpha $, то другой равен ${90}^circ -alpha $:
Это утверждение может показаться очевидным. И оно действительно является таковым. Однако деление прямого угла на части встречается в задачах настолько часто, что я не мог не упомянуть об этом.
Кроме того, начинающие ученики часто не замечают такие углы на чертежах. Поэтому сейчас мы будем отрабатывать эту теорему на реальных задачах.
4. Простые задачи
Начнём с простых задач.
Задача 1. На рисунке $ABbot MN$, $angle NOT={37}^circ $, $angle BOT+angle NOS={125}^circ $. Найдите углы $MOS$ и $SOT$.
Решение. Пусть $angle NOS=x$. Тогда из равенства
[angle BOT+angle NOS={125}^circ ]
получаем, что $angle BOT={125}^circ -x$. С другой стороны, углы $BOT$ и $NOT$ в сумме дают 90°. Потому
[begin{align}{125}^circ -x+{37}^circ &={90}^circ \ x&={72}^circ end{align}]
Теперь мы можем найти угол $SOT$:
[begin{align}angle SOT &=angle NOS+angle NOT= \ &={72}^circ +{37}^circ = \ &={109}^circ end{align}]
Кроме того, углы $MOS$ и $NOS$ — смежные, поэтому их сумма равна 180°. Отсюда получаем:
[begin{align}angle MOS&={180}^circ -angle NOS= \ &={180}^circ -{72}^circ = \ &={108}^circ end{align}]
Оба требуемых угла найдены. Задача решена.
Задача 2. Дан угол $AMC$, равный 140°. Внутри этого угла проведены лучи $MN$ и $MK$, причём $MNbot MC$ и $MKbot MA$. Найдите угол $KMN$.
Решение. Заметим, что угол $AMC$ составлен из углов $AMN$ и $CMN$, причём $angle CMN={90}^circ $ по условию. Найдём угол $AMN$:
[begin{align}angle AMN &=angle AMC-angle NMC= \ &={140}^circ -{90}^circ = \ &={50}^circ end{align}]
Точно так же найдём угол $CMK$, который вместе с углом прямым $AMK$ образует исходный угол $AMC$:
[begin{align}angle CMK &=angle AMC-angle AMN= \ &={140}^circ -{90}^circ = \ &={50}^circ end{align}]
Осталось найти искомый угол $KMN$:
[begin{align}angle KMN &=angle AMC-angle AMN-angle CMK= \ &={140}^circ -{50}^circ -{50}^circ = \ &={40}^circ end{align}]
Готово! Мы нашли нужный угол. Он равен 40 градусов.
Задача 3. Прямые $a$, $b$ и $c$ пересекаются в одной точке. Известно, что $abot b$ и $angle 1={36}^circ $. Найдите углы 2, 3 и 4.
Решение. Углы 1 и 3 — вертикальные, поэтому они равны:
[angle 3=angle 1={36}^circ ]
Кроме того, углы 1 и 2 вместе образуют прямой угол, поэтому их сумма равна 90 градусов:
[begin{align}angle 1+angle 2 &={90}^circ \ angle 2 &={90}^circ -angle 1= \ &={90}^circ -{36}^circ = \ &={54}^circ end{align}]
Наконец, углы 2 и 4 — тоже вертикальные, поэтому они тоже равны:
[angle 4=angle 2={54}^circ ]
Итого мы нашли все требуемые углы. Они равны 54, 36 и 54 градуса.
Задача 4. На рисунке угол $AMC$ — развёрнутый, луч $MBbot AC$, угол $KMN={90}^circ $. Докажите, что $angle BMN=angle CMK$.
Решение. Пусть $angle BMK=x$. Тогда, поскольку $ACbot MB$, углы $BMK$ и $CMK$ в сумме дают 90°. Отсюда получаем, что
[angle CMK={90}^circ -x]
С другой стороны, по условию задачи угол $NMK$ — прямой. Этот угол состоит из углов $BMN$ и $BMK$, поэтому
[angle BMN={90}^circ -x]
Видим, что углы $CMK$ и $BMN$ равны одной и той же величине: ${90}^circ -x$. Следовательно, эти углы равны, что и требовалось доказать.
5. Злые задачи
Деление задач на простые и сложные весьма условно. Часто «сложными» называют многошаговые задачи и доказательства.
Задача 5. Дан угол $AMB$, равный 64°. Из вершины этого угла проведены лучи $MC$ и $MD$, причём $MCbot MA$ и $MDbot MB$. Кроме того, полученный тупой угол $AMD$ содержит в себе лучи $MB$ и $MC$, которые деля этот угол на три части. Найдите углы $CMD$ и $AMD$.
Решение. Эта задача похожа на задачу 2. Взгляните на чертёж:
Поскольку угол $AMC$ — прямой, можем найти угол $BMC$:
[begin{align}angle BMC &={90}^circ -angle AMB= \ &={90}^circ -{64}^circ \ &={26}^circend{align}]
С другой стороны, угол $BMD$ — тоже прямой, поэтому можем найти угол $CMD$:
[begin{align}angle CMD &={90}^circ -angle BMC= \ &={90}^circ -{26}^circ = \ &={64}^circend{align}]
Вновь, как и в задаче 2, получили, что углы $AMB$ и $DMC$ равны. Но это не относится к делу. Найдём угол $AMD$, представив его как сумму углов $AMB$ и $BMD$:
[begin{align}angle AMD &=angle AMB+angle BMD= \ &={64}^circ +{90}^circ = \ &={154}^circ end{align}]
Задача 6. Дан прямой угол $AMB$. Луч $MC$ делит этот угол на два острых угла: $AMC$ и $BMC$. Угол между биссектрисами углов $AMC$ и $AMB$ равен 18°. Найдите углы $AMC$ и $BMC$.
Решение. Вот это уже довольно интересная задача. Взгляните на чертёж:
Красным цветом обозначена биссектриса прямого угла $AMB$. Она разбивает этого угол на два маленьких угла по 45°.
Синим цветом обозначена биссектриса искомого угла $AMC$. Обозначим половинки этого угла за $x$ (имеется в виду, что каждая из половин угла $AMC$ содержит по $x$ градусов).
Но тогда угол между биссектрисами — это часть угла между стороной $MA$ прямого угла $AMB$ и биссектрисой этого же угла. Откуда получаем уравнение
[begin{align}{45}^circ &=x+{18}^circ \ x &={45}^circ -{18}^circ ={27}^circ end{align}]
Но тогда угол $AMC$ будет вдвое больше:
[angle AMC=2x={54}^circ ]
А угол $BMC$, который дополняет $angle AMC$ до прямого, можно найти по формуле
[begin{align}angle BMC &={90}^circ -angle AMC= \ &={90}^circ -{54}^circ ={36}^circend{align}]
Итого искомые углы равны 54 и 36 градусов.
Задача 7. Два равных тупых угла имеют общую сторону. Две другие стороны этих углов взаимно перпендикулярны. Найдите величину тупого угла.
Решение. Пусть два равных тупых угла содержат по $x$ градусов. Вместе с прямым углом (т.е. углом в 90 градусов) они образуют полный поворот, т.е. 360 градусов. Получаем уравнение:
[begin{align}2x+{90}^circ&={360}^circ\ 2x &={270}^circ \ x &={135}^circend{align}]
Задача 8. Из вершины развёрнутого угла проведены два луча, которые делят этот угол на три равные части. Докажите, что биссектриса среднего угла перпендикулярна сторонам развёрнутого угла.
Доказательство. Обозначим развёрнутый угол как $AOD$, а дополнительные лучи — $OB$ и $OC$. Биссектриса угла $BOC$ — это луч $MO$ (отмечен красным цветом).
Поскольку углы $AOB$, $BOC$ и $COD$ равны и в сумме образуют развёрнутый угол, их градусные меры также равны и составляют треть от 180°:
[angle AOB=angle BOC=angle COD={60}^circ ]
Кроме того, поскольку $OM$ — биссектриса, то углы $BOM$ и $COM$ равны между собой:
[angle BOM=angle COM={30}^circ ]
Однако угол $AOM$ составлен из углов $AOB$ и $BOM$, поэтому
[begin{align}angle AOM &=angle AOB+angle BOM= \ &={60}^circ +{30}^circ ={90}^circ end{align}]
Получили, что $OMbot AD$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы

- Что такое смежные углы

- Комбинаторика в задаче B6: легкий тест

- Задача B15 — исследование функции с помощью производной

- Координаты вершин правильного тетраэдра

- Задача B4: обмен валют в трех различных банках

Введение
Все вы помните, что такое прямой угол. В математике и в жизни прямые углы встречаются довольно часто. Если вы рассмотрите квадрат, то заметите, что стороны квадрата пересекаются под прямым углом. Если рассмотреть железнодорожное полотно, можно увидеть, что рельсы и шпалы расположены под прямым углом друг относительно друга; стены дома чаще всего делают под прямым углом к фундаменту и т. д.
Перпендикулярность прямых, отрезков и лучей
В математике есть специальное обозначение для прямых, которые пересекаются под прямым углом. Такие прямые называют перпендикулярными. Записывают это так: ![]() . Читается: «
. Читается: «![]() перпендикулярна
перпендикулярна ![]() ».
».
Перпендикулярными бывают и отрезки. Отрезки называются перпендикулярными, когда прямые, которые их содержат, перпендикулярны. Данное утверждение легко понять, вспомнив квадрат – прямые, содержащие соседние стороны квадрата, перпендикулярны, значит, и отрезки (стороны) перпендикулярны.
Отрезки, представленные на рисунке 1, также перпендикулярны. (См. Рис. 1.) Почему?

Рис. 1. Перпендикулярные отрезки
Если эти отрезки продлить до прямых, то прямые пересекутся под прямым углом. Значит, если прямые перпендикулярны, то и отрезки тоже перпендикулярны, хотя и не пересекаются. (См. Рис. 2.)

Рис. 2. Если перпендикулярны прямые, то перпендикулярны и отрезки, лежащие на них
Лучи называют перпендикулярными, если прямые, содержащие эти лучи, перпендикулярны. (См. Рис. 3 и 4.)

Рис. 3. Перпендикулярные лучи

Рис. 4. Непересекающиеся перпендикулярные лучи
Построение перпендикулярных прямых
Есть несколько способов:
- С помощью чертежного угольника, т. к. две его стороны образуют прямой угол.
- С помощью транспортира – отметить угол
 и провести прямые, которые его образуют.
и провести прямые, которые его образуют. - С помощью циркуля и линейки (с этим способом вы познакомитесь в 7 классе).
Особенность перпендикулярных прямых
Почему именно такой тип прямых выделили в отдельный класс? Почему не говорим отдельно о прямых, которые просто пересекаются друг с другом под каким-то другим углом, например ![]() ? Ответ следующий. При пересечении прямых у нас образуются углы, чаще всего они не равны. (См. Рис. 5.)
? Ответ следующий. При пересечении прямых у нас образуются углы, чаще всего они не равны. (См. Рис. 5.)

Рис. 5. ![]()
Но если мы говорим о перпендикулярных прямых, то это единственный случай, когда образовавшиеся углы равны между собой – все они прямые. (См. Рис. 6.)

Рис. 6. ![]()
Именно поэтому эти прямые и выделили, тем более в жизни мы с ними сталкиваемся чаще, чем с прямыми, пересекающимися под каким-либо другим углом.
Вопросы, связанные с перпендикулярными прямыми
1. На некоторой прямой отметили точку. (См. Рис. 7.)
![]()
Рис. 7. Точка на прямой
Сколько прямых можно провести через эту точку так, чтобы они были перпендикулярны исходной прямой? Ответ: только одну. Нужно приложить угольник и провести соответствующую прямую. (См. Рис. 8.)

Рис. 8. Через точку на прямой можно провести только одну прямую, перпендикулярную данной
2. Дана прямая и точка вне её. (См. Рис. 9.)

Рис. 9. Прямая и точка вне её
Сколько прямых проходят через эту точку так, что они перпендикулярны исходной прямой? Ответ: одна прямая. Опять же, это можно сделать с помощью угольника. (См. Рис. 10.)

Рис. 10. Через точку вне прямой можно провести только одну прямую, перпендикулярную данной
Параллельность прямых, отрезков и лучей
Мы говорили о пересекающихся прямых. Но бывает же так, что прямые не пересекаются. С этим мы сталкиваемся и в жизни – у лыжников во время спуска правая лыжня и левая не пересекаются; или дорожки в бассейне – они также не пересекаются; или железнодорожное полотно – рельсы не пересекаются. Для непересекающихся прямых также есть специальное название. Прямые на плоскости, которые не пересекаются, называются параллельными.
Очень важно здесь добавить «на плоскости», потому что, когда в 10 классе вы столкнетесь с прямыми в пространстве, окажется, что есть прямые, которые не пересекаются, но и не являются параллельными. Сейчас же речь идет о плоскости, и на плоскости есть два случая: прямые либо пересекаются, либо параллельны (не пересекаются).
Для параллельных прямых есть специальная запись: ![]() . Читается: «
. Читается: «![]() параллельна
параллельна ![]() ».
».
По аналогии с перпендикулярными отрезками и лучами имеются также определения параллельных отрезков и лучей. Отрезки называются параллельными, если они лежат на параллельных прямых. Лучи называются параллельными, если они лежат на параллельных прямых. (См. Рис. 11.)

Рис. 11. Параллельные отрезки и лучи
Таким образом, когда мы говорим о дорожках в бассейне, речь идет скорее о параллельных отрезках (дорожки ограничены), нежели о прямых.
Вопросы, связанные с параллельными прямыми
Верно ли, что если два отрезка не пересекаются, то они параллельны? Ответ: нет, не верно. Приведем контрпример. (См. Рис. 12.)

Рис. 12. Контрпример
Эти два отрезка не пересекаются, но они не являются параллельными, т. к. прямые, содержащие их, пересекаются. Аналогично с лучами – если лучи не пересекаются, они не обязательно параллельны. (См. Рис. 13.)

Рис. 13. Лучи не пересекаются, но и не являются параллельными
Примеры, которые мы приводили в начале урока, также могут быть контрпримерами – лучи и отрезки не пересекались, но и не являлись параллельными, потому что они перпендикулярны (См. Рис. 1. и Рис. 4.)
Построение параллельных прямых
Рассмотрим конструкцию, состоящую из трех прямых ![]() и
и ![]() , где
, где ![]() . (См. Рис. 14.)
. (См. Рис. 14.)

Рис. 14. Данная конструкция
Тогда что мы можем сказать про прямые ![]() и
и ![]() ? Судя по картинке, они параллельны. Доказать мы этого пока не можем, но тем не менее это как раз и есть способ построения параллельных прямых. То есть параллельные прямые строятся через перпендикулярность – сначала проводят прямую, перпендикулярную исходной, (в нашем случае
? Судя по картинке, они параллельны. Доказать мы этого пока не можем, но тем не менее это как раз и есть способ построения параллельных прямых. То есть параллельные прямые строятся через перпендикулярность – сначала проводят прямую, перпендикулярную исходной, (в нашем случае ![]() ), а потом проводят прямую, перпендикулярную второй (в нашем случае
), а потом проводят прямую, перпендикулярную второй (в нашем случае ![]() ).
).
Отметим, что из указанных фактов следует параллельность противоположных сторон квадрата и прямоугольника – они перпендикулярны одной и той же стороне.
Есть еще один интересный факт. Проведем две параллельные прямые, а также третью прямую, которая параллельна первой, то есть ![]() . (См. Рис. 15.)
. (См. Рис. 15.)

Рис. 15. ![]()
Судя по рисунку ![]() тоже. Этот факт верен, но, опять же, доказывать мы его будем в 7 классе.
тоже. Этот факт верен, но, опять же, доказывать мы его будем в 7 классе.
Заключение
На этом уроке мы познакомились с понятиями параллельных и перпендикулярных прямых; мы выяснили, какие отрезки и лучи называют перпендикулярными, а какие – параллельными; узнали, как строятся перпендикулярные прямые.
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: ИОЦ «Мнемозина», 2014 – 264 с.
- Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. – М. «Просвещение»: 2-е изд., перераб. – М.: 2010; Ч.2 – 128 с.
- Виленкин Н.Я. и др. Математика. Учебник для 6 класса. – М.: ИОЦ «Мнемозина», 2013 – 288 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Yaklass.ru (Источник).
- Shkolo.ru (Источник).
- Shkolo.ru (Источник).
Домашнее задание
- Найдите перпендикулярные отрезки (См. Рис. 1.)

Рис. 1.



















