Объём параллелепипеда
равен
смешанному произведению векторов
на которых он построен:
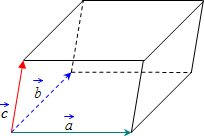
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела – всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах

Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Объем параллелепипеда, построенного на векторах онлайн
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:

Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела – всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Объем параллелепипеда и пирамиды построенного на трех векторах
№ 1
Найти объём параллелепипеда, построенного на векторах , , .
Решение
Объём параллелепипеда, построенного на векторах a, b, c численно равен модулю смешанного произведения этих векторов.
V = | abc |
V = | -7 | = 7
№ 2
Найти объём пирамиды, построенной на векторах , , .
Решение
Объём пирамиды, построенной на векторах a, b, c равен 1/6 объёма параллелепипеда, построенного на этих векторах.
Объём параллелепипеда, построенного на векторах a, b, c численно равен модулю смешанного произведения этих векторов.
V = | abc |/6
V = | -7 | /6= 7/6
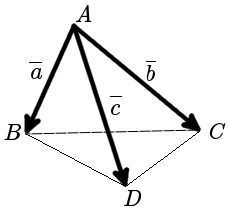
№ 3
Найти объём тетраэдра ABCD.
Решение
Построим векторы AB, AC, AD.
, , .
Объём тетраэдра, построенного на векторах AB, AC, AD равен 1/6 объёма параллелепипеда, построенного на этих векторах.
Объём параллелепипеда, построенного на векторах AB, AC, AD численно равен модулю смешанного произведения этих векторов.
V = | AB · AC· AD |/6
V = | 12 | /6 = 12/6 = 2
[spoiler title=”источники:”]
http://mathforyou.net/online/vectors/volume/parallelepiped/
http://ludmilav2.narod.ru/index/0-65
[/spoiler]
Онлайн калькулятор, для расчета объема параллелепипеда и тетраэдра, если определены координаты всех вершин.
| Введите вершину A | |||
| Введите вершину B | |||
| Введите вершину C | |||
| Введите вершину D | |||
| Объем Параллелепипед | |||
| Объем Тетраэдра |
Формула объема Параллелепипеда и Тетраэдра
Объем Параллелепипеда (Pv):

Объем Тетраэдра (Tv)=Pv/6
где,
- (x1,y1,z1) вершина A,
- (x2,y2,z2) вершина B,
- (x3,y3,z3) вершина C,
- (x4,y4,z4) вершина D,
людей нашли эту статью полезной. А Вы?
Онлайн калькулятор расчета объема параллелепипеда позволяет быстро и точно получить результат. Для вычисления объема потребуется выбрать необходимую формулу расчета и ввести имеющиеся значения. В зависимости от исходных параметров объем геометрического тела можно вычислить несколькими способами: через стороны фигуры; через стороны в основании и его высоту; через определитель. Также онлайн можно рассчитать объем наклонного параллелепипеда.
Что такое параллелепипед в геометрии
В геометрии параллелепипедом называют геометрическую фигуру в основании которой лежит параллелограмм. При чем все грани фигуры являются параллелограммами. Выделяют 2 вида геометрической фигуры: прямоугольный параллелепипед, в котором 4 грани имеют форму прямоугольника, и прямой параллелепипед, где все стороны фигуры – прямоугольники.
Прежде чем вычислять объем параллелепипеда, следует ознакомиться с самим понятием объема.
В повседневной жизни человека окружают разные объекты (физические тела), которые занимают определенное пространство (в зависимости от размера самого тела) – некий объем.
Существует 2 понятия значения термина “объем”:
- определенная величина, которая характеризует содержание какого-либо предмета;
- с геометрической точки зрения – величина, которая характеризует размер какого-либо тела в пространстве.
Объем определяет форма и размер тела. При необходимости объем можно измерить как и другие величины. Объем измеряется в кубических единицах и выражается в положительных значениях.
Существует несколько способов вычисления объема параллелепипеда:
- через его стороны;
- через стороны в основании и его высоту;
- через определитель;
- формула вычисления объема наклонного параллелепипеда.
По стандартной формуле объем параллелепипеда будет равняться произведению его высоты на площадь его основания:
V = S * h
- V – объем;
- S – площадь основания геометрического тела;
- h – высота фигуры.
Пример: Как найти объем параллелепипеда, если площадь основания (S) составляет 15 см2, высота (h) равна 6 см. Используя формулу, подставляем значения: V = 15 * 6 = 90 см3
Эта формула может применяться для определения объема любого геометрического тела:
- наклонная фигура, в которого боковые грани расположены не перпендикулярно основанию;
- прямая или прямоугольная геометрическая фигура, в которой боковые грани – прямоугольники;
- ромбоэдр – геометрическая фигура, у которой грани – ромбы;
- куб – фигура в геометрии, у которой все грани – равные квадраты.
Расчет объема параллелепипеда через его стороны
Вычислить объем фигуры через его стороны можно при помощи следующей формулы:
V = a * b * c
Где:
- V – объем тела;
- a – ширина;
- b – длина;
- c – высота.
Пример расчета
Необходимо вычислить объем параллелепипеда, высота которого равна 8 см., ширина – 12 см., длина – 6 см.
с = 8 см.;
а = 12 см;
b = 6 см.
Известные показатели подставляем в калькулятор объема параллелепипеда и получаем результат: V = 12 * 6 * 8 = 576 см3
Расчет объема геометрического тела через его стороны в основании и высоту фигуры
Вычислить объем геометрического тела через его стороны в основании и высоту можно по следующей формуле:
V = a * b * h
Где:
- V – объем фигуры;
- a, b – стороны тела;
- h – высота геометрического тела.
Также для расчета параметров объема параллелепипеда используют формулу: V = S * h
Где:
- V – искомый объем;
- S – площадь основания фигуры;
- h – высота тела.
Основанием геометрической фигуры является прямоугольник, площадь которого высчитывается по формуле: S = a * b * h
Где:
- S – площадь основания фигуры;
- a, b – стороны фигуры;
- h – высота тела.
Пример расчета
Как найти объем параллелепипеда, в основании которого – прямоугольник, если известны следующие значения: одна сторона основания равна 5 см., вторая сторона – 6 см., высота фигуры составляет 11 см.?
Условные обозначения:
- a – одна сторона основания – 5 см.;
- b – другая сторона основания – 6 см.;
- h – высота – 11 см.;
- V – объем фигуры.
Для решения задачи потребуется подставить известные значения в формулу: V = a * b * h = 5 * 6 * 11 = 330 см3
Пример расчета
Рассчитать объем геометрического тела, площадь основания которого составляет 8 см3, высота – 4 см.
Результат можно получить быстро и точно при помощи калькулятора объема параллелепипеда, подставив числа в формулу и нажав “рассчитать”:
V = S * h = 8 * 4 = 32 см3
Расчет объема параллелепипеда через определитель
Еще одним способом рассчитать объем фигуры можно назвать метод расчета через определитель. Известно, что при расчетах смешанное произведение векторов может иметь отрицательное значение, а объем фигуры всегда представляет собой положительное число. Поэтому для получения результата смешанного произведения при вычислении объема геометрического тела, которое построено на векторах (определителе), берется по модулю:
→ → →
V = |a * (b * c)|
Следовательно, для получения значения объема параллелепипеда, который построен на векторах, необходимо найти смешанное произведение этих векторов. При этом полученный результат берется по модулю.
Пример расчета
Параллелепипед построен на векторах, координаты которых:
→
a = (ax, ay, az)
→
b = (bx, by, bz)
→
c = (cx, cy, cz)
Таким образом, объем фигуры – определитель, который состоит из имеющихся координат:
|ax ay az|
V = |bx by bz|
|cx cy cz|
Вычислить объем параллелепипеда через смешанное значение векторов с координатами:
→
a = (3,4,6)
→
b = (2,5,5)
→
c = (4,6,8)
Подставляем значения в формулу и получаем следующее уравнение:
|3 4 6|
V = |2 5 5| = 3 * 5 * 8 + 4 * 5 * 4 + 6 * 2 * 6 – 6 * 5 * 4 – 3 * 5 * 6 – 4 * 2 * 8 = 120 + 80 + 72 – 120 – 90 – 64 = – 2
|4 6 8|
Так как получившееся значение объема – отрицательное число, то для результата берется модуль данного числа и получаем V = 2 см3
Расчет объема наклонного параллелепипеда
Наклонным параллелепипедом называется геометрическая фигура, у которой боковые грани располагаются под непрямым углом относительно ее оснований.
Для поиска объема наклонного параллелепипеда используется следующая формула:
V = S * h
V – искомый объем, S – площадь основания фигуры, h – высота.
Таким образом, площадь основания геометрического тела умножается на его высоту, опущенную на это основание из противоположного угла.
Чтобы рассчитать площадь основания, следует знать, что в основании данной фигуры находится параллелограмм, площадь которого высчитывается по следующим формулам:
- через основание и высоту: S = a * h, где а – основание (сторона), h – высота;
- по стороне и высоте, которая опущена на основание: S = b * h, где b – сторона, h – высота;
- по двум сторонам и углу между ними: S = a * b *sin (α)°
Как пользоваться калькулятором объёма параллелепипеда
На странице онлайн калькулятора можно рассчитать объем геометрической фигуры онлайн. Для расчета достаточно задать имеющиеся параметры и нажать на кнопку “рассчитать”. Вычисления производятся в мм., см., м. Результат выводится в см3.
Пользователю доступны некоторые преимущества при использовании онлайн-калькулятора:
- экономится время благодаря автоматизации подсчета;
- возможность определить объем параллелепипеда по имеющимся значениям;
- простой и удобный интерфейс калькулятора.
Таким образом, при использовании онлайн калькулятора не требуется самостоятельно производить все расчеты формул и значений, что существенно экономит время. К тому же, онлайн калькулятор выдает максимально точные расчеты. Еще одним преимуществом онлайн калькулятора является его доступность в любое время. Главным критерием его использования является лишь наличие интернета.
Параллелепипед — это призма, основанием которой является параллелограмм.
Онлайн-калькулятор объема параллелепипеда
Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.
Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.
Формула объема прямоугольного параллелепипеда
Объемом такого параллелепипеда называется произведение всех его трех измерений: длины, ширины, высоты. Вычисляется он так:
V=a⋅b⋅cV=acdot bcdot c
a,b,ca, b, c — длина, ширина и высота прямоугольного параллелепипеда.
Рассмотрим несколько примеров.
Найти объем прямоугольного параллелепипеда, если известны его длина, равная 5 см.5text{ см.}, ширина, имеющая длину 10 см.10text{ см.} и высота длиной в 7 см.7text{ см.}
Решение
a=5a=5
b=10b=10
c=7c=7
Сразу подставляем в формулу численные значения:
V=a⋅b⋅c=5⋅10⋅7=350 см3V=acdot bcdot c=5cdot 10cdot 7=350text{ см}^3
Ответ
350 см3.350text{ см}^3.
Формула объема наклонного параллелепипеда
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания наклонного параллелепипеда;
hh — его высота.
Вычислить объем наклонного параллелепипеда, если в его основании лежит прямоугольник со сторонами в 4 см.4text{ см.} и 5 см.5text{ см.}, а высота его равна 10 см.10text{ см.}
Решение
a=4a=4
b=5b=5
h=10h=10
Находим площадь основания, то есть площадь прямоугольника:
Sосн=a⋅b=4⋅5=20S_{text{осн}}=acdot b=4cdot 5=20
Сам объем равен:
V=Sосн⋅h=20⋅10=200 см3V=S_{text{осн}}cdot h=20cdot 10=200text{ см}^3
Ответ
200 см3.200text{ см}^3.
Формула объема параллелепипеда через определитель
Альтернативным способом нахождения объема параллелепипеда является вычисление смешанного произведения векторов, на которых построен данный параллелепипед.
Пусть параллелепипед построен на векторах a⃗vec{a}, b⃗vec{b} и c⃗vec{c} с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующего параллелепипеда это определитель, составленный из этих координат:
V=∣axayazbxbybzcxcycz∣V=begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем параллелепипеда через смешанное произведение векторов, координаты которых таковы: a⃗=(2,3,5)vec{a}=(2, 3, 5), b⃗=(1,4,4)vec{b}=(1, 4, 4), c⃗=(3,5,7)vec{c}=(3, 5, 7).
Решение
a⃗=(2,3,5)vec{a}=(2, 3, 5)
b⃗=(1,4,4)vec{b}=(1, 4, 4)
c⃗=(3,5,7)vec{c}=(3, 5, 7)
По формуле:
V=∣235144357∣=2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7=56+36+25−60−40−21=−4V=begin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 – 5cdot4cdot3 – 2cdot4cdot5 – 3cdot1cdot7 = 56 + 36 + 25 – 60 – 40 – 21 = -4
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=4 см3V=4text{ см}^3
Ответ
4 см3.4text{ см}^3.
У вас не получается решить задачу по геометрии? Наши эксперты помогут вам!
