Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
и
где q1=(m1, p1) направляющий вектор прямой L1, а q2=(m2, p2) направляющий вектор прямой L2.
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
Из определения скалярного произведения:
где |q1| и |q2| модули направляющих векторов q1 и q2 соответственно, φ -угол между векторами q1 и q2.
Из выражения (1.3) получим:
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
и
Решение. Прямая (1.5) имеет направляющий вектор q1=(m1, p1)=(3, 4), а прямая (1.6) − q2=(m2, p2)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m1, p1, m2, p2 в (1.4):
Упростим и решим:
Найдем угол φ
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
Ответ.
Угол между прямыми равен:
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
Сделаем преобразования с выражением (1.7):
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
Пример 2. Определить, параллельны ли прямые
и
Решение. Прямая (1.10) имеет направляющий вектор q1=(m1, p1)=(3, 3), а прямая (1.11) − q2=(m2, p2)=(−2, −2). Тогда
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
и
Решение. Прямая (1.14) имеет направляющий вектор q1=(m1, p1)=(3, 1), а прямая (1.15) − q2=(m2, p2)=(−2, 6). Тогда
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
и
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
Из определения скалярного произведения двух векторов, имеем:
где |n1| и |n2| модули нормальных векторов n1 и n2 соответственно, φ -угол между векторами n1 и n2.
Из уравнения (19) получим
Пример 4. Найти угол между прямыми
и
Решение. Прямая (1.21) имеет нормальный вектор n1=(A1, B1)=(5, −2), а прямая (1.22) − n2=(A2, B2)=(1, 3). Задача определения угла между прямыми L1 и L2 сводится к определению угла между векторами n1 и n2. Из определения скалярного произведения векторов имеем: (n1,n2)=|n1||n2|cosφ. Тогда
Подставляя значения A1, B1, A2, B2 в (1.23), получим:
Упростим и решим:
Найдем угол φ:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
и
Решение. Прямая (1.26) имеет нормальный вектор n1=(A1, B1)=(4, 2), а прямая (1.27) − n2=(A2, B2)=(2, 1). Тогда подставляя значения A1, B1, A2, B2 в (1.24), получим
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
и
Решение. Прямая (1.29) имеет нормальный вектор n1=(A1, B1)=(4, −1), а прямая (1.30) − n2=(A2, B2)=(2, 8). Тогда подставляя значения A1, B1, A2, B2 в (28), получим
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
и
где q1=(m1, p1, l1) направляющий вектор прямой L1, а q2=(m2, p2, l2) направляющий вектор прямой L2.
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
Из определения скалярного произведения:
где |q1| и |q2| модули направляющих векторов q1 и q2 соответственно, φ -угол между векторами q1 и q2.
Из выражения (2.3) получим:
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
и
Решение. Прямая (2.5) имеет направляющий вектор q1=(m1, p1, l1)=(1, 1, 3), а прямая (2.6) − q2=(m2, p2, l2)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m1, p1, l1, m2, p2, l2 в (2.4):
Упростим и решим:
Найдем угол φ
Ответ.
Угол между прямыми равен:
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
Отметим, что любую пропорцию  нужно понимать как равенство ad=bc.
нужно понимать как равенство ad=bc.
Пример 2. Определить, параллельны ли прямые
и
Решение. Прямая (2.9) имеет направляющий вектор q1=(m1, p1, l1)=(3, 2, 4), а прямая (2.10) − q2=(m2, p2, l2)=(6, 4, 8). Тогда
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
и
Решение. Прямая (2.9) имеет направляющий вектор q1=(m1, p1, l1)=(1, 2, 0), а прямая (2.10) − q2=(m2, p2, l2)=(2, 4, 0). Подставляя значения m1, p1, l1, m2, p2, l2 в (2.8), получим
Выражение (2.13) нужно понимать так:
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
и
Решение. Прямая (2.16) имеет направляющий вектор q1=(m1, p1, l1)=(3, 2, 1), а прямая (2.17) − q2=(m2, p2, l2)=(4, −6, 0). Тогда
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми – размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.

Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α – β
tg γ = tg (α – β) = tg α – tg β1 + tg α ·tg β = k1 – k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых

Если a – направляющий вектор первой прямой и b – направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x – x0 l = y – y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых

Если a – вектор нормали первой прямой и b – вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; –k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a – направляющий вектор первой прямой и b – вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости

Пример 1. Найти угол между прямыми y = 2x – 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 – k21 + k1·k2
=
2 – (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°

Пример 2. Найти угол между прямыми y = 2x – 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x – 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x – 23 = y4 => y = 43x – 83 (k2 = 43)
tg γ =
k1 – k21 + k1·k2
=
-23 – 431 + (-23)·43
=
-631 – 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a – направляющий вектор первой прямой, а b – направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x – x0 l = y – y0m = z – z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t – 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} – направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x – 23
=
y4
=
z – 35
и –
x – 22
= 1 – 3y =
3z – 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
–x – 22 = x – 2-2
1 – 3y = 1 + y-1/3 = y – 1/3-1/3
3z – 52 = z – 5/32/3
Получено уравнение второй прямой в канонической форме
x – 2-2 = y – 1/3-1/3 = z – 5/32/3
{-2; -13; 23} – направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 – 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
Угол между прямыми на плоскости
Определение.
Углом между прямыми называется наименьший
из двух смежных углов, образованных
этими прямыми.
Для
решения вопроса о нахождении угла между
прямыми достаточно заменить прямые их
направляющими векторами и находить
острый угол между векторами.
Пусть
прямые ℓ1
и ℓ2
заданы общими уравнениями в прямоугольной
декартовой системе координат О
:
ℓ1:
![]()
= 0,
ℓ2:
![]()
= 0.
Направляющие
векторы этих прямых имеют координаты
1(В1,
– А1)
и
2(В2,
– А2).
Пусть угол между прямыми равен .
Тогда
cos
=
![]()
или
cos
=
![]()
.
(7)
При
решении задач часто сталкиваемся с
нахождением угла между прямыми, когда
прямые ℓ1
и ℓ2
задаются
уравнениями с угловым коэффициентом
(не забываем, что прямые ℓ1
и ℓ2
не параллельны оси Оу):
ℓ1:
![]()
,
ℓ2:
![]()
.
Если
переписать эти уравнения в общем виде,
то получим
ℓ1:
![]()
= 0,
ℓ2:
![]()
= 0.
Соответственно,
их направляющие векторы
1(1,
k1)
и
2(1,
k2),
и формула (7) принимает вид:
cos
=
![]()
.
Более
интересна формула для угла между прямыми
ℓ1
и ℓ2
:
![]()
=
![]()
.
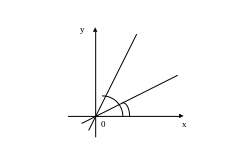
Действительно,
![]()
,
![]()
(см. рисунок). Тогда
один из углов между прямыми ℓ1
и ℓ2
:
= |![]()
|.
Так как
=
|
![]()
|
= |![]()
|,
то
=
.
Замечание.
Если ℓ1
ℓ2,
то
– не существует и
![]()
= –1.
Взаимное расположение двух прямых на плоскости
Пусть
прямые ℓ1
и ℓ2
заданы общими уравнениями в О
![]()
:
ℓ1:
= 0,
ℓ2:
= 0.
Вопрос
о взаимном расположении двух прямых
можно решить алгебраическим путем, а
именно, исследуя решение системы линейных
уравнений
![]()
Как
известно, система имеет единственное
решение только в единственно случае,
когда коэффициенты при неизвестных не
пропорциональны
![]()
.
Следовательно,
1.
ℓ1
ℓ2
ℓ1
ℓ2
.
2.
ℓ1||ℓ2
ℓ1
ℓ2
![]()
(![]()
![]()
).
3.
ℓ1
=
ℓ2
=
![]()
( прямые совпадают).
Расстояние от точки до прямой
Пусть
прямая ℓ задана общим уравнением в О
:
ℓ:
= 0.
Нормальный
вектор прямой имеет координаты:
![]()
.
Выберем произвольно точку М0(![]()
)
и найдем расстояние от точки М0
до прямой ℓ.

Из
точки М0
опустим
перпендикуляр на прямую ℓ
и обозначим
основание
перпендикуляра
М1(![]()
).
Так как М1
ℓ, то
![]()
= 0 и
С
= – (![]()
).
(8)
Искомое
расстояние равно |М1М0|.
С другой стороны
![]()
||
![]()
и, следовательно, угол
между ними равен или 0, или .
Поэтому:
(
,
)
= |
|
|
|cos
=
|
|
|
|
=
|
|![]()
.
Запишем
полученное равенство в координатной
форме.
Имеем:
(![]()
.
Поэтому,
учитывая (8) получим:
(
,
)
=
![]()
=
![]()
=
![]()
.
Учитывая,
что скалярное произведение векторов
может быть отрицательным, будем
рассматривать его по абсолютной величине
и находим
|
|
= |
|,
|М1М0|
=
![]()
.
(9)
Знак
трехчлена Ах
+ Ву + С
Пусть
прямая ℓ задана общим уравнением в О
:
ℓ:
= 0.
Нормальный
вектор прямой имеет координаты:
.
От произвольной точки
![]()
прямой
ℓ откладываем представитель
![]()
вектора
.

Как
известно прямая ℓ разбивает плоскость
на две открытые полуплоскости, которые
обозначим
и ,
причем полуплоскость
содержит отрезок
![]()
.
Тогда,
как нетрудно заметить, если точка М(![]()
)
расположена в полуплоскости ,
то угол между векторами
![]()
и
![]()
будет острый. Если точка М
расположена в полуплоскости ,
то угол между векторами
и
будет тупой. Рассматривая скалярные
произведения этих векторов, получим:
-
Если
точка М
расположена в полуплоскости ,
то (
,

)
> 0. -
Если
точка М
расположена
в полуплоскости ,
то (
,)
< 0.
Записывая
1 и 2 в координатной форме, получим:
М
![]()
>
0,
М
<
0.
Учитывая,
что точка
![]()
ℓ, (см (8)) получим:
М
![]()
> 0, (10)
М
< 0. (11)
Таким
образом, строгие неравенства (10), (11)
являются уравнениями открытых
полуплоскостей. Если неравенства
нестрогие, т.е.
≥ 0,
(12)
0.
(13),
то
они являются уравнениями полуплоскостей
(вместе с граничной прямой ℓ).
Пример.
В прямоугольной декартовой системе
координат на плоскости заданы точки:
А(2; −1), В(−1;
3), С(4; −5).
1)
Составить уравнения прямой АВ
в канонической,
параметрической и общей формах. Определить
координаты ее нормального вектора.
2)
Определить угловой коэффициент прямой
(АС)
и отрезки, отсекаемые ею на осях координат.
3)
Найти косинус угла между прямыми (АВ)
и (АС).
4)
Найти длину высоты треугольника АВС,
проведенной из вершины С и составить
уравнение прямой, содержащей этот
отрезок.
Решение.
1. Прямую (АВ)
можно задать точкой А(2;
−1) и вектором
![]()
,
тогда каноническое и параметрическое
задания данной прямой будут выглядеть
следующим образом:
![]()
(1)
и
![]()
где
![]()
R.
(2)
Из
канонического уравнения (1) равносильными
переходами получим ее общее уравнение:
![]()
,
![]()
.
(3)
Из
уравнения (3) найдем координаты нормального
вектора этой прямой:
![]()
.
2.
Аналогично пункту (1) можно получить
общее уравнение прямой (АС):
2x
+ y
− 3 = 0.
Откуда
y
= −2x
+ 3.
Следовательно,
угловой коэффициент этой прямой k
= − 2.
Уравнение
прямой (АС)
запишем в виде: 2x
+ y
= 3 и, разделив
обе части уравнения на 3, получим
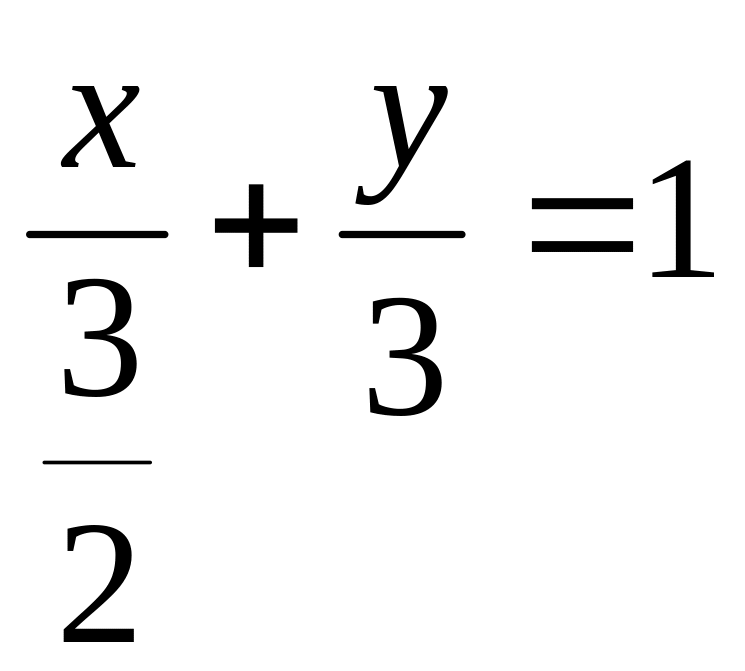
.
Мы
получили уравнение прямой в отрезках.
Отсюда находим точки пересечения прямой
с осями координат:
![]()
,
B(0;3)
3.
Для нахождения косинуса угла между
прямыми (АВ)
и (АС)
используем следующую формулу:
![]()
,
где
![]()
–угл между прямыми,
k1,
k2
– угловые коэффициенты данных прямых.
Во второй части задания мы нашли k2
= −2.
Общее
уравнение прямой (АВ)
получено в первой части задания:
4x
+ 3y
− 5 = 0, откуда
![]()
и k1=
![]()
.
Следовательно,

.
Итак,
![]()
.
4
.
Длину
высоты
![]()
можно рассматривать как расстояние от
точки С(4;−5).до прямой (АВ):
![]()
.
Т
H
аким образом,
![]()
.
Формула расстояния от точки до прямой
известна:
![]()
.
Следовательно,
![]()
.
Итак,
|CH|=0,8.
Прямую
(CH)
можно задать точкой С(4;
-5) и нормальным
вектором
![]()
.
Поэтому −3
∙(x
− 4) + 4 ∙(y
+5)=0,
3x
– 4y
– 32 = 0 –
уравнение прямой (CH).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение натуральной величины угла
Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.
Задача
Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.

Последовательность построений:
- В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
- Через точку K” проводим перпендикуляр к f”. На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O”. По линии связи определяем положение т. O’.
- Находим величину радиуса R поворота точки K. Для этого перпендикулярно O”K” откладываем отрезок K”K0 = yk – yo. Таким образом, R равен O”K0 – гипотенузе прямоугольного треугольника O”K”K0.
- Проводим дугу радиусом R до её пересечения с перпендикуляром O”K” в точке K”1. Соединяем K”1 c точками 1” и 2”. Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K”1.
Более подробную информацию о методе вращения вокруг линии уровня, который мы здесь использовали, вы можете найти на следующей странице.
Определение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называют плоский угол, стороны которого параллельны данным прямым. На изображении, приведенном ниже, прямые e и d скрещивающиеся и друг с другом не пересекаются. Чтобы найти угол между ними, выполним ряд графических построений:

Описание решения
- На любом свободном месте чертежа отмечаем точку S. Располагаем её произвольно (проекции S” и S’ показаны на рисунке).
- Через точку S проводим прямые a и b так, чтобы они были параллельны e и d. В нашем случае a||e, b||d соответственно.
- Строим горизонталь h, которая будет играть роль оси вращения. Перпендикулярно h’ из точки S’ проводим прямую. Она пересекает h’ в т. O’ – горизонтальной проекции центра вращения.
- Определяем радиус поворота R как гипотенузу треугольника O’S’S0. При этом катет S’S0 равен разности удаления точек S” и O” от горизонтальной плоскости.
- Находим т. S’1 на пересечении дуги радиуса R с прямой S’O’. Соединяем S’1 c точками 1′ и 2′, которые своего положения не меняют. Угол ϕ при вершине S’1 искомый. Задача решена.
Похожие задачи:
- Построение угла между прямой и плоскостью
- Построение угла между двумя плоскостями
Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.

Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).

Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.

Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD). 
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:

Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.

Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
