116
117
дифференциальные уравнения
второго порядка
с постоянными
коэффициентами
13.1. Структура решения неоднородного
линейного
дифференциального уравнения второго
порядка
с постоянными коэффициентами
Уравнение вида
![]() ,
,
где pиq– вещественные числа, называется
линейным неоднородным уравнением
второго порядка с постоянными
коэффициентами.
Общее решение этого уравнения
представляет собой сумму частного
решения неоднородного уравнения yч.н.и общего решения соответствующего
однородного уравненияyо.о.,
то естьy=yч.н.+yо.о.. Это
утверждение составляет содержание
теоремы о структуре общего решения
неоднородного линейного дифференциального
уравнения второго порядка с постоянными
коэффициентами.
Напомним, уравнение является однородным,
если f(x)
равно нулю. Для того чтобы решить
однородное дифференциальное уравнение,
необходимо составить характеристическое
уравнение![]() .
.
При его решении возможны следующие три
случая.
Случай 1. Если корни k1,k2 различны, то
общее решение однородного уравнения
имеет вид:
![]() .
.
Случай 2. Если k1 =k2 =k,
то общее решение однородного уравнения
имеет вид:
![]() .
.
Случай 3. Если
![]() ,
,
то общее решение однородного уравнения
имеет вид:
![]() ,
,
где
![]() ,
,![]() .
.
13.2. Нахождение частных решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Частное решение линейного неоднородного
уравнения зависит от вида правой части
уравнения, то есть от функции
![]() .
.
Если
![]() ,
,
где![]() –данный многочлен степени
–данный многочлен степени![]() ,
,
то частное решение линейного неоднородного
уравнения имеет вид:
![]() ,
,
где
![]() – многочлен степени
– многочлен степени![]() с неизвестными коэффициентами, которые
с неизвестными коэффициентами, которые
нужно найти,
![]() – число корней характеристического
– число корней характеристического
уравнения, равных нулю.
Если
![]() ,
,
то частное решение линейного неоднородного
уравнения имеет вид:
![]() ,
,
где
![]() – многочлен степени
– многочлен степени![]() с неизвестными коэффициентами,
с неизвестными коэффициентами,
![]() – кратность корня характеристического
– кратность корня характеристического
уравнения![]() .
.
Если
![]() ,
,
где![]() ,
,![]() и
и![]() – известные числа, то частное решение
– известные числа, то частное решение
линейного неоднородного уравнения
имеет вид:
![]()
где
![]() ,
,![]() – неизвестные коэффициенты,
– неизвестные коэффициенты,
![]() – число корней характеристического
– число корней характеристического
уравнения, равных![]() .
.
13.3. Примеры решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Рассмотрим примеры решения неоднородных
дифференциальных уравнений второго
порядка с постоянными коэффициентами.
Пример 1.Найти общее решение уравнения![]() .
.
Решение.Характеристическое уравнение![]() имеет корниk1 =
имеет корниk1 =
0,k2 = 1. Общее
решение однородного уравнения тогда
имеет вид:
![]() .
.
Найдем частное решение неоднородного
уравнения. Так как 0 является корнем
характеристического уравнения кратности
т = 1, то частное решение имеет вид:
![]() .
.
Найдем
![]() и
и![]() :
:![]() ,
,![]() .
.
Теперь подставим производные в исходное
уравнение, получим:
![]() .
.
Приравнивая коэффициенты при одинаковых
степенях
![]() ,
,
получим систему алгебраических уравнений:
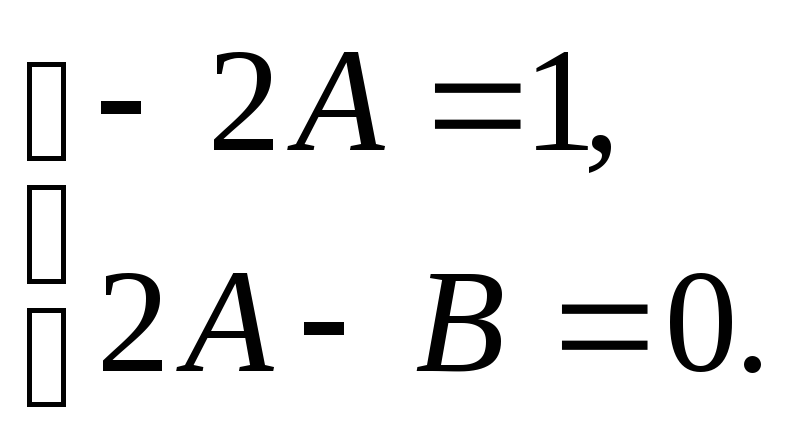
Решая систему, находим, что
![]() ,
,![]() .
.
Итак,![]() .
.
Тогда общее решение неоднородного
уравнения примет вид:
![]() .
.
Пример 2.Найти общее решение уравнения![]() .
.
Решение. Характеристическое уравнение
имеет вид:![]() ,
,
которое имеет корниk1
= 2,k2 = 3.
Следовательно, общее решение однородного
уравнения примет вид:
![]() .
.
Так как
![]() = 1 не является корнем характеристического
= 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:![]() .
.
Подставив
![]()
![]() и
и![]() в исходное уравнение, получим:
в исходное уравнение, получим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Приравняем коэффициенты при одинаковых
степенях
![]() ,
,
получим систему уравнений:
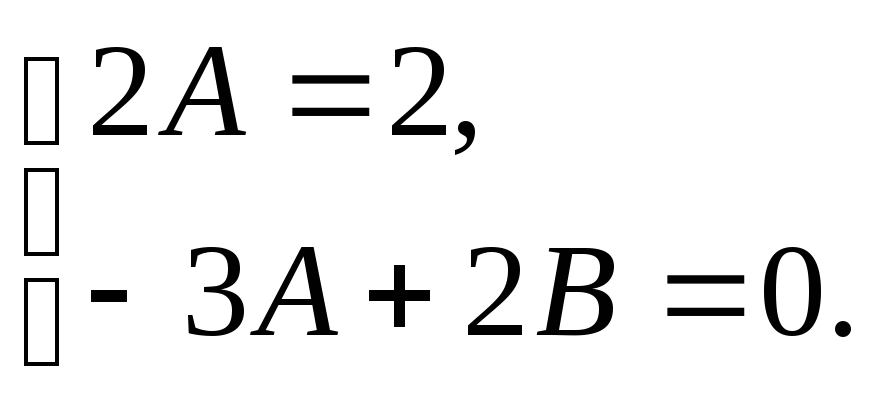
Откуда находим, что
![]() ,
,![]() .
.
Находим общее решение неоднородного
уравнения:
![]()
Пример 3.Найти частное решение
уравнения![]() ,
,
удовлетворяющее начальным условиям![]() ,
,![]() .
.
Решение. Характеристическое уравнениеk2+ 1 = 0 действительных
корней не имеет. Найдем![]() и
и![]() :
:
![]() ,
,![]() .
.
Общее решение однородного уравнения
имеет вид:
![]() .
.
Найдем частное решение неоднородного
уравнения. Так как 2 не является корнем
характеристического уравнения, то
![]() ;
;
![]() ;
;
![]() .
.
Подставим
![]() и
и![]() в исходное уравнение, получим:
в исходное уравнение, получим:
![]() ;
;
![]() .
.
Из последнего равенства получим систему
уравнений:
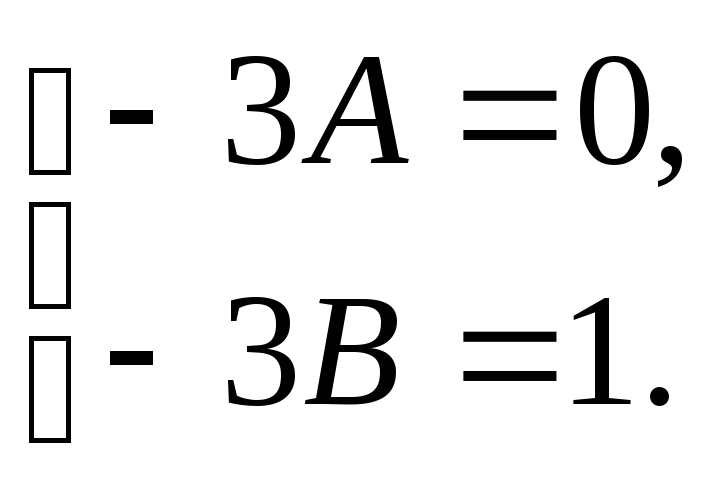
Откуда следует, что
![]() ,
,![]() .
.
Тогда общее решение неоднородного
уравнения имеет вид:
![]() .
.
Для того чтобы найти частное решение
исходного уравнения, подставим начальные
условия в полученное решение. Имеем:
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,![]() .
.
Тогда получаем, что частное решение,
удовлетворяющее начальным условиям
![]() ,
,![]() ,
,
имеет вид:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим линейное неоднородное дифференциальное уравнение (ЛНДУ) порядка ![]()
![]() Или коротко
Или коротко ![]() , где
, где ![]() .
.
Уравнение ![]() , левая часть которого совпадает с левой частью ЛНДУ, называют Соответствующим данному ЛНДУ однородным уравнением.
, левая часть которого совпадает с левой частью ЛНДУ, называют Соответствующим данному ЛНДУ однородным уравнением.
Теорема (о структуре общего решения ЛНДУ).
Общее решение ЛНДУ Порядка ![]() с непрерывными на некотором интервале
с непрерывными на некотором интервале ![]() коэффициентами
коэффициентами ![]() равно сумме общего решения соответствующего однородного уравнения
равно сумме общего решения соответствующего однородного уравнения ![]() и любого частного решения
и любого частного решения ![]() ЛНДУ, т. е.
ЛНДУ, т. е. ![]() .
.
Доказательство. В первую очередь, подставим функцию ![]() В исходное уравнение и убедимся в том, что она действительно является решением ЛНДУ:
В исходное уравнение и убедимся в том, что она действительно является решением ЛНДУ:
![]()
При выводе были использованы линейные свойства линейного дифференциального оператора ![]() и то, что функция
и то, что функция ![]() Есть общее решение ОЛДУ, так что
Есть общее решение ОЛДУ, так что ![]() , а функция
, а функция ![]() Есть частное решение НЛДУ, так что
Есть частное решение НЛДУ, так что ![]() .
.
Далее, чтобы доказать, что данное решение является общим, необходимо для заданных начальных условий ![]() найти единственную комбинацию
найти единственную комбинацию ![]() Произвольных постоянных, обеспечивающих решение задачи Коши.
Произвольных постоянных, обеспечивающих решение задачи Коши.
Дифференцируя функцию ![]()
![]() Раз, и подставляя в нее и во все ее производные заданные начальные условия, получим систему линейных уравнений относительно произвольных постоянных следующего вида:
Раз, и подставляя в нее и во все ее производные заданные начальные условия, получим систему линейных уравнений относительно произвольных постоянных следующего вида:

Определителем этой системы является Вронскиан ![]() , который не равен нулю, поскольку по условию теоремы решения
, который не равен нулю, поскольку по условию теоремы решения ![]() образуют фундаментальную систему решений соответствующего ОЛДУ. При условии
образуют фундаментальную систему решений соответствующего ОЛДУ. При условии ![]() данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных
данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных ![]() , которое обозначим как
, которое обозначим как ![]() .
.
Таким образом, сумма линейной комбинации фундаментальных решений вида ![]() и частного решения
и частного решения ![]() Является решением, получена из общего решения при некоторых значениях
Является решением, получена из общего решения при некоторых значениях ![]() Произвольных постоянных и по построению удовлетворяет начальным условиям, что и требовалось доказать.
Произвольных постоянных и по построению удовлетворяет начальным условиям, что и требовалось доказать.
Если известна фундаментальная система решений ![]() соответствующего ОЛДУ и, следовательно, его общее решение
соответствующего ОЛДУ и, следовательно, его общее решение ![]() , то для определения частного решения
, то для определения частного решения ![]() НЛДУ порядка
НЛДУ порядка ![]() можно воспользоваться Методом Лагранжа вариации произвольных постоянных.
можно воспользоваться Методом Лагранжа вариации произвольных постоянных.
Этот метод заключается в том, что частное решение ![]() НЛДУ ищут в виде
НЛДУ ищут в виде
![]() ,
,
Т. е. в виде линейной комбинации ![]() неизвестных функций
неизвестных функций ![]() и
и ![]() заранее вычисленных фундаментальных решений
заранее вычисленных фундаментальных решений ![]() соответствующего ОЛДУ.
соответствующего ОЛДУ.
Предварительно находят производные ![]() из системы алгебраических уравнений следующего вида:
из системы алгебраических уравнений следующего вида:

Определителем этой системы является Вронскиан ![]() , который не равен нулю при любом
, который не равен нулю при любом ![]() , поскольку решения
, поскольку решения ![]() образуют фундаментальную систему решений соответствующего ОЛДУ.
образуют фундаментальную систему решений соответствующего ОЛДУ.
При условии ![]() данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных
данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных ![]() , которое представим в виде
, которое представим в виде ![]() равенств
равенств ![]() .
.
Интегрируя каждое из полученных равенств, получим набор первообразных ![]() для функций
для функций ![]() .
.
Окончательно, получаем функцию ![]() ,
,
Которая, как доказано в общей теории, является частным решением ЛНДУ при условии непрерывности на некотором интервале ![]() функций
функций ![]() .
.
Отметим, что для произвольного НЛДУ порядка ![]() нет общего способа построения системы фундаментальных решений
нет общего способа построения системы фундаментальных решений ![]() . Таким образом, методом Лагранжа можно воспользоваться только тогда, когда эту фундаментальную систему каким-либо способом удается найти. Если НЛДУ порядка
. Таким образом, методом Лагранжа можно воспользоваться только тогда, когда эту фундаментальную систему каким-либо способом удается найти. Если НЛДУ порядка ![]() имеет числовые коэффициенты
имеет числовые коэффициенты ![]() , то фундаментальная система решений
, то фундаментальная система решений ![]() , соответствующего ОЛДУ, находится всегда и достаточно просто. В этом случае для нахождения частного решения
, соответствующего ОЛДУ, находится всегда и достаточно просто. В этом случае для нахождения частного решения ![]() всегда можно использовать метод Лагранжа.
всегда можно использовать метод Лагранжа.
Теорема (о наложении решений ЛНДУ).
Если правая часть ЛНДУ представлена в виде суммы нескольких функций, так что
![]() , и
, и ![]() есть частные решения неоднородных уравнений
есть частные решения неоднородных уравнений ![]() , то сумма этих частных решений
, то сумма этих частных решений ![]() есть некоторое частное решение исходного ЛНДУ.
есть некоторое частное решение исходного ЛНДУ.
Доказательство. Подставим функцию ![]() В исходное уравнение и убедимся в том, что эта функция действительно является решением ЛНДУ:
В исходное уравнение и убедимся в том, что эта функция действительно является решением ЛНДУ:
![]()
![]() .
.
При выводе были использованы линейные свойства линейного дифференциального оператора ![]() и условия теоремы. Таким образом, теорема полностью доказана.
и условия теоремы. Таким образом, теорема полностью доказана.
Частным случаем ЛНДУ являются линейные неоднородные дифференциальные уравнения порядка ![]() с постоянными числовыми коэффициентами
с постоянными числовыми коэффициентами ![]() вида
вида ![]() .
.
Так как постоянные функции ![]() непрерывны на любом промежутке, то по теореме о структуре общего решения ЛНДУ для того, чтобы найти общее решение
непрерывны на любом промежутке, то по теореме о структуре общего решения ЛНДУ для того, чтобы найти общее решение ![]() данного уравнения достаточно построить фундаментальную систему решений
данного уравнения достаточно построить фундаментальную систему решений ![]() соответствующего однородного уравнения, найти некоторое частное решение
соответствующего однородного уравнения, найти некоторое частное решение ![]() ЛНДУ и представить общее решение в следующем виде:
ЛНДУ и представить общее решение в следующем виде:
![]() .
.
Рассмотрим на примере ЛНДУ второго порядка с постоянными коэффициентами, как находится его общее решение с использованием метода Лагранжа для отыскания частного решения.
Пример. Найти общее решение уравнения ![]() .
.
На первом этапе ищется общее решение соответствующего однородного уравнения ![]() Его характеристическое уравнение имеет вид
Его характеристическое уравнение имеет вид ![]() Корни характеристического уравнения находятся по общей формуле вычисления корней квадратного уравнения и в данном случае равны
Корни характеристического уравнения находятся по общей формуле вычисления корней квадратного уравнения и в данном случае равны ![]() ,
, ![]() .
.
В соответствии с общей теорией функции ![]() ,
, ![]() являются линейно независимыми, и для уравнения второго порядка образует фундаментальную систему решений.
являются линейно независимыми, и для уравнения второго порядка образует фундаментальную систему решений.
Таким образом, общее решение соответствующего однородного уравнения имеет вид
![]() .
.
Заменим в общем решении ![]() Постоянные
Постоянные ![]() Неизвестными функциями
Неизвестными функциями ![]() И в соответствии с методом неопределенных коэффициентов будем искать частное решение НЛДУ в виде
И в соответствии с методом неопределенных коэффициентов будем искать частное решение НЛДУ в виде ![]() .
.
Предварительно для НЛДУ второго порядка решается система уравнений

Линейная относительно производных неизвестных функций ![]() .
.
Для данного уравнения указанная система имеет вид

Определителем этой системы является Вронскиан ![]() который всегда отличен от нуля, что позволяет найти неизвестные по формулам Крамера
который всегда отличен от нуля, что позволяет найти неизвестные по формулам Крамера
 ,
,  .
.
Интегрируя полученные дифференциальные уравнения и выделяя первообразные их правых частей ![]() ,
, ![]() , находим неизвестные функции в виде
, находим неизвестные функции в виде ![]() ,
, ![]() . Отсюда, частное решение данного НЛДУ равно
. Отсюда, частное решение данного НЛДУ равно
![]() .
.
Окончательно, общее решение данного уравнения записывается в виде
![]() .
.
Пример. Найти общее решение уравнения ![]() .
.
На первом этапе ищется общее решение соответствующего однородного уравнения ![]() Его характеристическое уравнение имеет вид
Его характеристическое уравнение имеет вид ![]() Корни характеристического уравнения находятся с использованием общей формулы вычисления корней квадратного уравнения и в данном случае равны
Корни характеристического уравнения находятся с использованием общей формулы вычисления корней квадратного уравнения и в данном случае равны ![]() ,
, ![]() ,
, ![]() .
.
В соответствии с общей теорией функции ![]() ,
, ![]() ,
, ![]() являются линейно независимыми, и для уравнения третьего порядка образует фундаментальную систему решений.
являются линейно независимыми, и для уравнения третьего порядка образует фундаментальную систему решений.
Таким образом, общее решение соответствующего однородного уравнения имеет вид
![]() .
.
Заменим в общем решении ![]() Постоянные
Постоянные ![]() Неизвестными функциями
Неизвестными функциями ![]() И в соответствии с методом неопределенных коэффициентов Лагранжа будем искать частное решение НЛДУ в следующем виде:
И в соответствии с методом неопределенных коэффициентов Лагранжа будем искать частное решение НЛДУ в следующем виде:
![]() .
.
Для данного НЛДУ третьего порядка система уравнений, линейная относительно производных неизвестных функций ![]() имеет вид:
имеет вид:

Определителем этой системы является Вронскиан
![]()
Который отличен от нуля, что позволяет найти неизвестные ![]() По формулам Крамера в следующем виде:
По формулам Крамера в следующем виде: ![]() ,
, ![]() ,
, ![]() .
.
Интегрируя полученные дифференциальные уравнения, находим неизвестные функции ![]() ,
, ![]() ,
, ![]() . Отсюда, частное решение данного НЛДУ равно
. Отсюда, частное решение данного НЛДУ равно ![]() .
.
Окончательно, общее решение данного уравнения записывается в виде
![]() .
.
Пусть правая часть линейного неоднородного дифференциального уравнения порядка ![]() с постоянными числовыми коэффициентами имеет Специальный вид:
с постоянными числовыми коэффициентами имеет Специальный вид:
1) ![]() ,
,
2) ![]() ,
,
Где ![]() – вещественные числа,
– вещественные числа, ![]() И
И![]() – полиномы степеней
– полиномы степеней ![]() и
и ![]() .
.
Как и ранее, чтобы найти общее решение ![]() данного уравнения достаточно построить фундаментальную систему решений
данного уравнения достаточно построить фундаментальную систему решений ![]() соответствующего однородного уравнения, найти некоторое частное решение
соответствующего однородного уравнения, найти некоторое частное решение ![]() ЛНДУ и представить общее решение в виде
ЛНДУ и представить общее решение в виде ![]() .
.
Однако если правая часть ЛНДУ имеет специальный вид, то частное решение уравнения ![]() также имеет структуру, аналогичную правой части, и может быть найдено по Методу неопределенных коэффициентов. Этот метод несколько проще метода вариации произвольных постоянных, так как не включает в себя операцию интегрирования функций.
также имеет структуру, аналогичную правой части, и может быть найдено по Методу неопределенных коэффициентов. Этот метод несколько проще метода вариации произвольных постоянных, так как не включает в себя операцию интегрирования функций.
1) Рассмотрим вначале ЛНДУ с постоянными коэффициентами второго порядка со специальной частью первого вида ![]() .
.
В этом случае частное решение ![]() дифференциального уравнения ищем в виде
дифференциального уравнения ищем в виде
![]() ,
,
Т. е. выбираем полином той же степени, что и в правой части, только с неизвестными заранее коэффициентами ![]() , а число
, а число ![]() назначаем равным числу
назначаем равным числу ![]() в правой части.
в правой части.
Показатель ![]() степенной функции
степенной функции ![]() выбирают равным нулю, если число
выбирают равным нулю, если число ![]() не совпадает ни с одним корнем характеристического уравнения, и равным кратности корня характеристического уравнения в случае совпадения числа
не совпадает ни с одним корнем характеристического уравнения, и равным кратности корня характеристического уравнения в случае совпадения числа ![]() с каким-либо корнем.
с каким-либо корнем.
Рассмотрим на конкретных примерах ЛНДУ второго порядка, как находится его общее решение с использованием метода неопределенных коэффициентов для отыскания частного решения ![]() .
.
Пример. Найти общее решение уравнения ![]() .
.
На первом этапе ищется общее решение соответствующего однородного уравнения ![]() . Его характеристическое уравнение
. Его характеристическое уравнение ![]() имеет корни
имеет корни ![]() ,
, ![]() . Следовательно, фундаментальная система решений имеет вид
. Следовательно, фундаментальная система решений имеет вид ![]() ,
,![]() , а общее решение соответствующего однородного уравнения есть
, а общее решение соответствующего однородного уравнения есть ![]() .
.
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как ![]() не совпадает ни с одним корнем характеристического уравнения, то
не совпадает ни с одним корнем характеристического уравнения, то ![]() и частное решение будем искать в виде
и частное решение будем искать в виде
![]() .
.
Вычислив производные ![]() ,
,![]() И подставив
И подставив ![]() ,
,![]() и
и ![]() в исходное уравнение получим (после сокращения на
в исходное уравнение получим (после сокращения на ![]() ) следующее тождество:
) следующее тождество:
![]() .
.
Сравнивая коэффициенты обеих частей этого тождества, получим систему трех линейных уравнений для определения неизвестных коэффициентов:
![]() ,
,
Откуда ![]() .
.
Итак, ![]() , и, следовательно, общее решение уравнения имеет вид
, и, следовательно, общее решение уравнения имеет вид ![]() .
.
Пример. Найти общее решение уравнения ![]() .
.
На первом этапе ищется общее решение соответствующего однородного уравнения ![]() . Его характеристическое уравнение
. Его характеристическое уравнение ![]() имеет двукратный корень
имеет двукратный корень ![]() . Следовательно, фундаментальная система решений имеет вид
. Следовательно, фундаментальная система решений имеет вид ![]() ,
,![]() , а общее решение соответствующего однородного уравнения есть
, а общее решение соответствующего однородного уравнения есть ![]() .
.
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как ![]() совпадает с двукратным корнем характеристического уравнения, то
совпадает с двукратным корнем характеристического уравнения, то ![]() и частное решение будем искать в виде
и частное решение будем искать в виде
![]() .
.
Вычислив производные ![]() ,
,![]() И подставив
И подставив ![]() ,
,![]() и
и ![]() в исходное уравнение получим (сократив на
в исходное уравнение получим (сократив на ![]() и сравнив коэффициенты при одинаковых степенях
и сравнив коэффициенты при одинаковых степенях ![]() ) следующие значения для неопределенных коэффициентов:
) следующие значения для неопределенных коэффициентов: ![]() .
.
Следовательно, ![]() , а общее решение данного уравнения имеет вид
, а общее решение данного уравнения имеет вид ![]() .
.
2) Рассмотрим далее ЛНДУ с постоянными коэффициентами второго порядка со специальной частью второго вида ![]() .
.
В этом случае частное решение уравнения ![]() ищем в виде
ищем в виде
![]() ,
,
Т. е. выбираем полиномы при косинусе и синусе наибольшей степени, из имеющихся в правой части, с неизвестными заранее коэффициентами ![]() и
и ![]() , а числа
, а числа ![]() ,
, ![]() назначаем равными числам
назначаем равными числам ![]() ,
, ![]() , стоящим в правой части.
, стоящим в правой части.
Показатель ![]() степенной функции
степенной функции ![]() выбирают равным нулю, если комплексное число
выбирают равным нулю, если комплексное число ![]() , не совпадает ни с одним комплексным корнем характеристического уравнения, и равным кратности комплексного корня характеристического уравнения в случае совпадения числа
, не совпадает ни с одним комплексным корнем характеристического уравнения, и равным кратности комплексного корня характеристического уравнения в случае совпадения числа ![]() с каким-либо комплексным корнем.
с каким-либо комплексным корнем.
Рассмотрим на конкретных примерах ЛНДУ второго порядка, как находится его общее решение с использованием метода неопределенных коэффициентов для отыскания частного решения ![]() .
.
Пример. Найти частное решение уравнения ![]() .
.
На первом этапе ищется общее решение соответствующего однородного уравнения ![]() . Его характеристическое уравнение
. Его характеристическое уравнение ![]() имеет два различных комплексных корня
имеет два различных комплексных корня ![]() ,
,![]() . Следовательно, фундаментальная система вещественных решений имеет вид
. Следовательно, фундаментальная система вещественных решений имеет вид ![]() ,
, ![]() , а общее решение соответствующего однородного уравнения есть
, а общее решение соответствующего однородного уравнения есть ![]() .
.
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как комплексная пара сопряженных чисел ![]() правой части исходного уравнения совпадает с комплексной парой корней кратности один характеристического уравнения, то
правой части исходного уравнения совпадает с комплексной парой корней кратности один характеристического уравнения, то ![]() и частное решение будем искать в виде
и частное решение будем искать в виде
![]() .
.
Вычислив производные ![]() ,
,![]() И подставив
И подставив ![]() , и
, и ![]() в исходное уравнение получим следующее тождество:
в исходное уравнение получим следующее тождество: ![]() . Сравнивая коэффициенты при синусе и косинусе, найдем следующие значения для неопределенных коэффициентов:
. Сравнивая коэффициенты при синусе и косинусе, найдем следующие значения для неопределенных коэффициентов: ![]() . Следовательно,
. Следовательно, ![]() , а общее решение данного уравнения имеет вид
, а общее решение данного уравнения имеет вид ![]() .
.
| < Предыдущая | Следующая > |
|---|
Решение линейного неоднородного дифференциального уравнения состоит из двух частей: решения соответствующего однородного уравнения и непосредственно решения неоднородного. Поэтому на первом шаге решается уравнение без учета правой части. Затем ищется решение в зависимости от вида правой части. И, наконец, эти решения складываются.
О решении однородного уравнения читайте в статье.
Правая часть вида Pn(x)P_n(x) — многочлен степени nn
Решение ищется в виде
y~=Qn(x)xs,tilde y=Q_n(x) x^s,
где Qn(x)Q_n(x) – многочлен той же степени, что и в правой части. Показатель степени ss равен количеству нулевых корней характеристического уравнения.
y′′−y′−2y=x2−3x+1y”-y^prime-2y=x^2-3x+1
k2−k−2=0k^2-k-2=0
k1=−1;k2=2k_1=-1;k_2=2
yo=C1e−x+C2e2xy_o=C_1 e^{-x}+C_2 e^{2x}
Теперь рассмотрим правую часть. Она представляет собой многочлен второй степени, при этом нулевых корней у характеристического уравнения нет (ss=0), следовательно, решение нелинейного уравнения ищем в виде
y~=Ax2+Bx+Ctilde y=Ax^2+Bx+C
Первая производная
y~′=2Ax+Btilde y^prime=2Ax+B
Вторая производная
y~′′=2Atilde y”=2A
Подставляем их в начальное уравнение
2A−(2Ax+B)−2(Ax2+Bx+C)=x2−3x+12A-(2Ax+B)-2(Ax^2+Bx+C)=x^2-3x+1
−2Ax2+(−2A−2B)x+(2A−B−2C)=x2−3x+1-2Ax^2+(-2A-2B)x+(2A-B-2C)=x^2-3x+1
Коэффициенты при равных степенях должны быть равны
{−2A=1−2A−2B=−32A−B−2C=1begin{cases}
-2A=1
\-2A-2B=-3
\2A-B-2C=1
end{cases}
{A=−12B=32−A=32−(−12)=2C=−1+2A−B2=−1begin{cases}
A=-frac{1}{2}
\B=frac{3}{2}-A=frac{3}{2}-left(-frac{1}{2}right)=2
\C=frac{-1+2A-B}{2}=-1
end{cases}
Получаем
y~=−12×2+2x−1tilde y=-frac{1}{2}x^2+2x-1
И окончательно
y=yo+y~=C1e−x+C2e2x−12×2+2x−1y=y_o+tilde y = C_1 e^{-x}+C_2 e^{2x}-frac{1}{2}x^2+2x-1
Правая часть вида eαxPne^{alpha x}P_n
Решение ищется в виде
y~=eαxQn(x)xs,tilde y= e^{alpha x}Q_n(x) x^s,
где Qn(x)Q_n(x) – многочлен той же степени, что и в правой части. Показатель степени ss равен количеству кратных корней характеристического уравнения, которые при это еще равны αalpha.
y′′+3y′+2y=ex(x+1)y” +3y^prime +2y= e^{x}(x+1)
k1=−2;k2=−1k_1=-2; k_2=-1
yo=C1e−2x+C2e−xy_o=C_1 e^{-2 x}+ C_2 e^{- x}
Теперь рассмотрим правую часть. Она содержит многочлен первой степени, при этом корней, равных единицу (в правой части α=1alpha=1) у характеристического уравнения нет (ss=0), следовательно, решение нелинейного уравнения ищем в виде
y~=ex(Ax+B)tilde y= e^{ x}(Ax+B)
Первая производная
y~′=ex(Ax+B)+ex⋅A=ex(Ax+A+B)tilde y^prime= e^{ x}(Ax+B)+ e^{ x}cdot A= e^{ x}(Ax+A+B)
Вторая производная
y~′′=ex(Ax+A+B)+ex⋅A=ex(Ax+2A+B)tilde y”= e^{ x}(Ax+A+B)+ e^{ x}cdot A = e^{ x}(Ax+2A+B)
Подставляем их в начальное уравнение
ex(Ax+2A+B)+3ex(Ax+A+B)+2ex(Ax+B)=ex(x+1)e^{ x}(Ax+2A+B)+3e^{ x}(Ax+A+B)+2e^{ x}(Ax+B)= e^{x}(x+1)
(Ax+2A+B)+3(Ax+A+B)+2(Ax+B)=x+1(Ax+2A+B)+3(Ax+A+B)+2(Ax+B)= x+1
6Ax+5A+6B=x+16Ax+5A+6B=x+1
Коэффициенты при равных степенях должны быть равны
{6A=15A+6B=1{A=16B=136begin{cases}
6A=1
\5A+6B=1
end{cases}
begin{cases}
A=frac{1}{6}
\B=frac{1}{36}
end{cases}
Получаем
y~=ex(16x+136)tilde y= e^{ x}left(frac{1}{6}x+frac{1}{36}right)
И окончательно
y=yo+y~=C1e−2x+C2e−x+ex(16x+136)y=y_o+tilde y = C_1 e^{-2 x}+ C_2 e^{- x}+ e^{ x}left(frac{1}{6}x+frac{1}{36}right)
Правая часть вида eαx(Pncosβx+Qmsinβx)e^{alpha x}left(P_ncos beta x +Q_msin beta xright)
Решение ищется в виде
y~=eαx(Rlcosβx+Qlsinβx)xstilde y= e^{alpha x} left(R_lcos beta x +Q_lsin beta xright) x^s
Многочлены, входящие в решение имеют максимальную степень из тех, что содержат многочлены правой части l=max(n;m)l=max(n;m). Далее рассматриваются корни характеристического уравнения, и если они комплексные и равны α±βialphapmbeta i, где αalpha и βbeta из правой части, то s=1s=1 (не забываем, что мы рассматриваем уравнения второй степени, поэтому больше 1 в данном случае ss не может быть).
y′′+3y′+2y=exsin3xy” +3y^prime +2y= e^{x}sin 3x
k1=−2;k2=−1k_1=-2; k_2=-1
yo=C1e−2x+C2e−xy_o=C_1 e^{-2 x}+ C_2 e^{- x}
Проанализировав правую часть, видим, что решение необходимо искать в виде
y~=ex(Acos3x+Bsin3x)tilde y= e^{x}(Acos 3 x +Bsin 3 x)
Первая производная
y~′=ex(Acos3x+Bsin3x)+ex(−3Asin3x+3Bcos3x)=tilde y^prime = e^{x}(Acos 3x+Bsin 3x)+ e^{x}(-3Asin 3 x +3Bcos 3 x)=
=ex(−3Asin3x+3Bcos3x+Acos3x+Bsin3x)= e^{x}(-3Asin 3x+3Bcos 3x+ Acos 3x+Bsin 3x )
Вторая производная
y~′′=ex(−3Asin3x+3Bcos3x+Acos3x+Bsin3x)+tilde y”= e^{x}(-3Asin 3x+3Bcos 3x+ Acos 3x+Bsin 3x )+
+ex(−9Acos3x−9Bsin3x−3Asin3x+3Bcos3x)=+ e^{x}(-9Acos 3x-9Bsin 3x- 3Asin 3x+3Bcos 3x )=
=ex(−6Asin3x+8Acos3x+8Bsin3x−6Bcos3x)= e^{x}(-6Asin 3x+8Acos 3x+8Bsin 3x-6Bcos 3x)
Подставляем их в начальное уравнение
−ex(−6Asin3x+8Acos3x+8Bsin3x−6Bcos3x)+- e^{x}(-6Asin 3x+8Acos 3x+8Bsin 3x-6Bcos 3x) +
+3ex(−3Asin3x+3Bcos3x+Acos3x+Bsin3x)++3 e^{x}(-3Asin 3x+3Bcos 3x+ Acos 3x+Bsin 3x )+
+2ex(Acos3x+Bsin3x)=exsin3x+2 e^{x}(Acos 3 x +Bsin 3 x)= e^{x}sin 3x
Приводим подобные
−15Aexsin3x−3Aexcos3x−3Bexsin3x+15Bexcos3x=exsin3x-15Ae^x sin 3x-3Ae^x cos 3x-3Be^x sin 3x +15Be^x cos 3x= e^{x}sin 3x
Коэффициенты при одинаковых функциях должны быть равны
{−15A−3B=1−3A+15B=0{A=−578B=−178begin{cases}
-15A-3B=1
\-3A+15B=0
end{cases}
begin{cases}
A=-frac{5}{78}
\B=-frac{1}{78}
end{cases}
Получаем
y~=ex(−578cos3x−178sin3x)tilde y= e^{x}(-frac{5}{78}cos 3 x -frac{1}{78}sin 3 x)
И окончательно
y=yo+y~=C1e−2x+C2e−x+ex(−578cos3x−178sin3x)y=y_o+tilde y = C_1 e^{-2 x}+ C_2 e^{- x} + e^{x}(-frac{5}{78}cos 3 x -frac{1}{78}sin 3 x)
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} – 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} – 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t – 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = – int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$ |
| Ответ |
| $$y = x^4 – x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x – cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y”)=0$
- Без переменной $x$: $F(y,y’,y”)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
