Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
Задана точка M0(x0, y0, z0) и прямая L:
Построить уравнение плоскости α, проходящей через точку M0 и перпендинулярной прямой L.
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n={A, B, C} имеет следующий вид:
Направляющий вектор прямой L имеет вид q={m, p, l}. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:
Упростим уравнение (3):
где D=−mx0−px0−lx0.
Таким образом уравнение (4) определяет плоскость, проходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1).
Ответ. Уравнение плоскости прпоходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1) имеет вид (4).
Пример 1. Найти уравнение плоскости α, проходящую через точку M0(3, −1, 2) и перпендикулярной прямой L:
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n={A, B, C} представляется формулой (2).
Направляющий вектор прямой L имеет следующий вид: :
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
Подставляя координаты точки M0 и направляющего вектора q в (8), получим:
Упростим уравнение (9):
Ответ: Уравнение плоскости, проходящей через точку M0(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:
Решение. Приведем параметрическое уравнение (11) к каноническому виду:
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n={A, B, C} представляется формулой:
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:
Подставляя координаты точки M0 и направляющего вектора q в (13), получим:
Упростим уравнение (13):
Ответ. Уравнение плоскости, проходящей через точку M0(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).
Ученик
(92),
на голосовании
2 года назад
Голосование за лучший ответ
Павел Коржов (который А.)
Гений
(96168)
2 года назад
Для плоскости Ax+By+Cz+D = 0 вектор (А, В, С) является нормалью к ней. В данном случае он сонаправлен с данной прямой, а ее напр-й вектор суть (-1,1,2). Поэтому положим А=-1, В=1, С=2 и найдем D подстановкой данной точки А (2,-8,-4).
Ересь ЕресеваяМастер (1138)
2 года назад
Павел Александрович, Вы мизантроп? Считаете ли Вы, что математику в должной мере способен познать лишь человек с определенной психической составляющей личности?
Skip to content
matematicus.ru
matematicus включает разделы – высшая математика, аналитическая геометрия в пространстве и на плоскости, теория вероятностей, Arduino, Android Studio, Excel, программирование, программы, Windows, ошибки, таблицы, формулы, примеры, физика, химия
Уравнение плоскости, проходящей через точку перпендикулярно к прямой
Плоскость, проходящая через данную точку М0(х0; у0; z0) и перпендикулярная к данной прямой:
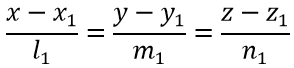
имеет нормальный вектор N{ι1, m1, n1} и представляется уравнением:
l1(x-x1) + m1(y-y1) + n1(z-z1)=0
или в векторной форме:
a1(r−r0)=0
Пример
Плоскость, проходящая через точку (9; -3; 7) и перпендикулярная к прямой:
$frac{x}{0} = frac{y}{4} = frac{{z — 3}}{4}$
, представляется уравнением:
4⋅(у+3)+4⋅(z-7)=0
4у+4z−16=0
4257
Уравнение плоскости, которая проходит через точку перпендикулярно прямой
1. Найти уравнение плоскости, которая проходит через точку 
, перпендикулярно прямой 
.
Решение.
Прямая имеет направляющий вектор 
. Плоскость, перпендикулярная прямой 
, также перпендикулярна ее направляющему вектору. То есть вектор является нормальным для искомой плоскости.
Уравнение плоскости, которая проходит через точку $(x_0, y_0, z_0)$ перпендикулярно вектору $(A, B, C)$ имеет вид
$A(x-x_0)+B(y-y_0)+C(z-z_0)=0.$
Уравнение плоскости, которая проходит через точку $(x_0, y_0, z_0)$ перпендикулярно вектору $(A, B, C)$ имеет вид
$A(x-x_0)+B(y-y_0)+C(z-z_0)=0.$
Запишем уравнение плоскости, проходящей через точку перпендикулярно вектору :
Ответ: 
2. Напишите уравнение плоскости, проходящей через точку 
и параллельной плоскости 
:
.
Решение.
: 
Нормали параллельных плоскостей равны.
– уравнение плоскости, которая проходит через заданную точку 
перпендикулярно вектору 
.
Уравнение искомой плоскости:
Ответ: 
.
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Взаимное положение прямой и плоскости в пространстве
Прямая в просторные может пересекать плоскость, может быть параллельной ей, а также может принадлежать плоскости. Но, независимо от них взаимного положения, можно говорить об углу между ними.
Пусть плоскость $P$ задана общим уравнением $Acdot x+Bcdot y+Ccdot z+D=0$, а прямую $L$ задано параметрическими уравнениями $x=x_{0} +mcdot t$, $y=y_{0} +ncdot t$, $z=z_{0} +pcdot t$.
Углом между прямой $L$ и плоскостью $P$ будем называть любой угол из двух сопредельных острого и тупого углов, образованных прямой и ее проекцией на плоскость. Если величина какого-то одного из них $varphi $, то величина второго $pi -varphi $.
Вместо угла $varphi $ между прямой $L$ и плоскостью $P$ рассмотрим угол $theta $ между направляющим вектором прямой и нормальным вектором плоскости, то есть угол между векторами $overline{R}=mcdot overline{i}+ncdot overline{j}+pcdot overline{k}$ и $overline{N}=Acdot overline{i}+Bcdot overline{j}+Ccdot overline{k}$. Этот угол тоже может быть одним из двух сопредельных острого и тупого углов: $theta $ или $pi -theta $. Между углами $varphi $ и $theta $ существует связь, а именно: если угол $theta $ острый, то $varphi =frac{pi }{2} -theta $ (острый) или $varphi =frac{pi }{2} +theta $ (тупой); если угол $theta $ тупой, то $varphi =theta -frac{pi }{2} $ (острый) или $varphi =frac{3cdot pi }{2} -theta $ (тупой).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Косинус угла $theta $ можно найти за формулой $cos theta =frac{Acdot m+Bcdot n+Ccdot p}{sqrt{A^{2} +B^{2} +C^{2} } cdot sqrt{m^{2} +n^{2} +p^{2} } } $ (см. лекцию 10.1). После этого нужно вычислить угол $0
Важный случай имеем, когда $cos theta =0$. Это означает, что прямая параллельная плоскости. Итак, условие параллельности прямой и плоскости имеет вид $Acdot m+Bcdot n+Ccdot p=0$. Условие перпендикулярности прямой и плоскости совпадает с условием коллинеарности нормального вектора плоскости и направляющего вектора прямой, то есть $frac{A}{m} =frac{B}{n} =frac{C}{p} $.
Для того, чтобы найти координаты точки сечения плоскости $P$ и прямой $L$, подставим параметрические уравнения прямой в общее уравнение плоскости:
Отсюда получаем формулу: $t=-frac{Acdot x_{0} +Bcdot y_{0} +Ccdot z_{0} +D}{Acdot m+Bcdot n+Ccdot p} $.
При вычислении $t$ возможные три случая:
- Знаменатель не равняется нулю $Acdot m+Bcdot n+Ccdot pne 0$. Тогда параметр $t$ имеет единое значение, которое нужно подставить в параметрические уравнения прямой $L$. При этом будет получено координаты нужной точки сечения.
- Знаменатель равняется нулю $Acdot m+Bcdot n+Ccdot p=0$, но числитель нулю не равняется $Acdot x_{0} +Bcdot y_{0} +Ccdot z_{0} +Dne 0$. Тогда решение поставленной задачи отсутствующий, поскольку прямая $L$ плоскость $P$ не пересекает. Это бывает тогда, когда прямая параллельная плоскости.
- Знаменатель равняется нулю $Acdot m+Bcdot n+Ccdot p=0$, и числитель также равняется нулю $Acdot x_{0} +Bcdot y_{0} +Ccdot z_{0} +D=0$. Тогда поставленная задача имеет множество решений. Это бывает тогда, когда прямая $L$ принадлежит плоскости $P$.
«Перпендикулярность прямой и плоскости» 👇
Отметим, что принадлежности прямой плоскости можно рассматривать, как частный случай параллельности прямой и плоскости.
Задача 1
В пространстве задана точка $Pleft(x_{0} ,y_{0} ,z_{0} right)$. Точка $O$ — начало координат. Найти уравнение плоскости, проходящей через точку $P$перпендикулярно вектору $overline{OP}=x_{0} cdot overline{i}+y_{0} cdot overline{j}+z_{0} cdot overline{k}$.
Поскольку вектор $overline{OP}$ перпендикулярен плоскости, которая проходит через точку $P$, то, очевидно, что указанные точка и вектор эту плоскость определяют однозначно.
Чтобы найти уравнение плоскости, выберем на ней произвольную точку $Mleft(x,y,zright)$ и найдем связь ее координат с координатами точки $P$. Рассмотрим вектор $overline{PM}=left(x-x_{0} right)cdot overline{i}+left(y-y_{0} right)cdot overline{j}+left(z-z_{0} right)cdot overline{k}$. Независимо от положения точки $M$ на плоскости, векторы $overline{OP}$ и $overline{PM}$ взаимно перпендикулярны.
Отсюда следует, что скалярное произведение этих векторов равняется нулю $overline{OP}cdot overline{PM}=0$. Подставим в это уравнение координаты векторов:
[overline{OP}cdot overline{PM}=left(x_{0} cdot overline{i}+y_{0} cdot overline{j}+z_{0} cdot overline{k}right)cdot left(left(x-x_{0} right)cdot overline{i}+left(y-y_{0} right)cdot overline{j}+left(z-z_{0} right)cdot overline{k}right)=]
[=x_{0} cdot left(x-x_{0} right)+y_{0} cdot left(y-y_{0} right)+z_{0} cdot left(z-z_{0} right)=x_{0} cdot x+y_{0} cdot y+z_{0} cdot z-x_{0}^{2} -y_{0}^{2} -z_{0}^{2} =0.]
Отсюда получаем общее уравнение искомой плоскости $Acdot x+Bcdot y+Ccdot z+D=0$, где $A=x_{0} $, $B=y_{0} $, $C=z_{0} $, $D=-x_{0}^{2} -y_{0}^{2} -z_{0}^{2} $.
Задача 2
Найти уравнение плоскости, перпендикулярной оси $Ox$ и проходящей через точку $Mleft(3;; 1;; 2right)$.
Плоскость, которая перпендикулярна оси $Ox$, параллельна координатной плоскости $yOz$. Следовательно, уравнение этой плоскости имеет вид $Acdot x+Bcdot y+Ccdot z+D=0$, в котором $B=0$ и $C=0$, то есть $Acdot x+D=0$.
Уравнению этой плоскости должны удовлетворять координаты точки $Mleft(3;; 1;; 2right)$. Получаем: $Acdot 3+D=0$, то есть $D=-Acdot 3$.
Уравнение искомой плоскости $Acdot x+D=0$ приобретает вид $Acdot x-Acdot 3=0$, то есть $Acdot left(x-3right)=0$.
Таким образом, уравнение искомой плоскости $x-3=0$.
Задача 3
Через две заданные точки $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$ и $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$ провести плоскость перпендикулярно к данной плоскости $acdot x+bcdot y+ccdot z+d=0$.
Известно, что некоторая плоскость $Acdot x+Bcdot y+Ccdot z+D=0$, которая проходит через две заданные точки, удовлетворяет двум уравнениям $Acdot left(x-x_{1} right)+Bcdot left(y-y_{1} right)+Ccdot left(z-z_{1} right)=0$ и $Acdot left(x_{2} -x_{1} right)+Bcdot left(y_{2} -y_{1} right)+Ccdot left(z_{2} -z_{1} right)=0$. Условие перпендикулярности обеих плоскостей имеет вид: $acdot A+bcdot B+ccdot C=0$. Полученная однородная система трех уравнений с тремя неизвестными $A$, $B$ и $C$ имеет ненулевое решение только тогда, когда определитель основной матрицы системы равняется нулю: $left|begin{array}{ccc} {x-x_{1} } & {y-y_{1} } & {z-z_{1} } \ {x_{2} -x_{1} } & {y_{2} -y_{1} } & {z_{2} -z_{1} } \ {a} & {b} & {c} end{array}right|=0$. Данное уравнение является уравнением нужной плоскости.
Задача 4
Найти проекцию заданной точки $M_{0} left(x_{0} ,y_{0} ,z_{0} right)$ на заданную плоскость $Acdot x+Bcdot y+Ccdot z+D=0$.
Пусть точка $M_{0} $ проецируется на плоскость в точку $Pleft(x,y,zright)$. Построим вектор $overline{M_{0} P}=left(x-x_{0} right)cdot overline{i}+left(y-y_{0} right)cdot overline{j}+left(z-z_{0} right)cdot overline{k}$. Этот вектор коллинеарен нормальному вектору плоскости $overline{N}=Acdot overline{i}+Bcdot overline{j}+Ccdot overline{k}$. Применяем условие коллинеарности векторов: $frac{x-x_{0} }{A} =frac{y-y_{0} }{B} =frac{z-z_{0} }{C} $. Эти два уравнения вместе с уравнением плоскости $Acdot x+Bcdot y+Ccdot z+D=0$ образуют систему трех уравнений с тремя неизвестными $x$, $y$ и $z$. Решив ее, найдем координаты точки $P$.
Задача 5
Через точки $Cleft(2;6;-1,75right)$ и $Dleft(2;-3;6right)$ провести плоскость перпендикулярно плоскости, общее уравнение которой $21cdot x+28cdot y+24cdot z-168=0$.
Уравнение нужной плоскости имеет вид $left|begin{array}{ccc} {x-x_{1} } & {y-y_{1} } & {z-z_{1} } \ {x_{2} -x_{1} } & {y_{2} -y_{1} } & {z_{2} -z_{1} } \ {a} & {b} & {c} end{array}right|=0$.
Этот определитель вычисляем посредством разворачивания по элементам первой строки:
[left|begin{array}{ccc} {x-2} & {y-6} & {z-left(-1,75right)} \ {2-2} & {left(-3right)-6} & {6-left(-1,75right)} \ {21} & {28} & {24} end{array}right|=left|begin{array}{ccc} {x-2} & {y-6} & {z+1,75} \ {0} & {-9} & {7,75} \ {21} & {28} & {24} end{array}right|=]
[=-433cdot x+162,75cdot y+189cdot z+220,25=0.]
Итак, уравнение перпендикулярной плоскости:
[-433cdot x+162,75cdot y+189cdot z+220,25=0.]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
