Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой
Критерий среднего выигрыша
Формула критерия среднего выигрыша
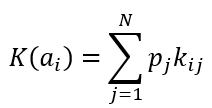
Формула оптимального решения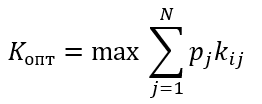
Пример

Пусть даны вероятности, p1=0.2 p2=0.1 p3=0.3 p4=0.2, тогда получаем
K(a1)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a2)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a3)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a4)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
Kопт=max{0.27; 0.48; 0.43; 0.51}=0.51
В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.
Критерий Вальда или пессимизма
Формула критерия Вальда или максимина
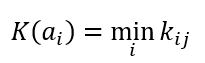
Формула оптимального решения по критерию Лапласа
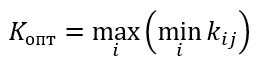
Пример

K(a1)=min(0.4;0.5;0.3;0.4)=0.3
K(a2)=min(0.3;0.2;0.3;0.5)=0.2
K(a3)=min(0.6;0.3;0.3;0.2)=0.2
K(a4)=min(0.4;0.5;0.2;0.3)=0.2
Kопт=max{0.3; 0.2; 0.2; 0.2}=0.3
По критерию Вальда оптимальным решением является выбор первой программы.
Критерий максимакса или оптимизма
Формула критерия максимакса
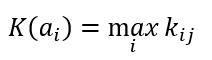
Формула оптимального решения по критерию максимакса
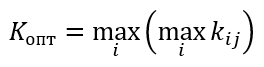
Пример

K(a1)=max(0.4;0.5;0.3;0.4)=0.5
K(a2)= max (0.3;0.2;0.3;0.5)=0.5
K(a3)= max (0.6;0.3;0.3;0.2)=0.6
K(a4)= max (0.4;0.5;0.2;0.3)=0.5
Kопт=max{0.5; 0.5; 0.6; 0.5}=0.6
По критерию максимакса оптимальным решением является выбор третьей программы.
Критерий Лапласа
Формула критерия Лапласа
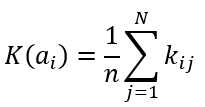
Формула оптимального решения по критерию Лапласа

Пример

Решение
K(a1)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a2)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a3)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a4)=0.25*(0.4+0.5+0.2+0.3)=0.35
Kопт=max{0.4; 0.325; 0.35; 0.35}=0.4
По критерию Лапласа оптимальным решением является выбор первой программы.
Критерий Гурвица
Пример

Формула критерия Гурвица
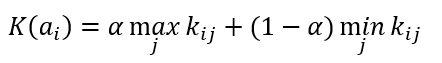
Формула оптимального решения по Гурвица критерию

Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.
Пусть α=0.7
K(a1)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a2)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a3)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a4)= 0.7* 0.5+(1-0.7)*0.2=0.41
Kопт=max{0.44; 0.41; 0.48; 0.41}=0.48
По критерию Гурвица оптимальным решением является выбор третьей программы.
Критерий Сэвиджа или минимакса (критерий потерь)
Формула критерия Сэвиджа для построения матрицы потерь

Формула для выбора максимального значения из матрицы потерь

Формула оптимального решения по критерию Сэвиджа
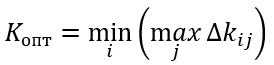
Для примера

Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида

K(a1)= max{0.2; 0; 0; 0.1}=0.2
K(a2)= max{0.3; 0.3; 0; 0}=0.3
K(a3)= max{0; 0.2; 0; 0.3}=0.3
K(a4)= max{0.2; 0; 0.1; 0.2}=0.2
Kопт=min{0.2; 0.3; 0.3; 0.2}=0.2
По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.
Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.
Сочетание стратегий
Аi
и Пj
является случайным и дает результат –
выигрыш (ущерб) – аi,j:
аi,j
0 – положительный – прибыль
аi,j
0 – отрицательный – убыток
аi,j
= 0 – нулевой
Природа ущерба и
прибыли в каждом конкретном случае
может быть различной, а сам ущерб и
прибыль должны быть строго обоснованы,
т.к. от них зависит выбор оптимального
решения. В примере: удовлетворение
потребности в агрегатах связано с
сокращением простоев автомобиля в
ремонте, что приносит прибыль АТП.
Излишний запас вызывает дополнительные
затраты на хранения: убыток. Отсутствие
агрегата: убыток. Прибыль и ущерб
оцениваются в стоимостном выражении
(у.е.) или в баллах.
Таблица 2.
Условия определения выигрыша
|
Ситуации |
Выигрыш в у.е. |
||
|
Убыток |
Прибыль |
||
|
1. |
Хранение на |
а = -1 |
– |
|
2. |
Удовлетворение |
– |
а = +2 |
|
3. |
Отсутствие |
а = -3 |
– |
*Примечание
-
Варианты
выигрышейСитуации
1
2
3
1
2
3
4
5
-1
-2
-3
-4
-2
-1
+2
+3
+4
+5
+4
+3
-3
-4
-5
-6
-6
-5
4. Формирование платежной матрицы.
Платежная матрица
составляется по условиям рассматриваемого
примера запаса агрегатов и их потребности
и принятой системы определения выигрыша
(а примере принимаем 1ый
вариант условий определения выигрышей
(см. табл. 2.)).
Таблица 3.
Платежная матрица выигрышей для сочетания всех возможных стратегий.
|
Стратегия Аi |
Число агрегатов |
Необходимое |
Минимальный |
||||
|
П1 |
П2 |
П3 |
П4 |
П5 |
|||
|
0 |
1 |
2 |
3 |
4 |
|||
|
А1 |
0 |
0 |
-3 |
-6 |
-9 |
-12 |
-12 |
|
А2 |
1 |
-1 |
2 |
-1 |
-4 |
-7 |
-7 |
|
А3 |
2 |
-2 |
1 |
4 |
1 |
-2 |
-2 |
|
А4 |
3 |
-3 |
0 |
3 |
6 |
3 |
-3 |
|
А5 |
4 |
-4 |
-1 |
2 |
5 |
8 |
-4 |
|
Максимальный |
0 |
2 |
4 |
6 |
8 |
– |
Пример расчета:
1) Сочетание
стратегий А2
и П4
(при потребности три агрегата на складе
имеется один агрегат); выигрыш составит:
а24
= 1
2 (одно требование удовлетворительно)
– 2
3 (две заявки не удовлетворительны) = 2 –
6 = -4.
2) Сочетание
стратегий А4
и П2
(при потребности одного агрегата на
складе имеются три агрегата); выигрыш
составит: а42
= 1
2 (одно требование удовлетворительно)
– 2
1 (два агрегата не востребованы) = 2 – 2 =
0 и т.д.
5. Выбор стратегии
организаторов складского хозяйства.
При известных
вероятностях каждого состояния Пj
выбирается стратегия Аi,
при которой математическое ожидание
выигрыша будет максимальным. Для этого
вычисляют средний выигрыш по каждой
строке для i-й
стратегии по формуле:
![]()
(1)
Например, для
стратегии А1
(по 1му
варианту вероятностей замены данного
количества агрегатов (см. табл. 1.)):
![]()
Результаты расчетов
сводятся в матрицу выигрышей.
Таблица 4.
Матрица выигрышей
|
Пj(ni) Аi |
П1 (n1 |
П2 (n2 |
П3 (n3 |
П4 (n4 |
П5 (n5 |
Средний выигрыш |
|
А1 |
0 |
-1,2 |
-1,8 |
-0,9 |
-1,2 |
-5,1 |
|
А2 |
-0,1 |
0,8 |
-0,3 |
-0,4 |
-0,7 |
-0,7 |
|
А3 |
-0,2 |
0,4 |
1,2 |
0,1 |
-0,2 |
1,3 |
|
А4 |
-0,3 |
0 |
0,9 |
0,6 |
0,3 |
1,5 – а4 |
|
А5 |
-0,4 |
-0,4 |
0,6 |
0,5 |
0,8 |
1,1 |
|
Вероятности |
-0,1 |
0,4 |
0,3 |
0,1 |
0,1 |
– |
Вывод: оптимальной
стратегией организаторов складского
хозяйства в примере является стратегия
А4,
предусматривающая хранение на складе
3 (три) агрегата.
6. Сравнение
оптимальной стратегии со средневзвешенной
потребностью в агрегатах.
Расчет на основе
вероятностей без учета экономических
последствий дает средневзвешенное
количество расходуемых за смену
агрегатов:
![]()
(2)
![]()
Средняя потребность
в агрегатах: nр
= 1,7 (2) агрегатов. Оптимальный запас
агрегатов n0
= 3 агрегата.
7. Определение
экономического эффекта от использования
оптимальной стратегии:
![]()
(3)
где – выигрыш при
оптимальной стратегии (иметь на складе
3 агрегата);
– то же при
средневзвешенной стратегии (иметь на
складе 2 агрегата) (табл. 2.4.)
![]()
В отчете необходимо
заполнить таблицы 1 и 2 в соответствии
выданным вариантам вероятностей и
выигрышей, заполнить таблицы 3 и 4 и
расчеты по пунктам 6 и 7.
Литература:
-
Кузнецов Е.С.
Управление технической эксплуатацией
автомобилей. М.: Транспорт, 1990. – 272 с.
Министерство
образования и науки РФ
Тольяттинский
государственный университет
Кафедра: «Техническая
эксплуатация автомобилей и восстановление
деталей»
Управление
техническими системами
Контрольная работа
«Принятие управляющих
решений в условиях риска»
Вариант:
|
Выполнил студент |
|||
|
Номер зачетной |
|||
|
подпись |
Ф.И.О. |
Принял преподаватель
|
Петин Ю.П. |
|||
|
подпись |
Тольятти 2006
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математические формулы в лотерее являются частью теории вероятностей и комбинаторной математики.
Что же мы подразумеваем под этим интуитивным понятием вероятности? С точки зрения математики возможны две различные интерпретации этого сугубо абстрактного понятия. В первой из них понятие вероятности ассоциируется с частотой появления данного события в серии опытов, в каждом из которых анализируемое событие может появиться или не появиться. Такое событие математики называют случайным.
Как вычислить вероятность?
Существует так называемый закон больших чисел, справедливость которого доказывается в теории вероятностей. Согласно этому закону, в любой серии опытов при увеличении их числа, частота появления случайного события всегда стабильно стремится к одной и той же величине и это предельное значение можно принять за вероятность Р(А) (probability — на английском языке):
![]()
Таким образом, согласно этому утверждению, чтобы найти вероятность события, нужно провести достаточно длинную серию опытов и полученную частоту выразить в процентах.
А нельзя ли определить вероятность выигрыша априори, то есть до начала опытов? Оказывается, что в ряде случаев это возможно. Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем:
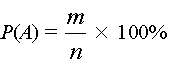
то — есть вероятность появления события А равна отношению числа m — благоприятных событий для А к полному числу n — возможных элементарных событий, выраженному в процентах.
Рассмотрим теперь задачу, более близкую к нашим интересам. А эти интересы в данном случае связаны с подсчетом вероятностей угадывания цифр в розыгрышах Лото 6/49. По правилам этой игры, требуется угадать шесть отобранных (счастливых) номеров из общего количества имеющихся в наличии сорока девяти. Для наглядности заштрихуем «счастливые номера», как это показано на рисунке.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
Какова вероятность того, что перевернутый номер окажется заштрихованным? Очевидно, она и в этом случае равна отношению числа благоприятных для нас исходов (заштрихованных номеров, а их число равно 6) к полному числу всех возможных исходов (то есть полному числу номеров, число которых 49). Таким образом, вероятность угадать одну из шести отобранных номеров равна 6/49, а вероятность не угадать, соответственно — 43/49.
Если сложить теперь вероятности этих двух возможных исходов, то, как и следовало ожидать, сумма всех вероятностей окажется равной 1. Конечно, хоть что-нибудь, но должно же случиться с достоверностью (то есть с вероятностью 100%). Как говорят, уж если не выиграю, то проиграю.
При второй попытки полное число оставшихся номеров, уже становится равным 48 (один номер уже был разыгран в первом туре). Таким образом, для всех возможных вариантов исхода получаем:
- Если в первом туре был угадан заштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 5/48, а вероятность выпадения незаштрихованного номера составит 43/48. - Если в первом туре был угадан незаштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 6/48, а вероятность выпадения незаштрихованного номера составит 42/48.
Таким образом, при двух подходах жеребьевки возможны четыре варианта результата (первый подход + второй подход):
1) угадал + не угадал: p = 6/49 x 43/48 = 0,1097
2) не угадал + угадал: p = 43/49 x 6/48 = 0,1097
3) угадал + угадал: p = 6/49 x 5/48 = 0,0128
4) не угадал + не угадал: p = 43/49 x 42/48 = 0,7679
Нетрудно убедиться, что и в этом случае сумма вероятностей равна 1.
Как вычислить количество всех возможных результатов?
Легко заметить, что по мере увеличения количества подходов общее количество возможных вариантов результата увеличивается очень быстро, а именно: общее количество возможных вариантов результата для n подходов розыгрышей равно 2n (2 в степени n).
Например, при трех подходах у нас уже будет 23 = 8 возможных вариантов результата:
1) угадал + угадал + угадал: вероятность = 0,0011
2) угадал + угадал + не угадал: вероятность = 0,0117
3) угадал + не угадал + угадал: вероятность = 0,0117
4) не угадал + угадал + угадал: вероятность = 0,0117
5) угадал + не угадал + не угадал: вероятность = 0,0980
6) не угадал + угадал + не угадал: вероятность = 0,0980
7) не угадал + не угадал + угадал: вероятность = 0,0980
8) не угадал + не угадал + не угадал: вероятность = 0,6698
Как вычислить количество комбинаций?
Зная общее количество возможных вариантов, давайте теперь выясним, сколько из этих вариантов содержат угаданные числа. Количество этих вариантов на самом деле является количеством всех возможных комбинаций угаданных заштрихованных чисел.
Предположим, что мы отметили шесть произвольных чисел и хотим узнать, сколько существует вариантов, в которых будет угадано 4 цифры из 6. Число способов, которыми можно угадать 4 из этих 6 номеров, математики называют числом сочетаний и обозначают его ![]() . Эта запись читается так: «число сочетаний из шести по четыре».
. Эта запись читается так: «число сочетаний из шести по четыре».
Предположим, что угаданы числа 12, 14, 30 и 36. Сколько вариантов существует для такого угадывания? Число 12 может быть угадано в любой из 6 попыток, то-есть может быть названо 1-м, 2-м, 3-м, 4-м, 5-м или 6-м. Следовательно, для угадывания числа 12 существует 6 различных вариантов. Второе число 14 может быть угадано в любой из оставшихся пяти попытках, следовательно, для его угадывания имеется 5 различных вариантов. Продолжая эти рассуждения, легко прийти к выводу, что для угадывания числа 30 существует 4 различных варианта, а числа 36 — 3 варианта. Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.
Но не все эти варианты различны. Предположим, что эти числа были угаданы в первых же четырех попытках. Тогда все эти варианты, соответствующие различной последовательности заполнения «счастливых» номеров в тех же самых попытках (всего 24 варианта), фактически представляют 1 вариант (число перестановок 4 элементов равно 4х3х2х1=24).

Окончательно для искомого числа сочетаний мы получили формулу:
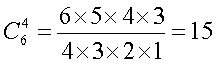
Эта формула для числа сочетаний является справедливой и при любых других количествах отмеченных чисел и количествах «угаданных». В общем случае можно сформулировать следующее правило: для того, чтобы определить количество возможных вариантов с m угаданными числами для отмеченных n чисел, необходимо вычислить число сочетаний:
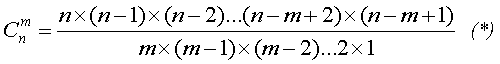
В этой формуле число сомножителей в числителе и знаменателе одинаково и равно m.
Также по этой формуле рассчитывается общее количество возможных комбинаций для игр в лотереи. А для Лото 6 из 49 получаем:
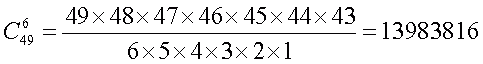
На основе формулы (*) заполняется таблица с количеством выигрышей для каждой категории выигрышей, в зависимости от того, сколько чисел было отмечено и сколько чисел было угадано. См. В качестве примера таблицу для Лото 6/49.
Средний выигрыш одной комбинации
Теперь перейдем к оценке выигрышей, которые рассчитываются на основе среднего выигрыша одного игрового варианта, разыгранного для каждой призовой категории. Средний выигрыш представляет собой вероятность возникновения этого выигрыша, умноженную на общую сумму денег, предложенную для данной призовой категории.
Согласно математическим расчетам, средние значения выигрыша для каждого рубля, потраченного в простой игровой системе и в развернутой игровой системе, одинаковы, независимо от того, сколько чисел было отмечено. Но все же различие между этими двумя игровыми системами существует.
Если мы возьмем статистическую характеристику для большого количества участников игры, то заметим, что при увеличении количества отмеченных чисел в билете в целом, выигрыши становятся крупнее, но вероятность более мелких выигрышей при этом резко уменьшается. Отсюда можно сделать вывод, что если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее будет развернутая система игры, но если не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то лучше подойдет простая система игры.
Вероятность последовательных неудач
Какова вероятность длинной серии неудач, если ставить в каждом туре на одну и ту же комбинацию? Существует формула, которая называется формулой Бернулли. Она позволяет найти вероятность того, что в результате участия в n турах игры количество туров без единого выигрыша будет равно m:
![]()
где q определяет вероятность «несчастного» случая только для одного тура т.е. не были угаданы 6, 5 и 4 номеров и определяется формулой:
![]()
где ![]() ,
, ![]() и
и ![]() вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.
вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.
Для примера, на основе формулы Бернулли и некоторых исходных статистических данных были получены следующие результаты вероятностей неудач для 4 розыгрышей:
1) Не было ни одного выигрыша: m = 4, P = 0,02 (2%)
2) Был один выигрыш: m = 3, P = 0,13 (13%)
3) Было два выигрыша: m = 2, P = 0,33 (33%)
4) Было три выигрыша: m = 1, P = 0,37 (37%)
5) Все туры были выигрышными: m = 0, P = 0,15 (15%)
2% + 13% + 33% + 37% + 15% = 100%
Как видим, вероятность последовательных проигрышей с одной и той же комбинацией чисел уменьшается с увеличением количества участий, но появление выигрыша не гарантирует того, что он будет большим.
И все-таки, несмотря на то, что непредсказуемость результатов азартной игры является ее основной чертой, нельзя ли избрать какую-то оптимальную стратегию? Единственный совет, который можно дать в этом случае — это рационально выбрать определенную систему игры и последовательно придерживаться её.
Любую хозяйственную деятельность
человека можно рассматривать как игру с природой. В широком смысле под природой
будем понимать совокупность неопределенных факторов, влияющих на эффективность
принимаемых решений.
Управление любым объектом
осуществляется путем принятия последовательности управленческих решений. Для принятия решения
необходима информация (совокупность сведений о состоянии объекта управления и
условиях его работы). В тех случаях когда отсутствует
достаточно полная информация, возникает неопределенность в принятии решения. Причины этого могут быть
различны: требующаяся для полного обоснования решения информация принципиально
не может быть получена (неустранимая неопределенность); информация не может быть
получена своевременно, к моменту принятия решения; затраты, связанные с
получением информации, слишком высоки. По мере совершенствования средств сбора, передачи и обработки информации неопределенность
управленческих решении будет уменьшаться. К этому нужно стремиться.
Существование неустранимой неопределенности связано со случайным характером
многих явлений. Например, в торговле, случайный характер изменения спроса
делает невозможным его точное прогнозирование, a, следовательно, и формирование
идеально точного заказа на поставку товара. Принятие решения в этом случае
связано с риском. Приемка партии товара на основании выборочного контроля также
связана с риском принятия решения в условиях неопределенности. Неопределенность
может быть снята путем полного контроля всей партии, однако это может оказаться
слишком дорогостоящим мероприятием. В сельском хозяйстве, например, с целью
получения урожая человек предпринимает ряд действии (пашет землю, вносит
удобрения, борется с сорняками и т. п.). Окончательный результат (урожай)
зависит от действий не только человека, но и природы (дождь, засуха, вечер и т.
п.). Из приведенных примеров видно, что
полностью исключить неопределенность в управлении экономической системой
нельзя, хотя, повторим, к этому нужно стремиться. В каждом конкретном случае
следует принимать во внимание степень риска при принятии управленческих
решений, по возможности максимально учитывать имеющуюся информацию с целью
уменьшения неблагоприятных последствий, которые могут возникнуть из-за
ошибочных решений.
Две стороны, участвующие в игре,
будем называть игрок I и игрок II. Каждый из игроков располагает конечным
набором действий (чистых стратегий), которые он может применять в процессе
игры. Игра имеет повторяющийся,
циклический характер. о
каждом цикле игроки выбирают одну из своих стратегии, что однозначно определяет
платеж
. Интересы игроков
противоположны. Игрок I старается вести игру так, чтобы платежи были как можно
большими. Для игрока II желательны как можно меньшие значения платежей (с
учетом знака). Причем в каждом цикле выигрыш одного из игроков в точности
совпадает с проигрышем другого. Игры такого типа называются играми с нулевой
суммой.
Решить игру – значит определить
оптимальное поведение игроков. Решение игр является предметом теории игр.
Оптимальное поведение игрока инвариантно относительно изменения всех элементов
платежной матрицы на некоторую величину.
В общем случае определение оптимального
поведения игроков связано с решением двойственной пары задач линейного
программирования. В отдельных случаях могут быть использованы более простые
методы. Часто платежную матрицу удается упростить путем удаления из нее строк и
столбцов, соответствующих доминируемым стратегиям
игроков, доминируемой называется стратегия, все
платежи которой не лучше соответствующих платежей некоторой другой стратегии и
хотя бы один из платежей хуже соответствующего платежа этой другой стратегии,
называемой доминирующей.
В обычной стратегической игре
принимают участие «разумные и антагонистические» противники (противоборствующие
стороны). В таких играх каждая из сторон предпринимает именно те действия,
которые наиболее выгодны ей и менее выгодны противнику. Однако очень часто неопределенность, сопровождающая
некоторую операцию, не связана с сознательным противодействием противника, а
зависит от некой, не известной игроку I объективной действительности (природы).
Такого рода ситуации принято называть играми с природой. Игрок II – природа – в
теории статистических игр не является разумным игроком, так как рассматривается
как некая незаинтересованная инстанция, которая не выбирает для себя
оптимальных стратегий. Возможные состояния природы (ее стратегии) реализуются
случайным образом. В исследовании операций оперирующую сторону (игрока I) часто
называют статистиком, а сами операции – играми статистика с природой или
статистическими играми.
Рассмотрим игровую постановку
задачи принятия решения в условиях неопределенности. Пусть оперирующей стороне
необходимо выполнить операцию в недостаточно известной обстановке относительно
состояний которой можно сделать
предположений. Эти предположения
будем рассматривать как стратегии природы.
Оперирующая сторона в своем распоряжении имеет
возможных стратегий –
. Выигрыши игрока I
при каждой паре стратегий
и
– предполагаются известными и заданы платежной
матрицей
.
Задача заключается в определении
такой стратегии (чистой или смешанной), которая лри
ее применении обеспечила бы оперирующей стороне наибольший выигрыш.
Выше уже говорилось, что
хозяйственная деятельность человека может рассматриваться как игра с природой.
Основной особенностью природы как игрока является ее не заинтересованность в
выигрыше.
Анализ матрицы выигрышей игры с
природой начинается с выявления и отбрасывания
дублирующих и заведомо невыгодных стратегий лица, играющего с природой. Что
касается стратегий природы, то ни одну из них отбросить нельзя, так как каждое
из состояний природы может наступить случайным образом, независимо от действий
игрока I. Ввиду того что природа не противодействует
игроку I, может показаться, что игра с природой проще стратегической игры. На
самом деле это не так. Противоположность интересов игроков в стратегической
игре в некотором смысле как бы снимает неопределенность, чего нельзя сказать о
статистической игре. Оперирующей стороне в игре с природой легче в том
отношении, что она скорее .всего выиграет больше, чем
в игре против сознательного противника. Однако ей труднее принять обоснованное
решение, так как в игре с природой неопределенность ситуации сказывается в
гораздо более сильной степени.
После упрощения платежной матрицы
игры с природой целесообразно не только оценить выигрыш при той или иной
игровой ситуации, но и определить разность между максимально возможным
выигрышем при данном состоянии природы и выигрышем, который будет получен при
применении стратегии
в тех же условиях. Эта разность в теории игр
называется риском.
Природа меняет состояние
стихийно, совершенно не заботясь о результате игры. В антагонистической игре мы
предполагали, что игроки пользуются оптимальными (в определенном выше смысле)
смешанными стратегиями. Можно предположить, что природа применяет наверняка не
оптимальную стратегию. Тогда какую? Если бы существовал ответ на этот вопрос,
то принятие решения лицом, принимающим решения (ЛПР) сводилось бы к
детерминированной задаче.
Если вероятности
состояний
природы известны, то пользуются критерием
Байеса, в соответствии с которым оптимальной считается чистая стратегия
, при которой максимизируется
средний выигрыш:
Критерий Байеса предполагает, что
нам хотя и неизвестны условиях выполнения операций (состояния природы)
, но известны их вероятности
.
С помощью такого приема задача о
выборе решения в условиях неопределенности превращается в задачу о выборе
решения в условиях определенности, только принятое решение является оптимальным
не в каждом отдельном случае, а в среднем.
Если игроку
представляются в равной мере правдоподобными
все состояния
природы, то иногда полагают
и, учитывая, «принцип недостаточного
основания» Лапласа, оптимальной считают чистую стратегию
, обеспечивающую:
Если же смешанная стратегия
природы неизвестна, то в зависимости от гипотезы о поведении природы можно
предложить ряд подходов для обоснования выбора решения ЛПР. Свою оценку
характера поведения природы будем характеризовать числом
, которое можно связывать со
степенью активного «противодействия» природы как игрока Значение
соответствует наиболее пессимистичному
отношению ЛПР в смысле «содействия» природы в достижении им наилучших
хозяйственных результатов. Значение
соответствует наибольшему оптимизму ЛПР. Как
известно, в хозяйственной деятельности указанные крайности опасны. Скорее
всего, целесообразно исходить из некоторого промежуточного значения
. В этом случае используется
критерий Гурвица, согласно которому наилучшим решением ЛПР является чистая
стратегия
, соответствующая условию:
Критерий Гурвица (критерий
«оптимизма-пессимизма») позволяет руководствоваться при выборе рискового
решения в условиях неопределенности некоторым средним результатом
эффективности, находящимся в поле между значениями по критериям «максимакса» и «максимина» (поле между этими значениями
связано посредством выпуклой линейной функции).
В случае крайнего пессимизма ЛПР
указанный критерий называется критерием
Вальда. Согласно этому критерию, наилучшей считается максиминная
стратегия. Это критерий крайнего
пессимизма. По этому критерию ЛПР выбирает ту стратегию, которая гарантирует в
наихудших условиях максимальный выигрыш:
Такой выбор соответствует
наиболее робкому поведению ЛПР, когда он предполагает наиболее, неблагоприятное
поведение природы, боится больших потерь. Можно предположить, что он не получит
больших выигрышей. Согласно критерию Сэвиджа, следует
выбирать чистую стратегию
соответствующую условию:
где риск
.
Критерий Сэвиджа
(критерий потерь от «минимакса») предполагает, что из всех возможных вариантов
«матрицы решений» выбирается та альтернатива, которая минимизирует размеры
максимальных потерь по каждому из возможных решений. При использовании этого
критерия «матрица решения» преобразуется в «матрицу риска», в которой вместо
значений эффективности проставляются размеры потерь при различных вариантах
развития событий.
Недостатком критериев Вальда, Сэвиджа и Гурвица
является субъективная оценка поведения природы. Хотя указанные критерии и дают
некоторую логическую схему принятия решений, резонно все же задать вопрос: «А
почему сразу не выбрать субъективное решение, вместо того чтобы иметь дело с
разными критериями?» Несомненно, определение решения по различным критериям помогает
ЛПР оценить принимаемое решение с различных позиций и избежать грубых ошибок в
хозяйственной деятельности.
Задача
После
нескольких лет эксплуатации оборудование может оказаться в одном из трех
состояний:
-
требуется профилактический ремонт;
требуется замена отдельных деталей и узлов;
требуется капитальный ремонт.
В
зависимости от ситуации руководство предприятия может принять следующие
решения:
-
отремонтировать оборудование своими силами, что потребует затрат
;
вызвать специальную бригаду ремонтников, расходы в этом случае составят
;
заменить оборудование новым, реализовав устаревшее по остаточной стоимости.
Совокупные затраты на этот мероприятие составят
.
Требуется
найти оптимальное решение данной проблемы по критерию минимизации затрат с
учетом следующих предположений:
|
|
|
|
|
| a | 4 | 6 | 9 |
| b | 5 | 3 | 7 |
| c | 20 | 15 | 6 |
| q | 0.4 | 0.45 | 0.15 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Игра парная, статистическая. В игре участвуют
2 игрока: руководство предприятия и природа.
Под природой в данном случае понимаем
совокупность внешних факторов, которые определяют состояние оборудования.
Стратегия руководства:
–
отремонтировать оборудование своими силами
–
вызвать бригаду специалистов
–
заменить оборудование новым
Стратегия природы – 3 возможных состояния
оборудования.
– требуется профилактический ремонт;
– следует заменить отдельные детали и узлы;
– требуется капитальный ремонт.
Расчет платежной матрицы и матрицы рисков
Поскольку элементы матрицы – затраты,
то будем считать их выигрышными но со знаком минус. Платежная матрица:
|
|
|
|
|
|
|
|
-4 | -6 | -9 | -9 |
|
|
-5 | -3 | -7 | -7 |
|
|
-20 | -15 | -6 | -20 |
|
|
0.4 | 0.45 | 0.15 |
Составляем матрицу рисков:
|
|
|
|
|
|
|
|
(-4)-(-4)=0 | (-3)-(-6)=3 | (-6)-(-9)=3 | 3 |
|
|
(-4)-(-5)=1 | (-3)-(-3)=0 | (-6)-(-7)=1 | 1 |
|
|
(-4)-(-20)=16 | (-3)-(-15)=12 | (-6)-(-6)=0 | 16 |
Критерий Байеса
Определяем средние выигрыши:
По критерию Байеса оптимальной является стратегия
–
вызвать бригаду специалистов
Критерий Лапласа
Примем
Определим средние выигрыши:
По критерию Лапласа оптимальной является стратегия
– вызвать бригаду специалистов
Критерий Вальда
По критерию Вальда оптимальной является стратегия
– вызвать бригаду специалистов
Критерий Сэвиджа
По критерию Сэвиджа оптимальной
является стратегия
-вызвать
бригаду специалистов.
Критерий Гурвица
:
По критерию Гурвица оптимальной является стратегия
–
вызвать бригаду специалистов
Ответ: По всем критериям
оптимальной является стратегия «Вызвать бригаду специалистов».
Добрый день.
Уже три недели прошло с выхода заметки «От Колмогорова к Максвеллу, Лапласу, Байесу», уже более сотни интереснейших комментариев написано, множество копий сломано, несколько заблуждений сформулировано и разобрано. Иногда, к сожалению, собеседники переходили на личности, называли высказывания друг друга чушью, не убедившись, что правильно поняли друг друга. Но не зря борьбу за правду называют борьбой.
Комментарии к той записи сами по себе очень интересны (и продолжение темы, начатой в заметке, конечно, скоро будет опубликовано), но сегодня я предлагаю начать обсуждать интересную задачу из тех комментариев, в которой неожиданным образом показывает себя понятие «средний выигрыш». Ну а для тех, кто не очень любит теорию вероятностей, есть специально заготовленная коллекция «пирожков» (спасибо всем, кто вспомнил свои любимые «пирожки» в комментариях!).
Итак, задача:
Представьте, что вы изобрели такую стратегию игры на фондовой бирже, что она позволяет с вероятностью 90% удваивать торговый капитал, а с вероятностью 10% полностью его терять. Ясно, что с такой стратегией нельзя подставлять под риск весь свой капитал — какой-то процент надо держать в запасе, чтобы всегда можно было возобновить игру, когда «черный лебедь» слизнет весь торговый капитал. Вопрос: какую долю капитала было бы оптимально использовать для игры, а какую всегда сохранять?
Тонкость этой задачи в том, что надо сначала определить, что такое «оптимально» (вспомните задачу Бертрана, в которой понятное и простое условие можно было понимать самыми разными способами). Многие считают, что в этой задаче достаточно посчитать математическое ожидание выигрыша, чтобы определить, на какую сумму играть.
Давайте проделаем это. Пусть x (число от 0 до 1) — доля капитала, которую мы всегда сохраняем. Каким будет средний выигрыш M1(x) за одну игру?
M1(x) = 0.9 * (x + 2 * (1 – x)) + 0.1 * x
(т.е. с вероятностью 90% мы удвоим капитал (1-x), сохранив сумму x, а с вероятностью 10% у нас останется только x).
Давайте найдём x, чтобы функция M1(x) приняла максимальное значение. M1(x) = 1.8 – 0.8 * x. Получается, что чем меньше x, тем выше средний выигрыш. Пожалуй, тут не поспоришь, при одной игре с такими выгодными условиями неразумно оставлять себе хоть что-то, а стоит играть на все.
А что будет при серии из двух игр? Давайте вычислим M2(x).
M2(x) = 0.9^2 * (x + 2 * (1 – x))^2 + 0.1^2 * x^2 + (1 – 0.9^2 – 0.1^2) * (x + 2 * (1-x)) * x
(т.е. с вероятностью 81% [0.9 в квадрате] нам повезёт удвоить капитал дважды, сохраняя на каждом этапе долю x от него, с вероятностью 1% мы дважды проиграем [и сохраним тогда всего x^2 денег], а в остальных случаях мы один раз удвоим капитал (1-x), сохранив x, а один раз «умножим его на x», причём, неважно, в каком порядке).
Найдём x, при котором M2(x) имеет максимальное значение:
M2(x) = 0.64 * x^2 – 2.88 * x + 3.24.
Легко видеть, что эта функция задаёт параболу, ветви которой идут вверх, а наименьшее значение принимается при x > 1. Другими словами, максимальное значение на интервале [0, 1] функция M2(x) принимает в при x=0. Получается, и в серии из двух игр выгоднее не оставлять часть капитала, а «играть на все».
И так далее.
Теперь возникает вопрос: если бытовая интуиция говорит нам «сохрани хоть сколько-то, чтобы иметь возможность возобновить выгодную игру, если вдруг не повезёт», а сухая математическая наука говорит «выгоднее всего играть на всю сумму», то кому верить?
Ну и попутно ещё масса вопросов:
– Верно ли, что математическое ожидание выигрыша будет максимальным при нулевом x для любого количества игр?
– Что такое «оптимальная стратегия» при такой игре? (не «какой она является», а «как понять, что найденная стратегия является оптимальной»)
– Какую сумму x вы бы откладывали от имеющихся денег, если бы планировали сыграть большое количество игр (например, миллион игр)? А если бы всего 3 игры? А если 10 игр?
Хорошей недели!
