Как найти равнодействующую силу системы сходящихся сил

Содержание:

1. Система сходящихся сил
2. Равнодействующая системы сходящихся сил
3. Разложение силы по заданным направлениям
4. Разложение силы по двум заданным направлениям
5. Разложение силы по трем заданным направлениям
6. Проекция силы на ось и плоскость
7. Аналитический способ определения равнодействующей
8. Условия и уравнения равновесия системы сходящихся сил
9. Геометрическое условие равновесия
10. Аналитические условия равновесия. Уравнения равновесия
11. Методика решения задач на равновесие
12. Примеры решения задач на равновесие под действием системы сходящихся сил
13. Система сходящихся сил и решение задач
14. Условия равновесия системы совпадающих сил
15. Геометрический метод решения задач
16. Аналитический метод решения задач
17. Проекция силы на ось и на плоскость
18. Аналитические условия равновесия системы совпадающих сил
19. Образец выполнения  и решения задач на темы С2
20. Система сходящихся сил на плоскости
21. Геометрическое условие равновесия системы сходящихся сил
22. Геометрический метод решения задач
23. Аналитические условия равновесия системы сходящихся сил
24. Примеры решения задач на тему: Система сходящихся сил

Система сходящихся сил – это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Система сходящихся сил

Определение:

Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил. Системы сходящихся сил могут быть плоскими и пространственными.

Нехай на тверде тіло діє система збіжних сил , лінії дії яких перетинаються в точці О (рис. 2.1, а).

Используя теорему 1.1, § 1.3, перенесем силы вдоль линий их действия в точку В и получим эквивалентную систему сил, приложенных к твердому телу в одной точке (рис. 2.1, б), которую еще называют пучком.

Равнодействующая системы сходящихся сил

Силы, приложенные в одной точке твердого тела, можно добавлять, используя аксиому о параллелограмм сил. Пусть к телу в точке О приложена система n сходящихся сил (рис. 2.2, а).

Найдем равнодействующую сил  и (рис. 2.2, а):

(индекс в обозначении равнодействующей соответствует количеству положительных сил).

К равнодействующей добавим силу . Получим

Составим равнодействующую с последней силой и получим равнодействующую n сил. Итак,  есть система сходящихся сил эквивалентна одной силе – равнодействующей, которая равна векторной сумме этих сил и приложена в точке пересечения линий их действия 

Как видно из рис. 2.2, б, построение параллелограммов сил эквивалентна построении векторного многоугольника сил. Для системы сил, изображенной на рис. 2.2, б, векторный многоугольник сил построим следующим образом: к концу вектора присоединим вектор, геометрически ровный , а с его конца отложим вектор и так далее. Вектор, проведенный из точки приложения первой силы до конца вектора , является равнодействующей силой . Полученный таким образом многоугольник называется силовым или многоугольником сил. 

Замыкающая сторона силового многоугольника, которая направлена против его обхода, определяет равнодействующую как по величине, так и по направлению (Рис. 2.2, б). Определение равнодействующей системы сходящихся сил по правилу параллелограмма или силового многоугольника называется геометрическим способом определения равнодействующей.

В случае плоской системы сходящихся сил силовой многоугольник используется для графического определения равнодействующей. Изображая силы в определенном масштабе, величину равнодействующей силы определим непосредственным измерением ее на чертеже. Геометрический способ определения равнодействующей используется в графостатици.

Разложение силы по заданным направлениям

Разложить данную силу на несколько составляющих – значит найти такую систему нескольких сил, для которых данная сила равнодействующей. Эта задача является
неопределенной и имеет однозначное решение лишь при задании дополнительных условий. Такими дополнительными условиями могут, например, быть: 1) задания двух направлений, вдоль которых должны действовать составляющие силы; 2) задания
модулей обеих составляющих сил; 3) задания модуля одной составляющей силы и
направление второй. Рассмотрим два частных случая.

Разложение силы по двум заданным направлениям

Задача сводится к построению такого параллелограмма, у которого сила, которая разлагается, является диагональю, а стороны параллельны заданным направлениям. Например, на рис. 2.3, а, показано, что сила розкладаеься по направлениям АВ и AD на силы  и – составляющие силы (сила и прямые АВ и АD лежат в одной плоскости).

Разложение силы по трем заданным направлениям

Если заданные направления АВ, АС и АD не лежащих в одной плоскости, то задача является определенной и сводится к построению такого параллелепипеда, в которого диагональ является заданной силой , а ребра параллельны заданным направлениям и определяют составляющие (рис. 2.3, б).

Проекция силы на ось и плоскость

Аналитический способ решения задач статики основывается на понятии о проекции силы на ось. Проекция силы на ось является алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и силой (Рис. 2.4)

Отметим, что:

Проекцией силы на плоскость Oxy называется вектор, который
соединяет проекции начала и конца вектора на эту плоскость (рис. 2.5).

В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной. Она характеризуется не только своим модулем, но и направлением в плоскости Oxу. Модуль проекции силы на плоскость 

 

где θ – угол между направлением силы и плоскостью. В некоторых случаях для определения проекции силы на ось выгоднее найти сначала ее проекцию на плоскость,
в которой эта ось лежит, а потом найденную проекцию на плоскость спроектировать на эту ось.

Например, в случае, изображенном на рис. 2.5, таким способом найдем, что: 

При решении многих задач механики удобно задавать силу через ее проекции на оси прямоугольной декартовой системы координат (рис. 2.6):

где , – проекции силы на соответствующие оси координат; – единичные орты осей  По известным проекциями силы на оси координат можно определить модуль силы и углы, которые она образует с координатными осями, по формулам:

Аналитический способ определения равнодействующей

Кроме геометрического существует еще и аналитический способ определения равнодействующей системы сходящихся сил. Если равенство (2.1) спроектируем на оси
декартовой системы координат (рис. 2.2, а), то получим:

где – проекции равнодействующей на оси координат; , – проекции силы на оси координат.

Итак, проекция равнодействующей системы сходящихся сил на эту ось равна алгебраической сумме проекций составляющих сил на эту же ось.

Поскольку формулы (2.7) определяют проекции равнодействующей на три взаимно перпендикулярные оси, то модуль и направление равнодействующей вычисляются по формулам:

Условия и уравнения равновесия системы сходящихся сил

По определению уравновешенной системы сил имеем

а для системы сходящихся сил (см. § 2.2) получили

Сравнивая эквивалентности (а) и (б), получим векторное условие равновесия: для равновесия системы сходящихся сил необходимо и достаточно, чтобы ее равнодействующая была равна нулю: 

Векторное равенство (2.9) является необходимым и достаточным условием равновесия
системы сходящихся сил. Условия, которым при этом должны удовлетворять самые силы, можно выразить в геометрической или аналитической форме.

Геометрическое условие равновесия

Как известно, равнодействующая – это замыкающая сторона силового многоугольника (рис. 2.2, б). Условие (2.9) будет выполняться только тогда, когда конец последней силы совместится с началом первой силы при построении силового многоугольника, то есть когда силовой многоугольник будет замкнутым. Необходимым и достаточным условием равновесия системы сходящихся сил есть замкнутость ее силового многоугольника (рис. 2.2, в).

Аналитические условия равновесия. Уравнения равновесия

Аналитические условия равновесия системы сходящихся сил вытекают из условия (2.9), согласно которой модуль равнодействующей равна нулю. Используя формулу (2.8), получаем или, согласно с (2.7),

Это означает, что для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на три взаимно перпендикулярные
оси равны нулю.

Равенства (2.10) называются аналитическими условиями равновесия системы сходящихся сил.

Для случая плоской системы сходящихся сил будем иметь:

Итак, задачи на равновесие системы сходящихся сил можно решать двумя способами – геометрически и аналитически. Первый способ удобен для плоской системы сходящихся сил.

Аналитические условия равновесия (2.10) или (2.11), расписаны для конкретной задачи, в которые входят неизвестные параметры, реакции связей, активные силы, расстояния, углы и т.д., называются уравнениями равновесия.

При решении задач статики реакции связей всегда есть неизвестными величинами. Для их определения используют условия равновесия той или другой системы сил.

Задачи, в которых число неизвестных величин равно числу уравнений равновесия, в которые они входят, называются статически определенными. Системы, для которых это имеет место, называются статически определенными.

Задачи, в которых число неизвестных величин больше, чем число уравнений равновесия, в которые входят эти величины, называются статически неопределенными. Системы, для которых это имеет место, называются статически неопределенными.

Методика решения задач на равновесие

Все задачи на равновесие желательно решать по такой методике.

1. Следуя масштаба, сделать четкий схематический рисунок к задачи.

2. Выбрать объект равновесия. Последним может быть точка, тело или
система тел, к которым приложено заданные и неизвестные силы. Если заданы
силы действуют на одно тело, а неизвестные – на второе, то необходимо рассматривать
равновесие системы тел в целом или последовательно равновесие каждого тела.
3. Изобразить на рисунке все заданные силы, приложенные к объекту равновесия.

4. Условно освободить объект равновесия от наложенных связей, а их действие заменить реакциями связей. Изобразить на рисунке реакции связей.
5. Выяснить, какая система сил действует на объект равновесия и условия равновесия рационально использовать.
6. В соответствии с условиями равновесия составить уравнение равновесия или выполнить соответствующие графические построения.
7. Решить уравнение равновесия, найти неизвестные величины и проанализировать полученные результаты.
Все расчеты в процессе решения задачи рекомендуется выполнять в общем виде, а числовые значения подставлять только в конечные алгебраические выражения.

Примеры решения задач на равновесие под действием системы сходящихся сил

Задача 2.1. Однородная горизонтальная балка, вес которой, содержится в равновесии шарнирно-неподвижной опорой А и шарнирнорухомою опорой В (рис. 2.7). Определить реакции опор.

Решение. Объектом равновесия выберем балку АВ, на которую действует одна заданная сила приложенная посередине длины балки (рис. 2.7, б).

Мысленно освободимся от связей. Линия действия реакции  перпендикулярна к плоскости, на которую опирается шарнирно-подвижная опора В. Известная точка приложения реакции (точка А). Очевидно, что балка находится в равновесии под действием трех непараллельных сил, которые лежат в одной плоскости. Найдем точку пересечения линий их действия. Для этого продолжим линии действия сил и  до пересечения в точке О. Согласно теореме о трех непараллельных силах, линия действия реакции должна пройти через точку В (по линии АО) (Рис. 2.7, б).

Балка находится в равновесии под действием трех сходящихся сил . Используем геометрическое условие равновесия и построим замкнутый треугольник сил (рис. 2.7, в). Для этого в выбранном масштабе отложим вектор силы  с начала которого проведем прямую, параллельную линии АО, а с конца – прямую, параллельную линии ВО. Точка пересечения этих прямых определит конец вектора и начало вектора . С треугольника сил определим величины неизвестных реакций  и .

Поскольку в , а линия действия силы является медианой и высотой основы АВ, поэтому также . Перенесем найдены углы на силовой треугольник. Решив его, получим 

Задача 2.2. Вертикальный стояк подъемного крана опирается на подпятник A и подшипник В (рис. 2.8, а). В точке С действует вертикальная нагрузка Р = 20 кН. Высота стояка АВ равна 2 м, вылет стрелы крана – 4 м. Найти опорные реакции при условии, что кран находится в
равновесии.

Решение. Рассмотрим равновесие крана. На него действует заданная сила приложена в точке С. Применим принцип освобождения от связей и найдем направление реакций связей. Линия действия реакции в подшипнике – горизонтальная; линия действия реакции подпятника – неизвестно. поскольку три силы , взаимно уравновешенные (кран находится в равновесии), лежат в одной плоскости и непараллельные, то они должны пересекаться в одной точке согласно теореме о трех силы. Найдем точку пересечения D линий действия сил  и и соединим с ней точку А (рис. 2.8, б). прямая AD будет линией действия реакции . Данную задачу также решим, используя геометрическую условие равновесия сходящейся системы сил. построим
замкнутый силовой треугольник (рис. 2.8, в). Видим, что треугольник сил подобен треугольника АВD (рис. 2.8, б). С подобия треугольников записываем отношение соответствующих сторон:

откуда определяем величины реакции связей  и 

Задачи 2.1, 2.2 могут быть решены аналитическим способом, с использованием условий равновесия произвольной плоской системы сил (см. раздел 6).

Задача 2.3. Груз Р весом 2 кН содержится в равновесии лебедкой D с помощью каната, перекинутого через блок B (рис 2.9, а). пренебрегая трением на блоке, определить усилия в стержнях AB и CВ, считая, что крепления в точках A, B и С – шарнирные. Углы показано на рис. 2.9, а. Размерами блока и весом стержней пренебречь.

Решение. Объект равновесия выбираем блок B, который рассматриваем как точку. К нему приложена заданная сила тяжести груза . Мысленно освободимся от связей и заменим действие их на блок В реакциями связей. Поскольку стержни АВ и ВС погружены в точке В, а их соединения – шарнирные, то они могут быть только или растянутыми или сжатыми,
то есть реакции стержней будут направлены вдоль их осей.

Стержень АВ является растянутый, поэтому его реакция будет направлена от точки В к
точки А, стрижень ВС – сжат, и его реакция направлена от точки С к точке В. Натяжение каната ВD будет направлен по линии каната, и, поскольку трением между блоком и канатом
пренебрегаем, то.

На блок В действует система сходящихся сил, расположенных в плоскости рисунка. Для решения задачи используем аналитические условия равновесия. Для этого выберем систему координат с началом в точке В (рис. 2.9, б) и запишем два уравнения равновесия (2.11):

Решим эти уравнения и определим неизвестные величины:

Анализируя полученные результаты, мы видим, что усилия и полученные со знаком «+». Это означает, что действительно стержень AB работает на растяжение, а стержень ВС – на сжатие.

Задача 2.4. Найти усилия, возникающие в стержнях АВ, АС и AD (рис. 2.10) под действием
силы и силы тяжести груза  подвешенного в точке А. Плоскость прямоугольника АВОС – горизонтальная, крепления стержней в точках A, B, C, D – шарнирные, сила  и груз Р находятся в вертикальной плоскости OAD. углы показаны на рисунке.

Решение. Объект равновесия выберем узел А. На него действуют заданные силы и   Мысленно освободим узел А от связей. Реакции идеальных жестких стержней   и  направлены по осям стержней.

На узел А действует пространственная система сходящихся сил. Выберем систему координат с началом в точке О и запишем уравнение равновесия (2.10):

Решим полученную систему уравнений и определим неизвестные величины усилий в стержнях:

Полученные результаты свидетельствуют о том, что стержни АВ и АС работают на растяжение, а стержень АD – на сжатие.

Система сходящихся сил и решение задач

Система сходящихся сил – это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух.

Условия равновесия системы совпадающих сил

Совпадающими называются силы, линии действия которых
пересекаются в одной точке.

Если все силы по линиям их действия перенести в эту точку, то получим эквивалентную систему сил, которая приложена к одной точке. Равнодействующая  системы прилагаемых к одной точки сил, приложенная к той же точке и изображается замыкающим вектором силового многоугольника, который построен на прибавляемых силах. Равнодействующая  равняется векторной сумме прибавляемых сил:

Поскольку система смежных сил может быть заменена одной силой (равнодействующей), то необходимым и достаточным условием равновесия тела под действием системы совпадающих сил является равенство нуля этого равнодействующего:

Геометрически это уравнение означает, что в построенном многоугольнике конец последнего вектора совпадает с началом первого, то есть многоугольник представляет
собой замкнутую фигуру.

В случае, когда на тело действуют три уравновешенные совпадающие силы, силовой (векторный) многоугольник сводится к силовому треугольнику. Решение задачи на равновесие в этом случае сводится к нахождению сторон треугольника с помощью тригонометрических формул.
 

Теорема о трех непараллельных силах. Если тело находится в равновесии под действием трех непараллельных сил, то линии действия этих сил обязательно пересекаются в одной точке и лежат в одной плоскости, то есть силы образуют плоскую систему совпадающих сил.

Теорема о трех силах облегчает решение задачи на равновесие твердого тела в том случае, когда направление одной из сил неизвестно. Найдя точку пересечения линий действий двух сил, направления которых известны, можно определить направление линии действия третьей силы, поскольку она должна проходить через точку приложения этой силы и точку пересечения линий действий первых двух сил.
 

Геометрический метод решения задач

Непосредственное использование сил многоугольника для решение задач статики сводится к геометрическому построению в масштабе векторного многоугольника с
дальнейшим определением неизвестных элементов с помощью тригонометрических формул. При решении задач на равновесие твердого тела геометрическим методом рекомендуется соблюдать следующий порядок:

1. Выделить объект равновесия;

2. Показать на чертежах точки примера и направления активных сил, действующих на объект равновесия;

3. Выяснить характер связей и возможные направления их реакций;

4. Построить замкнутый силовой многоугольник (построение надо начинать с силы, которая известна как по модулю, так и по направлению);

5. Из силового многоугольника найти неизвестные величины.
 

Аналитический метод решения задач

Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.

Проекция силы на ось и на плоскость

Общим способом определения модуля и направления равнодействующей является аналитический, который тоже следует из условия (C2.1) и базируется на аналитическом методе обозначения силы.
Аналитический метод обозначения силы заключается в том, что, выбрав некоторую прямоугольную систему координат (рис.C2.1), силу раскладывают по правилу параллелепипеда на три составляющие,

Алгебраические значения длин направленных отрезков и называются
проекциями силы на оси  и  и обозначаются  и 

Если и  – единичные векторы,  которые направленны по  осями  и  соответственно, а  и  –  проекции силы на эти оси, то

Модуль и направление силы по известным проекциям на
три взаимно перпендикулярные оси  и  можно получить из формул:

При определении проекции силы на ось возможны 4 случаи (рис.C2.2).

1. Вектор силы образует острый угол  с положительным направлением координатной оси (черта С2.2, а). В этом случае проекция силы на ось  положительная и по модулю  равна:

2. Вектор силы образует с положительным направлением оси тупой угол (рис.С2.2, б). В этом случае проекция силы на ось отрицательная и по модулю равна:

3. Вектор силы образует прямой угол с осью  (рис.С2.2, в.). В этом случае проекция силы на ось равняется нулю:

4. Сила параллельна к координатной оси. В этом случая сила проецируется на ось в натуральную величину со знаком плюс, когда ее направление совпадает с положительным направлением оси (рис.С2.2, г), и со знаком минус в противоположном случае (рис.С2.2, д):

В некоторых случаях для нахождения проекции силы на ось удобнее сначала найти ее проекцию на плоскость, в которой лежит эта ось, а уже затем спроектировать найденную проекцию на нужную ось.

Например, в случае, что изображен на рис. 2.3, сначала лучше спроектировать
силу  на плоскость  и получить проекцию  а уже затем найти проекции силы на оси  и  и  Тогда:

 

Аналитические условия равновесия системы совпадающих сил

Пусть силы образуют систему совпадающих сил, тогда равнодействующая  равна их геометрической сумме и тогда по теореме о проекции равнодействующей на оси системы координат:

Если тело под действием заданной системы сил находится в равновесии, то  итак  или с учетом (С2.7) получаем следующие условия равновесия тела под действием системы совпадающих сил:

Таким образом, для равновесия пространственной системы совпадающих сил необходимо и достаточно, чтобы сумма проекций этих сил на каждую из трех
координатных осей равнялась нулю.

При решении задачи аналитическим способом до трех первых пунктов, приведенных в разделе С2.2, надо добавить следующие:

4. Выбрать декартовую систему координат 

5. Составить уравнение равновесия твердого тела в проекциях на оси координат;

6. Решить полученную систему уравнений равновесия и найти неизвестные величины.

Образец выполнения  и решения задач на темы С2

Задача 1

Задано:

 
 

Определить: натяжение  нити ВС; реакцию  стержня АВ.
 

Решение.

Центр шарнира точка В находится в равновесии под действием сил натяжения нитей
 , и реакции невесомого стержня  Причем  по модулю равняется 
(п. С1.4, задача 1).

Таким образом, точка В находится в равновесии под действием трех сил, лежащих в одной плоскости и линии действия которых пересекаются в одной точке.

Величину и направление реакции  и величину натяжения нити  определим геометрически, воспользовавшись условием равновесия системы смежных сил в векторной форме:

Для решения уравнения (1) построим силовой (векторный) треугольник (рис.2).

Для этого из произвольной точки Р (полюса) отложим вектор  величина которого
нам известна. Поскольку векторный треугольник должен быть замкнутым, то с начала этого вектора проведем направление а с конца – направление  до взаимного пересечения (точка С).

Векторы  и  направим таким образом, чтобы векторный треугольник был замкнутым.

Определив углы  треугольника, можно записать теорему синусов:

Отсюда получим:

Ответ:  

Задача 2

Задано: 

 
Определить: натяжение нити  и реакции   и стержней AD и BD.
 

Решение. Шарнир D находится в равновесии под действием силы тяжести   натяжения нити  реакций  и  невесомых стержней АD и BD (п.С1.4, задача 2).

Реакции  и  направим вдоль стержней от D, примем, что стержни растянуты.

Все силы приложены к одной точке D и для определение неизвестных реакций можно воспользоваться аналитическими условиями равновесия системы совпадающих сил.

С точкой О свяжем пространственную систему координат, направив ось  перпендикулярно плоскости АВС, а оси  и  расположим в этой плоскости.

Спроектировав все силы на оси выбранной системы координат, достанем:

Из уравнения (1) находим: 
Выразим из уравнения (2) натяжение нити и  подставим в уравнение (3):

Откуда:

Если при решении задачи какая-то из реакций приобретает отрицательное значение, то это означает, что направление этой реакции надо изменить на противоположное. Тогда, действительное направление реакций и  невесомых стержней DA и DB противоположно изображенным на рисунке, а сами стержни будут не растянутыми, как указывалось в начале, а сжатыми.
Ответ: 

Система сходящихся сил на плоскости

Система сходящихся сил на плоскости – это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух.

Геометрическое условие равновесия системы сходящихся сил

Сходящимися называются силы, линии действия которых пересекаются в одной точке (рис.2.1, а).

Если перенести все силы вдоль линии их действия в эту точку, получим эквивалентную систему сил, приложенных к одной точке.

Равнодействующая данной системы сил, которые проходят через точку , приложена к этой же точке и изображается замыкающей стороной силового многоугольника, который построен (рис.2.1, б)

на прилагаемых силах, то есть равнодействующая равна векторной сумме прилагаемых сил:

Поскольку система сходящихся сил может быть заменена одной силой – равнодействующей, то необходимым и достаточным условием равновесия тела под действием системы сходящих сил является равенство нулю этой равнодействующей:

Геометрически это условие состоит в том, чтобы конец последнего вектора совпадал с началом первого в векторном (силовом) многоугольнике, построенном из сил системы, то есть силы должны образовывать замкнутый многоугольник.

Если тело находится в равновесии под действием трех сходящихся сил, то силовой многоугольник сводится к силовому треугольнику. Решения же задачи о равновесии в этом случае требует нахождения неизвестных элементов треугольника с помощью тригонометрических формул или измерений.

При решении задач на равновесие тела под действием трех сил часто приходится пользоваться теоремой о трех силах:

Если тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил обязательно пересекаются в одной точке, то есть силы образуют сходящуюся систему сил.

Теорема о трех непараллельных силах облегчает решение задач на равновесие твердого тела в тех случаях, когда направление одной из трех сил неизвестное. Определив точку пересечения линий действия двух сил, направление которых известно, можно указать направление линии действия третьей силы, поскольку она должна пройти через точку приложения этой силы и точку пересечения линий действия первых двух сил.

Геометрический метод решения задач

Непосредственное использование многоугольника сил при решение задач статики приводит к геометрическим построениям с последующим определением неизвестных элементов с помощью, например, формул тригонометрии.

При решении задач на равновесие твердого тела геометрическим методом рекомендуется придерживаться следующего порядка:

1. Выделить объект, который будет рассматриваться в равновесии.
2. Установить и показать на схеме активные силы, действующие на тело.
3. Выяснить характер связей и установить направления их реакций.
4. Построить замкнутый силовой многоугольник (построение надо начинать с сил, известных по модулю и по направлению).
5. Из силового многоугольника определить неизвестные силы.

Аналитические условия равновесия системы сходящихся сил

Наиболее общим способом определения модуля и направления равнодействующей является аналитический, который базируется на аналитическом определении силы.

Если выбрать некоторую прямоугольную систему координатных осей (рис.2.2.), то силу по правилу параллелограмма (в данном случае – прямоугольника) можно разложить на две составляющие и .

Алгебраические значения длин направленных отрезков и называются проекциями силы на оси  и  и обозначаются и .

Если и единичные векторы, что направлены по осям  и , а 

Модуль и направление силы по известным проекциям на взаимно перпендикулярные оси ,  находят из следующих формул:

При определении проекции силы на ось возможны следующие случаи (рис.2.3):

Рис. 2.3

1. Сила образует острый угол  с положительным направлением оси (рис.2.3, а). В этом случае проекция силы на ось имеет положительный знак и по модулю равна

2. Сила образует с положительным направлением оси тупой угол (рис.2.3, б). В этом случае ее проекция на координатную ось имеет отрицательный знак и равна

3. Сила образует прямой угол с координатной осью (рис.2.3, в). В этом случае проекция силы на ось равна нулю: 

4. Сила параллельна координатной оси (рис.2.3, г, д). В этом случае сила проецируется в натуральную величину и проекция положительна, если ее направление совпадает с положительным направлением оси (рис.2.3, г), и отрицательная, если направление силы совпадает с отрицательным направлением оси (рис.2.3, д).

Если силы представляют собой систему сходящихся сил, то равнодействующая равна их геометрической сумме, а ее проекции на оси:

Поскольку модуль равнодействующей определяется по формуле

то тело под действием системы сходящихся сил будет находиться в равновесии, когда , а это возможно, когда и . В результате получим следующие аналитические условия равновесия тела под действием системы сходящихся сил:

Таким образом, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций всех этих сил на каждую из координатных осей равнялись нулю.

При решении задач аналитическим способом нужно выполнить три первых пункта, указанные в параграфе 2.2, а затем следующие:

4. Выбрать декартову систему координат .

5. Составить уравнения равновесия твердого тела в проекциях на эти оси координат.

6. Решить систему составленных уравнений и определить неизвестные величины.

Примеры решения задач на тему: Система сходящихся сил

Задача № 1

Идеальный стержень удерживается в равновесии нерастяжимой нитью . К шарниру стержня на нити подвешено тело весом (рис.2.4).

Определить натяжение нити и реакцию стержня , если

Решение. Рассмотрим равновесие узла (рис.2.4). К узлу приложена сила , которая перенесена вдоль линии действия от центра масс тела к точке , натяжение нити и реакция стержня . Таким образом, узел  находится в равновесии под действием трех сил , и , которые лежат в одной плоскости и имеют одну и ту же точку пересечения.

Величину и направление усилия и величину натяжения нити определим геометрическим методом, воспользовавшись геометрическим условием равновесия плоской системы сходящихся сил. Запишем геометрическое условие равновесия системы действующих сил на точку :

Согласно записанному векторному уравнению построим силовой треугольник.

Для этого с произвольной точки (рис. 2.5) отложим в некотором масштабе вектор . С точки начала вектора проведем прямую, параллельную линии действия реакции , а с точки конца вектора  – прямую, параллельную линии действия реакции . Проведенные прямые пересекутся в точке , образовав треугольник . Укажем направление сил, руководствуясь тем, что при добавлении векторов начало каждого следующего вектора должно исходить из конца предыдущего.

Найти неизвестные величины можно или померив соответствующие стороны силового треугольника, или, по известным углам треугольника из теоремы синусов:

Откуда: 

Ответ: 

Задача № 2

Нить с двумя телами на концах и перекинута через блоки  и  (рис.2.6). В точке к нити, находящейся между блоками, прикрепил груз При равновесии системы нить  образовала с горизонталью угол , а нить .

Определить вес тел и . Силами трения в блоках пренебречь.

Решение. Сначала выясним, равновесие какого объекта надо рассмотреть при решении задачи. По условию задачи нужно определить вес тела и вес тела , которые приложены к центрам масс тел и направлены вертикально вниз. Каждое тело натягивает нить с силой, равной его весу. Блок меняет направление нити, а соответственно, и направление силы натяжения нити. Силы и  по модулю, равны и , но направлены вдоль и .

Поскольку прямые и пересекаются в точке , к которой можно приложить и заданную силу , то при решении задачи надо рассматривать равновесие точки .

Таким образом, на объект равновесия, точку (рис.2.6), действуют силы натяжения ветки нити ; натяжения ветки нити ; весы тела . (Вес тел и учитывать не надо, поскольку они приложены не к объекту равновесия точки ).

Составим уравнение равновесия. Для этого, выберем систему координат с началом в точке , спроецируем силы на оси и составим уравнение равновесия.

Для проекций на ось  достанем:

Знак проекции – плюс, поскольку она направлена по положительному направлению оси . Знак проекции – минус, поскольку она направлена по отрицательному направлению оси . Проекция силы на ось равна нулю.

Сумма проекций всех сил на ось равна:

Проекции сил и  имеют знак плюс, поскольку направлены по положительному направлению оси . Проекция силы  имеет знак минус, поскольку направлена по отрицательному направлению оси.

С учетом численных значений тригонометрических функций и величины , уравнения примут вид:

Найдя из первого уравнения:

и подставив во второе, получим:

Ответ: 

Задача № 3

Однородный стержень (рис.2.7), что прикреплено к вертикальной стенке с помощью шарнира , удерживается под углом к вертикали с помощью троса , который образует угол со стержнем.

Определить величину и направление реакции петли, если вес стержня 

Решение. Задачу решим геометрическим и аналитическим способами, используя теорему о равновесии тела под действием 3-х сил.

Рассмотрим равновесие стержня . На стержень действует активная сила – сила тяжести и реакции связей: натяжение троса ; реакция цилиндрического шарнира .

Направление натяжения троса известное – реакция направлена вдоль троса к точке . Направление реакции шарнира предварительно указать нельзя. Для определения направления реакции воспользуемся теоремой о трех силах, так как стержень находится в равновесии под действием трех сил , и .

Найдем точку пересечения линий действия силы тяжести и натяжение троса  – это точка . Согласно теореме о трех силах, линия действия реакции тоже должна пройти через эту точку.

На рис.2.7 равнобедренный (углы при вершинах и равны ). Поскольку линия действия () силы тяжести проходит через середину стержня и представляет собой среднюю линию , то точка делит сторону пополам.

Соответственно, отрезок является одновременно высотой, медианой и биссектрисой треугольника .

Таким образом

После определения направления реакции , можно переходить к вычислению величин реакций.

Запишем геометрическое условие равновесия системы сил, действующих на стержень :

Согласно записанному векторному уравнению построим замкнутый силовой треугольник (рис.2.8). 

Для этого из произвольной точки в некотором масштабе проводим вектор силы тяжести  . Через точку  проводим прямую, параллельную линии действия реакции , а через точку конца вектора проводим прямую, параллельную линии действия натяжения .

Проведенные прямые пересекаются в точке , образовав силовой треугольник . Поскольку (рис. 2.7) и . ( рис. 2.8) подобные, то

Из силового треугольника находим:

Решим задачу аналитическим способом. Для этого выберем прямоугольную систему координат (рис.2.7) и составим уравнение равновесия в проекциях на оси:

Из первого уравнения выразим и подставим во второе уравнение:

Отсюда получим:

Ответ: 

Балка (рис.2.9) закреплена шарнирно-неподвижной опорой в точке и шарнирно-подвижной в точке . К середине балки под углом приложена сила

Определить реакции опор  и  для двух случаев наклона подвижной опоры (рис.2.9, а и 2.9, б). Весом балки пренебречь.

Решение. Рассмотрим равновесие балки , изображенной на рис.2.9,а. На балку действует активная сила и реакции опор  и  (рис. 2.10). Опора шарнирно-подвижная, ее реакция направлена перпендикулярно опорной поверхности. Поскольку, в данном случае опорная поверхность параллельна оси балки, то реакция перпендикулярна . Опора шарнирно-неподвижная и направление ее реакции предварительно указать нельзя.

Для определения направления реакции (угла  ) воспользуемся теоремой о трех силах. Линии действия силы и реакции пересекаются в точке . Таким образом, линия действия тоже должна пройти через точку .

С рис.2.10 видно, что – равнобедренный и прямоугольный, то есть . Откуда:

Теперь перейдем к определению величин реакций опор.

Составим уравнение равновесия сил в проекциях на оси выбранной системы координат :

С учетом числовых значений:

В результате получим:

Ответ: 

Перейдем к определению реакций опор балки , что изображена на рис.2.9,б.

В этом случае, реакция составляет с осью балки угол . Линия действия реакции (рис.2.11) проходит через точку , в которой пересекаются линии действия силы и реакции .

Определим угол между реакцией и осью балки :

Составим уравнение равновесия для системы сил, действующей на балку:

С учетом числовых данных:

Добавив уравнение получим:

Подставив значение в первое уравнение, найдем :

Ответ: 

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Момент силы
3. Пара сил
4. Произвольная система сил
5. Плоская произвольная система сил
6. Трение
7. Расчет ферм
8. Расчет усилий в стержнях фермы
9. Пространственная система сил
10. Произвольная пространственная система сил
11. Плоская система сходящихся сил
12. Пространственная система сходящихся сил
13. Равновесие тела под действием пространственной системы сил
14. Естественный способ задания движения точки
15. Центр параллельных сил
16. Параллельные силы
17. Система произвольно расположенных сил
18. Сосредоточенные силы и распределенные нагрузки
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Содержание:

Система сходящихся сил:

Рассмотрим одну из важных систем сил — систему сходящихся сил. Для этой системы сил следует рассмотреть приведение ее к простейшему виду и установить условия равновесия.

Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке — центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т. е. расположенными в одной плоскости.

Приведение к равнодействующей силе

Рассмотрим общий случай пространственной системы сходящихся сил. Так как сила, действующая на твердое тело, есть вектор скользящий, то можно считать, что силы системы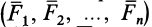

Применяя к первым двум силам пучка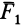

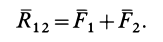
Затем по правилу параллелограмма складываем силы 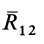и  и 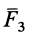получаем их равнодействующую:

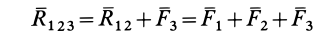
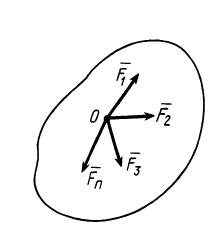
Рис. 12

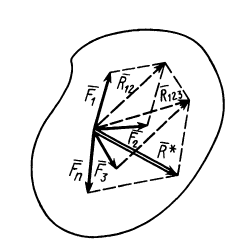
Рис. 13

и т. д. Продолжая процесс векторного сложения сил для всех 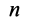сил, получим

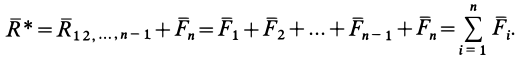
Таким образом, система 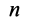сходящихся сил эквивалентна одной силе 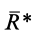, которая и является равнодействующей этой системы сил.

Процесс последовательного применения к силам правила параллелограмма, или их векторного сложения, приводит к построению силового многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой (рис. 14). Равнодействующая сила 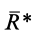в силовом многоугольнике соединяет начало первой силы с концом последней, т. е. изображается замыкающей силового многоугольника, который в общем случае является незамкнутым. Силы в силовом многоугольнике можно изображать в любой последовательности. От этого изменится форма силового многоугольника, а замыкающая не изменится; следовательно, не изменится и равнодействующая сила.

Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской— плоской. Для плоской системы сходящихся сил равнодействующую силу можно определить графически путем построения замыкающей силового многоугольника в выбранном для сил масштабе. Для пространственной системы сходящихся сил пришлось бы силовой многоугольник строить в пространстве из стержней.

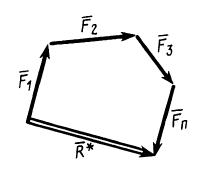
Рис. 14

Итак, система сходящихся сил в общем случае приводится к одной силе—равнодействующей этой системы сил, которая изображается замыкающей силового многоугольника, построенного на силах системы. Линия действия равнодействующей силы проходит через центр пучка параллельно замыкающей силового многоугольника.

Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться известной из геометрии теоремой о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось.

Так как равнодействующая сила 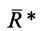является замыкающей силового многоугольника, или векторной суммой сил, то

Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим

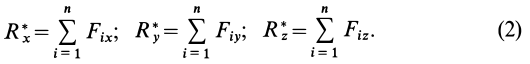
По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам

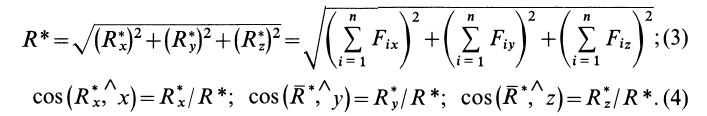
В формуле (3) перед квадратным корнем всегда берут знак плюс, так как определяется модуль равнодействующей силы.

В случае плоской системы сходящихся сил одну из координатных осей, обычно 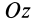, выбирают перпендикулярной силам, тогда каждая из сил пучка даст проекцию на эту ось, равную нулю, а следовательно, будет равна нулю и проекция равнодействующей силы на эту ось, т. е.

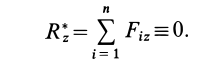
Условия равновесия системы сходящихся сил

Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпасть с началом первой силы. Такой силовой многоугольник называют замкнутым (рис. 15). Получено условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.

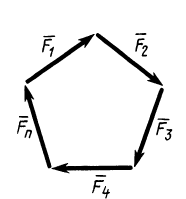
Рис. 15

Для определения неизвестных сил при равновесии более предпочтительным является использование условий равновесия системы сходящихся сил в аналитической форме. Так как при равновесии системы сходящихся сил равнодействующая сила должна быть равна нулю (силовой многоугольник замкнут), то из этого следует, что равно нулю подкоренное выражение в (3), состоящее из суммы положительных величин. Таким образом, равны нулю квадраты каждой из величин подкоренного выражения, а следовательно, равны нулю и сами величины. Получаем условия равновесия пространственной системы сходящихся сил в аналитической форме:

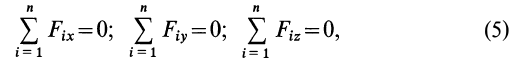
т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.

В случае плоской системы сходящихся сил одну из осей координат, обычно 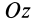, выбирают перпендикулярной силам, а две другие оси—соответственно в плоскости сил. Тогда третье условие из (5) превратится в тождество 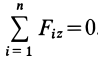. Отбрасывая его, получаем

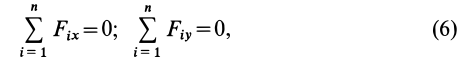
т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю.

Проецирование силы на оси координат

Если дана сила 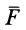, то ее проекции на прямоугольные оси координат вычисляются по формулам

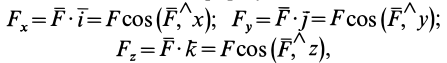
где 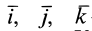— единичные векторы, направленные по осям координат. Косинусы углов силы с осями координат удовлетворяют условию

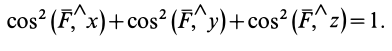
Из трех углов независимыми являются только два.

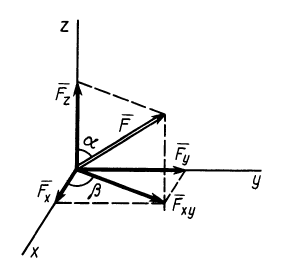
Рис. 16

При проецировании силы на прямоугольные оси координат целесообразно использовать тоже два угла. Для этого предварительно силу разлагают на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-либо оси координат, например 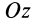, а другая находится в координатной плоскости двух других осей, в нашем случае — координатной плоскости 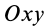(рис. 16). Получаем

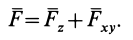
Проецируя векторы векторного равенства на координатные оси, имеем

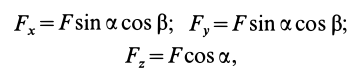
так как

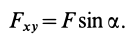
При проецировании использованы только два угла: 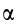и .

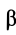Векторные величины 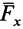, , 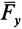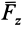называются составляющими силы 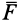по осям координат. Скалярные величины 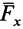, , 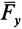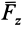являются проекциями силы 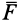на оси координат. Таким образом, силу на оси координат проецируют обычно в два приема. Сначала ее проецируют на одну из осей и на координатную плоскость двух других осей. Проекция силы на плоскость является вектором. Этот вектор затем проецируют на оси координат, расположенные в плоскости.

Пример 1.

Подъемный кран, имеющий вертикальную ось вращения 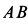, состоит из стержней, скрепленных шарнирами. Ось крана закреплена с помощью подпятника 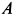и подшипника 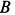(рис. 17, а). Считая стержни и весь кран невесомыми, определить силы реакций в подпятнике и в подшипнике, усилия в стержнях 1, 2, 3, 4, если известны размеры 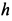и 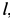, а также углы 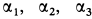. Стержни 2 и 5 горизонтальны. Кран с помощью троса 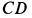удерживает груз, сила тяжести которого равна .

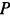Решение. Считая кран твердым телом, освободим его от связей, которыми являются подпятник и подшипник, заменив их силами реакций связей. Сила реакции подшипника (цилиндрический шарнир) перпендикулярна его оси. Направление силы реакции подпятника заранее не известно и подлежит определению. На весь кран, находящийся в равновесии, действуют три силы: 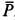, , 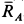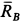(рис. 17,6). Линии действия этих сил должны пересекаться в одной точке, т. е. линия действия силы  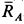должна пройти через точку 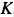, в которой пересекаются линии действия сил 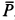и 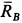. Три силы должны образовывать также замкнутый силовой треугольник. Отложим силу 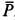в выбранном масштабе и проведем через ее начало и конец линии, параллельные силам  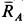и 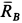. В полученном силовом треугольнике три силы должны быть направлены друг за другом (рис. 17, в). Из полученного прямоугольного треугольника находим

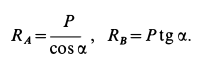
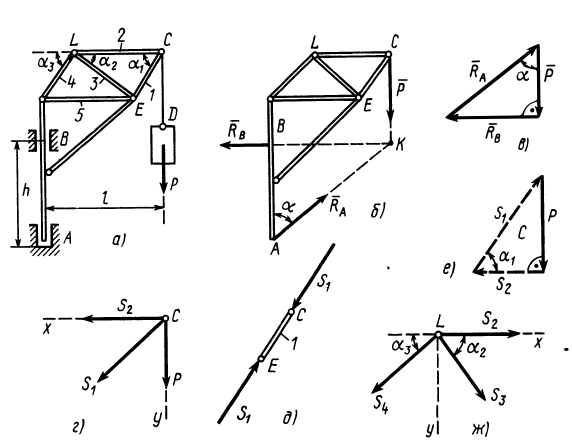
Рис. 17

Из геометрического треугольника

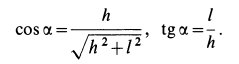
Для определения усилий в стержнях 1 и 2 применим метод вырезания узлов. Для этого рассмотрим равновесие отдельного шарнира или узла С. На этот узел действуют сила Р через трос и силы реакций стержней 1 и 2, которые следует мысленно отбросить. Силы реакций стержней на узел должны быть направлены по стержням, так как на эти стержни между их шарнирами другие силы не действуют. Стержни являются шарнирными. (Условимся силы реакций стержней направлять от узла (рис. 17, г) и знак вектора у сил на рисунке не ставить, чтобы не увеличивать без необходимости число обозначений для одинаковых по числовому значению сил.)

Выбрав в точке 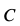оси координат, составим условия равновесия для плоской системы сходящихся сил, действующих на узел :

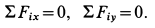
Эти условия в рассматриваемом случае принимают форму в проекциях на оси:

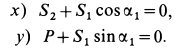
Из полученных уравнений получаем:

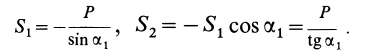
Знак 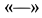у 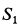показывает, что направление этой силы противоположно принятому, т. е. направлено к узлу. Рассматривая равновесие отдельного стержня 1, убеждаемся, что на него действуют только две силы со стороны узлов и 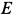. Эти силы должны быть при равновесии равны по модулю и противоположны по направлению. Узел действует на стержень 1 с силой 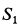 , противоположной по направлению силе действия стержня на узел 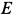(рис.17, д). Таким образом, получаем, что при рассмотрении равновесия узла , когда 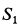имеет отрицательное значение, стержень 1 будет сжат;  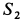получили с плюсом. Следовательно, стержень 2 будет испытывать растяжение.

На узел действуют три силы, и они поэтому должны образовывать замкнутый силовой треугольник. Построение силового треугольника следует начать с известной силы 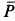, проводя через ее концы линии, параллельные неизвестным по значению силам реакций стержней (рис. 17, е). Из силового треугольника можно определить силы 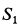и .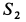

Из уравнений равновесия или силового треугольника можно определить только две неизвестные силы. Поэтому при дальнейшем решении задачи следует переходить к рассмотрению равновесия узла, на который действуют не более двух неизвестных сил. Таким узлом является узел 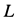. На узел 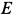действуют три неизвестные силы. При рассмотрении равновесия узла 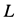будем направлять силы реакций стержней опять от этого узла (рис. 17,ж) независимо от ранее полученных знаков для них. В уравнения равновесия уже известную силу 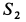следует подставить со знаком плюс, полученным для нее ранее. Условия равновесия сил, действующих на узел 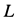, имеют форму:

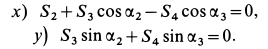
Из этих уравнений находим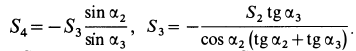

Подставляя в выражение для 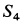полученное значение 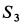, получим

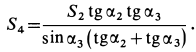
Усилие 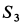 при положительном 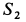отрицательно. Следовательно, стержень 3 сжат. Усилие 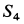положительно. Поэтому стержень 4 растянут.

Для узла 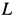можно построить также замкнутый силовой треугольник и решить задачу нахождения неизвестных сил геометрически.

Пример 2.

Груз с силой тяжести 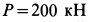 прикреплен с помощью троса к шарниру 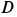, который крепится к вертикальной стене тремя стержнями, два из которых расположены в горизонтальной плоскости, а третий — в вертикальной, с помощью шарниров. Сила сопротивления груза от ветра 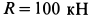горизонтальна и параллельна стене. Определить силу натяжения троса и усилия в стержнях, считая стержни невесомыми, если 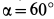, 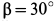(рис. 18, а).

Решение. На находящийся в равновесии груз 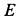действует система трех сходящихся сил, расположенных в вертикальной_ плоскости, параллельной стене. Это сила тяжести 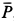, сила сопротивления 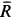и сила натяжения троса 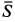, направленная по нему (рис. 18,6). Сила 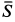должна уравновесить равнодействующую сил 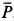и 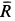. Следовательно,

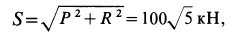
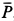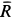так как силы и перпендикулярны. Сила 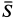составляет с вертикалью угол 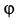, для которого

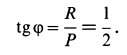
Рассмотрим равновесие шарнира 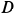, на который действуют силы реакции трех стержней 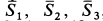, направленные по стержням, и сила натяжения троса, равная 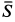(рис. 18, в). Имеем пространственную систему сходящихся сил, условия равновесия которой имеют форму

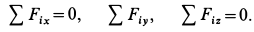
В рассматриваемом случае для выбранных осей координат имеем:

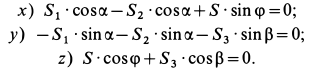
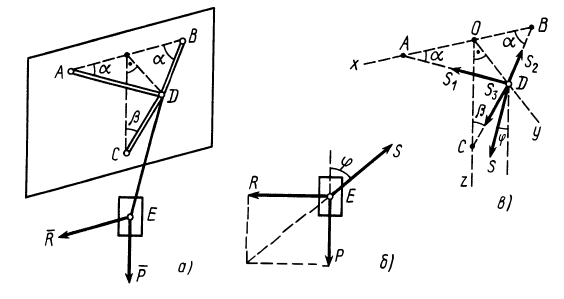
Рис. 18

Так как

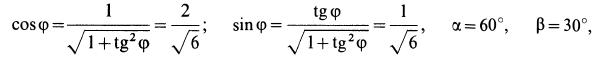
то система уравнений принимает форму

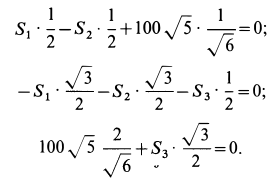
Решая эту систему уравнений, получаем:

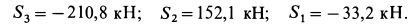
Усилия в стержнях направляли от рассматриваемого узла и получил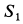и и 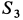со знаком минус, a  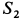— со знаком плюс. Это служит указанием, что стержни 1 и 3 подвергаются сжатию, а стержень 2 — растяжению.

Силы, сходящиеся в одной точке

Если на точку А действуют n сил, расположенных в одной плоскости (рис. 22), то эти силы можно сложить геометрически, построив многоугольник векторов, который в нашем случае называется многоугольником сил.

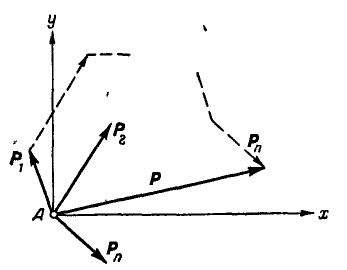
Рис. 22.

Обозначая равнодействующую сил через Р, можем написать:

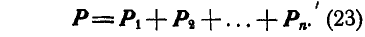
Проектируя равнодействующую и составляющие на координатные оси, проведенные через точку А, по формуле (3) имеем:

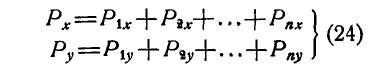
Величину равнодействующей находим по формуле (7):

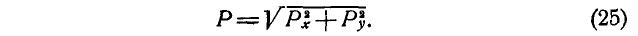
Направление равнодействующей определяем по формулам (6):

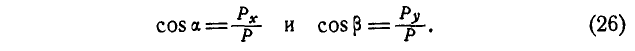
Может оказаться, что при построении многоугольника сил конец последней силы совпадет с началом первой; в этом случае многоугольник сил получается замкнутым, равнодействующая сила равна нулю и силы находятся в равновесии. Таким образом, геометрическое условие равновесия сил, приложенных к точке, заключается в том, что многоугольник этих сил должен быть замкнут.        

В этом случае Р=0, а поэтому и 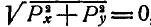   , а это может быть при условии, когда 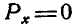и 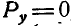, что возможно, если:

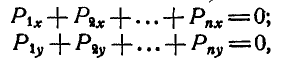
или сокращенно:

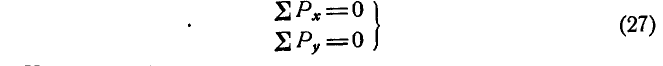
Уравнения (27) называются уравнениями равновесия сил, приложенных к точке, и выражают аналитические условия равновесия этих сил.

Рассмотрим равновесие трех сил 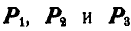, действующих на тело (рис. 23).

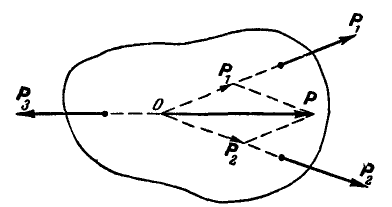
Рис. 23.

Пусть в точке О пересекаются линии действия любых двух сил, например 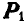и 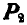, тогда эти силы можно перенести в точку О и по правилу параллелограмма заменить одной силой Р.

Теперь на тело уже действуют две силы Р и А, равновесие которых по аксиоме 2 возможно, если они будут направлены по одной прямой.

Отсюда заключаем, что три силы, действующие на тело, и расположенные в одной плоскости, могут находиться в равновесии только тогда, когда их линии действия пересекаются в одной точке.

• Заказать решение задач по теоретической механике

Задача 1.

К точке В шарнирного кронштейна АВС (рис. 24, а) подвешен груз Q = 100 кГ. Определить усилия 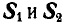в стержнях ВА и ВС.

Решение. Для определения усилия 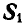в стержне ВА, который является связью для точки В, освободимся от связи и введем реакцию стержня, которая, согласно аксиоме 6, будет равна и прямо цретивоположна искомому усилию 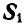(рис. 24, б). Теперь точка В находится в равновесии под действием двух сил 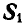и 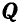и имеет возможность двигаться по дуге окружности радиуса ВС (рис. 24, б). Поэтому равновесие точки В возможно будет только тогда, когда равнодействующая этих двух сил 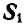и 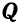пойдет по направлению оси стержня ВС. Но это равносильно тому, что проекция ее на направление 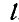, перпендикулярное к стержню ВС, будет равна нулю, или, что то же, сумма проекций составляющих на это направление равна нулю: 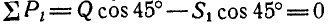, откуда .

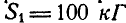Для нахождения усилия 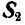 в стержне ВС поступаем аналогично. Устраняем связь ВС и взамен ее вводим реакцию 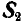(рис. 24, в); тогда точка В должна находиться в равновесии под действием двух сил 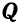и 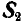. Проектируя эти силы на направление у возможного движения точки В, получим условие равновесия точки В в виде: 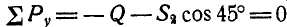, откуда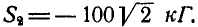

При решении этой задачи можно было бы освободиться одновременно от обеих связей ВА и ВС, вводя взамен их реакции связе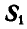й и 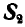(рис. 24,г).

Тогда для свободной точки В можно написать два уравнения равновесия (27) в виде:

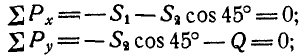
отсюда находим, что 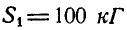и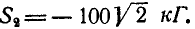

Знак минус у 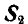указывает на то, что направление реакции нами выбрано неправильно и это направление следует изменить на обратное. На рисунке 24, д дано правильное направление стрелок реакций связей.

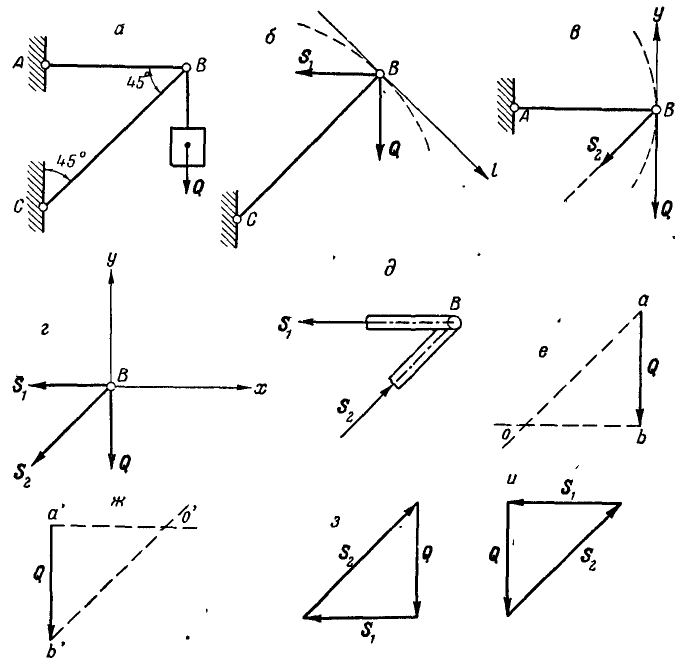
Рис. 24.

При неподвижной точке В реакция направленная от узла, будет растягивать стержень, а реакция 58, направленная к узлу, будет сжимать стержень, что ясно видно из чертежа.

Решим теперь эту задачу геометрическим способом. Все силы, заданные и реактивные, действующие на точку В, взаимно уравновешиваются, а поэтому многоугольник этих сил должен быть замкнут. На этом основании проводим вектор, равный силе 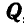, и из начала и конца этого вектора проводим направления, параллельные линиям действия реакций связей ВА и ВС (рис. 24, е или 24, ж); в пересечении этих направлений получаем точку О или О’.

Так как многоугольник сил, действующих на точку В, должен быть замкнут, то стрелки всех сил в полученном многоугольнике сил, в нашем случае – треугольнике (рис. 24, е или 24, ж), должны быть расположены в одном направлении. Исходя из заданного направления силы , получим правильное направление стрелок реактивных сил 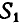 и 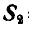(рис. 24, з или 24, м).

Выбрав один из полученных треугольников сил, замечаем, что сила 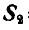, перенесенная параллельно самой себе на стержень 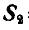(рис. 24, а или 24, д), будет направлена к узлу В, следовательно, стержень ВС — сжат, а сила 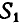направленная от узла В, будет растягивать стержень ВА. Из полученного треугольника сил (рис. 24, з или 24, и) имеем:

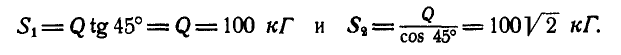
При решении дальнейших задач аналитическим способом стрелки неизвестных реакций стержней будём направлять всегда от рассматриваемого нами узла; тогда знак минус у модуля реакции какого-либо стержня будет указывать на то, что рассматриваемый нами стержень сжат.

Задача 2.

Определить усилия в стержнях АВ и ВС при действии в шарнире В силы Q=100 кГ, если АВ = ВС =5 м, BD = 0,5 м и шарниры А и С расположены на одной горизонтали (рис. 25, а).

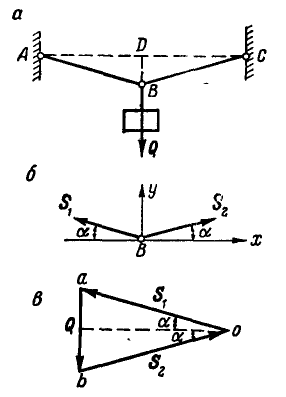
Рис. 25.

Решение. Решим сначала задачу аналитическим способом, для чего рассмотрим равновесие точки В, находящейся под действием трех сил: заданной силы 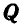и реакций связе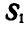й и 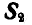(рис. 25, б).

Применяя уравнения равновесия (27), имеем:

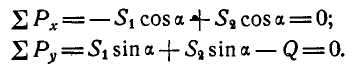
Из первого уравнения находим: 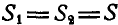; тогда второе уравнение примет вид: 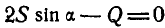, откуда 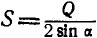. Из  ΔABD  имеем: 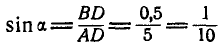, поэтому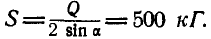 

Знак плюс у S указывает на то, что оба стержня ВА и ВС растянуты.

Для решения этой задачи геометрическим способом, построим треугольник равновесия 0ab (рис. 25,в), из которого сразу находим правильное направление реакци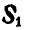и и 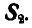. Далее 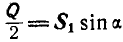, или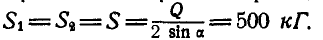

Задача 3.

Однородный цилиндр (рис. 26,а) весом 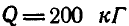опирается на гладкую плоскость, наклоненную под 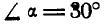к горизонту и удерживается в равновесии горизонтальным канатом 0С. К оси цилиндра О приложена сила Р=400 кГ, направленная параллельно плоскости. Найти реакцию N плоскости и натяжение Т каната ОС.

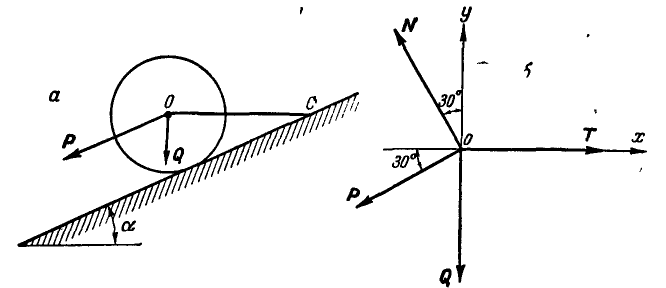
Рис. 26.

Решение. Решим задачу аналитическим способом. Освободившись от связей (рис. 26,6) и составляя для точки О уравнения равновесия (27), имеем:

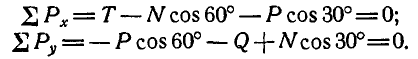
Подставляя вместо Р и Q их значения и решая полученные уравнения, находим неизвестные силы:

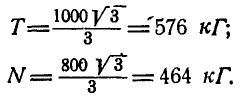
Задача 4.

Жесткое колено ABCD (рис. 27,а), могущее вращаться вокруг шарнира В, опирается в точке D на гладкий уступ. Пренебрегая весом колена, определить реакции связей в точках В и D, если в точке А колена приложена сила Р=100 кГ.

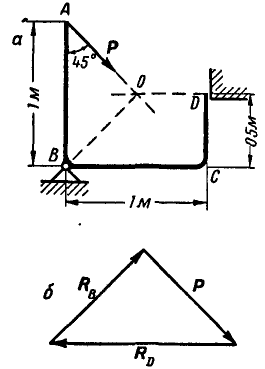
Рис. 27.

Решение. Так как колено находится в равновесии, то три силы, действующие в точках А, В и D, должны пересекаться в одной точке. Продолжаем линию действия силы Р  и реакции в точке D, направленной перпендикулярно к плоскости уступа, до взаимного пересечения в точке О; тогда линия действия реакции шарнира В пройдет обязательно через точку О. 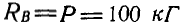На рисунке 27, б дано построение треугольника равновесия трех сил , из которого следует, что и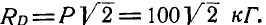

Задача 5.

При подъеме плуга на стоянке (рис. 30) поворачивают коленчатый рычаг АВС, вращая рукоятку силой Р. Какова при этом должна быть величина силы Р, если вес части плуга, передающейся на коленчатый рычаг, вращающийся вокруг шарнира В, равен Q = 30 кГ, длина рукоятки АВ = 0,6 м и радиус колеса плуга г = 0,25 м.

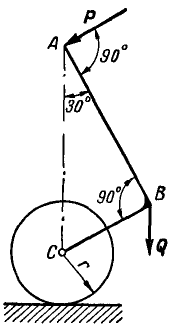
Рис. 30.

Решение. Строим для сил, приложенных к коленчатому рычагу, треугольник равновесия. Из подобия треугольника равновесия и соответствующего треугольника на чертеже находим силу Р.

Ответ: Р = 11 кГ.

Равнодействующая
системы сходящихся сил –
сила, оказывающая на твёрдое тело такое же механическое действие, как и данная система приложенных ктелу сил. В простейших случаях (например, для сил, приложенных в одной точке или расположенных в однойплоскости) равнодействующую можно найти, последовательно применяя закон параллелограмма сил.Равнодействующую имеет не всякая система сил, например, пара сил или две силы, не лежащие в одной
плоскости, равнодействующей не имеют.

Определение
равнодействующей системы сил аналитическим
способом

Величина
равнодействующей равна векторной
(геометрической) сумме векторов системы
сил. Определяем равнодействующую
геоме­трическим способом. Выберем
систему координат, определим про­екции
всех заданных векторов на эти оси (рис.
3.4а). Складываем проекции всех векторов
на оси х и у (рис. 3.46).

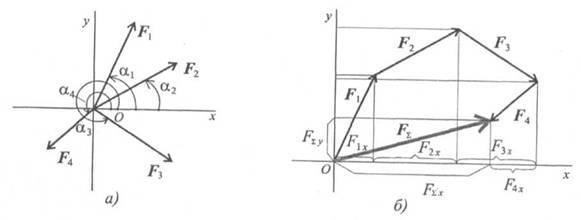
Рис.3.4

FΣч  = Flx + F2x + F3x
+ F4x; FΣн = Fly + F2y + F3y + F4y;

;  .

Модуль (величину)
равнодействующей можно найти по известным
проекциям:

 .

Направление вектора
равнодействующей можно определить по
величинам и знакам косинусов углов,
образуемых равнодействую­щей с осями
координат (рис. 3.5). Растяжение сжатие
Продольные силы и определение напряжений.

;

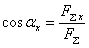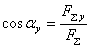
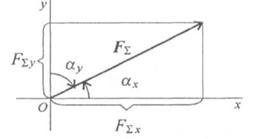
Рис.3.5

Условия равновесия
плоской системы сходящихся сил в
аналитической форме. Исходя из того,
что равнодействующая равна нулю, получим:

  FΣ = 0.

Условия равновесия
в аналитической форме можно сформулиро­вать
следующим образом:

Плоская
система сходящихся сил находится в
равновесии, ес­ли алгебраическая
сумма проекций всех сил системы на любую
ось равна нулю. Система уравнений
равновесия плоской сходящейся системы
сил:.

7. Условие равновесия системы сходящихся сил в аналитической и геометрической формах

Равновесие
системы сходящихся сил.

Из законов меха­ники
следует, что твердое тело, на которое
действуют взаимно уравновешенные
внешние силы, может не только находиться
в покое, но и совершать движение, которое
мы назовем движением «по инер­ции».
Таким движением будет, например,
поступательное равномерное и прямолинейное
движение тела.

Отсюда получаем
два важных вывода:

1) Условиям равновесия
статики удовлетворяют силы, действующие
как на покоящееся тело, так и на тело,
движущееся «по инерции».

2) Уравно­вешенность
сил, приложенных к свободному твердому
телу, является необходимым, но не
достаточным условием равновесия (покоя)
самого тела; в покое тело будет при этом
находиться лишь в том случае, если оно
было в покое и до момента приложения к
нему уравнове­шенных сил.

Для равновесия
приложенной к твердому телу системы
сходя­щихся сил необходимо и достаточно,
чтобы равнодействующая этих сил была
равна нулю. Условия, которым при этом
должны удовле­творять сами силы, можно
выразить в геометрической или
аналити­ческой форме.

1. Геометрическое
условие равновесия. Так
как равнодействующая   сходящихся
сил определяется как замыкающая сторона
силового многоугольника, построенного
из этих сил, то   может
обратиться в нуль тогда и только тогда,
когда конец последней силы в многоугольнике
совпадает с началом первой, т.
е. когда много­угольник замкнется.

Следовательно,
для равновесия системы, сходящихся сил
необ­ходимо и достаточно, чтобы силовой
многоугольник, построен­ный из этих
сил, был замкнут.

2. Аналитические
условия равновесия. Аналитически
равнодействующая системы сходящихся
сил определяется формулой

.

Так
как под корнем стоит сумма положительных
слагаемых, то R обратится
в нуль только тогда, когда одновременно ,
т. е. когда действующие на тело силы
будут удовлетворять равенствам:

Равенства
выражают условия
равновесия в аналитической форме: для
равновесия пространственной системы
сходящихся сил необходимо и достаточно,
чтобы суммы проекций этих сил на каждую
из трех координатных осей были равны
нулю.

Если все действующие
на тело сходящиеся силы лежат в одной
плоскости, то они образуют плоскую
систему сходящихся сил. В случае плоской
системы сходящихся сил получим, очевидно,
только два условия равновесия

Равенства выражают
также необходимые условия (или уравнения)
равновесия свободного твердого тела,
находящегося под действием сходящихся
сил.

Теорема
о трех силах. Уравновешенная
плоская система трех непараллельных
сил является сходящейся.

Условие
«плоская» в формулировке теоремы не
является необходимым  можно
убедиться, что любая уравновешенная
система трех сил всегда будет плоской.
Это следует из условий равновесия
произвольной пространственной системы
сил, которые будут рассмотрены далее.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Системой сходящихся сил называют группу двух, трех и более сил, приложенных к телу, линии действия которых пересекаются в некоторой точке.

Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, … F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

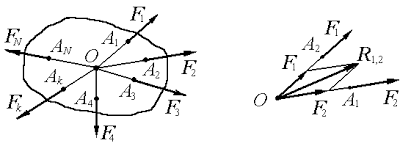
Рисунок 1

В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

(F₁, F₂) ~ R_1,2,

где R_1,2=F₁+F₂.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R^*_1,2 и силы F₃, тогда

(R_1,2 F₃) ~ (F₁, F₂, F₃) ~ R_1,2,3,

где R_1,2,3=F₁+F₂+F₃ и т.д.

Для системы N сил окончательно будем иметь

(F₁ F₂ … F_N) ~ R^*,

R^*= F₁ + F₂ + … + F_N= ∑F_i .          (1)

На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.

Силовой многоугольник

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄.

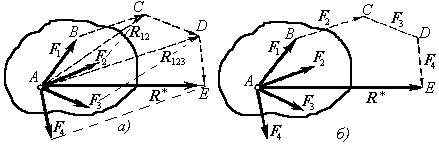
Рисунок 2

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.

Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

R_x = ∑ F_kx ,      
R_y = ∑ F_ky ,    
R_z = ∑ F_kz .       (2)

Тогда величина равнодействующей определится следующей формулой:

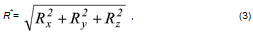
или

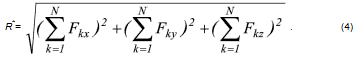
Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

cos α = R_x/R,      cos β = R_y/R,     cos γ = R_z/R.       (5)

Здесь  α ,  β ,  γ — углы между положительным направлением осей координат и равнодействующей.

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.

Примеры решения задач >
Условия равновесия системы сходящихся сил >

§ 3. Система сходящихся сил. Способы нахождения равнодействующей системы сходящихся сил

Система сил, линии действия которых пересекаются в одной точ­ке, называется системой сходящихся сил.

Система сходящихся сил либо приводится к равнодействующей, либо находится в равновесии.

Теорема. Равнодействующая системы сходящихся сил равна век­торной сумме этих сил.

Действительно, пусть к абсолютно твердому телу приложена система сил F_1, F₂, …, F_n, линии действия которых пересекаются в некоторой точке О (рис. 9). Мы могли бы складывать последова­тельно эти силы по аксиоме о параллелограмме сил. Однако этот путь очень длинен. Пользуясь правилом геометрического сложения векторов, сразу построим многоугольник сил F₁, F₂, …,F_n, замыкающая сторона которого и будет равнодействующей силой R.

Изложенный способ определения равнодействующей является геометрическим. Однако равнодействующую силу R можно определить и аналитически, по проекциям на неподвижные оси декартовой системы координат, выбрав за начало координат точку О пересечения линий действия системы сходящихся сил.

Равновесие системы сходящихся сил.

Рекомендуемые материалы

Условия равновесия системы сходящихся сил

Если система сходящихся сил находится в равновесии, механи­ческим условием равновесия является равенство нулю равнодейст­вующей силы. Получим

 или                                                          R = 0

Так как векторная сумма сил равна нулю, то многоугольник сил является замкнутым (начало первого вектора силы и конец по­следнего совпадают).

Таким образом, при равновесии системы сходящихся сил много­угольник сил является замкнутым (условие равновесия в геометри­ческой или графической форме).

В аналитической форме условия равновесия системы сходящихся сил заключаются в следующем.

Если пространственная система сходящихся сил находится в рав­новесии, то алгебраическая сумма проекций этих сил на каждую из трех координатных осей должна равняться нулю (на две оси, если система сходящихся сил расположена на плоскости).

Поскольку в случае равновесия указанной системы сил их рав­нодействующая равна нулю (R = 0), то равны нулю и ее проекции на оси координат, т. е. R_х = 0, R_у = 0, R_г = 0. На основании (1.10) получим

       

Для плоской сходящейся системы сил имеем

     

 Условия (1.13) и (1.14) в аналитической форме называются также уравнениями равновесия. Для статической определенности задачи число неизвестных не должно превышать числа уравнений равно­весия.

Момент силы относительно точки и оси. Главный вектор и главный момент. Пара сил. Момент силы относительно точки

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на силу. Итак, по определению (рис. 12),

 

Обозначая длину перпендикуляра, опущенного из центра момента на линию действия силы, через h (величину h в дальнейшем будем называть плечом), можно модуль вектора Мо (F) представить в виде произведения Fh, т. е.

|М₀(F)|  =М₀(F) = Fh.

Таким образом, момент силы относительно   точки — это вектор, направленный   перпендикулярно   к   плоскости,   содержащей   силу и точку, в ту часть пространства,.

Для аналитического определения момента силы относительно точки выберем произвольную систему координат О_xyz с началом в точке О (рис. 13) и обозначим проекции радиуса-вектора г и силы F на координатные оси О_x, О_Y, О_z, соответственно через х, у, z и X, У, Z. Заметим, что проекции х, у, z радиуса-вектора г точки прило­жения силы одновременно означают координаты этой точки. Тогда, спроектировав обе части векторного равенства (1.15) на оси координат, получим  выражение момента силы относительно точки в анали­тической форме в виде трех его проекций на координатные оси:

                                                       ,

                                                       .

Теорема о моменте равнодействующей системы

сходящихся сил (теорема Вариньона)

Момент силы относительно оси

Моментом силы относительно оси называется проекция на ату ось момента силы относительно произвольной точки на оси. Момент силы F относительно оси Оz обозначается через М_z (F). Таким обра­зом,

М

      Момент силы относительно оси, как будет показано в динамике, является физической величиной, характеризующей вращательное движение твердого тела.

Согласно определению, моменты силы относительно координат­ных осей выражаются величинами (1.18), т. е. соответственно равны проекциям

М    М_У(F) = zХ -хZ;    М

Укажем практический способ определения момента силы относи­тельно оси.

 Главный вектор и главный момент системы сил

Главным вектором R системы сил   F₁,F₂ … , F_n называется векторная сумма этих сил, т. е.

R=

Таким образом, главный вектор системы сил можно определить геометрически с помощью многоугольника сил.

Аналитически главный вектор определяется тремя своими проекциями на координатные оси;

R

  R 

R

Главным моментом Мо системы сил F_1: F₂, …, F_n относительно точки называется векторная сумма моментов этих сил относительно этой точки, т. е

M

Таким образом, главный момент системы сил относительно точки можно определить геометрически с помощью многоугольника момен­тов этих сил относительно данной точки.

Аналитически главный момент относительно точки определяется тремя своими проекциями на координатные оси:

M

M

M

или

;   ;   

Заметим, что понятия главного вектора и равнодействующей системы сил не тождественны. Как мы увидим в следующей главе, не всякая система сил имеет равнодействующую. Если же система сил и приводится к равнодействующей, то последняя, хотя геометрически и равна главному вектору, но имеет вполне определенную линию действия, в то время как главный вектор (также и главный момент) является свободным вектором.

В лекции “3. Архитектура операционной системы” также много полезной информации.

Пара сил

Парой сил называется система двух параллельных сил, равных по величине, направленных в противоположные стороны и приложенных к твердому телу.

Пара сил может быть ориентирована положи­тельно (против часовой стрелки в правой системе координат) и отрицательно (по часовой стрелке в левой системе координат). Очевидно, что с переходом от правой системы координат к левой ориентация пары сил изменяется на противоположную. Кратчайшее рас­стояние Н между линиями действия сил пары называется ее плечом.

Главный вектор пары сил равен нулю. Пусть силы F и —F пары приложены соответственно в точках А и В. Определим главный мо­мент пары сил относительно какой-либо точки О. Главный момент пары сил не зависит от выбора центра момен­тов; он обозначается М и называется моментом пары сил:

1                    М₀ = М = В А х F.

Итак, момент пары сил — это свободный вектор, по модулю равный М = Fh и направленный перпендикулярно плоскости ее действия так, чтобы с вершины этого вектора пара сил была ориентирована положительно.