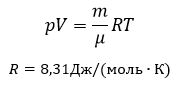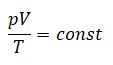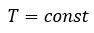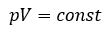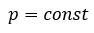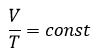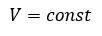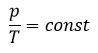Уравнение состояния идеального газа определяет связь температуры, объема и давления тел.
- Позволяет определить одну извеличин, характеризующих состояние газа, по двум другим (используется в термометрах);
- Определить, как протекают процессы при определенных внешних условиях;
- Определить, как меняется состояние системы, если она совершает работу или получает тепло от внешних тел.
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
– универсальная газовая постоянная, R = kNA
Уравнение Клапейрона (объединенный газовый закон)
Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный.
Количественные зависимости между двумя параметрами газа одной и той же массы при неизменном значении третьего параметра называют газовыми законами.
Газовые законы
Закон Бойля – Мариотта
Первый газовый закон был открыт английским ученым Р. Бойлем (1627—1691) в 1660 г. Работа Бойля называлась «Новые эксперименты, касающиеся воздушной пружины». И действительно, газ ведет себя подобно сжатой пружине, в этом можно убедиться, сжимая воздух в обычном велосипедном насосе.
Бойль изучал изменение давления газа в зависимости от объема при постоянной температуре. Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим (от греческих слов isos — равный, therme — тепло).
Независимо от Бойля несколько позднее французский ученый Э. Мариотт (1620—1684) пришел к тем же выводам. Поэтому найденный закон получил название закона Бойля—Мариотта.
Произведение давления газа данной массы на его объем постоянно, если температура не меняется
pV = const
Закон Гей-Люссака
Сообщение об открытии еще одного газового закона было опубликовано лишь в 1802 г., спустя почти 150 лет после открытия закона Бойля—Мариотта. Закон, определяющий зависимость объема газа от температуры при постоянном давлении (и неизменной массе), был установлен французским ученым Гей-Люссаком (1778— 1850).
Относительное изменение объема газа данной массы при постоянном давлении прямо пропорционально изменению температуры
V = V0 αT
Закон Шарля
Зависимость давления газа от температуры при постоянном объеме экспериментально установил французский физик Ж. Шарль (1746—1823) в 1787 г.
Ж. Шарль в 1787 г., т. е. раньше, чем Гей-Люссак, установил и зависимость объема от температуры при постоянном давлении, но он своевременно не опубликовал своих работ.
Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
p = p0 γT
| Название | Формулировка | Графики |
|
Закон Бойля-Мариотта– изотермический процесс |
Для данной массы газа произведение давления на объем постоянно, если температура не меняется |
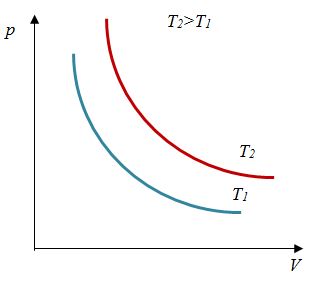   |
|
Закон Гей-Люссака– изобарный процесс |
Для данной массы газа отношение объема к температуре постоянно, если давление не меняется |
   |
|
Закон Шарля– |
Для данной массы газа отношение давления к температуре постоянно, если объем не меняется |
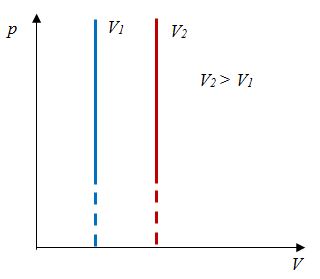   |
Графические задачи


Для
данной массы газа при постоянном объеме
V
= const
давление газа изменяется линейно с
температурой (закон Шарля):
![]()
(5)
где
ро –
давление газа при 0оС,
р –
давление газа при температуре t,
V
–
термический коэффициент давления газа
для изохорического процесса (или
изохорный коэффициент давления, или
термический
коэффициент давления).
Уравнение
(5), называемое уравнением
изохоры
(процесс,
происходящий при постоянном объеме,
называется изохорическим),
выражает
закон Шарля. Этот закон был открыт им в
1787 году.
Термический
коэффициент давления любого вещества
для изохорического процесса
определяют как
![]()
(6).
Индекс
V
у
производной показывает, что она берется
при V
=
const.
Для идеального газа в соответствии с
выражением (5) этот коэффициент будет
равен
![]()
(7)
Термический
коэффициент объемного расширения
представляет
собой относительное изменение давления
при изменении температуры на 1 К при
изохорическом процессе. Относительное
изменение давления определяется по
отношению к давлению, соответствующему
нормальным условиям, то есть при 0оС.
Экспериментально
установлено, что для идеального газа
![]()
(8).
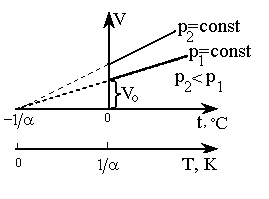
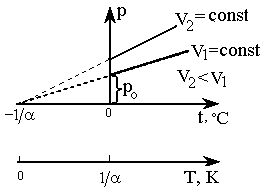
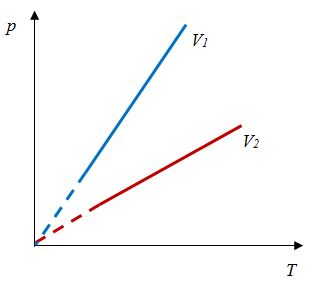
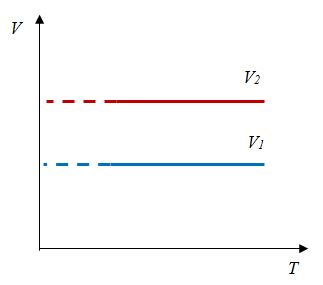
Согласно
формулам (2) и (5), изобарический и
изохорический процессы представляются
на графиках прямыми линиями (изобарами
и изохорами) (рис. 2, 3), проходящими
наклонно к оси температур и пересекающими
ее в точке
![]()
,
определяемой из условия 1 + t
= 0. Если перенести начало отсчета в эту
точку, то происходит переход к шкале
Кельвина (рис. 2, 3), откуда Т = t
+
![]()
.
Точка
![]()
принята
за начало отсчета новой шкалы температур,
называемой термодинамической шкалой
(шкалой Кельвина), или абсолютной шкалой.
Температура, отсчитываемая по этой
шкале, называется термодинамической;
ноль этой шкалы называется нолем
Кельвина.
|
|
|
Рис. 2. Изобары |
|
|
|
Рис. 3. Изохоры |
Вводя в формулы
(2), (5) термодинамическую температуру,
законам Гей-Люссака и Шарля можно придать
более удобный вид:
![]()
(9)
![]()
(10).
Или
![]()
для
р
= const,
m =
const, (11)
![]()
для
V = const,
m =
const (12).
Уравнение состояния идеального газа
Величинами,
определяющими состояние газа являются:
давление р,
под
которым
находится газ, его температура Т
и
объем V,
занимаемый
определенной
массой газа. Их называют макропараметрами
состояния.
Перечисленные
три величины не являются независимыми.
Каждая
из них является функцией двух других.
Уравнение, связывающее
все три величины – давление, объем и
температуру газа для
данной его массы, называется уравнением
состояния
и
может быть
в общем виде записано так:
f(р,
V,
T)
= 0.
Это
значит, что состояние газа определяется
только двумя параметрами
(например, давлением и объемом, давлением
и температурой
или, наконец, объемом и температурой),
третий параметр однозначно
определяется двумя другими. Если
уравнение состояния известно в явном
виде, то любой параметр можно вычислить,
зная
два других.
Давление,
концентрация газа n
и температура связаны между собой как:
p
= nkT, (13)
где
k
–
постоянная Больцмана, равная 1,380662.10-23
Дж/К.
Если
в объеме V
содержится N
частиц,
то по определению
n
= N/V (14)
подставив
(13)
в (14), получим, что
pV = NkT
(15)
Это
уравнение, в которое входят
все три параметра состояния, и является
уравнением состояния идеальных газов.
Его
можно преобразовать так, чтобы в него
вместо недоступного прямому измерению
числа частиц N
входила
легко измеряемая масса газа m.
Для
такого преобразования воспользуемся
понятием о моле.
Молем
вещества называется такое его количество,
масса которого, выраженная в граммах,
равна относительной молекулярной массе
М вещества (иногда говорят: молекулярному
весу, молярной массе). Моль любого
вещества содержит одно и то же число
молекул.
Число
частиц в одном моле, одинаковое для всех
веществ, называется числом
Авогадро
NА,
которое
равно
NА
= 6,0220943
.
1023
моль-1.
Можно,
таким образом, определить моль как
единицу особой величины
–
количества
вещества.
Если
разделить число молекул N в данной массе
газа на число Авогадро NА,
то
получим число молей
в этой массе газа
=
N/NА (16)
Но
эту же величину можно получить, разделив
массу m
газа
на его молярную массу М
=
m/М (17)
Из выражений (16),
(17) получим выражение для N:
![]()
(18)
Подставим
выражение (18) в формулу (15). Тогда уравнение
состояния примет вид:
![]()
(19).
В
это уравнение входят две универсальные
константы: число Авогадро NА
и
постоянная Больцмана k.
Произведение
универсальных констант тоже является
универсальной константой. Она получила
название универсальной
газовой постоянной
R
= NАk (20)
R
= 8,31414 Дж/(моль.К).
Подставив (20) в
уравнение (19), получим:
![]()
(21).
Представленное
в таком виде уравнение состояния
идеального газа называют уравнением
Менделеева – Клапейрона.
Это уравнение связывает макроскопические
параметры состояния для газа. Уравнение
(21) описывает равновесное состояние
газа, когда его параметры во всем объеме
не зависят от времени (иначе говоря,
остаются неизменными по всему объему).
Реализовать такие условия трудно.
Поэтому определить идеальный газ можно
еще и так: газ, подчиняющийся уравнению
Менделеева – Клапейрона
во всем диапазоне изменения температуры
и давления, называется идеальным.
Одна из форм записи
уравнения состояния имеет вид
![]()
(22)
Это
уравнение носит название уравнения
Клапейрона.
Согласно этому уравнению произведение
давления газа данной массы на его объем,
деленное на абсолютную температуру,
есть величина постоянная, не зависящая
от состояния, в котором находится газ.
Сравнив выражения (21) и (22), можно увидеть,
что для одного моля газа
![]()
.
Практическая
часть
Экспериментальная
установка для исследования экспериментальных
газовых законов приведена на рис. 4.
В
стеклянном корпусе (1) находится шприц
с подвижным поршнем (2). Под стеклянным
корпусом, не касаясь его, расположена
плитка (3). Датчик давления (4), подключают
к входу S1
устройства Cobra
(5). Короткая резиновая трубка-переходник
(6) соединяет датчик давления со шприцом.
Этот датчик позволяет автоматически
производить измерение давления во
внутренней камере шприца. Стеклянную
емкость через отверстие (7) заполняют
водой. В воду помещают магнитную мешалку.
Можно перемешивать воду, обеспечивая
равномерный прогрев воздуха во внутренней
камере шприца, поднося магнит (9) к
стеклянному корпусу (1). В отверстие (8),
закрытое специальной пробкой с отверстием,
помещают термодатчик (10), также подключив
его к разъему S2
устройства Cobra
(5).

















Рис.
4. Схема установки для
исследования газовых законов.
1
– стеклянный корпус; 2 – подвижный
поршень (шприц находится внутри
стеклянного корпуса); 3 – плитка; 4 –
датчик давления; 5 – устройство Cobra;
6 – резиновая трубка-переходник; 7, 8 –
отверстия в стеклянном корпусе; 9 –
магнит;10 – термодатчик.
Осуществить
изотермический процесс можно при
комнатной температуре, изменяя объем
воздуха в шприце, перемещая поршень
(2). Давление при этом будет меняться,
что автоматически зафиксирует датчик
давления (4). Температуру при этом будет
фиксировать термодатчик (10).
Изобарический
и изохорический процессы можно изучать
одновременно. Температуру воздуха в
шприце можно увеличить при нагревании
воды, находящейся в стеклянном корпусе.
Для этого используют плитку (3). Нагревание
воздуха в шприце приведет к его расширению,
поршень будет перемещаться таким
образом, чтобы давление оставалось
равным атмосферному (р = const).
Фиксируя вручную изменение объема
воздуха и соответствующую температуру
по показаниям термодатчика (10), можно
получить данные о зависимости V(T)
для изобарического процесса.
В
то же время, можно получить данные о
зависимости р(Т) для изохорического
процесса, возвращая поршень (2) в исходное
положение (к начальному объему, то есть
поддерживая V
= const)
после повышения температуры на
определенную величину Т
(например, 5К). Давление автоматически
будет фиксировать датчик давления (4).
Во
всех случаях количество воздуха в шприце
остается неизменным, то есть
=
const.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Онлайн калькулятор поможет рассчитать какое будет конечное давления идеального газа от изменения температуры, при условии, что объем газа остается постоянным. Зависимость давления от температуры в этом случае описывается законом Гей-Люссака (законом Шарля).
Формула: P2 = P1×T2/T1
Где:
P1 – начальное давление;
P2 – конечное давление;
T1 – начальная температура (в Кельвинах);
T2 – конечная температура (в Кельвинах).
Например, данный калькулятор поможет приблизительно определить зависимость давления в шинах от температуры.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Относительное изменение – давление
Cтраница 1
Относительное изменение давления – – приблизительно пропорционально квадрату отношения скорости движения потока газа о) к скорости звука а. Поэтому можно сделать заключение, что при росте отношения скорости потока газа к скорости звука свойство сжимаемости газа сказывается все в большей степени. Следовательно, скорость звука является критерием сжатия газа.
[1]
А относительное изменение давления уменьшается.
[3]
Если принять относительное изменение давления равным 25 %, то полезный объем аккумулятора ( накопленный объем масла) А К будет составлять примерно 25 % общей ( конструктивной) его емкости. В большинстве случаев полезный объем аккумулятора составляет от 15 до 20 % общего конструктивного его объема.
[4]
Член при относительном изменении давления о в уравнении (V.26) представляет собой безразмерный коэффициент самовыравнивания, по величине обратный коэффициенту усиления К.
[5]
С ростом параметра А относительное изменение давления уменьшается.
[6]
К l / o – относительное изменение давления, приходящееся на 1 С изменения температуры ( Т0 – абсолютная температура при начальных условиях); для температур порядка от – 20 до 20 С значения К ъ 0.3 – г – 0 4 % / С.
[7]
Кроме того, при изоэнтропических движениях относительные изменения давления и плотности пропорциональны [ разд.
[8]
В левой части этих равенств стоит относительное изменение давления пара одного из компонентов в результате того, что он входит в состав раствора. Из формул видно, что относительное изменение равновесного давления пара одного из компонентов равно концентрации другого компонента. В частности, когда растворенное вещество нелетуче, первая из формул (108.3) означает, что относительное изменение упругости насыщенного пара растворителя равно концентрации растворенного вещества.
[9]
Как следует из соотношения (4.58), относительное изменение давления влаги в корке при консолидации, кроме проницаемости корки и пласта, зависит также от ее толщины L и толщины модели пласта Ln. В случае расчета для условий скважины, необходимо брать достаточно удаленную зону, как это делается для пластовых систем.
[10]
В левой части этих равенств стоит относительное изменение давления пара одного из компонентов в результате того, что он входит в состав раствора. Из формул видно, что относительное изменение равновесного давления пара одного из компонентов равно концентрации другого компонента. В частности, когда растворенное вещество нелетуче, первая из формул (108.3) означает, что относительное изменение упругости насыщенного пара растворителя равно концентрации растворенного вещества.
[11]
Иногда при расчете пневмотранспорта рассматривается коэффициент относительного изменения давления а, являющийся отношением полного перепада давления при пневмотранспорте к потере напора при движении незапыленного потока с той же скоростью, с какой движется транспортирующий агент.
[12]
Показать, что для любой бегущей акустической волны относительное изменение давления dp / p в данной точке равно отношению скорости частицы к скорости звука, умноженному на ycp / cv, где ср и с – теплоемкости вещества среды соответственно при постоянном давлении и постоянном объеме.
[13]
На рис. 4.8 – 4.13 представлены временные характеристики относительного изменения давления c &i и флегмового числа аю в зависимости от возмущающих и управляющих воздействий, модуль которых приведен к одной величине. Пунктирные кривые относятся к аппарату В ( R oo), сплошные воспроизводят динамические свойства аппарата С ( У.
[15]
Страницы:
1
2
3
Преподаватель который помогает студентам и школьникам в учёбе.
Газовые законы в физике – формулы и определения с примерами
Содержание:
Газовые законы:
С помощью уравнения состояния идеального газа можно исследовать процессы, при которых сохраняются постоянными масса газа и один из его макроскопических параметров.
Газовыми законами называются законы, определяющие количественную зависимость между двумя макроскопическими параметрами газа данной массы 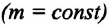
Изопроцессами (греч.: izos – “равный “) называются процессы, протекающие в газах данной массы 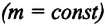
Закон Бойля-Мариотта
Этот закон был определен в 1662 году английским физиком Робертом Бойлем (1627-1691) и в 1676 году французским физиком Эдом Мариоттом (1620-1684).
Для данной массы газа при неизменной температуре произведение давления газа на его объем постоянно 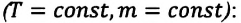

Для данной массы газа при неизменной температуре произведение давления начального состояния 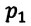 на его первоначальный объем
на его первоначальный объем 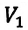 равно произведению значений этих параметров
равно произведению значений этих параметров 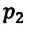 и
и 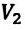 произвольного состояния:
произвольного состояния:
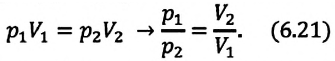
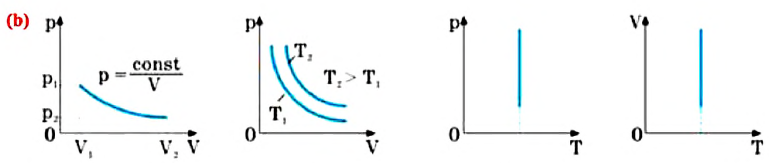
Изотермическим называется процесс изменения состояния данной массы идеального газа при постоянной температуре 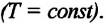 В изотермическом процессе давление газа и его объем обратно пропорциональны друг другу (b).
В изотермическом процессе давление газа и его объем обратно пропорциональны друг другу (b).
Закон Гей-Люссака
Этот закон был экспериментально установлен в 1802 году французским физиком Джозефом Луи Гей-Люссаком (1778-1850).
Для данной массы газа при неизменном давлении отношение объема газа к его абсолютной температуре постоянно 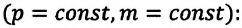
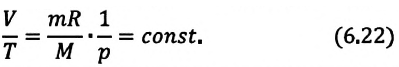
При неизменном давлении отношение первоначального объема газа 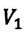 к его первоначальной температуре
к его первоначальной температуре 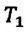 равно отношению параметров
равно отношению параметров 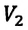 к
к 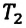 в произвольном состоянии:
в произвольном состоянии:

Закон Гей-Люссака можно выразить и так:
Для данной массы идеального газа при неизменном давлении относительное
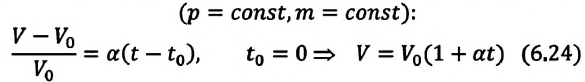
Где 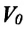 -объем идеального газа при постоянном давлении при температуре 0°С,
-объем идеального газа при постоянном давлении при температуре 0°С, 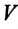 -объем конечного состояния,
-объем конечного состояния, 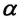 — коэффициент объемного расширения. Опыты показывают, что при нагревании любого разряженного газа на
— коэффициент объемного расширения. Опыты показывают, что при нагревании любого разряженного газа на 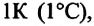 при постоянном давлении, его объем увеличивается приблизительно на
при постоянном давлении, его объем увеличивается приблизительно на 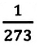 часть объема первоначального состояния:
часть объема первоначального состояния:
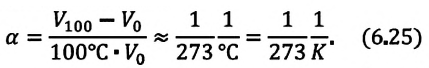
Изобарным называют процесс изменения состояния данной массы идеального газа при постоянном давлении 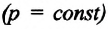 (с). При изобарном процессе объем данной массы газа прямо пропорционален его температуре.
(с). При изобарном процессе объем данной массы газа прямо пропорционален его температуре.
- Заказать решение задач по физике
Закон Шарля
Этот закон экспериментально определил в 1787 году французский физик Шарль Жак Александр Сезар (1746-1823):
Для данной массы газа при постоянном объеме отношение давления газа к его абсолютной температуре остается неизменным 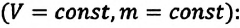
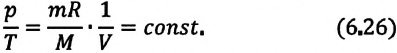
Отношение первоначального давления 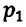 газа к его температуре
газа к его температуре 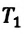 равно отношению параметров
равно отношению параметров 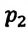 к
к 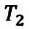 в произвольном состоянии:
в произвольном состоянии:

Закон Шарля можно выразить и так:
Для данной массы идеального газа при неизменном объеме относительное изменение давления прямо пропорционально изменению температуры 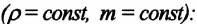
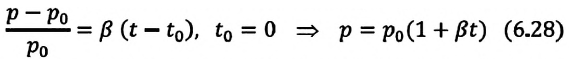
Где 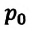 – давление начального состояния идеального газа (при температуре
– давление начального состояния идеального газа (при температуре 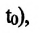
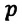 — давление конечного состояния (при температуре
— давление конечного состояния (при температуре 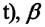 – коэффициент изменения давления. Из опытов было определено, что при нагревании любого разряженного газа на
– коэффициент изменения давления. Из опытов было определено, что при нагревании любого разряженного газа на 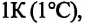 при постоянном объеме, его давление увеличивается приблизительно на
при постоянном объеме, его давление увеличивается приблизительно на 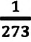 часть давления первоначального состояния:
часть давления первоначального состояния:
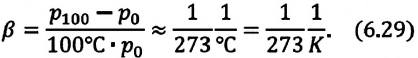
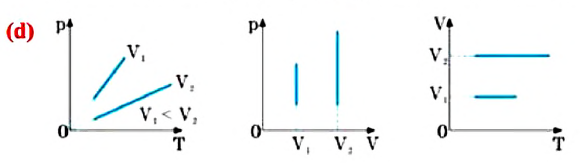
Изохорным называется процесс изменения состояния данной массы идеального газа при постоянном объеме 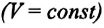 (d). При изохорном процессе давление данной массы газа прямо пропорционально его температуре.
(d). При изохорном процессе давление данной массы газа прямо пропорционально его температуре.
Закон Дальтона
Этот закон в 1801 году установил английский исследователь Джон Дальтон (1766-1844):
Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов:
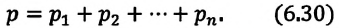
Парциальное давление — это давление отдельно взятого газа из газовой смеси.
Закон Авогадро
Этот закон, как предположение, был выдвинут в 1811 году итальянским физиком Амедео Авогадро (1776-1856). В последующем это предположение было подтверждено многочислеными опытами.
В равных объемах различных газов, взятых при одинаковых температурах и давлении, содержится одинаковое число молекул. Например, число молекул в 1 моле произвольного газа равно: 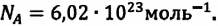 При нормальных условиях объём 1 моля газа равен 22,4 л (л/моль). Этот объём называют молярным объёмом идеального газа.
При нормальных условиях объём 1 моля газа равен 22,4 л (л/моль). Этот объём называют молярным объёмом идеального газа.
- Взаимодействие молекул
- Агрегатное состояние вещества
- Зависимость размеров тел от температуры
- Световые явления
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Движение молекул в физике в газах, жидкостях и твёрдых телах
- Скорость движения молекул газа