РАДИОАКТИВНЫЙ
РАСПАД
Ядра
атомов состоят из протонов р,
электрический заряд, которых равен
элементарному заряду, и незаряженных
частиц нейтронов n.
Эти частицы также называют нуклонами.
Ядра
атомов обозначают теми же символами
периодической системы, что и сами атомы.
При этом слева внизу указывается
зарядовое число Z
(заряд ядра в единицах элементарного
заряда), а вверху – массовое число А
(число нуклонов в ядре).
Ядра, содержащие
одинаковое число протонов, но разное
число нейтронов называются изотопами.
Так же изотопами называются и атомы,
ядра которых удовлетворяют этому
условию. Известно около 1500 изотопов,
примерно пятая часть из которых стабильна.
Между нуклонами
в ядре действуют ядерные силы. Поэтому
чтобы разделить ядро на отдельные
нуклоны необходимо затратить некоторую
энергию называемую энергией связи Ес.
При передаче энергии нуклонам их масса
возрастает. Поэтому сумма масс свободных
нуклонов, больше массы ядра на величину
называемую дефектом массыm:
m
= Z mp
+ (A – Z) mn
– mя. (1)
Энергия связи
Есравна:
Ес=mс2(2)
Если дефект
массы измерять в а.е.м., то:
Ес= 931![]() ·m; (2.1)
·m; (2.1)
Удельной
энергией связи Есуназывается
величина равная энергии связи, приходящейся
на один нуклон ядра:
![]() (3)
(3)
Процесс
взаимодействия атомного ядра с
элементарной частицей или другим ядром,
приводящий к преобразованию ядра (или
ядер) называют ядерной реакцией.
В ядерных
реакциях выполняются законы сохранения:
-
Электрического
заряда; -
Суммарного
числа нуклонов; -
Энергии;
-
Импульса.
Энергия
ядерной реакции (или тепловой эффект
реакции) равна:
Q= (m-m)c2: (4),
где m,m,
суммы масс покоя частиц соответствено
до и после реакции. Массы изотопов,
необходимые для решения задач, приведены
в таблице 3.1.
Радиоактивным
распадом называется спонтанное
превращение одних атомных ядер в другие,
сопровождаемое испусканием элементарных
частиц.
Радиоактивный
распад подчиняется следующему закону:
для данного ядра, находящегося в
определенном энергетическом состоянии,
вероятность его распада в единицу
времени есть величина постоянная.
Этот закон
позволяет получить зависимость числа
не распавшихся ядер от времени, которую
также иногда называют законом
радиоактивного распада:
N=Noe–![]() t , (5)
t , (5)
где Nо– начальное число ядер,![]() –
–
постоянная распада.
Радиоактивный
распад можно характеризовать периодом
полураспада Т1/2, т.е. временем, за
которое распадается половина начального
числа ядер изотопа. Т1/2 и![]() связаны соотношением:
связаны соотношением:
 , (6)
, (6)
поэтому:
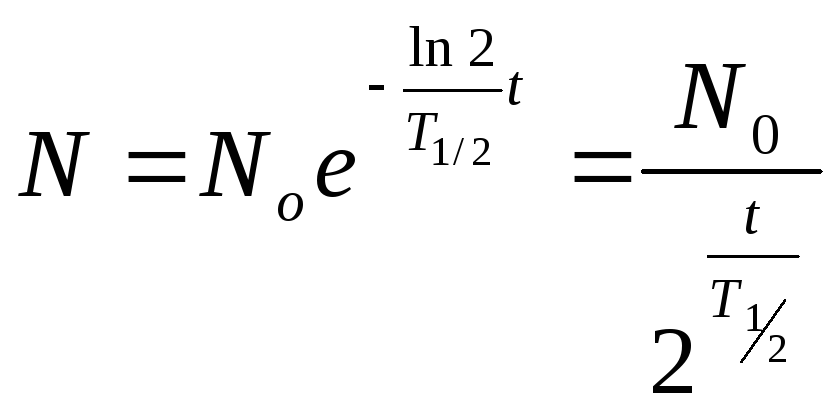 . (7)
. (7)
Среднее время жизни ядра равно:
 . (8)
. (8)
Радиоактивные вещества характеризуются
активностью – А, которая определяется
как число распадов ядер, происходящих
в препарате в единицу времени.
Активность вещества также зависит от
времени:
А = Аоe–![]() t. (9)
t. (9)
В системе СИ
активность изотопов измеряется в
Беккерелях: 1 Бк = 1![]() .
.
Применяется также внесистемная единица
активности Кюри (Кu).
1 Кu= 3,7 1010Бк – активность примерно 1
г радия.
Примеры решения задач
Задача 1.Определить энергию, необходимую
для разделения ядра 10Ne20на ядро углерода6С12и две
альфа-частицы, если известно, что удельные
энергии связи в ядрах10Ne20;6С12и2He4соответственно равны: 8,03; 7,68 и 7,07 МэВ на
нуклон.
Решение.
При образовании
ядра 10Ne20из
свободных нуклонов выделилась бы
энергия:
ЕNe=Ecу·А = 8,03 20 = 160,6 МэВ.
Соответственно
для ядра 612С и двух ядер24He:
Ес= 7,68 ·12 = 92,16
МэВ,
ЕНе= 7,07· 8 = 56,56
МэВ.
Тогда при
образовании 1020Ne
из двух ядер24Heи ядра612С выделилась бы
энергия:
![]() E
E
= ENe
– Ec
– EHe
![]() E
E
= 160,6 – 92,16 – 56,56 = 11,88 МэВ.
Такую же
энергию необходимо затратить на процесс
разделения ядра 1020Neна612С и 224H.
Ответ.
![]() Е
Е
= 11,88 МэВ.
Задача 2. При
соударении
![]() -частицы
-частицы
с ядром бора5В10произошла
ядерная реакция, в результате которой
образовалось ядро атома водорода и
неизвестное ядро. Определить это ядро
и найти энергетический эффект ядерной
реакции.
Решение.
Запишем уравнение
реакции:
5В10
+ 2Не4![]() 1Н1
1Н1
+ zХА
Из
закона сохранения числа нуклонов
следует, что:
10
+ 4 + 1 + А; А = 13
Из
закона сохранения заряда следует, что:
5
+ 2 = 1 +Z;
Z
= 6
По
таблице Менделеева находим, что
неизвестное ядро есть ядро изотопа
углерода 6С13.
Энергетический
эффект реакции рассчитаем по формуле
(4). В данном случае:
Q
=
![]()
Массы
изотопов подставим из таблицы (3.1):
![]() Q
Q
=
![]()
МэВ.
Ответ:
zХА
= 6С13;
Q
= 4,06 МэВ.
Задача
3. Какое количество теплоты выделилось
при распаде 0,01 моля
![]() –
–
радиоактивного изотопа за время, равное
половине периода полураспада? При![]() –
–
распаде ядра выделяется энергия 5,5 МэВ.
Решение:
Согласно формуле
(7)
![]() =
=![]()
.
Тогда, число
распавшихся ядер равно:
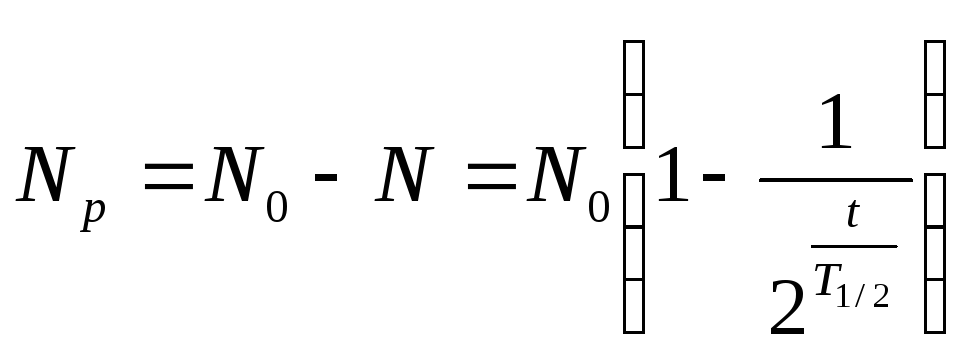 .
.
Так
как
![]() ν0,
ν0,
то:
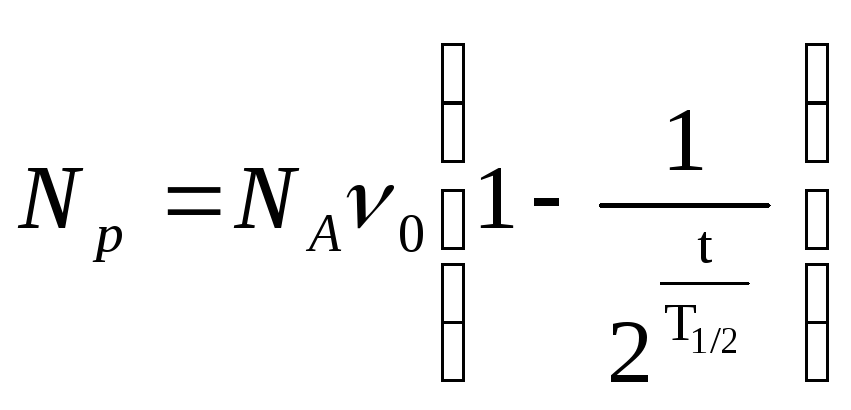 .
.
Поскольку
при одном распаде выделяется энергия
равная Е0
= 5,5 МэВ = 8,8·10-13
Дж, то:
Q
= Eo
Np
= NAoEo(1
–
![]()
![]() )
)![]() ,
,
Q
= 6,0210230,018,810-13(1
–
![]() )
)
= 1,55109
Дж
Ответ:
Q
= 1,55 ГДж.
Задачи для самостоятельного
решения.
3.1
Определить дефект масс, энергию связи
и удельную энергию связи изотопа углерода
6С12.
3.2
Какую энергию необходимо затратить,
чтобы разделить ядро кислорода 8O16
на отдельные нуклоны? Какова величина
дефекта масс этого ядра ?
3.3
Найти энергию, которую необходимо
затратить, чтобы разделить ядро лития
3Li6
а)на три равные части; б) на альфа –
частицу и ядро дейтерия.
3.4
Найти энергию, которую необходимо
затратить, чтобы разделить ядро углерода
6C12
а) на две одинаковые части; б) на три
одинаковые части.
3.5
В приведенной термоядерной реакции
установить ядро, обозначенное символом
«х», и рассчитать энергетический эффект
реакции
х
+ х →2He4+2n
3.6
Решить задачу 3.5 для реакции х + х →2He4+2
1H1
3.7
Решить задачу 3.5 для реакции 3Li6
+ 3Li6
→x+2He4+1H1
3.8
В приведенных ниже термоядерных реакциях
установить ядра, обозначенные символом
«х», указать, в какой из них выделяется
больше энергии и рассчитать эту энергию:
а)
x + 1H2
→2He4+1H3+1H1
б)
3Li6
+ x →2He4+2He3+n
3.9
Решить задачу 3.8 для следующих реакций:
а)
x + 1H3
→5B11+2He4+n
б)
6C13
+ 1H3
→x+1H2
3.10
Решить задачу для следующих реакций:
а)
6C12
+ x →7N14+2He4
б)
6C12
+ 3Li6
→8O16+x
3.11
Дописать схему ядерной реакции, установив
ядро, обозначенное символом «х».
Определить энергетический эффект
реакции в расчете на один нуклон 3Li6
+ 1H1
→2x+n
.
3.12
Какую энергию необходимо затратить,
чтобы разделить на отдельные нуклоны
ядра 3Li7
и 4Ве7?
Почему для изотопа 4Ве7
эта энергия меньше, чем для 3Li7?
3.13
Атомное ядро, поглотив гамма-квант с
длиной волны 0.47 пм перешло в возбужденное
состояние и распалось на отдельные
нуклоны. Суммарная кинетическая энергия
всех нуклонов Т=26.3 МэВ. Определить
энергию связи ядра.
3.14
Определить энергию, необходимую для
разделения ядра 10Ne20
на ядро углерода 6C12
и две альфа-частицы, если известно, что
удельные энергии связи в ядрах 10Ne20,
6C12,
2He4
соответственно равны: 8.3; 7.68; 7.07 МэВ на
нуклон.
3.15
При бомбардировке ядер лития 3Li7
протонами с энергией 1МэВобразуются
две альфа-частицы, имеющие одинаковые
скорости и движущиеся под одинаковыми
углами с направлением движения протона.
Определить скорость альфа-частиц.
Написать схему ядерной реакции.
3.16
Энергия связи ядра кислорода 8O16
равна 139,8 МэВ, а ядра фтора 9F19
– 147,8 МэВ. Какую минимальную энергию
нужно затратить, чтобы удалить один
протон из ядра фтора? Написать схему
реакции.
3.17
Написать схему альфа-распада ядра
88Ra226
. Считая, что до распада ядро радия
покоилось, найти отношение импульсов
и кинетических энергий продуктов
распада.
3.18
Написать схему альфа-распада ядра
94Pu238
. Вычислить энергию, выделяющуюся при
таком распаде, если энергия связи
материнского ядра равна
1801,3
МэВ, а у дочернего – 1778,5 МэВ.
3.19
Написать схему альфа-распада ядра
84Po210
. Вычислить энергию, выделяющуюся при
таком распаде, если у материнского ядра
энергия связи равна 1645.2 МэВ, а у
дочернего – 1622.3 МэВ .
3.20
Ядро висмута 83Bi210
может испытывать как альфа-распад, так
и бета-распад. Написать схемы распадов.
Для альфа-распада вычислить выделившуюся
энергию, если материнское ядро имеет
энергию связи равную1644.8 МэВ , а дочернее
-1621.6 МэВ.
3.21
При электронном распаде ядра 12Mg28
образуется новое радиоактивное ядро,
в результате распада которого получается
стабильный изотоп. Написать схему обоих
распадов. Считая массу покоя антинейтрино
равной нулю, рассчитать энергию,
выделяемую при обоих распадах, если
энергия связи ядра 12
Mg28
равна
231,6 МэВ, а у конечного продукта распада
– 236.5 МэВ.
3.22
В результате позитронного распада ядра
14Si26
образуется ядро, которое при β+
– распаде становится ядром стабильного
изотопа. Написать схемы обоих распадов.
Считая массу покоя нейтрино равной
нулю, найти энергию, выделяемую при
обоих распадах, если энергия связи
исходного ядра равна 243.8 МэВ , а конечного
– 255.2 МэВ.
3.23
Альфа-частица, обладающая кинетической
энергией 5.3 МэВ вызывает ядерную реакцию
4Be9
+ 2He4
→ 6C12
+ n.
Нейтрон вылетает под прямым углом к
направлению движения альфа-частицы.
Какова кинетическая энергия ядра
углерода ?
3.24
Найти энергетический эффект реакции
4Be9
+ 1H1
→ 2He4
+ 3Li6,
если известно, что кинетические энергии
протона и альфа-частицы равны соответственно
5.45 МэВ и 4 МэВ, причем альфа-частица
вылетела под углом 90 o
к направлению движения протона.
Ядро-мишень 4Ву9
неподвижно.
3.25
Деление ядер урана 92U235
под действием медленных нейтронов может
осуществляется, например, по схеме
92U235
+ n → 54Xe140
+ x + 2n . Установить ядро обозначенное
символом «х» . Продукты деления в
результате ряда β–
– распадов превращаются в стабильные
ядра 58Ce140
и 40Zr94
. Написать схемы этих β–
– распадов. Считая, что энергии связи
ядер U235,
Ce140
и Zr94
равны соответственно 1783.8 ; 1117.9 ; 814.7 МэВ
, а масса покоя антинейтрино равна нулю,
найти суммарную энергию, выделяющуюся
в процессе деления и при последующих
превращениях ядер.
3.26
Период полураспада изотопа 15P32
равен 14 дней. Во сколько раз уменьшится
активность препарата за 20 дней ? За какое
время активность уменьшится в 9 раз ?
3.27
Счетчик альфа-частиц установленный
вблизи радиоактивного препарата, при
первом измерении за минуту регистрировал
1600 частиц, а через 4 часа только 400 частиц.
Найти период полураспада изотопа.
Сколько частиц за одну минуту будет
регистрировать счетчик через 6 часов ?
3.28
Найти период полураспада радиоактивного
изотопа, если его активность через 10
суток уменьшилась на 25 % по сравнению с
первоначальной. Через какое время
останется 25 % исходного количества ядер
этого изотопа.
3.29
Активность радиоактивного изотопа за
20 суток уменьшилась в 3 раза. Найти
среднее время жизни этих ядер этого
изотопа. Во сколько раз уменьшится
активность через 60 суток ?
3.30
Количество ядер радиоактивного изотопа
за 6 месяцев уменьшилась в 8 раз. Найти
период полураспада этого изотопа. За
какое время количество ядер уменьшится
в 32 раза ?
3.31
Из каждого миллиона атомов радиоактивного
изотопа каждую секунду распадается 100
атомов. Во сколько раз уменьшится
исходное число ядер этого изотопа за
время 10000 с . Найти период полураспада
этого изотопа.
3.32
Найти период полураспада и среднее
время жизни ядер радиоактивного изотопа,
если за 5 часов распадается 25 % от
начального количества ядер. Какая часть
ядер от их начального числа останется
через 10 часов ?
3.33
Счетчик радиоактивного излучения,
помещенный вблизи изотопа Na24
в начале регистрировал 204 отсчета за
одну секунду. Через сутки он регистрирова
лишь 68 отсчетов в секунду. Найти период
полураспада изотопа. За какое время
активность препарата уменьшится в 17
раз.
3.34
Период полураспада ядер трития 1H3
составляет 12 лет . Найти активность
0.001 моля “сверхтяжелой воды”. Какое
количество ядер гелия 2He3
образуется в результате распада ядер
трития за 6 лет ?
3.35
Какое количество гелия (в молях) образуется
из 0.002 молей альфа-радиоактивного
препарата за время равное удвоенному
значению периоду полураспада? Какое
число ядер изотопа останется нераспавшимся
за это время?
3.36
Какое количество теплоты выделится при
распаде 0.01 моля альфа-радиоактивного
изотопа за время, равное половине периода
полураспада. Энергия, которая выделяется
при альфа-распаде составляет 5.5 МэВ.
3.37
10 миллиграмм альфа-радиоактивного
препарата висмута Bi214
с периодом полураспада 20 минут заключены
в герметичную капсулу, объемом 10 см3
. Найти приращение давления в капсуле
(за счет образования гелия) через 10 мин.
после ее закрытия, если температура
капсулы 300 К ?
3.38
В калориметре , теплоемкость которого
С равна 1000 Дж/К, помещены 0.001 моля
радиоактивного препарата. Через 60 мин.
после начала опыта температура колориметра
увеличилась на 0.6 К . Считая, что при
распаде ядра выделяется энергия 3.5 МэВ
найти период полураспада изотопа.
3.39
При альфа-распаде полония Po210
в течении 1 часа образовался гелий,
который при нормальных условиях занял
объем 89.5 см3.
Определить исходную массу полония, если
период его полураспада Т = 138 дней.
3.40
В калориметр поместили моля
альфа-радиоактивного препарата Bi214
с периодом полураспада 20 минут. Какова
теплоемкость калориметра, если через
10 минут после начала опыта его температура
повысилась на 20 К ? При распаде ядра
выделяется энергия примерно 5 МэВ.
|
Название постоянной |
Значение |
|
Постоянная Заряд электрона (e) Масса Скорость Постоянная Постоянная |
1,3810-23Дж/К 1,610-19 9,110-31 3,0108 6,6310-34 1,097107 |
Таблица 3.1
|
Символ |
Масса, а.е.м. |
Символ |
Масса, а.е.м. |
Символ |
Масса, а.е.м. |
|
0n1 |
1,00867 |
3L6 |
6,01513 |
6C12 |
12,00000 |
|
1H1 |
1,00783 |
3Le7 |
7,01601 |
6C13 |
13,00335 |
|
1H2 |
2,01410 |
4Be7 |
7,01693 |
6C14 |
14,00324 |
|
1H3 |
3,01605 |
4Be9 |
9,01219 |
7N14 |
14,00307 |
|
2He3 |
3,01603 |
5B10 |
10,01294 |
8O16 |
15,99491 |
|
2H4 |
4,00260 |
5B11 |
11,00930 |
8O17 |
16,99913 |
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Можно получать энергию как за счет управляемого распада ядер некоторых элементов, так и за счет слияния мелких ядер в более крупные в процессе так называемой реакции термоядерного синтеза.
Согласно теории относительности, масса представляет собой особую форму энергии, о чем и свидетельствует известная формула Эйнштейна E = mc2. Из нее следует возможность преобразования массы в энергию и энергии в массу. И такие реакции на внутриатомном уровне вещества реально имеют место. В частности, часть массы атомного ядра может превращаться в энергию, и происходит это двумя путями. Во-первых, крупное ядро может распасться на несколько мелких — такой процесс называется реакцией распада. Во-вторых, несколько более мелких ядер могут объединиться в одно более крупное — это так называемая реакция синтеза. Реакции ядерного синтеза во Вселенной распространены очень широко — достаточно упомянуть, что именно из них черпают энергию звезды. Ядерный распад сегодня служит одним из основных источников энергии для человечества — он используется на атомных электростанциях. И при реакции распада, и при реакции синтеза совокупная масса продуктов реакции меньше совокупной массы реагентов. Эта-то разница в массе и преобразуется в энергию по формуле E = mc2.
Распад
В природе уран встречается в форме нескольких изотопов, один из которых — уран-235 (235U) — самопроизвольно распадается с выделением энергии. В частности, при попадании достаточно быстрого нейтрона в ядро атома 235U последнее распадается на два крупных куска и ряд мелких частиц, включая, обычно, два или три нейтрона. Однако сложив массы крупных фрагментов и элементарных частиц, мы недосчитаемся определенной массы по сравнению с массой исходного ядра до его распада под воздействием удара нейтрона. Эта-то недостающая масса и выделяется в виде энергии, распределенной среди получившихся продуктов распада — прежде всего, кинетической энергии (энергии движения). Стремительно движущиеся частицы разлетаются от места распада и сталкиваются с другими частицами вещества, разогревая их.
Они представляют собой стремительно разлетающиеся от места распада частицы, при этом далеко они не улетают, врезаясь в соседние атомы вещества и разогревая их. Таким образом, энергия, порождаемая ядерным распадом, преобразуется в теплоту окружающего вещества.
В уране, добываемом из природной урановой руды, изотопа урана-235 содержится всего 0,7% от общей массы урана — остальные 99,3% приходятся на долю относительно устойчивого (слабо радиоактивного) изотопа 238U, который просто поглощает свободные нейтроны, не распадаясь под их воздействием. Поэтому для использования урана в качестве топлива в ядерных реакторах его нужно предварительно обогатить — то есть довести содержание радиоактивного изотопа 235U до уровня не менее 5%.
После этого уран-235 в составе обогащенного природного урана в атомном реакторе распадается под воздействием бомбардировки нейтронами. В результате из одного ядра 235U выделяется в среднем 2,5 новых нейтрона, каждый из которых вызывает распад еще 2,5 ядер, и запускается так называемая цепная реакция. Условием для продолжения незатухающей реакции распада урана-235 является превышение числа выделяемых распадающимися ядрами нейтронов числа нейтронов, покидающих урановый конгломерат; в этом случае реакция продолжается с выделением энергии.
В атомной бомбе реакция носит умышленно неконтролируемый характер, в результате чего за доли секунды распадается огромное число ядер 235U и выделяется колоссальная по своей разрушительности взрывная энергия. В атомных реакторах, используемых в энергетике, реакцию распада необходимо строго контролировать с целью дозирования выделяемой энергии. Хорошим поглотителем нейтронов является кадмий — его-то обычно и используют для управления интенсивностью распада в реакторах АЭС. Кадмиевые стержни погружают в активную зону реактора до уровня, необходимого для снижения скорости выделения свободной энергии до технологически разумных пределов, а в случае падения энерговыделения ниже необходимого уровня частично выводят стержни из активной зоны реакции, после чего реакция распада интенсифицируется до необходимого уровня. Выделившаяся тепловая энергия затем в обычном порядке (посредством турбогенераторов) преобразуется в электрическую.
Синтез
Термоядерный синтез — реакция прямо противоположная реакции распада по своей сути: более мелкие ядра объединяются в более крупные. Самая распространенная во Вселенной реакция вообще — это реакция термоядерного синтеза ядер гелия из ядер водорода: она непрерывно протекает в недрах практически всех видимых звезд. В чистом виде она выглядит так: четыре ядра водорода (протона) образуют атом гелия (2 протона + 2 нейтрона) с выделением ряда других частиц. Как и в случае реакции распада атомного ядра совокупная масса образовавшихся частиц оказывается меньше массы исходного продукта (водорода) — она и выделяется в виде кинетической энергии частиц-продуктов реакции, за счет чего звезды и разогреваются.
В недрах звезд реакция термоядерного синтеза происходит не единовременно (когда сталкиваются 4 протона), а в три этапа. Сначала из двух протонов образуется ядро дейтерия (один протон и один нейтрон). Затем, после попадания в ядро дейтерия еще одного протона, образуется гелий-3 (два протона и один нейтрон) плюс другие частицы. И наконец, два ядра гелия-3 сталкиваются, образуя гелий-4, два протона, а также другие частицы. Однако по совокупности эта трехэтапная реакция дает чистый эффект образования из четырех протонов ядра гелия-4 с выделением энергии, уносимой быстрыми частицами, прежде всего фотонами (см. Эволюция звезд).
Естественная реакция термоядерного синтеза происходит в звездах; искусственная — в водородной бомбе. Увы, человек до сих пор не сумел найти средств для того, чтобы направить термоядерный синтез в управляемое русло и научиться получать за счет него энергию для использования в мирных целях. Однако ученые не теряют надежды на достижение положительных результатов в области получения «мирной и дешевой» термоядерной энергии уже в обозримом будущем — для этого главное научиться удерживать высокотемпературную плазму либо посредством лазерных лучей, либо посредством сверхмощных тороидальных электромагнитных полей (см. Критерий Лоусона).
См. также:
Задачи, тесты
А. А.
Найдин,
< naidin_anatoli@mail.ru >, МОУ гимназия № 44, г. Новокузнецк, Кемеровская обл.
Расчёт энерговыделения при ядерной реакции
Всё прекрасное так же трудно, как и редко…
Спиноза
Расчёт энерговыделения при ядерных реакциях традиционно труден для учеников средней школы, однако происходящие внутри атомного ядра процессы всегда вызывают у них живой интерес. В школьных учебниках на примерах показано, как определить энергию связи ядра и энергетический выход ядерной реакции, однако совсем не обсуждаются условия протекания ядерной реакции и другие способы расчёта энерговыделения. Попробуем этот недочёт устранить, сгруппировав решаемые на уроке задачи так, чтобы они образовали систему задач, которая будет развивать ученика. Напомним, что ядерные реакции – превращения атомных ядер при взаимодействии с частицами, в том числе с фотонами или друг с другом.
Для протекания ядерной реакции необходимо сближение частиц до расстояний порядка 10–13 см. Что конкретно произойдёт с ядром, зависит от энергии налетающей частицы и энергии связи нуклонов: частица может быть захвачена ядром атома и вызвать ядерную реакцию, может расщепить ядро на фрагменты, может отлететь от ядра при упругом ударе. Ядерные реакции подчиняются законам сохранения электрического заряда, энергии, импульса.
Примеры ядерных реакций (запись комментируют учащиеся):
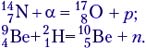
Ядерные реакции могут протекать как с выделением, так и с поглощением энергии. Причём эта энергия по порядку величины в 106 раз больше, чем при химической реакции! Произведём расчёт энерговыделения на примере ядерной реакции:
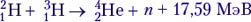
(такие ядерные реакции называются реакциями синтеза):
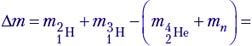 2,01410 а.е.м. + 3,01605 а.е.м. – (4,00260 + 1,00866) а.е.м. = 0,01889 а.е.м. = 0,013136 · 10–27 кг.
2,01410 а.е.м. + 3,01605 а.е.м. – (4,00260 + 1,00866) а.е.м. = 0,01889 а.е.м. = 0,013136 · 10–27 кг.
E = Δmc2 = 0,28221 · 10–11 Дж ≈ 17,6 МэВ.
Ядерные реакции деления покажем на примере одной из возможных схем деления изотопа урана 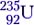 :
:
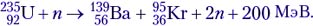
Эта реакция идёт при взрыве атомной бомбы, а также в недрах ядерного реактора. Расчёт энерговыделения производить не будем, но на будущее будем знать, что в среднем на одну реакцию деления изотопа урана выделяется около 200 МэВ энергии.
Реакцию распада удобно показать на примере реакции 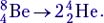 Эта реакция интересна тем, что попытки создать ядро
Эта реакция интересна тем, что попытки создать ядро 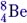 путём двойного α-цикла природа «предпринимала» во время Большого Взрыва, предпринимает и сейчас – в недрах звёзд. Однако это ядро неустойчиво и практически сразу распадается на две α-частицы. Благодаря этому Вселенная в основном состоит из водорода и гелия, а концентрация более тяжёлых элементов в ней незначительна.
путём двойного α-цикла природа «предпринимала» во время Большого Взрыва, предпринимает и сейчас – в недрах звёзд. Однако это ядро неустойчиво и практически сразу распадается на две α-частицы. Благодаря этому Вселенная в основном состоит из водорода и гелия, а концентрация более тяжёлых элементов в ней незначительна.
Сокращённую запись уравнения ядерной реакции покажем на примере реакции 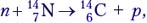 которую записывают в виде
которую записывают в виде 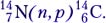
«Установленное Эйнштейном соотношение является основанием для дальнейших, значительно более важных выводов. Радиоактивная отслойка является с этой точки зрения одной из возможностей получения из материи огромных запасов энергии, техническое использование таких запасов энергии в принципе не представляется невыполнимым и совсем недавно Резерфорд получил, по-видимому, подобные количества энергии, – правда, в микроскопическом масштабе, когда ему удалось разложить азот путём радиоактивного расщепления. Но не нужно предаваться иллюзии, будто техническая добыча указанной здесь энергии является вопросом непосредственного будущего и что этим будет достигнуто обесценивание угля; с другой стороны, нельзя возражать и против того, что тут раскрывается одна из серьёзнейших технических проблем».
В.Нернст, 1918
Теперь в процессе решения задач ученикам можно продемонстрировать и другие методы расчёта энерговыделения при ядерной реакции.
«Прибавь ещё один оттенок к радуге…»
У.Шекспир
Задача 1. Одной из наиболее известных реакций термоядерного синтеза является реакция слияния дейтерия и трития: 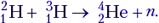 Какая энергия выделяется в этой реакции? Энергия связи дейтерия 2,228 МэВ, трития 8,483 МэВ, гелия 28,294 МэВ.
Какая энергия выделяется в этой реакции? Энергия связи дейтерия 2,228 МэВ, трития 8,483 МэВ, гелия 28,294 МэВ.
Решение. В данной реакции происходит разделение ядер дейтерия и трития на составляющие их частицы, на что затрачивается энергия связи, после чего образуется ядро гелия с выделением энергии. Энергетический выход реакции: Е = 28,294 МэВ – (2,228 МэВ
+ 8,483 МэВ) = 17,583 МэВ. Энергию связи любого ядра ученики уже могут рассчитывать, поэтому для них не представляет большого труда рассчитать энергетический выход любой ядерной реакции таким способом.
Задача 2. Определите энергию реакции 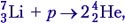 если известно, что энергии связи на один нуклон в ядрах
если известно, что энергии связи на один нуклон в ядрах 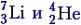 равны соответственно 5,60 и 7,06 МэВ.
равны соответственно 5,60 и 7,06 МэВ.
Решение. Под действием протона ядро лития разрушается, на что затрачивается энергия связи, но при этом возникают два ядра гелия и выделяется энергия Е = 2(4 ∙ 7,06 МэВ/нуклон) – 7 ∙ 5,60 МэВ/нуклон = 17,28 МэВ.
Задача 3. В ядерной реакции 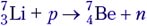 протоны налетают на покоящиеся ядра лития. Если энергия налетающих протонов Е = 1,92 МэВ, то нейтроны, образующиеся в реакции, покоятся. Оцените, какая энергия поглощается в данной реакции. При какой минимальной энергии налетающих протонов эта реакция может идти?
протоны налетают на покоящиеся ядра лития. Если энергия налетающих протонов Е = 1,92 МэВ, то нейтроны, образующиеся в реакции, покоятся. Оцените, какая энергия поглощается в данной реакции. При какой минимальной энергии налетающих протонов эта реакция может идти?
Решение. Это первый пример ядерной реакции, в которой энергия поглощается (Еп). В лабораторной системе отсчёта имеем движущийся со скоростью υ протон и покоящееся ядро лития (рис. а). После ядерной реакции нейтрон неподвижен, а ядро бериллия приобретает некоторую скорость V (рис. б).

По закону сохранения импульса, mpυ = mBeV. Зная массовое число каждой частицы, находим V = (1/7)υ. В лабораторной системе отсчёта 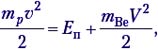 откуда Еп=6/7.
откуда Еп=6/7.
Теперь выясним, при какой минимальной энергии налетающих протонов Е′ эта реакция вообще может идти. В системе отсчёта «центр масс системы протон–ядро лития», которая движется вправо с некоторой скоростью υ′, их импульс mp(υ – υ′) – mLiυ′ = 0, откуда υ′ = 1/8 υ. Если протон обладает минимальной энергией Е′, то в данной системе отсчёта вся она поглощается и возникшие в реакции частицы не разлетаются: 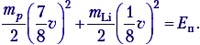 Учитывая, что mLi = 7mp , получим
Учитывая, что mLi = 7mp , получим 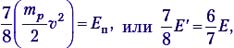 или откуда Е′= 48/49Е.
или откуда Е′= 48/49Е.
Задача 4. Если направить поток протонов на кусок льда из тяжёлой воды D2O, то при минимальной кинетической энергии протонов Е = 1,4 МэВ происходит ядерная реакция с образованием ядер  Какую минимальную энергию надо сообщить ядрам дейтерия, чтобы при их попадании на кусок льда из обычной воды произошла та же ядерная реакция?
Какую минимальную энергию надо сообщить ядрам дейтерия, чтобы при их попадании на кусок льда из обычной воды произошла та же ядерная реакция?
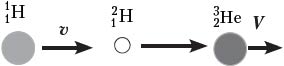
Решение. Запишем закон сохранения импульса и закон сохранения энергии для данной реакции V:
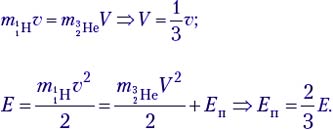
где Еп – энергия, поглощаемая в данной реакции.
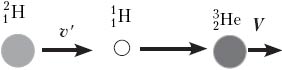
Запишем закон сохранения импульса и закон сохранения энергии для случая, когда ядра дейтерия попадают на кусок льда из обычной воды:
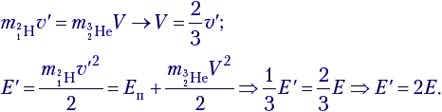
Задача 5. В реакции 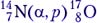 налетающая α-частица имеет кинетическую энергию 7,68 МэВ. Возможна ли такая реакция? Если да, то чему равна полная кинетическая энергия продуктов реакции?
налетающая α-частица имеет кинетическую энергию 7,68 МэВ. Возможна ли такая реакция? Если да, то чему равна полная кинетическая энергия продуктов реакции?
Решение. Найдём дефект массы: 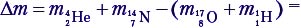 4,00260 + 14,00307 – (16,99913 + 1,00782) = –0,0013 а.е.м.
4,00260 + 14,00307 – (16,99913 + 1,00782) = –0,0013 а.е.м.
Эта реакция идёт с поглощением энергии! Еп = 1,2 МэВ.
Запишем закон сохранения импульса и закон сохранения энергии для этой реакции:
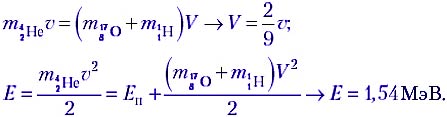
Энергии налетающей частицы вполне достаточно для того, чтобы данная реакция протекала! Полная кинетическая энергия продуктов распада Е – Еп = 6,14 МэВ.
Литература
- Джанколи Д. Физика. – М.: Мир, 1989.
- Савченко О.Я. Задачи по физике. – Новосибирск: НГУ, 1999.
Закон радиоактивного распада.
Закон радиоактивного распада установлен Ф. Содди.
Опытным путем Э. Резерфорд установил, что активность радиоактивного распада убывает с течением времени. Для каждого радиоактивного вещества существует интервал времени, на протяжении которого активность убывает в 2 раза, т. е. период полураспада Т данного вещества. Например, для ядра ![]() период T=1600 лет. Следовательно, если взять 1г Ra, через 1600 лет его будет 1/2 г, а через 3200 лет— 1/4 г. Таким образом, исходное количество радия должно обратится в нуль спустя бесконечный промежуток времени.
период T=1600 лет. Следовательно, если взять 1г Ra, через 1600 лет его будет 1/2 г, а через 3200 лет— 1/4 г. Таким образом, исходное количество радия должно обратится в нуль спустя бесконечный промежуток времени.
Математическое выражение
Пусть число радиоактивных атомов N0, время t=0.
Через t2=T число нераспавшихся ядер N=N0/2
Через t2=2T останетсяN=N0/22,
Через t3-=3T таких ядер окажетсяN=N0/23— и т. д.
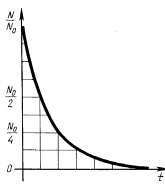
Следовательно, в конце промежутка времени t= nT нераспавшихся ядер останется N=N0/2n . Так как n=t/T, то ![]() . Это закон, которому подчиняется распад большого количества радиоактивных ядер.
. Это закон, которому подчиняется распад большого количества радиоактивных ядер.
У радиоактивных элементов Т имеет различную величину, например, ![]() имеет период полураспада Т=1,4.1010 лет, а у криптона
имеет период полураспада Т=1,4.1010 лет, а у криптона ![]() период полураспада Т=1,4 с. У искусственно созданных элементов с Z > 100 период полураспада составляет сотые и тысячные доли секунды.
период полураспада Т=1,4 с. У искусственно созданных элементов с Z > 100 период полураспада составляет сотые и тысячные доли секунды.
![]()
Ядерные силы
(сильное или ядерное взаимодействие – т.к. во много раз больше кулоновских сил). Силы притяжения, связывающие протоны и нейтроны в ядре, называются ядерными силами.Первые попытки объяснить – И.Е. Тамм. Теория создана Х. Юкава (1936). Свойства:
- На расстояниях порядка 10-13см сильные взаимодействия соответствуют притяжению, при уменьшении расстояния – отталкиванию.
- Независимы от наличия электрического заряда (свойство зарядовой независимости) Одинаковая сила действует и на протон и на нейтрон.
- Взаимодействуют с ограниченным числом нуклонов (свойство насыщения).
- Короткодействующие: быстро убывают, начиная с r ≈ 2,2.10-15 м.
Радиус действия
Относит интенсивность.
Ядерное
10-15м
1
Эл.-маг.
?
1/137
Слабое
10-13м
Гравитационное
?
10-33
Энергия связи ядра
Энергия, которая необходима для полного расщепления ядра на отдельные нуклоны, называется энергией связи. Энергия связи очень велика. При синтезе 4 г гелия выделяется такое же количество энергии, как при сжигании двух вагонов каменного угля.
1эВ=1,6.10-19Дж
1 а.е.м.=1,67-10-27 кг
Формула для вычисления энергии связи:
![]()
![]() – дефект массы.
– дефект массы.
![]()
В атомной физике массу удобно выражать в атомных единицах массы: 1 а.е.м.=1,67-10-27 кг. Коэффициент связи энергии и массы (равный с2): с2= 931,5 МэВ/аем.
с2= 931,5 МэВ/аем.
Удельная энергия связи
Энергия связи, приходящаяся на один нуклон в ядре, т. е. энергия, которую необходимо затратить, чтобы удалить из ядра один нуклон называется удельной энергией связи;
![]() где А — массовое число.
где А — массовое число.
![]()
При плавлении льда на 1 молекулу: 0,06 эВ;
При парообразовании воды на 1 молекулу: 0,4 эВ;
Для разрыва молекулы водорода на атомы: 4,5 эВ;
Для ионизации атома водорода: 13,6 эВ;
Для отделения нейтрона от ядра дейтерия: 1,1 МэВ.
Электронвольт
1 эВ = 1,6.10-19Дж
1МэВ = 1,6.10-13Дж
- У ядер средней части периодической системы Менделеева с массовым числом 40 <= А <= 100 удельная энергия максимальна. Наиболее устойчивы от 50 до 60.
- У ядер, для которых А>100, удельная энергия связи плавно убывает.
- У ядер, для которых А<40, удельная энергия скачкообразно убывает.
-
Максимальной удельной энергией обладают ядра, у которых число протонов и нейтронов четное (
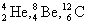 ), а минимальной— ядра, у которых число протонов и нейтронов нечетное (
), а минимальной— ядра, у которых число протонов и нейтронов нечетное ( ).
).
Таким образом, энергетически выгодны два способа высвобождения внутренней энергии: деление тяжелых ядер (цепная ядерная реакция) и синтез легких ядер (термоядерная реакция).
График зависимости удельной энергии связи
от массового числа:
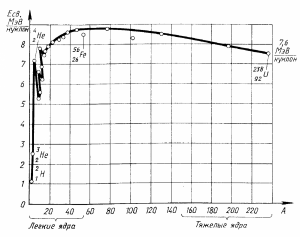
Ядерные реакции – превращения атомных ядер, вызванные их взаимодействиями с различными частицами или друг с другом.
Символическая запись: А + а ® В + b. При написании ядерных реакций используются з-нысохранения заряда и массового числа (числа нуклонов).
Примеры:
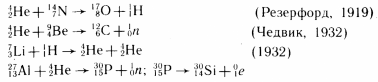
![]() (искусственная радиоактивность, И. и Ф. Жолио-Кюри, 1934).
(искусственная радиоактивность, И. и Ф. Жолио-Кюри, 1934).
Энергетический выход ядерной реакции – разность между суммарной энергией связи частиц, участвующих в реакции и продуктов реакции.
Реакции, происходящие с выделением энергии, наз. экзотермическими, с поглощением – эндотермическими.
Недавно проводил очередные занятия по физике со своими учениками и заметил некоторые трудности в решении задач на радиоактивный распад. По моим наблюдениям в школе и в интернете разбираются самые тривиальные задачи на распад. Задачи из ЕГЭ бывают немного сложнее. Но для интереса я добавил в статью разборы еще 6 задач, которые смело можно назвать задачами «со звёздочкой*», то есть повышенной сложности. На написание теории и подробные решения было потрачено много времени, поэтому, если Вам понравится статья, поддержите своей активностью.
💡 Крупные статьи я выкладываю в pdf в своём канале в telegram Репетитор IT mentor. Подписывайтесь, там публикуется контент, которого на Дзен не будет.
Прежде всего хотелось бы сделать замечание. Для успешного решения задач по физике (в целом, любых задач) Вам понадобятся:
◼ 1. Уверенные знания в математике на уровне физ-мат лицея (это минимум)
◼ 2. Базовые знания по дифференциальному и интегральному исчислению, а также умение применять начальные условия (НУ) и граничные условия (ГУ).
◼ 3. Понимание ограничений и сути процесса ( у вас не должны получаться отрицательная масса или отрицательное время, дробное количество, околосветовые скорости макроскопических объектов )
◼ 4. Хорошее воображение, 3D-видение эксперимента у себя в голове, а также возможность представить как выглядит график функции, описываемой в определенном законе (например: закон радиоактивного распада).
◼ 5. Умение разбивать большую задачу на малые подзадачи (например: определить амплитуду колебаний изображения математического маятника — у вас две задачи: механическая и оптическая — решайте их отдельно, потом сшивайте).
◼ 6. Чувствуйте абстракции. Вы никогда не решите задачу, если попытаетесь учесть всё. Пример: определите траекторию полёта камня, брошенного под углом к горизонту с учётом… эффекта Магнуса, динамического сопротивления ветра, фазы Луны, функции плотности воздуха, динамики вихрей потоков воздуха, распада вещества, из которого состоит камень, термодинамического расширения камня. Сложно? Вот поэтому чувствуйте абстракции.
◼ 7. Программирование. Да… внезапно. Для физики полезно знать какой-нибудь язык программирования. Попробуйте решенную задачу замоделировать и закодить в виде графической анимации. Так ваши решения станут куда более интересными и наглядными. А меняя входные параметры, вы станете лучше понимать поведение физических систем.
Основные определения
Радиоактивность – свойство некоторых нуклидов подвергаться радиоактивному распаду.
Радиоактивность – превращение одних атомных ядер в другие ядра, сопровождающееся испусканием различных частиц и электромагнитного излучения. На латыни radio – излучаю, activus – действенный.
Радиоактивность – самопроизвольное превращение неустойчивых изотопов одного химического элемента в изотоп другого элемента, сопровождающееся испусканием элементарных частиц, ядер и жесткого электромагнитного излучения.
Нуклид – разновидность атома, характеризуемая числом протонов и нейтронов, а в некоторых случаях энергетическим состоянием ядра.
Радионуклид – нуклид, испускающий ионизирующее излучение.
Радиация или ионизирующее излучение – это частицы или гамма-кванты, энергия которых достаточна велика, чтобы при воздействии на вещество создавать ионы и катионы (т.е. ионизировать молекулы на своём пути).
Ионизирующее излучение – поток заряженных или нейтральных частиц и квантов электромагнитного излучения, прохождение которых через вещество приводит к ионизации и возбуждению атомов или молекул среды. По своей природе делится на фотонное (гамма-излучение, тормозное излучение, рентгеновское излучение) и корпускулярное (альфа-излучение, электронное, протонное, нейтронное, мезонное).
Теория для решения задач
Закон радиоактивного распада – закон, который описывается зависимость интенсивности радиоактивного распада от времени и от количества радиоактивных атомов в образце. Закон был открыт Фредериком Содди и Эрнестом Резерфордом. Оба получили Нобелевскую премию. Они обнаружили закон экспериментальным путем. Ещё в далеком 1903 году в работах «Сравнительное изучение радиоактивности радия и тория» этот закон формулировался:
Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии.
То есть скорость превращения всё время пропорционально количеству элементов, ещё не подвергнувшихся превращению.
Данную формулировку можно записать в виде дифференциального уравнения: dN/dt = – λ·N, где dN – изменение количества ядер за время dt.
Это изменение отрицательно, потому что при распаде уменьшается количество оставшихся элементов. Опытным путем было установлено, что эта скорость распада dN/dt пропорционально количеству оставшихся ядер N и некоторой постоянной λ, которая называется постоянной распада и характеризует вероятность радиоактивного распада за единицу времени (имеет размерность 1/c). Данное уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными. Решение подобных уравнений можно найти в любом учебнике по высшей математике.
В итоге решение будет иметь вид N = N₀ · exp(- λ·t) :
Отсюда видно, что число радиоактивных атомов какого-либо вещества уменьшается со временем по экспоненциальному (показательному) закону. Помимо постоянной распада λ используются другие характеристики.
Среднее время жизни
Зная закон распада, можно посчитать среднее время жизни радиоактивного атома. Вспоминаем, что dN обозначает количество атомов, которое распадется за время от t до t + dt. Тогда среднее время можно будет найти подобно тому, как мы ищем среднее или математическое ожидание случайной непрерывной величины:
В вычислениях была использована формула для интегрирования по частям. Теория интегрирования также описана в любой книге с конспектами по высшей математике (или математическому анализу, или интегральному исчислению).
Подставим результат для тау (время жизни τ) в экспоненциальную зависимость в формуле распада:
Отсюда видно, что за среднее время жизни τ число радиоактивных атомов образца ( а также его активность – количество распадов в секунду) уменьшается в e ≈ 2.718 раз.
Период полураспада
И всё же большей популярностью пользуется другая характеристика для радиоактивных элементов. Называется она периодом полураспада T. Если немного подумать, то из названия понятно, что это время, в течение которого количество радиоактивных атомов исходного элемента уменьшается в 2 раза. Выведем связь этой величины с постоянной распада:
A – массовое число (число нуклонов в составе ядра атома)
Z – атомный номер в таблице Менделеева (число протонов в ядре)
Для нейтрального атома:
Законы сохранения в распадах
При радиоактивном распаде сохраняются следующие параметры:
1. Заряд. Электрический заряд не может создаваться или исчезать. Общий заряд до и после реакции должен сохраняться, хотя может по-разному распределяться среди различных ядер и частиц. Единичный положительный и отрицательный заряды нейтрализуют друг друга. Аналогично, возможно для нейтральной частицы (типа нейтрона) произвести один заряд каждого знака.
2. Массовое число или число нуклонов. Число нуклонов после реакции должно быть равно числу нуклонов до реакции.
3. Общая энергия. Кулоновская энергия и энергия эквивалентных масс должна сохраняться во всех реакциях и распадах.
4. Импульс и угловой момент. Сохранение линейного импульса ответственно за распределение кулоновской энергии среди ядер, частиц и/или электромагнитного излучения. Угловой момент относится к спину частиц.
Потенциальная энергия взаимодействия α-частицы и остаточного ядра с зарядом Z·e
Вид волновой функции можно получить из решения уравнения Шредингера для взаимодействия ядра атома и α-частицы. Способы решения можно почитать в книгах по физике вузовского уровня или в книгах по ММФ (методы математической физики). В целом, для понимания вам будет полезна теория решения дифференциальных уравнений из конспектов лекций по высшей математике или конкретно по теме – дифференциальное и интегральное исчисление.
По причинам исторического характера ядро He называют альфа-частицей. Установлено, что многие тяжелые ядра с зарядовым числом Z > 82 (Z = 82 имеет свинец) испытывают радиоактивный распад с испусканием альфа-частицы. В альфа-частице удельная энергия связи больше, чем в тяжелых ядрах, поэтому альфа-распад возможен энергетически. К примеру, образце урана U-238 испускает альфа-частицы с периодом полураспада 4.5 млрд. лет. Самопроизвольно происходит реакция:
Спустя 4.5 млрд. лет половина ядер урана U-238 распадается. Разность масс U-238 и продуктов распада равна энергии 4.2 МэВ. Рисунок выше позволяет получить представление о том, почему происходит альфа-распад. Ea – кинетическая энергия вылетающей альфа-частицы. Первоначально альфа-частицы находится в области I и может быть описана стоячей волной с амплитудой Ψвнутр (волновая функция в данной области пространства). Однако, возможно проникновение сквозь барьер, потому что в области вдали от ядра имеется небольшой «хвост» волновой функции Ψвнеш. Вероятность вылета альфа-частицы в момент её соударения с барьером можно оценить выражением: |Ψвнеш|²/|Ψвнутр|².
Число таких столкновений в 1 секунду приблизительно v/2R, где v – скорость альфа-частицы в области I. Таким образом, вероятность испускания альфа-частицы в единицу времени можно записать так:
В образце, содержащем n ядер, число распадов в секунду (скорость уменьшения n) равна
Отсюда с помощью интегрирования и подстановки начальных условий можно снова получить закон радиоактивного распада:
Можно получить ещё одну формулу для оценки периода полураспада:
Формула иллюстрирует применение квантовой механики для объяснения радиоактивности. Квантовая механика дает исчерпывающее объяснение альфа-распада и других радиоактивных превращений. Природа вероятности интересна тем, что если в силу редкой случайности текущее ядро уцелело на протяжении большого числа периодов полураспада, то эта предыстория абсолютно не влияет на вероятность распада в будущем. Этот же эффект имеет место при бросании монеты. Если у вас пять раз выпал орёл, вероятность шестой раз выпасть орлу остаётся по-прежнему равной 0.5.
Вероятность распада ядер одного вещества всегда одна и та же, независимо от их возраста. Допустим, половина ядер какого-либо изотопа распадается за один год. Какое-то ядро, избежавшее распада в первый год, по-прежнему будет иметь вероятность ½ распасться на протяжении второго года. Если сохранится на протяжении двух лет, то вероятность распада на третий год снова будет ½.
💡 Теперь перейдем к практике и поучимся решать основные задачи. Здесь имеются две задачи из ЕГЭ по физике, но также я добавил более сложные задачи, которые не встречались мне в ЕГЭ, однако встречались в вузовской программе для физиков.
Практика решения задач
Задача 1. Какая доля радиоактивных ядер распадается через интервал времени, равный половине периода полураспада? Ответ приведите в процентах и округлите до целых.
Решение:
Задача 2. После крупной радиационной аварии, произошедшей в 1986 году на Чернобыльской атомной электростанции, некоторые участки местности оказались сильно загрязнены радиоактивным изотопом цезия-137 с периодом полураспада 30 лет. На некоторых участках норма максимально допустимого содержания цезия-137 была превышена в 1000 раз. Через сколько периодов полураспада после загрязнения такие участки местности вновь можно считать удовлетворяющими норме? Ответ округлите до целого числа.
Решение:
Задача 3. Период полураспада элемента 1 в три раза больше периода полураспада элемента 2. За некоторое время число атомов элемента 1 уменьшилось в 8 раз. Во сколько раз за это же время уменьшилось число атомов элемента 2?
Решение:
Задача 4*. Вычислить постоянную распада λ для изотопов радия:
а) ²¹⁹Ra; б) ²²⁶Ra; в) ²³⁰Ra. Чему равна вероятность распада изотопов радия за время t = 1 час ?
Решение:
Задача 5*. При определении периода полураспада короткоживущего радиоактивного изотопа использовался счётчик импульсов. За минуту в начале наблюдения было насчитано Δn₀ = 250 импульсов, а через время τ = 1 час было зарегистрировано Δn = 92 импульса. Чему равен период полураспада данного изотопа?
Решение:
Задача 6*. Известно, что из радиоактивного полония ²¹⁰Po массой m = 2.5 грамм за время t = 32 дня в результате его распада образуется гелий объемом V = 40 см³ при нормальных условиях: p₀ = 10⁵ Па и τ₀ = 273 К. Определить по этим данным период полураспада данного изотопа полония.
Решение:
Задача 7*.Оценить количество тепла, которое выделяет полоний ²¹⁰Po массой m = 1 мг за время, равное периоду полураспада этих ядер, если испускаемые α-частицы имеют кинетическую энергию Wα = 5.3 МэВ.
Решение:
Задача 8*. Пусть в ядре урана ²³⁸U альфа-частица сталкивается с потенциальным барьером 5·10²⁰ раз в секунду и Ψвнеш/Ψвнутр = 10⁻¹⁹.
а) Какова вероятность распада этого ядра в 1 сек ?
б) Каково среднее время жизни этого ядра?
Решение:
Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram
