Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
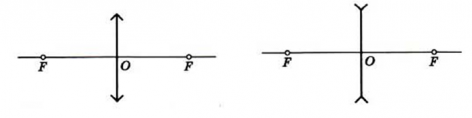
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
Внимание!
Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
Определение
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
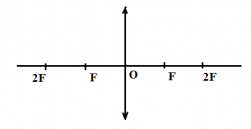
Построение изображения в собирающей линзе
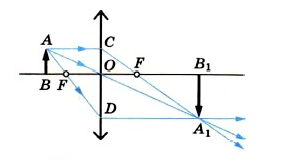
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Два вида лучей при построении изображений в линзе
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
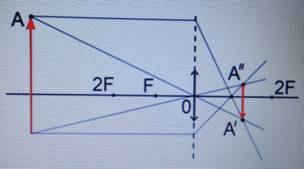 |
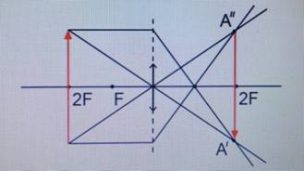
Предмет располагается за двойным фокусом.
Изображение:
|
 |
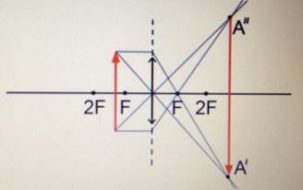
Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
|
 |
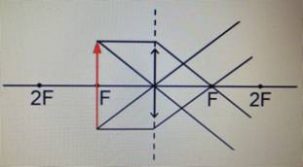
Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
|
 |
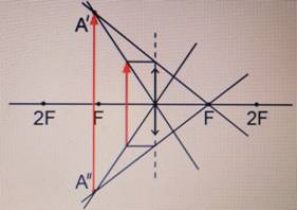
Предмет находится в фокальной плоскости.
Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. |
 |
Предмет располагается между линзой и фокусом.
Изображение:
|
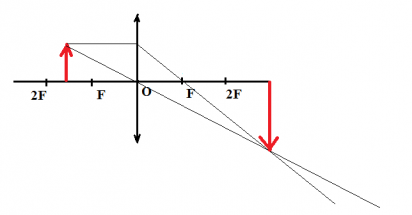
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
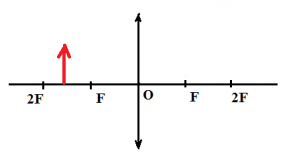
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
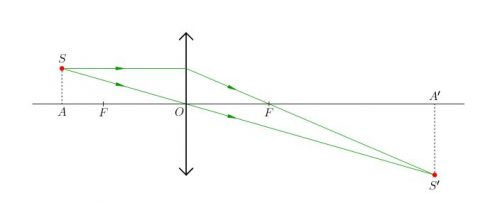
Частный случай — построение изображения точки
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.
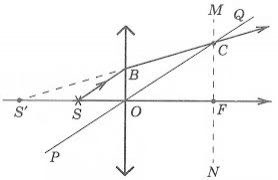
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
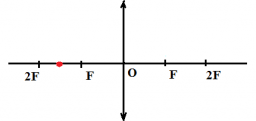
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
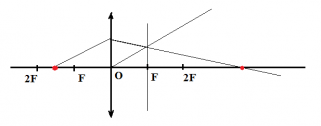
Построение изображения в рассеивающей линзе
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).
Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
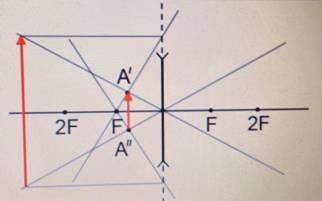
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
Пример №3. Построить изображение предмета в рассеивающей линзе.
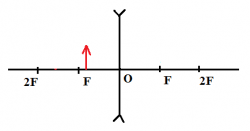
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
Определение
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
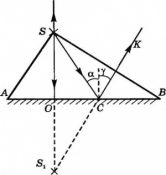
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Внимание!
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
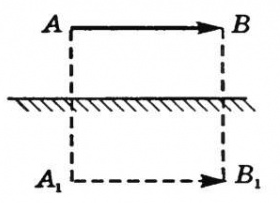
Изображение и сам предмет всегда симметричны относительно зеркала.
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
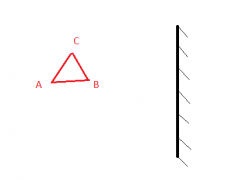
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
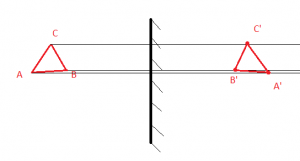
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760
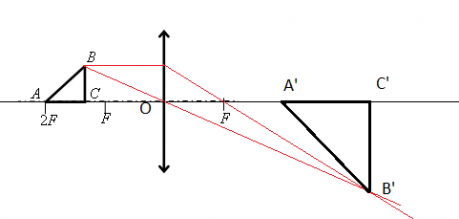
 Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18181
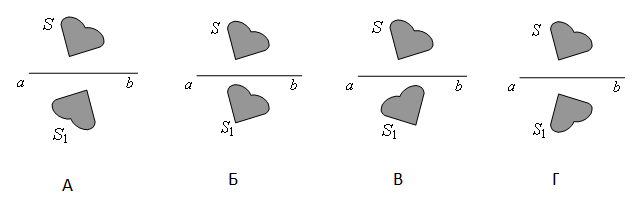
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Ответ: Г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18876
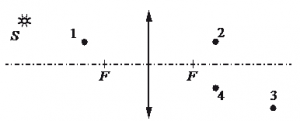 Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?
Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?
Алгоритм решения
1.Построить изображение точки.
Решение
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
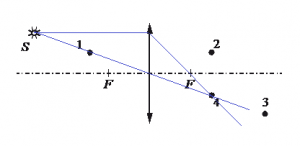
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 32.3k
В
данной теме будет рассмотрено решение задач на построение изображений в линзе.
Задача
1.
На рисунке изображен предмет АВ и собирающая линза. Постройте
изображение предмета если он находится а) за двойным фокусом б) между фокусом
и двойным фокусом.
РЕШЕНИЕ
Изобразим
на чертеже собирающую линзу, её главную оптическую ось, фокусы и двойные
фокусы.
Двойной
фокус – это точка, находящаяся на оптической оси на расстоянии от оптического
центра, вдвое большем, чем фокусное расстояние. Изобразим предмет АВ,
находящийся за двойным фокусом.
Точка
А находится на оптической оси линзы, поэтому её изображение тоже будет находится
на оптической оси. Чтобы получить изображение точки В, понадобится два
луча. Один направим параллельно оптической оси, а второй – через оптический
центр. Лучи, проходящие через оптический центр, не преломляются, поэтому легко
можем продолжить последний луч. Луч, параллельный оптической оси преломляется,
и после преломления проходит через фокус линзы. На пересечении этих лучей и
формируется изображение точки В, которое обозначим как B’.
Точка A’
будет
находится на главной оптической оси.
Во
втором случаи поступаем таким же образом используя два луча.
Таким
образом, получено действительное и перевёрнутое изображение. Только в этот раз
оно является увеличенным и находится за двойным фокусом.
Задача
2.
На рисунке указан источник света и его изображение в линзе. Также на рисунке
указана главная оптическая ось линзы. На основании этих данных, найдите
положение оптического центра линзы, её фокусов, а также определите тип линзы.
РЕШЕНИЕ
В
первую очередь, проведём прямую через источник света и его изображение (она называется
побочной оптической осью). Точка пересечения этой прямой с главной оптической
осью является оптическим центром линзы.
Обозначим
на нашем чертеже линзу. От источника света направим луч на линзу параллельно
главной оптической оси. Известно, что луч преломляясь идёт через фокус и через
изображение (или же, через изображение идёт продолжение луча). Проведём
пунктирную прямую через точку, в которой луч падает на линзу и через изображение
источника света. Точка, в которой данная прямая пересекает главную оптическую
ось и будет являться фокусом линзы.
Теперь,
с уверенностью можно сказать, что прямая, которую построили является
продолжением преломлённого луча. По характеру преломления луча или, исходя из
того, что изображение мнимое и находится ближе фокуса, можно заключить, что
линза является рассеивающей.
Задача
3.
На рисунке изображен луч АВ, прошедший через рассевающую линзу. Также,
на рисунке указаны положения фокусов линзы. Постройте ход падающего луча.
РЕШЕНИЕ
Отметим
на чертеже оптический центр линзы. Поскольку имеются положения фокусов линзы, можно
провести фокальную плоскость. Теперь проведём продолжение преломлённого луча до
пересечения с фокальной плоскостью. Точку пересечения обозначим за F’.
Через
эту точку и оптический центр линзы пройдёт побочная оптическая ось. Луч, идущий
вдоль этой оси пройдёт, не меняя своего направления (поскольку он пройдёт через
оптический центр). Луч, параллельный побочной оси, преломляется таким образом,
что продолжение преломлённого луча пройдёт через точку F’.
Таким образом, построен падающий луч.
Задача
4.
Постройте изображение предмета АВ в соответствии с указанным рисунком.
РЕШЕНИЕ
Здесь
сложность заключается в том, что предмет проходит через фокус, причём, таким
образом, что часть предмета находится на расстоянии, ближе фокусного, а часть –
между фокусом и двойным фокусом.
Можно
попытаться разбить предмет на два отрезка: AF
и FB. Очевидно, что
изображения и того, и другого отрезка будут уходить в бесконечность, поскольку,
точка F, естественно,
находится на фокусном расстоянии от линзы. А, как изветно, изображения
предметов, находящихся на фокусном расстоянии от линзы, не формируются (или
формируются в бесконечности).
Однако,
следует заметить, что луч, идущий в направлении от точки А к точке В
преломляется таким образом, что преломлённый луч параллелен главной оптической
оси. Можно построить продолжение этого луча.
Таким
образом, все точки изображения предмета АВ будут лежать на прямой,
проходящей через указанный луч и его продолжение. Проведём прямую через точку А
и оптический центр до пересечения с указанной ранее прямой. В точке пересечения
получится изображение точки А, которое обозначим как A’.
Аналогично,
проведём прямую через оптический центр и точку D
– таким образом, получим точку B’.
Если попытаться получить изображения других точек аналогичным способом, то можно
убедиться, что изображение данного предмета получается разрозненным (то есть,
делится на две части). Действительно, ведь изображение той части предмета,
которая находится перед фокусом, является мнимым, а изображение части,
находящейся между фокусом и двойным фокусом является действительным.
Задача
5.
На рисунке указан предмет, который находится на таком расстоянии от линзы, что
его изображение является действительным и увеличенным ровно в 2 раза. Постройте
это изображение и найдите длину отрезка A’C’,
если длина отрезка AB
равна 15 см, а длина
отрезка A’B’
равна 35 см. Угол BAC
прямой.
РЕШЕНИЕ
Отметим
на чертеже фокусы и двойные фокусы линзы. Отметим эти точки таким образом,
чтобы наш предмет находился между фокусом и двойным фокусом, поскольку именно в
этом случае получается действительное и увеличенное изображение (которое будет
находится за двойным фокусом). Итак, чтобы построить изображение, необходимо
получить изображения точек А, В и С. Построим эти точки
используя два луча.
Т.к.
изображение больше предмета в два раза, то
По
теореме Пифагора
Ответ: 18 см.
В уроках «Изображение светящейся точки, даваемое линзой» и «Изображение предмета, даваемое линзой», мы уже рассматривали построение различных изображений. Также в этих уроках находятся памятки для построения изображения точки или предмета, которые могут вам пригодиться.
В данном уроке представлены дополнительные интересные задачи на построение изображений. И, конечно, вы можете ознакомиться с их решением, разбором построения и итоговым чертежом.
Задача №1
На рисунке 1 показан ход светового луча, падающего на рассеивающую линзу. Выполнив необходимые построения, найдите положения фокусов линзы и положение изображения светящейся точки $S$.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Если луч падает параллельно оптической оси на рассеивающую линзу и преломляется, то продолжение этого преломленного луча пересечет оптическую ось в мнимом фокусе рассеивающей линзы.
Поэтому мы продолжим преломленный луч (отмечен синим цветом) до пересечения с оптической осью. Точка пересечения — это мнимый фокус $F$. Отметим его на чертеже (рисунок 2, а).
С другой стороны от линзы отмерим точно такое же фокусное расстояние и отметим второй фокус линзы.
Теперь нужно построить изображение светящейся точки (рисунок 2, б). Один преломленный луч у нас на чертеже уже есть (использовать мы будем его продолжение). Значит, нужно провести второй луч.
Выберем и проведем на чертеже луч, проходящий через оптический центр линзы $O$. После прохождения через линзу он не изменит направления своего распространения. Поэтому его продолжение совпадет с падающим лучом $SO$.
В итоге, на пересечении двух продолжений преломленных лучей мы получаем мнимое изображение светящейся точки $S_1$.
Задача №2
На рисунке 3 изображены положения главной оптической оси линзы, источника света $S$ и его изображения $S_1$. С помощью этих данных постройте оптический центр, отметьте на чертеже саму линзу и ее фокусы.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
В этой задаче у нас уже есть изображение светящейся точки. Обычно, когда мы занимаемся его построением, мы используем два световых луча. Один из них — это луч, проходящий через оптический центр $O$, который лежит на оптической оси линзы. После прохождения через линзу (ее оптический центр) он не изменяет своего направления.
А изображение $S_1$ лежит на пересечении этого луча с другим. Значит, мы можем соединить точки $S$ и $S_1$ друг с другом (рисунок 4, а).
Полученная прямая $SS_1$ пересекает оптическую ось в точке — это и есть оптический центр $O$. Отметим его на рисунке.
Зная положение оптического центра, мы можем отметить на чертеже и саму линзу. Какая это будет линза: собирающая или рассеивающая? Изображение $S_1$ является действительным, так как оно находится по другую сторону от линзы и явно будет на пересечении двух преломленных лучей. Действительное изображение мы можем получить только с помощью собирающей линзы (рисунок 4, б).
Теперь у нас на чертеже есть: оптическая линза, оптическая ось, оптический центр $O$, точка $S$, ее изображение $S_1$, падающий луч $SO$ и преломленный луч $OS_1$. Построим ход второго луча.
Луч $SC$ падает на линзу параллельно ее оптической оси. По определению, после преломления он должен пройти через фокус линзы и пересечься с другим преломленным лучом.
Этот преломленный луч будет выходить из точки $C$ и пересекаться с другим преломленным лучом в точке $S_1$. Отметим на чертеже этот луч $CS_1$ (рисунок 4, в).
Он пересек оптическую ось в точке — это и есть фокус линзы $F$. Чтобы отметить второй фокус, нужно отложить такое же фокусное расстояние с другой стороны линзы.
Задача №3
Постройте оптический центр, отметьте линзу и ее фокусы на чертеже, используя данные рисунка 5.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
По аналогии с построением в предыдущей задаче соединим прямой точку $S$ и ее изображение $S_1$. Но в этом случае прямая $SS_1$ не пересекла оптическую ось. Продолжим ее до пересечения, чтобы получить положение оптического центра $O$ (рисунок 6, а).
Мы видим, что точка и ее изображение находятся по одну сторону от линзы (ее оптического центра). Значит, изображение $S_1$ — мнимое. В точке $S_1$ должны пересечься продолжения преломленных лучей. Это возможно, если мы будем использовать рассеивающую линзу. Отметим ее на чертеже (рисунок 6, б).
Луч $SO$ после прохождения сквозь линзу не изменит своего направления. Продолжение преломленного луча совпадает с самим падающим лучом $SO$.
Проведем второй луч, идущий параллельно оптическое оси — луч $SС$. После прохождения сквозь линзу продолжение преломленного луча пересекается с продолжением другого преломленного луча $SO$ в точке $S_1$. Продолжим его до пересечения с оптической осью.
Так мы получили положение мнимого фокуса $F$ (рисунок 6, в). Чтобы отметить второй фокус, нужно отложить такое же фокусное расстояние с другой стороны линзы.
Задача №4
Постройте изображение предмета, расположение которого показано на рисунке 7. Охарактеризуйте его.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
На исходном рисунке 7 изображена выпуклая линза — собирающая. Отметим саму линзу и ее оптический центр $O$ на чертеже. Обозначим крайние точки предмета точками $A$ и $B$ (рисунок 8, а).
Начнем построение изображения предмета. Так как обе его точки не лежат на оптической оси, то и изображение нужно будет строить сначала для одной точки, а потом — для второй.
Займемся построением изображения точки $A$ (рисунок 8, б). Проведем два падающих луча $AC$ и $AO$. Луч $AO$ после преломления не изменит своего направления, а луч $AC$ преломится в линзе и после пройдет через фокус $F$.
Продолжим эти два преломленных луча до пересечения друг с другом. Получим изображение $A_1$.
Теперь построим изображение точки $B$ (рисунок 8, в). На линзу падают лучи $BO$ и $BD$. После преломления они пересекутся в точке $B_1$.
Соединим точки $A_1$ и $B_1$. Так мы получили изображение предмета $A_1B_1$. Охарактеризуем его.
Полученное изображение предмета:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 2F$
Описывая положение изображения в последнем пункте, под величиной $f$ мы принимаем расстояние от изображения предмета до линзы.
Задача №5
Постройте изображение предмета, находящегося в фокусе собирающей и рассеивающей линз (рисунок 9). Сравните полученные изображения.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Начнем с построения изображения предмета, даваемого собирающей линзой (рисунок 10, а). Из точки выходят два луча $AC$ и $AO$. Как видно из чертежа после прохождения сквозь линзу преломленные лучи параллельны друг другу — они никогда не пересекутся. Значит, изображения мы не получим.
Теперь построим изображение предмета в рассеивающей линзе (рисунок 10, б). Из крайней точки $A$ выходят два луча $AC$ и $AO$. Так как линза рассеивающая, изображение точки $A_1$ мы получим на пересечении продолжений преломленных лучей. Опустим перпендикуляр на оптическую ось и получим точку $B_1$. Соединим полученные точки друг с другом — получим изображение предмета $A_1B_1$.
Если предмет находится в фокусе собирающей линзы, то мы не получим его изображения.
Если предмет находится в фокусе рассеивающей линзы, то изображение предмета:
1. Мнимое
2. Уменьшенное
3. Прямое
4. $f < F$
Описывая положение изображения в последнем пункте, под величиной $f$ мы принимаем расстояние от изображения предмета до линзы.
Задача №6
Постройте изображение предмета, расположенного от собирающей линзы на расстоянии $3F$ (рисунок 11).
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Из точка $A$ на линзу падают лучи $AC$ и $AO$ (рисунок 12). После прохождения сквозь линзу они преломляются и пересекаются друг с другом в точке $A_1$ — изображении точки $A$.
Опустим перпендикуляр на оптическую ось и получим точку $B_1$ — изображение точки $B$. Соединим точки $A_1$ и $B_1$ между собой и получим изображение предмета $A_1B_1$.
Охарактеризуем полученное изображение. При этом $d$ — это расстояние от предмета до линзы, а $f$ — расстояние от изображения предмета до линзы.
Если $d = 3F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
2. $2F > f >F$
Задача №7
Постройте изображение предмета, расположенного от собирающей линзы на расстоянии $4F$ (рисунок 13). Сравните его с изображением предмета, полученным в задаче №6.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Построим изображение точки $A$ (рисунок 14). Из нее выходят два луча: $AC$ и $AO$. После преломления они пересекаются в точке $A_1$. Опустим перпендикуляр на оптическую ось, чтобы получить изображение точки $B$ — $B_1$.
Соединим точки $A_1$ и $B_1$ между собой и получим изображение предмета $A_1B_1$.
Охарактеризуем полученное изображение. При этом $d$ — это расстояние от предмета до линзы, а $f$ — расстояние от изображения предмета до линзы.
Если $d = 4F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
2. $2F > f >F$
Сравнивая полученное изображение предмета с изображением, полученным в предыдущей задаче, мы уже можем сделать определенные выводы. Для полной картины используем полученное изображение в задаче, рассмотренной в уроке «Изображение предмета, даваемое линзой». Там предмет находился в двойном фокусе линзы, а его полученное изображение было действительным, перевернутым, равным по размеру предмету и находилось в двойном фокусе с другой стороны линзы.
Тогда мы можем сделать вывод:
по мере отдаления предмета от линзы на двойное фокусное расстояние и дальше, действительное и перевернутое изображение предмета уменьшается и приближается к фокусу линзы, но никогда не окажется в нем.
Постройте изображение предмета, расположение которого показано на рисунке 15, и охарактеризуйте его.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Хоть одна из крайних точек предмета и находится на оптической оси, сам предмет расположен под углом к ней. Поэтому, при построении изображения необходимо будет отдельно строить изображения крайних точек $A$ и $B$.
Начнем с более сложного построения. Построим изображение точки, лежащей на оптической оси линзы — точки $B$ (рисунок 16).
Луч $BO$ проходит через оптический центр и после преломления не изменит своего направления. Эти лучи лежат оптической оси линзы.
Произвольный луч $BC$ падает на линзу. Теперь нам нужно построить ход этого луча после преломления в линзе. Для этого проведем побочную оптическую ось $MN$, параллельную этому лучу.
Далее отметим на чертеже фокальную плоскость, перпендикулярную оптической оси и проходящую через фокус $F$ (обозначена на рисунке пунктирной линией-перпендикуляром, опущенным в точку $F$).
Побочная оптическая ось $MN$ пересечет фокальную плоскость в точке $F’$ — побочном фокусе.
Преломленный луч будет проходить через этот побочный фокус. Соединим точки $C$ и $F’$ — получим преломленный луч $CF’$. Продолжим его до пересечения с первым преломленным лучом (который совпадает с оптической осью). На этом пересечении мы получаем точку $B_1$ — изображение точки $B$.
Теперь привычным для нас способом построим изображение точки $A$ (рисунок 17).
Лучи $AD$ и $AO$ после преломления в линзе пересекаются в точке $A_1$. Соединим точки $A_1$ и $B_1$ и получим изображение предмета $A_1B_1$.
Полученное изображение предмета, находящегося от линзы на расстоянии $2F > d >F$:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 3F$
Ох, уж эти линзы. Задач по этой теме немного, но они могут застать врасплох даже перспективного ученика. А все дело в том, что при минимальном количестве формул, эта тема содержит множество «НО», мешающих разложить все по полочкам в голове.
Предлагаю выделить 5 минут, чтобы полностью сформировать базу, достаточную для решения всех задач по этой теме внутри границ ОГЭ по физике. Достаточно всего лишь внимательно прочитать, понять и запомнить.
Что такое линза?
Линза – это прозрачное тело, ограниченное с двух сторон (или с одной из сторон) криволинейной поверхностью.
Линза может быть собирающей или рассеивающей.
У собирающих линз середина толще краёв, у рассеивающих – наоборот.
Прямая, проходящая через центры кривизны поверхностей линзы называется главной оптической осью. Если параллельно этой оси пустить пучок света, то после прохождения лучей через собирающую линзу они пересекутся в одной точке, называемой фокусом линзы. Расстояние от оптического центра линзы до фокуса называют фокусным расстоянием F. Если мы говорим о рассеивающей линзе, то фокус будет находиться со стороны самого предмета, а фокусное расстояние, соответственно, будет отрицательным.
Фокусное расстояние зависит только от толщины линзы и от значения преломления n материала, из которого сделана линза.
Важно также понимать, что при решении задач часто используют тонкие линзы, т.е. линзы, толщиной которой можно пренебречь. Это делается для того, чтобы главная оптическая ось пересекала линзу в одной точке, которая называется оптическим центром линзы O. Лучи через оптический центр проходят без преломления.
Построение изображения в тонкой линзе.
Для построения изображения точки, которая не лежит на главной оптической оси, необходимо построить:
– луч, проходящий через оптический центр линзы (без преломления);
– луч, идущий к линзе параллельно главной оптической оси и пересекающий после линзы ее фокус.
На пересечении этих лучей и будет располагаться изображение.
Важно понимать, что полноценное, т.е. действительное изображение точки можно получить только в собирающей линзе, т.к. только в этом случае после всех отражений и преломлений лучи, вышедшие из одной точки предмета, могут собраться в одну точку.
Рассеивающая линза всегда дает только мнимое изображение, т.е. изображение, которое возникает при пересечении продолжений расходящегося пучка лучей. Собирающая линза может давать как мнимое, так и действительное изображение.
Построение изображения предмета в тонкой линзе
В задачах ОГЭ предмет, как правило, представлен в виде двух точек, соединенных между собой жирным отрезком. Отрезок расположен перпендикулярно главной оптической оси и берет на ней свое начало, т.е. одна из точек всегда расположена на этой оси. Построение изображения начинается с точки, лежащей на другом конце этого отрезка согласно алгоритму, описанному выше. Для построения изображения всего предмета достаточно просто опустить перпендикуляр с точки пересечения лучей (места изображения точки) на главную оптическую ось.
Как и в случае с изображением точки, изображение предмета в рассеивающей линзе является мнимым. Кроме того, оно всегда прямое и уменьшенное.
А вот характер изображения, полученного с помощью собирающей линзы, зависит от положения предмета относительно линзы. Следует запомнить эту таблицу, а лучше самостоятельно перерисовать все эти случаи для понимания логики построения, т.к. вероятность попадания подобного вопроса достаточно высока.
Теперь, когда есть понимание, как строится изображение предмета в линзе, необходимо понимать зависимость фокусного расстояния от расстояний предмета (d) и изображения (f) до линзы: 1/F=1/d+1/f.
Также стоит запомнить величину оптическая сила D. Она определяет преломляющую способность линз и оптических систем линз и измеряется в диоптриях (дптр). Оптическая сила обратно пропорциональна фокусному расстоянию, т.е. D = 1/F, а раз существует такая зависимость, оптическая сила, как и фокусное расстояние, зависит только от характеристики самой линзы, а не от расстояний d (от предмета до линзы) и, соответственно, f (от изображения до линзы).
ИТАК, прошло, как и обещал, 5 минут. Решим теперь в качестве примера задачу из демонстрационного варианта ОГЭ по изученной теме.
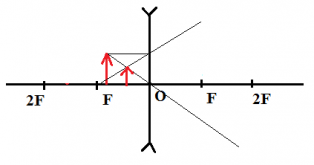
В первую очередь обращаем внимание, что линза собирающая (ориентируемся по вертикальным стрелкам).
Сложность этого задания в том, что предмет представляется точкой, лежащей на основной оптической оси, что не совсем стандартно и удобно для представления. Однако для правильного решения достаточно вспомнить зависимость изображения от расстояния предмета от линзы. В нашем случае это расстояние равно 2F, а значит, изображение должно быть на таком же расстоянии. В нашем случае это линия 2.
Спасибо всем, кто дочитал этот пост, надеюсь, он был полезным.
Не забудьте поставить лайк и подписаться на мой канал, чтобы полезные и интересные посты выходили как можно чаще 🙂
Для введённых нами линз существует два условно разных типа задач:
- задачи на построение в собирающей и рассеивающей линзах
- задачи на формулу для тонкой линзы
Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения преломлённых в линзах лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от линз. Для собирающей и рассеивающей линзу существуют рассмотренные (не нами) траектории распространения луча (рис. 1) от источника .

Рис.1. Собирающая и рассеивающая линзы (ход лучей)
Для собирающей линзы (рис. 1.1) лучи:
- синий. Луч, идущий вдоль главной оптической оси, после преломления проходит через передний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
- красный. Луч, идущий через передний фокус, после преломления распространяется параллельно главной оптической оси.
Пересечение любых из этих двух лучей (чаще всего выбирают лучи 1 и 2) дают изображение ().
Для рассеивающей линзы (рис. 1.2) лучи:
- синий. Луч, идущий параллельно главной оптической оси, преломляется так, что продолжения луча проходит через задний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
Пересечение продолжений рассмотренных лучей даёт изображение ().
Аналогично сферическому зеркалу, получим набор изображений от предмета, расположенного на различных расстояниях от зеркала. Введём те же обозначения: пусть — расстояние от предмета до линзы,
— расстояние от изображения до линзы,
— фокусное расстояние (расстояние от фокуса до линзы).
Для собирающей линзы:
(источник находится очень далеко от линзы). В этом случае мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси линзы.

Рис. 2. Собирающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе проходят через фокус, то точка фокуса и является точкой пересечения преломлённых лучей, тогда она же и есть изображение источника (точечное, действительное).
(источник находится за двойным фокусным расстоянием) (рис. 3).

Рис. 3. Собирающая линза (источник за двойным фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения преломившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.
(источник находится ровно в двойном фокусе) (рис. 4).

Рис. 4. Собирающая линза (источник в двойном фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.
(источник между фокусом и двойным фокусом) (рис. 5)

Рис. 5. Собирающая линза (источник между двойным фокусом и фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.
(источник находится ровно в фокусе собирающей линзы) (рис. 6)

Рис. 6. Собирающая линза (источник в фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). В этом случае, оба преломлённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.
(источник находится между фокусом и главным оптическим центром) (рис. 7)

Рис. 7. Собирающая линза (источник перед фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Однако преломлённые лучи расходятся, т.е. сами преломлённые лучи не пересекутся, зато могут пересечься продолжения этих лучей. Точка пересечения продолжений преломлённых лучей — изображение (увеличенное, мнимое, прямое). Положение — по ту же сторону, что и предмет.
Для рассеивающей линзы построение изображений предметов практически не зависит от положения предмета, так что ограничимся произвольным положением самого предмета и характеристикой изображения.
(источник находится очень далеко от линзы). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 8). Пустим два луча параллельно главной оптической оси линзы.

Рис. 8. Рассеивающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе должны проходить через фокус (свойство фокуса), однако после преломления в рассеивающей линзе лучи должны расходится. Тогда в фокусе сходятся продолжения преломившихся лучей. Тогда точка фокуса и является точкой пересечения продолжений преломлённых лучей, т.е. она же и есть изображение источника (точечное, мнимое).
- любое другое положение источника (рис. 9).

Рис. 9. Рассеивающая линза (произвольное положение источника)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (продолжение отражённого луча проходит через передний фокус) и идущего через главный оптический центр линзы (не преломляется). Тогда изображением будет пересечение продолжений преломлённых лучей.
Второй тип задач связан с формулой тонкой линзы. Такие задачи основываются на числовых данных параметров, характеризующих положение источника, изображения или фокуса линзы. Рассмотрим произвольную систему (рис. 10). Пусть положение источника (), изображения (
) и фокуса системы (
) задано.

Рис. 10. Формула тонкой линзы
Тогда взаимосвязь между параметрами положения элементов можно описать формулой:
(1)
Важно: для использования формулы (1) необходимо помнить правило расстановки знаков. Если линза собирающая, то , если рассеивающая, то
. В случае действительных предметов и изображений:
,
, а в случае мнимых предметов и изображений:
и
.
И последним параметром, характеризующим линзы или систему линз, является оптическая сила линзы (). Её нахождение довольно простое:
(2)
Размерность оптической силы линзы: м
=дптр (диоптрии). Оптическая сила собирающей линзы положительна, рассеивающей — отрицательна.
Вывод: задачи с линзами, в целом, разделены на два класса. Задачи на построение основываются на рисунках 2-9. Достаточно проанализировать ход лучей и найти изображение (рис.1). Численные значения в дано указывают на задачи на формулу тонкой линзы (1).
