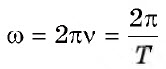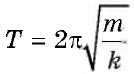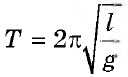Математический маятник .
Математический маятник представляет из себя груз на нити.
Формула периода математического маятника:
(T=2 pi sqrt{dfrac{l}{g}} )
(l ) – длина нити
1. Вычислить период (T) математического маятника, если длина его подвеса
(l=0,9 м ) , ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
2. Вычислить период (T) математического маятника, если длина его подвеса
(l=2,5 м ) , ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 3.
Вычислить период (T) математического маятника, если длина его подвеса
(l=62,5 см ) , ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти длину подвеса математического маятника, если его период ( T=1,884 с )
, ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 5.
Какую длину подвеса должен иметь математический маятник, чтобы его период был равен 3,14 с ?
Ускорение свободного падения ( g=10м/с^2 ; )
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 6.
При проведении лабораторной работы по вычислению ускорения свободного падения
математический маятник длиной (l=1 м ) совершил за время (t=34 с )
17 колебаний.
Какое значение ускорения свободного падения получено из данных опыта?
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 6.(Другое решение вывод формулы в общем виде)
При проведении лабораторной работы по вычислению ускорения свободного падения
математический маятник длиной (l=1 м ) совершил за время (t=34 с )
17 колебаний.
Какое значение ускорения свободного падения получено из данных опыта?
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти длины (l_1 и l_2 ) математических маятников, если
за одно и то же время один математический маятник совершает (N_1=50 ) колебаний, а другой (N_2=30 )
колебаний.
Разность длин маятников (l_2-l_1=0,32 метра )
Дать ответ в сантиметрах
Показать ответ
Показать решение
Видеорешение
Задачи на Механические колебания с решениями
Формулы, используемые на уроках «Задачи на Механические колебания».
Название величины |
Обозначение |
Единица измерения |
Формула |
Амплитуда колебаний |
A |
м |
|
Период колебаний |
T |
с |
T = 1 / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = 1 / T ;v = N / t |
Число колебаний за какое-то время |
N |
N = t /T ;N = vt |
|
Время |
t |
с |
t = NT ;t = N / v |
Циклическая частота колебаний |
ω |
Гц |
|
Период колебаний пружинного маятника |
T |
c |
|
Период колебаний математического маятника |
T |
c |
|
Уравнение гармонических колебаний |
x(t) = Asin(ωt+φ0) |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.


Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.

Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
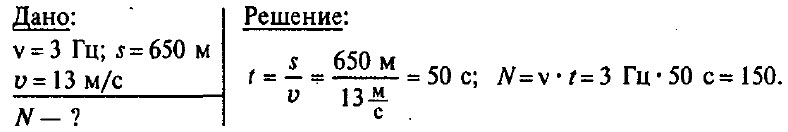
Задача № 8.
Гармоническое колебание описывается уравнением
![]() Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
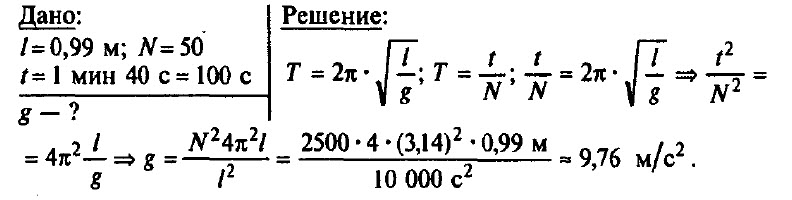
Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.


Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Колебательное движение. Математический маятник
- Механические колебания
- Математический маятник
- Параметры колебаний математического маятника
- Задачи
- Лабораторная работа №4. Исследование колебаний математического маятника
п.1. Механические колебания
Кроме прямолинейного и криволинейного движения, с которыми мы уже познакомились, существует еще один вид механического движения – колебательный.
Механические колебания – это движения тел, которые в той или иной степени повторяются через определенные промежутки времени.
Примеры колебательных движений:
- движение маятника в часах;
- колебание автомобиля на рессорах;
- покачивание деревьев на ветру;
- раскачивание качели;
- сокращения сердца и легких;
- движение крыльев насекомых и птиц.
п.2. Математический маятник
Математическим маятником называют тело, подвешенное на длинной нерастяжимой нити, размеры которого значительно меньше длины нити.
Нить считается нерастяжимой и невесомой, а тело – материальной точкой на этой нити.
 |
В положении равновесия тело (шарик) находится внизу. Отклонение от положения равновесия называют смещением тела, обозначают буквой x и измеряют в метрах (в СИ). Наибольшее смещение маятника от положения равновесия называют амплитудой колебаний, обозначают буквой A. В проекции на горизонтальную ось OX смещение изменяется в интервале (-Aleq xleq A). В положении равновесия x=0. Если маятник после смещения в положение 1, прошел положение равновесия 2, отклонился в положение 3, опять прошел положение 2, и вернулся в положение 1, говорят, что маятник совершил полное колебание. |
п.3. Параметры колебаний математического маятника
Период колебаний математического маятника – это время, за которое маятник совершает одно полное колебание. Период колебаний равен: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
На поверхности Земли (gapprox 9,8 м/с^2)
Частота колебаний математического маятника – это количество полных колебаний, которые маятник совершает за единицу времени: $$ f=frac 1T=frac{1}{2pi}sqrt{frac gL} $$
Период и частота колебаний – взаимно обратные величины
Период в СИ измеряют в секундах, частоту – в герцах: 1 Гц=1 c-1
Формула для периода колебаний справедлива для небольших отклонений маятника (на угол порядка 15-20° от положения равновесия).
п.4. Задачи
Задача 1. Маятник совершил 3 полных колебания за 9 с. Найдите период и частоту его колебаний. Чему равна длина нити, на которой подвешен маятник (ответ дайте в см, с округлением до целых)?
Дано:
(N=3)
(t=9 c)
__________________
(T, f, L-?)
Период колебаний: (T=frac tN)
Частота колебаний: (f=frac 1T=frac Nt)
Длина нити: $$ T=2pisqrt{frac Lg}Rightarrow sqrt{frac Lg}=frac{T}{2pi}Rightarrow frac Lg=left(frac{T}{2pi}right)^2Rightarrow L=gleft(frac{T}{2pi}right)^2 $$ Подставляем: begin{gather*} T=frac 93=3 (c)\ f=frac 13 (Гц)\ L=9,8cdotleft(frac{3}{2pi}right)^2approx 2,234 (м)approx 223 (см) end{gather*} Ответ: 3 с; 1/3 Гц; 223 см
Задача 2. Математический маятник колеблется с частотой 20?тиы кГц. Найдите период колебаний и число колебаний в минуту.
Дано:
(f=20 кГц=2cdot 10^4 Гц)
(t=1 мин=60 с)
__________________
(T, N-?)
Период колебаний: (T=frac 1f)
Частота колебаний за время (t: N=ft)
Подставляем: begin{gather*} T=frac{1}{2cdot 10^4}=0,5cdot 10^{-4} (c)=50cdot 10^{-6} (c)=50 (мкс)\ N=2cdot 10^4cdot 60=1,2cdot 10^6 end{gather*} Ответ: 50 мкс; 1,2·106
Задача 3. Расстояние от улья до цветочного поля 600 м. Пчела летит за нектаром со скоростью 8 м/с и машет крылышками с частотой 440 Гц. Возвращаясь в улей с нектаром, пчела летит со скоростью 5 м/с и машет крылышками с частотой 320 Гц. Найдите разность в количестве взмахов крылышками на пути туда и обратно.
Дано:
(s=600 м )
(v_1=8 м/с)
(f_1=440 Гц)
(v_2=5 м/с)
(f_2=320 Гц)
__________________
(triangle N-?)
Время полета из улья за нектаром (t_1=frac{s}{v_1})
Количество взмахов крылышками (N_1=f_1 t_1=f_1frac{s}{v_1})
Аналогично количество взмахов на пути назад (N_2=f_2frac{s}{v_2})
Найдем каждое из (N): begin{gather*} N_1=440cdotfrac{600}{8}=33000\ N_2=320cdotfrac{600}{5}=38400 end{gather*} На пути обратно пчела с грузом делает больше взмахов. Искомая разность: $$ triangle N=N_2-N_1=38400-33000=5400 $$ Ответ: 5400
Задача 4. Определите длину математического маятника с периодом колебаний 1с, если он находится: а) на Луне ((g_л=1,6 м/с^2)); б) на Марсе ((g_м=3,6 м/с^2)). Ответ запишите в см, с точностью до десятых.
Дано:
(T=1 с )
(g_л=1,6 м/с^2 )
(g_м=3,6 м/с^2)
__________________
(L_л, L_м-?)
Длина нити: begin{gather*} T=2pisqrt{frac Lg}Rightarrowsqrt{frac Lg} =frac{T}{2pi}Rightarrowfrac Lg=left( frac{T}{2pi}right)^2Rightarrow L = gleft(frac{T}{2pi}right)^2 end{gather*} На Луне: $$ L_л=1,6cdotleft(frac{1}{2pi}right)^2approx 0,0405 (м)approx 4,1 (см) $$ На Марсе: $$ L_м=3,6cdotleft(frac{1}{2pi}right)^2approx 0,0912 (м)approx 9,1 (см) $$ Ответ: 4,1 см; 9,1 см
п.5. Лабораторная работа №4. Исследование колебаний математического маятника
Цель работы
Исследовать, от каких величин зависит период колебаний математического маятника.
Теоретические сведения
При малых отклонениях (порядка 15-20° от вертикали) период колебаний математического маятника определяется формулой: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
Для работы принять (gapprox 9,80665 м/с^2).
При заданном периоде колебаний для длины маятника получаем: $$ L=gleft(frac{T}{2pi}right)^2 $$
Приборы и материалы
Два лабораторных грузика по 100 г, крепкая нить (1,5-2 м), линейка (30-50 см), штатив, секундомер.
Ход работы
1. Рассчитайте длину нитей, необходимых для создания маятников с периодами колебаний (T_1=1 с; T_2=2 с).
2. Закрепите один грузик на нити и подвесьте его на штативе так, чтобы длина подвеса была равна расчетной длине (L_1).
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний. Повторите опыт 5 раз. Проведите расчеты для определения периода колебаний (T_{1 эксп}) по методике, изложенной в лабораторной работе №2 (см. §4 данного справочника).
4. Теперь подвесьте грузик так, чтобы длина подвеса была равна расчетной длине (L_2). Повторите серию из 5 экспериментов и определите (T_{2 эксп}).
5. При длине подвеса (L_2) подвесьте к первому грузику второй. Повторите серию из 5 экспериментов и определите (T ‘). Сравните (T ‘) и (T_{2 эксп}).
6. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Расчет длины нитей begin{gather*} L=gleft(frac{T}{2pi}right)^2\ T_1=1 c, L_1=9,80665cdotleft(frac{1}{2pi}right)^2approx 0,248 (м)=24,8 (см)\ T_2=2 c, L_1=9,80665cdotleft(frac{2}{2pi}right)^2approx 0,9994 (м)=99,4 (см) end{gather*}
Определение (T_{1 эксп})
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1 c)
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 9,7 | 10,2 | 9,8 | 9,9 | 10,3 | 50 |
| (triangle c) | 0,3 | 0,2 | 0,2 | 0,1 | 0,3 | 1 |
begin{gather*} t_{cp}=frac{50}{5}=10\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(10,0pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{1 эксп}=frac{1}{10}(t_0pmtriangle t), T_{1 эксп}=(1,00pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{1 эксп}}cdot 100text{%}=frac{0,02}{1}cdot 100text{%}=2,0text{%} $$
Определение (T_{2 эксп})
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 19,7 | 20,1 | 19,8 | 20,2 | 19,7 | 99,5 |
| (triangle c) | 0,2 | 0,2 | 0,1 | 0,3 | 0,2 | 1 |
begin{gather*} t_{cp}=frac{99,5}{5}=19,9\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,9pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{2 эксп}=frac{1}{10}(t_0pmtriangle t), T_{2 эксп}=(1,99pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{2 эксп}}cdot 100text{%}=frac{0,02}{1,99}cdot 100text{%}approx 1,0text{%} $$
Определение (T ‘) (с двумя грузиками)
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 20,2 | 19,7 | 19,6 | 20,0 | 20,3 | 99,8 |
| (triangle c) | 0,24 | 0,26 | 0,36 | 0,04 | 0,34 | 1,24 |
begin{gather*} t_{cp}=frac{99,8}{5}=19,96\ triangle_{cp}=frac{1,24}{5}approx 0,25 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,25right}=0,25 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,96pm 0,25) c end{gather*} Период колебаний в 10 раз меньше: $$ T’=frac{1}{10}(t_0pmtriangle t), T’=(1,996pm 0,025) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T’}cdot 100text{%}=frac{0,025}{1,996}cdot 100text{%}approx 1,3text{%} $$
Полученные на опыте интервалы для (T_{2 эксп}) и (T’) (одинаковая длина нити (L_2) и разные массы грузиков – 100 г и 200 г соответственно): begin{gather*} 1,97leq T_{2 эксп}leq 2,01\ 1,971leq T’leq 2,021 end{gather*} Таким образом, (T_{2 эксп}approx T’), т.е. период колебаний математического маятника не зависит от массы груза.
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе с помощью расчетной формулы были определены длины нитей подвеса для маятников с периодами колебаний (T_1=1 с; T_2=2 с).
Полученный на опыте период колебаний для подвеса с (L_1=24,8 см) с грузиком 100 г равен $$ T_{1 эксп}=(1,00pm 0,02) c, delta=2,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 100 г равен $$ T_{2 эксп}=(1,99pm 0,02) c, delta=1,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 200 г равен $$ T’=(1,996pm 0,025) c, delta=1,3text{%} $$ Формула (T=2pisqrt{frac Lg}) данными экспериментами подтверждена.
Период колебаний математического маятника зависит от длины подвеса и не зависит от массы грузика на подвесе.
Трепещите и радуйтесь: сегодня занимаемся решением задач по теме «Механические колебания и волны».
И конечно, подписывайтесь на наш телеграм-канал, чтобы получать полезную рассылку каждый день. Не важно, технарь вы, или гуманитарий – интересно будет всем.
Задачи по теме механические колебания и волны с решениями
Здесь мы постарались собрать несколько типовых и при этом разноплановых задач на механические колебания.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Гармонические колебания
Условие
Точка совершает колебания по гармоническому закону. Амплитуда колебаний равна 5 см, а период – 4 секунды. Каковы максимальная скорость колеблющейся точки и её ускорение?
Решение
Запишем уравнение гармонических колебаний:
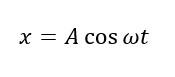
Здесь омега – циклическая частота:
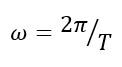
Скорость и ускорение точки вычисляются по формулам механики:
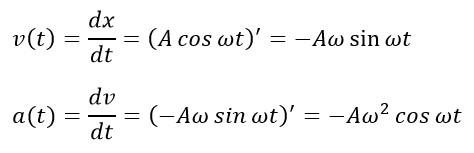
Модули ускорения и скорости максимальны тогда, когда значение тригонометрической функции в выражениях равно единице:

Ответ: 8 см/с; 12 см/с^2.
Задача №2. Длина волны
Условие
Какова длина волны основного тона ноты «ля» частотой 435 Гц? Скорость звука в воздухе принять равно 340 м/с.
Решение
Известно, период – величина, обратная частоте. А длина волны связана с периодом колебаний и скоростью их распространения соотношением:
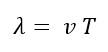
Тогда можно записать:
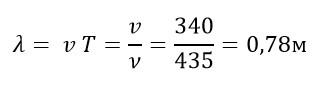
Ответ: 0,78 м.
Задача №3. Затухающие колебания
Условие
Груз массой 0,2 кг подвешен на пружине и помещен в масло. Коэффициент сопротивления r в масле равен 0,5 кг/с. Коэффициент жесткости пружины k равен 50 Н/м. Найти частоту затухающих колебаний груза.
Решение
Циклическая частота затухающих колебаний можно определяется по формуле:

Теперь определим обычную частоту:

Ответ: 2,51 Гц.
Задача №4. Эффект Доплера
Условие
Гудок неподвижного электровоза дает сигнал с частотой 300 Гц. Какова кажущаяся частота гудка для пассажира, который в другом поезде приближается к электровозу со скоростью 40 м/с? Удаляется от него с той же скоростью?
Подробнее про эффект Доплера читайте в отдельной статье нашего блога.
Решение
Формула, связывающая испускаемую и воспринимаемую частоты при эффекте Доплера:

Здесь с – скорость волн в среде (в нашем случае скорость звука), u – скорость приемника относительно среды, v – скорость источника относительно среды. Когда поезд приближается:
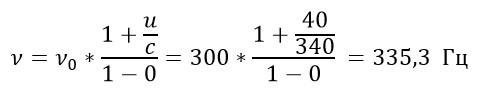
При движении от источника звука:
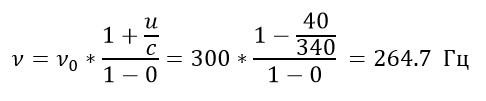
Ответ: 335,3 Гц; 264,7 Гц.
Задача №5. Математический маятник
Условие
Математический маятник колеблется с амплитудой А и максимальной скоростью Vm. Найти длину маятника l.
Решение
Запишем уравнение гармонических колебаний математического маятника:
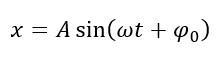
Взяв первую производную, получим скорость и выразим период:
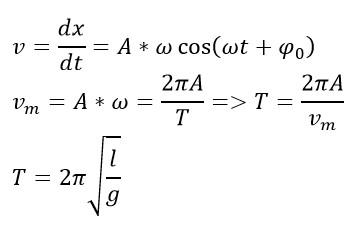
В итоге получаем:

Ответ: см. решение.
Вопросы на тему «Механические колебания и волны»
Вопрос 1. Что такое волна?
Ответ. Волна – это колебания, распространяющиеся в среде с течением времени. Волны могут иметь разную физическую природу, они бывают механические, электромагнитные и т.д.
Вопрос 2. Что такое колебание?
Ответ. Колебание – процесс изменения состояний системы, в той или иной степени повторяющийся во времени.
Принципиальное отличие волн от колебаний: при колебаниях отсутствует перенос энергии.
Вопрос 3. Приведите примеры механических колебаний в повседневной жизни.
Ответ. Механические колебания:
- маятник часов;
- раскачивающиеся качели;
- вибрации гитарной струны;
- качка корабля на волнах и т.д.
Вопрос 4. Приведите примеры механических волн.
Ответ. Механические волны:
- звук;
- морские волны;
- сейсмические волны.
Вопрос 5. Какие колебания называются гармоническими?
Ответ. Гармонические колебания – это колебания, в которых изменение какой-либо физической величины происходит по закону синуса или косинуса.
Держите под рукой полезные формулы, которые пригодятся при решении задач. А перед тем как начать самостоятельно решать задачи, рекомендуем ознакомиться с универсальной памяткой.
Нужна помощь в решении задач и прочих студенческих заданий? Профессиональный студенческий сервис готов оказать ее в любое время, обращайтесь за консультациями к проверенным специалистам.
«Мир,
в котором мы живём,
удивительно
склонен к колебаниям….
Колеблются
даже атомы,
из
которых мы состоим».
Данная
тема посвящена решению задач на математический маятник.
Задача
1.
Математический маятник совершил 30 колебаний за минуту. Найдите период и
частоту колебаний, а также длину маятника.
|
ДАНО: |
СИ |
РЕШЕНИЕ Период колебаний можно определить по формуле Частота колебаний рассчитывается по формуле Период колебаний математического маятника рассчитывается Преобразуем эту формулу и выразим из неё длину маятника |
|
|
Ответ:
период – 2 с, частота – 0,5 Гц, длина маятника – 99 см.
Задача
2.
При уменьшении длины математического маятника на 2 см, период его колебаний
уменьшается в 1,5 раза. Найдите первоначальную длину маятника.
|
ДАНО: |
СИ |
РЕШЕНИЕ Период колебаний математического маятника определяется по В соответствии с этим, Т.к. период колебаний уменьшился в 1,5 раза, то получаем Преобразуем полученную |
|
|
Ответ:
3,6 см.
Задача
3.
Математический маятник, проходя нижнюю точку имеет скорость 1 м/с, а его
длина равна 20 см. Определите вертикальное отклонение маятника от положения
равновесия в момент времени t = 5 с,
если в начальный момент времени маятник находится на максимальной высоте.
|
ДАНО: |
СИ |
РЕШЕНИЕ Поскольку в начальный момент Запишем уравнение гармонических Исходя из начального Запишем закон сохранения энергии, который выполняется для Тогда Циклическая частота Т.к амплитуда и циклическая То уравнение гармонических А по прошествии 5 с |
|
|
Ответ:
4,5 см.
Задача
4.
Шарик массой 200 г, подвешенный на нити совершает колебания. Шарику сообщили
заряд 300 мкКл и поместили всю систему в электростатическое поле, линии
напряжённости которого направлены вертикально вниз. После этого циклическая
частота колебаний увеличилась вдвое. Найдите напряжённость поля.
|
ДАНО: |
СИ |
РЕШЕНИЕ Циклическая частота Сила тяжести Электростатическая сила В электростатике заряд – это Запишем теперь выражение для Для конечной циклической Т.к. по условию задачи Преобразуем данную формулу и
|
|
|
Ответ:
1960 Н/Кл.
Задача
5.
Материальная точка на нерастяжимой нити длиной 0,3 м совершает колебания,
так что максимальный угол отклонения нити от вертикали составляет 30º.
Найдите положение материальной точки в момент времени t = 5 с
в системе отсчёта, связанной с положением равновесия. В начальный момент
времени точка находится в положении равновесия.
|
ДАНО: |
РЕШЕНИЕ Запишем уравнение Очевидно, что амплитуда Циклическая частота математического Тогда с учётом того, что Уравнения гармонических Тогда координаты точки через |
|
|
Ответ:
(–4,8 см; 1,3 см).