8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:

(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:
 (8.17 – формула Медианы)
(8.17 – формула Медианы)
где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:

Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):

Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
![]() Загрузка…
Загрузка…
Как рассчитать моду из таблицы частот (с примерами)
17 авг. 2022 г.
читать 2 мин
Мода таблицы частот представляет значение, которое встречается чаще всего.
На практике может быть:
- Нулевые режимы , если ни одно значение не встречается чаще, чем любое другое.
- Один режим , если одно значение встречается чаще всего.
- Несколько режимов , если несколько значений встречаются чаще всего.
Чтобы определить режим таблицы частот, вам просто нужно определить значение (я) с самой высокой частотой.
В следующих примерах показано, как найти моду различных таблиц частот.
Пример 1: Поиск моды из таблицы частот (нулевые моды)
Следующая таблица частот показывает количество домашних животных, принадлежащих 10 разным семьям в определенном районе:
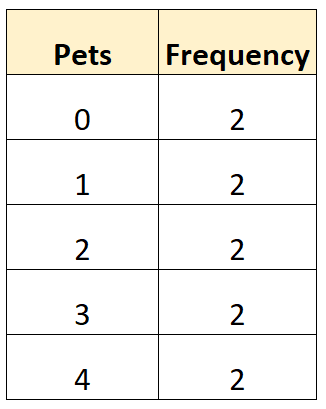
Обратите внимание, что каждое значение в таблице имеет одинаковую частоту.
Это означает, что для этой конкретной таблицы частот нет режима, поскольку каждое значение встречается одинаковое количество раз.
Пример 2: Поиск режима из таблицы частот (один режим)
В следующей таблице частоты показано общее количество побед 17 футбольных команд в определенной лиге:
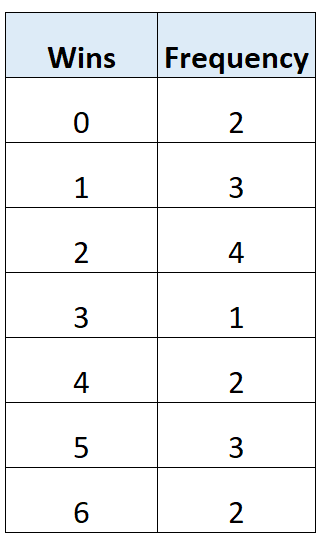
Количество выигрышей с наибольшей частотой – 2 выигрыша.
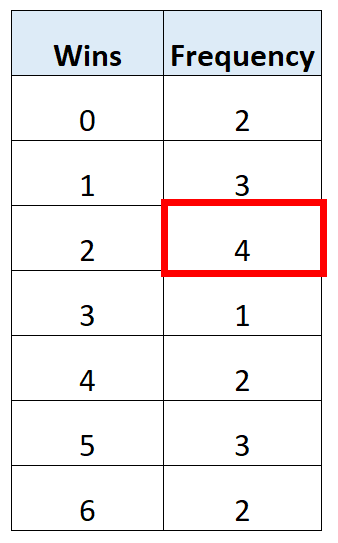
Таким образом, мода для этой таблицы частот равна 2 .
Пример 3: Поиск режима из таблицы частот (несколько режимов)
В следующей таблице частот показан размер домохозяйства различных домохозяйств в определенном районе:
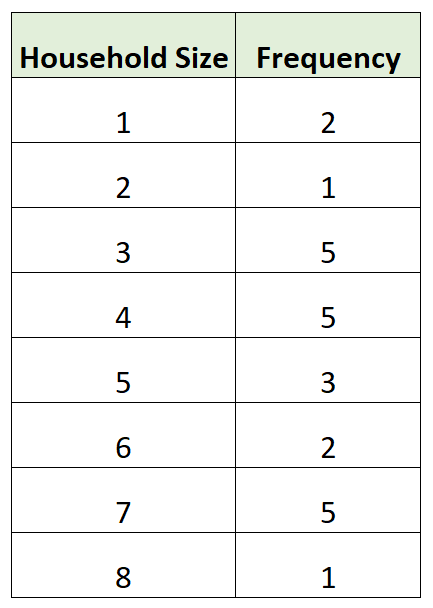
Размеры домохозяйств с наибольшей частотой составляют 3 , 4 и 7 .
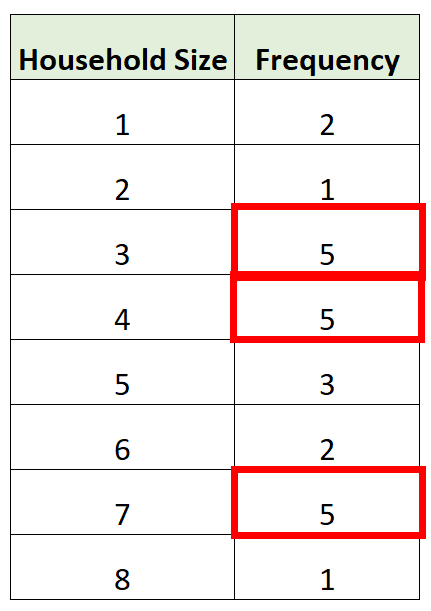
Таким образом, эта таблица частот фактически имеет три моды: 3 , 4 и 7 .
Дополнительные ресурсы
Как рассчитать медиану из таблицы частот
Как рассчитать среднее значение из таблицы частот
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
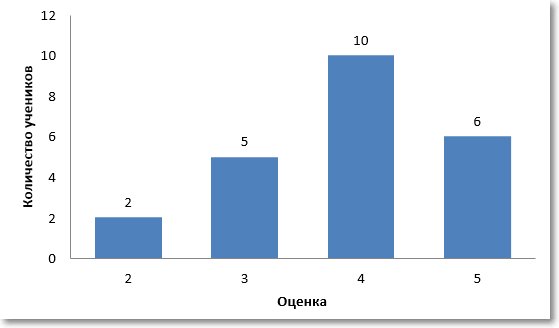
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
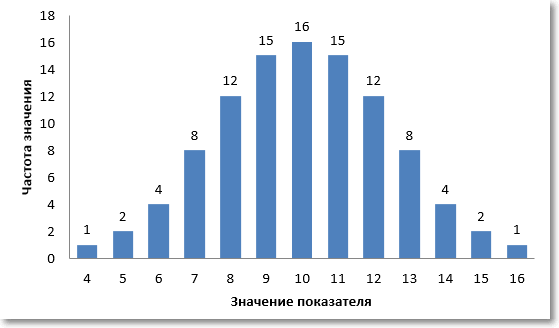
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
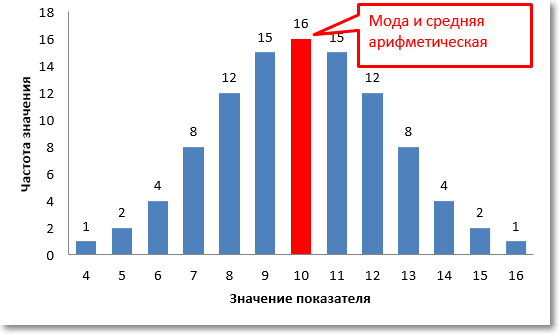
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
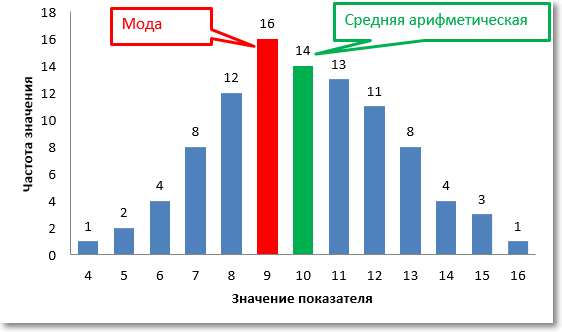
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
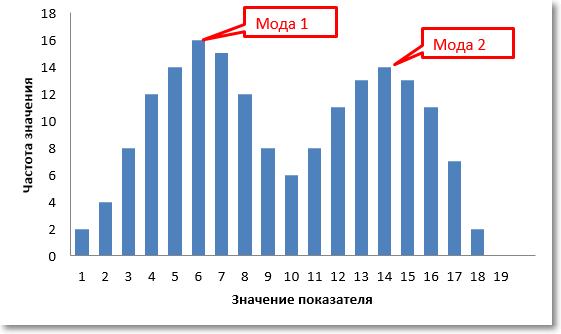
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
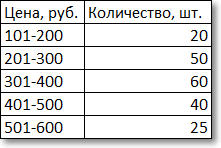
Для наглядности изобразим соответствующую диаграмму.
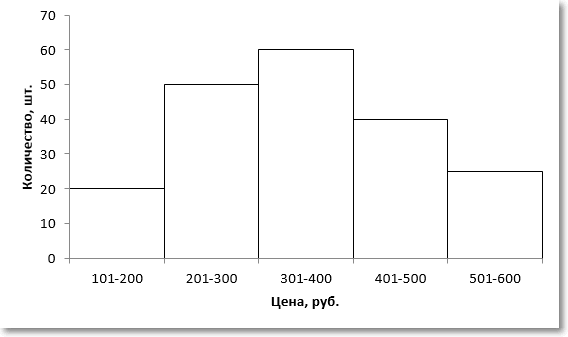
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
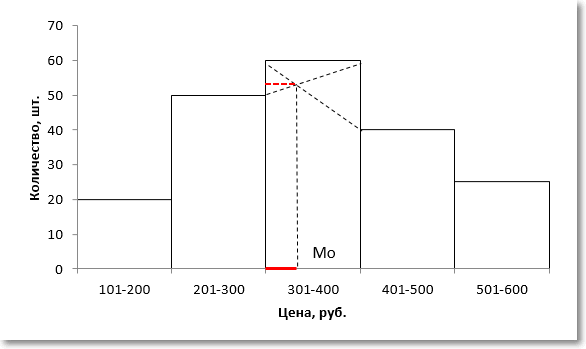
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
![]()
Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
![]()
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
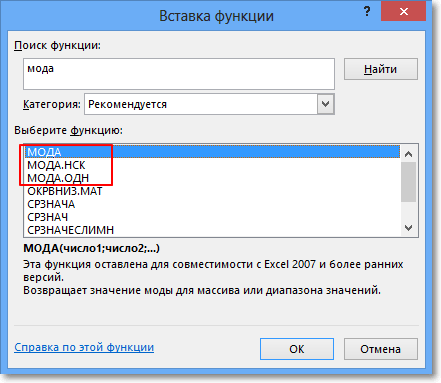
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Следующая статья посвящена медиане.
До встречи на statanaliz.info.
Поделиться в социальных сетях:
Мода
и медиана –
особого рода средние, которые используются
для изучения структуры вариационного
ряда. Их иногда называют структурными
средними, в отличие от рассмотренных
ранее степенных средних.
Мода
– это величина признака (варианта),
которая чаще всего встречается в данной
совокупности, т.е. имеет наибольшую
частоту.
Мода
имеет большое практическое применение
и в ряде случаев только мода может дать
характеристику общественных явлений.
Медиана
– это варианта, которая находится в
середине упорядоченного вариационного
ряда.
Медиана
показывает количественную границу
значения варьирующего признака, которой
достигла половина единиц совокупности.
Применение медианы наряду со средней
или вместо нее целесообразно при наличии
в вариационном ряду открытых интервалов,
т.к. для вычисления медианы не требуется
условное установление границ отрытых
интервалов, и поэтому отсутствие сведений
о них не влияет на точность вычисления
медианы.
Медиану
применяют также тогда, когда показатели,
которые нужно использовать в качестве
весов, неизвестны. Медиану применяют
вместо средней арифметической при
статистических методах контроля качества
продукции. Сумма абсолютных отклонений
варианты от медианы меньше, чем от любого
другого числа.
Рассмотрим
расчет моды и медианы в дискретном
вариационном ряду:
|
Стаж, |
Число |
Накопленные |
|
1 |
2 |
2 |
|
3 |
4 |
6 |
|
4 |
5 |
(11) |
|
8 |
4 |
15 |
|
10 |
1 |
16 |
|
ИТОГО: |
16 |
– |
Определить моду и медиану.
Мода
Мо =
4 года, так как этому значению соответствует
наибольшая частота f
= 5.
Т.е.
наибольшее число рабочих имеют стаж 4
года.
Для
того, чтобы вычислить медиану, найдем
предварительно половину суммы частот.
Если сумма частот является числом
нечетным, то мы сначала прибавляем к
этой сумме единицу, а затем делим пополам:
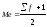
Ме=16/2=8
Медианой
будет восьмая по счету варианта.
Для
того, чтобы найти, какая варианта будет
восьмой по номеру, будем накапливать
частоты до тех пор, пока не получим сумму
частот, равную или превышающую половину
суммы всех частот. Соответствующая
варианта и будет медианой.
Ме
= 4 года.
Т.е.
половина рабочих имеет стаж меньше
четырех лет, половина больше.
Если
сумма накопленных частот против одной
варианты равна половине сумме частот,
то медиана определяется как средняя
арифметическая этой варианты и
последующей.
Вычисление
моды и медианы в интервальном вариационном
ряду
Мода
в интервальном вариационном ряду
вычисляется по формуле
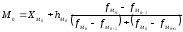
где ХМ0
– начальная
граница модального интервала,
hм0
– величина модального интервала,
fм0,
fм0-1,
fм0+1
– частота
соответственно модального интервала,
предшествующего модальному и последующего.
Модальным
называется такой интервал, которому
соответствует наибольшая частота.
Пример
1
|
Группы |
Число |
Накопленные |
|
1 |
2 |
3 |
|
До |
4 |
4 |
|
2-4 |
23 |
27 |
|
4-6 |
20 |
47 |
|
6-8 |
35 |
82 |
|
8-10 |
11 |
93 |
|
свыше |
7 |
100 |
|
ИТОГО: |
100 |
– |
Определить
моду и медиану.
Решение.
Модальный
интервал [6-8], т.к. ему соответствует
наибольшая частота f
= 35. Тогда:
Хм0=6,
fм0=35
hм0=2,
fм0-1=20
fм0+1=11

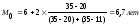
Вывод:
Наибольшее число рабочих имеет стаж
примерно 6,7 лет.
Для
интервального ряда Ме вычисляется по
следующей формуле:

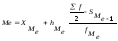
где Хме
–
нижняя граница медиального интервала,
hме
– величина медиального интервала,
![]() –
–
половина суммы частот,
fме
– частота медианного интервала,
Sме-1
–сумма
накопленных частот интервала,
предшествующего медианному.
Медианный
интервал – такой интервал, которому
соответствует кумулятивная частота,
равная или превышающая половину суммы
частот.
Определим
медиану для нашего примера.
Найдем:
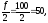
т.к
82>50, то медианный интервал [6-8].
Тогда:
Хме
=6, fме
=35,
hме
=2, Sме-1=47,
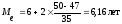
Вывод: Половина рабочих имеет стаж
меньше 6,16 лет, а половина имеет стаж
больше, чем 6,16 лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.
Расчёт структурных характеристик
вариационного ряда распределения.
Студент
должен:
знать:
– область применения и методику расчёта структурных
средних величин;
уметь:
– исчислять структурные средние величины;
– формулировать вывод по полученным результатам.
Методические указания
В
статистике исчисляются мода и медиана, которые относятся к структурным средним,
так как их величина зависит от строения статистической совокупности.
Расчёт моды
Модой называется значение признака
(варианта), чаще всеговстречающееся в изучаемой
совокупности. В дискретном ряду распределения модой будет варианта с наибольшей
частотой.
Например: Распределение проданной женской обуви по размерам характеризуется
следующим образом:
|
Размер |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
|
Количество |
8 |
19 |
34 |
108 |
72 |
51 |
6 |
2 |
В этом ряду
распределения модой является 37 размер,
т.е. Мо=37 размер.
Для
интервального ряда распределения мода определяется по формуле:
![]()
где ХMo –
нижняя граница модального интервала;
hMo – величина модального интервала;
fMo –
частота модального интервала;
fMo–1 и
fMo+1 – частота интервала соответственно
предшествующего модальному и следующего за ним.
Например:
Распределение рабочих по стажу работы характеризуется следующими данными.
|
Стаж работы, лет |
до 2 |
2-4 |
4-6 |
6-8 |
8-10 |
10 и более |
|
Число рабочих, чел. |
4 |
23 |
20 |
35 |
11 |
7 |
Определить моду
интервального ряда распределения.
Мода интервального ряда составляет
![]()
Мода всегда бывает
несколько неопределённой, т.к. она зависит от величины групп и точного
положения границ групп. Мода широко применяется в коммерческой практике при
изучении покупательского спроса, при регистрации цен и т.п.
Расчёт медианы
Медианой в статистике называется варианта,
расположенная в середине упорядоченного ряда данных, и которая делит
статистическую совокупность на две равные части так, что у одной половины
значения меньше медианы, а у другой половины – больше её. Для определения
медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания
или убывания индивидуальных значений признака.
В дискретном
упорядоченном ряду с нечётным числом членов медианой будет варианта,
расположенная в центре ряда.
Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7
лет, т.е. Ме=7 лет
Если дискретный
упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя
арифметическая из двух смежных вариант, стоящих в центре ряда.
Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду
имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя
арифметическая из этих значений и будет медианой ряда
![]()
Чтобы определить медиану для
сгруппированных данных, необходимо считать накопленные частоты.
Например: По имеющимся данным определим медиану размера обуви
|
Размер обуви |
Количество проданных пар |
Сумма накопленных частот |
|
34 |
8 |
8 |
|
35 |
19 |
8+19=27 |
|
36 |
34 |
27+34=61 |
|
37 |
108 |
61+108=169 |
|
38 |
72 |
– |
|
39 |
51 |
– |
|
40 |
6 |
– |
|
41 |
2 |
– |
|
Итого |
300 |
Для
определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание
итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот
ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная
сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е.
37 и есть медиана ряда.
Если
же сумма накопленных частот против одной из вариант равна точно половине суммы
частот ряда, то медиана определяется как средняя арифметическая этой варианты и
последующей.
Например: По имеющимся данным определим медиану заработной платы рабочих
|
Месячная заработная плата, тыс.руб. |
Число рабочих, чел. |
Сумма накопленных частот |
|
14,0 |
2 |
2 |
|
14,2 |
6 |
2+6=8 |
|
16,0 |
12 |
8+12=20 |
|
16,8 |
16 |
– |
|
18,0 |
4 |
– |
|
Итого: |
40 |
– |
Медиана будет равна: ![]()
Медиана
интервального вариационного ряда распределения определяется по формуле:
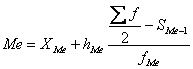
Где ХМе – нижняя граница медианного интервала;
hMe –
величина медианного интервала;
∑f
– сумма частот ряда;
fМе – частота медианного интервала;
Например: По имеющимся данным о распределении предприятий по численности
промышленно – производственного персонала рассчитать медиану в интервальном
вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
7 |
4+7=11 |
|
400-500 |
30 |
11+30=41 |
|
500-600 |
19 |
– |
|
600-700 |
15 |
– |
|
700-800 |
5 |
|
|
Итого: |
80 |
Определим, прежде всего,
медианный интервал. В данном примере сумма накопленных частот, превышающих половину
суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный
интервал, т.е. интервал, в котором находится медиана ряда. Определим её
значение
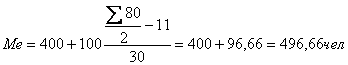
Если же сумма накопленных частот
против одного из интервалов равна точно половине суммы частот ряда, то медиана
определяется по формуле:
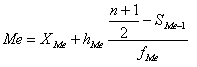
где n – число
единиц в совокупности.
Например: По имеющимся данным о распределении предприятий по
численности промышленно – производственного персонала рассчитать медиану в
интервальном вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
6 |
4+6=10 |
|
400-500 |
30 |
10+30=40 |
|
500-600 |
20 |
40+20=60 |
|
600-700 |
15 |
– |
|
700-800 |
5 |
|
|
Итого: |
80 |
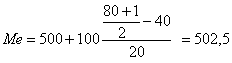 чел
чел
Моду и медиану в
интервальном ряду можно определить
графически:
моду
в дискретных рядах – по полигону распределения, моду в интервальных рядах – по
гистограмме распределения, а медиану – по кумуляте.
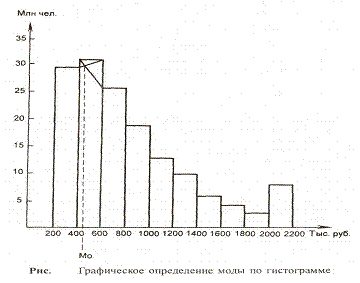
Мода интервального ряда распределения
определяется по гистограмме распределения определяют
следующим образом. Для этого выбирается самый высокий прямоугольник, который
является в данном случае модальным. Затем правую вершину модального
прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.
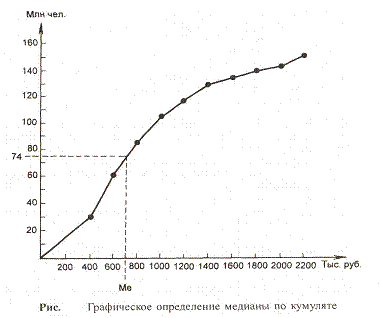
Медиана рассчитывается по
кумуляте. Для её определения из точки на шкале
накопленных частот (частостей), соответствующей 50%,
проводится прямая, параллельная оси абсцисс, до
пересечения с кумулятой. Затем из точки пересечения
указанной прямой с кумулятой опускается перпендикуляр
на ось абсцисс. Абсцисса точки пересечения является медианой.
Кроме моды и медианы в вариантных рядах могут быть
определены и другие структурные характеристики – квантили. Квантили
предназначены для более глубокого изучения структуры ряда распределения.
Квантиль – это значение
признака, занимающее определенное место в упорядоченной по данному признаку
совокупности. Различают следующие виды квантилей:
– квартили – значения признака, делящие упорядоченную
совокупность на четыре
равные части;
– децили
– значения признака, делящие упорядоченную совокупность на десять
равных частей;
– перцентели –
значения признака, делящие упорядоченную совокупность на сто равных частей.
Таким образом, для характеристики положения центра ряда распределения
можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя
центра распределения необходимо исходить из следующих рекомендаций:
–
для устойчивых социально-экономических
процессов в качестве показателя центра используют среднюю
арифметическую. Такие процессы характеризуются симметричными распределениями, в
которых ![]() ;
;
–
для неустойчивых процессов положение
центра распределения характеризуется с помощью Mo
или Me. Для асимметричных процессов предпочтительной
характеристикой центра распределения является медиана, поскольку занимает
положение между средней арифметической и модой.
