У этого термина существуют и другие значения, см. Метод (значения).
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства.
Описание метода[править | править код]
Обоснование[править | править код]
Чтобы численно решить уравнение 


Для наилучшей сходимости метода в точке очередного приближения 


В предположении, что точка приближения «достаточно близка» к корню 


С учётом этого функция 
При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение.
В этом случае алгоритм нахождения численного решения уравнения 
По теореме Банаха последовательность приближений стремится к корню уравнения 
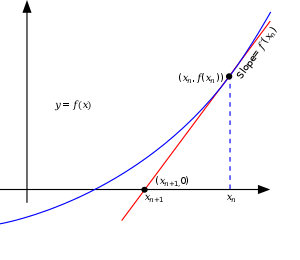
Иллюстрация метода Ньютона (синим изображена функция 



Геометрическая интерпретация[править | править код]
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть 1) вещественнозначная функция 

2) существует искомая точка 

3) существуют 

для ![{displaystyle xin (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260bb1d0fcbae53c2e7a917c0ada3962ebf17bdd)
и
для 
4) точка 

Тогда формула итеративного приближения 
может быть выведена из геометрического смысла касательной следующим образом:
где 
к графику
в точке 
Следовательно (в уравнении касательной прямой полагаем 

Если 

Если 



до тех пор, пока точка «не вернётся» в область поиска

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения 
2) Случаи граничного (в точке 


3) С геометрической точки зрения равенство
означает, что касательная прямая к графику
в точке

параллельна оси
и при
не пересекается с ней в конечной части.
4) Чем больше константа 

тем для
пересечение касательной к графику 


то есть тем ближе значение 

Итерационный процесс начинается с некоторого начального приближения

причём между
и искомой точкой
не должно быть других нулей функции

то есть «чем ближе
к искомому корню 
тем лучше». Если предположения о нахождении 
Для предварительно заданных 
итерационный процесс завершается если


В частности, для матрицы дисплея 

исходя из масштаба отображения графика 
то есть если 



Алгоритм[править | править код]
- Задается начальное приближение
.
- Пока не выполнено условие остановки, в качестве которого можно взять
или
(то есть погрешность в нужных пределах), вычисляют новое приближение:
.
Пример[править | править код]
Иллюстрация применения метода Ньютона к функции  с начальным приближением в точке с начальным приближением в точке  . .
|
|
|---|---|
|
График последовательных приближений. |
График сходимости. |
| Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум. |
Рассмотрим задачу о нахождении положительных 








Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
Условия применения[править | править код]
Иллюстрация расхождения метода Ньютона, применённого к функции 

Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры[править | править код]
-
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём ноль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст ноль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
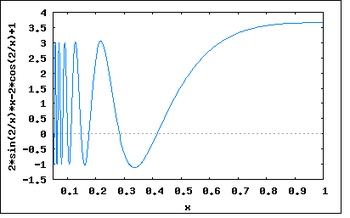
График производной функции 

-
- Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.
Рассмотрим функцию:
Тогда 

В окрестности корня производная меняет знак при приближении 


Таким образом 

-
- Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.
Рассмотрим пример:
Тогда 


На очередном шаге имеем 
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и 
-
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда 

Ограничения[править | править код]
Пусть задано уравнение 

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы 
на
, то есть
сут и не равна нулю;
на
, то есть
ограничена;
на
, и
;
Причём длина рассматриваемого отрезка 
- на
существует корень
уравнения
;
- если
, то итерационная последовательность сходится к этому корню:
;
- погрешность может быть оценена по формуле
.
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию 
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная
равномерно отделена от нуля;
- её вторая производная
должна быть равномерно ограничена.
Историческая справка[править | править код]
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения 

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений 
В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
Обобщения и модификации[править | править код]
Иллюстрация последовательных приближений метода одной касательной, применённого к функции 

Метод секущих[править | править код]
Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

Таким образом, основная формула имеет вид
Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618…
Замечания. 1) Для начала итерационного процесса требуются два различных значения


2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только
(и в ходе вычислений — временно 

для метода секущих требуется сохранение




3) Применяется, если вычисление 
(например, требует большого количества машинных ресурсов: времени и/или памяти).
Метод одной касательной[править | править код]
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения 
При таком выборе 

и если отрезок, на котором предполагается наличие корня 






Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.
Метод Ньютона-Фурье[править | править код]
Метод Ньютона-Фурье – это расширение метода Ньютона, выведенное Жозефом Фурье для получения оценок на абсолютную ошибку аппроксимации корня, в то же время обеспечивая квадратичную сходимость с обеих сторон.
Предположим, что f(x) дважды непрерывно дифференцируема на отрезке [a, b] и что f имеет корень на этом интервале. Дополнительно положим, что f′(x), f″(x) ≠ 0 на этом отрезке (например, это верно, если f(a) < 0, f(b) > 0, и f″(x) > 0 на этом отрезке). Это гарантирует наличие единственного корня на этом отрезке, обозначим его α. Эти рассуждения относятся к вогнутой вверх функции. Если она вогнута вниз, то заменим f(x) на −f(x), поскольку они имеют одни и те же корни.
Пусть x0 = b будет правым концом отрезка, на котором мы ищем корень, а z0 = a – левым концом того же отрезка. Если xn найдено, определим
которое выражает обычный метод Ньютона, как описано выше. Затем определим
где знаменатель равен f′(xn), а не f′(zn). Итерации xn будут строго убывающими к корню, а итерации zn – строго возрастающими к корню. Также выполняется следующее соотношение:
,
таким образом, расстояние между xn и zn уменьшается квадратичным образом.
Многомерный случай[править | править код]
Обобщим полученный результат на многомерный случай.
Пусть необходимо найти решение системы:
Выбирая некоторое начальное значение ![{displaystyle {vec {x}}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ae4aca0e44306357efc8a4653f758b4d984a42f)
![{displaystyle {vec {x}}^{[j+1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/731295798153991209f20aaf78929acff1a3a6fa)
где ![{displaystyle {vec {x}}^{[j]}=(x_{1}^{[j]},;x_{2}^{[j]},;ldots ,;x_{n}^{[j]}),quad j=0,;1,;2,;ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/84da9bf66616a56d35d1971525796f1cd57fab79)
Применительно к задачам оптимизации[править | править код]
Пусть необходимо найти минимум функции многих переменных 

где 

В более удобном итеративном виде это выражение выглядит так:
В случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
Метод Ньютона — Рафсона[править | править код]
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где
Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением ![{displaystyle H(f({vec {x}}^{[0]}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deb9b2bfeb49d385250170d0ec25c37a5772da8b)

Применительно к задачам о наименьших квадратах[править | править код]
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где 



Тогда очередной шаг 
Метод Гаусса — Ньютона[править | править код]
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое 



Таким образом, когда норма 



Обобщение на комплексную плоскость[править | править код]

Бассейны Ньютона для полинома пятой степени 
До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексной переменной. При этом процедура остаётся неизменной:
Особый интерес представляет выбор начального приближения 
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Реализация[править | править код]
Scala[править | править код]
object NewtonMethod { val accuracy = 1e-6 @tailrec def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = { val x1 = x0 - f(x0) / dfdx(x0) if (abs(x1 - x0) < e) x1 else method(x1, f, dfdx, e) } def g(C: Double) = (x: Double) => x*x - C def dgdx(x: Double) = 2*x def sqrt(x: Double) = x match { case 0 => 0 case x if (x < 0) => Double.NaN case x if (x > 0) => method(x/2, g(x), dgdx, accuracy) } }
Python[править | править код]
from math import sin, cos from typing import Callable import unittest def newton(f: Callable[[float], float], f_prime: Callable[[float], float], x0: float, eps: float=1e-7, kmax: int=1e3) -> float: """ solves f(x) = 0 by Newton's method with precision eps :param f: f :param f_prime: f' :param x0: starting point :param eps: precision wanted :return: root of f(x) = 0 """ x, x_prev, i = x0, x0 + 2 * eps, 0 while abs(x - x_prev) >= eps and i < kmax: x, x_prev, i = x - f(x) / f_prime(x), x, i + 1 return x class TestNewton(unittest.TestCase): def test_0(self): def f(x: float) -> float: return x**2 - 20 * sin(x) def f_prime(x: float) -> float: return 2 * x - 20 * cos(x) x0, x_star = 2, 2.7529466338187049383 self.assertAlmostEqual(newton(f, f_prime, x0), x_star) if __name__ == '__main__': unittest.main()
PHP[править | править код]
<?php // PHP 5.4 function newtons_method( $a = -1, $b = 1, $f = function($x) { return pow($x, 4) - 1; }, $derivative_f = function($x) { return 4 * pow($x, 3); }, $eps = 1E-3) { $xa = $a; $xb = $b; $iteration = 0; while (abs($xb) > $eps) { $p1 = $f($xa); $q1 = $derivative_f($xa); $xa -= $p1 / $q1; $xb = $p1; ++$iteration; } return $xa; }
Octave[править | править код]
function res = nt() eps = 1e-7; x0_1 = [-0.5,0.5]; max_iter = 500; xopt = new(@resh, eps, max_iter); xopt endfunction function a = new(f, eps, max_iter) x=-1; p0=1; i=0; while (abs(p0)>=eps) [p1,q1]=f(x); x=x-p1/q1; p0=p1; i=i+1; end i a=x; endfunction function[p,q]= resh(x) % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1; p=-25*x.^4+16*x.^3-36*x.^2+22*x-2; q=-100*x.^3+48*x.^2-72*x+22; endfunction
Delphi[править | править код]
// вычисляемая функция function fx(x: Double): Double; begin Result := x * x - 17; end; // производная функция от f(x) function dfx(x: Double): Double; begin Result := 2 * x; end; function solve(fx, dfx: TFunc<Double, Double>; x0: Double): Double; const eps = 0.000001; var x1: Double; begin x1 := x0 - fx(x0) / dfx(x0); // первое приближение while (Abs(x1-x0) > eps) do begin // пока не достигнута точность 0.000001 x0 := x1; x1 := x1 - fx(x1) / dfx(x1); // последующие приближения end; Result := x1; end; // Вызов solve(fx, dfx,4));
C++[править | править код]
#include <stdio.h> #include <math.h> #define eps 0.000001 double fx(double x) { return x * x - 17;} // вычисляемая функция double dfx(double x) { return 2 * x;} // производная функции typedef double(*function)(double x); // задание типа function double solve(function fx, function dfx, double x0) { double x1 = x0 - fx(x0) / dfx(x0); // первое приближение while (fabs(x1 - x0) > eps) { // пока не достигнута точность 0.000001 x0 = x1; x1 = x0 - fx(x0) / dfx(x0); // последующие приближения } return x1; } int main () { printf("%fn", solve(fx, dfx, 4)); // вывод на экран return 0; }
C[править | править код]
typedef double (*function)(double x); double TangentsMethod(function f, function df, double xn, double eps) { double x1 = xn - f(xn)/df(xn); double x0 = xn; while(abs(x0-x1) > eps) { x0 = x1; x1 = x1 - f(x1)/df(x1); } return x1; } //Выбор начального приближения xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A; double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная //Пример вызова функции double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1)
Haskell[править | править код]
import Data.List ( iterate' ) main :: IO () main = print $ solve ( x -> x * x - 17) ( * 2) 4 -- Функция solve универсальна для всех вещественных типов значения которых можно сравнивать. solve = esolve 0.000001 esolve epsilon func deriv x0 = fst . head $ dropWhile pred pairs where pred (xn, xn1) = (abs $ xn - xn1) > epsilon -- Функция pred определяет достигнута ли необходимая точность. next xn = xn - func xn / deriv xn -- Функция next вычисляет новое приближение. iters = iterate' next x0 -- Бесконечный список итераций. pairs = zip iters (tail iters) -- Бесконечный список пар итераций вида: [(x0, x1), (x1, x2) ..].
Литература[править | править код]
- Акулич И. Л. Математическое программирование в примерах и задачах : Учеб. пособие для студентов эконом. спец. вузов. — М. : Высшая школа, 1986. — 319 с. : ил. — ББК 22.1 А44. — УДК 517.8(G).
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров : Учеб. пособие. — М. : Высшая школа, 1994. — 544 с. : ил. — ББК 32.97 А62. — УДК 683.1(G). — ISBN 5-06-000625-5.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М. : Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М. : Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М. : Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М. : Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М. : Наука, 1970. — С. 575—576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М. : МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
См. также[править | править код]
- Метод простой итерации
- Двоичный поиск
- Метод дихотомии
- Метод секущих
- Метод Мюллера
- Метод хорд
- Метод бисекции
- Фрактал
- Численное решение уравнений
- Целочисленный квадратный корень
- Быстрый обратный квадратный корень
Ссылки[править | править код]
- «Бассейны Ньютона» на сайте fractalworld.xaoc.ru
- «Исаак Ньютон» на сайте www.scottish-wetlands.org
- «Математические работы Канторовича» на сайте Института математики СО РАН
- Hazewinkel, Michiel, ed. (2001), Newton method, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W. Newton’s Method (англ.) на сайте Wolfram MathWorld.
- Newton’s method, Citizendium.
- Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
- Wu, X., Roots of Equations, Course notes.
Решение уравнения методом Ньютона
Метод
Ньютона, алгоритм Ньютона (также известный
как метод касательных) — это итерационный
численный метод нахождения корня (нуля)
заданной функции.
Достоинства
метода Ньютона:
Метод Ньютона – самый быстрый способ
нахождения корней уравнений: обычно
заданная точность достигается за 2-3
итерации. Очень быстрая сходимость по
сравнению с методом половинного деления
и методом простой итерации к заданной
точности.
Недостаток:
громоздкий алгоритм: на каждой итерации
необходимо вычислять значение функции
и ее первой производной.
Значение
корня новой итерации вычисляется по
формуле
![]()

Алгоритм
-
Задается
начальное приближение x0. -
Пока
не выполнено условие остановки, в
качестве которого можно взять

или

(то есть погрешность в нужных пределах),
вычисляют новое приближение:[1].
Производные
функции
-

; -

; -

если

>0

если
<0
Точное значение корня
Первое
уравнение – кубическое уравнение
Решение
кубического уравнения по формуле Кардано
Кубическое
уравнение в каноническом виде:
![]()
Обозначим
дискриминант кубического уравнения
![]()
По
формулам Кардано 3 корня уравнения
определяются следующим образом:

где

При
этом количество корней уравнения
определяются следующим образом:
Если
![]()
, уравнение имеет три действительных
корня.
Если
![]()
,
уравнение имеет один действительный и
два комплексно сопряженных корня.
Если
![]()
, уравнение имеет два действительных
корня. Если p = q = 0, уравнение имеет один
действительный корень [2].
Разрабатываемая
функция будет вычислять только первый
корень. При наличии других действительных
корнях будет сообщать об этом.
Наше
уравнение имеет вид:
Следовательно

Вычисление
корня по формуле Кардано:
float
al, be,//альфа, бетта
p,
q,//коэффициенты канонического уравнения
de;//дискриминант
(дельта)
p
= b / a;
q
= c / a;
de
= pow(p / 3, 3) + pow(q / 2, 2);
al
= pow(-q / 2 + pow(de, 0.5), (float)1/3);
be
= pow(-q / 2 – pow(de, 0.5), (float)1/3);
if(de
<= 0)
cout<<“nYravnenie
imeet neskol’ko deistvitelnuh kornei.”;
return
al + be;
Второе
уравнение – тригонометрическое уравнение
Найдем
точное решение уравнения





Уравнение
имеет множество корней. Нас интересует
ближайший корень к точке x0,
следовательно, необходимо найти ближайшее
целое значение k.



Тогда
точное решение будет в соответствии с
найденным k:
int
k;
k
= (x0 – asin(-c / a) + b) / (2 * M_PI);
return
asin(-c / a) + 2 * M_PI * k – b;
Третье
уравнение – логарифмическое уравнение



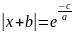
Два
возможных точных решения:


Нам
необходимо выбрать ближайший к x0.
То есть сравниваем расстояния х1х0 и
х2х0 и выбираем ближайший:
if
(fabs(exp(-c / a) – b – x0) < fabs(-exp(-c / a) – b – x0))
return
exp(-c / a) – b;
else
return
-exp(-c / a) – b
Абсолютная и относительная погрешность вычисления
Абсолютная
погрешность вычисления находится как
модуль разности между точным и приближенным
решением [3].
А
относительной погрешностью приближённого
числа называется отношение абсолютной
погрешности приближённого числа к
самому этому числу в процентном
соотношении.
Так
в нашем случае
fabs(pribl
– toch)
– абсолютная погрешность;
fabs(pribl
– toch)
/ toch
* 100 – относительная погрешность.
Где
pribl
– приближенное решение интеграла
(методом левых прямоугольников), toch
– точное решение интеграла.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$$
f(x) = 0
$$
Единственные требования, накладываемые на функцию $f$ — что у неё есть хотя бы один корень и что она непрерывна и дифференцируема на интервале поиска.
#Описание алгоритма
Алгоритм начинает с какого-то изначального приближения $x_0$ и затем итеративно строит лучшее решение, строя касательную к графику в точке $x = x_i$ и присваивая в качестве следующего приближения $x_{i+1}$ координату пересечения касательной с осью $x$. Интуиция в том, что если функция $f$ «хорошая», и $x_i$ уже достаточно близок к корню, то $x_{i+1}$ будет ещё ближе.
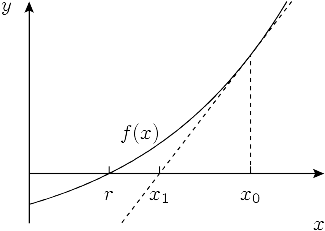
Чтобы получить точку пересечения для $x_i$, нужно приравнять уравнение касательной к нулю:
$$
0 = f(x_i) + (x_{i+1} – x_i) f'(x_i)
$$
откуда можно выразить
$$
x_{i+1} = x_i – frac{f(x_i)}{f'(x_i)}
$$
Метод Ньютона крайне важен в вычислительной математике: в большинстве случаев именно он используется для нахождения численных решений уравнений.
#Поиск квадратных корней
В качестве конкретного примера рассмотрим задачу нахождения квадратных корней, которую можно переформулировать как решение следующего уравнения:
$$
x = sqrt n iff x^2 = n iff f(x) = x^2 – n = 0
$$
Если в методе Ньютона подставим $f(x) = x^2 – n$, мы получим следующее правило:
$$
x_{i+1} = x_i – frac{x_i^2 – n}{2 x_i} = frac{x_i + n / x_i}{2}
$$
Если нам нужно посчитать корень с некоторой заданной точностью $epsilon$, можно на каждой итерации делать соответствующую проверку:
const double eps = 1e-9;
double sqrt(double n) {
double x = 1;
while (abs(x * x - n) > eps)
x = (x + n / x) / 2;
return x;
}
Алгоритм успешно сходится к правильному ответу для многих функций, однако это происходит надежно и доказуемо только для определенного множества функций (например, выпуклых). Другой вопрос — как быстра эта сходимость, если она происходит.
#Скорость сходимости
Запустим метод Ньютона для поиска квадратного корня $2$, начиная с $x_0 = 1$, и посмотрим, сколько первых цифр оказались правильными после каждой итерации:
1.0000000000000000000000000000000000000000000000000000000000000 1.5000000000000000000000000000000000000000000000000000000000000 1.4166666666666666666666666666666666666666666666666666666666675 1.4142156862745098039215686274509803921568627450980392156862745 1.4142135623746899106262955788901349101165596221157440445849057 1.4142135623730950488016896235025302436149819257761974284982890 1.4142135623730950488016887242096980785696718753772340015610125 1.4142135623730950488016887242096980785696718753769480731766796
Можно заметить, что число корректных цифр примерно удваивается после каждой итерации. Такая прекрасная скорость сходимости не просто совпадение.
Чтобы оценить скорость сходимости численно, рассмотрим небольшую относительную ошибку $delta_i$ на $i$-ой итерации и посмотрим, насколько меньше станет ошибка $delta_{i+1}$ на следующей итерации.
$$
|delta_i| = frac{|x_n – x|}{x}
$$
В терминах относительных ошибок, мы можем выразить $x_i$ как $x cdot (1 + delta_i)$. Подставляя это выражение в формулу для следующей итерации и деля обе стороны на $x$ получаем
$$
1 + delta_{i+1} = frac{1}{2} (1 + delta_i + frac{1}{1 + delta_i}) = frac{1}{2} (1 + delta_i + 1 – delta_i + delta_i^2 + o(delta_i^2)) = 1 + frac{delta_i^2}{2} + o(delta_i^2)
$$
Здесь мы разложили $(1 + delta_i)^{-1}$ в ряд Тейлора в точке $0$, используя предположение что ошибка $d_i$ мала: так как последовательность $x_i$ сходится к $x$, то $d_i ll 1$ для достаточно больших $n$.
Наконец, выражая $delta_{i+1}$, получаем
$$
delta_{i+1} = frac{delta_i^2}{2} + o(delta_i^2)
$$
что означает, что относительная ошибка примерно возводится в квадрат и делится пополам на каждой итерации, когда мы уже близки к решению. Так как логарифм $(- log_{10} delta_i)$ примерно равен числу правильных значимых цифр числа $x_i$, возведение ошибки в квадрат соответствует удвоению значимых цифр ответа, что мы и наблюдали ранее.
Это свойство называется квадратичной сходимостью, и оно относится не только к нахождению квадратных корней. Оставляя формальное доказательство в качестве упражнения, можно показать, что в общем случае
$$
|delta_{i+1}| = frac{|f”(x_i)|}{2 cdot |f'(x_n)|} cdot delta_i^2
$$
что означает хотя бы квадратичную сходимость при нескольких дополнительных предположениях, а именно что $f’(x)$ не равна нулю и $f’’(x)$ непрерывна.
Содержание
§
Вспомогательная страница к разделу
☞
ПОЛИНОМ ОДНОЙ ПЕРЕМЕННОЙ
Метод Ньютона решения уравнения
Метод применяется для решения широкого класса уравнений, но в настоящем разделе мы будем излагать его только в применении к уравнению алгебраическому.
Пусть $ f_{}(x) $ — полином с вещественными коэффициентами, $ deg f ge 2 $, и $ lambda $ обозначает его корень,
лежащий на интервале $ ]a,b[ $. Пусть, кроме того, $ f^{prime}(x)ne 0 $ на указанном интервале,
тогда $ lambda_{} $ — единственный корень полинома на $ ]a,b[ $.
При произвольном $ x_0 in ]a,b[ $ выпишем формулу Тейлора
$$f(x)=f(x_0)+f'(x_0)(x-x_0)+dots ,$$
ограничившись в ней двумя первыми слагаемыми. Вместо уравнения $ f_{}(x)=0 $
будем рассматривать его линейное приближение $ f(x_0)+f'(x_0)(x-x_0)=0 $.
Утверждается, что достаточно часто (в смысле выбора точки $ x_{0} $) решение этого уравнения, т.е. точка
$$
x_1= x_{0}-frac{f(x_{0})}{f'(x_{0})}
$$
лежит ближе к (неизвестному нам заранее) значению корня $ lambda $, чем точка $ x_{0} $. Можно утверждать и большее: при подходящем выборе $ x_{0} $ итерационная
последовательность
$$
left{ x_j= x_{j-1}-frac{f(x_{j-1})}{f'(x_{j-1})} right}_{j=1}^{infty}
$$
будет сходиться к $ lambda_{} $ при $ jto + infty $.
Метод поиска вещественного решения уравнения $ f(x)=0 $ построением указанной последовательности известен как метод Ньютона или же (см.
☟
ПУНКТ) как метод каcательных.
И
Биографические заметки о Ньютоне
☞
ЗДЕСЬ.
Т
Теорема 1. Если полином $ f_{}(x) $ не имеет кратных корней и последовательность $ {x_j}_{j=1}^{infty} $ сходится к конечному
пределу, то этот предел является корнем $ f_{}(x) $.
Доказательство. Пусть
$$ lim_{jto + infty} x_j = A , $$
тогда и
$$lim_{jto + infty} x_{j-1} = A . $$
По непрерывности $ f_{}(x) $ и $ f^{prime}(x) $ будет выполнено
$$lim_{jto + infty} f(x_{j-1})= f(A) , quad lim_{jto + infty} f^{prime}(x_{j-1})= f^{prime}(A) , $$
и, по предположению, числа $ f(A) $ и $ f^{prime}(A) $ не могут одновременно обращаться в нуль. Если бы число $ f^{prime}(A) $ было равно нулю, то
последовательность $ {x_j}_{j=1}^{infty} $ была бы неограниченной, а у нее же, по предположению теоремы, существует конечный предел. Следовательно
$ f^{prime}(A)ne 0 $.
При переходе в равенстве
$$
x_j= x_{j-1}-frac{f(x_{j-1})}{f'(x_{j-1})}
$$
к пределу при $ jto + infty $, равенство должно сохраниться:
$$ A= A- frac{f(A)}{f'(A)} quad Rightarrow quad frac{f(A)}{f'(A)}=0 quad
Rightarrow quad f(A)=0 .$$
♦
Наша задача теперь заключается в подборе такого стартового (начального) значения $ x_{0} $,
чтобы последовательность $ {x_j}_{j=1}^{infty} $ сходилась к определенному корню полинома, например, лежащему на данном интервале $ [a,b] $. Нам
потребуется следующий результат из математического анализа.
Т
Теорема 2. Если функция $ F_{}(x) $ и ее производные
$ F^{prime}(x) $ и $ F^{prime prime}(x) $ непрерывны в $ ]a,b[ $, то для
любых значений $ x_{} $ и $ x_{0} $ из этого интервала будет справедлива
формула Тейлора с остаточным членом в форме Лагранжа:
$$
F(x)equiv F(x_0)+F^{prime}(x_0)(x-x_0)+ frac{F^{prime prime}(c)}{2!}(x-x_0)^2
$$
где значение $ c_{} $ принадлежит интервалу $ ]x_0,x[ $ при $ x>x_0 $ или
$ ]x,x_0[ $ при $ x<x_0 $.
Т
Теорема 3. Если для $ f(x)in mathbb R[x] $ на интервале $ ]a,b[ $ выполнены условия:
а) $ f(a)f(b)<0 $;
б) $ f^{prime}(x) $ и $ f^{prime prime}(x) $ не имеют корней на $ ]a,b[ $;
то при любом выборе $ x_{0} $ таком, что
$$
operatorname{sign} f(x_0) = operatorname{sign} f^{prime prime}(x)
$$
последовательность $ {x_j}_{j=1}^{infty} $ монотонно сходится к единственному корню полинома $ f_{}(x) $, лежащему на $ ]a,b[ $.
Доказательство. Существование корня $ lambda in ]a,b[ $ гарантировано теоремой Больцано; его единственность на рассматриваемом интервале
является следствием предположения б) и теоремы Ролля.
Для определенности, будем предполагать $ f^{prime}(x)>0 $ и
$ f^{prime prime}(x)>0 $ на $ ]a,b[ $, иначе говоря, функция
возрастает и выпукла вниз; согласно правилу
выбора начальной точки $ x_{0} $ мы должны взять ее из условия $ f(x_0)>0 $, т.е.
ближе к правому концу интервала. Имеем, следовательно $ x_0>lambda $.
Докажем, что значение $ x_{1} $, вычисляемое по формуле
$$
x_1= x_{0}-frac{f(x_{0})}{f'(x_{0})} ,
$$
будет удовлетворять условиям $ lambda < x_1 < x_0 $.
Правое из этих неравенств очевидно следует из формулы, определяющей $ x_{1} $:
из $ x_{0} $ вычитается положительная величина. Для доказательства неравенства
$ x_{1} > lambda $ запишем для $ f_{}(x) $ формулу Тейлора с остаточным членом в форме Лагранжа:
$$
f(x)equiv f(x_0)+f^{prime}(x_0)(x-x_0)+ frac{f^{prime prime}(c)}{2!}(x-x_0)^2
.
$$
Подставим вместо $ x_{} $ значение корня $ lambda_{} $:
$$
0=f(x_0)+f^{prime}(x_0)(lambda-x_0)+ frac{f^{prime prime}(c)}{2!}(lambda-x_0)^2
,
$$
перенесем первые два слагаемые в левую часть и поделим получившееся равенство
на $ f^{prime}(x_0) $:
$$
left(x_{0}-frac{f(x_{0})}{f^{prime}(x_{0})} right) – lambda =
frac{f^{prime prime}(c)}{2!, f^{prime}(x_{0})}(lambda-x_0)^2
.
$$
В левой части получили $ x_1 – lambda $.
По предположению, $ f^{prime prime}(c)>0 $ и $ f^{prime}(x_{0})>0 $,
следовательно правая часть неотрицательна. Итак, $ x_1 > lambda $.
Совершенно аналогично доказывается, что $ lambda < x_2 < x_1 $ и т.д.
Последовательность $ {x_j}_{j=1}^{infty} $ монотонно убывает и ограничена
снизу. Такая последовательность всегда сходится, и ее предел
должен принадлежать интервалу $ [lambda, x_0] $. По доказанному в теореме $ 1_{} $
она сходится к какому-то корню полинома $ f(x) $, но
тогда она сходится именно к $ lambda_{} $, поскольку другого корня на $ [a,b] $
у полинома нет.
♦
=>
При выполнении условий теоремы $3$ скорость сходимости последовательности метода Ньютона оценивается неравенством
$$
|x_j-lambda|le frac{M}{2m} |x_{j-1}-lambda|^2 ; quad mbox{здесь} quad m= min_{xin [a,b]} | f^{prime}(x)|, M=
max_{xin [a,b]} | f^{prime prime}(x)| , .
$$
П
Пример. Найти положительный корень полинома $ x^5-4, x -2 $ с точностью до $ 0.001 $.
Решение.
На основании правила знаков Декарта делаем вывод, что $ f_{}(x) $ имеет положительный корень и этот корень единствен. Далее, $ f(1)<0,f(2)>0 $
и, на основании теоремы Больцано, этот корень принадлежит интервалу $ ]1,2[ $.
Далее,
$$f^{prime}(x)=5,x^4-4>0, f^{prime prime}(x)>0 quad
npu quad xin ]1,2[ ,$$
т.е. мы находимся точно в условиях случая, рассмотренного в доказательстве теоремы $ 3_{} $.
Запускаем итерационную последовательность, полагая $ x_0=2 $:
$$x_1 =x_0-frac{x_0^5-4, x_0 -2}{5, x_0^4 -4}=frac{65}{38} approx 1.710526316
. $$
Далее, последовательное применение формулы метода Ньютона дает:
$$
begin{array}{lll}
x_2 &= x_1- displaystyle frac{x_1^5-4, x_1 -2}{5, x_1^4 -4}
=frac{2399816418}{1537339039} &approx 1.561019630 , \
x_3 &= x_2- displaystyle frac{x_2^5-4, x_2 -2}{5, x_2^4 -4}
& approx 1.521115751 , \
x_4 & & approx 1.518522614 , \
x_5 & & approx 1.518512153 .
end{array}
$$
Ответ. $ lambda approx 1.518 $.
Геометрическая интерпретация: метод касательных
Геометрическая интерпретация метода Ньютона заключается в следующем. Для определенности предположим,
что $ f^{prime}(x)>0,, f^{prime prime}(x)>0 $ на $ ]a,b[ $. Возьмем $ x_{0} $
ближе к правому концу указанного интервала, т.е. пусть $ f(x_0)>0 $.
Проведем касательную к графику функции $ y=f(x) $ в точке $ (x_0,f(x_0)) $:
$$frac{y-f(x_0)}{x-x_0}=f^{prime}(x_0) $$
и найдем ее точку пересечения $ (x_1,y_1) $ с осью абсцисс.

Легко вычислить координаты этой точки:
$$y_1=0, x_1=x_0 – frac{f(x_0)}{f^{prime}(x_0)} ;$$
иначе говоря, $ x_{1} $ определяется как раз по формуле метода Ньютона.
Из рисунка видно (а в теореме $ 3_{} $ строго доказывается), что
точка $ x_{1} $ лежит ближе к неизвестному нам значению корня $ lambda_{} $
полинома $ f_{}(x) $, чем точка $ x_{0} $. Поэтому имеет смысл повторить процедуру:
построить касательную к графику в точке $ (x_1,f(x_{1})) $, найти ее
пересечение $ (x_{2},y_2) $ с осью абсцисс и т.д.

В конце концов, монотонно
убывающая и ограниченная снизу последовательность точек $ x_0,x_1,x_2,dots $
попадет в сколь угодно малую окрестность $ lambda_{} $. Эти геометрические
соображения обосновывают и другое название метода Ньютона; он также называется методом касательных.
Выбор стартового значения ближе к правому концу интервала
обеспечивает монотонное убывание последовательности $ {x_j}_{j=1}^{infty} $
также в случае когда на этом интервале имеют место неравенства $ f^{prime}(x)<0 $ и $ f^{prime prime}(x)<0 $; в двух
же оставшихся случаях
$$ f^{prime}(x)<0,, f^{prime prime}(x)>0 quad u quad f^{prime}(x)>0,, f^{prime prime}(x)<0 $$
последовательность будет сходиться к $ lambda_{} $, монотонно возрастая, если
выбрать $ x_{0} $ ближе к левому концу интервала.
Чувствительность корней
Если мы хотим найти приближенное значение корня полинома применением
метода Ньютона, то мы должны предварительно дать оценку точности вычислений: сколько значащих цифр мы должны сохранять в промежуточных выкладках, чтобы гарантировать достоверность получаемых результатов?
Это порождает более общую задачу оценки чувствительности корней,
т.е. оценки их изменения при некотором возмущении коэффициентов полинома. Обсуждение этой задачи
☞
ЗДЕСЬ.
Развитие
Методу Ньютона можно дать интерпретацию, отличную от изложенной в пункте МЕТОД КАСАТЕЛЬНЫХ. Если выполнены условия теоремы $ 3 $, то на интервале $ [a,b] $ существует обратная функция к $ y=f(x) $, т.е. функция $ x=varphi(y) $ такая что
$$ f(varphi(y)) equiv y quad mbox{ или, эквивалентно } quad varphi(f(x)) equiv x , . $$
Если эту функцию удается построить, то поиск корня уравнения $ f(x)=0 $ на интервале $ [a,b] $ сведется к вычислению значения $ varphi (0) $.
Проблема состоит в том, что как правило, представить обратную функцию в виде конечной комбинации сравнительно простых функций не представляется возможным даже для полиномиальных $ f(x) $. Но, по крайней мере, для таких функций можно представить обратную функцию в виде ряда Тейлора в окрестности некоторой точки $ x_0 in [a,b] $:
$$
varphi(y)=x_0+ B_1(y-f(x_0))+B_2(y-f(x_0))^2+ dots
$$
при
$$
B_1=frac{1}{f^{prime}(x_0)} , B_2 = – frac{f^{prime prime}(x_0)}{2[f^{prime}_x(x_0)]^3} ,
B_3=frac{3,[f^{prime prime}(x_0)]^2- f^{prime}_x(x_0)f^{prime prime prime}(x_0) }{6[f^{prime}_x(x_0)]^5} ,
dots
$$
Бесконечного количества слагаемых мы не вычислим, но если ограничиться первыми двумя, то получим линейное приближение обратной функции
$$
varphi(y)approx x_0+ frac{1}{f^{prime}(x_0)}(y-f(x_0)) ,
$$
из которого получаем приближение корня первого порядка
$$
varphi(0) approx x_0 – frac{f(x_0)}{f^{prime}(x_0)} ,
$$
т.е. в точности формулу первой итерации метода Ньютона.
Если взять три слагаемых разложения, то приближение корня второго порядка получается в виде
$$
varphi(0) approx x_0 – frac{f(x_0)}{f^{prime}(x_0)} – frac{f^2(x_0)f^{prime prime}(x_0)}{2[f^{prime}(x_0)]^3} ,
$$
и т.д. Посчитаем итерации, задаваемые этой функцией,
$$
left{ x_{j}=
x_{j-1} – frac{f(x_{j-1})}{f^{prime}(x_{j-1})} – frac{f^2(x_{j-1})f^{prime prime}(x_{j-1})}{2[f^{prime}(x_{j-1})]^3} right}_{j=1}^{infty}
$$
необходимые для решения примера из пункта МЕТОД НЬЮТОНА.
П
Пример. Найти корень полинома $ x^5-4, x -2 $ на интервале $[1,2] $ с точностью до $ 0.001 $.
Решение. При выборе $ x_0 =2 $ требуемая точность достигается за три итерации
$$
x_1 = frac{22255}{13718} approx 1.622321,
x_2approx 1.521381, x_3 approx 1.518512 , .
$$
По сравнению с пятью итерациями метода Ньютона — существенный выигрыш. Проблема только в том, что каждая итерация теперь стоит дороже: она более сложна при вычислении.
Метод Галлея (касательных гипербол)
Геометрическая идея, лежащая в основе метода Галлея1), обобщает идею метода касательных. К графику функции $ y=f(x) $ строится гипербола вида
$$ (x-alpha)(y-beta)=k , $$
имеющая в точке $ (x_0,f(x_0)) $ касание с графиком второго порядка, т.е. значения функции
$$
y=beta+frac{k}{x-alpha} ,
$$
а также значения ее первой и второй производных в точке $ x_0 $ совпадают с соответствующими значениями для функции $ f_{}(x) $.
В качестве очередного приближения $ x_{1} $ к неизвестному корню $ lambda_{} $ берется точка пересечения гиперболы с осью абсцисс.
$$
left{x_j=x_{j-1}- frac{f(x_{j-1})f^{prime}(x_{j-1})}{left[f^{prime}(x_{j-1})right]^2-frac{1}{2}f(x_{j-1})f^{prime prime}(x_{j-1})} right}_{j=1}^{infty} .
$$
Эта же формула может быть формально получена применением формулы метода Ньютона к функции $ f(x)/sqrt{pm f^{prime}(x)} $ (имеющей корни, совпадающие с корнями $ f_{}(x) $).

Обобщения
Целые числа
Задача. Для заданного натурального числа $ B_{} $ установить является ли оно полным квадратом и в этом случае определить $ sqrt{B} $.
Следующий результат получается «округлением» итераций метода Ньютона, примененного к уравнению $ x^2-B=0 $.
Т
Теорема.
Пусть $ B_0 $ — произвольное целое такое, что $ B_0^2>B $. Последовательность
$$
B_j =
begin{array}{c}
leftlfloor
begin{array}{c}
B_{j-1}+ leftlfloor displaystyle frac{B}{B_{j-1}} rightrfloor_{} \
hline
2
end{array}
rightrfloor
\
end{array}
quad npu jin {1,2,dots } ,
$$
монотонно убывая, сойдется за конечное число шагов к значению
$ leftlfloorsqrt{B} rightrfloor $, если только число $ B+1 $ не является
полным квадратом. Здесь $ lfloor rfloor $ означает целую часть числа.
Доказательство
☞
ЗДЕСЬ.
Комплексные числа
Формально ничто не мешает нам применить последовательность
метода Ньютона для поиска мнимых корней полинома $ f_{}(x) $. Можно доказать комплексный
аналог теоремы $ 3_{} $ , а также показать сходимость итерационной
последовательности к конкретному корню полинома при условии, что
стартовое (начальное) значение выбирается достаточно близко к искомому корню.
Интересно посмотреть на поведение последовательности уже для самых
простых случаев. Пусть, например,
$$ f(z)=z^3-1 , , $$
т.е. наша задача
заключается в поиске трех корней кубических из $ 1_{} $:
$$1,quad -frac{1}{2} + mathbf i
frac{sqrt{3}}{2} ,quad
-frac{1}{2} – mathbf i
frac{sqrt{3}}{2} . $$
Комплексный вариант последовательности метода Ньютона:
$$
left{z_j = frac{2,z_{j-1}^3+1}{3,z_{j-1}^2} right}_{j=1}^{infty}
$$
при задании стартового значения $ z_{0} $ «выведет» нас при $ jto infty $
к какому-то значению корня. Итак, вся комплексная плоскость может быть
поделена на три «области притяжения» каждого из корней. Раскрасим
эти множества в разные цвета. Какова будет граница между этими областями?
— Оказывается, эта граница имеет так называемую фрактальную структуру; и каждая граничная
точка любой области является также граничной для двух других
областей2).

.
Если начальную точку $ z_0 $ выбрать на этой границе, то последовательность метода Ньютона будет бесконечно долго скакать по ней, не сходясь ни к какому корню. При выборе $ z_0 $ близко к границе, мы, теоретически, должны получить последовательность, сходящуюся к какому-то корню. Однако ошибки округления, накапливающиеся с каждой итерацией, могут снова привести к непредсказуемости ни качества сходимости (к конкретному корню) ни количества итераций, требуемых для достижения заданной точности.
Системы нелинейных уравнений с несколькими неизвестными
Проблемы сходимости комплексного варианта метода Ньютона, отмеченные в предыдущем пункте, наследуются и обобщением метода Ньютона для задачи решения системы нелинейных уравнений с несколькими неизвестными. Действительно, задача поиска комплексных корней уравнения $ z^3-1=0 $ эквивалентна поиску вещественных решений системы уравнений
$$ x^3-3, xy^2-1=0, 3, x^2y-y^3=0 , . $$
§
Развитие метода Ньютона для решения системы уравнений
$$
f(x,y)=0, g(x,y)=0
$$
при $ f, g $ — произвольных полиномах с вещественными коэффициентами обсуждается
☞
ЗДЕСЬ
Задачи
Источники
[1]. Березин И.С., Жидков Н.П. Методы вычислений. Т.2. М.Физматгиз. 1960
[2]. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948
Численные методы решения нелинейных уравнений
Корни нелинейных уравнений
Пусть дано нелинейное уравнение
где — функция, определенная и непрерывная на некотором промежутке. В некоторых случаях на функцию
могут быть наложены дополнительные ограничения, например, непрерывность первой и второй производных, что специально оговаривается. Функция
может быть задана в виде алгебраического многочлена или трансцендентной функции (тогда ей соответствует алгебраическое или трансцендентное уравнение).
Требуется найти корни нелинейного уравнения (3.1), т.е. числа которые путем подстановки их в (3.1) превращают уравнение в верное числовое равенство. Числа
называются также нулями функции
.
На практике часто бывает выгодно уравнение (3.1) заменить равносильным ему уравнением (уравнения равносильны, если имеют одинаковые корни):
(3.2)
где функции — более простые, чем функция
. Тогда при задании уравнения в виде (3.1) нулями функции
являются точки пересечения
с осью
(рис. 3.1,д), а при задании в виде (3.2) — абсциссы точек пересечения функций
и
(рис. 3.1,б).
Замечания
1. Если — алгебраический многочлен, то уравнение (3.1) называется также алгебраическим n-й степени:
(3.3)
где — действительные числа, коэффициенты уравнения.
2. На практике встречаются задачи нахождения корней уравнения , левая часть которого задана сеточной функцией
(рис. 3.2).
Число есть корень уравнения (3.1) кратности
, если при
вместе с функцией
обращаются в нуль ее производные до (k-1)-го порядка включительно, т.е.
, а
. Корень кратности к = 1 называется простым. На рис 3.1,с простыми корнями являются
, a корни
— кратные.
В соответствии с классическим результатом Галуа алгебраическое уравнение (3.1) при не имеет решения в замкнутом (формульном) виде. Сеточные уравнения вообще не имеют формульных решений. Поэтому корни алгебраических
, трансцендентных и сеточных уравнений, как правило, определяются приближенно с заданной точностью.
Решение осуществляется в два этапа:
Первый этап. Находятся отрезки , внутри каждого из которых содержится один простой или кратный корень
(см. рис. 3.1). Этот этап называется процедурой отделения корней. По сути на нем осуществляется грубое нахождение корней
.
Второй этап. Грубое значение каждого корня уточняется до заданной точности одним из численных методов, в которых реализуются последовательные приближения. Порядок (скорость) сходимости метода определяется так же, как в методе простых итераций.
Отделение корней уравнения
Для отделения действительных корней полезно определять заранее число корней, а также верхнюю и нижнюю границы их расположения. Для этого используется ряд теорем.
Теорема 3.1 (о числе корней алгебраического уравнения (3.3)). Алгебраическое уравнение (3.3) n-й степени имеет ровно корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.
Теорема 3.2 (о свойстве парной сопряженности комплексных корней уравнения (3.3)). Если — корень алгебраического уравнения (3.3) кратности
, то число
также является корнем той же кратности.
Следствие. Алгебраическое уравнение нечетной степени имеет по крайней мере один действительный корень.
Теорема 3.3 (об оценке модулей корней уравнения (3.3)). Пусть
где — коэффициенты уравнения
. Тогда модули всех корней
уравнения удовлетворяют неравенству
(3.4)
т.е. корни уравнения расположены в кольце.
Следствие. Числа и
являются соответственно нижней и верхней границами положительных корней алгебраического уравнения:
. Аналогично числа
и
служат нижней и верхней границами отрицательных корней уравнения:
.
Приведем полезные теоремы, используемые для более точного установления границ действительных корней алгебраических уравнений.
Теорема 3.4 (теорема Лагранжа о верхней границе положительных корней уравнения (3.3)). Пусть и
— первый отрицательный коэффициент в последовательности
— наибольшая из абсолютных величин отрицательных коэффициентов. Тогда за верхнюю границу положительных корней уравнения (3.3) может быть принято число
(3.5)
Теорема 3.5 (о нижних и верхних границах положительных и отрицательных корней алгебраического уравнения). Пусть — верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
.
Тогда положительные корни и отрицательные корни
уравнения (3.3) удовлетворяют неравенствам
(3.6)
Теорема 3.6 (теорема Декарта о количестве действительных корней алгебраических уравнений). Число положительных корней (с учетом их кратностей) алгебраического уравнения
равно числу перемен знаков в последовательности коэффициентов
(коэффициенты, равные нулю, не учитываются) многочлена
или меньше этого числа на четное число. Число
отрицательных корней (с учетом их кратностей) алгебраического уравнения
равно числу перемен знаков в последовательности
многочлена
или меньше этого числа на четное число.
Теорема 3.7 (теорема Гюа о необходимом условии действительности всех корней алгебраического уравнения). Если алгебраическое уравнение (3.3) имеет все действительные корни, то квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов.
Следствие. Если при каком-нибудь выполнено неравенство
, то уравнение (3.3) имеет по крайней мере одну пару комплексных корней.
Для отделения корней применяется следующая теорема.
Теорема 3.8. Если функция , определяющая уравнение
, на концах отрезка
принимает значения разных знаков, т.е.
, то на этом отрезке содержится по крайней мере один корень уравнения. Если же
непрерывна и дифференцируема и ее первая производная сохраняет знак внутри отрезка
, то на
находится только один корень уравнения.
Способы отделения корней
В вычислительной практике обычно используются следующие способы отделения корней:
1) средствами машинной графики: функция представляется на дисплее и приближенно определяются отрезки, которым принадлежат точки
;
2) средствами математического анализа с помощью исследования функций и построения графиков (см. рис. 3.1,д);
3) формированием простых функций и
таких, что получается равносильное уравнение в виде (3.2), и дальнейшим построением графиков этих функций (см. рис. 3.1,б).
▼ Примеры 3.1-3.3
Пример 3.1. Определить число положительных и отрицательных корней, а также их границы для уравнения
Решение
В данной задаче . Согласно теореме 3.1 уравнение имеет пять корней. Поскольку
, то по следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный корень.
Оценим модули корней по теореме 3.3. Так как
то или
, т.е. все корни лежат внутри данного кольца. По следствию из теоремы 3.3 это означает, что положительные корни удовлетворяют неравенству
, а отрицательные — неравенству
.
Применим теоремы 3.4 и 3.5 для уточнения приведенных результатов. Найдем верхнюю границу положительных корней. Так как — первый отрицательный коэффициент в последовательности
, то
, а
— наибольшая из абсолютных величин отрицательных коэффициентов. Следовательно,
.
Найдем нижнюю границу положительных корней. Составим уравнение:
или (старший коэффициент должен быть положительным). Для этого уравнения
, поэтому
. Отсюда
.
Уточним границы отрицательных корней. Составим уравнение:
или
.
Для этого уравнения , поэтому
. Составим уравнение
или . Для этого уравнения
, поэтому
. Отсюда находим:
. Заметим, что данный результат совпадает с полученным ранее.
Исследуем структуру корней уравнения. Так как квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов, то по теореме 3.7 необходимое условие действительности всех корней уравнения выполняется.
На основе теоремы 3.6 определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена . Так как число перемен знака
, то число положительных корней равно трем или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты многочлена
. Так как число перемен знаков
, то число отрицательных корней равно двум или меньше на четное число, т.е. их вообще нет.
Пример 3.2. Отделить корни кубического уравнения .
Решение
Согласно теореме 3.1 уравнение имеет три корня, среди которых по крайней мере один действительный (следствие из теоремы 3.2, поскольку это уравнение нечетной степени).
Оценим модули корней уравнения по теореме 3.3. Так как
, то
или
.
Отсюда и
.
Определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена . Так как число перемен знака
(нулевой коэффициент не учитывается), то число положительных корней равно двум или меньше на четное число, т.е. они отсутствуют. Далее выписываем коэффициенты многочлена
. Так как число перемен знака
(нулевой коэффициент не учитывается), то число отрицательных корней равно единице.
Отделим корни третьим способом. Для этого преобразуем уравнение к равносильному виду (3.2): и найдем точки пересечения фафиков
и
(рис. 3.3).
Очевидно, корень уравнения .
Пример 3.3. Отделить корни уравнения третьего порядка .
Решение
Метод половинного деления
Пусть дано уравнение и отделен простой корень
, т.е. найден такой отрезок
, что
и на концах отрезка функция имеет значения, противоположные по знаку
. Отрезок
называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция
имеет разные знаки (рис. 3.5).
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
Алгоритм метода половинного деления
1. Найти начальный интервал неопределенности одним из методов отделения корней, задать малое положительное число
. Положить
.
2. Найти середину текущего интервала неопределенности: .
3. Если , то положить
, а если
, то принять
. В результате находится текущий интервал неопределенности
.
4. Если , то процесс завершить:
. Приближенное значение корня можно найти по формуле
.
Если , положить
и перейти к п.2.
Замечания
1. Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза:
Из последнего соотношения можно оценить число итераций для достижения заданной точности
Отсюда видно, что, например, для достижения точности при
необходимо выполнить примерно десять итераций.
2. К достоинствам метода следует отнести то, что он позволяет найти простой корень уравнения любых непрерывных функций
при любых значениях
таких, что
. Недостатки метода — он не обобщается на системы нелинейных уравнений и не может использоваться для нахождения корней четной кратности.
▼ Примеры 3.4-3.6
Пример 3.4. Найти корень уравнения методом половинного деления с точностью
и
.
Решение
Пример 3.5. Найти корень уравнения методом половинного деления с точностью
.
Решение
В примере 3.3 были отделены корни уравнения. Уточним корень, лежащий на отрезке . Результаты расчетов поместим в табл. 3.2.
В результате найден интервал и приближенное значение корня
.
Пример 3.6. Отделить корни трансцендентного уравнения и найти один из корней с точностью
.
Решение
1. Можно отделить корни уравнения, преобразовав его к равносильному виду и определив абсциссу точек пересечения графиков функций
и
. При этом
.
2. Уточним корень. Результаты расчетов приведем в табл. 3.3.
Вычисления показывают, что .
Поэтому .
Метод хорд
Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого отрезок делится не пополам, а в отношении
.
Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки
и
(рис. 3.6).
Уравнение хорды имеет вид
. Полагая
и
, получаем
Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:
(рис. 3.7,д) и
(рис. 3.7,б). Случай
сводится к рассматриваемому, если уравнение записать в форме:
. Первому случаю (см. рис. 3.7,д) соответствует формула (3.7), а второму случаю (3.8) (см. рис. 3.7,б):
(3.7)
(3.8)
В первом случае остается неподвижным конец , а во втором случае конец
.
Замечание. Для выявления неподвижного конца используется условие , где
или
. Если неподвижен конец
, применяется формула (3.7), а если конец
, — формула (3.8).
Пример 3.7. Найти корень уравнения методом хорд с точностью
.
Решение
Рассмотрим задачу нахождения корня на отрезке (см. пример 3.2). Так как
, a
на отрезке
, то
и, следовательно, имеем второй случай (см. рис. 3.7,б).
Положим . Тогда по формуле (3.8) получаем
Так как , то положим
и продолжим процесс:
Так как , то положим
и продолжим процесс:
Поскольку , положим
Так как , положим
Поскольку , положим
Так как , положим
Поскольку , положим
Так как , то корень уравнения
. Из анализа поведения
следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Метод простых итераций
Пусть известно, что корень уравнения
лежит на отрезке
.
Методика решения задачи
1. Уравнение равносильным преобразованием привести к виду
. Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия
(
— некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой
и кривой
(рис. 3.8).
2. Задать начальное приближение и малое положительное число
. Положить
.
3. Вычислить следующее приближение:
(3.9)
4. Если , итерации завершаются и
. Если
, положить
и перейти к п.3.
Замечание. В качестве условия завершения итераций при известном значении может быть использовано неравенство
Проблемы сходимости и единственности численного решения, являющиеся главными при использовании этого метода, решаются и исследуются с помощью понятия о сжимающем отображении и теоремы о достаточном условии сходимости метода.
Отображение (функция) называется сжимающим в области
с коэффициентом
, если для любых двух
из
выполнено неравенство
(3.10)
Теорема 3.9 (о сходимости метода простых итераций и единственности получаемого численного решения)
Пусть выполнены условия:
1. Нелинейное уравнение имеет решение
.
2. Отображение является сжимающим в области
с некоторым коэффициентом
.
Тогда:
а) решение является единственным решением в области
;
б) последовательность , определяемая по отображению на основе итерационного процесса, сходится к решению
со скоростью геометрической прогрессии, т.е. при выборе
из условия
, где
— некоторое малое число, справедливо неравенство
Теорема 3.9 утверждает, что при выполнении условий 1,2 существует окрестность такая, что если взять
в этой окрестности и вычислять
по формуле (3.9), то в результате с любой наперед заданной точностью можно вычислить
, соответствующее искомому (единственному) корню. Но так как эта окрестность неизвестна, то можно взять произвольное
. Если при этом вычисляется последовательность
, сходящаяся к некоторому значению
, то в силу теоремы
. Если сходимость отсутствует, то надо взять другое
и повторить расчет.
Теорема 3.10 (о достаточном условии сходимости метода простых итераций). Пусть выполнены условия:
1. Функция имеет производные для всех
.
2. Существует число , такое, что
для всех
.
Тогда отображение является сжимающим в
с коэффициентом сжатия х и последовательность
, определяемая на основе итерационного процесса, сходится к решению
, то есть
при
.
▼ Доказательство
В силу условия 1 справедлива теорема Лагранжа о конечных приращениях:
для
,
где — точка, лежащая между
и
. Но тогда с учетом условия 2 и замены
ее мажорантой
получим
т.е. отображение — сжимающее, и, таким образом, последовательность
сходится к некоторому
. Но тогда в силу непрерывности
в
имеет место равенство
.
Геометрическая интерпретация процесса сходимости и расходимости в зависимости от выполнения или невыполнения достаточного условия сходимости представлена на рис. 3.9.
Из рис. 3.9 видно, что при и при
(см.рис. 3.9,д,б) итерационные последовательности
сходятся к
. Причем в первом случае реализуется односторонняя (монотонная) сходимость, а во втором — двусторонняя (немонотонная). При
(см.рис. 3.9,в,г) процесс расходится несмотря на то, что точка
очень близка к
. Процессы на рис. 3.9,а,б соответствуют сжимающему отображению.
Преобразование уравнения к равносильному виду
может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования
, дающие сжимающие отображения.
1. Можно заменить уравнение на равносильное
, где
. Тогда, принимая правую часть этого уравнения за
и раскрывая
, получаем условие
(3.11)
Таким образом, можно найти константу на отрезке
так, чтобы удовлетворялись неравенства (3.11). При этом надо стремиться получить такую постоянную
, которая бы больше отличалась от нуля, и тогда будет реализовы-ваться более быстрая сходимость.
Можно показать, что абсолютная погрешность метода оценивается по формуле (эта оценка выражается через два последовательных приближения)
(3.12)
или по формуле (эта оценка выражается через два приближения и
)
(3.13)
Из оценки следует условие выхода из итерационного процесса. Если значение неизвестно, то выход осуществляется по условию
2. Уравнение заменяется равносильным (где знак в правой части выбирается из условия
):
при
,
3. Можно выразить из уравнения
так, чтобы для полученного уравнения
выполнялось условие сходимости
в окрестности искомого корня.
Замечание к доказательству. Выполнение условия не гарантирует близости к точному решению (на рис. 3.10 достигается область, где условие окончания выполняется, но корень
расположен достаточно далеко от этой области).
▼ Примеры 3.8-3.10
Пример 3.8. Методом простых итераций с точностью уточнить корень трансцендентного уравнения
, причем искомый корень
.
Решение
Пример 3.9. Найти решение уравнения методом простых итераций с точностью
и
.
Решение
Пример 3.10. Найти корни уравнения методом простых итераций с точностью
.
Решение
1. Преобразуем уравнение к виду .
В примере 3.3 была выполнена операция отделения корней и получены отрезки .
Можно показать, что на отрезках функция
удовлетворяет условию
.
На отрезке используем другой вид уравнения:
. Также легко проверить, что функция
удовлетворяет достаточному условию сходимости на отрезке
.
2. В качестве начальных приближений выберем:
– точку на отрезке
;
– точку на отрезке
;
– точку на отрезке
;.
В поставленной задаче .
3,4. Выполним расчеты по формуле
с начальными значениями и
и по формуле
с начальным значением .
Результаты расчетов занесены в табл. 3.6–3.8.
В результате получены приближенные значения корней:
Обратим внимание на сильное различие в числе итераций, потребовавшихся для нахождения корней (табл. 3.6) и
(табл. 3.7), с помощью одной и той же формулы. Заметим, что в окрестности корня
значения модуля производной функции
равны:
С другой стороны, в окрестности корня имеем:
Анализ результатов показывает, что чем меньше значения модуля производной , тем быстрее сходимость.
Метод Ньютона для решения нелинейных уравнений
Метод Ньютона (метод касательных, или метод линеаризации) является одним из наиболее популярных численных методов. Он быстро сходится (имеет квадратичную сходимость) и допускает различные модификации, приспособленные для решения векторных задач и сеточных уравнений. Однако этот метод эффективен при весьма жестких ограничениях на характер функции
1) существование второй производной функции на множестве
;
2) удовлетворение первой производной условию для всех
;
3) знакопостоянство для всех
.
Поэтому его желательно использовать совместно с другими методами, например методом половинного деления, чтобы достигнуть диапазона , где указанные условия начинают выполняться.
Геометрическая интерпретация метода Ньютона состоит в следующем. Задается начальное приближение . Далее проводится касательная к кривой
в точке
(рис. 3.11), т.е. кривая заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс. Процесс построения касательных и нахождения точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины
.
Получим расчетную формулу метода Ньютона. Вместо участка кривой (точка
соответствует
) возьмем участок
— касательную, проведенную в точке
). Для этого отрезка справедливо конечное соотношение:
где — угол наклона касательной в точке
к оси абсцисс. Разрешая это соотношение относительно
, получаем
. Повторяя процесс, находим общую формулу:
(3.14)
Подчеркнем, что если отбросить итерационный индекс, то (3.14) записывается в виде нелинейного уравнения
(3.15)
которое, однако, на не равносильно исходному, а является таковым только в одной точке при
. Поэтому данный метод не служит разновидностью метода простых итераций.
Применим теперь для вывода формулы (3.14) метод линеаризации. Положим, что итерационный процесс имеет вид
(3.16)
где — поправка к k-му приближению, которую необходимо найти. Предполагая, что
имеет непрерывную вторую производную, разложим
по формуле Тейлора относительно точки
где . Учитывая, что
(это соответствует нахождению точки пересечения с осью абсцисс), и оставляя только линейную (относительно
) часть разложения (отсюда и название — метод линеаризации), записываем линейное относительно
уравнение
Отсюда выражается поправка . Подставляя
в (3.16), получаем (3.14).
Теорема 3.11 (о достаточных условиях сходимости метода Ньютона). Пусть выполняются следующие условия:
1. Функция определена и дважды дифференцируема на
.
2. Отрезку принадлежит только один простой корень
, так что
.
3. Производные на
сохраняют знак, и
.
4. Начальное приближение удовлетворяет неравенству
(знаки функций
и
в точке
совпадают).
Тогда с помощью метода Ньютона (3.14) можно вычислить корень уравнения с любой точностью.
Замечания
1. Метод Ньютона характеризуется вторым порядком сходимости вблизи корня и первым порядком — вдали от него. Данную оценку проверяем для двух случаев, когда находится далеко от корня
(это возможно на первых итерациях) и когда
располагается вблизи
.
Первый случай. Пусть отрезок не мал. Тогда на основе теоремы Лагранжа получим (где
)
(3.17)
Преобразуем с использованием (3.17) итерационную формулу (3.14) (где ):
В силу монотонности последовательности имеем
Таким образом, вдали от корня получаем линейную сходимость
, где
.
Второй случай. Пусть теперь отрезок мал, т.е. итерации выполняются вблизи корня. Тогда, полагая, что указанные выше предположения 1–4 теоремы 3.10 выполнены, разложим функцию
в окрестности корня
относительно точки
, учитывая члены до второго порядка. Получим
где (
— малая величина). Из данного соотношения выражаем
Но первые два слагаемых в правой части в соответствии с (3.14) равны . Тогда будем иметь
Из последнего соотношения следует оценка погрешности (k+1)-го приближения через погрешность k-го приближения:
(3.18)
где принято . Оценка (3.18) свидетельствует о квадратичной сходимости метода касательных вблизи корня. С вычислительной точки зрения это означает, что на каждом приближении количество верных цифр результата удваивается.
2. Для нахождения комплексных корней уравнения можно также использовать (3.14) в форме (где
— комплексная переменная)
Метод Ньютона может применяться не только для нахождения простых корней, но для определения кратных корней, т.е. когда на отрезке содержащем корень, не выполняется условие
(условие 2 теоремы 3.11). Наряду с теоремой 3.11 удобно также пользоваться следующей теоремой.
Достаточные условия сходимости метода Ньютона
Теорема 3.12 (достаточные условия сходимости метода Ньютона). Пусть:
а) дана функция , где
— открытый интервал, и
;
б) для некоторого выполняется условие
при всех
из
.
Если уравнение имеет решение
, то существует некоторое
, такое, что если
, то последовательность
, задаваемая формулой (3.14), существует и сходится к
. Более того, справедлива оценка
Здесь обозначение означает, что функция
непрерывна по Липшицу с константой
на множестве
, то есть
для любых
из
.
Замечания
1. Требование теоремы 3.12, чтобы производная имела ненулевую нижнюю границу в
, определяет, что значение
должно быть ненулевым для квадратичной сходимости метода Ньютона. Если же
, то
является кратным корнем, а метод Ньютона сходится лишь линейно.
2. Выполнение условий теоремы 3.12 гарантирует сходимость метода Ньютона только из “хорошего” начального приближения .
3. Метод Ньютона является локально сходящимся, так как он сходится с определенной скоростью к истинному решению при условии, что стартует в достаточной близости от этого решения.
Методика решения задачи
1. Задать начальное приближение так, чтобы выполнялось неравенство
, а также малое положительное число
. Положить
.
2. Вычислить по формуле
.
3. Если , процесс завершить и положить
.
Если , положить
и перейти к п.2.
▼ Примеры 3.11-3.14
Пример 3.11. Методом Ньютона с точностью уточнить корень трансцендентного уравнения
, причем искомый корень
.
Решение
Можно проверить, что на множестве удовлетворяются условия 1, 2, 3 теоремы 3.11, обеспечивающие сходимость метода касательных.
1. Зададим начальное приближение из условия 4. Так как для справедливо
на множестве
, то
, поэтому
.
2,3. Результаты расчетов по формуле (3.14) помещены в табл. 3.9.
Из табл. 3.9 можно сделать следующие выводы:
1. Для достижения заданной точности, проверяемой по модулю разности , потребовалось выполнить три приближения. Если же выход организовать по условию
, то достаточно двух приближений.
2. Вблизи корня количество верных цифр в результатах
удваивается, так что все цифры в
являются верными, тогда как в
верными являются первые три цифры после запятой.
3. Скорость сходимости метода Ньютона выше скорости сходимости метода простых итераций (та же точность была достигнута за пять итераций).
Пример 3.12. Методом Ньютона найти корень уравнения .
Решение
Пример 3.13. Найти корни уравнения методом Ньютона с точностью
.
Решение
Процедура отделения корней была выполнена в примере 3.3. В качестве отрезков , которым принадлежат корни уравнения, выберем
.
Так как , то есть
, производные
сохраняют знак при
, то условия сходимости выполняются.
Так как , то есть
, и производные
сохраняют знак при
, то условия сходимости на этом отрезке тоже выполняются.
Так как , то есть
, и производные
сохраняют знак при
, то условия сходимости выполняются.
1. Зададим начальные приближения: на отрезке выберем
, так как
; на отрезке
выберем
, так как
; аналогично на отрезке
выберем
. В поставленной задаче
.
2,3. Результаты расчетов по формуле (3.14) приведены в табл. 3.11–3.13.
В результате получены приближенные значения корней:
Пример 3.14. Найти корень уравнения методом Ньютона с точностью
.
Решение
Очевидно, уравнение имеет один кратный корень . Согласно замечанию к теореме 3.12 применение метода Ньютона для решения поставленной задачи сопровождается линейной сходимостью (табл. 3.14).
Полученное приближенное решение .
Метод касательных
Метод касательных, являясь весьма эффективным средством численного анализа, к сожалению, имеет достаточно жесткие ограничения. Действительно, он не может применяться для сеточных уравнений (см. рис. 3.2); при нарушении знакопостоянства производных (рис. 3.12); при существовании неограниченных вторых производных и др. Так, если даже условие знакопостоянства нарушено вдали от корня, где выбрано , а вблизи корня выполняется, то все равно метод касательных неприменим (см. рис. 3.12), если не произвести сужения начального отрезка.
Кроме того, если функция очень сложная, то будет сложной и ее производная, и поэтому на каждой итерации приходится рассчитывать две функции, что снижает эффективность метода касательных.
В силу этого в ряде случаев могут оказаться более предпочтительными модификации метода касательных. Рассмотрим три из них.
Упрощенный метод Ньютона. Методика его применения совпадает с изложенной ранее, но вместо формулы (3.14) используется
Отличие от метода Ньютона заключается в том, что производная функции подсчитывается только в точке начального приближения, а на последующих итерациях не уточняется. Процесс последовательных приближений отражен на рис. 3.13. Первая итерация совпадает с первой итерацией метода Ньютона. На последующих итерациях соответствующие отрезки параллельны касательной, проведенной в начальной точке.
Для этой модификации снимаются некоторые ограничения метода касательных, например условие знакопостоянства производных. Сходимость упрощенного метода Ньютона линейная.
Пример 3.15. Найти корень уравнения упрощенным методом Ньютона.
Решение
Корень уравнения отделен в примере 3.2: .
1. Выберем начальное приближение и зададим
и
.
2,3. Выполним расчеты по формуле (3.19):
Результаты расчетов приведены в табл. 3.15.
При получено решение
, а при
— решение
. Очевидно, по сравнению с методом Ньютона сходимость замедляется (см. пример 3.12).
Метод Ньютона-Бройдена
Этот метод позволяет увеличить скорость сходимости последовательных приближений благодаря использованию формулы
(3.20)
где — число, которое выбирается на каждой итерации так, чтобы уменьшить значение
по сравнению с
. При
метод Ньютона-Бройдена совпадает с методом Ньютона.
Как правило, при плохой сходимости или ее отсутствии полагают (рис. 3.14,д), а при хорошей сходимости для
полагают
(это ускоряет сходимость (рис. 3.14,б)).
На рис. 3.14 прямоугольниками отмечены точки , полученные при
, — поправка, соответствующая методу Ньютона, а точки
получены по методу Ньютона-Бройдена.
Метод секущих
В этом методе производная функции подсчитывается с помощью конечно-разностных соотношений:
– в точке используется формула
, где
— малая положительная величина;
– в точках , используется формула
.
Вычисленное значение определяет тангенс угла наклона секущей (рис. 3.15).
Методика применения метода секущих совпадает с описанной ранее, но вместо (3.14) используется формула
(3.21)
Замечания
1. Метод секущих является более экономичным по сравнению с методом Ньютона по количеству функций, подлежащих расчету: на каждой итерации в методе секущих необходимо рассчитать только значение , так как величина
уже подсчитана на предыдущей итерации.
2. Метод секущих может применяться и для решения сеточных уравнений. Для сеточной функции производные в методе секущих определяются так же, но для определения в промежуточных точках осуществляется аппроксимация (как правило, интерполяция) функции
(рис. 3.16). На этом рисунке штриховой линией показана аппроксимационная кривая.
3. Для всех описанных модификаций скорость сходимости по сравнению с методом касательных снижается:
. Однако для некоторых из них (метод секущих) значение
и может достигать
.
Пример 3.16. Методом секущих найти корень уравнения с точностью
.
Решение
1. Зададим начальное приближение (см. пример 3.12).
2. Для вычисления зададим
. Тогда
Отсюда .
Дальнейшие расчеты выполняются по формуле (3.21):
Результаты расчетов приведены в табл. 3.16.
Очевидно, метод сходится чуть хуже метода Ньютона (см. пример 3.12), однако скорость сходимости выше линейной.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.










![{displaystyle x_{n}in (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5f21fd665315688b00234e990e4e815e427b5b)

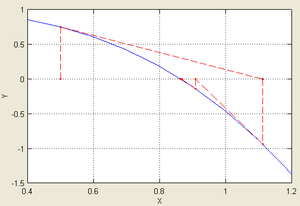


















![{displaystyle f_{i}+sum _{k=1}^{n}{frac {partial f_{i}}{partial x_{k}}}(x_{k}^{[j+1]}-x_{k}^{[j]})=0,qquad i=1,;2,;ldots ,;m,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc7f4c706fe7cadefee1e80477d0e3648a358b7f)
![{displaystyle nabla f({vec {x}}^{[j]})+H({vec {x}}^{[j]})({vec {x}}^{[j+1]}-{vec {x}}^{[j]})=0,quad j=1,;2,;ldots ,;n,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a93eebcf171c9964de5dc34316c1c362df1d719)
![{displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7746807ee2e9f155ca9bc3d0d82822e9d0ba810)
![{displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-lambda _{j}H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c868e602fce2d22f00f7113f6c4c2af899e1578)
![{displaystyle lambda _{j}=arg min _{lambda }f({vec {x}}^{[j]}-lambda H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]})).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c90586d6156feccbfe6a6d006966c3b1b5b276d)



![left[J^{T}({vec {x}})J({vec {x}})+sum _{{i=1}}^{m}f_{i}({vec {x}})H_{i}({vec {x}})right]{vec {p}}=-J^{T}({vec {x}}){vec {f}}({vec {x}}).](https://wikimedia.org/api/rest_v1/media/math/render/svg/98c37fe7b2533841a5672c30db2a479588a0b887)


