Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током |
| Напечатано:: | Гость |
| Дата: | Понедельник, 15 Май 2023, 18:00 |
Оглавление
- Самоиндукция
- Наблюдение самоиндукции
- Энергия магнитного поля
- Примеры решения задач
- Упражнение 24
Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797–1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?
Самоиндукция. Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока I в контуре, то
Коэффициенту пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил название «коэффициент самоиндукции»:
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.
Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,
Если индуктивность контура не изменяется во времени, т. е. L = const, то
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома где R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.
От теории к практике
Какой должна быть скорость изменения силы тока, чтобы в катушке с индуктивностью L = 0,20 Гн возникла ЭДС самоиндукции = 4,0 В?
![]()
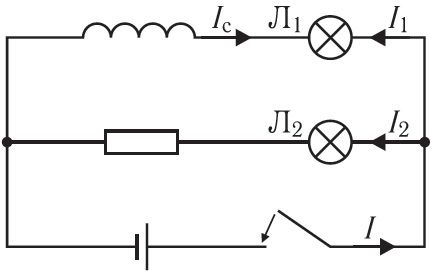
Наблюдение самоиндукции. Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка Л2 начинает светиться практически сразу, а лампочка Л1 — с заметным запаздыванием. При возрастании силы тока I1, созданного источником на участке, образованном катушкой и лампочкой Л1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции Iс направлен навстречу току источника. В результате рост силы тока I1 источника замедляется, и сила тока I1 — |Iс| не сразу достигает своего максимального значения.
![]()
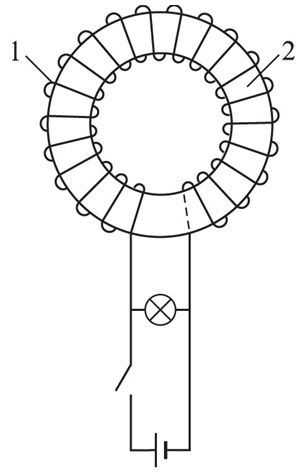
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки с большим количеством витков 1, намотанных на железный сердечник 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 185.1). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.
Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений . Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.
![]()
Энергия магнитного поля. Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
При замыкании цепи, состоящей из источника тока с ЭДС , катушки с индуктивностью L и резистора, сопротивление которого R, сила тока в цепи начнёт возрастать и появится ЭДС самоиндукции
.
Тогда в соответствии с законом Ома сила тока в цепи .
Значит, .
Умножив полученное равенство на IΔt, где Δt — достаточно малый промежуток времени, в течение которого сила тока I остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: .
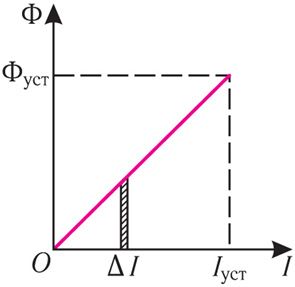
В процессе установления тока, когда сила тока I и магнитный поток Ф = LI возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся в резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени Δt при преодолении ЭДС самоиндукции в процессе установления тока (рис. 185.2):
δAдоп = ФΔI.
Полная дополнительная работа Адоп, равная сумме элементарных дополнительных работ δAдоп в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(I) (см. рис. 185.2).
Эта работа превращается в энергию магнитного поля катушки, поэтому:
где L — индуктивность контура; I — сила тока.
От теории к практике
Какова индуктивность катушки, если при силе тока I = 2,0 А энергия магнитного поля катушки Wм = 1,2 Дж?

![]()
1. Что называют самоиндукцией?
2. В каких опытах можно наблюдать явление самоиндукции?
3. От чего зависит ЭДС самоиндукции?
4. Что называют индуктивностью? В каких единицах в СИ её измеряют?
5. Как вычислить энергию магнитного поля катушки с током?
![]()
6. Почему для создания электрического тока в цепи с катушкой индуктивности источник тока должен затратить энергию?
Примеры решения задач
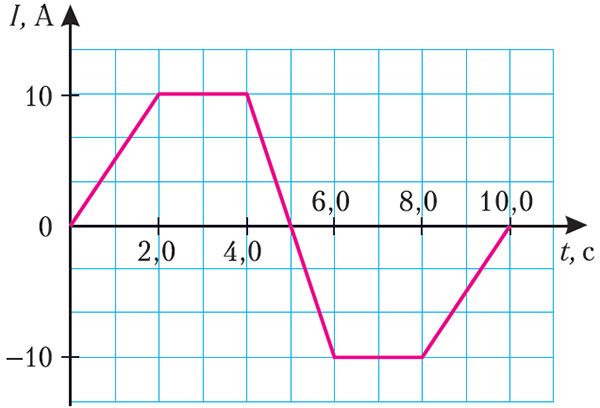
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
Дано:
L = 40 мГн = 4,0 · 10–2 Гн
— ?
Решение: ЭДС самоиндукции . Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
Таким образом,
Ответ: = 0,40 В.
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
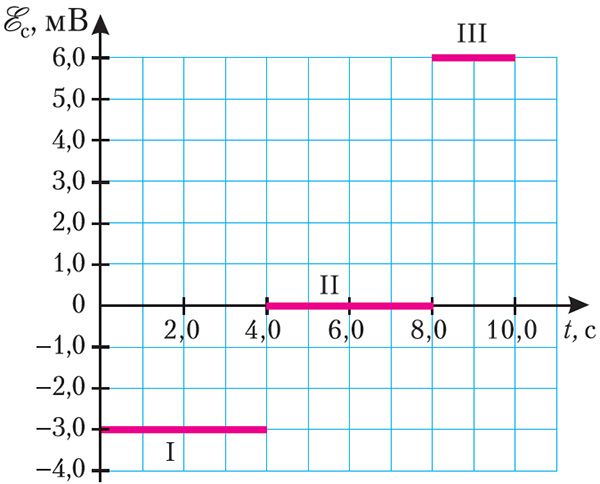
Дано:
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔII — ? ΔIII — ?
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции = –3,0 мВ, на участке III —
= 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
;
.
;
.
На участке II графика = 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки .
Следовательно,
.
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
![]()
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Дано:
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
= ‒14,0 В
Фс — ?
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: . Следовательно,
. Тогда
.
Приращение энергии магнитного поля катушки
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.
Упражнение 24
1. Сила тока, проходящего по замкнутому проводящему контуру, I = 1,2 А. Магнитное поле этого тока создаёт магнитный поток Ф = 3,0 мВб через поверхность, ограниченную контуром. Определите индуктивность контура.
2. При равномерном изменении силы тока в катушке на ΔI = –4,0 А за промежуток времени Δt = 0,10 с в ней возникает ЭДС самоиндукции = 20 В. Определите индуктивность катушки.
3. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 1,2 Гн, при равномерном изменении силы тока от I1 = 2,0 А до I2 = 6,0 А за промежуток времени Δt = 0,60 с. Определите приращение энергии магнитного поля при заданном изменении силы тока.
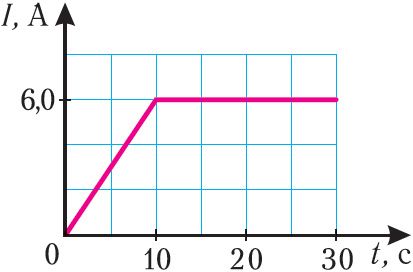
4. На рисунке 188 представлен график зависимости силы тока в катушке, индуктивность которой L = 10 мГн, от времени. Определите ЭДС самоиндукции через промежутки времени t1 = 10 с и t2 = 20 с от момента начала отсчёта времени.
5. Сила тока в катушке равномерно уменьшилась от I1 = 10 А до I2 = 5,0 А. При этом энергия магнитного поля изменилась на ΔWм = –3,0 Дж. Определите индуктивность катушки и первоначальное значение энергии магнитного поля.
6. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 0,12 Гн, при равномерном уменьшении силы тока от I1 = 8,0 А, если за промежуток времени t1 = 0,20 с энергия магнитного поля уменьшилась в α = 2,0 раза.
![]()
7. Энергия магнитного поля катушки с индуктивностью L1 = 0,5 Гн больше энергии магнитного поля катушки с индуктивностью L2 в α = 1,5 раза. Определите индуктивность второй катушки, если отношение собственного магнитного потока через поверхности, ограниченные витками второй катушки, к собственному магнитному потоку через поверхности, ограниченные витками первой катушки, .

Самоиндукция
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.
Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.
Ситуация 1 .Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).

Рис. 1. Вихревое поле препятствует увеличению тока
Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.
Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.
Ситуация 2 . Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).

Рис. 2. Вихревое поле поддерживает убывающий ток
Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.
Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.
Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре.
При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.
При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).
Индуктивность
Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока:
. Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока:
.
Коэффициент пропорциональности обозначается и называется индуктивностью контура:
(1)
Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).
Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея
приобретает вид:
(2)
Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.
Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.

Рис. 3. Самоиндукция при замыкании цепи
В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).
Ключ вначале разомкнут.
При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.
Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.
Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.

Рис. 4. Самоиндукция при размыкании цепи
Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.
При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).
Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.
Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.
Электромеханическая аналогия
Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой
в механике.
1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.
Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.
2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.
При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.
На самом деле эти электромеханические аналогии простираются довольно далеко; они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.
Энергия магнитного поля
Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?
Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.
Чтобы разогнать тело массы из состояния покоя до скорости
, внешняя сила должна совершить работу
. Тело приобретает кинетическую энергию, которая равна затраченной работе:
.
Чтобы после замыкания цепи ток в катушке индуктивности достиг величины
, источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).
Индуктивность служит аналогом массы
; сила тока
является очевидным аналогом скорости
. Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:
(3)
(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).
Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.
Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени
. В течение этого промежутка приращение силы тока равно
; величина
считается настолько малой, что
много меньше, чем
.
За время по цепи проходит заряд
. Вихревое электрическое поле совершает при этом отрицательную работу:
Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):
Интегрируя это от нуля до , найдем работу источника
, которая затрачивается на создание тока
:
Эта работа превращается в энергию магнитного поля созданного тока, и мы приходим к формуле (3).
Разберем задачи ЕГЭ по физике по темам: “Самоиндукция”, “Магнитный поток”, “Индуктивность”, “Электромагнитная индукция”.
Задача 1. На катушке сопротивлением 8,2 Ом и индуктивностью 25 мГн поддерживается постоянное напряжение 55 В. Сколько энергии выделится при размыкании цепи? Какая средняя ЭДС самоиндукции появится при этом в катушке, если энергия будет выделяться в течение 12 мс?
Дано:
R = 8,2 Ом;
L= 25 мГн = Гн;
t = 12 мс = 12;
Найти:
Wм – ? Eis – ?
Решение:
Решение любой задачи по физике должно начинаться с создания модели, которая поясняет ситуацию, описанную в данной задачи. В качестве модели может выступать чертеж, пояснительный рисунок, электрическая схема.
Для этой задачи необходимо начертить электрическую схему.

На схеме изображены катушка индуктивности, источник тока, поддерживающий на ней постоянное напряжение, ключ.
При замкнутом ключе через катушку протекает постоянный электрический ток, величину которого можно рассчитать, используя закон Ома для участка цепи. Катушка аналогична резистору, подключенному в эту цепь.
Энергия магнитного поля рассчитывается по формуле:
(Дж).
Стоит обратить внимание, что эта формула аналогична формуле кинетической энергии в механике:
При размыкании ключа, через катушку начинает протекать уже переменный ток. Поэтому магнитный поток, пронизывающий катушку, меняется. В самой катушке возникает ЭДС индукции, так как в ней течёт переменный ток. Тем самым, возникает явление самоиндукции.
Используя закон электромагнитной индукции в виде приходим к расчету второй неизвестной величины этой задачи:
(B).
В этих расчетах мы не учитывали знак (-), который указан в законе электромагнитной индукции. Смысл этого знака заключен в учёте правила Ленца, определяющего направление индукционного тока. Но так как о направлении индукционного тока речь в задаче не идет, то в расчетах именно получено значение модуля ЭДС самоиндукции.
Ответ: 0,56 Дж, 14 В.
Задача 2. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 15 с. Ответ выразите в мкВ.

Решение
Решение любых графических задач необходимо начинать с «чтения» самого графика. В этой задаче рассматривается зависимость силы тока от времени в цепи, содержащей катушку индуктивности. Необходимо обратить внимание на те интервалы времени, в течение которых происходит изменение силы тока. С изменением этой величины связано изменение магнитного потока и, как следствие, возникновение ЭДС самоиндукции. Сила тока меняется в интервале от 0 до 5 с, от 5 до 10 с и от 15 до 20 с. В интервале от 10 до 15 с сила тока постоянна, изменение магнитного потока не происходит, поэтому . Для участка от 5 до 10 с надо применить закон электромагнитной индукции
.
Для модуля ЭДС самоиндукции, т.е. без учета направления индукционного тока, этот закон будет иметь вид:
.
Данные для расчета необходимо взять из графической зависимости, учитывая при этом перевод в систему «СИ».
(мкВ).
Ответ: 2 мкВ.
Задача 3. Катушка, обладающая индуктивностью , соединена с источником питания с ЭДС
и двумя одинаковыми резисторами
. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.

В момент времени ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения –
Определите значение силы тока
Внутренним сопротивлением источника тока пренебречь.
Решение
В данной задаче необходимо рассмотреть две ситуации, которые происходят до и после замыкания ключа.
- До замыкания ключа в цепи устанавливается постоянная сила тока, которая определяется законом Ома для полной цепи
. Так как по условию внутренним сопротивлением источника можно пренебречь, то
(A).
- После замыкания ключа параллельно к первому резистору подключается второй, имеющий такое же сопротивление. Тогда общее сопротивление цепи можно рассчитать, как
Таким образом, внешнее сопротивление цепи уменьшается в 2 раза.
Наличие в цепи катушки индуктивности, в которой возникает ЭДС самоиндукции, препятствует мгновенному нарастанию силы тока (по аналогии с механикой – тело большой массы не может быстро изменить свою скорость). Поэтому сила тока плавно увеличивается до некоторого значения - Так как ЭДС самоиндукции с течением времени уменьшается до нулевого значения, то ток в цепи будет возрастать в 2 раза, так как общее сопротивление уменьшается также в 2 раза.
(A).
Ответ: 6 А.
Задача 4. Катушка Проволочная рамка площадью 60 см2 помещена в однородное магнитное поле так, что плоскость рамки перпендикулярна вектору индукции . Проекция
индукции магнитного поля на нормаль к плоскости рамки изменяется во времени t согласно графику на рисунке.

Из приведенного ниже списка выберите все верные утверждения о процессах, происходящих в рамке.
- Модуль ЭДС электромагнитной индукции, возникающий в рамке, максимален в интервале от 0 до 1мс.
Ответ. Согласно закону электромагнитной индукции
Т.е. максимальное значение ЭДС индукции будет наблюдаться на интервале максимального измененияс течением времени. В интервале от 0 до 1 мс скорость изменения проекции
наибольшая.
Утверждение верное. - Магнитный поток через рамку в интервале от 2 до 4 мс равен 12 мВб.
Ответ. Формула для расчета магнитного потока имеет вид
В данном временном интервале проекцияпостоянна и равна 2 Тл.
(Вб) = 12 (мВб).
Утверждение верное. - Модуль ЭДС электромагнитной индукции, возникающей в рамке, в интервале от 4 до 6 мс равен 6 В.
Ответ. Согласно закону электромагнитной индукции
(B).
Утверждение неверное. - Модуль скорости изменения магнитного потока через рамку минимален в интервале от 0 до 1 мс.
Ответ. В той задаче изменение магнитного потока связано с изменением проекциииндукции магнитного поля. В интервале от 0 до 1 мс проекция
меняется быстрее всего, потому и изменение магнитного потока максимальное.
Утверждение неверное. - Модуль ЭДС электромагнитной индукции, возникающей в рамке, равен нулю в интервале времени от 2 до 4 мс.
Ответ. Согласно закону электромагнитной индукции
В интервале от 2 до 4 мс проекцияне изменяется, потому
и
.
Тогда в проволочной рамке ЭДС индукции не возникает.
Утверждение верное.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самоиндукция» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
→
2.3 Магнитное поле, индуктивность
2.3 Магнитное поле, индуктивность
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
Магнитное поле, индуктивность
Основные положения и соотношения
1. Закон Био — Савара — Лапласа выражает значение магнитной индукции, определяемой элементом тока I dl → на расстоянии r от него в однородной среде (рис. 1)
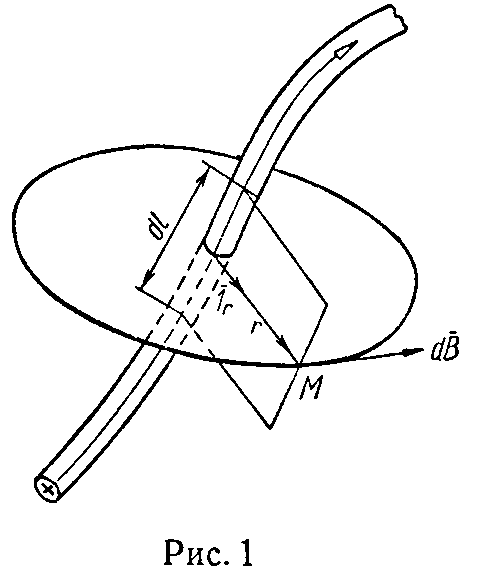
dB → =μ⋅ I⋅[ dl → × 1 r → ] 4π r 2 , (1)
здесь
1 r → – единичный вектор, направленный от центра элемента тока I dl → в точку М, в которой определяется магнитная индукция;
r — расстояние от центра элемента тока до той же точки;
µ — абсолютная магнитная проницаемость среды, равная µ0·µr;
µr — магнитная проницаемость (относительная магнитная проницаемость);
μ 0 =4π⋅ 10 −7 Гн м – магнитная постоянная.
В формуле (1) использовали векторное произведение [ a → × b → ]≡ a → × b →
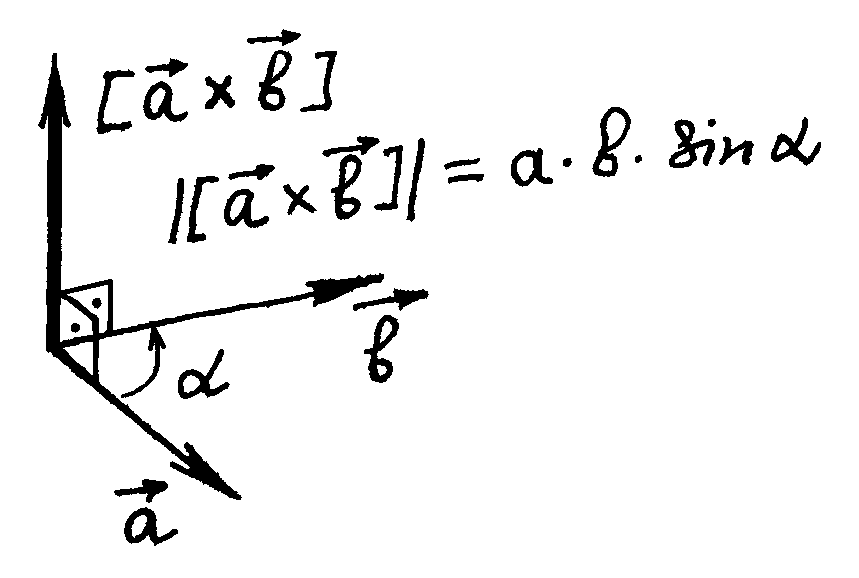
Закон Био — Савара — Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био — Савара — Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
Связь между векторами напряженности магнитного поля и магнитной индукцией выражается формулой
B → =μ⋅ H → . (2)
Величина напряженности магнитного поля тока, протекающего по прямому проводнику конечной длины l (рис. 2) в некоторой точке, находящейся на расстоянии a от проводника, равна
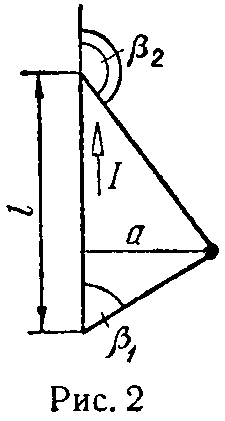
H= I 4π⋅a ⋅( cos β 1 −cos β 2 ). (3)
Направление вектора H → определяется правилом винта; так, в рассматриваемой на рис. 2 точке вектор H → направлен от читателя за чертеж.
Величина напряженности магнитного поля прямого и бесконечно длинного тока в точке, отстоящей на расстоянии a от оси провода, несущего ток, равна
H= I 2π⋅a . (4)
Величина напряженности магнитного поля кругового тока в некоторой точке на его оси (рис. 3) определяется по формуле
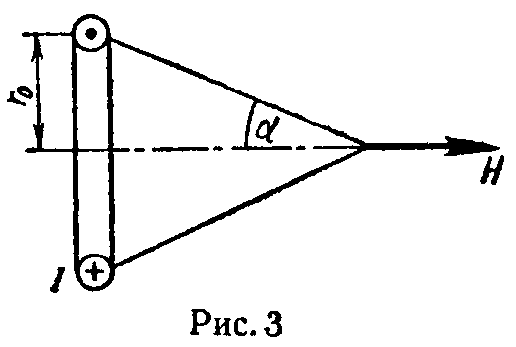
H= I 2 r 0 ⋅si n 3 α, (5)
здесь r0 — радиус витка, по которому протекает круговой ток, α — угол, под которым виден радиус витка из точки, в которой определяется напряженность поля.
Напряженность магнитного поля в центре плоскости витка определяется по формуле
H= I 2 r 0 . (6)
Напряженность магнитного поля соленоида. Величина напряженности магнитного поля в некоторой точке на оси цилиндрического соленоида (рис. 4)
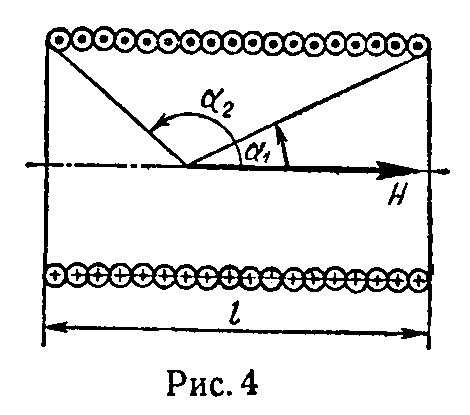
H= w⋅I 2l ⋅( cos α 1 −cos α 2 ), (7)
здесь w — общее число витков соленоида.
Величина напряженности магнитного поля на оси очень длинного цилиндрического соленоида
H= w⋅I l . (8)
Направление вектора H → и здесь определяется правилом винта.
По этой же формуле находится напряженность магнитного поля на оси кольцевого соленоида (тороида). В этом случае l — длина средней линии магнитной индукции, считается совпадающей с кольцевой осью соленоида.
2. Закон полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
? H → dl → = ∑ I . (9)
Формулы (4) и (8) являются непосредственными результатами применения закона полного тока.
3. Поток вектора магнитной индукции сквозь поверхность S
Φ= ∫ S B → dS → . (10)
4. Сила Лоренца. Сила, испытываемая зарядом q, движущимся со скоростью v в магнитном поле с индукцией В, определяется по формуле
F → =q⋅[ v → × B → ]. (11)
Макроскопическим проявлением силы Лоренца является сила Ампера.
Закон Ампера. Сила (рис. 5), действующая на элемент провода dl → с током I , помещенный в магнитное поле с индукцией B → (сила Ампера),
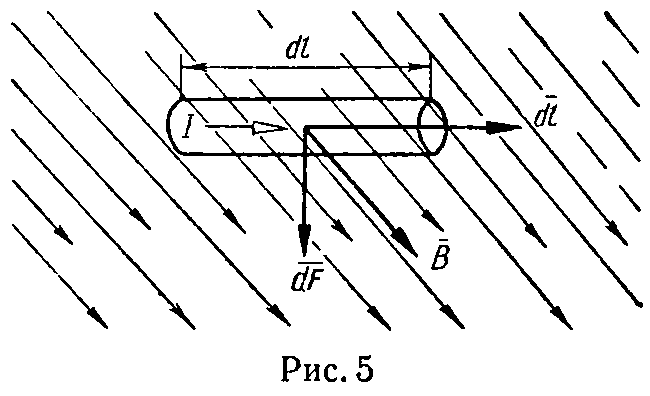
dF → =I⋅[ dl → × B → ]. (12)
Прямолинейный проводник длиной l, помещенный в однородное магнитное поле с индукцией B → под углом α к вектору B → , испытывает силу
F → =I⋅[ l → × B → ]=I⋅l⋅B⋅sinα⋅ 1 n → , (13)
где 1 n → – единичный вектор, нормальный к плоскости, проведенной через векторы l → и B → .
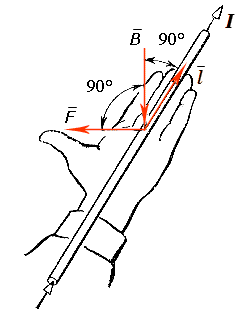
Направление силы Ампера F определяется правилом левой руки.
5. Работа сил поля при перемещении в нем на расстояние ds элемента проводника длиною dl с током I равна (рис. 6)
dW=I⋅dΦ, (14)
здесь dФ — магнитный поток через поверхность, описанную проводником при его перемещении.
Работа, производимая при перемещении замкнутого контура с неизменным по величине током в постоянном магнитном поле, определяется выражением
W=I⋅( Φ 2 − Φ 1 ), (15)
где Ф1 и Ф2 — величины магнитного потока, пронизывающего контур в начальном и конечном положениях.
6. Расчет магнитных цепей. Основанием к расчету служат: первый закон Кирхгофа для магнитных цепей и закон полного тока.
Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к контуру, образованному средними магнитными линиями магнитной цепи и имеет вид
F=ΣwI= ? H → dl → . (16)
Величина F называется магнитодвижущей силой (МДС).
Выражение
F=ΣwI= ∑ k=1 n Φ k R мk (17)
называют вторым законом Кирхгофа для магнитных цепей и формулируют следующим образом: алгебраическая сумма магнитодвижущих сил (ΣwI) в замкнутом контуре магнитной цепи равна алгебраической сумме магнитных напряжений ( ∑ k=1 n Φ k R мk ) в том же контуре.
В формуле (17) R мk = l k μ k S k – магнитное сопротивление участка цепи с сечением Sk, с длиною средней магнитной линии lk и с абсолютной магнитной проницаемостью материала µk.
Отметим, что для расчета стальной магнитной цепи формулой (17) пользуются редко, так как Rмk не может рассматриваться как постоянная величина (величина магнитной проницаемости стали и других ферромагнитных материалов зависит от их намагниченности).
При расчете магнитодвижущей силы для воздушного зазора напряженность магнитного поля определяется по формуле
H 0 = B μ 0 . (18)
7. Закон электромагнитной индукции. Величина индуктированной ЭДС
e=− dΨ dt , (19)
где Ψ — потокосцепление. Оно может быть выражено произведением величины магнитного потока на число витков, с которыми он сцеплен
Ψ= ∑ w⋅Φ . (20)
8. Общее выражение для статической индуктивности проводника, витка, катушки
L= Ψ I . (21)
9. ЭДС, индуктированная в прямолинейном проводнике, движущемся с равномерной скоростью v в однородном магнитном поле, равна
e = B·l·v·sinα, (22)
где α — угол между направлениями векторов v → и B → .
10. Величина ЭДС самоиндукции
e L =−L di dt . (23)
11. Индуктивность соленоида
L= μ⋅ w 2 ⋅S l , (24)
здесь w — число витков, S — сечение соленоида, l — длина средней линии магнитной индукции.
Эта же формула приближенно подходит для расчета индуктивности длинной однослойной катушки цилиндрической формы (l/D > 50), где l/D –отношение длины катушки к диаметру ее витков.
12. Для вычисления индуктивности коротких цилиндрических катушек без стального сердечника применяется формула
L=k⋅ μ 0 ⋅ w 2 ⋅S l , (25).
где коэффициент k является функцией отношения диаметра D катушки к ее длине l его значения приведены в таблице 1.
Таблица 1 — Значения коэффициент k(D/l)
|
D/l |
k |
D/l |
k |
|
0,00 |
1,0000 |
1,00 |
0,6884 |
|
0,10 |
0,9588 |
0,80 |
0.6581 |
|
0,20 |
0,9201 |
0,60 |
0.5697 |
|
0,40 |
0,8499 |
0,40 |
0,4719 |
|
0,60 |
0,7885 |
0,20 |
0,3108 |
|
0,80 |
0,7351 |
0,10 |
0,2033 |
|
1,00 |
0,6884 |
13. Индуктивность двухпроводной линии
L= μ 0 l π ln D r + μ⋅l 4π , (26)
здесь D — расстояние между осями проводов, r — радиус провода, l — длина линии, µ — абсолютная магнитная проницаемость проводов линии.
Для проводников, изготовленных не из ферромагнитных материалов, пользуются следующей приближенной формулой, в которой отсутствует слагаемое, выражающее внутреннюю индуктивность
L= μ 0 l π ln D r . (27)
Индуктивность однопроводной линии
L= μ 0 l 2π ln 2h r , (28)
где h — высота провода над землей.
14. Общее выражение для взаимной индуктивности двух контуров
M= w 1 Φ 21 I 2 = w 2 Φ 12 I 1 , (29)
здесь w1 и I1 — число витков и ток, проходящий в первом контуре, Ф21 — часть общего магнитного потока, определяемого током второго контура и пронизывающего первый контур, w2 и I2 — число витков и ток, проходящий во втором контуре, Ф12 — часть общего магнитного потока, определяемого током первого контура и пронизывающего второй контур.
15. Электродвижущая сила взаимоиндукции двух контуров с токами
e 1M =− w 1 d Φ 21 dt =−M d i 2 dt , e 2M =− w 2 d Φ 12 dt =−M d i 1 dt , (30)
здесь e1M — ЭДС, наведенная в первом контуре вследствие изменения во времени сцепляющейся с ним части магнитного потока Ф21, определяемого током во втором контуре, со скоростью d Φ 21 dt , e2M — ЭДС, наведенная во втором контуре вследствие изменения во времени сцепляющейся с ним части магнитного потока Ф12, определяемой током в первом контуре, со скоростью d Φ 12 dt .
16. Взаимная индуктивность двух кольцевых соленоидов, имеющих общий сердечник, число витков которых w1 и w2, определяется по приближенной формуле
M= μ w 1 w 2 S l , (31)
здесь S — сечение сердечника, l — длина средней линии магнитной индукции.
Взаимная индуктивность между двумя параллельными двухпроводными линиями a1a2 и b1b2 длиною l (рис. 7)
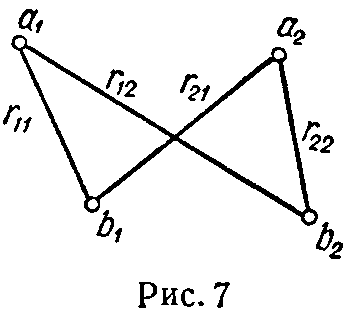
M= μ 0 l 2π ln r 12 r 21 r 11 r 22 . (32)
Расстояния считаются между осями проводов. Радиусы проводов предположены малыми по сравнению с расстояниями между ними.
17. Заряд, прошедший через проводящий контур. Количество индуктированного электричества, прошедшего через проводящий контур, имеющий w витков, при изменении сцепленного с ним магнитного потока от величины Ф1 до величины Ф2
Q= w r ( Φ 2 − Φ 1 ), (33)
здесь r — сопротивление контура, w — число витков.
18. Коэффициент магнитной связи двух контуров
k= M L 1 L 2 . (34)
Пределы изменения коэффициента магнитной связи
0 ≤ k ≤ 1.
Коэффициент рассеяния
σ = 1 — k2. (35)
19. Энергия магнитного поля
W= L⋅ I 2 2 = I⋅Ψ 2 , (36)
где Ψ — потокосцепление.
Удельная энергия магнитного поля (на единицу объема)
w= dW dV = B⋅H 2 = μ H 2 2 . (37)
Энергия магнитного поля может быть выражена через удельную энергию посредством интеграла
W= ∫ V B⋅H 2 dV . (38)
здесь V — объем пространства, занятый магнитным полем.
20. Полная магнитная энергия системы двух индуктивно связанных контуров с токами I1 и I2
W= L 1 I 1 2 2 + L 2 I 2 2 2 ±M⋅ I 1 I 2 . (39)
Упражнения и задачи
Задача 1. Вычислить и построить кривую, зависимости напряженности магнитного поля неограниченно длинного коаксиального кабеля (рис. 8) в функции расстояния r от его оси, если по кабелю проходит постоянный ток I = 1 А.
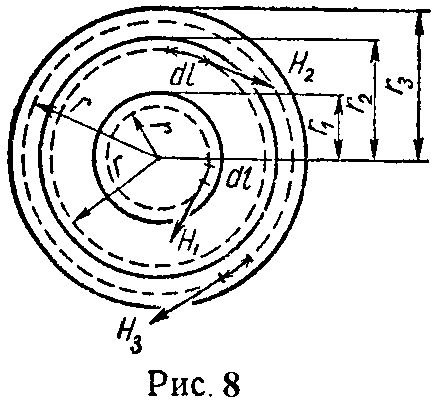
Радиус внутреннего проводника r1 = 2 мм, радиусы трубы r2 = 7,2 мм и r3 = 7,5 мм.
Плотность тока по сечению каждого проводника распределена равномерно.
Решение
Для определения напряженности магнитного поля (ввиду симметрии) воспользуемся законом полного тока.
Область внутреннего проводника (0 ≤ r ≤ r1)
Проведем окружность радиуса r < r1 с центром на оси провода. В любой ее точке напряженность H1 вследствие симметрии имеет одно и то же значение и совпадает по направлению с элементом длины окружности . Беря линейный интеграл напряженности магнитного поля вдоль этой окружности, по закону полного тока получим
? H 1 → dl → = ? H 1 dlcos( H 1 → , dl → ) = H 1 ⋅ ? dl = H 1 ⋅2πr=I( r ),
где под I(r) надо понимать ток, проходящий в части сечения проводника, находящейся внутри контура циркуляции.
Плотность тока во внутреннем проводнике
δ 1 = I π r 1 2 .
Ток, проходящий через часть сечения проводника, имеющую радиус r < r1,
I( r )= δ 1 π r 2 = I⋅ r 2 r 1 2 .
Итак,
H 1 ⋅2πr= I⋅ r 2 r 1 2 ,
отсюда
H 1 = I⋅r 2π r 1 2 .
После подстановки числовых значений получим
H 1 = I⋅r 2π r 1 2 = 1⋅r 2π⋅ 0,002 2 =39800⋅r ( А м ).
Область полости трубы (r1 ≤ r ≤ r2)
Применим закон полного тока к окружности радиуса r, проведенной в сечении трубы
? H 2 → dl → = ? H 2 dl = H 2 ⋅ ? dl = H 2 ⋅2πr=I,
отсюда
H 2 = I 2πr = 0,159 r ( А м ).
Область трубы (r2 ≤ r ≤ r3)
Применим закон полного тока к окружности радиуса r, проведенной в сечении трубы
? H 3 → dl → = ? H 3 dl = H 3 ⋅ ? dl = H 3 ⋅2πr= ∑ I .
Здесь под ΣI надо понимать сумму токов, находящихся внутри окружности радиуса r, т. е. весь ток I, проходящий по внутреннему проводу, и ток, проходящий по части сечения кольца трубы, обходимой контуром циркуляции, причем этот последний ток должен быть взят со знаком минус (так как по трубе протекает обратный ток).
Плотность тока в трубе
δ 2 = I π( r 3 2 − r 2 2 ) ; ∑ I =I− δ 2 ( π r 2 −π r 2 2 )=I⋅ r 3 2 − r 2 r 3 2 − r 2 2 .
Итак,
H 3 ⋅2πr=I⋅ r 3 2 − r 2 r 3 2 − r 2 2 ,
отсюда
H 3 =I⋅ r 3 2 − r 2 2π( r 3 2 − r 2 2 )⋅r = 2,03 r −36100⋅r ( А м ),
Область пространства вне кабеля (r3 ≤ r)
Для всех точек пространства вне кабеля напряженность магнитного поля H4 = 0. Это вытекает из закона полного тока при любом контуре интегрирования, охватывающем весь кабель.
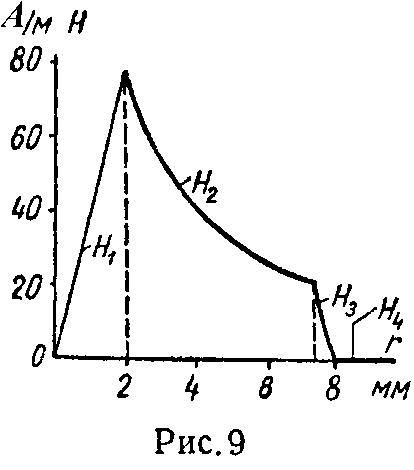
На рис. 9 представлена кривая изменения напряженности магнитного поля в функции r.
Задача 2. Вдоль длинного трубчатого провода, радиусы сечения которого r1 и r2, протекает постоянный ток I (рис. 10).
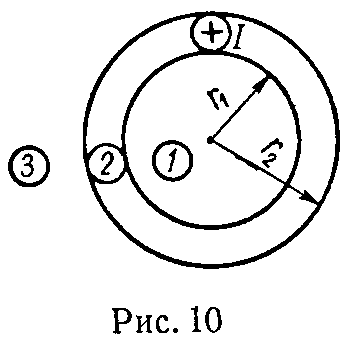
Вычислить и построить кривую зависимости напряженности магнитного поля в функции r — расстояния от точки до оси провода для областей 1 (внутри трубы), 2 (в стенках трубы), 3 (вне трубы). Даны: r1 = 2 см; r2 = 3 см, I = 10 А.
Ответ: внутри трубы (0 ≤ r ≤ r1) H1 = 0; в стенках трубы (r1 ≤ r ≤ r2) H 2 = r 2 −4 πr А см ; вне трубы (r2 ≤ r) H 3 = 5 πr А см .
Задача 3. Построить кривую напряженности магнитного поля вдоль оси x для двухпроводной линии (рис. 11), оси проводов которой отстоят друг от друга на расстоянии D = 30 см.
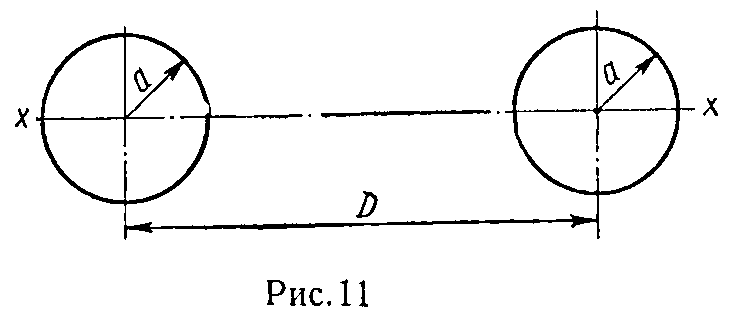
Радиус проводов a = 4 мм. Ток в прямом и обратном проводе I = 200 А. Весь ток, протекающий в проводе, следует считать сосредоточенным в его оси.
Задача 4. Два провода линии электропередачи Л1 и Л2 и две пары телефонных проводов (a1a2 и b1b2 расположены параллельно друг другу (рис. 12, а).
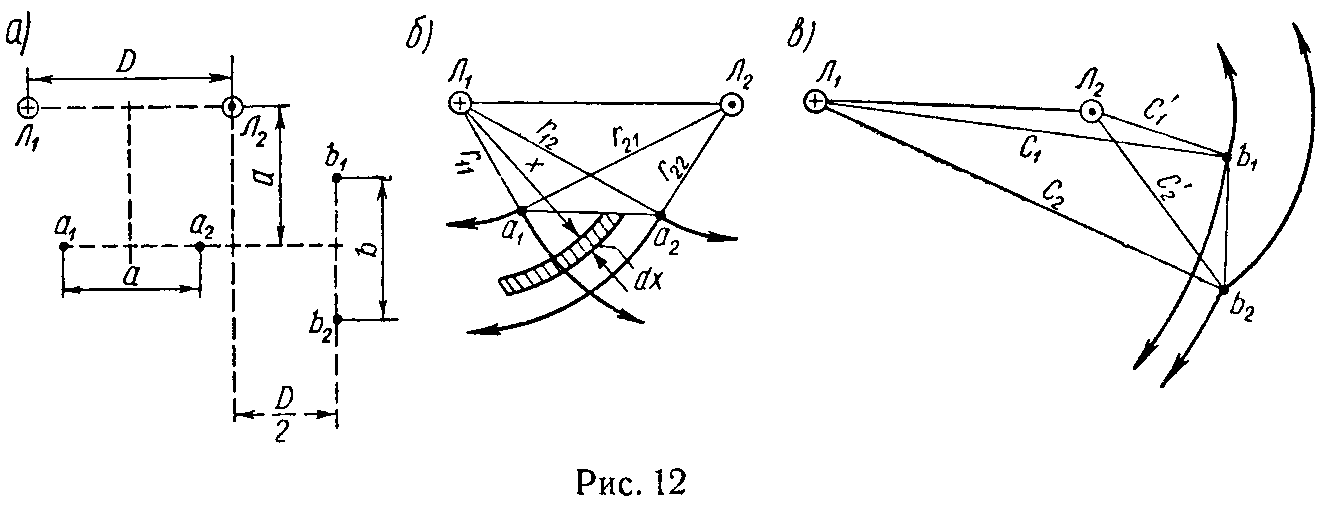
Если по проводам линии передачи проходит ток I = 150 А, то чему будет равно потокосцепление на 1 км с телефонной линией a1a2 и с телефонной линией b1b2. Даны: D = 90 см; a = b = 30 см.
Решение
Найдем потокосцепление линии Л1Л2 с линией a1a2 (рис. 12, б). Поток, определяемый током, проходящим через провод Л1, и пронизывающий линию a1a2, с учетом формул (2), (4) и того, что dS = ldx, где l — длина линии, будет равен
Φ Л 1 = ∫ r 11 r 12 BdS = ∫ r 11 r 12 μ I 2πx ldx = μ⋅I⋅l 2π ln r 12 r 11 .
Поток, определяемый током, проходящим через провод Л2, будет равен
Φ Л 2 = μ⋅I⋅l 2π ln r 21 r 22 = Φ Л 1 .
Так как
r 11 = r 22 = 30 2 + 30 2 =42,4 см и r 12 = r 21 = 30 2 + 60 2 =67 см,
то общий поток
Φ= Φ Л 1 + Φ Л 2 =2 μ 0 ⋅I⋅l 2π ln r 12 r 11 =2 4π⋅ 10 −7 ⋅150⋅ 10 3 2π ln 67 42,4 =27,5⋅ 10 −3 Вб.
Аналогично найдем, что потокосцепление линии Л1Л2 с линией b1b2 (рис. 12, в) будет равно
Φ= μ 0 ⋅I⋅l 2π ln c 1 ⋅ c ′ 2 c 2 ⋅ c ′ 1 =7,4⋅ 10 −3 Вб.
Задача 5. На кольцевой эбонитовый сердечник намотано w = 800 витков, по которым проходит ток I = 10 А (рис. 13).
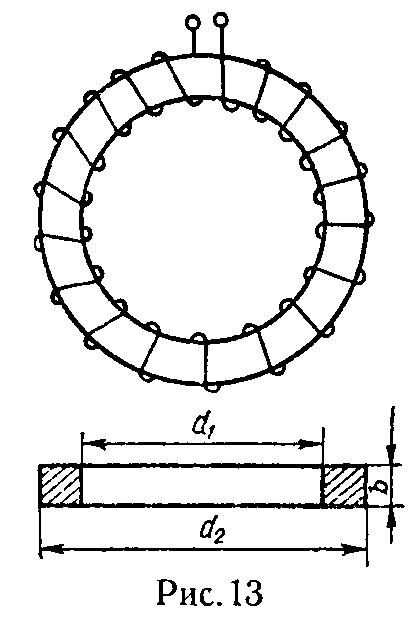
Учитывая неравномерность индукции по сечению сердечника, вычислить значение магнитного потока, проходящего через сердечник.
Внутренний диаметр сердечника d1 = 20 см, внешний диаметр d2 = 25 см, толщина сердечника b = 4 см.
Сравнить полученные результаты с теми, которые будут, если предположить, что индукция по всему сечению сердечника неизменна и равна индукции, соответствующей осевой линии.
Указание. Найти напряженность магнитного поля в любой точке сечения сердечника, пользуясь законом полного тока.
Ответ: Φ= μIwb 2π ln d 2 d 1 ; Φ приб = μIw l ср S, где S= d 2 − d 1 2 b.
Задача 6. Прямолинейный проводник, длина которого равна 40 см, перемещается со скоростью 25 м/сек под углом α = 30° к линиям однородного магнитного поля, имеющего магнитную индукцию, равную 1 Вб/м2. Определить величину ЭДС, индуктированной в проводнике.
Ответ: 5 В.
Задача 7. В однородном магнитном поле, индукция которого B, находится проволока aOb, изогнутая под углом α, по которой скользит проводник MN с равномерной скоростью v (рис. 14).
Вектор магнитной индукции перпендикулярен плоскости угла aOb. Все проводники обладают сопротивлением r0 на единицу длины. Найти выражения для наводимой ЭДС и тока, протекающего в контуре a1Ob1.
Решение
Обозначим отрезок a1b1 через h, а переменный отрезок Ob1 — через x.
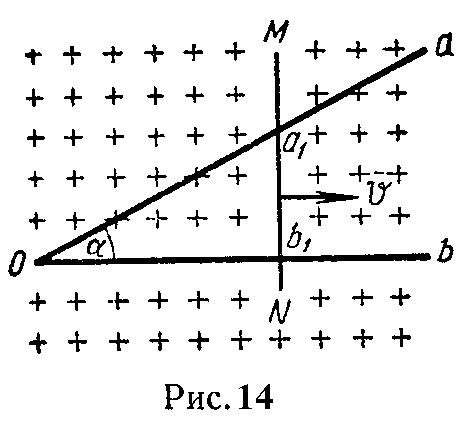
Площадь треугольника a1Ob1 равна
S= x⋅h 2 = x 2 tgα 2 .
Магнитный поток, пронизывающий контур треугольника,
Φ=B⋅S= B 2 tgα⋅ x 2 .
Имея в виду, что dx/dt = v, по формуле (19) найдем выражение для наводимой ЭДС
e=− dΦ dt =− dΦ dx dx dt =− 2x⋅tgα⋅B 2 ⋅v=B⋅v⋅x⋅tgα;
ЭДС растет пропорционально x, ибо этой величине пропорциональна активная часть a1b1 перемещающегося проводника MN.
Сопротивление контура проводника a1Ob1a1
r= r 0 ⋅( x+h+ x cosα )= r 0 ⋅x⋅( 1+tgα+ 1 cosα ).
Заметим, что величина сопротивления также возрастает пропорционально расстоянию x.
Искомый ток
i= e r =− B⋅v⋅sinα r 0 ⋅( 1+sinα+cosα ) =const,
т.е. по контуру протекает постоянный ток.
Задача 8. В однородном магнитном поле, индукция которого В = 0,5 Вб/м2, вокруг оси О вращается с равномерной скоростью прямоугольная рамка (рис. 15). Построить кривые изменения магнитного потока, пронизывающего рамку и наводимой в рамке ЭДС в функции времени. Рамка делает 1500 об/мин, ее размеры: a = 10 см, b = 20 см.
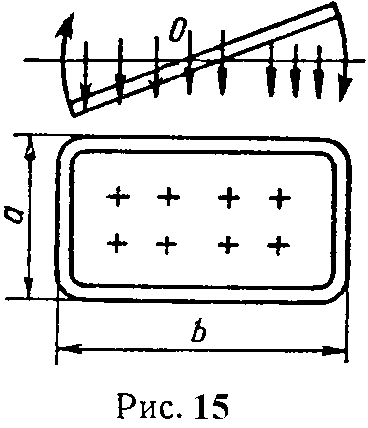
Как изменятся частота и величина максимальной ЭДС, наведенной в рамке, если: а) индукцию увеличить в 2 раза, б) сторону a увеличить в 2 раза, в) скорость вращения увеличить в 2 раза.
Ответ: Ф = 0,01cos50πt Вб, e = 1,57sin50πt В; а) и б) частота не изменится, Em увеличится в 2 раза; в) частота и Em увеличатся в 2 раза.
Задача 9. Круглый виток, радиус которого равен 5 см, находится в однородном магнитном поле, перпендикулярном плоскости витка, и изменяется с течением времени по уравнению В = Вmsinωt. Построить кривые изменения во времени магнитного потока, пронизывающего виток и наводимой в нем ЭДС, если Вm = 8000 Гс и ω = 628 1/с.
Единица индукции магнитного поля в системе единиц СИ Тесла (Тл), а в системе единиц СГСМ Гаусс (Гс). Соотношение между единицами: 1 Тл = 10000 Гс.
Ответ: Ф = 6,28·10–3sinωt Вб, e = –3,95cosωt В.
Задача 10. Построить кривую ЭДС, наводимой магнитным потоком в катушке, имеющей w =100 витков. Поток в функции времени изменяется согласно рис. 16, а, б, в, г.
Во всех случаях Фm = 10–2 Вб. Данные кривых:
а) для рис. 16, a t1 = t2 = 0,005 с;
б) для рис. 16, б t1 = 0,005 с, t2 = 0,0025 с;
в) для рис. 16, в t1 = 0,005 с, t2 = t3 = 0,0025 с;
г) для рис. 16, г t1 = 0,0025 с, t2 = t4 = 0,005 с; t3 = 0,01 с.
Решение
а) Наводимая ЭДС определяется по формуле (19).
На первом участке в интервале времени от нуля до t1 поток возрастает; за время dt происходит положительное приращение потока dФ (рис. 16, д). Вследствие линейного характера кривой отношение dФ/dt есть величина постоянная.
Величина наводимой ЭДС будет равна
e=−w dΦ dt =−w Φ m t 1 =−100 10 −2 0,005 =−200 В.
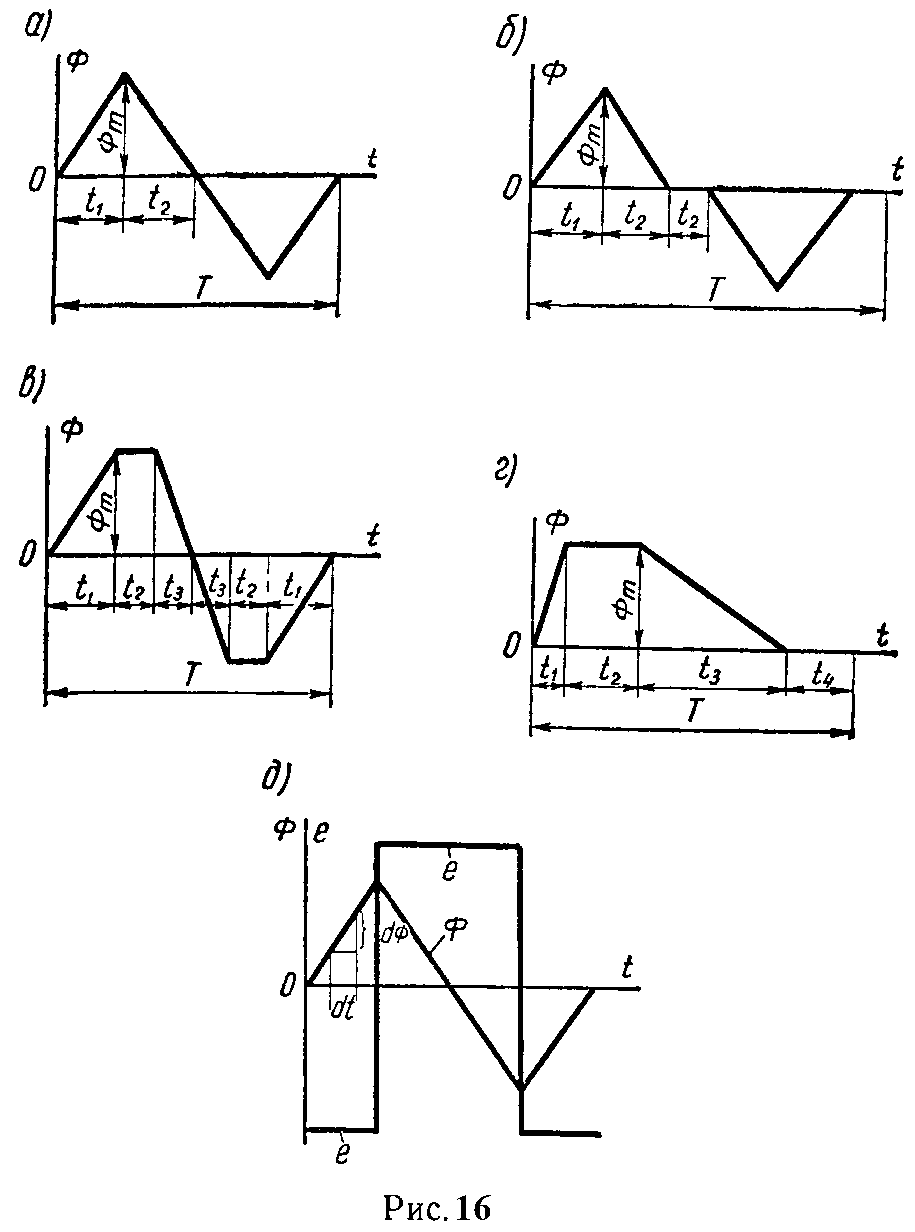
На втором участке t2 происходит спад кривой потока по прямой линии и, следовательно, dФ/dt также есть величина постоянная, но имеющая отрицательный знак; за время dt поток получает отрицательное приращение (dФ < 0); наводимая ЭДС равна
e=−w dΦ dt =+200 В.
На третьем участке за время dt поток продолжает убывать; и dФ/dt есть величина отрицательная; наводимая ЭДС равна +200 В; на четвертом участке магнитный поток возрастает с той же скоростью, что и на первом участке; наводимая ЭДС равна –200 В.
На рис. 16, д начерчена кривая наводимой ЭДС.
Задача 11. В центре цилиндрической катушки длиною l = 30 см и диаметром D = 10 см, состоящей из w = 400 витков, помещен виток, ось которого совпадает с осью катушки (рис. 17).
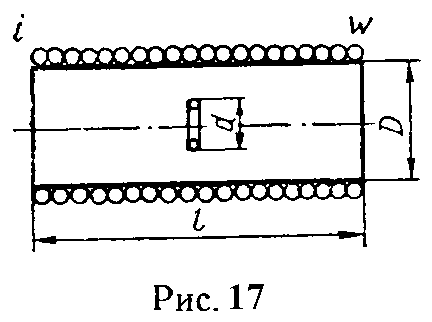
По катушке проходит ток
i = Imsinωt (Im = 4 А, ω = 314 с–1).
Определить взаимную индуктивность катушки и витка и ЭДС, наводимую в витке, если диаметр витка d = 0,5 см.
Ввиду малости размеров витка по сравнению с размерами катушки при расчете принять, что магнитная индукция, определяемая током в катушке во всех точках, лежащих в плоскости витка, будет такой же, как и в центре витка.
Полагая, что виток, перпендикулярный к оси цилиндрической катушки, расположен на расстоянии x от ее центра, построить кривую зависимости взаимной индуктивности катушки и витка в функции x.
Для построения кривой подсчет произвести для различных точек при изменении x от нуля до +l (соседние значения x брать через каждые 5 см).
Ответ: M = 31,2·10–9 Гн = 31,2 нГн; e = –39,2cos314t мкВ.
|
x, см |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
M, нГн |
31,2 |
30,7 |
26,3 |
16,1 |
4,63 |
1,62 |
0,72 |
Задача 12. Катушка прямоугольной формы, средние размеры сторон которой равны a = 8 см, b = 15 см, содержащая w = 20 витков тонкой проволоки, находится в плоскости проводов двухпроводной линии передачи энергии, по которой проходит ток I = 100 А (рис. 18).
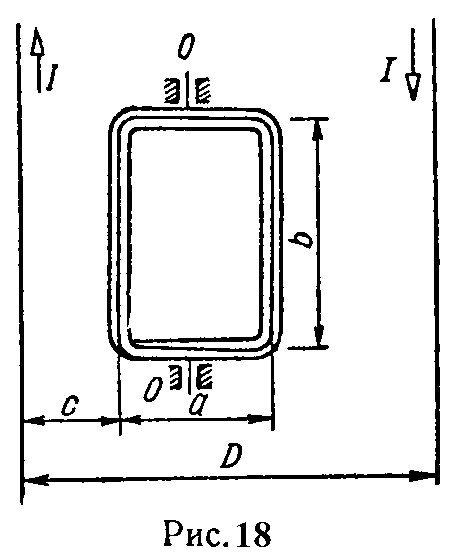
Расстояние между осью левого провода и серединой ближайшей стороны катушки c = 2 см. Расстояние между проводами линии D = 20 см.
Чему равна энергия потока взаимной индукции линии и катушки? Какова сила, действующая на катушку, если по ней проходит ток I = 0,5 А? Определить количество индуктированного в рамке электричества при ее повороте вокруг оси OO на 180°, если сопротивление катушки r = 0,08 Ом.
Примечание. Следует иметь в виду, что энергия потока взаимной индукции
W= w⋅Φ⋅I 2 ,
где Ф — магнитный поток, пронизывающий катушку, а I — ток в линии, определяющий этот поток.
Ответ: 6,6 мДж; 0,109 Гн; 33·10–4 Кл.
Задача 13. Определить индуктивность катушки, если известно, что при прохождении через нее синусоидального тока i = Imsinωt амплитуда (максимальная величина) наведенной ЭДС самоиндукции равна Em.
Дано Im = 2 А; ω = 5000 с–1; Em = 200 В.
Решение
По формуле (23) находим выражение для мгновенной величины электродвижущей силы самоиндукции, наводимой в катушке,
e L =−L di dt =−ωL I m cosωt.
Коэффициент при cosωt является амплитудой ЭДС самоиндукции, наведенной в катушке, т.е.
E m =ωL I m ,
откуда
L= E m ω I m = 200 5000⋅2 =0,02 Гн.
Задача 14. Определить индуктивность цилиндрической катушки без стального сердечника, имеющей w витков, длину l и сечение S. Расчет провести при следующих данных: a) w1 = 300, l1 = 60 см, S1 = 1 см2; б) w2 = 200, l2 = 60 см, S2 = 10 см2.
Решение
Индуктивность катушки вычисляем по формуле (25) с учетом коэффициента k, являющегося функцией отношения диаметра катушки к ее длине; значения k приведены в таблице 1.
а) Диаметр катушки найдем из формулы
S 1 = π D 1 2 4 ; D 1 = 4 S 1 π =1,13 см;
затем определяем коэффициент k1
k 1 = l 1 D 1 = 60 1,13 ≈53.
Так как k1 >50, то индуктивность находим по формуле (24)
L 1 = μ 0 ⋅ w 1 2 ⋅ S 1 l 1 = 4π⋅ 10 −7 ⋅ 300 2 ⋅1⋅ 10 −4 0,6 =18,8⋅ 10 −6 Гн=18,8 мкГн.
б) Найдем D2 и k2
D 2 = 4 S 2 π =3,57 см; k 2 = l 2 D 2 = 60 3,57 ≈16,8; D 2 l 2 = 3,57 60 =0,0595.
По таблице 1 находим, что отношению D/l = 0 соответствует k = 1, а отношению D/l = 0,1 соответствует k = 0,9588; путем интерполирования находим k, соответствующее отношению D2/l2 = 0,0595.
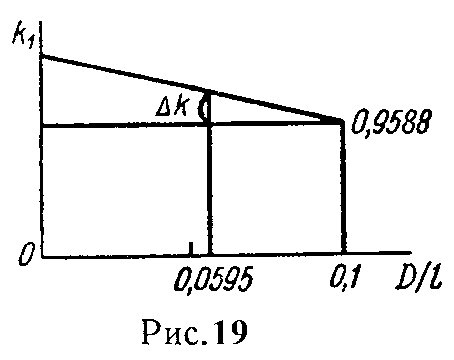
Из рис. 19 определяем
Δk 1−0,9588 = 0,1−0,0595 0,1 ,
откуда Δk = 0,0167, следовательно,
k = 0,9588 + Δk = 0,9588 + 0,0167 = 0,9755,
по формуле (25) находим индуктивность
L 2 =k μ 0 ⋅ w 2 2 ⋅ S 2 l 2 =81,5⋅ 10 −6 Гн=81,5 мкГн.
Задача 15. Индуктивность короткой цилиндрической катушки (для которой D:l = 1), имеющей 500 витков, равна 0,01 Гн. Определить индуктивность катушки, имеющей то же число витков и такую же длину, но у которой отношение D:l = 0,4.
Ответ: 2 мГн.
Задача 16. Определить индуктивность катушки, состоящей из 400 витков, намотанной на кольцевой сердечник, изготовленный из листовой электротехнической стали Э11, если ток I = 1 А. Сердечник имеет квадратное сечение. Радиусы: R1 = 3 см, R2 = 4 см.
Чему будет равна индуктивность, если в тороиде сделать зазор δ = 0,5 мм (рис. 20).
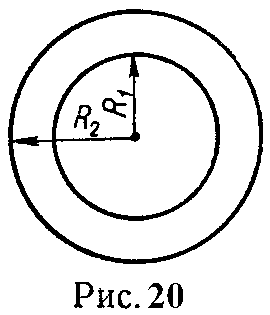
Указание. Надо рассчитать магнитную цепь, а для определения L воспользоваться формулой (21).
Ответ: 57,4 мГн; 32,8 мГн.
Задача 17. Катушка из 600 витков навита на стальной тороид, поперечное сечение которого равно 40 см2. Индуктивность катушки равна L1 = 2,5 Гн. Чему равна длина воздушного промежутка, который необходимо сделать в сердечнике для уменьшения индуктивности до 2 Гн?
При решении задачи принять, что магнитная проницаемость сердечника постоянна и очень велика по сравнению с единицей.
Решение
Магнитное сопротивление катушки без зазора
R 1 = l μS .
Для уменьшения индуктивности катушки в 1,25 раза ее магнитное сопротивление должно увеличиться в 1,25 раза, т. е. положив сечение пути потока в воздухе равным с сечением сердечника, получим
R 2 = l μS + δ μ 0 S =1,25 R 1 =1,25 l μS .
где δ — длина воздушного зазора, отсюда
δ S =0,25 l μ r S , l μ r =4δ.
Индуктивность катушки, определяемая по формуле (24), равна
L 1 = μ r μ 0 ⋅ w 2 ⋅S l ,
отсюда
l μ r = μ 0 ⋅ w 2 ⋅S L 1 .
Сравнивая два выражения для отношения l к µr, получим
4δ= μ 0 ⋅ w 2 ⋅S L 1 .
Отсюда рассчитывается необходимая длина воздушного зазора
δ= μ 0 ⋅ w 2 ⋅S 4 L 1 = 4π⋅ 10 −7 ⋅ 600 2 ⋅40⋅ 10 −4 4⋅2,5 =0,00018 м=0,18 мм.
Задача 18. На сердечник, изготовленный из листовой электротехнической стали Э11, имеющий регулируемый воздушный зазор, намотана катушка. Когда воздушный промежуток уменьшен до нуля, индуктивность катушки равна 3,5 Гн. При каком воздушном зазоре индуктивность катушки будет равна 2,5 Гн, если при зазоре в 1 мм ее индуктивность равна 2 Гн?
Принять, что абсолютная магнитная проницаемость сердечника постоянна.
Ответ: 0,53 мм.
Задача 19. Определить индуктивность 1 км воздушной медной двухпроводной линии, радиус проводов которой равен 2 мм и расстояние между осями проводов равно 30 см.
Ответ: 2 мГн.
Задача 20. Определить индуктивность 1 км воздушной медной однопроводной линии, радиус провода которой равен 2,5 мм. Расстояние провода от земли 5 м.
Ответ: 1,656 мГн.
Задача 21. Найти взаимную индуктивность на 1 км между двумя параллельными линиями a1a2 и b1b2 (рис. 21). Радиусы проводов считать малыми по сравнению с расстояниями между их осями, заданными на рис. 21.
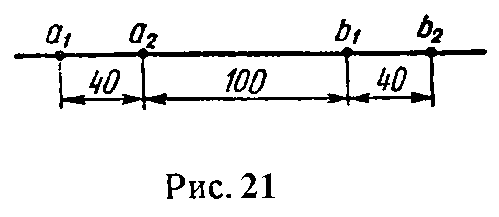
Решение
Расчет взаимной индуктивности проведем по формуле (32). Чтобы ею воспользоваться найдем расстояния: от оси первого провода первой линии до оси первого провода второй линии
r11 = a1b1 = 140 см;
от оси первого провода первой линии до оси второго провода второй линии
r12 = a1b2 = 180 см;
от оси второго провода первой линии до оси первого провода второй линии
r21 = a2b1 = 100 см;
и, наконец, от оси второго провода первой линии до оси второго провода второй линии
r22 = a2b2 = 140 см.
Искомая взаимная индуктивность
M= μ 0 l 2π ln r 11 r 22 r 12 r 21 = 4π⋅ 10 −7 2π ln 140⋅140 180⋅100 =17,2⋅ 10 −6 Гн=17,2 мкГн.
Задача 22. Четыре длинных прямых параллельных провода расположены в вершинах квадрата (рис. 22).
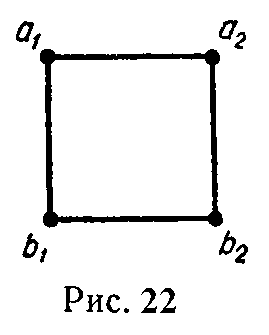
Провода a1a2 образуют одну цепь, провода b1b2 — другую. Чему равна взаимная индуктивность этих цепей на 1 км, если сторона квадрата равна 20 см? Радиусы проводов считать достаточно малыми (например, 1,5–2 мм).
Ответ: 0,1386 мГн.
Задача 23. Найти взаимную индуктивность двух катушек, изображенных на рис. 23.
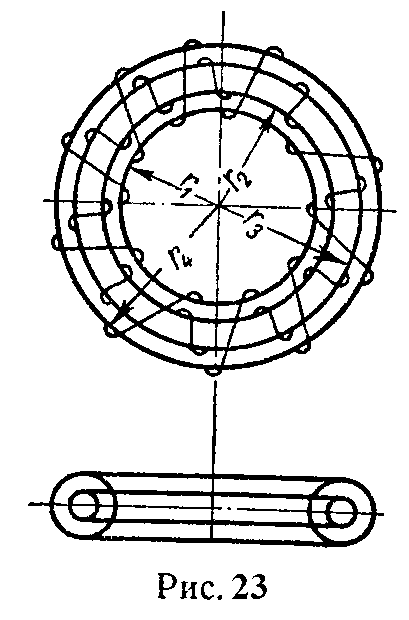
Число витков наружной катушки w1 = 200, число витков внутренней катушки w2 = 500; r1 = 8 см, r2 = 10 см, r3 = 12 см, r4= 14 см.
Решение
Взаимная индуктивность определяется по формуле (31), в которой под S надо понимать ту площадь, которая пронизывается потоком, сцепленным как с током первой так и с током второй катушки, т.е. площадь сечения меньшей катушки S2 равна
S 2 = π d 2 2 4 = π ( r 3 − r 2 ) 2 4 = 3,14⋅ 0,02 2 4 =3,14⋅ 10 −4 м 2 .
Полагая распределение магнитной индукции равномерным по сечениям обеих катушек, найдем
M= μ 0 w 1 w 2 S 2 2π r 1 + r 4 2 = 4π⋅ 10 −7 ⋅200⋅500⋅3,14⋅ 10 −4 2π⋅0,11 =57⋅ 10 −6 Гн=57 мкГн.
Задача 24. Под линией электропередачи Л1Л2 подвешены бронзовые провода линии связи a1a2 (рис. 24).
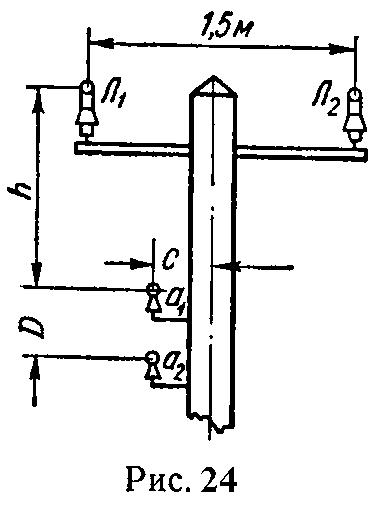
Определить индуктивность одного километра линии a1a2, диаметр проводов которой d = 3 мм, а расстояние между осями проводов D = 30 см.
Чему равна взаимная индуктивность на 1 км длины между линиями Л1Л2 и a1a2, если расстояния равны: h = 100 см, c = 25 см.
Какая электродвижущая сила наводится в линии связи, если по линии электропередачи протекает ток
i = Imsinωt,
где Im = 600 А, ω = 314 с–1.
Ответ: L = 2,12 мГн, M = 14 мкГн; e = –2,54cosωt В.
Задача 25. Определить взаимную индуктивность двух круговых витков, имеющих общую ось (рис. 25).
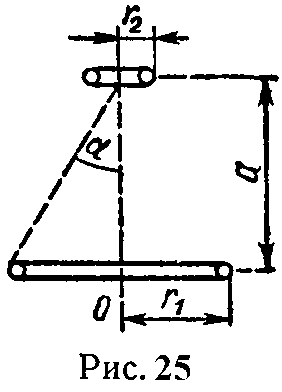
Радиусы витков r1 = 4 см, r2 = 0,5 см. Принять, что напряженность магнитного поля, определяемая током в большем витке во всех точках, лежащих в плоскости второго витка (внутри его), будет такой же, как и в центре второго витка.
Задачу решить для двух случаев: а) a = 0, б) a = 3 см.
На какое расстояние от центра 0 надо удалить второй виток, чтобы взаимная индуктивность составляла 1% от взаимной индуктивности в случае, когда плоскости витков совпадают.
Указание. Положив, что по большему витку проходит ток I, надо вычислить напряженность магнитного поля, созданную этим током в центре меньшего витка; умножив найденное значение H на магнитную постоянную и площадь, ограниченную меньшим витком, найти величину магнитного потока, пронизывающего этот виток. Разделив этот поток на ток I, получают искомую взаимную индуктивность (формула 29).
Ответ: а) 1,23 нГн; б) 0,63 нГн, 18,2 см.
Задача 26. На кольцо, изготовленное из литой стали, средний диаметр которого равен 25 см, навиты две катушки. Радиус поперечного сечения кольца 2 см. В первой катушке 250 витков, во второй — 500 витков. Относительную магнитную проницаемость стали принять постоянной и равной 1000. Определить индуктивность каждой катушки и их взаимную индуктивность (полагая распределение магнитной индукции в сечении кольца равномерным).
Ответ: L1 = 125,6 мГн; L2 = 502,4 мГн; M = 251,2 мГн.
Задача 27. Цилиндрическая катушка длиною в 1 м и диаметром в 10 см имеет 1000 витков. Вторая катушка, поперечное сечение которой 0,5 см2, а длина 1 см, имеет 10 витков. Катушки расположены так, что их оси совпадают.
Принять, что магнитная индукция, определяемая током первой катушки во всех точках, лежащих внутри второй катушки, будет такой же, как и в центре второй катушки. Определить взаимную индуктивность катушек, в случаях: а) когда их центры совпадают, б) когда центр второй катушки расположен на одном из концов первой катушки, в) когда их центры удалены друг от друга на 60 см.
Ответ: а) 0,625 мкГн; б) 0,314 мкГн; в) 0,033 мкГн.
Задача 28. Определить взаимную индуктивность двух катушек, индуктивности которых 0,04 и 0,16 Гн, а коэффициент связи равен 0,75.
Ответ: M = 0,06 Гн.
Задача 29. Определить коэффициент рассеяния двух катушек, индуктивности которых 30 и 120 мГн, а взаимная индуктивность равна 0.03 Гн.
Ответ: σ = 0,75.
Задача 30. Определить энергию магнитного поля цилиндрической катушки, содержащей 500 витков. Длина катушки равна 10 см. диаметр равен тоже 10 см; по виткам катушки проходит ток в 2 А. Среда — воздух.
Указание. Сначала следует вычислить индуктивность катушки по формуле (25), а затем энергию магнитного поля по формуле (36).
Ответ: 0,034 Дж.
Задача 31. Чему равна энергия магнитного поля катушки, имеющей 1000 витков и индуктивность которой равна 2 мГн, если магнитный поток, определяемый проходящим по катушке током, равен 2·10–5 Вб.
Ответ: 0,1 Дж.
Задача 32. Исходя из выражения интеграла магнитной энергии
W= ∫ V μ H 2 2 dV ,
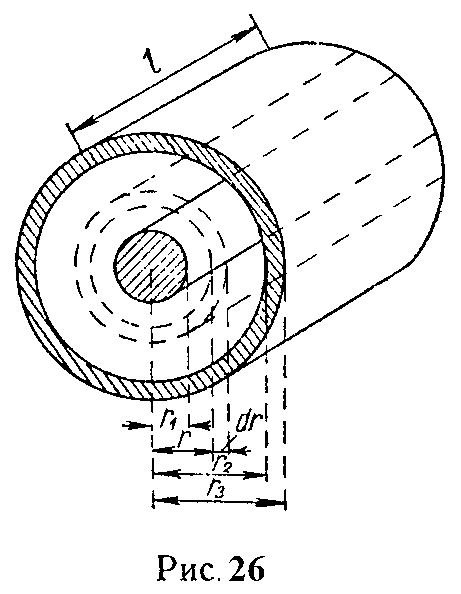
определить полную индуктивность коаксиального кабеля длиною l = 1 км, радиус внутреннего проводника которого r1 = 2 мм, внутренний радиус внешнего проводника r2 = 7,2 мм, внешний радиус внешнего проводника r3 = 7,5 мм (рис. 26).
Относительную магнитную проницаемость материала внутреннего и внешнего проводника, а также пространства между проводниками принять равной 1.
Определить энергию магнитного поля на 1 м длины кабеля, запасаемую во внутреннем проводе, между проводом и трубой и внутри трубы, если I = 1 А.
Указание. Индуктивность следует определить из выражения
L⋅ I 2 2 = ∫ V μ H 2 2 dV ,
которое следует применить по отдельности к области внутри внутреннего проводника, к полости трубы и к области внешнего проводника. При расчете энергии каждый раз надо рассматривать малый трубчатообразный объем (рис. 26)
dV = 2πr·dr·l.
Значение напряженности поля в каждой из областей было найдено в задаче 1.
В результате решения должно быть получено для внутренней индуктивности внутреннего проводника L’ = 0,05 мГн, то же для внешнего проводника L” = 0,0045 мГн, и для внешней индуктивности Lвне = 0,256 мГн. Полная индуктивность
L = L’ + L” + Lвне = 0,31 мГн.
Искомую энергию следует определять по формуле (36).
Задача 33. По двум катушкам, индуктивности которых равны L1 = 0,5 Гн, L2 = 1 Гн, а их взаимная индуктивность составляет M = 0,5 Гн, проходят токи I1 = 6 А, I2 = 4 А. Определить полную магнитную энергию этой системы.
Ответ: 29 Дж.
 удельная энергия магнитного поля,
удельная энергия магнитного поля,
энергия магнитного поля,
коэффициент магнитной связи,
взаимная индуктивность,
индуктивность однопроводной линии,
индуктивность двухпроводной линии,
индуктивность соленоида,
ЭДС самоиндукции,
индуктивность,
закон электромагнитной индукции,
второй закон Кирхгофа для магнитных цепей,
первый закон Кирхгофа для магнитных цепей,
сила Ампера,
закон Ампера,
сила Лоренца,
закон полного тока,
магнитная постоянная,
закон Био Савара Лапласа
Цель работы
Целью данной работы
является изучение явления электромагнитной
индукции и его законов, измерение
индуктивности катушки, исследование
зависимости индуктивности катушки от
силы тока, протекающего по ее обмотке,
а также индуктивности катушки, ее полного
и индуктивного сопротивлений от частоты
переменного тока.
Краткая теория.
Всякий контур, по
которому течет ток, пронизывается
магнитным полем, созданным этим током.
Если сила тока в контуре меняется, то
изменяется и сцепленный с контуром
магнитный поток, поэтому вследствие
явления электромагнитной индукции в
контуре возникает ЭДС.
Возникновение ЭДС
в контуре при изменении силы тока в нем
называется самоиндукцией. В соответствии
с законом Фарадея величина ЭДС
индукции пропорциональна скорости
изменения магнитного потока, пронизывающего
контур, то есть,
![]() (2.07.1)
(2.07.1)
Магнитный поток,
создаваемый током, протекающим в контуре,
называется потоком самоиндукции s.
Поток самоиндукции пропорционален
индукции магнитного поля, создаваемого
этим током, которая, в свою очередь,
пропорциональна величине силы тока в
контуре. Поэтому магнитный поток
самоиндукции пропорционален величине
силы тока
![]() , (2.07.2)
, (2.07.2)
где L – индуктивность
контура.
Индуктивность
контура – это
скалярная физическая величина,
характеризующая способность контура
создавать поток самоиндукции и зависящая
от его формы, размеров и магнитной
проницаемости среды. Из (2.07.2) следует,
что индуктивность контура измеряется
величиной магнитного потока, сцепленного
с контуром, при силе тока в нем равной
1 А. За единицу измерения индуктивности
в системе СИ принимается 1 Гн – это
индуктивность такого контура, с которым
сцеплен магнитный поток в 1 Вб при
силе тока в контуре, равной 1 А.
При
неизменной индуктивности закон Фарадея
для самоиндукции выглядит следующим
образом:
![]() (2.07.3)
(2.07.3)
т. е. ЭДС
самоиндукции пропорциональна скорости
изменения силы тока в контуре. В
соответствии с законом Фарадея можно
дать другое определение индуктивности.
Индуктивность определяется величиной
ЭДС,
возникающей в контуре, при изменении в
нем силы тока на 1 А за 1 с. Тогда,
согласно (2.07.3), 1 Гн – это
индуктивность такого контура, в котором
индуцируется ЭДС,
равная 1 В, при изменении в нем силы
тока на 1 А за 1 с. Знак минус в
формуле (2.07.3) отражает правило Ленца,
согласно которому самоиндукция
противодействует всякому изменению
силы тока в контуре и представляет собой
аналогию с инерцией в механике.
В электрической
цепи наличие индуктивности приводит к
возникновению добавочного индуктивного
сопротивления катушки переменному току
![]() ,
,
(2.07.4)
где – частота
переменного тока.
Модуль
полного сопротивления Z
катушки переменному току определяется
по закону Ома
![]() (2.07.5)
(2.07.5)
где U
и I – эффективные
значения напряжения и силы тока в
катушке.
Полное сопротивление
катушки Z
складывается из сопротивления катушки
в цепи постоянного тока R
(омического или активного сопротивления)
и индуктивного сопротивления XL
в соответствии с формулой:
![]() . (2.07.6)
. (2.07.6)
или, подставив
![]()
![]() (2.07.7)
(2.07.7)
из которого можно
выразить индуктивность катушки L
![]() (2.07.8)
(2.07.8)
Соотношение
(2.07.8) лежит в основе опыта по определению
индуктивности. Для того, чтобы определить
индуктивность, необходимо измерить
частоту переменного тока, действующее
значение силы переменного тока,
протекающего через катушку, действующее
значения напряжения на катушке и
омическое сопротивление катушки.
Индуктивность
длинного соленоида с сердечником может
быть рассчитана по формуле
![]() , (2.07.9)
, (2.07.9)
где – магнитная
проницаемость сердечника;
![]() – магнитная
– магнитная
постоянная;n – число
витков, приходящихся на единицу длины
катушки; V – объем
катушки.
Измеряя индуктивность
катушки, можно определять магнитную
проницаемость материала, из которого
изготовлен сердечник. В частности, таким
способом можно определять магнитную
проницаемость горных пород. Определив
индуктивность катушки с сердечником
из исследуемой породы Lс
и без
сердечника L0,
по отношению этих индуктивностей LС/L0
определяют
.
Определение магнитной проницаемости
горных пород и минералов необходимо
для изучения вопросов, связанных с
установлением качества железных руд и
железистых пород, магнитным обогащением
полезных ископаемых, с разведкой рудных
тел, исследованием трещиноватости
массива горных пород.
Выполнение работы
Необходимые
приборы:
лабораторный стенд, внутри которого
смонтированы все элементы схемы;
генератор периодических сигналов;
цифровой вольтметр. Рабочая схема опыта
показана на рис. 18 и на панели стенда.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.
В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).
Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.
Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.
Расчет индуктивности
Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:
B=μ0nI,
где I является обозначением тока в соленоиде, n = Ne указывает число витков на единицу длины соленоида.
Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:
Φ=B·S·N=μ0n2Sl
Таким образом, индуктивность соленоида будет выражена формулой:
L=μ0n2S·l=μ0n2V,
где V=Sl – объем соленоида, содержащий магнитное поле.
Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ, при заданном токе I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:
Lμ=μ·L=μ0·μ·n2·V.
ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:
δинд=δL=-∆Φ∆t=-L∆I∆t.
ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.
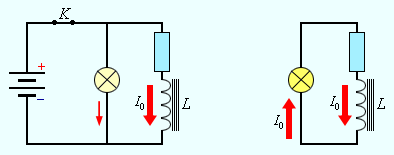
Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.
Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как R полное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.
Ток в цепи составляет:
I=δLR=-LR∆I∆t
Выражение для ΔQ можем записать так:
∆Q=-L·I·∆I=-Φ(I)∆I
В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:
Q=LI022
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
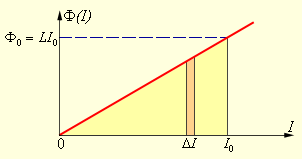
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
