Рассмотрим
проводник с током, имеющий форму
окружности радиуса R
(рис.4.5 ).
Определим магнитную индукцию в его
центре.
Каждый
элемент тока
![]() создает
создает
магнитное поле индукцией![]() ,
,
перпендикулярное к плоскости витка.
![]() .
.
(4.19)
В се
се
вектора![]() направлены одинаково, поэтому их
направлены одинаково, поэтому их
векторное сложение сведется к сложению
их модулей. Тогда
![]() .
.
Так
как
![]() ,
,
то для магнитной индукции в центре
кругового тока получаем:
![]() .
.
(4.20)
О пределим
пределим
магнитную индукцию в любой точке на оси
кругового тока. Обозначимx
расстояние от плоскости контура до
некоторой точки на оси (рис.4.6).
Так
как вектор
![]() ,
,
то модуль вектора![]() равен:
равен:
![]() .
.
(4.21)
Вектор
![]() перпендикулярен плоскостям, проходящим
перпендикулярен плоскостям, проходящим
через![]() и
и![]() (рис.4.6). От всех элементов тока будет
(рис.4.6). От всех элементов тока будет
образовываться «конус» векторов![]() .
.
Разложим
вектор
![]() на две составляющие: перпендикулярную
на две составляющие: перпендикулярную
и параллельную оси:![]() .
.
Применим принцип суперпозиции полей,
получим:
![]()
Нетрудно
убедиться, что векторная сумма всех
перпендикулярных составляющих равна
нулю, и результирующий вектор
![]() будет направлен вдоль оси тока. Вклад
будет направлен вдоль оси тока. Вклад
в него будут вносить только параллельные
оси составляющие векторов![]() .
.
Тогда
![]() .
.
(4.22)
Из треугольника
(см. рис.4.6) следует:
![]() .
.
(4.23)
Подставим выражение
(4.21) в формулу (4.23), получим:
![]() .
.
(4.24)
Возьмём
интеграл:
![]() ,
,
получим:
![]() ,
,
или
![]() .
.
(4.25)
Так
как
![]() , то окончательно получим:
, то окончательно получим:
![]() .
.
(4.26)
При
x=0
формула (4.26) переходит в (4.20).
4.5. Магнитный момент витка с током
Рассмотрим
замкнутый контур с током (рис. 4.7).
Обозначим
![]() –
–
единичный вектор положительной
нормали к контуру. Этот вектор связан
с направлением тока правилом правого
винта.
Магнитным
моментом контура с током называется
вектор
![]() ,
,
равный
![]() .
.
(4.27)
Здесь
S
– площадь,
охватываемая контуром. Если контур
круговой, то
![]() ,
,
тогда
![]()
 .
.
(4.28)
Для
магнитной индукции на оси кругового
тока было получено выражение:
![]() .
.
(4.29)
Во
многих случаях приходиться иметь дело
с замкнутыми токами, размеры которых
малы по сравнению с расстояниями до
точки наблюдения. Такие токи принято
называть элементарными. (Пример:
движущийся по замкнутой орбите электрон).
На
больших расстояниях от контура x>>R
и можно пренебречь вторым слагаемым в
знаменателе, тогда
![]() .
.
(4.30)
Умножим
числитель и знаменатель этого выражения
на π,
получим:
![]() ,
,
(4.31)
где
![]() .
.
Произведение
силы тока на площадь контура равно по
величине магнитному моменту контура.
Так как векторы
![]() и
и![]() направлены
направлены
одинаково, то
![]() .
.
(4.32)
Индукция
магнитного поля, созданного элементарным
током, пропорциональна его магнитному
моменту.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Магнитный момент

3.4. Магнитный момент

3.4.1. По круговому витку радиусом R = 5 см течёт постоянный ток силой I = 10 А. Определить магнитный момент витка.
1. Магнитный момент контура с током определяется уравнением
 , (1)
, (1)
 . (2)
. (2)

3.4.2. Короткая квадратная катушка с длиной стороны а = 0,1 м содержит N = 1000 витков тонкого провода. Определить магнитный момент катушки при силе тока I = 1 А.
1. Магнитный момент N витков будет равен сумме магнитных моментов всех витков, составляющих данную измерительную катушку
 . (1)
. (1)
3.4.3. Магнитный момент витка с током равен pm = 0,2 Дж/Тл. Определить силу тока в витке, если его радиус равен R = 5 см.
1. Запишем уравнение магнитного момента кругового витка с током и определим из него величину силы тока
 . (1)
. (1)
3.4.4. Напряжённость магнитного поля кругового витка с током составляет Н = 200 А/м. Магнитный момент витка равен pm = 1 А×м2. Определить силу тока в витке и его радиус.
1. Напряжённость кругового витка с током и его магнитный момент определяются следующими уравнениями
 (1)
(1)
2. Выразим из уравнения напряжённости магнитного поля силу тока и подставим её в уравнение магнитного момента, что позволит найти его радиус
 . (2)
. (2)
3. Так как, из уравнения напряжённости  , то
, то
 . (3)
. (3)

3.4.5. На оси кольца с током I на расстоянии r = 1 м от его центра напряжённость магнитного поля составляет В = 10 нТл. Считая радиус кольца много меньшим заданного расстояния R > R
 , (1)
, (1)
и выразим силу тока
 . (2)
. (2)
2. Подставим значение силы тока в уравнение магнитного момента
 . (3)
. (3)
3.4.6. Электрон в невозбуждённом атоме водорода движется по круговой орбите радиусом R = 50 пм. Найти величину магнитного момента pm эквивалентного кругового тока и механический момент сил Mz(F), относительно оси вращения электрона при помещении атома в магнитное поле индукцией В = 0,1 Тл. Вектор магнитной индукции параллелен плоскости орбиты вращающегося электрона.
1. Силу эквивалентного тока определим, воспользовавшись уравнением (4), полученном в задаче 3.2.1
 , (1)
, (1)
где е @ 1,6×1Кл – заряд электрона, me @ 1×1кг, e0 @ 9×1Ф/м – электрическая постоянная.
2. Магнитный момент такого эквивалентного тока определится как
 . (2)
. (2)
3. Механический момент относительно оси вращения z, действующий на атом водорода, помещённый в магнитное поле с индукцией В, равен
 , (2)
, (2)
Поскольку вектор магнитного момента перпендикулярен плоскости орбиты, то  , другими словами
, другими словами
 . (3)
. (3)
3.4.7. Электрон в атоме водорода движется по круговой орбите известного радиуса. Найти отношение магнитного момента pm к моменту импульса L орбитального движения электрона.
1. Орбитальную скорость электрона определим из условия его нахождения на стационарной круговой орбите
 , (1)
, (1)
где k = 1/(4pe0) @ 9×1012 м/Ф – постоянная величина, R – радиус орбиты, е, me – заряд и масса электрона.
2. Сила эквивалентного тока при круговом движении электрона
 . (2)
. (2)
3. Магнитный момент кругового тока
 . (3)
. (3)
4. Момент импульса электрона при его орбитальном движении
 . (4)
. (4)
5. Отношение магнитного момента к моменту импульса
 . (5)
. (5)

3.4.8. Тонкий стержень длиной l = 0,2 м несёт распределённый заряд Q = 240 нКл. Стержень вращается с постоянной угловой скоростью w = 10 рад/с вокруг оси перпендикулярной стержню и проходящей через его середину. Определить магнитный момент рm, возникающий при вращении заряженного стержня и отношение магнитного момента к его моменту количества движения L, если масса стержня составляет m = 12 г.
1. Распределённый заряд стержня можно представить в виде сосредоточенного заряда, создающего эквивалентный q = Q/3, сила тока в этом случае определится как
 . (1)
. (1)
2. Магнитный момент эквивалентного кругового тока
 . (2)
. (2)
3. Для определения отношения магнитного момента к моменту импульса воспользуемся уравнением (5) предыдущей задачи
 . (3)
. (3)
3.4.9. Тонкое кольцо радиусом R = 10 см несёт заряд Q = 10 нКл. Кольцо вращается равномерно с частотой n = 10 с -1 относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент, создаваемый круговым током pm и отношение магнитного момента к моменту импульса кольца pm/L, если его масса равна m = 10 г

1. Если выделить вспомогательную площадку d, расположив её перпендикулярно сечению кольца, то можно видеть, что через это сечение в единицу времени будет протекать заряд Q. Эквивалентная сила тока, вызванная вращением заряженного кольца, определится как
 , (1)
, (1)
2. Магнитный момент вращающегося заряженного кольца в этом случае будет равен
 . (2)
. (2)
3. Момент импульса кольца относительно оси вращения Оz
 . (3)
. (3)
4. Отношение магнитного момента кольца к моменту импульса
 . (4)
. (4)
3.4.10. Кольцо, геометрические параметры которого и заряд соответствуют предыдущей задаче, вращается с частотой n = 10 c – 1 вокруг оси, проходящей через один из его диаметров. Определить магнитный момент заряженного вращающегося кольца pm и отношение магнитного момента к моменту количества движения pm/L.

1. В данном случае, в виду симметрии кольца относительно оси вращения, распределённый заряд кольца Q можно представить в виде двух сосредоточенных зарядов q = Q/2, расположенных в диаметрально противоположных точках. Сила эквивалентного тока в этом случае запишется следующим образом
 . (1)
. (1)
2. Магнитный момент вращающегося таким образом заряженного кольца определится уравнением
 . (2)
. (2)
3. Отношение pm/L
 . (3)
. (3)
3.4.11. Диск радиусом R = 10 см несёт равномерно распределённый по поверхности заряд Q = 0,2 мкКл. Диск равномерно вращается с частотой n = 20 с – 1 относительно оси, проходящей через центр диска и перпендикулярной его плоскости. Определить магнитный момент pm кругового тока, создаваемого диском и отношение магнитного момента к моменту импульса диска pm/L, если масса диска равна m = 0,1 кг.

1. На одной поверхности диска распределён заряд q = Q/2, поэтому эквивалентный ток, создаваемый вращающимся диском определится как
 . (1)
. (1)
2. Магнитный момент эквивалентного тока, создаваемого вращающимся диском, несущим заряд, определится в этом случае как
 . (2)
. (2)
3. Момент импульса вращающегося диска равен произведению момента инерции диска на его угловую скорость
 . (3)
. (3)
4. Отношение магнитного момента диска к его моменту импульса равно
 . (4)
. (4)

3.4.12. Тонкостенная металлическая сфера радиусом R = 0,1 м с равномерно распределённым по поверхности зарядом Q = 3 мкКл. Сфера вращается равномерно вокруг с угловой скоростью w = 10 рад/с относительно оси, проходящей через центр сферы. Найти магнитный момент pm кругового тока, создаваемый вращением сферы и отношение магнитного момента к моменту импульса, если масса сферы m = 0,1 кг.
1. Магнитный момент эквивалентного тока вращающейся заряженной сферической оболочки
 . (1)
. (1)
2. Отношение магнитного момента к моменту импульса
 . (2)
. (2)

3.14.13. Сплошной шар радиусом R = 10 см несёт заряд Q = 200 нКл, равномерно распределённый по объёму. Шар вращается относительно оси, проходящей через центр шара, с угловой скоростью w = 10 рад/с. Определить магнитный момент эквивалентного кругового тока, создаваемого вращающимся заряженным шаром и сферы и отношение магнитного момента к моменту импульса, если масса сферы m = 100 кг.
1. Эквивалентный заряд, создающий круговой ток определится как
 . (1)
. (1)
2. Эквивалентный электрический ток, возникающий при вращении заряженного шара
 . (2)
. (2)
3. Магнитный момент, создаваемый равномерно заряженной вращающейся сферой
 . (3)
. (3)
4. Момент импульса сплошного шара определяется его моментом инерции J и угловой скоростью w
 . (4)
. (4)
5. Отношение магнитного момента заряженного вращающегося шара к его моменту импульса
 . (5)
. (5)
3.5. Контур в магнитном поле

3.5.1. Круговой контур радиусом R = 5 см, по которому течёт ток силой I = 4 A, находится в магнитном поле напряжённостью Н = 2 кА/м. Плоскость витка составляет угол a = 600 с направлением вектора напряжённости. Определить механический момент, действующий на контур.
1. Определим величину магнитной индукции поля
 . (1)
. (1)
2. Механический момент, действующий на круговой виток с током
 , (2)
, (2)
 . (3)
. (3)
3.5.2. Круговой контур радиусом R = 0,1 м закреплён так, что может вращаться вокруг оси, совпадающей с одним из его диаметров, совпадающим с магнитным меридианом поля Земли. Горизонтальная составляющая магнитной индукции нашей планеты равна Вх = 20 мкТл. По контуру пустили ток силой I = 10 А. Какой момент сил Mz(F) должен быть приложен к контуру, чтобы сохранялась его первоначальная ориентация?

1. При пропускании по контуру тока возникнет собственное магнитное поле и появится магнитный момент pm
 , (1)
, (1)
наличие которого обусловит его взаимодействие в внешним магнитным полем, в данном случае, горизонтальной составляющей магнитного поля Земли. Такое взаимодействие количественно можно охарактеризовать механическим моментом сил
 ,
,
 . (2)
. (2)
3.5.3. Измерительная часть гальванометра представляющая собой квадратную рамку с размерами а = 4 см и b = 1,5 см, на которую намотано N = 200 витков провода. Рамка помещена в магнитное поле с индукцией В = 0,1 Тл, так что плоскость рамки параллельна вектору индукции внешнего поля. Определить механический момент Mz(F), приложенный к рамке и величину магнитного момента рамки при пропускании по проводнику тока силой I = 1 мА.

1. Определим величину магнитного момента рамки при пропускании заданного тока
 . (1)
. (1)
2. Найдём величину механического момента сил, возникающего при взаимодействии собственного магнитного поля рамки с внешним полем
 , (1)
, (1)
поскольку вектор магнитного момента контура совпадает с направлением нормали к плоскости, в которой располагается контур, то угол между векторами pm и B равен 900, другими словами
 . (2)
. (2)
3.5.4. Короткая катушка площадью поперечного сечения s = 150 см2, содержит N = 200 витков провода, по которому пропускается ток силой I = 4 A. Катушка помещена в магнитное поле напряжённостью Н = 8 кА/м. Определить магнитный момент катушки рm и момент сил, действующий на катушку со стороны внешнего поля, если ось катушки составляет с линиями индукции угол a = 600.
1. Магнитный момент катушки
 . (1)
. (1)
2. Механический момент сил, действующий на рамку
 , (2)
, (2)
 . (3)
. (3)
3.5.5. Рамка гальванометра, содержащая N = 200 витков тонкого провода, подвешена на упругой нити. Поперечное сечение рамки равно s = 1 см2. Нормаль к плоскости кольца перпендикулярна линиям магнитной индукции внешнего поля с В = 5 мТл. При пропускании через гальванометр постоянного тока силой I = 2 мкА рамка повернулась на угол j = 300. Определить постоянную кручения нити С (коэффициент упругости).
1. Найдём величину магнитного момента рамки при пропускании по ней тока
 . (1)
. (1)
2. Определим величину механического момента под действием, которого рамка повернётся на заданный угол j
 . (2)
. (2)
3. Крутящий момент, действующий на нить пропорционален углу закручивания j и упругой постоянной С
 . (3)
. (3)
3.5.6. По рамке квадратной формы из тонкой проволоки массой m = 2×10 – 3 кг пропускают постоянный ток, силой I = 6 А. Рамка подвешена за середину одной из сторон на неупругой нити. Определить период малых колебаний рамки Т в магнитном поле с индукцией В = 2 мкТл, считая затухание не существенным.

1. Малые колебания рамки с током в магнитном поле будут возникать вследствие преобразования потенциальной энергии поля в кинетическую энергию крутильных колебаний, т. е. вращательного движения. Считая систему консервативной, закон сохранения энергии можно записать так
 (1)
(1)
где  – максимальное значение потенциальной энергии, кинетическая энергия вращательного движения в данном случае определится величиной момента инерции рамки и периодом её колебаний:
– максимальное значение потенциальной энергии, кинетическая энергия вращательного движения в данном случае определится величиной момента инерции рамки и периодом её колебаний:  , где J – момент инерции колеблющегося вокруг оси вращения тела, Т – период колебаний.
, где J – момент инерции колеблющегося вокруг оси вращения тела, Т – период колебаний.
2. Перепишем уравнение закона сохранения энергии с учётом полученных значений потенциальной и кинетической энергии
 . (2)
. (2)
3. Найдём период малых крутильных колебаний рамки
 . (3)
. (3)

2.5.7. Проволочное кольцо массой m = 3 г подвешено на неупругой нити в однородном магнитном поле. По кольцу течёт постоянный ток силой I = 2 А. Период малых крутильных колебаний кольца вокруг вертикальной оси составляет Т = 1,2 с. Определить величину магнитной индукции.
1. Закон сохранения механической энергии применительно к колеблющемуся кольцу представляется как процесс преобразования потенциальной энергии взаимодействия магнитных полей в кинетическую энергию вращательного движения
 , (1)
, (1)
где К – кинетическая энергия вращательного движения, J – момент инерции кольца относительно оси вращения, w – циклическая частота крутильных колебаний.
2. Потенциальная энергия будет максимальной, как это видно из уравнения (1), при совпадении по направлению векторов магнитного момента кольца и вектора индукции магнитного поля
 , (2)
, (2)
 . (3)
. (3)
3.6. Магнитный диполь
3.6.1. По бесконечно длинному проводнику пропускают постоянный ток силой I = 100 A. На расстоянии r = 0,1 м в плоскости проводника расположен магнитный диполь, вектор магнитного момента которого pm = 1 мА×м2 перпендикулярен проводнику. Найти силу F, действующую на магнитный диполь.

1. Магнитный диполь, помещённый в однородное поле, под действием механического момента сил будет менять свою ориентацию. Запишем уравнение механического момента и выразим действующую силу F
 , (1)
, (1)
 . (2)
. (2)
2. Определим величину магнитной индукции поля В, создаваемого бесконечным проводником с током в точке расположения магнитного диполя
 . (3)
. (3)
3. Подставим в уравнение (2) величину В и значение механического момента, с учётом того что вектор pm перпендикулярен вектору магнитной индукции
 . (4)
. (4)
3.6.2. Определить неоднородность магнитного поля  , в котором максимальная сила, действующая на точечный диполь равна Fmax = 1 мН. Магнитный момент диполя составляет pm = 2 мА×м2.
, в котором максимальная сила, действующая на точечный диполь равна Fmax = 1 мН. Магнитный момент диполя составляет pm = 2 мА×м2.
1. Сила, действующая на диполь в магнитном поле, определяется уравнением
 . (1)
. (1)
2. Поскольку, по условию задачи задано максимальное значение силы Fmax, то  , другими словами
, другими словами
 . (2)
. (2)
3.6.3. Круговой контур радиусом R = 0,2 м расположен в плоскости меридиана. В центре контура расположена магнитная стрелка, которая при пропускании по витку тока отклонилась на угол a = 90 от плоскости магнитного меридиана. Определить силу тока I, протекающего по контуру. Величину горизонтальной составляющей индукции магнитного поля Земли принять равной Вх = 20 мкТл.

1. В отсутствии собственного магнитного поля контура стрелка компаса реагирует только на магнитное поле Земли, на её горизонтальную составляющую Вх. При пропускании по контуру постоянного электрического тока, возникает собственное магнитное поле контура с индукцией

 . (1)
. (1)
2. На магнитную стрелку, таким образом, будут действовать два поля, под действием которых она займёт положение, соответствующее условию равновесия полей. Математически это можно выразить из соотношения модулей векторов индукции, угол между линиями действия которых составляет a = 90
 . (2)
. (2)
3.6.4. Определить число витков катушки N тангенс – гальванометра, при котором сила тока, текущего по обмотке, численно равна тангенсу угла отклонения магнитной стрелки, помещённой в центре обмотки. Радиус катушки равен R = 0,25 м. Ось катушки перпендикулярна плоскости магнитного меридиана Земли.
1. Магнитная индукция поля, создаваемого круглой катушкой тангенс – гальванометра определится как
 . (1)
. (1)
2. Условие равновесного положения стрелки компаса запишем по аналогии с уравнением (2) предыдущей задачи
 , (2)
, (2)
где Вх = 20 мкТл – горизонтальная составляющая магнитного поля Земли. По условию задачи tga численно равен силе тока в катушке, поэтому уравнение (2) можно переписать следующим образом
 . (3)
. (3)
3.6.5. Длинный прямолинейный соленоид содержит n = 5 витков на каждый сантиметр длины. Соленоид расположен перпендикулярно плоскости магнитного меридиана Земли (Вх = 20 мкТл). Внутри соленоида, в его центре находится магнитная стрелка, ориентированная первоначально по магнитному полю планеты. При пропускании по обмотке соленоида постоянного электрического тока стрелка отклоняется на угол a = 600. Найти силу тока.

1. Определим величину магнитной индукции поля, создаваемого соленоидом
 . (1)
. (1)
2. При возникновении в соленоиде магнитного поля стрелка компаса изменит свою ориентацию, повернувшись относительно оси вращения на угол a, новое положение стрелки будет характеризоваться равновесием между магнитными полями Земли и соленоида. Это условие равновесия можно охарактеризовать уравнением (2) предыдущей задачи
 . (2)
. (2)
3.7. Заряд, движущийся в магнитном поле
3.7.1. Найти величину силы Лоренца, приложенную к электрону, влетевшему в магнитное поле со скоростью v = 4×106 м/с в однородное магнитное поле под углом a = 300 к линии индукции. Магнитная индукция составляет B = 0,2 Тл.
1. Сила Лоренца, возникающая в магнитном поле при перемещении там заряда, определяется уравнением
 , (1)
, (1)
где е @ 1,6×1Кл – заряд электрона.
 . (2)
. (2)
3.7.2. Вычислить радиус дуги окружности R, которую опишет протон в магнитном поле с индукцией В = 15 мТл, если скорость протона перпендикулярна вектору индукции и равна v = 2 Мм/с.
1. Нахождение электрона на криволинейной траектории характеризуется следующим уравнением равновесия сил
 , (1)
, (1)
где  – заряд протона, mp @ 1,67×1кг – масса протона, a = 900 Þ sina = 1.
– заряд протона, mp @ 1,67×1кг – масса протона, a = 900 Þ sina = 1.
2. Выразим из уравнения (1) радиус кривизны
 . (2)
. (2)
3.7.3. Дважды ионизированный атом гелия, именуемый в простонародии a – частицей, движется в магнитном поле напряжённостью Н = 100 кА/м по окружности радиусом R = 0,1 м. Определить скорость частицы.
1. Заряд a – частицы по модулю равен заряду двух электронов
 (1)
(1)
масса a – частицы, состоящей из двух протонов и двух нейтронов равна
 . (2)
. (2)
2. Движение заряженной частицы по криволинейной траектории даже с постоянной по модулю скоростью обусловлено возникновением нормального ускорения |an| = v2/R. Приравняем силу инерции, действующую на a – частицу к силе Лоренца
 , (3)
, (3)
поскольку движение происходит по круговой траектории, то a – частица влетает перпендикулярно вектору индукции магнитного поля, а это значит, что sina = 1. Таким образом,
 . (4)
. (4)
3.7.4. Ион, несущий один элементарный заряд, движется в однородном магнитном поле с индукцией В = 0,015 Тл по круговой траектории радиусом R = 0,1 м. Определить импульс иона р.
1. Перепишем уравнение (3) предыдущей задачи применительно к рассматриваемому в настоящей задаче случаю
 . (1)
. (1)
3.7.5. Некая частица, несущая заряд, эквивалентный одному электрону, влетает в магнитное поле с индукцией В = 0,5 Тл. Определить момент импульса L, которым обладает частица при движении по дуге окружности радиусом R = 0,2 см.
1. Запишем уравнение, определяющее нахождение частицы на криволинейной траектории
 . (1)
. (1)
2. Момент импульса относительно мгновенной оси вращения численно равен произведению импульса частицы на радиус кривизны траектории
 , (2)
, (2)
чтобы в уравнении (1) образовать момент импульса, необходимо обе части этого уравнения умножить на R2
 . (3)
. (3)
3.7.6. Электрон движется в магнитном поле с индукцией В = 0,02 Тл по круговой траектории радиусом R = 0,01 м. Определить кинетическую энергию электрона, выразив её в джоулях и электрон-вольтах.
1. Запишем условие движения электрона по круговой траектории
 , (1)
, (1)
и определим его линейную скорость
 . (2)
. (2)
2. Кинетическая энергия электрона
 . (3)
. (3)
3. Выразим значение энергии в электрон-вольтах
 . (4)
. (4)

3.7.7. Частица, несущая на себе электрический заряд, влетает в среду, пронизанную линиями индукции однородного магнитного поля. В результате взаимодействия с атомами вещества, частица теряет половину своей первоначальной энергии. Во сколько раз будет отличаться радиус кривизны траектории z в начале и конце пути?
1. Запишем силовое условие нахождения движущейся заряженной частицы на криволинейной траектории при её вхождении в область пространства, занятого магнитным полем перпендикулярно линиям магнитной индукции
 , (1)
, (1)
где z – радиус кривизны траектории, m – масса частицы, q – заряд частицы, v – скорость частицы, В – индукция магнитного поля.
2. При перемещении в среде, занятой неизменным магнитным полем (B = const) в уравнении (1) будут изменяться две величины: скорость v и кривизна траектории z. С другой стороны по условию задачи известно, что кинетическая энергия уменьшается в два раза. При постоянстве массы частицы, это означает, что для скорости частицы можно записать следующие соотношения
 . (2)
. (2)
3. Решим уравнение (1) относительно скорости
 . (3)
. (3)
4. Запишем уравнение (2) для начального и конечного положения частицы на криволинейной траектории
 (4)
(4)
5. Поделим уравнения системы (4) почленно
 . (5)
. (5)

3.7.8. Заряженная частица, летящая в однородном магнитном поле по дуге окружности с радиусом кривизны z1 = 2 см, попадает в свинцовую мишень в виде пластины. При выходе из пластины, вследствие потери энергии радиус кривизны траектории уменьшился до величины z2 = 1 см. Найти относительное изменение энергии частицы.
1. При попадании частицы в свинец (Pb), при прочих равных условиях будет, вследствие взаимодействия с ионами и электронами свинца, уменьшаться её скорость. Перепишем систему уравнений (4) применительно к рассматриваемому случаю
 , (1)
, (1)
отношение кинетических энергий частицы в начальном и конечном положениях будет равно отношению квадратов радиусов кривизны.
2. Определим далее относительное изменение кинетической энергии
 , (2)
, (2)
 . (3)
. (3)

3.7.9. Протон, будучи разогнан ускоряющей разностью потенциалов U = 600 B попал в однородное магнитное поле с величиной магнитной индукции В = 0,3 Тл и начал двигаться по круговой траектории. Вычислить радиус окружности R по которой движется протон.
1. Протон обладает положительным элементарным зарядом q = |e| =1,6×1Кл и массой m = 1,67×1кг. Проходя ускоряющую разность потенциалов, протон приобретает скорость
 . (1)
. (1)
2. Запишем далее условия нахождения протона на круговой траектории радиуса R
 (2)
(2)
 . (3)
. (3)
3.7.10. Заряженная частица со скоростью v = 2×106 м/с влетает в однородное магнитное поле с индукцией B = 0,52 Тл. Определить, что это за частица, если известно, что она описала в магнитном поле окружность радиусом R = 4 см.
1. Запишем условие движения заряженной частицы в магнитном поле по круговой траектории
 . (1)
. (1)
2. Для частицы фиксированной величиной является удельный заряд, т. е. отношение заряда частицы к её массе. Определим это отношение для заданных условий
 . (2)
. (2)
3. Очевидно, что частицей является протон, обладающий зарядом |e| @ 1,6×1Кл и массой mp @ 1,67×1кг, потому что
 . (3)
. (3)
3.7.11. Заряженная частица, пройдя ускоряющую разность потенциалов U = 2000 В, движется в однородном магнитном поле с индукцией В = 15,1 мТл перпендикулярно линиям индукции. Найти удельный заряд частицы, если радиус окружности, которую она описала в поле, равен R = 1 см.
1. Запишем уравнение скорости, с которой частица влетает в магнитное поле, с учётом её разгона в электрическом поле
 . (1)
. (1)
2. Условие нахождения частицы на круговой орбите позволяет определить удельный заряд частицы и её линейную скорость
 (2)
(2)
 , (3)
, (3)

3.7.12. Частица, несущая электрический заряд, перемещается в однородном магнитном поле по круговой траектории радиуса R = 1 мм обладая при этом кинетической энергией К = 1 кэВ. Определить силу F, действующую на частицу со стороны поля.
1. Запишем уравнение кинетической энергии частицы и силовое условие её движения по круговой траектории
 , (1)
, (1)
 . (2)
. (2)
2. Сравнивая уравнения (1) и (2), можно видеть, что из уравнения (1) можно выразить комбинацию величин mv2 и подставить в уравнение (2)
 . (3)
. (3)
3.7.13. Электрон движется в однородном магнитном поле с индукцией В = 0,1 Тл перпендикулярно линиям индукции по траектории с радиусом кривизны z = 0,5 см. Определить силу Лоренца, действующую на частицу
1. Запишем условие нахождения электрона на криволинейной траектории и выразим из него скорость
 . (1)
. (1)
2. Подставим значение скорости в уравнение силы Лоренца
 , (2)
, (2)
где m @ 1×1кг – масса электрона, е @ 1,6×1Кл – заряд электрона.
3. Подставим величины, заданные по условию задачи и табличные данные в уравнение (2)
 . (3)
. (3)
3.7.14. Протон с кинетической энергией К = 1 МэВ влетел в однородное магнитное поле перпендикулярно линиям индукции (В = 1 Тл). Какое расстояние должен пройти электрон в области, занятой магнитным полем, чтобы изменить направление своего движения на противоположное?
1.Влетая в магнитное поле в точке А, перпендикулярно вектору магнитной индукции В, электрон начнёт под действием силы Лоренца двигаться по криволинейной траектории и описав полуокружность, в точке С будет иметь скорость противоположную по направлению начальной скорости. Задача, таким образом, сводится к определению радиуса кривизны траектории z.
2. Запишем условие нахождение протона на круговой орбите
 , (2)
, (2)
и выразим из него радиус кривизны z
 , (3)
, (3)
где |e| @ 1,6×1Кл – заряд протона, mp = 1,67×1кг – масса протона, v – скорость протона
3. Скорость электрона найдём по величине заданной кинетической энергии

 . (4)
. (4)
4. Подставим значение скорости из уравнения (4) в уравнение (3)
 . (5)
. (5)
5. Длина полуокружности l определится как
 . (6)
. (6)
3.7.15. Электрон движется по круговой траектории в однородном магнитном поле напряжённостью Н = 104 А/м. Определить период вращения электрона.
1. Период вращения электрона Т связан с его линейной скоростью и радиусом окружности, по которой он путешествует
 . (1)
. (1)
2. Подставим значение скорости в условия нахождения электрона на круговой орбите и разрешим полученное соотношение относительно искомой величины
 . (2)
. (2)
3.7.16. Определить частоту вращения n электрона по круговой орбите в однородном магнитном поле с индукцией В = 0,2 Тл.
1. Воспользуемся уравнением (2) предыдущей задачи, переписав его для частоты вращения n
 . (2)
. (2)
3.7.17. Два иона, имеющие одинаковый заряд и различные массы проходят одинаковую ускоряющую разность потенциалов, перед тем как попасть в однородное магнитное поле. При движении в пространстве, занятом полем ионы описывают окружности радиусами R1 = 5 см и R2 = 2,5 см. Найти отношение их масс m1/m2.
1. Определим скорости, приобретаемые ионами при прохождении ими ускоряющей разности потенциалов
 , (1)
, (1)
 . (2)
. (2)
2. Запишем далее условия движения электрона по круговой орбите
 . (3)
. (3)
3. Поскольку левые части уравнений (3) одинаковые, то их можно объединить. С учётом значения скоростей из уравнений (2), перепишем уравнение (3) следующим образом
 , (4)
, (4)
 , (5)
, (5)
 . (6)
. (6)
3.7.18. Электрон из состояния покоя, прошёл разность потенциалов U = 250 B и попал в однородное магнитное поле под углом a = 600 к линиям индукции (В = 0,51 Тл). Определить шаг винтовой линии h, по которой движется электрон в области пространства, занятого полем.

1. Определим величину скорости v0, приобретенную электроном при прохождении им ускоряющей разности потенциалов U
 , (1)
, (1)
 . (2)
. (2)
2. Запишем уравнения проекций скорости на выбранные оси координат, одна из которых, Оx совпадает с направлением вектора магнитной индукции В, а вторая Oy – перпендикулярна этому вектору
 . (3)
. (3)
3. Как это было принято в кинематике, сложное движение электрона целесообразно разложить на два более простых: на поступательное движение со скоростью vx = v0cosa и вращательное движение с линейной скоростью vy = v0sina.
4. Условие вращательного движения электрона определится в этом случае равенством
 . (4)
. (4)
5. Шаг спирали h, по которой движется электрон, определим из условия поступательного перемещения в течение периода
 . (5)
. (5)
6. Перепишем уравнение (4) таким образом, чтобы в него вошёл период Т
 . (6)
. (6)
7. С другой стороны, из уравнения (4) можно выразить радиус R
 . (7)
. (7)
8. Подставим далее значение периода обращения электрона Т из уравнения (7) в уравнение (5)
 (8)
(8)
3.7.19. Электрон движется в однородном магнитном поле с индукцией В = 9×10 – 3 Тл по винтовой линии радиусом R = 1 см и шагом h = 7,8 см. Определить период обращения электрона и его скорость.
1. Поскольку по условию задачи заданы радиус круговой орбиты и шаг винтовой линии, то электрон влетает в магнитное поле под некоторым углом по отношению к направлению вектора магнитной индукции.
2. Определим угол, под которым влетает электрон в магнитное поле из следующих соображений
 , (1)
, (1)
где Т – период вращения электрона, R – радиус орбиты вращательной составляющей движения, vx, vy – проекции скорости электрона v0 на оси координат, одна их которых, Ох совпадает с направлением вектора магнитной индукции, a – угол между вектором скорости электрона и вектором магнитной индукции
 . (2)
. (2)
3. Определим скорость, с которой электрон влетел в магнитное поле из условия его вращения по круговой орбите
 . (3)
. (3)
4. Период вращения электрона определится из чисто кинематических соображений
 (4)
(4)
3.7.20. Электрон движется по круговой траектории в однородном магнитном поле со скоростью v = 0,9 c (c = 3×108 м/с – скорость света в вакууме). Магнитная индукция поля В = 0,01 Тл. Определить радиус окружности с учётом увеличения массы электрона со скоростью.
1. Масса электрона при заданной скорости, в соответствии с уравнениями специальной теории относительности будет отличаться от его массы покоя m0 @ 1×1кг
 . (1)
. (1)
2. Запишем далее условие нахождения электрона на круговой орбите с учётом релятивистского увеличения массы
 , (2)
, (2)
где е @ 1,6×1Кл – заряд электрона, R – радиус окружности, по которой движется электрон.
3. Решим уравнение (2) относительно радиуса R
 . (3)
. (3)
4. Без учёта релятивистского увеличения массы электрона радиус его круговой орбиты составит
 . (4)
. (4)
3.8. Совместное действие электрических и магнитных полей
на заряженные частицы
3.8.1. Электрическое поле возбуждено перпендикулярно магнитному полю, причём, напряжённость электрического поля Е = 105 В/м, а индукция магнитного поля – В = 0,1 Тл. Перпендикулярно полям, не отклоняясь от прямолинейной траектории, движется заряженная частица. Определить скорость частицы.

1. Описанное движение частицы, несущей положительный заряд q возможно при равенстве модулей сил Кулона и Лоренца и их противоположном направлении, когда
 , (1)
, (1)
 . (2)
. (2)
3.8.2. Заряженная частица, двигаясь перпендикулярно скрещенным под прямым углом электрическому (Е = 4×105 В/м) и магнитному (В = 0,25 Тл) не испытывая отклонения при определённом значении скорости v. Определить значение скорости и возможные отклонения Dv от этой величины, если указанные параметры полей могут обеспечиваться с точностью, не превышающей 0,2%.
1. Величину скорости, при которой будет обеспечено движение частицы без отклонения от прямолинейной траектории, определим, воспользовавшись уравнением (2) предыдущей задачи
 . (1)
. (1)
2. Определим далее, заданные по условию задачи, величины отклонений напряжённости электрического поля и индукции магнитного поля
 (2)
(2)
 . (3)
. (3)
3. Диапазон скоростей Dv при которых будет обеспечиваться сохранение первоначального направления движения частицы
 . (4)
. (4)
3.8.3. Протон, будучи ускоренным разностью потенциалов U = 800 B, из состояния покоя, попадает в скрещенные под прямым углом поля. Магнитное поле имеет индукцию В = 50 мТл. При какой напряжённости электрического поля Е протон будет через пространство, занятое полями двигаться прямолинейно?
1. Определим скорость протона при его разгоне, полагая массу протона mp @ 1,67×1кг, заряд – qp = |e| @ 1,6×1Кл
 . (1)
. (1)
2. Как показано в двух предыдущих задачах, движение частицы будет прямолинейным в том случае когда
 (2)
(2)
откуда следует, что
 . (3)
. (3)
3.8.4. Циклотрон предназначен для разгона протонов до энергий порядка W @ 5 МэВ. Каков должен быть радиус дуантов R при индукции магнитного поля В = 1Тл?
1. Определим значение скорости протона (mp @ 1,67×1кг, |e| @ 1,6×1Кл) в циклотроне
 . (1)
. (1)
2. Запишем условия вращения протона по круговой орбите
 . (2)
. (2)
6.3. Магнитное поле на оси кругового тока
Напряженность магнитного поля на оси кругового тока (рис. 6.17-1), создаваемого элементом проводника Idl, равна

поскольку в данном случае


Рис. 6.17. Магнитное поле на оси кругового тока (слева) и электрическое поле на оси диполя (справа)
При интегрировании по витку вектор  будет описывать конус, так что в результате «выживет» только компонента поля вдоль оси 0z. Поэтому достаточно просуммировать величину
будет описывать конус, так что в результате «выживет» только компонента поля вдоль оси 0z. Поэтому достаточно просуммировать величину


выполняется с учетом того, что подынтегральная функция не зависит от переменной l, а

Соответственно, полная магнитная индукция на оси витка равна

В частности, в центре витка (h = 0) поле равно

На большом расстоянии от витка (h >> R) можно пренебречь единицей под радикалом в знаменателе. В результате получаем

Здесь мы использовали выражение для модуля магнитного момента витка Рm , равное произведению I на площадь витка  Магнитное поле образует с круговым током правовинтовую систему, так что (6.13) можно записать в векторной форме
Магнитное поле образует с круговым током правовинтовую систему, так что (6.13) можно записать в векторной форме

Для сравнения рассчитаем поле электрического диполя (рис. 6.17-2). Электрические поля от положительного и отрицательного зарядов равны, соответственно,

так что результирующее поле будет

На больших расстояниях (h >> l) имеем отсюда

Здесь мы использовали введенное в (3.5) понятие вектора электрического момента диполя  . Поле Е параллельно вектору дипольного момента, так что (6.16) можно записать в векторной форме
. Поле Е параллельно вектору дипольного момента, так что (6.16) можно записать в векторной форме

Аналогия с (6.14) очевидна.
Силовые линии магнитного поля кругового витка с током показаны на рис. 6.18. и 6.19

Рис. 6.18. Силовые линии магнитного поля кругового витка с током на небольших расстояниях от провода
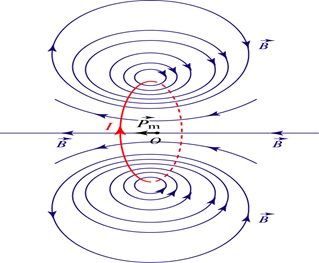
Рис. 6.19. Распределение силовых линий магнитного поля кругового витка с током в плоскости его оси симметрии.
Магнитный момент витка направлен по этой оси
На рис. 6.20 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг кругового витка с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.
Магнитные силовые линии для витка, ось которого лежит в плоскости пластинки, сгущаются внутри витка. Вблизи проводов они имеют кольцевую форму, а вдали от витка поле быстро спадает, так что опилки практически не ориентируются.

Рис. 6.20. Визуализация силовых линий магнитного поля вокруг кругового витка с током
Пример 1. Электрон в атоме водорода движется вокруг протона по окружности радиусом аB = 53 пм (эту величину называют радиусом Бора по имени одного из создателей квантовой механики, который первым вычислил радиус орбиты теоретически) (рис. 6.21). Найти силу эквивалентного кругового тока и магнитную индукцию В поля в центре окружности.

Рис. 6.21. Электрон в атоме водорода
Решение. Заряды электрона и протона одинаковы по величине (е) и противоположны по знаку. На электрон действует сила кулоновского притяжения протона, создающая центростремительное ускорение

откуда находим угловую скорость движения электрона по круговой орбите

Период обращения электрона вокруг ядра равен

Если представить себе воображаемую площадку, ортогональную траектории электрона, то за время Т через нее проходит заряд е. Поэтому сила эквивалентного тока равна

Скорость движения электрона равна v =  аB = 2,18·10 6 м/с. Движущийся заряд создает в центре орбиты магнитное поле
аB = 2,18·10 6 м/с. Движущийся заряд создает в центре орбиты магнитное поле

Этот же результат можно получить с помощью выражения (6.12) для поля в центре витка с током, силу которого мы нашли выше

Пример 2. Бесконечно длинный тонкий проводник с током 50 А имеет кольцеобразную петлю радиусом 10 см (рис. 6.22). Найти магнитную индукцию в центре петли.

Рис. 6.22. Магнитное поле длинного проводника с круговой петлей
Решение. Магнитное поле в центре петли создается бесконечно длинным прямолинейным проводом и кольцевым витком. Поле от прямолинейного провода направлено ортогонально плоскости рисунка «на нас», его величина равна (см. (6.9))

Поле, создаваемое кольцеобразной частью проводника, имеет то же направление и равно (см. 6.12)

Суммарное поле в центре витка будет равно

Дополнительная информация
Магнитное поле кругового тока
Рассмотрим магнитное поле постоянного тока /, текущего по проводу в форме окружности С радиуса а. Применим закон Био – Савара – Лапласа для определения магнитной индукции в центре кругового тока.
К расчету магнитного по^хя кругового тока
На рис. 6.2 изображены вектор dl, характеризующий произвольный малый
участок проводника с током, и вектор R , соединяющий этот участок с точкой О, в которой требуется определить магнитную инндукцию В . По определению векторного произведения из формулы (6.1)
следует, что вектор dB магнитной индукции поля, создаваемого рассматриваемым участком тока, перпендикулярен и
вектору dl , и вектору R . Таким образом, начало вектора dB находится в точке О, а сам вектор перпендикулярен плоскости контура С.
Так как векторы dl и R образуют прямой угол, модуль вектора dB согласно формуле (6.3) будет
Векторы dB магнитной индукции полей, создаваемых различными участками контура в точке О, совпадают по направлению. В таком случае их векторная сумма будет представлять собой вектор В , который имеет то же направление. При этом модуль этого вектора будет равен
сумме модулей векторов dB :
Интеграл от dl равен длине окружности:
Таким образом, придем к следующей формуле для магнитной индукции поля, создаваемого круговым током в центре окружности:
Модуль рт вектора магнитного момента кругового тока равен произведению силы тока на площадь круга:
Используя это соотношение, выражение (6.5) можно записать так:
В центре кругового витка с током вектор магнитной индукции направлен так же, как вектор магнитного момента рт. При этом справедливо соотношение
Отметим, что направление вектора магнитной индукции в центре кругового тока связано с направлением электрического тока правилом правого винта.
Линии в пространстве, к которым вектор В в любой точке является касательным, называются силовыми линиями магнитного поля. На рис. б.З изображены силовые линии магнитного поля кругового тока.
Рис. 6.8. Силовые линии магнитного поля кругового тока
[spoiler title=”источники:”]
http://online.mephi.ru/courses/physics/electricity/data/course/6/6.3.html
http://studme.org/312096/matematika_himiya_fizik/magnitnoe_pole_krugovogo_toka
[/spoiler]
Итак, элементарным током мы будем называть замкнутый ток, который удовлетворяет следующим условиям:
- Размеры контура бесконечно малы в сравнении с расстоянием до точек, в которых необходимо рассмотреть поле.
- Величины, которые характеризуют внешнее поле, постоянны (Точнее постоянны значения магнитной индукции и ее пространственные производные). Для любого замкнутого тока можно создать условия, при которых его считают элементарным.
Векторный потенциал элементарного тока
Выберем контур в виде параллелограмма, стороны которого $l_1,l_2, l_3,l_4 $(рис.1). Начало координат поместим в точку О на поверхности внутри параллелограмма. Так как параллелограмм бесконечно малый, то конкретное место положения точки значения не имеет.
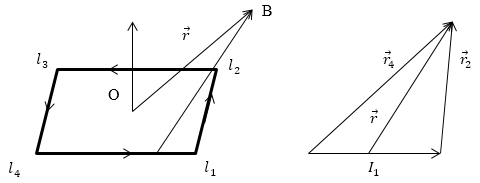
Рис. 1
Векторный потенциал магнитного поля ($overrightarrow{A}$) в точке B с радиус-вектором $overrightarrow{r}$ равен:
[overrightarrow{A}left(overrightarrow{r}right)=frac{{mu }_0}{4pi }Iintlimits_{l_1l_2l_3l_4}{frac{overrightarrow{dl}}{r}}left(1right).]
Так как параллелограмм маленький, то значение r можно считать постоянным и равным расстоянию от середины стороны параллелограмма до точки, в которой ищем поле. Соответственно перепишем уравнение (1):
[overrightarrow{A}left(overrightarrow{r}right)=frac{{mu }_0}{4pi }Ileft(frac{1}{r_1}intlimits_{l_1}{overrightarrow{dl}}+frac{1}{r_2}intlimits_{l_2}{overrightarrow{dl}}+frac{1}{r_3}intlimits_{l_3}{overrightarrow{dl}}+frac{1}{r_4}intlimits_{l_4}{overrightarrow{dl}}right)=frac{{mu }_0}{4pi }Ileft(frac{I_1}{r_1}+frac{I_2}{r_2}+frac{I_3}{r_3}+frac{I_4}{r_4}right)(2).]
Учтем, что:
[I_1=-I_3, I_2=-I_4left(3right).]
Для того чтобы преобразовать выражение (2) найдем:
[frac{I_1}{r_1}+frac{I_3}{r_3}=I_1left(frac{r_3-r_1}{r_1r_3}right)approx frac{I_1left(-{overrightarrow{l}}_2cdot overrightarrow{r}right)}{r^3},]
[frac{I_2}{r_2}+frac{I_4}{r_4}=I_2left(frac{r_4-r_2}{r_2r_4}right)approx frac{I_2left({overrightarrow{l}}_1cdot overrightarrow{r}right)}{r^3}left(4right),]
где бесконечно малыми величинами высоких порядков пренебрегаем. На рис.1 показаны геометрические построения для разъяснения того как получены равенства:
[overrightarrow{r_4}=overrightarrow{l_1}+overrightarrow{r_2}left(5right).]
Из равенства (5) получим:
[{r_4}^2={l_1}^2+{r_2}^2+2overrightarrow{l_1}overrightarrow{r_2}left(6right).]
Из уравнения (6) получим:
[{r_4}^2-{r_2}^2={l_1}^2+2overrightarrow{l_1}overrightarrow{r_2}to r_4-r_2=frac{{l_1}^2+2overrightarrow{l_1}overrightarrow{r_2}}{r_4+r_2}approx frac{overrightarrow{l_1}overrightarrow{r_2}}{r}left(7right).]
В выражении (7) мы сохранили члены только первого порядка малости по $overrightarrow{l_1}$. Таким образом, получено выражение (4). С учетом (4) выражение для векторного магнитного потенциала (2) примет вид:
[overrightarrow{A}left(overrightarrow{r}right)=frac{{mu }_0}{4pi }frac{I}{r^3}left[I_2left({overrightarrow{l}}_1overrightarrow{r}right)-I_1left({overrightarrow{l}}_2overrightarrow{r}right)right]=frac{{mu }_0}{4pi }frac{I}{r^3}left({overrightarrow{l}}_1times {overrightarrow{l}}_2right)times overrightarrow{r}left(8right),]
где использовано известное равенство их векторной алгебры:
[overrightarrow{A}times left(overrightarrow{B}times overrightarrow{C}right)=overrightarrow{B}left(overrightarrow{A}overrightarrow{C}right)-overrightarrow{C}left(overrightarrow{A}overrightarrow{B}right)left(9right).]
Используем то, что вектор элемента поверхности, которая обтекается током, равна:
[{overrightarrow{l}}_1times {overrightarrow{l}}_2=overrightarrow{S}left(10right).]
Перепишем уравнение (8), получим:
[overrightarrow{A}left(overrightarrow{r}right)=frac{mu_0}{4pi}frac{Ioverrightarrow{S} times overrightarrow{r}}{r^3}left(11right).]
Магнитный момент элементарного тока
Произведение:
[Ioverrightarrow{S}=overrightarrow{p_m}(12)]
называется магнитным моментом элементарного тока.
Из (12) очевидно, что эта величина по модулю равна произведению силы тока, который течет в контуре на площадь, которая охвачена им. Направление магнитного момента совпадает с положительной нормалью к поверхности S. Если использовать в записи векторного магнитного потенциала магнитный момент элементарного тока, то выражение (11) примет вид:
[overrightarrow{A}left(overrightarrow{r}right)=frac{{mu }_0}{4pi }frac{overrightarrow{p_m}times overrightarrow{r}}{r^3}left(13right).]
Основная единица измерения магнитного момента – $Аcdot м^2.$
Пример 2
Задание: Найдите магнитный момент $p_m $кругового витка с током если модуль вектора магнитной индукции в точке А равен В. Расстояние от центра кольца до точки А равно d (рис.2). Считайте ток элементарным.
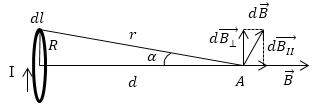
Рис. 2
Решение:
Выделим на круговом витке в током элемент тока $Idl$ . Для этого элемента запишем закон Био-Савара — Лапласа для вакуума, чтобы найти поле, которое создает этот ток в точке А:
[dB=frac{{mu }_0}{4pi }frac{Idl}{r^2}=frac{{mu }_0}{4pi }cdot frac{Idl}{R^2+d^2} left(2.1right),]
где $r$ — расстояние от $dl$ до точки A, $r^2=R^2+d^2, R$ — радиус витка с током.
[{dB}_{II}=Bsinalpha , sinalpha =frac{R}{sqrt{R^2+d^2}}left(2.2right).]
Подставим (2.1) в (2.2) получим:
[{dB}_{II}=frac{mu_0}{4pi}frac{IRdl}{{left(R^2+d^2right)}^{{3}/{2}}}left(2.3right).]
Используя принцип суперпозиции найдем полное поле, которое создает элементарный ток (виток с током) в точке А:
[B_{II}=intlimits^{2pi R}_0{frac{{mu }_0}{4pi }frac{IRdl}{{left(R^2+d^2right)}^{{3}/{2}}}}=frac{{mu }_0}{2}cdot frac{IR^2}{{left(R^2+d^2right)}^{{3}/{2}}}left(2.4right).]
В силу симметрии суммарный вклад в магнитную индукцию составляющей $B_{bot }равен нулю$. Следовательно, можно запить, что магнитная индукция поля в точке А равна:
[B=frac{{mu }_0}{2}cdot frac{IR}{{left(R^2+d^2right)}^{{3}/{2}}}left(2.5right).]
По условию, мы имеем дело с элементарным током, следовательно, $Rll d$. В таком случае, (2.5) преобразуется в формулу:
[B=frac{{mu }_0}{2}cdot frac{IR^2}{d^3}left(2.6right).]
Магнитный момент контура определен как:
[p_m=IS=Ipi R^2left(2.7right).]
Из (2.6) получим, что:
[IR^2=frac{2Bd^3}{{mu }_0}to p_m=frac{2pi Bd^3}{{mu }_0}.]
Ответ: $p_m=frac{2pi Bd^3}{{mu }_0}.$
Магнитный момент витка. Определение. Формула. Опыт
- admin
- 03.01.2022
- 0 comments
Магнитный момент витка с током это физическая величина, как и любой другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита.

Рисунок — 1 круговой виток с током
Круговой виток с током можно представить в виде короткого магнита. Причем этот магнит будет направлен перпендикулярно плоскости витка. Расположение полюсов такого магнита определяется с помощью правила буравчика. Согласно которому северный плюс будет находиться за плоскостью витка, если ток в нем будет двигаться по часовой стрелке.

Рисунок— 2 Воображаемый полосовой магнит на оси витка
На этот магнит, то есть на наш круговой виток с током, как и на любой другой магнит, будет воздействовать внешнее магнитное поле. Если это поле будет однородным, то возникнет вращающий момент, который будет стремиться развернуть виток. Поле буде поворачивать виток так чтобы его ось расположилась вдоль поля. При этом силовые линии самого витка, как маленького магнита, должны совпасть по направлению с внешним полем.
Если же внешнее поле будет не однородным, то к вращающему моменту добавится и поступательное движение. Это движение возникнет вследствие того что участки поля с большей индукцией будут притягивать наш магнит в виде витка больше чем участки с меньшей индукцией. И виток начнет двигаться в сторону поля с большей индукцией.
Величину магнитного момента кругового витка с током можно определить по формуле.
Формула — 1 Магнитный момент витка
Где, I ток протекающий по витку
S площадь витка с током
n нормаль к плоскости в которой находится виток
Таким образом, из формулы видно, что магнитный момент витка это векторная величина. То есть кроме величины силы, то есть ее модуля он обладает еще и направлением. Данное свойство магнитный момент получил из-за того что в его состав входит вектор нормали к плоскости витка.
Для закрепления материала можно провести несложный опыт. Для этого нам понадобится круговой виток, из медной проволоки подключённый к батареи питания. При этом подводящие провода должны быть достаточно тонкими и желательно свиты между собой. Это уменьшит их влияние на опыт.

Рисунок — 3 проволочный виток
Теперь подвесим виток на подводящих проводах в однородном магнитном поле, созданном скажем постоянными магнитами. Виток пока обесточен, и его плоскость располагается параллельно силовым линиям поля. При этом его ось и полюса воображаемого магнита будут перпендикулярны линиям внешнего поля.

Рисунок — 4 виток в однородном магнитном поле
При подаче тока на виток его плоскость повернется перпендикулярно силовым линиям постоянного магнита, а ось станет им параллельна. Причем направление поворота витка будет определяться правилом буравчика. А строго говоря, направлением, в котором течет ток по витку.
