Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
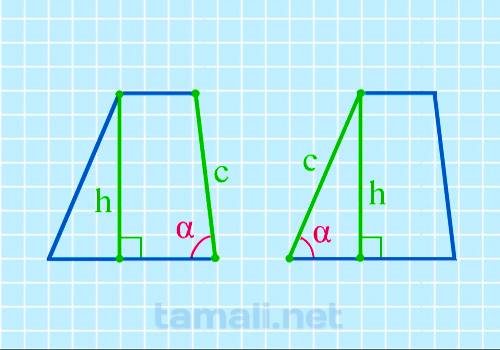
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
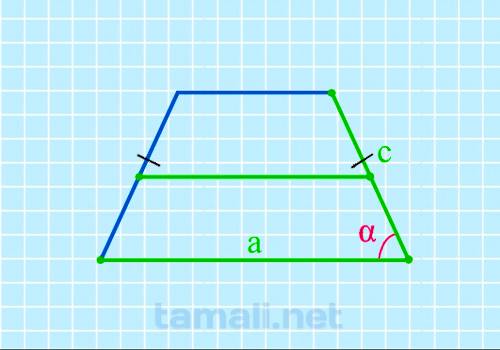
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
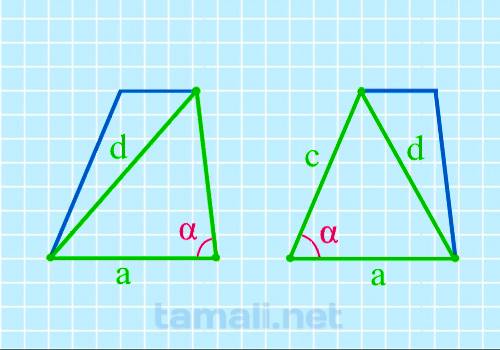
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
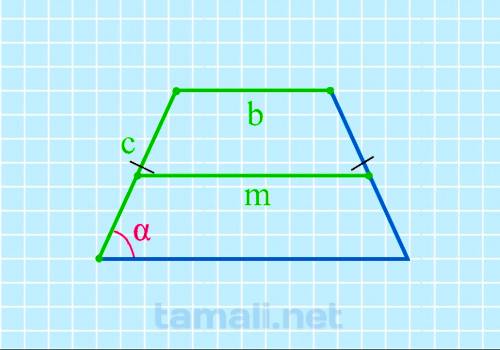
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
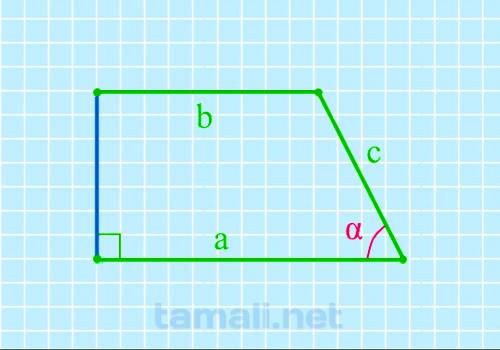
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
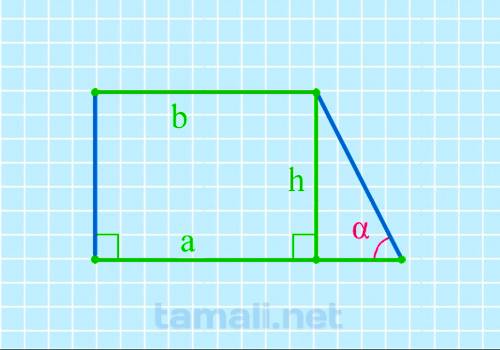
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
Как найти угол в трапеции
Трапеция – это плоский четырехугольник, у которого две противолежащие стороны параллельны. Они называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Инструкция
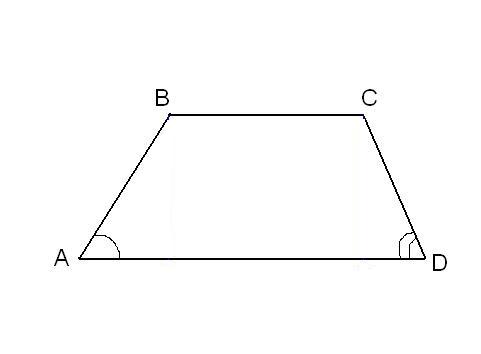
Задача нахождения произвольного угла в трапеции требует достаточного количества дополнительных данных. Рассмотрим пример, в котором известны два угла при основании трапеции. Пусть известны углы ∠BAD и ∠CDA, найдем углы ∠ABC и ∠BCD. Трапеция обладает таким свойством, что сумма углов при каждой боковой стороне равна 180°. Тогда ∠ABC = 180°-∠BAD, а ∠BCD = 180°-∠CDA.
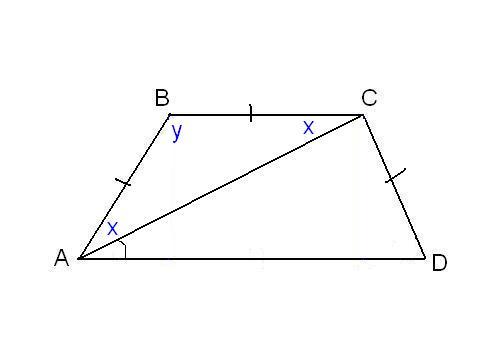
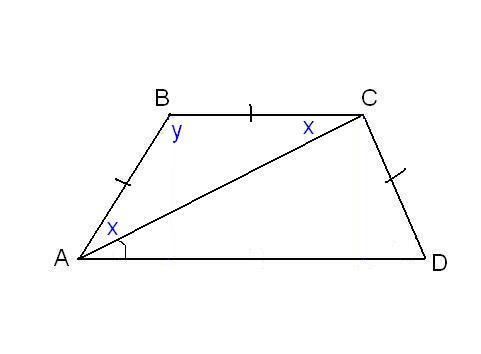
В другой задаче может быть указано равенство сторон трапеции и какие-нибудь дополнительные углы. Например, как на рисунке, может быть известно, что стороны AB, BC и CD равны, а диагональ составляет с нижним основанием угол ∠CAD = α.Рассмотрим треугольник ABC, он равнобедренный, так как AB = BC. Тогда ∠BAC = ∠BCA. Обозначим его x для краткости, а ∠ABC – y. Сумма углов любого треугольника равна 180°, из этого следует, что 2x + y = 180°, тогда y = 180° – 2x. В то же время из свойств трапеции: y + x + α = 180° и следовательно 180° – 2x + x + α = 180°. Таким образом, x = α. Мы нашли два угла трапеции: ∠BAC = 2x = 2α и ∠ABC = y = 180° – 2α.Так как AB = CD по условию, то трапеция равнобокая или равнобедренная. Значит, диагонали равны и равны углы при основаниях. Таким образом, ∠CDA = 2α, а ∠BCD = 180° – 2α.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.
Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.
Теперь применим это знание для решения задач из ОГЭ.
Задача №1
Для решения, воспользуемся свойством односторонних углов.
Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119
Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.
Точно также решается задача №2 с трапецией.
Меньший угол – это острый угол. Значит 180-131=49
Задача №3
Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.
Найдем меньший угол параллелограмма – он острый, равен 180-105=75
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Для этой теоремы подходят следующие задачи:
Задача №4
Решение:
Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66
Задача №5
Решение:
Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.
Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80
В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
как найти углы трапеции?
Мастер
(1553),
закрыт
14 лет назад
Дополнен 14 лет назад
ДАНО:
ВС-меньшее основание
На отрезке AD взята точка E, так что BE параллельна CD.
УГОЛ ABE=70 ГРАДУСОВ
УГОЛ BEA=50 ГРАДУСОВ
НАЙТИ:УГЛЫ ТРАПЕЦИИ
Елена
Мастер
(2376)
14 лет назад
у трапеции углы у оснований равны. Общая сумма углов – 360 градусов. Если известен хотя бы один угол (напр. угол у нижнего основания) , то второй угол у того же основания равен этому углу.
Сумму этих углов вычитаешь из 360 град, а полученное число делишь пополам. Это и будут углы у верхнего основания.
Это общее правило. А теперь решение.
В треугольнике АВЕ угол В = 70 град. , угол Е = 50 град. Сумма углов треугольника = 180 град.
Угол А = 180 – (70 + 50) = 60 град.
То есть углы А и Д трапеции по 60 град. Теперь ищем углы В и С трапеции (то есть АВС и ВСД)
360 – (60 + 60) = 240
240 : 2 = 120
Итого углы: А = 60 гр, В = 120 гр, С = 120 гр, Д = 60 гр
ЕленаМастер (2376)
14 лет назад
Kilimanjaro, я дико извиняюсь, лоханулась капитально. Ответ неправильный, это решение – для равнобедренной трапеции.
Спасибо Александру Шапошникову.
Павильный ответ
угол DAB=60
угол ABC=120
угол CDA=50
угол BCD=130.
Так что на лучший ответ я не заслуживаю. Выбери кого-то из тех, кто ответил правильно. Извини еще раз за то, что сбила тебя с толку
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
-
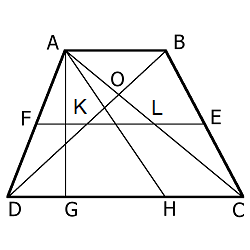
Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме
$$
FE = {AB + DC over 2}
$$ -
Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
-
Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е.
$$
KL = {DC – AB over 2}
$$ - Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции

- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции

Площадь трапеции через основания и высоту
$$
S = {AB + DC over 2} * AG
$$
Площадь трапеции через среднюю линию и высоту
$$
S = FE * AG
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC * BD over 2} * sin(∠AOD) = {AC * BD over 2} * sin(∠AOB)
$$
Площадь трапеции через четыре стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 – ({(DC – AB)^2 + AD^2 – BC^2 over 2 * (DC – AB)})^2}
$$
Формулы площади равнобедренной трапеции


Площадь трапеции через стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 – {(DC – AB)^2 over 4}}
$$
Площадь трапеции через стороны и угол
$$
S = AD * sin(∠ADC) * (DC – AD * cos(∠ADC))
$$
$$
S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC))
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC^2 over 2} * sin(∠AOD) = {AC^2 over 2} * sin(∠BOC)
$$
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$
S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB)
$$
Площадь трапеции если в нее вписана окружность
$$
S = {4 * R_В^2 over sin(∠ADC)} = {4 * R_В^2 over sin(∠DAB)}
$$
$$
S = {AB * DC over sin(∠ADC)} = {AB * DC over sin(∠DAB)}
$$
Формулы сторон произвольной трапеции

Основание через другое основание и среднюю линию
$$
AB = 2 * FE – DC
$$
$$
DC = 2 * FE – AB
$$
Основание через другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AG} * sin(∠AOD) – AB
$$
$$
AB = {AC * BD over AG} * sin(∠AOD) – DC
$$
Длины сторон
$$
DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
AB = DC – AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD)
$$
$$
AB = DC – AD * cos(∠ADC) – BC * cos(∠BCD)
$$
$$
AD = {AG over sin(∠ADC)}
$$
$$
BC = {AG over sin(∠BCD)}
$$
Формулы сторон равнобедренной трапеции


Длины сторон
$$
AD = {AG over sin(∠ADC)}
$$
$$
AD = {DC – AB over 2 * cos(∠ADC)}
$$
$$
DC = AB + 2 * AG * ctg(∠ADC)
$$
$$
AB = DC – 2 * AG * ctg(∠ADC)
$$
$$
DC = AB + 2 * AB * cos(∠ADC)
$$
$$
AB = DC – 2 * AB * cos(∠ADC)
$$
Длина основания через диагональ, боковую сторону и другое основание
$$
DC = {AC^2 – DA^2 over AB}
$$
$$
AB = {AC^2 – DA^2 over DC}
$$
Длина боковой стороны через диагональ и основания
$$
AD = sqrt{AC^2 – AB * DC}
$$
Длина основания через высоту, другое основание, диагонали и угол между ними
$$
DC = {AC^2 over AG} * sin(∠AOD) – AB
$$
$$
AB = {AC^2 over AG} * sin(∠AOD) – DC
$$
Длина основания через высоту, другое основание и площадь трапеции
$$
DC = {2 * S over AG} – AB
$$
$$
AB = {2 * S over AG} – DC
$$
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
$$
AD = {S over FE * sin(∠ADC)} = {S over FE * sin(∠DAB)}
$$
Длина боковой стороны через площадь трапеции, основания и угол при основании
$$
AD = {2 * S over (AB + DC) * sin(∠ADC)}
$$
$$
AD = {2 * S over (AB + DC) * sin(∠DAB)}
$$
Формулы сторон прямоугольной трапеции

Длины оснований
$$
DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD)
$$
$$
AB = DC – BC * cos(∠BCD) = DC – AD * ctg(∠BCD)
$$
$$
DC = AB + sqrt{BC^2 – AD^2}
$$
$$
AB = DC – sqrt{BC^2 – AD^2}
$$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AD} * sin(∠AOD) – AB
$$
$$
AB = {AC * BD over AD} * sin(∠AOD) – DC
$$
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG)
$$
DC = {2 * S over AD} – AB
$$
$$
AB = {2 * S over AD} – DC
$$
Формулы диагоналей произвольной трапеции

Длина диагоналей через четыре стороны
$$
BD = sqrt{BC^2 + DC * AB – {DC * (BC^2 – AD^2) over DC – AB}}
$$
$$
AC = sqrt{AD^2 + DC * AB – {DC * (AD^2 – BC^2) over DC – AB}}
$$
Длина диагоналей по теореме косинусов
$$
BD = sqrt{DC^2 + BC^2 – 2 * DC * BC * cos(∠BCD)}
$$
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * AD * cos(∠ADC)}
$$
Длина диагоналей через высоту
$$
BD = sqrt{AG^2 + (DC – AG * ctg(∠BCD))^2}
$$
$$
BD = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
$$
BD = sqrt{DC^2 + BC^2 – 2 * DC * sqrt{BC^2 – AG^2}}
$$
$$
AC = sqrt{AG^2 + (DC – AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2}
$$
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * sqrt{AD^2 – AG^2}}
$$
Длина диагоналей через стороны и другую диагональ
$$
BD = sqrt{AD^2 + BC^2 + 2 * DC * AB – AC^2}
$$
$$
AC = sqrt{AD^2 + BC^2 + 2 * DC * AB – BD^2}
$$
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
$$
BD = {AG * (DC + AB) over AC * sin(∠AOD)}
$$
$$
AC = {AG * (DC + AB) over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
$$
BD = {2 * S over AC * sin(∠AOD)}
$$
$$
AC = {2 * S over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
$$
BD = {2 * FE * AG over AC * sin(∠AOD)}
$$
$$
AC = {2 * FE * AG over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Формулы диагоналей равнобедренной трапеции


Длина диагоналей через стороны
$$
AC = sqrt{AD^2 + AB * DC}
$$
Длина диагоналей по теореме косинусов
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * AD * cos(∠ADC)}
$$
$$
AC = sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 – 2 * AB * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)}
$$
Длина диагоналей
$$
AC = sqrt{AG^2 + FE^2}
$$
$$
AC = sqrt{AG^2 + {(DC + AB)^2 over 4 }}
$$
$$
AC = sqrt{{AG * (AB + DC) over sin(∠AOD)}} = sqrt{{2 * S over sin(∠AOD)}} = sqrt{{2 * FE * AG over sin(∠AOD)}}
$$
Длина диагоналей через высоту основание и угол при основании
$$
AC = sqrt{AG^2 + (DC – AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
Длина диагоналей через сторону и высоту
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * sqrt{AD^2 – AG^2}}
$$
Формулы диагоналей прямоугольной трапеции

$$
BD = sqrt{AD^2 + AB^2}
$$
$$
AC = sqrt{AC^2 + DC^2}
$$
Формулы средней линии произвольной трапеции

Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC – AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и высоту
$$
FE = {S over AG}
$$
Формулы средней линии равнобедренной трапеции


Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC – AG * ctg(∠ADC) = AB + AG * ctg(∠ADC)
$$
Длина средней линии через основания, боковую сторону и высоту
$$
FE = DC – sqrt{AD^2 – AG^2} = AB + sqrt{AD^2 – AG^2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC^2 over 2 * AG} * sin(∠AOD) = {AC^2 over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и боковую сторону
$$
FE = {S over AD * sin(∠ADC)}
$$
Формулы средней линии прямоугольной трапеции

Длина средней линии через основания, высоту и угол при нижнем основании
$$
FE = DC – AG * {ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠BCD) over 2}
$$
Длина средней линии через основания, боковую сторону и угол при нижнем основании
$$
FE = DC – BC * {cos(∠BCD) over 2}
$$
$$
FE = AB + BC * {cos(∠BCD) over 2}
$$
Длина средней линии через основания и боковые стороны
$$
FE = DC – {sqrt{BC^2 – AD^2} over 2}
$$
$$
FE = AB + {sqrt{BC^2 – AD^2} over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Формулы высоты произвольной трапеции

Длина высоты через четыре стороны
$$
AG = sqrt{AD^2 – ({(DC – AB)^2 + AD^2 – BC^2 over 2 * (DC – AB)})^2}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC) = BC * sin(∠BCD)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC * BD over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC * BD over AB + DC} * sin(∠AOB)
$$
Длина высоты через среднюю линию, диагонали и углы между ними
$$
AG = {AC * BD over 2 * FE} * sin(∠AOD)
$$
$$
AG = {AC * BD over 2 * FE} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы высоты равнобедренной трапеции


Длина высоты через по сторонам
$$
AG = sqrt{AD^2 – {(DC – AB)^2 over 4}}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC)
$$
Длина высоты через основания и прилегающий угол к основанию
$$
AG = {DC – AB over 2} * tg(∠ADC)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC^2 over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC^2 over AB + DC} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы боковых сторон прямоугольной трапеции

Сторона AD
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
$$
BC = sqrt{AD^2 + (DC – AB)^2}
$$
Сторона BC через основания и угол ∠BCD
$$
BC = {DC – AB over cos(∠BCD)}
$$
Сторона BC через Сторону AD
$$
BC = {AD over sin(∠BCD)}
$$
Сторона BC через площадь, среднюю линию и угол ∠BCD
$$
BC = {S over FE * sin(∠BCD)}
$$
Сторона BC через площадь, основания и угол ∠BCD
$$
BC = {2 * S over (AB + DC) * sin(∠BCD)}
$$
