Лабораторная
работа №3
Решение логических
задач школьного курса повышенной
сложности
Алгебра логики – раздел математической
логики, изучающий высказывания,
рассматриваемые со стороны их логических
значений (истинности или ложности), и
логические операции над ними. Алгебра
логики возникла в середине 19 века в
трудах Дж. Буля и развивалась затем в
работах Ч. Пирса, П. С. Порецкого, Б.
Рассела, Д. Гильберта и др. Создание
алгебры логики представляло собой
попытку решать традиционные логические
задачи алгебраическими методами. С
появлением теории множеств (70-е гг. 19
в.) и дальнейшим развитием математической
логики (последняя четверть 19 в. — 1-я
половина 20 в.), предмет алгебры логики
значительно изменился. Основным предметом
алгебры логики стали высказывания. Под
высказыванием понимается каждое
предложение, относительно которого
имеет смысл утверждать, истинно оно или
ложно. Примеры высказываний: «кит —
животное», «все углы — прямые» и т.п.
Первое из этих высказываний является,
очевидно, истинным, а второе — ложным.
Употребляемые в обычной речи логические
связки «и», «или», «если…, то…»,
«эквивалентно», частица «не» и т. д.
позволяют из уже заданных высказываний
строить новые, более «сложные»
высказывания. Истинность или ложность
получаемых таким образом высказываний
зависит от истинности и ложности исходных
высказываний и соответствующей трактовки
связок как операций над высказываниями.
В отличие от обычной алгебры, изучающей
математические функции, алгебра логики
изучает логические функции. Известно,
что функция — это закон соответствия
между переменными. Следовательно,
логическая функция— это закон
соответствия между логическими
переменными.Логическая переменная— это такая переменная, которая может
принимать одно из двух возможных
значений: 0 («ложь») и 1 («истина»).
Логическим выражением называется
выражение, о котором можно сказать
истинно оно или ложно.
Примеры:
«5>8» – логическое выражение, т.к. о нем
можно сказать, что оно ложно.
«Эту девочку зовут Юля» – логическое
выражение.
«Подайте книгу» – это не логическое
выражение, т.к. о нем нельзя сказать,
истинно оно или ложно
Логическая функция может также принимать
два значения.
Таким образом, логические переменные
и функции определены на множестве двух
значений — {0,1}.
ЭВМ строятся из компонентов с двумя
устойчивыми состояниями. Одно состояние
обозначается нулем, другое — единицей.
На такие компоненты воздействуют
двоичные сигналы. Под воздействием
сигналов компоненты изменяют свои
состояния, т. е. состояние компонентов
или значения их выходных сигналов
зависят от значений воздействующих
сигналов. Очевидно, что функционирование
компонентов ЭВМ следует описывать
логическими функциями. По этой причине
алгебра логики находит непосредственное
и широкое применение при разработке и
использовании средств электронной
вычислительной техники.
Логические функции характеризуются
(задаются) так называемыми таблицами
истинности, или соответствия. Таблица
истинности— это таблица, устанавливающая
соответствие между возможными наборами
значений логических переменных и
значениями функций.
Основные логические функции
Функция
отрицания
Отрицание – это логическая функция от
одной переменной, которая принимает
единичное значение при нулевом значении
переменной и наоборот. Запись этой
функции:
F=![]() .
.
Конъюнкция может быть обозначена
следующими символами:
¬,¯, не, not.
Черта над переменной xявляется признаком отрицания (инверсии).
Таблица истинности этой функции
представлена на рис. 1а. Функция логического
отрицания описывает функционирование
логического элемента НЕ (рис. 1б).
Условно-графическое обозначение элемента
НЕ приведено на рис. 1в. Единичный сигнал
на выходе элемента НЕ появляется при
нулевом сигнале на входе (x=0,F=1) и, наоборот, нулевой
сигнал на выходе появляется при единичном
сигнале на входе (x=1,F=0). Графически отрицание
можно представить с помощью кругов
Эйлера (рис. 2).
а) б) в)
|
x |
F |
|
0 |
1 |
|
1 |
0 |
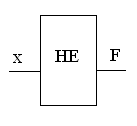
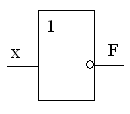
Рис. 1. Элемент НЕ

Рис. 2. Графическое представление
отрицания на множестве
Функция
логического умножения (конъюнкция)
Логическое умножение – это логическая
функция, по крайней мере, от двух
переменных, которая принимает единичное
значение при единичных значениях всех
переменных. Эта функция называется
также конъюнкцией. Элементарная
конъюнкция зависит от двух переменных.
Она принимает единичное значение только
тогда, когда и первая переменная и вторая
переменная равны единице. Возможны
различные варианты записи конъюнкции:
F=![]()
![]()
![]() ;F=
;F=![]() •
•![]() ;F=
;F=![]()
![]() ;F=
;F=![]() &
&![]() .
.
Конъюнкция может быть обозначена
следующими символами:
![]() ,
,
&, •, ∩, and, и.
Конъюнкция характеризуется таблицей
истинности, представленной на рис. 3а.
Из рассмотрения таблицы следует, что
эта функция принимает единичное значение
на наборе 4. Логическое умножение
описывает работу элемента И (рис. 3б).
Графически конъюнкцию можно представить
с помощью кругов Эйлера (рис. 4).
а)
б) в)
|
|
|
F |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
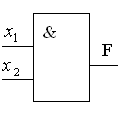
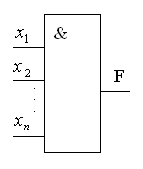
Рис. 3. Элемент И

Рис. 4. Графическое представление
конъюнкции на множествах
Конъюнкция на числовых множествах
(операция пересечения): {a,b,c}
![]() {b,c,d,e}={b,c}.
{b,c,d,e}={b,c}.
Единичный сигнал появляется на выходе
этого элемента только при наличии
единичного сигнала и на входе 1, и на
входе 2.
В общем случае элемент И может иметь n
входов (рис. 3в). При этом он реализует
конъюнкцию от n переменных, т.е.:
F=![]() •
•![]() •
•![]() •…•
•…•![]() .
.
Функция
логического сложения (дизъюнкция)
Логическое сложение – это логическая
функция, по крайней мере, от двух
переменных, которая принимает нулевое
значение при нулевых значениях всех
переменных. Эта функция называется
также дизъюнкцией. Таблица истинности
элементарной дизъюнкции представлена
на рис. 3а. Элементарная дизъюнкция
принимает единичное значение на наборах
1, 2, 3 и нулевое значение – только на
наборе 0. Функция записывается в одном
из двух видов: F=![]()
![]()
![]() илиF=
илиF=![]() +
+![]() .
.
Знак «плюс» не является алгебраическим,
т.к. при
![]() =1,
=1,
![]() =1
=1
дизъюнкцияF=![]() +
+![]() =1
=1
Дизъюнкция может быть обозначена
следующими символами:
![]() ,
,
+,![]() ,
,
or, или.
Дизъюнкция описывает функционирование
элемента ИЛИ (рис. 5б). Единичный сигнал
на выходе этого элемента возникает
тогда, когда или на входе 1, или на входе
2, или на двух входах единичные сигналы.
И только в том случае, когда на оба входа
поступают нулевые сигналы, на выходе
элементов появляется нулевой сигнал.
В общем случае элемент ИЛИ может иметь
n входов (рис. 5в). При этом он реализует
дизъюнкцию от n переменных.
а) б) в)
|
|
|
F |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
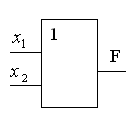
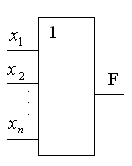
Рис. 5. Элемент ИЛИ

Рис. 6. Графическое представление
дизъюнкции на множествах
Дизъюнкция на числовых множествах
(операция объединения):
{a,b,c}![]() {b,c,d,e}={a,b,c,d,e}.
{b,c,d,e}={a,b,c,d,e}.
Равнозначность
(эквиваленция)
Равнозначность – это логическая функция
от двух переменных, которая принимает
единичное значение при одинаковых
значениях переменных. Одинаковые по
значению переменные называются
равнозначными, поэтому функция носит
название «равнозначность».
Запись функции:
F=![]()
![]() +
+![]()
![]() .
.
Таблица истинности функции равнозначности
представлена на рис. 7а. Эта функция
реализуется элементом равнозначности
(сравнения), который показан на рис. 7б.
Эквиваленция может быть обозначена
следующими символами:
~,
![]() ,
,![]() ,
,![]() .
.
Элемент используется для сравнения
двоичных сигналов.
|
|
|
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |

а)
б)
Рис. 7. Элемент равнозначности
Логическое
следование (импликация)
Обозначение логического следования:
F=![]() →
→![]() .
.
Высказывание F=![]() →
→![]() будем
будем
считать истинным во всех случаях, кроме
случая, когда![]() истинно, а
истинно, а![]() ложно. Таблица истинности представлена
ложно. Таблица истинности представлена
на рис. 8.
|
|
|
F= |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Рис. 8. Элемент импликации
Импликация может быть обозначена
следующими символами:→, ,.
Элемент
(штрих) Шеффера
Обозначение:
![]()
![]() ;
;![]() .
.
Другое название этой функции: «И-НЕ».
Высказывание
![]()
![]() будем считать ложным, когда
будем считать ложным, когда![]() и
и![]() равны единице. Таблица истинности
равны единице. Таблица истинности
представлена на рис. 9.
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Рис. 9. Элемент (штрих) Шеффера
Элемент
Вебба (стрелка Пирса)
Обозначение:
![]() ;
;![]() .
.
Высказывание
![]() будем считать истинным только тогда,
будем считать истинным только тогда,
когда оба операнда![]() и
и![]() равны нулю. Таблица истинности представлена
равны нулю. Таблица истинности представлена
на рис.10.
Другое название этой функции: «ИЛИ-НЕ».
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Рис. 10. Элемент Вебба (стрелка Пирса)
Сложение
по модулю 2.
Обозначение:
![]() ;
;![]() ;
;![]() XOR
XOR
![]() .
.
Высказывание
![]() будем считать истинным, если первый
будем считать истинным, если первый
операнд![]() не равен второму операнду
не равен второму операнду![]() .
.
Таблица истинности представлена на
рис. 11.
Другие названия этой функции: «исключающее
ИЛИ», «логическое ЛИБО», «неравносильность»,
«неэквивалентность», «логическое
сложение», «булево сложение».
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Рис. 11. Сложение по модулю 2
Коимпликация
Обозначение:
![]() ;
;![]() .
.
Высказывание
![]() будем считать истинным, если первый
будем считать истинным, если первый
операнд![]() равен 1, а второй операнд
равен 1, а второй операнд
![]() равен 0. Таблица истинности представлена
равен 0. Таблица истинности представлена
на рис. 12.
|
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Рис. 12 Таблица истинности функции
коимпликация
Приоритет операций в логическом
выражении, не содержащем скобок:
-
О
 трицание.
трицание. -
Конъюнкция, *, /, div,mod.
-
Дизъюнкция, +, -.
-
Операция отношения.
Для усиления операции используются
скобки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Булевы функции от одного и двух аргументов
Булевы функции получили свое название по имени замечательного английского математика Джорджа Буля (1815—1864), который первым начал применять математические методы в логике.
Происхождение булевых функций
В конце первой лекции отмечалось, что каждое из определений операций над высказываниями: отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности, — можно рассматривать как определение некоторого действия над символами 0 и 1, т. е. как определение некоторой функции, заданной на двухэлементном множестве и принимающей значения в том же множестве. Символом 0 обозначалось любое ложное высказывание, а символом 1 — любое истинное. Например, отрицание представляет собой в этом смысле функцию одного аргумента
, которая принимает следующие значения:
; конъюнкция представляет собой функцию двух аргументов
, принимающую следующие значения:
и т.д.
Во второй лекции эта мысль была развита дальше: отмечено, что каждая формула алгебры высказываний от
пропозициональных переменных
определяет по существу некоторую функцию от
аргументов, сопоставляющую любому набору длины
, составленному из элементов двухэлементного множества
, единственный элемент того же множества. Этот элемент является логическим значением того составного высказывания, в которое превращается данная формула, если вместо всех ее пропозициональных переменных подставить конкретные высказывания, имеющие соответствующие значения истинности. Легко понять, что высказывания (точнее, их содержание) здесь ни при чем. Функция, о которой идет речь, определяется структурой формулы
и определениями отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, которые понимаются как определения действий над символами
— элементами двухэлементного множества
.
В связи с этим естественно рассмотреть функции, заданные на двухэлементном множестве и принимающие значения в нем же безотносительно к формулам алгебры высказываний, т.е. сами по себе. Тогда функции, определяемые таблицами в определениях отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, а также функции, определяемые формулами алгебры высказываний, будут служить примерами таких функций. Такие функции, заданные и принимающие значения в двухэлементном множестве, появляющиеся в алгебре высказываний, носят название функций алгебры логики или булевых функций.
Введя понятие булевой функции, мы окончательно отрываемся от того содержательного смысла, который имели в виду в алгебре высказываний: пропозициональные переменные служили там обозначениями для высказываний языка. Теперь же остались только два символа 0 и 1 и понятие булевой функции. Чтобы еще более оттенить это обстоятельство, обозначим переменные, пробегающие множество , малыми буквами латинского алфавита
и будем называть их булевыми.
В этой лекции изучим некоторые свойства булевых функций и посмотрим, как эти функции могут применяться в алгебре высказываний и в теории релейно-контактных схем.
Булевы функции от одного аргумента
Определение 9.1. Булевой функцией от одного аргумента называется функция , заданная на множестве из двух элементов и принимающая значения в том же двухэлементном множестве.
Элементы двухэлементного множества будем обозначать 0 и 1. Таким образом, . Нетрудно перечислить все булевы функции от одного аргумента:
Составленная таблица означает, что, например, булева функция на аргументах 0 и 1 действует следующим образом:
и
. Всего имеется четыре различных булевых функций от одного аргумента:
— функция, тождественно равная 0 (тождественный нуль);
— тождественная функция;
— функция, называемая отрицанием;
— функция, тождественно равная 1 (тождественная единица).
Булевы функции от двух аргументов
Определение 9.2. Булевой функцией от двух аргументов называется функция , заданная на множестве
и принимающая значения в двухэлементном множестве
. Другими словами, булева функция от двух аргументов сопоставляет любой упорядоченной паре, составленной из элементов 0 и 1 (а таких упорядоченных пар будет четыре), либо 0, либо 1.
Перечислим все возможные булевы функции от двух аргументов в форме следующей таблицы:
Заметим: функции пронумерованы так, что номер функции, записанный в двоичной системе счисления, дает последовательность значений соответствующей функции. Например, двоичная запись числа 13 имеет вид: 1101. Соответствующая функция принимает следующие значения:
Многие из перечисленных функций имеют названия и специальные обозначения. Приведем их, сгруппировав функции в пары по тому принципу, что каждая функция из пары является отрицанием другой функции этой пары.
Первые две функции, которые рассматриваются, и
— тождественный ноль и тождественная единица.
Далее, функция называется конъюнкцией и обозначается
(или
). Таким образом,
. Конъюнкция принимает значение 1 в том и только в том случае, когда оба ее аргумента принимают значение 1. Отрицание конъюнкции, функция
, называется штрихом Шеффера и обозначается
. Таким образом,
. Эта функция принимает значение 0 в том и только в том случае, когда функция
принимает значение 1, т.е. в случае, когда оба ее аргумента принимают значение 1.
Функция называется дизъюнкцией и обозначается
. Таким образом,
. Функция
, являющаяся отрицанием функции
, носит название стрелка Пирса (или функция Вебба) и обозначается
. Итак,
.
Функция называется импликацией и обозначается
, т.е
. Аргумент
в этой функции называется посылкой импликации, а аргумент
— ее следствием. Отрицанием импликации является функция
. Специального названия она не имеет.
Функция называется антиимпликацией или обратной импликацией, потому что представляет собой импликацию с посылкой
и следствием
. Таким образом,
. Ее отрицанием является функция
, не имеющая названия.
Функция называется эквивалентностью и обозначается
, так что
. Она принимает значение 1 тогда и только тогда, когда оба ее аргумента принимают одинаковые значения. Функция
, являющаяся отрицанием функции
, называется сложением по модулю два, или суммой Жегалкина, и обозначается
.
Наконец остаются еще две пары функций. В первую пару входят функции и
. Первая из них принимает всегда те же самые значения, что и ее первый аргумент, т.е.
, а вторая функция является отрицанием первой:
. Во вторую пару входят функции
и
. Первая из них принимает всегда те же самые значения, что и ее второй аргумент, т.е.
, а вторая функция является отрицанием первой:
.
Теперь установим некоторые важнейшие свойства введенных функций. Две булевы функции и
называются равными, если каждому набору значений аргументов
обе функции сопоставляют один и тот же элемент из множества
, т.е.
для любых
. Например,
.
Из введенных простейших булевых функций можно строить с помощью суперпозиций более сложные булевы функции. Например, если в функцию вставить вместо аргумента
функцию
, то получим следующую сложную функцию:
. Если в нее в свою очередь вставить вместо аргумента
функцию
, то получим сложную функцию
. И так далее. В результате получаются булевы функции от трех, четырех и большего числа аргументов.
В следующих теоремах устанавливаются некоторые равенства одних булевых функций другим, выражающие свойства основных булевых функций.
Свойства дизъюнкции, конъюнкции и отрицания
Теорема 9.3. Для булевых функций выполняются следующие равенства:
а) (идемпотентность дизъюнкции и конъюнкции);
б) (коммутативность дизъюнкции и конъюнкции);
в) (ассоциативность дизъюнкции и конъюнкции);
г) ;
д) ;
е) (дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции);
ж) (законы поглощения);
з) (законы де Моргана);
и) ;
к) .
Доказательство. а) Свойство идемпотентности дизъюнкции и конъюнкции означает, что применение как одной из них, так и другой к двум одинаковым элементам дает этот же самый элемент. Доказательства данных равенств вытекают непосредственно из таблиц, определяющих дизъюнкцию и конъюнкцию. В самом деле, для дизъюнкции и для конъюнкции
.
б) Коммутативность (перестановочность) дизъюнкции означает, что значение функции не зависит от порядка ее аргументов. Это действительно так, потому что, согласно определению дизъюнкции, она принимает значение 1 тогда и только тогда, когда хотя бы один из ее аргументов (не имеет значения, какой именно) принимает значение 1, и принимает значение 0 тогда и только тогда, когда оба аргумента равны 0. Аналогична ситуация и с конъюнкцией.
в) Вместо слова “ассоциативность” используется также термин “сочетательность”. Докажем ассоциативность конъюнкции с помощью таблиц. Такой способ важен тем, что он может быть применен для доказательства (или опровержения) равенства между любыми двумя булевыми функциями. Итак, составляем последовательно таблицы значений булевых функций, суперпозиция которых дает левую часть тождества ассоциативности, а затем булевых функций, суперпозиция которых дает его правую часть, придавая всевозможные значения аргументам,
Сравнивая пятый и седьмой столбцы таблицы, видим, что они одинаковы, т.е. функции, стоящие в левой и правой частях Доказываемого равенства, принимают одинаковые значения при одинаковых наборах значений аргументов. А это означает, что функции и
действительно равны.
Составлением аналогичных таблиц может быть доказана и ассоциативность дизъюнкции. ссоциативность означает, что при многократном применении дизъюнкции или конъюнкции результат не будет зависеть от последовательности их применения, и потому все скобки, обозначающие эту последовательность, могут быть опущены. Так, будем писать
вместо
, а также вместо
, или —
вместо
и вместо
. Точно так же будем писать
вместо каждой из следующих равных между собой булевых функций:
Аналогичным образом будет использоваться запись и т.д.
г) Свойства сразу следуют из таблиц для дизъюнкции и конъюнкции. Первое свойство означает, что дизъюнкция любого элемента с элементом 1 дает снова элемент 1 (подобно тому как в арифметике умножение любого числа на нуль дает нуль). Второе свойство говорит о том, что относительно конъюнкции элемент 1 играет роль “нейтрального” элемента, т.е. такого элемента, конъюнкция которого с любым элементом не меняет его.
д) Аналогично двум предыдущим свойствам, эти свойства также легко вытекают из таблиц для дизъюнкции и конъюнкции. Здесь первое свойство говорит о “нейтральности” элемента 0 относительно дизъюнкции.
е) Для доказательства этих равенств можно воспользоваться рассмотренным выше методом таблиц, но можно использовать и ранее доказанные соотношения. Проверим, например, первое равенство. При его левая часть в силу свойств г) и б) равна
, а правая, в силу тех же свойств, равна
. Если же
, то левая часть доказываемого равенства становится, в силу свойств д) и б), равной
; но тому же самому становится равной и правая часть:
. Следовательно, функции
и
при одинаковых значениях аргументов дают равные значения, т. е. они равны.
Совершенно аналогичным путем можно доказать и второе тождество дистрибутивности. место слова “дистрибутивность” иногда употребляется термин “распределительность”. Отметим, что в обычной арифметике умножение дистрибутивно (распределительно) относительно сложения:
, но сложение, конечно, не дистрибутивно относительно умножения:
. Для булевых операций (функций) не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции.
ж) Снова при доказательстве можем пользоваться уже установленными свойствами. В самом деле, при левая часть первого равенства превращается в
, т. е. равна правой.
Если же , то левая часть рассматриваемого соотношения равна
, т. е. снова равна его правой части. Следовательно, первое равенство доказано. Аналогично проверяется второе равенство.
з) Для доказательства второго равенства положим сначала, что . Тогда его левая часть будет равна
, а правая —
. Если же
, то левая часть доказываемого тождества превратится в
, а его правая часть — в
. Следовательно, равенство выполняется. Аналогично проверяется первое равенство.
и) Если , то
. Если
, то
. Таким образом, первое равенство справедливо. Аналогично проверяется второе равенство.
к) Если , то
. Если
, то
. Следовательно,
.
Теорема полностью доказана.
Свойства эквивалентности, импликации и отрицания
Свойства эквивалентности и импликации только частично аналогичны свойствам дизъюнкции или конъюнкции.
Теорема 9.4. Для булевых функций справедливы следующие равенства:
а) ;
б) (коммутативность эквивалентности);
в) (ассоциативность эквивалентности);
г) ;
д) ;
е) ;
ж) ;
з) ;
и) ;
к) ;
л) ;
м) ;
н) .
Доказательство этих соотношений не представляет труда. Предлагается проделать их самостоятельно с помощью таблиц.
Заметим, что импликация не обладает ни свойством коммутативности, ни свойством ассоциативности. Предлагается самостоятельно исследовать вопрос о том, будут ли эквивалентность и импликация дистрибутивны (распределительны) одна относительно другой справа и слева.
Выражение одних булевых функций через другие
О взаимозависимостях булевых функций возникает много вопросов. Как выражаются одни булевы функции в виде суперпозиций других булевых функций? Можно ли все булевы функции выразить через какие-то одни и те же функции? Существует ли такая булева функция, через которую выражаются все остальные? И так далее. В следующей теореме приводятся основные выражения одних булевых функций через другие, которые можно использовать при получении новых зависимостей между булевыми функциями.
Теорема 9.5. Справедливы следующие равенства, выражающие одни булевы функции через другие:
а) ;
в) ;
г) ;
д) ;
е) ;
ж) ;
з) ;
и) ;
к) ;
л) ;
м) .
Доказательство. Для а) и б) доказательства равенств легко следуют из законов де Моргана (теорема 9.3, пункт з), если на обе части каждого из них “навесить” знак отрицания, а затем к левым частям полученных равенств применить равенство из теоремы 9.3, пункт к.
Для в) и г) равенства можно проверить с помощью общего метода таблиц, а можно воспользоваться равенством д), преобразуя, например, правую часть первого равенства. Тогда
При доказательстве были использованы, кроме того, соотношения теоремы 9.3, з, к, е, и, г.
д) Равенство легко проверяется с помощью таблиц.
ё) Докажите, построив таблицы.
ж) и к) Соотношения непосредственно видны из таблиц, определяющих функции штрих Шеффера и стрелку Пирса.
з) и л) Равенства уже отмечались при определении функций штрих Шеффера и стрелка Пирса.
и) Можно составить таблицы, а можно рассуждать следующим образом: .
первом равенстве использовано предыдущее соотношение з).
м) Докажите равенство подобно тому как было доказано равенство и), используя при этом соотношение л).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики)[1] от n аргументов — в дискретной математике — отображение Bn → B, где B = {0,1} — булево множество. Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n, обозначающее количество аргументов, называется арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения (n-я прямая степень) Bn называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается P2, а от n аргументов — P2(n). Переменные, принимающие значения из булева множества, называются булевыми переменными[2]. Булевы функции названы по фамилии математика Джорджа Буля.
При работе с булевыми функциями происходит полное абстрагирование от того содержательного смысла, какой предполагается в алгебре высказываний[2]. Тем не менее между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие, если[3]:
- установить взаимно-однозначное соответствие между булевыми и пропозициональными переменными;
- установить связь между булевыми функциями и логическими связками;
- оставить приоритет операций без изменений.
Основные сведения[править | править код]
Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2n. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 2(2n). Поэтому в этом разделе рассматриваются только простейшие и важнейшие булевы функции.
Практически все булевы функции низших арностей (0, 1, 2 и 3) получили исторически сложившиеся имена. Если значение функции не зависит от одной из переменных (то есть, по сути, для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная, не играя никакого «значения», называется фиктивной.
Таблицы истинности[править | править код]
Булева функция задаётся конечным набором значений, что позволяет представить её в виде таблицы истинности, например[4]:
| x1 | x2 | … | xn−1 | xn | f(x1, x2, …, xn) |
|---|---|---|---|---|---|
| 0 | 0 | … | 0 | 0 | 0 |
| 0 | 0 | … | 0 | 1 | 0 |
| 0 | 0 | … | 1 | 0 | 1 |
| 0 | 0 | … | 1 | 1 | 0 |
 |
 |
 |
 |
 |

|
| 1 | 1 | … | 0 | 0 | 1 |
| 1 | 1 | … | 0 | 1 | 0 |
| 1 | 1 | … | 1 | 0 | 0 |
| 1 | 1 | … | 1 | 1 | 0 |
Нульарные функции[править | править код]
При n = 0 количество булевых функций сводится к двум 220 = 21 = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
Таблица значений и названий нульарных булевых функций:
| Значение | Обозначение | Название | |
|---|---|---|---|
| 0 | F0,0 = 0 | тождественный ноль | |
| 1 | F0,1 = 1 | тождественная единица, тавтология |
Унарные функции[править | править код]
При n = 1 число булевых функций равно 221 = 22 = 4. Определение этих функций содержится в следующей таблице.
Таблица значений и названий булевых функций от одной переменной:
| x0=x | 1 | 0 | Обозначение | Название |
|---|---|---|---|---|
| 0 | 0 | 0 | F1,0 = 0 | тождественный ноль |
| 1 | 0 | 1 | F1,1 = x = ¬x = x’ = NOT(x) | отрицание, логическое «НЕТ», «НЕ», «НИ», инвертор, SWAP (обмен) |
| 2 | 1 | 0 | F1,2 = x | тождественная функция, логическое “ДА”, повторитель |
| 3 | 1 | 1 | F1,3 = 1 | тождественная единица, тавтология |
Бинарные функции[править | править код]
При n = 2 число булевых функций равно 222 = 24 = 16.
Таблица значений и названий булевых функций от двух переменных (в зависимости от области применения, функции имеют разные словесные названия, но один и тот же номер):
| x0=x | 1 | 0 | 1 | 0 | Обозначение функции | Название функции |
|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | F2,0 = 0 | тождественный ноль |
| 1 | 0 | 0 | 0 | 1 | F2,1 = x ↓ y = x NOR y = NOR(x,y) = x НЕ-ИЛИ y = НЕ-ИЛИ(x,y) = NOT(MAX(X,Y)) | стрелка Пи́рса – “↓” (кинжал Куайна – “†”), функция Ве́бба – “°”[5], НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, инверсия максимума |
| 2 | 0 | 0 | 1 | 0 | F2,2 = x > y = x GT y = GT(x,y) = x → y = x  y y
|
функция сравнения “первый операнд больше второго операнда”, инверсия прямой импликации, коимпликация[6] |
| 3 | 0 | 0 | 1 | 1 | F2,3 = y = y’ = ¬y = NOT2(x,y) = НЕ2(x,y) | отрицание (негация, инверсия) второго операнда |
| 4 | 0 | 1 | 0 | 0 | F2,4 = x < y = x LT y = LT(x,y) = x ← y = x  y y
|
функция сравнения “первый операнд меньше второго операнда”, инверсия обратной импликации, обратная коимпликация[6] |
| 5 | 0 | 1 | 0 | 1 | F2,5 = x = x’ = ¬x = NOT1(x,y) = НЕ1(x,y) | отрицание (негация, инверсия) первого операнда |
| 6 | 0 | 1 | 1 | 0 | F2,6 = x >< y = x <> y = x NE y = NE(x, y) = x ⊕ y = x XOR y = XOR(x,y) = XMAX(x,y) = x XMAX y | функция сравнения “операнды не равны”, сложение по модулю 2, исключающее «или», сумма Жегалкина[7], исключающий max |
| 7 | 0 | 1 | 1 | 1 | F2,7 = x | y = x NAND y = NAND(x,y) = x НЕ-И y = НЕ-И(x,y) = NOT(MIN(X,Y)) | штрих Ше́ффера, пунктир Чулкова[8], НЕ-И, 2И-НЕ, антиконъюнкция, инверсия минимума |
| 8 | 1 | 0 | 0 | 0 | F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x,y) = x И y = И(x,y) = min(x,y) | конъюнкция, 2И, минимум |
| 9 | 1 | 0 | 0 | 1 | F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x,y) | функция сравнения “операнды равны”, эквивалентность |
| 10 | 1 | 0 | 1 | 0 | F2,10 = YES1(x,y) = ДА1(x,y) = x | первый операнд |
| 11 | 1 | 0 | 1 | 1 | F2,11 = x ≥ y = x >= y = x GE y = GE(x,y) = x ← y = x ⊂ y | функция сравнения “первый операнд не меньше второго операнда”, обратная импликация (от второго аргумента к первому) |
| 12 | 1 | 1 | 0 | 0 | F2,12 = YES2(x,y) = ДА2(x,y) = y | второй операнд |
| 13 | 1 | 1 | 0 | 1 | F2,13 = x ≤ y = x <= y = x LE y = LE(x,y) = x → y = x ⊃ y | функция сравнения “первый операнд не больше второго операнда”, прямая (материальная) импликация (от первого аргумента ко второму) |
| 14 | 1 | 1 | 1 | 0 | F2,14 = x ∨ y = x + y = x OR y = OR(x,y) = x ИЛИ y = ИЛИ(x,y) = max(x,y) | дизъюнкция, 2ИЛИ, максимум |
| 15 | 1 | 1 | 1 | 1 | F2,15 = 1 | тождественная единица, тавтология |
При двух аргументах префиксная, инфиксная и постфиксная записи, по экономичности, почти одинаковы.
Некоторые функции, имеющие смысл в цифровой технике, например функции сравнения, минимум и максимум, не имеют смысла в логике, так как в логике, в общем случае, логические значения TRUE и FALSE не имеют жёсткой привязки к числовым значениям (например в TurboBasic’е, для упрощения некоторых вычислений, TRUE = -1, а FALSE = 0) и невозможно определить, что больше TRUE или FALSE, импликации же и др. имеют смысл и в цифровой технике и в логике.
Тернарные функции[править | править код]
При n = 3 число булевых функций равно 2(23) = 28 = 256. Некоторые из них определены в следующей таблице:
Таблица значений и названий некоторых булевых функций от трёх переменных, имеющих собственное название:
| x0=x | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | Обозначения | Названия |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| x2=z | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | F3,1 = x↓y↓z = ↓(x,y,z) = Webb2(x,y,z) = NOR(x,y,z) | 3ИЛИ-НЕ, функция Вебба, стрелка Пирса, кинжал Куайна – “†” |
| 23 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | F3,23 =  = ≥2(x,y,z) = ≥2(x,y,z)
|
Переключатель по большинству с инверсией, 3ППБ-НЕ, мажоритарный клапан с инверсией |
| 31 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | F3,31 = x OR (y AND z) = Gi,j = Gi,j-1 OR (Pi,j-1 AND Gi-1,j-1) | Оператор Valency-2 (валентность=2) в параллельно префиксных сумматорах |
| 126 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | F3,126 = (x≠y≠z) = [≠(x,y,z)] = NE(x,y,z) | Неравенство |
| 127 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | F3,127 = x|y|z = |(x,y,z) = NAND(x,y,z) | 3И-НЕ, штрих Шеффера |
| 128 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | F3,128 = x&y&z = &(x,y,z) = (x AND y AND z) = AND(x,y,z) = (x И y И z) = И(x,y,z) = min(x,y,z) | 3И, минимум |
| 129 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | F3,129 = (x=y=z) = [=(x,y,z)] = EQV(x,y,z) | Равенство |
| 150 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | F3,150 = x⊕y⊕z = x⊕2y⊕2z = ⊕2(x,y,z) | Тернарное сложение по модулю 2 |
| 184 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | F3,184 = ![{displaystyle [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af0bfedf9a4341d42ead3affff487ec9debd8365)
|
Условная дизъюнкция |
| 216 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | F3,216 = f1 | Разряд займа при тернарном вычитании |
| 232 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | F3,232 = f2 = [>=2(x,y,z)] = ≥2(x,y,z) = (x И y) ИЛИ (y И z) ИЛИ (z И x) | Разряд переноса при тернарном сложении, переключатель по большинству, 3ППБ, мажоритарный клапан |
| 254 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | F3,254 = (x+y+z) = +(x,y,z) = (x OR y OR z) = OR(x,y,z) = (x ИЛИ y ИЛИ z) = ИЛИ(x,y,z) = max(x,y,z) | ИЛИ, максимум |
При трёх и более аргументах префиксная (и постфиксная) запись экономичнее инфиксной записи.
Обычный вид записи функций — префиксный (перед операндами). При инфиксной (между операндами) записи функций функции называются операторами, а аргументы функции — операндами.
Полные системы булевых функций[править | править код]
Суперпозиция и замкнутые классы функций[править | править код]
Результат вычисления булевой функции может быть использован в качестве одного из аргументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции 
 |
 |
 |

|
|
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.
В качестве простейших примеров замкнутых классов булевых функций можно назвать множество 





Разумеется, множество 
Тождественность и двойственность[править | править код]
Две булевы функции тождественны друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. Тождественность функций f и g можно записать, например, так:

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:
 |
 |

|
 |

|
 |
 |
 |
 |

|
А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

Функция 


Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.
Полнота системы, критерий Поста[править | править код]
Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством 
Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:
Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с 
Пост доказал, что множество замкнутых классов булевых функций — счётное множество.
Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.
Представление булевых функций[править | править код]
Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее, чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций 

- Как построить по данной функции представляющую её формулу?
- Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
- В частности: существует ли способ приведения произвольной формулы к эквивалентной ей канонической форме такой, что две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
- Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
Дизъюнктивная нормальная форма (ДНФ)[править | править код]
Простой конъюнкцией или конъюнктом называется конъюнкция некоторого конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций.
Элементарная конъюнкция
- правильная, если каждая переменная входит в неё не более одного раза (включая отрицание);
- полная, если каждая переменная (или её отрицание) входит в неё ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
Например 
Совершенной дизъюнктивной нормальной формой или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: 
Легко убедиться, что каждой булевой функции соответствует некоторая ДНФ, а функции, отличной от тождественного нуля — даже СДНФ. Для этого достаточно в таблице истинности этой функции найти все булевы векторы, на которых её значение равно 1, и для каждого такого вектора 






Конъюнктивная нормальная форма (КНФ)[править | править код]
Конъюнктивная нормальная форма (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.
Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».
КНФ может быть преобразована к эквивалентной ей ДНФ путём раскрытия скобок по правилу:
которое выражает дистрибутивность конъюнкции относительно дизъюнкции. После этого необходимо в каждой конъюнкции удалить повторяющиеся переменные или их отрицания, а также выбросить из дизъюнкции все конъюнкции, в которых встречается переменная вместе со своим отрицанием. При этом результатом не обязательно будет СДНФ, даже если исходная КНФ была СКНФ. Точно также можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило
выражающее дистрибутивность дизъюнкции относительно конъюнкции. Результат нужно преобразовать описанным выше способом, заменив слово «конъюнкция» на «дизъюнкция» и наоборот.
Алгебраическая нормальная форма (АНФ или полином Жегалкина)[править | править код]
Алгебраическая нормальная форма (общепринятое название в зарубежной литературе) или полином Жегалкина (название, используемое в отечественной литературе) — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции («И», AND), а в качестве сложения — сложение по модулю 2 (исключающее «ИЛИ», XOR). Для получения полинома Жегалкина следует выполнить следующие действия:
- Получить СДНФ функции
- Все ИЛИ заменить на Исключающее ИЛИ
- Во всех термах заменить элементы с отрицанием на конструкцию: («элемент» «исключающее ИЛИ» 1)
- Раскрыть скобки по правилам алгебры Жегалкина и привести попарно одинаковые термы
Классификация булевых функций[править | править код]
- По количеству n входных операндов, от которых зависит значение на выходе функции, различают нульарные (n = 0), унарные (n = 1), бинарные (n = 2), тернарные (n = 3) булевы функции и функции от большего числа операндов.
- По количеству единиц и нулей в таблице истинности отличают узкий класс сбалансированных булевых функций (также называемых уравновешенными или равновероятностными, поскольку при равновероятных случайных значениях на входе или при переборе всех комбинаций по таблице истинности вероятность получения на выходе значения 1 равна 1/2) от более широкого класса несбалансированных булевых функций (так же называемых неуравновешенными, поскольку вероятность получения на выходе значения 1 отлична от 1/2). Сбалансированные булевы функции в основном используются в криптографии.
- По зависимости значения функции от перестановки её входных битов различают симметричные булевы функции (значение которых зависит только от количества единиц на входе) и несимметричные булевы функции (значение которых так же зависит от перестановки её входных бит).
- По значению функции на противоположных друг другу наборах значений аргументов отличают самодвойственные функции (значение которых инвертируется при инвертировании значения всех входов) от остальных булевых функций, не обладающих таким свойством. Нижняя часть таблицы истинности для самодвойственных функций является зеркальным отражением инвертированной верхней части (если расположить входные комбинации в таблице истинности в естественном порядке).
- По алгебраической степени нелинейности отличают линейные булевы функции (АНФ которых сводится к линейной сумме по модулю 2 входных значений) и нелинейные булевы функции (АНФ которых содержит хотя бы одну нелинейную операцию конъюнкции входных значений). Примерами линейных функций являются: сложение по модулю 2 (исключающее «ИЛИ», XOR), эквивалентность, а также все булевы функции, АНФ которых содержит лишь линейные операции сложения по модулю 2 без конъюнкций. Примерами нелинейных функций являются: конъюнкция («И», AND), штрих Шеффера («НЕ-И», NAND), стрелка Пирса («НЕ-ИЛИ», NOR), а также все булевы функции, АНФ которых содержит хотя бы одну нелинейную операцию конъюнкции.
Существенные и фиктивные переменные[править | править код]
Переменная булевой функции называется существенной, если для булевой функции существует два набора значений её аргументов, различающиеся лишь значением этой переменной и значения булевой функции на них различаются. Если значения этой функции на них совпадают, то переменная называется фиктивной. Переменная является существенной тогда и только тогда, когда она входит в совершенную ДНФ булевой функции или она входит в полином Жегалкина булевой функции.
Две булевы функции называются равными, если множества их существенных переменных равны и на любых двух равных наборах значений существенных переменных значения функций совпадают.[9]
См. также[править | править код]
- Булева алгебра
- Битовые операции
- Комбинационная логика
- Секвенциальная логика
- Троичная логика
- Троичные функции
- Логические элементы
Литература[править | править код]
- Алексеев В. Б. (лектор), Поспелов А.Д. (составитель). Дискретная математика (курс лекций, II семестр). — М.: Изд. отд. фак. Вычислит. математики и кибернетики МГУ им. М. В. Ломоносова, 2002. — 44 с.
- Быкова С. В., Буркатовская Ю. Б. Булевы функции: учебное пособие для студентов высших учебных заведений, обучающихся по специальности ВПО 010501 «Прикладная математика и информатика». — Томск: Томский гос. ун-т, 2010. — 190 с.
- Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике. — М.: ФИЗМАТЛИТ, 2009.
- Игошин В. И. Математическая логика и теория алгоритмов. — 2-е изд., стереотип.. — М.: Издательский центр «Академия», 2008. — 448 с.
- Кузнецов О. П. Дискретная математика для инженера. — СПб.: Лань, 2007. — 394 с.
- Учебные пособия кафедры математической кибернетики ВМиК МГУ (на сайте кафедры математической кибернетики МГУ ВМК).
- Ложкин С.А. Лекции по основам кибернетики : учеб. пособие по курсам «Основы кибернетики» и «Структур. реализация дискрет. функций». — М.: Изд. отд. фак. Вычислит. математики и кибернетики МГУ им. М. В. Ломоносова, 2004. — 254 с.
- Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2001. — 126 с.
- Самофалов К. Г., Романкевич А. М., Валуйский В. Н., Каневский Ю. С., Пиневич М. М. Прикладная теория цифровых автоматов. — Киев: Вища Школа, 1987. — С. 183—189. — 375 с.
- Яблонский С. В. Введение в дискретную математику. — М.: Высш. шк., 2006. — 384 с.
Ссылки[править | править код]
- ↑ Игошин, 2008, Глава 2. Булевы функции.
- ↑ 1 2 Игошин, 2008, с. 94.
- ↑ Игошин, 2008, с. 104-105.
- ↑ Самофалов, 1987.
- ↑ Элементарные булевы функции. Дата обращения: 9 ноября 2016. Архивировано 10 ноября 2016 года.
- ↑ 1 2 Избранные вопросы теории булевых функций. // А. С. Балюк и др. Под ред. С. Ф. Винокурова и Н. А. Перязева. — М.: ФИЗМАТЛИТ, 2001. — 192 с. — С. 13.
- ↑ Игошин, 2008, с. 96.
- ↑ И.А. Насыров. учебно-методическое пособие. Дата обращения: 20 ноября 2020. Архивировано 22 декабря 2019 года.
- ↑ Гаврилов Г. П., Сапоженко А.А. Сборник задач по дискретной математике. — М., Наука, 1977. — c. 44, 46, 47
Здравствуйте. Нашел функцию, которая позволяет сравнивать объекты между собой:
const compareObjects = (a, b) => {
if (a === b) return true;
if (typeof a != 'object' || typeof b != 'object' || a == null || b == null) return false;
let keysA = Object.keys(a), keysB = Object.keys(b);
if (keysA.length != keysB.length) return false;
for (let key of keysA) {
if (!keysB.includes(key)) return false;
if (typeof a[key] === 'function' || typeof b[key] === 'function') {
if (a[key].toString() != b[key].toString()) return false;
} else {
if (!compareObjects(a[key], b[key])) return false;
}
}
return true;
}Но не могу понять, для чего используется отрицание функции !compareObjects(a[key], b[key]). Впервые с таким сталкиваюсь. Непонятно, как в общем работает отрицание функций в JS и для чего это используется в данном конкретном примере.



