Intersection points can be beneficial in finding insights into the data, As intersections give the same values for different data sets. Excel can help to automate the task of finding the intersection point of two lines by using the =slope() and =intersection() function and replacing their values with the given equations. In this article, we will learn how to find the intersection point of two straight lines in excel.
Procedure to find Intersection
An intersection is a point where 2 curves have the same coordinates. The equation of a straight line can be written asy = mx + c, where m is the slope and c is the intercept of a line. For example, you are given two lines line1:y = m1x + c1 and line2:y1 = m2x + c2 wherem1, c1 are the slope and intersection of line1 andm2, c2 are the slope and intersection of line2. Considering the intersection point to be (a, b).
Following are the steps
Step 1: As, (a, b) is the intersection point of the two lines, which means that (a, b) satisfies the equation of both linesb = m1a + c1 i.e. andb = m2a + c2.
Step 2: Equating the values of b, to find the value of a,m1a+ c1 = m2 + c2. .
Step3: After rearranging the equation, the value of a comes out to be,![]() .
.
Step 4: Now, substitute the value of a in any of the equations to find the value of b,b = m1 + c1.
Excel Functions used in Calculating Intersection
There are two excel functions that are helpful in calculating the intersection point of a line.
=SLOPE(y_values, x_values)
The slope function calculates the average slope of a dataset. The slope function takes two arguments, the first argument is the values of y, and the second argument is the values of x.
=INTERCEPT(y_values, x_values)
The intercept function calculates the average intercept of a dataset. The intercept function takes two arguments, the first argument is the values of y, and the second argument is the values of x.
Calculating the intersection of lines in Excel
Generally, the equation of lines is not given, but the data points of the equation are given. We will calculate the intersection using the same procedure as explained above. For example, “Arushi” is a data analyst, and she has been given two data sets, each containing values of x and y. “Arushi” had drawn the graph of the two lines, and she wanted to find the intersection of the lines drawn from the given data set.

Following are the steps
Step 1: Firstly, we need to find the slope and intersection of both the lines. To do this, make four columns, A9:A12, specifying the name of the intercept and slope of each line.

Step 2: Cell C9 has to be filled with the slope of the line1. Use =SLOPE() function, to calculate the average slope of the given data points, i.e. =SLOPE(B4:B6, A4:A6).

Step 3: Press Enter. The slope of the line1 is 1.

Step 4: Cell C10 has to be filled with the slope of the line2. Use =SLOPE() function, to calculate the average slope of the given data points, i.e. =SLOPE(E4:E6, D4:D6).

Step 5: Press Enter. The slope of the line2 is 2.

Step 6: Cell C11 has to be filled with the intercept of the line1. Use =INTERCEPT() function to calculate the average intercept of the given data points, i.e., =INERCEPT(B4:B6, A4:A6).

Step 7: Press Enter. The intercept of the line1 is 0.

Step 8: Cell C12 has to be filled with the intercept of the line2. Use =INTERCEPT() function to calculate the average intercept of the given data points, i.e., =INERCEPT(E4:E6, D4:D6).

Step 9: Press Enter. The intercept of the line2 is -1.

Step 10: Now, we have the slope and intercept of both the lines. Now, we have to find the intersection point of the two lines. To do this, make two columns, A15:A16, specifying the name of the point of co-ordinates of the intersection.

Step 11: Cell B15 has to be filled with the x coordinate of lines intersection. Use the formula as explained above to calculate the x co-ordinate of lines intersection.

Step 12: Press Enter. The x coordinate of the intersection point is 1.

Step 13: Cell B16 has to be filled with the y co-ordinate of lines intersection. Use the formula as explained above to calculate the y co-ordinate of lines intersection.

Step 14: Press Enter. The y coordinate of the intersection point is 1.

Step 15: The intersection point of both lines is (1, 1). We can also see (1, 1) is the intersection point in the graph.

Last Updated :
22 Aug, 2022
Like Article
Save Article
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
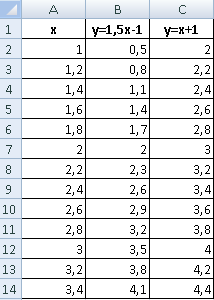
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
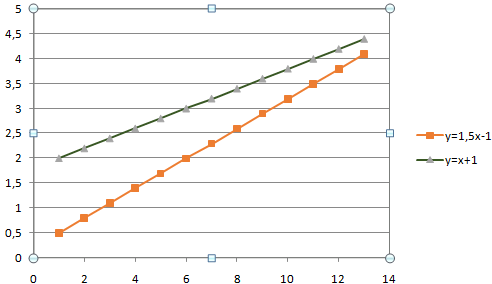
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
Находим точку пересечения графиков в Excel
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
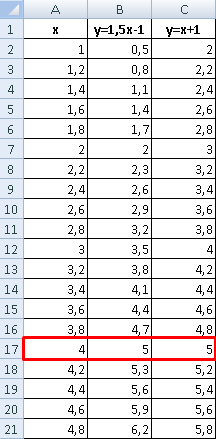
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
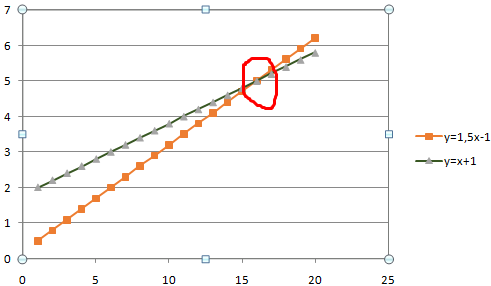
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
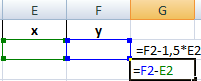
Вызываем меню «Поиск решения» – заполняем условия, необходимые для решения уравнений.
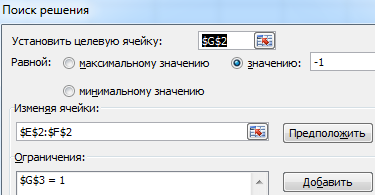
Нажимаем «Выполнить» – инструмент предлагает решение уравнений.
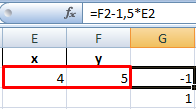
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
Существует три показателя, которые измерялись во времени.

По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
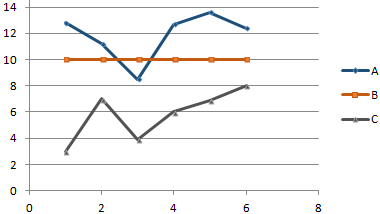
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
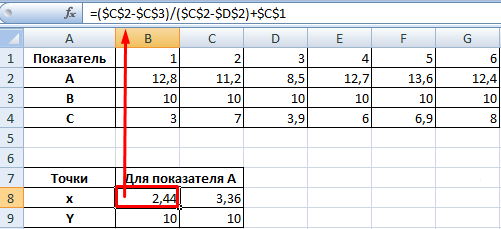
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
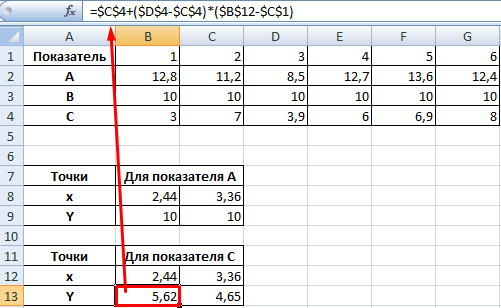
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
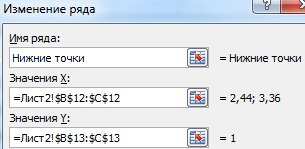
Получается такой рисунок:
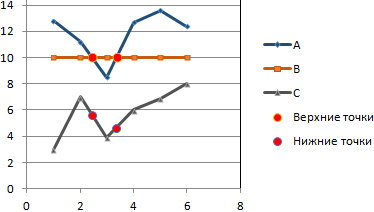
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
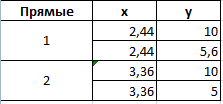
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
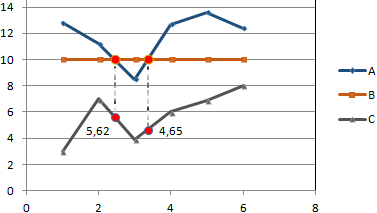
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
Хороший вопрос…
Задали мне тут недавно вопрос. Есть график, на котором имеем 3 показателя работы производства: удельный расход материала, норматив расхода и объём производства, а по горизонтальной оси временной период (недели, например).
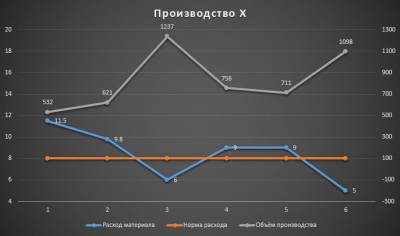
Исходные данные выглядят так:

Удельный расход материала зависит от объёма производства. Он то выше, то ниже норматива по итогам периода и возникает естественный вопрос показать на диаграмме те моменты времени и те объёмы производства, когда линия расхода пересекает линию норматива. Может быть эта проблема и лишена какого-то великого смысла, но тем не менее вопрос был задан, значит потребность такая у людей есть.
А это наша конечная цель:
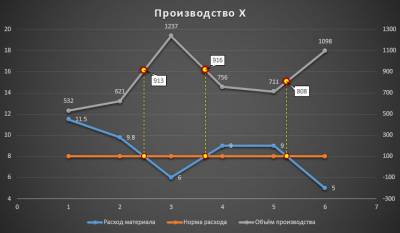
Скачать пример
ChartsIntersection.xlsx
Решение
Шаг 1
Для начала обратим внимание, что исходный тип диаграммы – График с маркерами.
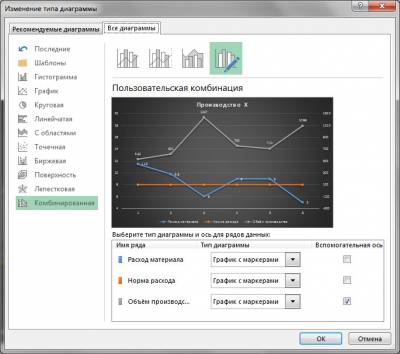
Ряды этого типа описываются так:
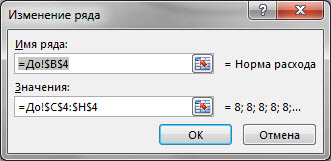
Заметьте, что тут нет значений координат по оси X, а есть только координаты по условной оси Y. Этим подразумевается, что условная ось X – общая для всех рядов, а также, что при их построении не используются значения, отличные от заранее фиксированного ряда оси X. Вот есть у нас периоды: 1, 2, 3 и т.д., нанесенные на ось Х, и использовать можно только их. Периода, где X=3.5 не существует для данного типа диаграммы.
Однако, нам для решения этой задачи необходимо, чтобы мы могли задавать любое значение X, в том числе промежуточные, так как наши линии как раз пересекаются где-то “между периодами”. Поэтому тип диаграммы мы меняем для всех рядов с “графика с маркерами” на “точечную с прямыми отрезками и маркерами“.
Следует упомянуть, что наш случай осложняется наличием двух вертикальных осей: основной и вспомогательной, так как значения расхода материала и объёма производства сильно друг от друга отличаются.
Шаг 2
Теперь нам необходимо нанести на диаграмму дополнительные ряды данных:
-
Точки пересечения линий расхода материала с нормами расхода. Таких точек у нас будет 3, исходя из условий примера. Эти точки нам необходимо будет расчитать, вспомнив школьный курс геометрии (см. лист Треугольники). В файле учебного примера на листе После в таблице N3:Q5 мы получили координаты нужных точек путем нехитрых формул. Тип диаграммы Точечная в отличие от рядов с показателями работы производства.
-
Точки пересечения найденных значений по оси X с объемом производства. Расчитывается в таблице N8:Q10 по близким формулам. Тип диаграммы Точечная.
-
Пунктирные линии, которые мы рисуем из эстетических соображений. Таблица с их координатами находится в N12:P18.
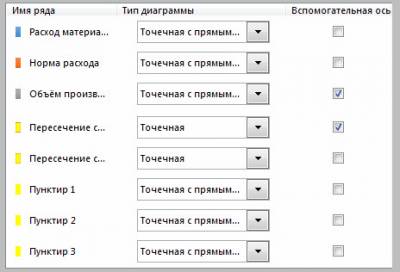
Добавляем ряды данных в соответствии с теми точками, которые мы расчитали. Щёлкните ПКМ по диаграмме и выберите “Выбрать данные…“, далее воспользуйтесь кнопкой “Добавить“.
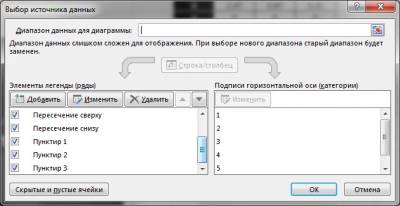
Пример одного из рядов:
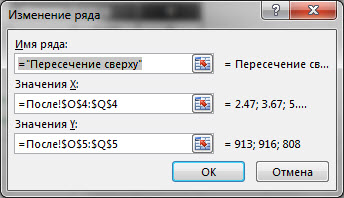
Шаг 3
Отформатируйте линии и маркеры новых рядов данных, так как вам необходимо. Готово! 🙂
|
Добрый день. Подскажите, как можно решить такую задачу: Имеется график “1”, который пересекается с графиком “RΣ” в одной точке. Как определить эту точку и опустить вертикальную линию из найденной точки на ось Х? Прикрепленные файлы
|
|
|
Sanja Пользователь Сообщений: 14849 |
На выбор Согласие есть продукт при полном непротивлении сторон. |
|
Думал Вы поможете, но подумав сделал. Как найти пересечения линий графиков и отобразить их на диаграмме. “Опыты” проводил на левым графиком. Координаты точки пересечения вычисляются правильно, если данная точка лежит в пределах 6 и 7 по Х. Если изменить данные, точка не будет вычисляться правильно. Прикрепленные файлы
|
|
|
MCH Пользователь Сообщений: 3886 |
У Вас график нелинейный, а Вы вычисляете линейную интерполяцию. |
|
PolosatiyKot Пользователь Сообщений: 16 |
#5 13.11.2017 12:24:18
Для меня эти слова не очень понятны. Немного доделал график и перенес значения, поэтому формула немного видоизменилась. Поставил значения искомой координаты под графиком и выделил синим цветом. Можете попросить Вас написать подобную формулу для другой точки пересечения, которая находится правее и так же выделена синим? Прикрепленные файлы
|
||
|
MCH Пользователь Сообщений: 3886 |
Подробнее опишите словами что нужно посчитать Как я понял: |
|
PolosatiyKot Пользователь Сообщений: 16 |
#7 13.11.2017 16:27:47
В таблице 2, которая находится под текстом необходимо, чтобы координата по оси “y” точки пересечения графиков “2” и “R бо” (Пресечение 2) вычислялись автоматически. Очень надеюсь, что достаточно понятно написал. Прикрепленные файлы
Изменено: PolosatiyKot – 13.11.2017 17:01:37 |
||
|
MCH Пользователь Сообщений: 3886 |
|
|
PolosatiyKot Пользователь Сообщений: 16 |
#9 13.11.2017 17:11:26 Большое спасибо. То, что было нужно, даже больше. Изменено: PolosatiyKot – 13.11.2017 17:12:28 |
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ОТРЕЗОК в Microsoft Excel.
Описание
Вычисляет точку пересечения линии с осью y, используя значения аргументов “известные_значения_x” и “известные_значения_y”. Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные аргументами “известные_значения_x” и “известные_значения_y”. Функция ОТРЕЗОК используется, если нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.
Синтаксис
ОТРЕЗОК(известные_значения_y; известные_значения_x)
Аргументы функции ОТРЕЗОК описаны ниже.
-
Известные_значения_y — обязательный аргумент. Зависимое множество наблюдений или данных.
-
Известные_значения_x — обязательный аргумент. Независимое множество наблюдений или данных.
Замечания
-
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
-
Если аргументы “известные_значения_y” и “известные_значения_x” содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.
-
Уравнение для точки пересечения линии линейной регрессии a с осью y имеет следующий вид:
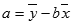
где наклон b вычисляется следующим образом:
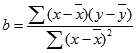
где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).
-
Алгоритм, лежащий в основе работы функций ОТРЕЗОК и НАКЛОН, отличается от алгоритма, на котором основана функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать в случае неопределенных и коллинеарных данных. Например, если точками данных аргумента “известные_значения_y” являются нули, а аргумента “известные_значения_x” — единицы, то справедливо указанное ниже.
-
От ПЕРЕХВАТ и НАКЛОН возвращают #DIV/0! ошибку “#ВЫЧИС!”. Алгоритмы ОТОКП и НАКЛОН предназначены для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
-
Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
-
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|
|
2 |
6 |
|
|
3 |
5 |
|
|
9 |
11 |
|
|
1 |
7 |
|
|
8 |
5 |
|
|
Формула |
Описание |
Результат |
|
=ОТРЕЗОК(A2:A6; B2:B6) |
Определяет точку пересечения линии с осью y, используя приведенные выше известные значения x и известные значения y |
0,0483871 |
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
