Как посчитать длину окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать длину окружности
Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
 Для того чтобы определить длину окружности вам необходимо знать её радиус или диаметр, либо её площадь. Зная хотя бы один из этих параметров, введите его в соответствующие поле и получите результат в виде длины окружности (длины дуги в 360 градусов).
Для того чтобы определить длину окружности вам необходимо знать её радиус или диаметр, либо её площадь. Зная хотя бы один из этих параметров, введите его в соответствующие поле и получите результат в виде длины окружности (длины дуги в 360 градусов).
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
её диаметр ?
Ответ:
0
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
её радиус ?
Ответ:
0
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
её площадь ?
Ответ:
0
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.
См. также
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое окружность?
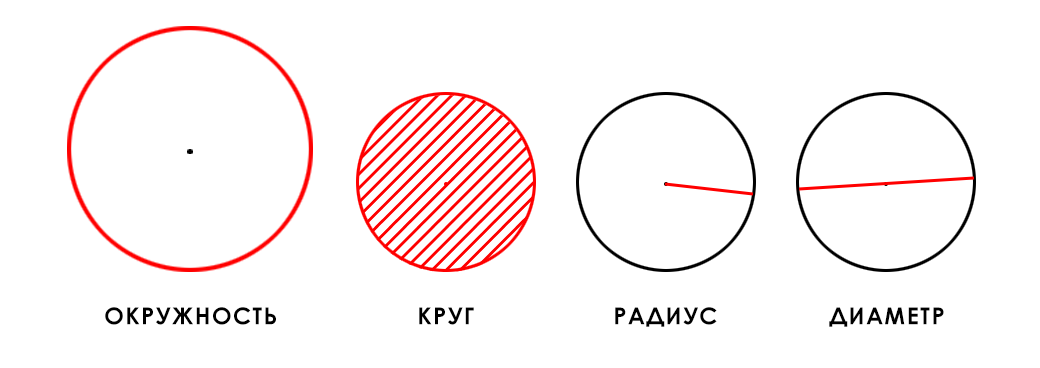
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
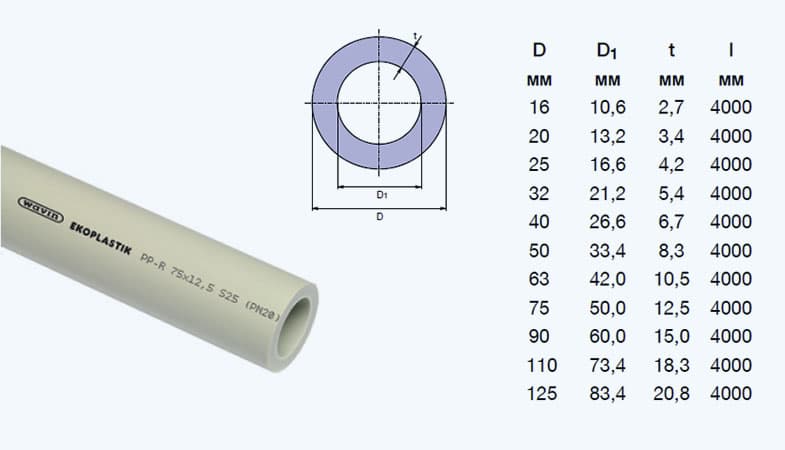
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.

Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как рассчитать периметр круга или длину окружности
На данной странице калькулятор поможет рассчитать периметр круга или длину окружности онлайн. Для расчета задайте радиус или диаметр.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
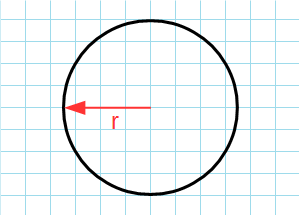
Формула для нахождения длины окружности или периметр круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
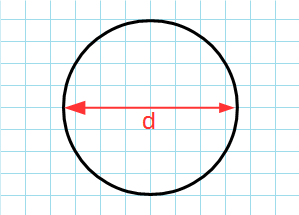
Формула для нахождения длины окружности или периметр круга через диаметр:
π – константа равная (3.14); d – диаметр.

{P = 2 pi R}
Найти длину окружности, которую часто называют периметром круга, поможет наш калькулятор. Для расчета просто введите радиус или диагональ окружности и получите ответ в режиме онлайн. Также мы приводим формулы для расчета длины окружности самостоятельно.
Содержание:
- калькулятор длины окружности
- формула длины окружности через радиус
- формула длины окружности через диаметр
- формула длины окружности через площадь круга
- примеры задач
Окружность — замкнутая плоская кривая у которой все ее точки удалены от данной точки (центра) на одинаковое расстояние (его называют радиус окружности) и лежат с ней в одной плоскости.
Перед тем, как говорить о вычислении длины окружности, необходимо познакомиться с основными понятиями. Нам необходимо понять значение терминов окружность, круг, радиус и диаметр. Графически они отображены на рисунке ниже.
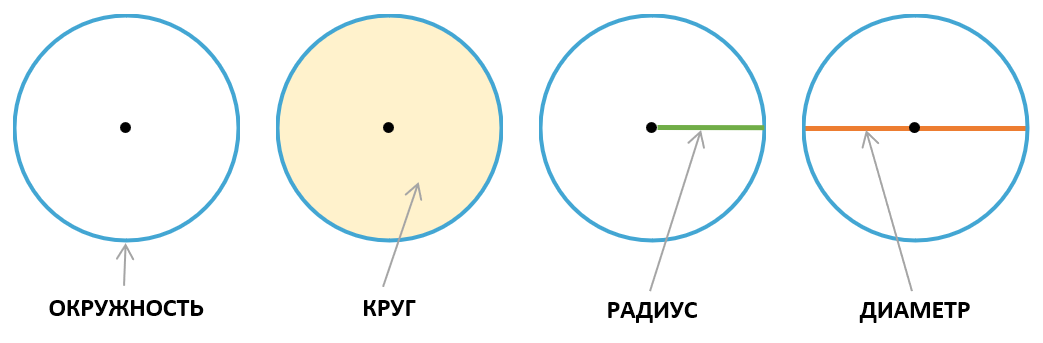
Формула длины окружности через радиус

{P = 2 pi R}
R – радиус окружности
Формула длины окружности через диаметр

{P = pi D}
D – диаметр окружности
Формула длины окружности через площадь круга
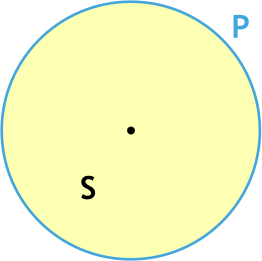
{P = sqrt{4S pi}}
S – площадь круга
Примеры задач на нахождение длины окружности
Задача 1
Найдите длину окружности, если её радиус равен 4.5см.
Решение
Воспользуемся первой формулой. Подставим значение радиуса и вычислим длину окружности:
P = 2 pi R = 2 pi cdot 4.5 = 9 pi : см approx 28.27433 : см
Ответ: {9 pi : см approx 28.27433 : см}
Проверить результат можно с помощью калькулятора .
Задача 1
Найдите длину окружности диаметр которой равен 1.8дм.
Решение
А в этом случае нам поможет вторая формула.
P = pi D = 1.8 pi = 1.8 pi : дм approx 5.65487 : дм
Ответ: {1.8 pi : дм approx 5.65487 : дм}
Проверим ответ .
Окружность представляет собой замкнутую кривую, все точки которой находятся на одинаковом расстоянии
от центра. Центр окружности – это точка, которая находится на равном расстоянии от всех точек,
расположенных на одной прямой. Также стоит различать два понятия: окружность и круг. Круг – это
просто часть некого пространства, которое ограничено окружностью. А окружностью представляет собой
совокупность точек на одной прямой. Понятия связаны, но имеют существенные различия.
- Длина окружности через радиус
- Длина окружности через диаметр
- Длина окружности через площадь круга
Через радиус
Для начала стоит сказать, что R- радиус окружности, Р – длина (периметр) окружности. Одним из самых
простых способов для ее вычисления является следующий:
Р = 2R * π
где R — Радиус.
Цифр после
запятой:
Результат в:
Пример. Дана окружность. Учащемуся требуется найти длину окружности, когда у него
есть только радиус. Радиус равен 15 см, тогда длина окружности? Решение. Находим неизвестную
величину по вышеупомянутой формуле: Р = 2R * π, восполняя данные, которые были указаны в условии. К
слову, π — это постоянная математическая величина. Чаще всего в ответах к заданиям она и
остается в таком виде, хотя у нее есть числовое значение, которое равно 3,14. Р = 2 * 15 * 3,14 = 9 см.
см. Решение не вызывает никаких вопросов, так как для нахождения неизвестной требуется только радиус
окружности.
Через диаметр
Диаметр – это радиус, который увеличили в два раза. Он тоже проходит через центр окружности и
касается контура, только уже в двух местах. Но через диаметр можно найти переменную – длину
(периметр) окружности. Это действие выполнимо благодаря следующей формуле:
P = D * π
где D – это диаметр окружности.
Цифр после
запятой:
Результат в:
Пример. Учащемуся необходимо найти длину (периметр) окружности. Из известных данных
только диаметр (D), который равен 20 см. Решение. Используем формулу, которая была указана выше и
подставим известные данные: Р = 20 * 3,14 = 6 см.
Через площадь окружности
Есть еще один способ, который поможет найти длину окружности. Этот способ основан на площади
окружности. Стоит упомянуть, что площадь можно найти по следующей формуле: S= πR², где S – это
площадь окружности, а R – радиус окружности. А длину окружности находят следующим образом:
P = √(S * 4π)
где S — это площадь окружности.
Цифр после
запятой:
Результат в:
Пример. Дана окружность, а учащемуся требуется найти ее длину (периметр). Он имеет
следующие данные: R = 3 см. Тогда чему равна длина окружности. Решение. Сначала требуется найти
площадь вышеуказанной фигуры: S = πR² = 3,14 * 9 = 28,26 см. Далее можно
уже находить и длину окружности, подставляя все уже известные данные в формулу, которая была
упомянута выше: P = √(S * 4π) = √(28,26 * 4 * 3,14) = 1,9 см.
Каждая окружность обладает некоторыми переменными, которые можно и нужно уметь различать. Например,
радиус – это расстояние от центра окружности до любой точки, которая лежит на окружности. Диаметр –
это то понятие, которое связано с радиусом. Он представляет собой отрезок, который проходит через
центр окружности и соединяет точки на этой же окружности, которые лежат напротив друг друга. Диаметр
– это увеличенный вдвое радиус. Любая фигура имеет площадь. Окружность не является
исключением. Таким образом, окружность является довольно важной фигурой, которая имеет множество
составляющих, которые позволяют находить ее длину несколькими способами.
