На чтение 11 мин Просмотров 5 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- Задача (условие, вопрос, схема, выражение, ответ). 1-й класс
- Схемы к задачам по математике 2 класс
- Задачи на нахождение суммы
- Задачи на увеличение уменьшение числа на несколько единиц
- Задачи на нахождение неизвестного слагаемого
- Задачи на нахождение остатка
- Задачи на нахождение неизвестного вычитаемого и слагаемого
- Задачи на разностное сравнение
- Задачи с косвенными вопросами
- Составные задачи на нахождение суммы
- Составные задачи на нахождение остатка
- Составные задачи на нахождение слагаемого и вычитаемого
- Составные задачи на нахождение третьего слагаемого
- Составные задачи на нахождение суммы
- Составные задачи на нахождение уменьшаемого
- Урок математики в 5 классе по теме «СХЕМА ДЛЯ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ЧИСЛОВЫХ ВЫРАЖЕНИЙ»
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
Задача (условие, вопрос, схема, выражение, ответ). 1-й класс
- Закрепление навыков устного счёта в пределах 10.
- Повторить составление выражений по рисункам, соотношение между целым и его частями.
- Уточнить термины, связанные с понятием «задача»: условие, вопрос, выражение, решение, ответ.
- Научить делать краткую запись в виде схем, познакомить с записью решения в тетради.
- Учить составлять задачи по схемам и числовым выражениям.
- Развивать мышление, речь, творческие способности.
- наглядность к устному счёту: ромашки, поезд, зайчик, Великий Математик;
- иллюстрация к задаче;
- плакаты: условие, вопрос, схема, выражение, решение, ответ;
- схемы к задачам;
- плакат (проверка № 5 с. 45).

— Ребята, сегодня на уроке мы отправляемся с вами путешествовать в страну Математики и нас будет сопровождать Великий Математик. Математика – это точная наука, требующая хороших знаний, чёткого выполнения всех арифметических действий.
— Какие действия мы с вами уже знаем? (Сложение и вычитание.)
— Во 2 классе мы познакомимся с умножением и делением.
— Сегодня на уроке мы будем заниматься наблюдениями, открывать математические закономерности, изучать новый материал.
1) Путешествовать мы с вами отправляемся на поезде, но прежде, чем наш поезд тронется, мы должны получить билеты. Для этого разделимся на команды и поиграем в игру «Кто быстрее?»
(Учащиеся выходят к доске и дописывают нужные числа.)

2) А теперь надо узнать № поезда. Для этого решим цепочку примеров:

Проверка (у каждого учащегося цифры, ответ показывает каждый с места).
(На доске картинка с зайчиком).

— Зайчик тоже хочет отправиться с нами путешествовать, но он не знает номер поезда, ему достался трудный пример. Он записан под цепочкой.
(Учащиеся записывают пример в тетради и решают.)
— Что вы заметили? (В примере выполнены те же действия, что и в цепочке. Значит ответ будет такой же 9.)
Значит Зайка едет в нашем поезде – берём его с собой.
Наш поезд отправился, давайте сосчитаем:
— Сколько пассажиров в каждом вагоне?
| 9-6 | 3 | 4+5 | 9 | 8-4 | 4 |
| 3+3 | 6 | 7-5 | 2 | 3+4 | 7 |
— Запишите их в порядке возрастания и вы отгадаете слово.
(На доске все картинки перемешаны, выходит ученик и располагает их в порядке возрастания.)
— Какое слово получилось? (Дети отвечают хором.)
IV. Знакомство с новым материалом.
Тема сегодняшнего урока: Задача.
Наш поезд делает I остановку в лесу. Рассмотрите иллюстрацию. Составьте задачу про детей.

«Мальчик и девочка пошли в лес за грибами. Мальчик нашёл 2 гриба, а девочка 4.Сколько всего грибов нашли дети?»
— Правильно. Без чего нет задачи? (Без вопроса.)
— В задаче всегда о чём-то спрашивается, без вопроса нет задачи. Это нужно хорошо понять и запомнить.
— Задачу можно разбить на 2 части:
- Условие – то, что известно.
- Вопрос – то, что неизвестно.
(На доске постепенно открываются плакаты: условие, вопрос, схема, выражение, решение, ответ.)
— Давайте повторим условие нашей задачи, вопрос.
— А теперь запишем в тетради: Задача.
— Ниже запишите выражение: 4 + 2.
— Найдите его значение: 4 + 2 = 6(гр.)
— Полученное равенство называют решением задачи, а значение выражения 6 грибов – ответом задачи.
Ответ: 6 грибов. (На доске записан образец записи.)
— Разобраться в этом помогает рисунок, но если числа большие то делать рисунок неудобно – слишком много предметов надо рисовать. На помощь приходит схема-отрезок, разбитый на части. Разбивая отрезок на части, мы получаем те же самые соотношения между частью и целым, что и при разбиении совокупностей предметов.

— Какой мы делаем вывод? (Наглядно представить содержание задачи можно сопоставив целое всему отрезку, а части – частям отрезка.)
— Что обозначает весь отрезок? (Число грибов, собранных детьми.)
— Что такое части? (Части отрезка.)
— Что обозначают части отрезка? (Грибы, собранные мальчиком и девочкой.)
— Что показывает знак вопроса? (Находят целое.)
— Каким действием решаем задачу? (Сложением.)
1) Следующая остановка нашего поезда «Поиграй-ка».
— А сейчас мы с вами немного поиграем.
— Великий Математик прислал конверты с задачами.
— Каждой группе нужно определить, что относится к условию, вопросу, найти схему, записать выражение, решение, назвать ответ.
А) Условие. Во дворе играли 6 ребят. Двое ушли домой.
Вопрос. Сколько ребят осталось во дворе?

Б) Условие. В хоре пело 4 мальчика и 6 девочек.
Вопрос. Сколько детей пело в хоре?

В) Условие. Из клетки улетело сначала 2 попугая, а потом ещё 3.
Вопрос. Сколько попугаев улетело из клетки?

2) Наш поезд продолжает путешествие.
— Следующая остановка: «Объясни-ка».
— Откройте учебник с. 44 урок 23 № 2.
— Что нужно сделать? (Соотнести записи в рамках с соответствующими терминами.)
— Назовите условие, вопрос, выражение, решение.
— Что обозначает весь отрезок? (Число конфет у девочки.)
— Его части? (Число конфет, которые она подарила и число конфет, которые у неё остались.)
— Почему задача решается вычитанием? (Ищем части.)
— Как найти часть? (Из целого вычитаем другую часть.)
3) Перейдём к №3. Составьте задачу по рисунку.
На столе лежали яблоки в 2-х вазах. В 1 вазе – 5 яблок, во 2 – 2 яблока.
— Сколько всего яблок лежало в двух вазах?
— Назовите условие, вопрос, выражение, решение.
— Что обозначает весь отрезок? (Все яблоки, лежащие на 1 и 2 вазе.)
— Его части? (1 ваза с яблоками, 2 – с яблоками.)
— Почему задача решается сложением? (Находим целое.)
4) Путешествие наше продолжается, но нам надо забрать багаж в камере хранения ( №5).
Расшифруем записи – код ячеек.
— Что нужно выполнить? (Составить выражение с заданным числовым значением и дорисовать картинки.) Выполните самостоятельно.
— Наше путешествие подходит к концу.
— И в последнем задании Великий Математик зашифровал слово.
— Если вы правильно выполните действие и сосчитаете, то узнаете слово (умница).
— Великий Математик считает, что вы все умницы, так как хорошо работали на уроке и правильно отвечали на все вопросы, и выполнили все задания.
— Что нового узнали, чем занимались на уроке?
Источник
Схемы к задачам по математике 2 класс
В этой ветке форума вы найдете основные типы задач для второго класса и схемы к ним. Теперь требования в начальной школе отличаются от тех требований, по которым учили нас в свое время. Раньше учили лишь записывать краткую запись, учителю важно было правильное решение и ответ. Теперь же обязательно требуется схема к задаче в виде одного или нескольких отрезков. На отрезках указываются данные и неизвестное.
Решение задачи у каждого ученика было по 3 ручки и 2 карандаша смотрите здесь
Задачи на нахождение суммы
У Сони было 4 синих карандаша и 3 коричневых. Сколько было всего карандашей у Сони?

Задачи на увеличение уменьшение числа на несколько единиц
Ване 8 лет, а его сестре – на 8 лет больше. Сколько лет сестре?

Задачи на нахождение неизвестного слагаемого
У кошки было 10 котят. 2 из них белого цвета, остальные — серого. Сколько серых котят было у кошки?

Задачи на нахождение остатка
.
У Вероники было 10 рублей. Она купила ручку за 8 рублей. Сколько денег осталось у Вероники?

Задачи на нахождение неизвестного вычитаемого и слагаемого
У Вики было 9 конфет. Когда несколько конфет Вика отдала друзьям, у нее осталось — 6. Сколько конфет подарила Вика?

Задачи на разностное сравнение
У Марины было 8 тетрадей, а у Маши — 5. На сколько больше тетрадей у Марины, чем у Маши?

Задачи с косвенными вопросами
Мама купила 7 кг вишни. что на 2 кг меньше, чем облепихи. Сколько кг облепихи купила мама?

Составные задачи на нахождение суммы
Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько всего фруктов купила хозяйка?

Составные задачи на нахождение остатка
Пете задали читать на лето 3 книги зарубежной литературы и 5 книг отечественной. После прочтения 6 книг, Пете осталось читать еще несколько. Cколько книг осталось прочитать Пете?

Составные задачи на нахождение слагаемого и вычитаемого
У кошки было 5 белых котят и 4 дымчатых. Когда несколько котят отдали, то их осталось 6. Сколько котят отдали?

Составные задачи на нахождение третьего слагаемого
Три друга – Миша, Саша и Ваня — получили за четверть 60 пятерок. Миша получил 10 пятерок, Саша – 20. Сколько пятерок получил Ваня?

Составные задачи на нахождение суммы
У Василисы 6 карамелек, шоколадных конфет на 4 меньше, мятных подушечек на 2 больше, чем шоколадных конфет. Сколько мятных подушечек у Василисы?

Составные задачи на нахождение уменьшаемого
Из пенала Витя взял 3 карандаша и 2 ручки. Сколько школьных принадлежностей в пенале было сначала, если в ней осталось 3 фломастера?

спасибо за схемы. но есть еще правила к схемам, а как они пишутся?
adoksana69, правил для составления схем нигде не видел. Нужно знать как, к каждому типу задач составляется схема. Ребенок справляется с заданием с помощью выработка навыка.
Источник
Урок математики в 5 классе по теме «СХЕМА ДЛЯ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ЧИСЛОВЫХ ВЫРАЖЕНИЙ»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Тема : Схема для вычисления значений числовых выражений
Цель : создание условий для закрепления знаний по теме урока; отработки умения составлять схемы для вычисления значений числовых выражений, развития вычислительных навыков, воспитания ответственного отношения к учебе
1) Выполните вычисления по схеме. Запишите выражение со скобками, соответствующее вычислительной схеме.


2) Составьте программу вычисления выражения:
Запишите эту программу в виде схемы. Найдите значение выражения.
1. Что такое команда? (Последовательность выполнения действий в выражении). № 630 (ниже дан образец выполнения).
Числовое выражение: 381 29 – 7248 : 24.
3) От результата выполнения команды 1 отнять результат выполнения команды 2.

3. Записать числовые выражения: № 646
5. Самостоятельная работа по вариантам.
Краткое описание документа:
Урок математики в 5 классе по теме «СХЕМА ДЛЯ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ЧИСЛОВЫХ ВЫРАЖЕНИЙ».
Цель : создание условий для закрепления знаний по теме урока; отработки умения составлять схемы для вычисления значений числовых выражений, развития вычислительных навыков, воспитания ответственного отношения к учебе.
1) Выполните вычисления по схеме. Запишите выражение со скобками, соответствующее вычислительной схеме.
2) Составьте программу вычисления выражения:
Запишите эту программу в виде схемы. Найдите значение выражения.
1. Что такое команда? (Последовательность выполнения действий в выражении). № 630 (ниже дан образец выполнения).
Числовое выражение: 381 × 29 – 7248 : 24.
3) От результата выполнения команды 1 отнять результат выполнения команды 2.
3. Записать числовые выражения: № 646
5. Самостоятельная работа по вариантам.

Курс повышения квалификации
Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 565 676 материалов в базе
Материал подходит для УМК

«Математика», Виленкин Н.Я., Жохов В.И. и др.
6. Сложение натуральных чисел и его свойства
Другие материалы
Оставьте свой комментарий
Добавить в избранное
- 31.03.2015 5138
- DOCX 23.1 кбайт
- 20 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Кислицина Лидия Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
![]()
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Онлайн-конференция о создании школьных служб примирения

В Египте нашли древние школьные «тетрадки»

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Объявлен конкурс дизайн-проектов для школьных пространств

Профессия педагога на третьем месте по популярности среди абитуриентов
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
Всякая хорошо решённая математическая задача
доставляет умственное наслаждение (Г. Гессе)
Умение решать задачи — показатель
математического развития учащихся, их
логического мышления. Ученикам нравится решать
то, что у них получается, то, что поддаётся
алгоритмизации. А текстовые задачи настолько
разнообразны, что порой трудно увидеть в
предлагаемой задаче уже знакомую. Чтобы научить
решать задачи надо сформировать умение выявлять
их математическую суть. Этому помогает
моделирование условия задачи с помощью
графических схем. Таким образом, научить решать
задачи — научить моделированию условия задачи и
переводу его с языка русского на язык
математический. Графическая модель задачи
помогает лучше понять условие, отношения величин
и облегчает процесс составления уравнений и их
систем.
Решение задачи с помощью уравнения состоит из
следующих шагов:
- Обозначение неизвестной величины буквой.
- Запись с помощью выражений информации, которая
содержится в условии задачи. - Составление уравнения.
- Решение уравнения.
- Запись ответа.
Многие трудности при решении задачи возникают
потому, что дети не умеют записывать в виде
выражений содержащуюся в условии задачи
информацию. Моделирование ситуации с помощью
схематических рисунков помогает переводу текста
условия задачи на математический язык выражений
и их равенств.
При изучении темы “Решение текстовых задач с
помощью уравнений” в курсе алгебры 8 класса, у
учащихся, как правило, возникают трудности при
работе с задачами на производительность труда
или так называемыми задачами на “совместный
труд”. В задачах такого типа сложный сюжет и его
не всегда легко перевести на язык чисел. Если
выделенный тип задач подвергнуть более
детальному рассмотрению, то получим следующие
результаты.
1. В задачах “на совместный труд”, используются
следующие величины:
• объём работы (если он неизвестен и не
является искомым, то принимается за 1);
• время выполнения работы;
• скорость выполнения работы
(производительность труда, т.е. объём работы,
выполняемый за единицу времени).
2. Для решения таких задач необходимо:
1) Определить скорость работы
(производительность труда) каждого объекта ![]()
2) Определить общую скорость выполнения работы ![]()
3) Найти общее время совместной работы ![]() .
.
В задачах на совместный труд объём работы может
быть известен, а может быть и нет.
При составлении графических схем к этим
задачам приходим к выводу, что схемы задач на
производительность труда похожи на схемы задач
на движение, в которых также участвуют три
величины: v; t; S. Таким образом, задачи на
производительность труда и задачи на движение
укладываются в одну схему:
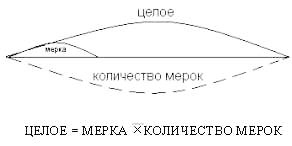
• В роли целого может выступать объём
работы или расстояние.
• В качестве мерки — скорость
движения или скорость работы
(производительность труда).
• Количество мерок может быть представлено временем
движения или временем выполнения работы.
Существуют ещё задачи, которые укладываются в
эту же схему.
Например, экономические, где в качестве величин
выступают: стоимость, цена, количество.
Есть мнение, что вообще все задачи
выстраиваются по одной схеме: нахождение целого,
если оно неизвестно, либо его составляющих.
Таким образом, целое можно найти двумя
способами:
|
I способ |
II способ |
|
Целое = часть + |
Целое = мерка (если целое нужно измерять) |
Рассмотрим примеры решения задач “на
совместный труд” с использованием графических
схем.
ЗАДАЧА №1: Малыш может съесть 600 граммов
варенья за 6 минут, а Карлсон в два раза быстрее.
За какое время они съедят это варенье вместе?
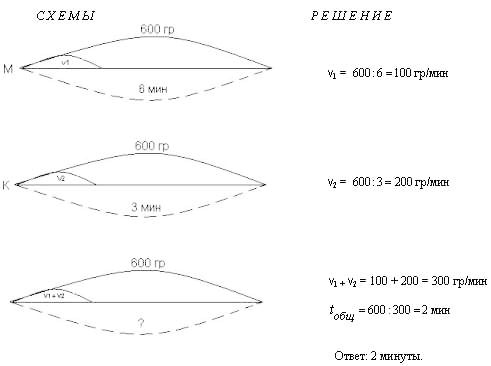
Теперь рассмотрим более сложную задачу “про
бассейны”.
ЗАДАЧА №2: Две трубы при совместном
действии могут наполнить бассейн за 4 часа. Если
бы сначала первая труба наполнила половину
бассейна, а затем её перекрыли и открыли вторую,
то наполнение бассейна было бы закончено за 9
часов. За сколько часов может наполнить этот
бассейн каждая труба в отдельности?
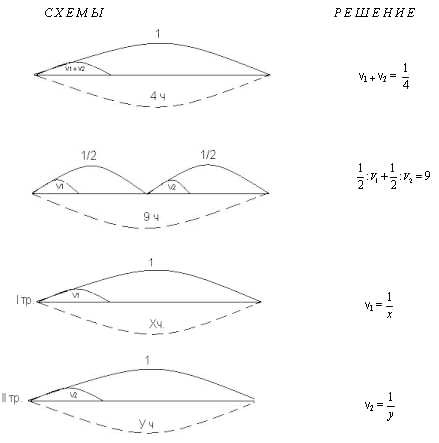
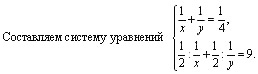
Решив её, получаем ответ 12 ч и 6 ч.
При решении текстовых задач учащимся можно
рекомендовать представлять условия в виде
графических схем. Этот приём помогает в анализе
ситуации, описанной в простой задаче, и даёт
способ решения сложных задач.
В заключение хотелось бы отметить, что изучение
способов решения задач нужно начинать не с
демонстрации учащимся решения, а подводить их к
“открытию” этого решения с помощью специально
подобранных подготовительных задач.
Очирова Жаргалма
Александровна учитель начальных классов МАОУ «СОШ№9»г.
Улан-Удэ
«Решение задач с
помощью схем»
Данная
работа является итогом десятилетнего опыта работы с опорными схемами в
начальных классах по математике. Как показывает практика, использование опорных
схем заметно повышает результативность обучению решению задач. Схемы легче
усваиваются детьми не только с высоким уровнем познания, но и детьми со
средним и низким уровнем успеваемости.
В
своей работе я использую опорные схемы из методических разработок по
математике по системе Эльконина – Давыдова. Ознакомление
младших школьников с решением задач производится в ходе выполнения практических
упражнений и эта работа ведётся в течение четырёх лет. Основная цель при решении
задач в 1-4 классах заключаются в том, чтобы создать у детей четкие и
правильные представления о способах решения данных задач, развить
пространственные представления, вооружить их навыками, имеющими большое
жизненно – практическое значение, и тем самым подготовить учеников к успешному применению
знаний в жизненных ситуациях.
Общее направление, в котором проходит изучение решению задач должно
быть от начала до конца активным, конкретным, наглядным. Все обучение следует
сопровождать практическими упражнениями, при этом учащиеся будут воспринимать
не только готовые схемы, но и сами будут создавать их.
Схемы –
большая помощь учителю на уроках математики.
Схема
даёт возможность наглядно представить соотношение между величинами. В процессе
определения и выбора схемы к задаче, уточняются связи между данными и искомыми
величинами, выбор действия решения. Дети видят, что известно и что нужно
найти, какие новые (промежуточные) данные потребуются им для ответа на основной
вопрос задачи.
Каждая схема представляет
определённый вид задач:
·
Нахождение суммы или одного из слагаемых.
·
Нахождение остатка, уменьшаемого или вычитаемого.
·
Увеличение или уменьшение числа на несколько единиц.
·
![]()
![]() На разностное сравнение.
На разностное сравнение.
Применение опорных схем
позволяет направить внимание детей на существенные признаки задач нового вида.
Формирование умения решать задачи является важным разделом
умственного воспитания, имеет широкое значение во всей познавательной
деятельности человека. Задача развития у младших школьников геометрических
представлений, способности к обобщению и анализу состоит в том, чтобы научить
их видеть математические (геометрические) образы в окружающей обстановке,
выделять их свойства, преобразовывать, изображать их на чертеже.
Для сравнения приведу пример краткой записи и схемы некоторых
задач, которые решаются в 1 – 2классах. Схема должна появляться на глазах у
ребенка.
Условные обозначения:
![]() – целое
– целое
– часть от целого
![]() – количество
– количество
![]()
– пунктирная линия обозначает некоторое количество
![]()
частей
– прямая линия обозначает целое или часть
Примерные
тексты задач:
Слайд 1-2.
1.
У Кати живут 4 черепахи и
несколько рыбок. Сколько животных у Кати, если рыбок 9?
![]() Черепах – 4 ?
Черепах – 4 ?
Рыбок– 9

4
9
?
(Обозначим количество
животных, которые живут у Кати, отрезком любой длины. Укажем сверху на отрезке
дужкой любой длины количество черепах, и второй дужкой – количество рыбок.
Дужкой внизу отметим количество всех животных. Найдем целое и отметим его
кружком, а части – треугольниками. Неизвестное находится в целом. Для того чтобы
найти целое – нужно сложить части.)
Слайд 3.
2.
Купили 4 красных, 3 синих
и несколько желтых шаров. Желтых было сколько, сколько красных и синих вместе.
Сколько желтых шаров?
![]()
![]() Красных шаров -4 ?
Красных шаров -4 ?
Синих шаров – 3
Желтых шаров – ?

3
4
?
(Аналогично покажем отрезками
красные и синие шары. Внизу начертим отрезок такой же длины, который покажет
количество желтых шаров. Неизвестное находится в целом. Чтобы найти целое –
нужно сложить части.)
Слайд 4.
3.
Длина ручки 14
см, а длина карандаша на 3 см короче. Чему равна длина карандаша?
Длина ручки – 14
см
Длина карандаша – ? на 3
см короче

14
3
?
 |
(Для того, чтобы показать что карандаш
короче ручки – вычеркнем небольшой отрезок. Неизвестное находится в части. Чтобы
найти часть – нужно из целого вычесть известную часть.)
Слайд 5.
4.
На катке было 15 детей.
Через час обедать ушли 4 мальчика и 3 девочки. Сколько детей осталось на катке?
Было – 15 д.
Ушли – ? 4
м. и 3 д.
Осталось – ? д.

15
? 3 4
 |
(Неизвестное находится в части. Для
того, чтобы найти часть нужно из целого вычесть известные части.)
Слайд 6.
5.
У Димы 14 рублей, у Кати 5
рублей. На сколько рублей у Кати меньше, чем у Димы?
![]() У Димы – 14
У Димы – 14
руб. на ?
У Кати – 5 руб.
![]()
5
![]()
![]()
![]()
14
![]()
![]()
![]()
![]()
?
 |
(Неизвестное находится в части. Чтобы найти
часть, нужно из целого вычесть известную часть.)
Слайд 7.
6.
В песочнице играют малыши:
6 девочек и несколько мальчиков. Мальчиков на 2 меньше, чем девочек. Сколько
всего малышей?
![]() Девочек
Девочек
–6 ?
Мальчиков – ? на 2 меньше

6
?
?
2
(Чтобы ответить на
основной вопрос задачи т.е. найти целое, нужно найти части. Это 6 и ?. Но 6 будет целым по
отношению к ? и 2, которые являются частями.
Как найти
неизвестную часть? Из известного целого вычесть известную часть: 6 – 2, а потом
прибавить вторую часть.)
Слайд 8.
7.
В гардеробе висят 43
пальто, плащей на 12 больше, чем пальто, а курток на 4 больше, чем плащей.
Сколько в гардеробе плащей? Сколько курток?
![]() Пальто –
Пальто –
43
![]()
![]()
![]() Плащей – ? на 12 больше
Плащей – ? на 12 больше
![]() Курток – ?
Курток – ?
на 4 больше

43
12
? 4
?
(Неизвестное находится в целом. Чтобы найти
целое нужно сложить части.)
Слайд 9.
8.
На 4 подоконника
расставили поровну 12 горшков с кактусами. Сколько горшков поставили на каждый
подоконник?
4 подок. – 12 горшк.
1 подок. – ? горшк.

12
?
4
(Пусть отрезок
обозначает количество горшков с кактусами 12 – целое.
На одном окне их
было ? – часть.
Чтобы не путать
количество горшков с количеством подоконников, обозначим подоконники пунктирной
дужкой 4 – количество неизвестных частей.
Неизвестное
находится в части. Чтобы его найти нужно целое разделить на количество.)
Слайд 10.
9.
Посадили 3 ряда кустов
смородины, по 8 кустов в ряду, и 18 кустов крыжовника. Сколько кустов посадили?
Смородины – ? к. 3 ряда по 8
кустов ?
Крыжовника – 18 кустов

? 18
8
3
?
 |
(Пусть 8 кустов в
одном ряду будет частью.
3 ряда – это
количество частей.
Всего кустов
смородины неизвестно. Неизвестное и будет целым.
Дорисуем до целого
отрезок, который обозначает кусты крыжовника.
Теперь целым
станет большой отрезок, а малое целое станет еще и частью для большого отрезка.
Чтобы ответить на
основной вопрос задачи нужно найти вторую неизвестную часть. Она является еще и
целым, которое можно найти если умножить часть на количество.)
Математика, 2 класс
Урок № 22. Решение текстовых задач. Запись решения выражением
Перечень вопросов, рассматриваемых в теме:
– Что такое встречное движение, расстояние?
– Как выполнять схематический чертёж к задачам на движение?
Глоссарий по теме:
Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.
Выражение – формула, выражающая какие–либо математические отношения.
Расстояние – пространственный промежуток, разделяющий два объекта, отрезок пути.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с.64.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.46.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.28.
- Математика. Проверочные работы. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 2-е изд. – М.: Просвещение, 2014. – с.30,31.
Теоретический материал для самостоятельного изучения
Расстояние – это путь, который прошёл какой-либо объект.
РАССТОЯНИЕ – промежуток в пространстве, разделяющий два объекта
Измеряя расстояние, мы будем использовать сокращённые записи.
1 МЕТР – 1м
1 ДЕЦИМЕТР – 1дм
1 САНТИМЕТР – 1 см
1 МИЛЛИМЕТР – 1 мм
Сегодня на уроке мы будем решать новые задачи – задачи на движение.
Длина аллеи 80 м. Два мальчика пошли навстречу друг другу. Один прошёл до встречи 45 м. Сколько прошёл до встречи другой мальчик?
Сделаем к задаче схематический чертёж.
Начертим отрезок, обозначающий длину всей дорожки, или расстояние между концами дорожки. Синей стрелкой обозначим длину дорожки. Укажем – 80 метров.



Мальчики шли навстречу друг другу с разных сторон дорожки. На чертеже это будем обозначать стрелками, которые показывают направление движения каждого мальчика.
Место встречи мальчиков будем обозначать флажком.



Теперь обозначим, что один мальчик прошёл до встречи 45 метров, а другой –
неизвестно. Поставим знак вопроса.



? м
45 м
Так выглядит схематический чертёж к задаче. По чертежу видно, что нам необходимо найти разность отрезков, выполнить вычитание.
Чтобы узнать, сколько метров до встречи прошёл второй мальчик, вычтем из длины всей дорожки длину пути, который прошёл первый мальчик.
80 – 45 = 35 (м) прошёл второй мальчик.
Второй мальчик прошёл до встречи 35 метров.
Решим вторую задачу:
Девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 30 м, другая на 4 метра меньше. Какой длины была дорожка?
Сделаем схематический чертёж к задаче.
Итак, нам надо найти длину всей дорожки. Для этого мы должны знать, сколько метров прошла каждая девочка. Мы знаем, сколько прошла первая девочка – 30 метров. А сколько прошла вторая девочка, нам надо узнать.



Будем решать задачу в два действия. Запишем первое действие:
1) 30 – 4 = 26 (м) прошла вторая девочка.
Вторая девочка прошла до встречи двадцать шесть метров.
Теперь можем ответить на вопрос задачи. Запишем второе действие:
2) 30 + 26 = 56 (м) длина дорожки.
Длина всей дорожки была 56 метров.
Вывод: Для решения задач на движение обычно выполняют чертёж, в котором стрелками показывают направление движения объектов. Движение может быть встречным или в противоположных направлениях.
Тренировочные задания.
1.Подберите схематический чертёж к задаче
Красная Шапочка отправилась в гости к бабушке. До дома бабушки нужно пройти 100 метров. Красная Шапочка уже прошла 70 метров. Сколько ей осталось пройти?




Правильные ответы:
Вторая схема.
2.Соедините каждый чертёж с карточкой, на которой записано соответствующее решение задачи.
 30 – 20
30 – 20
 30 + 20
30 + 20
 70 – 45
70 – 45
Правильные ответы:
 70 – 45
70 – 45
 30 + 20
30 + 20
 30 – 20
30 – 20
Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.
Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.
Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км – это известное расстояние. Неизвестные величины — это скорость и время.
Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.
Чтобы решить такую задачу потребуется составлять выражение. Принимать за “х” скорость первой или второй машины до встречи. За “у” время первой или второй машины также до встречи. Или обходиться одним “х”, а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а “решала” составляет выражения.
Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.

