Рассмотрим задачи на нахождение областей в комплексной плоскости, заданных неравенствами. Чтобы решить данные неравенства с комплексными числами, вначале необходимо перейти к декартовым координатам, т.е. перейти к действительному представлению.
Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z действительными переменными x и y, а именно z = x + iy, где
x = Re(z), y = Im(z).
Пример 1. Найти на комплексной плоскости множество точек, удовлетворяющих неравенству
|z + i| < 2.
Решение неравенства с комплексными числами начинается с представления числа в действительной форме. Неравенство примет вид:
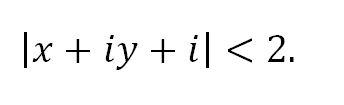
или

Для того, чтобы избавиться от ограждающего знака модуля, используют стандартную замену:
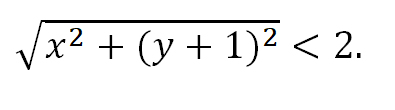
или
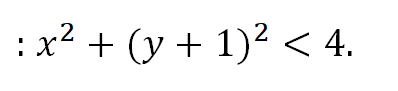
Как мы знаем из начальных уроков, |z| это модуль комплексного числа, х — действительная часть комплексного числа, y — это мнимая часть комплексного числа, которая находится в связке с мнимой единицей. Итоговый ответ, область решения — это часть плоскости, расположенная внутри круга
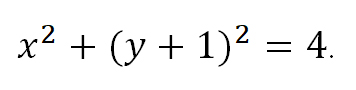
Пример 2. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству
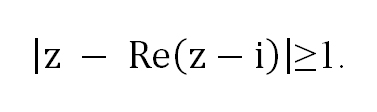
Заменяем переменную z представлением в действительной форме z = x + iy, приводим подобные члены, берем действительную часть от получившегося комплексного числа и
приводим к стандартному виду получившееся комплексное число:
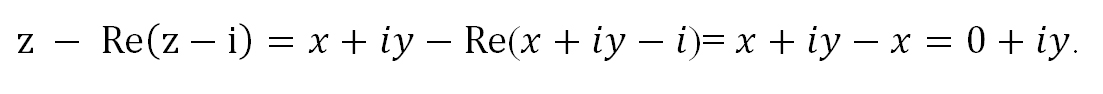
Областью решения неравенства
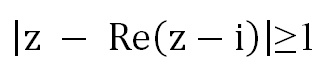
является плоскость, расположенная выше прямой у = 1. Рисунок не прикрепляю, все просто — чертим прямую у = 1 и штрихуем область выше этой прямой.
Чтобы изобразить область, заданную несколькими неравенствами, нужно изобразить области, задаваемые отдельными неравенствами, а затем найти их общую часть.
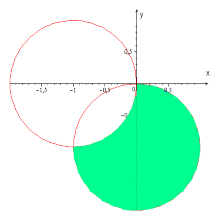
Пример 3. Построить область, заданную неравенствами

Вначале, заменяем z=x+iy, затем группируем подобные члены, чтобы сформировать действительное представление комплексного числа.
Первое неравенство задает внешнюю часть окружности радиуса 1 с центром в точке (-1; 0) с границей (белый круг). Второе неравенство задает внутреннюю часть окружности радиуса 1 с центром в точке (0; -1) без границы.
Сделаем рисунок в качестве графического доказательства. Область окружности, закрашенная зеленым цветом, является графическим ответом к решению заданного неравенства с комплексными числами:
Графический метод решения задач линейного программирования
1. Область решений линейных неравенств.
Пусть
задано линейное неравенство с двумя
переменными
![]() и
и![]()
![]()
![]() (1)
(1)
Если
величины
![]() и
и![]() рассматривать как координаты точки
рассматривать как координаты точки
плоскости, то совокупность точек
плоскости, координаты которых удовлетворяют
неравенству (1), называется областью
решений данного неравенства. Следовательно,
областью решений неравенства (1) является
полуплоскость с граничной прямой линией![]() .
.
Пример
1.
Найти полуплоскость, определяемую
неравенством
![]() .
.
Решение.
Строим прямую
![]() по двум точкам, например, по точкам
по двум точкам, например, по точкам
пересечения с осями координат (0; 4) и (6;
0). Эта линия делит плоскость на две
части, т.е. на две полуплоскости. Берем
любую точку плоскости, не лежащую на
построенной прямой. Если координаты
точки удовлетворяют заданному неравенству,
то областью решений является та
полуплоскость, в которой находится эта
точка. Если же получаем неверное числовое
неравенство, то областью решений является
та полуплоскость, которой эта точка не
принадлежит. Обычно для контроля берут
точку (0; 0).
Подставим
![]() и
и![]() в заданное неравенство. Получим
в заданное неравенство. Получим![]() .
.
Следовательно, полуплоскость «к нулю»
является областью решений данного
неравенства (заштрихованная часть
рис. 1).
Пример
2.
Найти полуплоскость, определяемую
неравенством
![]() .
.
Решение.
Строим прямую
![]() ,
,
например, по точкам (0; 0) и (1; 3). Т.к. прямая
проходит через начало координат, точку
(0; 0), то нельзя брать ее для контроля.
Возьмем, например, точку (– 2; 0) и подставим
ее координаты в заданное неравенство.
Получим![]() .
.
Это неверно. Значит, областью решений
данного неравенства будет та полуплоскость,
которой не принадлежит контрольная
точка (заштрихованная часть рис. 2).
2. Область решений системы линейных неравенств.
Пример.
Найти область решений системы неравенств:

Решение.
Находим область решений I-го
неравенства (рис. 1) и II-го
неравенства (рис. 2).
Все
точки части плоскости, где штриховка
наложилась, будут удовлетворять и
первому и второму неравенству. Таким
образом, получена область решений
заданной системы неравенств (рис. 3).
Если
к заданной системе неравенств добавить
условия
![]() и
и![]() ,
,
то область решений системы неравенств будет находиться только вI
будет находиться только вI
координатной четверти (рис. 4).
Принцип
нахождения решения системы линейных
неравенств не зависит от количества
неравенств, входящих в систему.
Примечание:
Область допустимых решений (ОДР) если
существует, то представляет собой
замкнутый или незамкнутый выпуклый
многоугольник.
3. Алгоритм графического метода решения злп
Если задача
линейного программирования содержит
только две переменные, то ее можно решить
графическим методом, выполняя следующие
операции:
-
Строим все
полуплоскости, соответствующие
ограничениям системы. -
Находим
область допустимых решений (ОДР), как
множество точек, в котором пересекаются
все построенные полуплоскости. -
Строим
вектор
 ,
,
выходящий из начала координат, где и
и – это коэффициенты при неизвестных в
– это коэффициенты при неизвестных в
целевой функции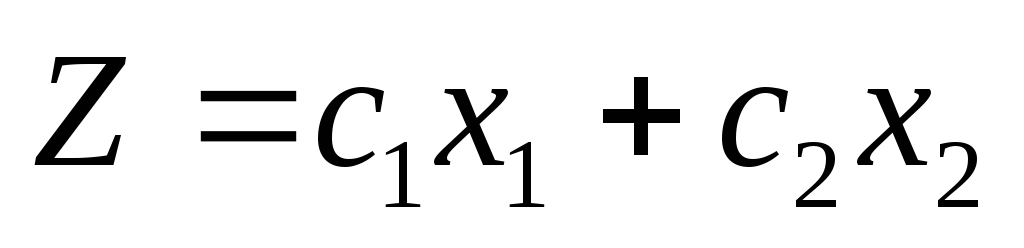 .
.
Этот вектор указывает направление
возрастания целевой функции. -
Перпендикулярно
вектору
 проводим так называемую линию уровня
проводим так называемую линию уровня (т.е. прямую
(т.е. прямую ,
,
проходящую через начало координат). -
Перемещаем
линию уровня
 параллельно самой себе в направлении
параллельно самой себе в направлении
вектора (если задача на максимум (max))
(если задача на максимум (max))
или в противоположном направлении
(если задача на минимум (min))
до тех пор, пока линия уровня имеет хотя
бы одну общую точку с ОДР. -
Находим
координаты
 этой общей крайней точки, решая систему
этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится. -
Подставляем
эти координаты в целевую функцию и
находим ее max
(или
min).
Пример.
Решить задачу линейного программирования
графическим методом
![]() max
max

Решение.
Третье и четвертое ограничения системы
– двойные неравенства, преобразуем их
к более привычному для подобных задач
виду
![]() ,
,
это![]() и
и![]() ,
,
т.о. первое из полученных неравенств![]() (или
(или![]() )
)
относится к условию неотрицательности,
а второе![]() к системе ограничений. Аналогично,
к системе ограничений. Аналогично,![]() это
это![]() и
и![]() .
.
Т.о. задача примет
вид
![]() max
max

![]() ,
,
![]()
Заменив знаки
неравенств на знаки точных равенств,
построим область допустимых решений
по уравнениям прямых:
![]()
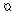


 ;
;
![]() ;
;![]() ;
;![]() .
.
Областью
решений неравенств является пятиугольник
ABCDE.
Построим
вектор
![]() .
.
Через
начало координат перпендикулярно
вектору
![]() проведем линию уровня
проведем линию уровня![]() .
.
И затем будем перемещать ее параллельно
самой себе в направлении вектора![]() до точки выхода из области допустимых
до точки выхода из области допустимых
решений. Это будет точкаС.
Найдем координаты этой точки, решив
систему, состоящую из уравнений первой
и четвертой прямых:

![]()

![]()
![]()
![]()
![]() .
.
Подставим
координаты точки С
в целевую функцию и найдем ее максимальное
значение
![]() Пример.
Пример.
Построить линии уровня
![]() и
и![]() для задачи линейного программирования:
для задачи линейного программирования:
![]()
max
(min)

Решение.
Область допустимых решений – открытая
область (рис. 6). Линия уровня
![]() проходит через точкуВ.
проходит через точкуВ.
Функция Z
имеет минимум в этой точке. Линию уровня
![]() построить нельзя, так как нет точки
построить нельзя, так как нет точки
выхода из области допустимых решений,
это значит, что![]() .
.
Задания
для самостоятельной работы.
-
Найти область
решений системы неравенств:
а)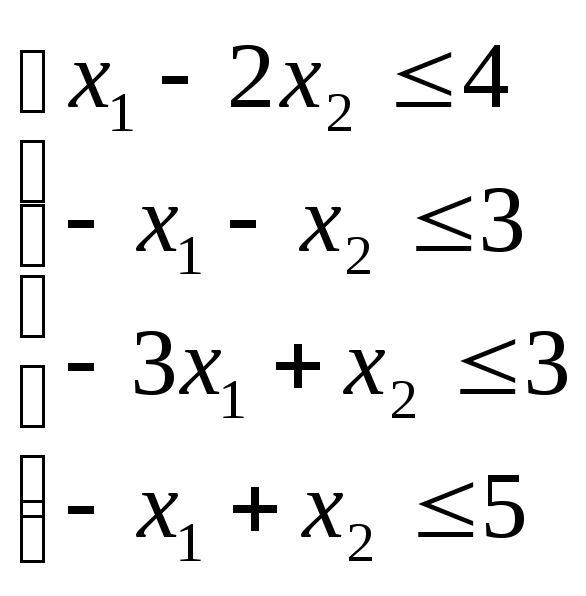 б)
б)
-
Решить графически
задачу линейного программирования
![]() min
min

-
Составить
экономико-математическую модель и
решить графически задачу линейного
программирования
Фирма
выпускает изделия двух видов А и
В. Изделия каждого вида обрабатывают
на двух станках (I
и II).
Время обработки одного изделия каждого
вида на станках, время работы станков
за рабочую смену, прибыль фирмы от
реализации одного изделия вида А и вида
В занесены в таблицу:
|
Станки |
Время |
Время |
|
|
А |
В |
||
|
I |
10 |
20 |
1300 |
|
II |
4 |
13 |
720 |
|
Прибыль |
0,3 |
0,9 |
Изучение рынка
сбыта показало, что ежедневный спрос
на изделия вида В никогда не превышает
спрос на изделия вида А более чем на 40
единиц, а спрос на изделия вида А не
превышает 90 единиц в день.
Определить план
производства изделий, обеспечивающий
наибольшую прибыль.
Область определения в уравнениях и неравенствах
Среди множества уравнений и неравенств выделить те , которые решаются с помощью нахождения ОДЗ
Скачать:
| Вложение | Размер |
|---|---|
| метод решения уравнений и неравенств | 67.88 КБ |
Предварительный просмотр:
§1.Нахождение области определения функции………………..…………………………….………5
§2. Область определения в уравнениях.………………………………………….…………………. 6
Тема: «Область определения в уравнениях и неравенствах».
Максакова Д.В., Забайкальский край, п.Карымское, МОУ «СОШ №5
п. Карымское с пришкольным интернатом»,11 класс.
Тема моей исследовательской работы «Область определения в уравнениях и неравенствах». На уроках алгебры область определения рассматривается при решении стандартных задач, но при конкурсном отборе и при подготовке к конкурсным экзаменам в ВУЗы, а также на олимпиадах встречаются задания, связанные с ограничением условий, которые требуют нестандартных приемов и подходов к решению. Кроме того, в части C тестов ЕГЭ часто встречаются задания, построенные на исследовании ОДЗ. Поэтому в настоящее время эта тема является актуальной.
Цель моей работы : найти среди множества уравнений и неравенств те, которые сводятся к изучению области определения, установить связь между уравнениями, неравенствами и системами уравнений и неравенств.
1) Просмотреть и изучить задания, связанные с ОДЗ.
2) Разбить их на группы, систематизировать знания о решении систем уравнений и неравенств.
При выполнении работы мне пришлось сравнивать различные методы, переходить от общих методов к частным, и наоборот. Также я обобщила информацию, собранную из различных источников. В связи с этим можно выделить следующие методы исследовательской деятельности: пошаговые, репродуктивные, логическое исследование.
В результате мной получены следующие результаты и выводы :
1) Во многих уравнениях и неравенствах область определения играет определяющую роль.
2) Чтобы найти ОДЗ, необходимо знать множество ограничений и свойств.
3) Нахождение ОДЗ не всегда необходимо.
Тема: «Область определения в уравнениях и неравенствах».
Максакова Д.В., Забайкальский край, п.Карымское, МОУ «СОШ №5 п. Карымское
с пришкольным интернатом»,11 класс.
Объектная область , в которой я проводила исследование, – алгебра.
Объект моего исследования – исследование ограничений в уравнениях и неравенствах.
Среди всех уравнений и неравенств я выбрала те, которые требуют изучение ОДЗ – предмет моего исследования .
Гипотеза : если правильно исследовать ОДЗ в уравнениях и неравенствах, то их решение значительно упростится.
Значит, если громоздкие выражения с помощью ограничений можно заменить несложными системами уравнений и неравенств, то можно сказать, что выбранная мною тема нужная и важная.
Свою работу я разбила на три параграфа. В первом параграфе я обобщила различные условия, при которых функция имеет ограничения, проиллюстрировала примерами процесс нахождения области определения функции.
Второй параграф был посвящен уравнениям, при решении которых ОДЗ играет ключевую роль. В этом же параграфе я рассмотрела ошибки при решении логарифмических уравнений, связанные с изменением ОДЗ, и случаи, когда задача определения ОДЗ оказывается сложной и абсолютно ненужной.
Свойства неравенств, которыми обусловлена их область определения, и промежутки возрастания и убывания функции были изучены в третьем параграфе.
Тема: «Область определения в уравнениях и неравенствах».
Максакова Д.В., Забайкальский край, п.Карымское, МОУ «СОШ №5п. Карымское
с пришкольным интернатом»,11 класс.
§1.Нахождение области определения функции
Процесс нахождения области определения функции состоит из двух этапов: составление системы ограничений и решение этой системы.
Чтобы составить систему ограничений нужно знать, чем вызваны ограничения:
При этом необходимо помнить, что выполнение преобразований заданной функции порой неправомерно. Разберем это на примере 1.
Найдите ОДЗ функций и
Решением является промежуток
При решении системы, составленной из ограничений, последовательно находят пересечения различных множеств, приближаясь к ответу. Пронаблюдаем это на примере.
Составим систему ограничений:
Рассмотрим еще несколько примеров.
§2.Область определения в уравнениях
Областью определения уравнения или областью допустимых значений (ОДЗ) уравнения называют множество тех значений неизвестного, при котором имеют смысл его левая и правая часть.
При решении уравнений, содержащих тригонометрические и логарифмические функции, ОДЗ играет ключевую роль. Покажем это на примерах.
На первый взгляд, в данном уравнении нет ограничений , но
при любых , значит 0 , тогда , то есть , ,
Найдите все значения , где , при котором уравнение имеет хотя бы одно решение, удовлетворяющее условию
Учитывая ограниченность функции , имеем:
Так как функция убывающая, получим
Тогда левая часть тоже имеет ограничения
Равенство , выполняется при ,
Учтем условие : , значит .
То есть , , так как , то ,
Часто при решении логарифмических уравнений используют прием логарифмирования обеих частей.
Найдем косинус от обеих частей уравнения:
Введем новую переменную: , , тогда
корней нет, значит .
Корень включает решение первого уравнения, то есть
Поскольку , , то левая часть равна 3, если
, только для четных , значит
Если , то функция убывает с ростом , следовательно, . Сложив почленно эти неравенства, будем иметь:
Следовательно, левая часть данного уравнения равна 1 тогда и только тогда, когда
То есть может принимать значения, а может принимать значения -1, 0. Тогда
то есть (3 и 4 четверть).
или – решения нет, так как , тогда , но учитывая то, что ,
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y = x + x – 2 или y = 5 · x 2 + 1 · x 3 , y = x x – 5 или y = x – 1 5 – 3 . Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y = f ( x ) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть ( 0 , + ∞ ) или такой [ − 3 , 1 ) ∪ [ 5 , 7 ) . Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y = x + 2 · x x 4 – 1 ;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y = x + 1 или y = 2 3 · x + 3 x ;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y = 5 · ( x + 1 ) – 3 , y = – 1 + x 1 1 3 , y = ( x 3 – x + 1 ) 2 , которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y = ln x 2 + x 4 или y = 1 + log x – 1 ( x + 1 ) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y = x 3 + t g 2 · x + 5 или y = c t g ( 3 · x 3 – 1 ) , так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y = a r c sin ( x + 2 ) + 2 · x 2 , y = a r c cos x – 1 + x , область определения которых определяется ни интервале от – 1 до 1 .
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y = x 4 + 2 · x 2 – x + 1 2 + 2 2 3 · x . Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y = 2 · x + 1 . Для вычисления ее значения можем определить x . Из выражения 2 · x + 1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y = 3 x – 1 , а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3 x – 1 знаменатель равняется нулю при х = 1 , поэтому искомая область определения данной функции примет вид ( − ∞ , 1 ) ∪ ( 1 , + ∞ ) и считается числовым множеством.
На рассмотрении примера y = x 2 – 5 · x + 6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x 2 − 5 · x + 6 ≥ 0 . После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как ( − ∞ , 2 ] ∪ [ 3 , + ∞ ) .
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция f f считается суммой n функций f 1 , f 2 , … , f n , иначе говоря, эта функция задается при помощи формулы y = f 1 ( x ) + f 2 ( x ) + … + f n ( x ) , тогда ее область определения считается пересечением областей определения функций f 1 , f 2 , … , f n . Данное утверждение можно записать как:
D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y = x 7 + x + 5 + t g x .
Заданная функция представляется как сумма четырех: степенной с показателем 7 ,степенной с показателем 1 , постоянной, функции тангенса.
По таблице определения видим, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) , D ( f 3 ) = ( − ∞ , + ∞ ) , причем область определения тангенса включает в себя все действительные числа, кроме π 2 + π · k , k ∈ Z .
Областью определения заданной функции f является пересечение областей определения f 1 , f 2 , f 3 и f 4 . То есть для функции существует такое количество действительных чисел, куда не входит π 2 + π · k , k ∈ Z .
Ответ: все действительные числа кроме π 2 + π · k , k ∈ Z .
Для нахождения области определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f 1 , f 2 , f 3 и f n , тогда существует такая функция f , которую можно задать при помощи формулы y = f 1 ( x ) · f 2 ( x ) · … · f n ( x ) , тогда ее область определения считается областью определения для всех функций.
Запишется D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Найти область определения функции y = 3 · a r c t g x · ln x .
Правая часть формулы рассматривается как f 1 ( x ) · f 2 ( x ) · f 3 ( x ) , где за f 1 является постоянной функцией, f 2 является арктангенсом, f 3 – логарифмической функцией с основанием e . По условию имеем, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) и D ( f 3 ) = ( 0 , + ∞ ) . Мы получаем, что
D ( f ) = D ( f 1 ) D ( f 2 ) D ( f n ) = ( – ∞ , + ∞ ) ( – ∞ , + ∞ ) D ( 0 , + ∞ ) = ( 0 , + ∞ )
Ответ: область определения y = 3 · a r c t g x · ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y = C · f ( x ) , где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y = C · f ( x ) – произведение постоянной функции и f . Область определения – это все действительные числа области определения D ( f ) . Отсюда видим, что область определения функции y = C · f ( x ) является – ∞ , + ∞ D ( f ) = D ( f ) .
Получили, что область определения y = f ( x ) и y = C · f ( x ) , где C является некоторое действительное число, совпадают. Это видно на примере определения корня y = x считается [ 0 , + ∞ ) , потому как область определения функции y = – 5 · x – [ 0 , + ∞ ) .
Области определения y = f ( x ) и y = − f ( x ) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y = log 3 x − 3 · 2 x .
Необходимо рассмотреть как разность двух функций f 1 и f 2 .
f 1 ( x ) = log 3 x и f 2 ( x ) = 3 · 2 x . Тогда получим, что D ( f ) = D ( f 1 ) D ( f 2 ) .
Область определения записывается как D ( f 1 ) = ( 0 , + ∞ ) . Приступим к области определения f 2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D ( f 2 ) = ( − ∞ , + ∞ ) .
Для нахождения области определения функции y = log 3 x − 3 · 2 x получим, что
D ( f ) = D ( f 1 ) D ( f 2 ) = ( 0 , + ∞ ) – ∞ , + ∞
Необходимо озвучить утверждение о том, что областью определения y = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 является множество действительных чисел.
Рассмотрим y = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 , где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы ( n + 1 ) -ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R .
Найти область определения f 1 ( x ) = x 5 + 7 x 3 – 2 x 2 + 1 2 .
Примем обозначение f за разность двух функций, тогда получим, что f 1 ( x ) = x 5 + 7 x 3 – 2 x 2 + 1 2 и f 2 ( x ) = 3 · x – ln 5 . Выше было показано, что D ( f 1 ) = R . Область определения для f 2 является совпадающей со степенной при показателе – ln 5 , иначе говоря, что D ( f 2 ) = ( 0 , + ∞ ) .
Получаем, что D ( f ) = D ( f 1 ) D ( f 2 ) = – ∞ , + ∞ ( 0 , + ∞ ) = ( 0 , + ∞ ) .
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y = f 1 ( f 2 ( x ) ) . Известно, что D ( f ) является множеством всех x из определения функции f 2 , где область определения f 2 ( x ) принадлежит области определения f 1 .
Видно, что область определения сложной функции вида y = f 1 ( f 2 ( x ) ) находится на пересечении двух множеств таких, где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . В стандартном обозначении это примет вид
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 )
Рассмотрим решение нескольких примеров.
Найти область определения y = ln x 2 .
Данную функцию представляем в виде y = f 1 ( f 2 ( x ) ) , где имеем, что f 1 является логарифмом с основанием e , а f 2 – степенная функция с показателем 2 .
Для решения необходимо использовать известные области определения D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) .
Тогда получим систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ – ∞ , + ∞ x 2 ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( – ∞ , + ∞ ) x 2 > 0 ⇔ x ∈ ( – ∞ , + ∞ ) x ∈ ( – ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( – ∞ , 0 ) ∪ ( 0 , + ∞ )
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Найти область определения функции y = ( a r c sin x ) – 1 2 .
Так как дана сложная функция, необходимо рассматривать ее как y = f 1 ( f 2 ( x ) ) , где f 1 является степенной функцией с показателем – 1 2 , а f 2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = [ − 1 , 1 ] . Теперь найдем все множества значений x , где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . Получаем систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ – 1 , 1 a r c sin x ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ – 1 , 1 a r c sin x > 0
Для решения a r c sin x > 0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [ − 1 , 1 ] , причем обращается в ноль при х = 0 , значит, что a r c sin x > 0 из определения x принадлежит промежутку ( 0 , 1 ] .
Преобразуем систему вида
x ∈ – 1 , 1 a r c sin x > 0 ⇔ x ∈ – 1 , 1 x ∈ ( 0 , 1 ] ⇔ x ∈ ( 0 , 1 ]
Область определения искомой функции имеет интервал равный ( 0 , 1 ] .
Ответ: ( 0 , 1 ] .
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y = f 1 ( f 2 ( … f n ( x ) ) ) ) . Область определения такой функции ищется из x ∈ D ( f n ) f n ( x ) ∈ D ( f n – 1 ) f n – 1 ( f n ( x ) ) ∈ D ( f n – 2 ) . . . f 2 ( f 3 ( . . . ( f n ( x ) ) ) ∈ D ( f 1 ) .
Найти область определения y = sin ( l g x 4 ) .
Заданная функция может быть расписана, как y = f 1 ( f 2 ( f 3 ( x ) ) ) , где имеем f 1 – функция синуса, f 2 – функция с корнем 4 степени, f 3 – логарифмическая функция.
Имеем, что по условию D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = [ 0 , + ∞ ) , D ( f 3 ) = ( 0 , + ∞ ) . Тогда областью определения функции – это пересечение множеств таких значений, где x ∈ D ( f 3 ) , f 3 ( x ) ∈ D ( f 2 ) , f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) . Получаем, что
x ∈ D ( f 3 ) f 3 ( x ) ∈ D ( f 2 ) f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ – ∞ , + ∞
Условие lg x 4 ∈ – ∞ , + ∞ аналогично условию l g x ∈ [ 0 , + ∞ ) , значит
x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ – ∞ , + ∞ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ 0 ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ lg 1 ⇔ x ∈ ( 0 , + ∞ ) x ≥ 1 ⇔ ⇔ x ∈ [ 1 , + ∞ )
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f 1 ( x ) f 2 ( x ) . Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f 2 ( х ) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Запишем функцию y = f 1 ( x ) f 2 ( x ) в виде y = f 1 ( x ) · ( f 2 ( x ) ) – 1 . Тогда получим произведение функций вида y = f 1 ( x ) с y = ( f 2 ( x ) ) – 1 . Областью определения функции y = f 1 ( x ) является множество D ( f 1 ) , а для сложной y = ( f 2 ( x ) ) – 1 определим из системы вида x ∈ D ( f 2 ) f 2 ( x ) ∈ ( – ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Значит, x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ∈ ( – ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Найти область определения y = t g ( 2 · x + 1 ) x 2 – x – 6 .
Заданная функция дробная, поэтому f 1 – сложная функция, где y = t g ( 2 · x + 1 ) и f 2 – целая рациональная функция, где y = x 2 − x − 6 , а область определения считается множеством всех чисел. Можно записать это в виде
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0
Представление сложной функции y = f 3 ( f 4 ( x ) ) , где f 3 –это функция тангенс, где в область определения включены все числа, кроме π 2 + π · k , k ∈ Z , а f 4 – это целая рациональная функция y = 2 · x + 1 с областью определения D ( f 4 ) = ( − ∞ , + ∞ ) . После чего приступаем к нахождению области определения f 1 :
x ∈ D ( f 4 ) 2 · x + 1 ∈ D ( f 3 ) ⇔ x ∈ ( – ∞ , + ∞ ) 2 x + 1 ≠ π 2 + π · k , k ∈ Z ⇔ x ≠ π 4 – 1 2 + π 2 · k , k ∈ Z
Еще необходимо рассмотреть нижнюю область определения y = t g ( 2 · x + 1 ) x 2 – x – 6 . Тогда получаем, что
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 ⇔ x ≠ π 4 – 1 2 + π 2 · k , k ∈ Z x ∈ – ∞ , + ∞ x 2 – x – 6 ≠ 0 ⇔ ⇔ x ≠ π 4 – 1 2 + π 2 · k , k ∈ Z x ≠ – 2 x ≠ 3
Ответ: множество действительных чисел, кроме – 2 , 3 и π 4 – 1 2 + π 2 · k , k ∈ Z .
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1 . Отсюда видно, что функция y = log f 2 ( x ) f 1 ( x ) имеет область определения, которая выглядит так:
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 . После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y = log a f 1 ( x ) и y = log a f 2 ( x ) можно определить из получившейся системы вида x ∈ D ( f 1 ) f 1 ( x ) > 0 и x ∈ D ( f 2 ) f 2 ( x ) > 0 . Иначе эту область можно записать в виде y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 , что означает нахождение y = log f 2 ( x ) f 1 ( x ) из самой системы вида
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 log a f 2 ( x ) ≠ 0 = x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
Обозначить область определения функции y = log 2 · x ( x 2 – 6 x + 5 ) .
Следует принять обозначения f 1 ( x ) = x 2 − 6 · x + 5 и f 2 ( x ) = 2 · x , отсюда D ( f 1 ) = ( − ∞ , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) . Необходимо приступить к поиску множества x , где выполняется условие x ∈ D ( f 1 ) , f 1 ( x ) > 0 , x ∈ D ( f 2 ) , f 2 ( x ) > 0 , f 2 ( x ) ≠ 1 . Тогда получаем систему вида
x ∈ ( – ∞ , + ∞ ) x 2 – 6 x + 5 > 0 x ∈ ( – ∞ , + ∞ ) 2 · x > 0 2 · x ≠ 1 ⇔ x ∈ ( – ∞ , + ∞ ) x ∈ ( – ∞ , 1 ) ∪ ( 5 , + ∞ ) x ∈ ( – ∞ , + ∞ ) x > 0 x ≠ 1 2 ⇔ ⇔ x ∈ 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ )
Отсюда видим, что искомой областью функции y = log 2 · x ( x 2 – 6 x + 5 ) считается множнство, удовлетворяющее условию 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Ответ: 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y = ( f 1 ( x ) ) f 2 ( x ) . Ее область определения включает в себя такие значения x , которые удовлетворяют системе x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Эта область позволяет переходить от показательно-степенной к сложной вида y = a log a ( f 1 ( x ) ) f 2 ( x ) = a f 2 ( x ) · log a f 1 ( x ) , где где a > 0 , a ≠ 1 .
Найти область определения показательно-степенной функции y = ( x 2 – 1 ) x 3 – 9 · x .
Примем за обозначение f 1 ( x ) = x 2 − 1 и f 2 ( x ) = x 3 – 9 · x .
Функция f 1 определена на множестве действительных чисел, тогда получаем область определения вида D ( f 1 ) = ( − ∞ , + ∞ ) . Функция f 2 является сложной, поэтому ее представление примет вид y = f 3 ( f 4 ( x ) ) , а f 3 – квадратным корнем с областью определения D ( f 3 ) = [ 0 , + ∞ ) , а функция f 4 – целой рациональной, D ( f 4 ) = ( − ∞ , + ∞ ) . Получаем систему вида
x ∈ D ( f 4 ) f 4 ( x ) ∈ D ( f 3 ) ⇔ x ∈ ( – ∞ , + ∞ ) x 3 – 9 · x ≥ 0 ⇔ ⇔ x ∈ ( – ∞ , + ∞ ) x ∈ – 3 , 0 ∪ [ 3 , + ∞ ) ⇔ x ∈ – 3 , 0 ∪ [ 3 , + ∞ )
Значит, область определения для функции f 2 имеет вид D ( f 2 ) = [ − 3 , 0 ] ∪ [ 3 , + ∞ ) . После чего необходимо найти область определения показательно-степенной функции по условию x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Получаем систему вида x ∈ – ∞ , + ∞ x ∈ – 3 , 0 ∪ [ 3 , + ∞ ) x 2 – 1 > 0 ⇔ x ∈ – ∞ , + ∞ x ∈ – 3 , 0 ∪ [ 3 , + ∞ ) x ∈ ( – ∞ , – 1 ) ∪ ( 1 , + ∞ ) ⇔ ⇔ x ∈ – 3 , – 1 ∪ [ 3 , + ∞ )
Ответ: [ − 3 , − 1 ) ∪ [ 3 , + ∞ )
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
Сумма, разность, произведение функций
f 1 , f 2 , . . . , f n
D ( f 1 ) , D ( f 2 ) , . . . , D ( f n )
y = f 1 ( f 2 ( f 3 ( . . . f n ( x ) ) ) )
Множество всех x , одновременно удовлетворяющих условиям
x ∈ D ( f n ) , f n ( x ) ∈ D ( f n – 1 ) , f n – 1 ( f n ( x ) ) ∈ D ( f n – 2 ) , . . . , f 2 ( f 3 ( . . . f n ( x ) ) ) ∈ D ( f 1 )
x ∈ D ( f 2 ) , f 2 ( x ) ∈ D ( f 1 )
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y = k · x
Обратная пропорциональность y = k x
Дробная y = f 1 ( x ) f 2 ( x )
В частности, если f 1 ( x ) , f 2 ( x ) – многочлены
Множество всех x , которые одновременно удовлетворяют условиям
x ∈ D ( f 1 ) , x ∈ D ( f 2 ) , f 2 ( x ) ≠ 0
y = log f 2 ( x ) f 1 ( x )
В частности, y = log a f 1 ( x )
В частности, y = log f 2 ( x ) a
x ∈ D ( f 1 ) , f 1 ( x ) > 0 , x ∈ D ( f 2 ) , f 2 ( x ) > 0 , f 2 ( x ) ≠ 1
x ∈ D ( f 1 ) , f 1 ( x ) > 0
x ∈ D ( f 2 ) , f 2 > 0 , f 2 ( x ) ≠ 1
| Функция | Ее область определения |
| R | |
| Линейная y = k · x + b | R |
| – ∞ , 0 ∪ 0 , + ∞ | |
| Квадратичная y = a · x 2 + b · x + c | R |
| y = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 | R |
| Целая рациональная | R |
| y = C · f ( x ) , где C – число | D ( f ) |
| y = f ( x ) n , где n – четное | x ∈ D ( f 1 ) , f ( x ) ≥ 0 |
| Показательно-степенная y = ( f 1 ( x ) ) f 2 ( x ) | x ∈ D ( f 1 ) , x ∈ D ( f 2 ) , f 1 ( x ) > 0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y = x 2 – 4 x – 2 и y = x + 2 являются разными функциями, так как первая определяется на ( − ∞ , 2 ) ∪ ( 2 , + ∞ ) , а вторая из множества действительных чисел. Из преобразования y = x 2 – 4 x – 2 = x – 2 x + 2 x – 2 = x + 2 видно, что функция имеет смысл при x ≠ 2 .
Область допустимых значений: теория и практика

Конкурс исследовательских и проектных работ учащихся
«ИНТЕЛЛЕКТУАЛЬНОЕ БУДУЩЕЕ МОРДОВИИ»
ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ:
ТЕОРИЯ И ПРАКТИКА
Автор: Малышева Оксана
2. Исторический очерк 4
3. «Место» ОДЗ при решении уравнений и неравенств 5-6
4. Особенности и опасность ОДЗ 7
5. ОДЗ – есть решение 8-9
6. Нахождение ОДЗ – лишняя работа.
Равносильность переходов 10-13
7. ОДЗ в ЕГЭ 14-15
8. Заключение 16
9. Литература 17
Уравнения и неравенства, в которых нужно находить область допустимых значений, не нашли места в курсе алгебры систематического изложения, возможно поэтому мои сверстники часто делают ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об области допустимых значений. Это и определило проблему данной работы.
В настоящей работе предполагается исследовать явление существования области допустимых значений при решении уравнений и неравенств разных типов; проанализировать данную ситуацию, сделать логически корректные выводы в примерах, где нужно учитывать область допустимых значений.
-
Опираясь на имеющийся опыт и теоретическую базу, собрать основные сведения об области допустимых значений и её использовании в школьной практике; Проанализировать решения разнообразных типов уравнений и неравенств (дробно-рациональных, иррациональных, логарифмических, содержащих обратные тригонометрические функции); Проверить ранее полученные при решении различных уравнений и неравенств результаты, убедиться в надёжности способов и методов их решения; Определить «место» области допустимых значений при решении уравнений и неравенств; Применить полученные материалы исследования в ситуации, которая отличается от стандартной, и использовать их при подготовке к ЕГЭ.
При решении этих задач использованы следующие методы исследования: анализ, статистический анализ, дедукция, классификация, прогнозирование.
Исследование начато с повторения известных функций, изучаемых в школьной программе. Область определения многих из них имеет ограничения.
Область допустимых значений встречается при решении: дробно-рациональных уравнений и неравенств; иррациональных уравнений и неравенств; логарифмических уравнений и неравенств; уравнений и неравенств, содержащих обратные тригонометрические функции.
Прорешав множество примеров из различных источников (пособий по ЕГЭ, учебников, справочников), выделили решение примеров по следующим принципам:
· можно решить пример и учесть ОДЗ (самый распространённый способ)
· можно решить пример, не учитывая ОДЗ
· можно только учитывая ОДЗ прийти к правильному решению.
Изучен анализ результатов ЕГЭ за прошедшие годы. Много ошибок было допущено в примерах, в которых нужно учитывать ОДЗ. Практическое значение работы заключается в том, что ее содержание, оценки и выводы могут быть использованы в преподавании математики в школе, при подготовке к итоговой аттестации школьников 9 и 11 классов.
2. Исторический очерк
Как и остальные понятия математики, понятие функции сложилось не сразу, а прошло долгий путь развития. В работе П. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. 1679) говорится: «Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется место». По существу здесь идёт речь о функциональной зависимости и её графическом изображении («место» у Ферма означает линию). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У И. Барроу («Лекции по геометрии», 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчётливом владении понятием функции. В геометрическом и механическом виде это понятие мы находим и у И. Ньютона. Однако термин «функция» впервые появляется лишь в 1692 у Г. Лейбница и притом не совсем в современном его понимании. Г. Лейбниц называет функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.
Первое определение функции в смысле, близком к современному, встречается у И. Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Л. Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств». Впрочем, уже Л. Эйлеру не чуждо и современное понимание функции, которое не связывает понятие функции с каким-либо аналитическим её выражением. В его «Дифференциальном исчислении» (1755) говорится: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функциями вторых».
С начала XIX века уже всё чаще и чаще определяют понятие функции без упоминания об её аналитическом изображении. В «Трактате по дифференциальному и интегральному исчислению» (1797—1802) С. Лакруа говорится: «Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних». В «Аналитической теории тепла» Ж. Фурье (1822) имеется фраза: «Функция f(x) обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям x, содержащимся между 0 и какой-либо величиной x». Близко к современному и определение Н. И. Лобачевского: «…Общее понятие функции требует, чтобы функцией от x называть число, которое даётся для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной». Там же немного ниже сказано: «Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе». Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое П. Дирихле (1837), неоднократно предлагалось и до него:
у есть функция переменной х (на отрезке  ), если каждому значению х (на этом отрезке) соответствует совершенно определённое значение у, причем безразлично, каким образом установлено это соответствие — аналитической формулой, графиком, таблицей, либо даже просто словами. [[1]]
), если каждому значению х (на этом отрезке) соответствует совершенно определённое значение у, причем безразлично, каким образом установлено это соответствие — аналитической формулой, графиком, таблицей, либо даже просто словами. [[1]]
3. «Место» области допустимых значений при решении уравнений и неравенств
При решении уравнений и неравенств часто возникает дилемма: находить область допустимых значений или нет, выбрать традиционный способ решения или воспользоваться нерациональным, объёмным, чтобы рассмотреть все варианты, не совершить ошибку и прийти, наконец, к верному решению.
Для начала вспомним методы решения уравнений и неравенств разных видов и уровней сложности, рассмотрим частные случаи.
1. При решении дробно-рациональных уравнений и неравенств знаменатель не должен равняться нулю.
2. Решение иррациональных уравнений и неравенств.
2.1. Простейшие иррациональные уравнения имеют вид  . Возведя обе части уравнения в квадрат, мы избавимся от иррациональности. Но обратим внимание на то, что возведение в квадрат, вообще говоря, не равносильное преобразование, и при возведении в квадрат мы можем получить лишние корни. Если корни получились целые, то несложно произвести проверку. Но в некоторых случаях производить проверку неудобно. Тогда используют сведение данного уравнения к равносильной системе:
. Возведя обе части уравнения в квадрат, мы избавимся от иррациональности. Но обратим внимание на то, что возведение в квадрат, вообще говоря, не равносильное преобразование, и при возведении в квадрат мы можем получить лишние корни. Если корни получились целые, то несложно произвести проверку. Но в некоторых случаях производить проверку неудобно. Тогда используют сведение данного уравнения к равносильной системе:
 .
.
В данном случае нет необходимости находить ОДЗ: из первого уравнения следует, что при полученных значения х выполняется неравенство:  .
.
2.2. Решением уравнения вида  является система:
является система:
 Поскольку в уравнение
Поскольку в уравнение  и
и  входят равноправно, то вместо неравенства
входят равноправно, то вместо неравенства  , можно включить неравенство
, можно включить неравенство  , и естественно, надо выбирать из них наиболее простое.
, и естественно, надо выбирать из них наиболее простое.
2.3. Схемы решения основных иррациональных неравенств:







3. Решение логарифмических уравнений и неравенств.
3.1. Схема решения логарифмического уравнения

Но проверить достаточно только одно условие ОДЗ.
3.2. Схема решения логарифмического неравенства вида  : 1)
: 1)  2)
2) 

4. Тригонометрические уравнения вида  равносильны системе
равносильны системе  (вместо неравенства
(вместо неравенства  в систему можно включить неравенство
в систему можно включить неравенство  ).
).
Уравнения  равносильны уравнению
равносильны уравнению 
4. Особенности и опасность области допустимых значений
На уроках математики от нас требуют нахождения ОДЗ в каждом примере. В то же время по математической сути дела нахождение ОДЗ вовсе не является обязательным, часто не нужно, а иногда и невозможно – и все это без какого бы то ни было ущерба для решения примера. С другой стороны, часто случается такое, что решив пример, школьники забывают учесть ОДЗ, записывают её как конечный ответ, учитывают лишь некоторые условия. Обстоятельство это хорошо известно, но «война» продолжается каждый год и, похоже, будет идти еще долго.
Рассмотрим, к примеру, такое неравенство:
 >
>
Здесь ищется ОДЗ, и неравенство решается. Однако при решении этого неравенства школьники иногда считают, что вполне можно обойтись без поиска ОДЗ, точнее, можно обойтись и без условия 
В самом деле, для получения верного ответа необходимо учесть и неравенство  , и
, и  .
.
А вот, например, решение уравнения: 
Решают его, естественно, избавляясь от логарифмов, но затем найденные значения нередко проверяются на выполнение системы трех таких неравенств: 
что равносильно работе с ОДЗ. Однако и в этом примере такая работа излишняя – достаточно проверить выполнение только двух из этих неравенств, причем любых двух.
Напомним, что всякое уравнение (неравенство) может быть сведено к виду  . ОДЗ – это просто область определения функции в левой части. То, что за этой областью надо следить, вытекает уже из определения корня как числа из области определения данной функции, тем самым – из ОДЗ. Вот забавный пример на эту тему. Дано уравнение
. ОДЗ – это просто область определения функции в левой части. То, что за этой областью надо следить, вытекает уже из определения корня как числа из области определения данной функции, тем самым – из ОДЗ. Вот забавный пример на эту тему. Дано уравнение  , и вопрос: «является ли число -1 корнем этого уравнения?» С одной стороны, при подстановке -1 в обе части мы получаем верное равенство, а значит, -1 является корнем. Но с другой стороны, функция
, и вопрос: «является ли число -1 корнем этого уравнения?» С одной стороны, при подстановке -1 в обе части мы получаем верное равенство, а значит, -1 является корнем. Но с другой стороны, функция  имеет областью определения множество положительных чисел (это, конечно, договоренность – рассматривать функцию
имеет областью определения множество положительных чисел (это, конечно, договоренность – рассматривать функцию  при,
при,  , но разумная), а тогда -1 не является корнем.
, но разумная), а тогда -1 не является корнем.
5. Область допустимых значений – есть решение
И наконец, в массе примеров нахождение ОДЗ позволяет получить ответ без громоздких выкладок, а то и вовсе устно.
1. ОД3 представляет собой пустое множество, а значит, исходный пример не имеет решений.
1)  2)
2)  3)
3) 

2. В ОДЗ находится одно или несколько чисел, и несложная подстановка быстро определяет корни.
1)  , х=3
, х=3
2)  Здесь в ОДЗ находится только число 1, и после подстановки видно, что оно не является корнем.
Здесь в ОДЗ находится только число 1, и после подстановки видно, что оно не является корнем.
3)  В ОДЗ находятся два числа: 2 и 3, и оба подходят.
В ОДЗ находятся два числа: 2 и 3, и оба подходят.
4)  >
>  В ОДЗ находятся два числа 0 и 1, и подходит только 1.
В ОДЗ находятся два числа 0 и 1, и подходит только 1.
Эффективно может использоваться ОДЗ в сочетании с анализом самого выражения.
5) 
 , а значит,
, а значит,  . Решая последнее неравенство, получим х 2. При этом
. Решая последнее неравенство, получим х 2. При этом  . Значит, исходное равенство невозможно и решений нет.
. Значит, исходное равенство невозможно и решений нет.
А теперь приведём пример, который был предложен учителем на уроке алгебры. Решить его сразу нам не удалось, но когда мы нашли ОДЗ, всё стало ясно.
Найдите целочисленный корень уравнения  Найдём ОДЗ:
Найдём ОДЗ:




Целочисленное решение возможно лишь при х=3 и х=5. Проверкой находим, что корень х=3 не подходит, а значит ответ: х=5.
6. Нахождение области допустимых значений – лишняя работа. Равносильность переходов.
Можно привести примеры, где ситуация ясна и без нахождения ОДЗ.
1. 
Равенство невозможно, ибо при вычитании из меньшего выражения большее должно получатся отрицательное число.
2.  .
.
Сумма двух неотрицательных функций не может быть отрицательной.
Приведу также примеры, где нахождение ОДЗ затруднено, а иногда просто невозможно.

И, наконец, поиски ОДЗ являются очень часто просто лишней работой, без которой прекрасно можно обойтись, доказав тем самым понимание происходящего. Тут можно привести громадное число примеров, поэтому выберем только наиболее типичные. Главным приемом решения являются в этом случае равносильные преобразования при переходе от одного уравнения (неравенства, системы) к другому.
1. . ОДЗ не нужна, ибо, найдя те значения х, при которых х2=1, мы не можем получить х=0.
. ОДЗ не нужна, ибо, найдя те значения х, при которых х2=1, мы не можем получить х=0.
2.  . ОДЗ не нужна, ибо мы выясняем, когда выполняется равенство подкоренного выражения положительному числу.
. ОДЗ не нужна, ибо мы выясняем, когда выполняется равенство подкоренного выражения положительному числу.
3.  . ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
. ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
4. 
ОДЗ не нужна, ибо подкоренное выражение равно квадрату некоторой функции, а потому не может быть отрицательным.
5.  ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
6.  . ОДЗ не нужна, так как выражение
. ОДЗ не нужна, так как выражение  всегда положительно.
всегда положительно.
7.  Для решения достаточно только одного ограничения для подкоренного выражения. В самом деле, из записанной смешанной системы следует, что и другое подкоренное выражение неотрицательно.
Для решения достаточно только одного ограничения для подкоренного выражения. В самом деле, из записанной смешанной системы следует, что и другое подкоренное выражение неотрицательно.
8.  ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
9.  ОДЗ не нужна, так как достаточно, чтобы были положительны два из трех выражений под знаками логарифма, чтобы обеспечить положительность третьего.
ОДЗ не нужна, так как достаточно, чтобы были положительны два из трех выражений под знаками логарифма, чтобы обеспечить положительность третьего.
10.  ОДЗ не нужна, так как положительность трёхчлена
ОДЗ не нужна, так как положительность трёхчлена  следует из условий системы неравенств.
следует из условий системы неравенств.
11.  ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.
Стоит, однако, заметить, что при решении способом равносильных преобразований помогает знание ОДЗ (и свойств функций).
Вот несколько примеров.
1.  . ОД3
. ОД3  , откуда следует положительность выражения в правой части, и возможно записать уравнение, равносильное данному, в таком виде
, откуда следует положительность выражения в правой части, и возможно записать уравнение, равносильное данному, в таком виде  . Полученный результат надо проверить по ОДЗ.
. Полученный результат надо проверить по ОДЗ.
2.  ОДЗ:
ОДЗ:  . Но тогда
. Но тогда  , и при решении этого неравенства не надо рассматривать случай, когда правая часть меньше 0.
, и при решении этого неравенства не надо рассматривать случай, когда правая часть меньше 0.
3.  . Из ОДЗ следует, что
. Из ОДЗ следует, что  , а потому случай, когда
, а потому случай, когда  , исключается.
, исключается.
В целом эффективность способа равносильных преобразований вроде бы ясна. С их помощью мы добираемся до ответа и без поисков ОДЗ. Значит ли это, что имеется некий универсальный способ и осталось только научиться им пользоваться? Но это не совсем так. Тому несколько причин. Теорем о равносильных преобразованиях довольно много, они непросты для запоминания, и уверенное владение ими – дело не простое. Часто, пользуясь равносильными преобразованиями, начинаешь ставить этот знак при любых переходах от одного уравнения к другому, как действительно равносильных, так и не являющихся таковыми. Теоремы же эти быстро забываются.
Еще одна сложность – при записи равносильности можно забыть выписать все условия, ее гарантирующие, но на ответе это может никак не отразиться. Вот два таких примера:
1.  Переход в общем виде выглядит так:
Переход в общем виде выглядит так:

В данном примере выражение под знаком логарифма, стоящего справа, всегда положительно. Поэтому применительно к этому примеру та часть условий равносильности, которая записана в виде совокупности, ничего не добавляет. Но дав такое решение, можно просто забыть об этой совокупности.
2. 
Возможны два случая: 0 1.
Значит, исходное неравенство равносильно следующей совокупности систем неравенств:




Первая система не имеет решений, а из второй получаем: x 1, откуда следует x  (-
(- ;1,3). Здесь допущена грубая ошибка, так как не рассмотрен случай 36 – 20x
;1,3). Здесь допущена грубая ошибка, так как не рассмотрен случай 36 – 20x
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/funktsii/kak-najti-oblast-opredelenija-funktsii/
http://pandia.ru/text/78/093/15148.php
[/spoiler]
Неравенством с одной переменной называют каждое из выражений вида:
 ,
,  ,
,  ,
,  ,
,
где знаки  ,
,  ,
,  ,
,  означают соответственно меньше, больше, меньше или равно, больше или равно.
означают соответственно меньше, больше, меньше или равно, больше или равно.
Например,  ,
,  ,
,  ,
,  ,
,  – примеры неравенств с одной переменной.
– примеры неравенств с одной переменной.
Решением неравенства называют значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
Решить неравенство – значит найти множество всех его решений или доказать, что неравенство не имеет решений.
Областью определения (областью допустимых значений) неравенства  называют общую часть областей определения функций
называют общую часть областей определения функций 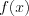 и
и 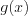 .
.
Равносильные неравенства
Два неравенства называют равносильными, если множества их решений совпадают или оба неравенства не имеют решений.
Например: 1) неравенства  и
и  равносильны, так как оба неравенства выполняются на множестве действительных чисел;
равносильны, так как оба неравенства выполняются на множестве действительных чисел;
2) неравенства  и
и  равносильны, так как оба неравенства не имеют решений;
равносильны, так как оба неравенства не имеют решений;
Решая неравенство, как правило, его заменяют более простым, но равносильным ему неравенством. Такие замены осуществляют на основании следующих утверждений:
1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получим неравенство, равносильное данному неравенству.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число или на одну и ту же функцию, положительную на области определения неравенства, то получим неравенство, равносильное данному неравенству.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число или на одну и ту же функцию, отрицательную на области определения неравенства, изменив при этом смысловой знак неравенства, то получим неравенство, равносильное данному.
4. Неравенства  и
и  , а также неравенства
, а также неравенства  и
и  равносильны.
равносильны.
5. Неравенства  и
и  равносильны для всех
равносильны для всех 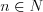 при условии, что значения выражений
при условии, что значения выражений 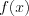 и
и 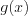 неотрицательные.
неотрицательные.
6. Неравенства  и
и  равносильны для всех
равносильны для всех 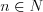 .
.
7. Неравенства ![sqrt[2n+1]{f(x)}< sqrt[2n+1]{g(x)} LaTeX formula: sqrt[2n+1]{f(x)}< sqrt[2n+1]{g(x)}](https://helpy.quali.me/uploads/formulas/fba645ad1ebd71ce03c560c56e25ab36b08ec1bc.1.1.png) и
и  равносильны для всех
равносильны для всех  .
.
Системы и совокупности неравенств с одной переменной
Рассмотрим два неравенства  и
и  .
.
Систему двух неравенств записывают в виде: 
Совокупность неравенств записывают в виде: 
Чтобы решить систему неравенств, необходимо найти множества решений каждого неравенства системы, тогда общая часть (пересечение) этих множеств и будет решением системы.
Чтобы решить совокупность неравенств, необходимо найти множества решений каждого неравенства совокупности, тогда объединение этих множеств и будет решением совокупности.
Метод интервалов
Метод интервалов основан на следующем свойстве двучлена: если отметить на координатной оси 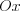 число
число  (рис. 7.1), то для любого
(рис. 7.1), то для любого  , находящегося справа от точки
, находящегося справа от точки  , двучлен
, двучлен  положителен, а слева от точки
положителен, а слева от точки  он отрицателен.
он отрицателен.


Рассмотрим дробно-рациональную функцию  где:
где:  .
.
Если  , то каждый из сомножителей
, то каждый из сомножителей  ,
,  ,
,  ,
,  положителен, и, следовательно, на промежутке
положителен, и, следовательно, на промежутке  имеем
имеем  (рис. 7.2). Если
(рис. 7.2). Если  , то множитель
, то множитель  , а остальные сомножители по-прежнему положительны. Значит, на промежутке
, а остальные сомножители по-прежнему положительны. Значит, на промежутке  имеем
имеем  . Однако при разложении левой части неравенства могут встретиться одинаковые множители.
. Однако при разложении левой части неравенства могут встретиться одинаковые множители.
Число  называют кратностью корня
называют кратностью корня  многочлена
многочлена  , а число
, а число  – k-кратным корнем этого многочлена.
– k-кратным корнем этого многочлена.
В процессе решения неравенств методом интервалов для удобства корни четной кратности будем наносить на координатную прямую дважды, а нечетной кратности – один раз. При переходе через корень четной кратности знаки значений функции не изменятся, а при переходе через корень нечетной кратности – изменятся.
При решении неравенств вида  и
и  корни числителя будем отмечать на координатной прямой «зачерненными» кружочками, а корни знаменателя – «пустыми», так как множество решений неравенства не должно содержать корней многочлена
корни числителя будем отмечать на координатной прямой «зачерненными» кружочками, а корни знаменателя – «пустыми», так как множество решений неравенства не должно содержать корней многочлена 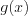 .
.
Наряду с алгебраическим подходом к решению неравенств можно использовать также и функциональный подход.
Приведем алгоритм решения методом интервалов неравенства вида  (
(  ,
,  ,
,  ), где функция
), где функция  может быть произвольной (рациональной, иррациональной, показательной, логарифмической, тригонометрической и т. д.):
может быть произвольной (рациональной, иррациональной, показательной, логарифмической, тригонометрической и т. д.):
1) запишем функцию  ;
;
2) найдем область определения функции;
3) найдем нули функции, решая уравнение  ;
;
4) нанесем нули функции на ее область определения;
5) определим знаки значений функции на одном из полученных промежутков;
6) определим знаки значений функции на остальных промежутках по правилу: при переходе через каждый нуль функции знаки значений функции изменяются (учитываем кратность нулей);
7) запишем решение неравенства, учитывая его смысловой знак.
Содержание:
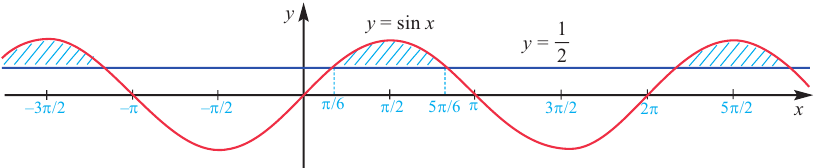
Для решение простейших тригонометрических неравенств можно использовать как единичную окружность, так и графики тригонометрических функций.
Пример 1.
Решим неравенство 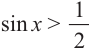
Решение:
Запишем решение в общем виде.
Решить данное неравенство значит, найти абсциссы множества точек графика функции 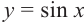 , ординаты которых больше
, ординаты которых больше 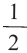 .
.
1.Построим график функции 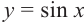 .
.
2.В одной системе координат построим график функции 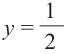 .
.
3.Отметим точки пересечения графиков.
4. Как видно, прямая 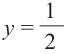 делит график функции
делит график функции 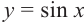 на две части. Абсциссы множества точек расположенные в верхней части от прямой
на две части. Абсциссы множества точек расположенные в верхней части от прямой 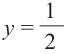 удовлетворяют неравенству. На интервале
удовлетворяют неравенству. На интервале 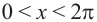 эти точки имеют абсциссы
эти точки имеют абсциссы 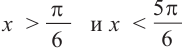 . Значит, решением неравенства на интервале
. Значит, решением неравенства на интервале 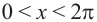 является множество точек, удовлетворяющих условию
является множество точек, удовлетворяющих условию 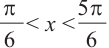
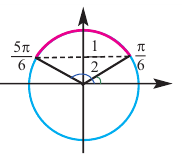
Также решения тригонометрических неравенств можно ясно увидеть на единичной окружности. Все остальные интервалы, удовлетворяющие решению неравенства получаются смещением интервала 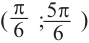 на расстояние длиной в
на расстояние длиной в  влево или вправо. Поэтому решения неравенства
влево или вправо. Поэтому решения неравенства 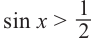 записываются так:
записываются так:
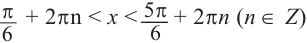 .
. 
Пример 2.
Решим неравенство 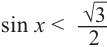
Решение:
Решения уравнения 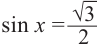 являются абсциссами точек пересечения графиков функций
являются абсциссами точек пересечения графиков функций 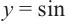 и
и 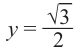 . Если один из корней, на промежутке длиной
. Если один из корней, на промежутке длиной 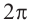 равен
равен 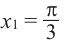 , то другой корень будет равен
, то другой корень будет равен 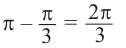 . На графике отметим точки пересечения с абсциссами
. На графике отметим точки пересечения с абсциссами 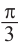 и
и 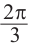 .
.
От каждой из них, по обе стороны, отметим ещё две точки – вправо от
точки 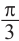 на
на 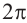 :
: 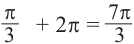 ,и влево от точки
,и влево от точки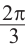 на
на 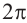 :
: 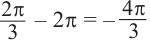
Они также являются абсциссами точек пересечения графиков.
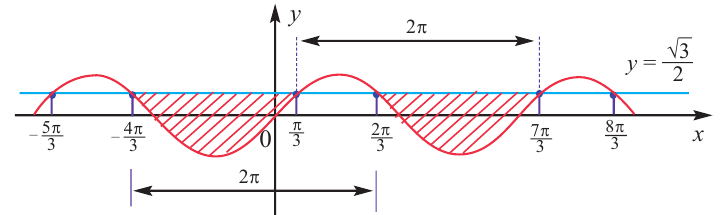
На промежутке (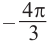
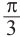 ) ординаты точек графика функции у = sin х меньше
) ординаты точек графика функции у = sin х меньше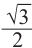 . Приняв во внимание период функции, решения неравенства
. Приняв во внимание период функции, решения неравенства 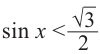 можно записать в виде:
можно записать в виде: 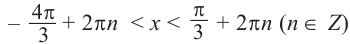 . Из графика видно, что интервал
. Из графика видно, что интервал 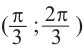 удовлетворяет решению неравенства
удовлетворяет решению неравенства 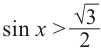 . Все остальные интервалы, удовлетворяющие неравенству
. Все остальные интервалы, удовлетворяющие неравенству 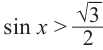 получаются смещением интервала
получаются смещением интервала 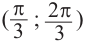 влево и вправо на отрезок длиной в
влево и вправо на отрезок длиной в 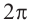 . Значит, в общем виде решения неравенства
. Значит, в общем виде решения неравенства 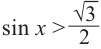 записываются так:
записываются так: 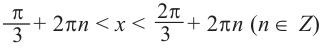 .
.
Пример 3.
Решим неравенство 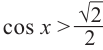
Решение:
Найдём абсциссы точек пересечения графиков функций 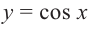
и 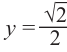 из уравнения
из уравнения 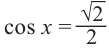 .
.
Получим: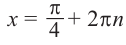 и
и 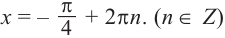
При 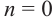 абсциссы точек пересечения будут равны
абсциссы точек пересечения будут равны 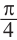 и
и 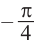 . Отметим эти точки на графике. От каждой из них, по обе стороны, отметим ещё две точки.
. Отметим эти точки на графике. От каждой из них, по обе стороны, отметим ещё две точки.
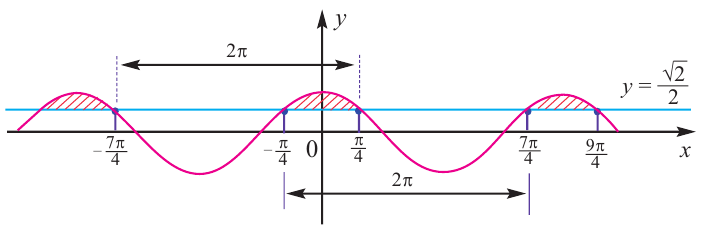
Отметим от точки 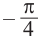 справа на расстоянии
справа на расстоянии 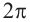 точку
точку
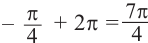 и от точки
и от точки 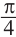 слева на расстоянии
слева на расстоянии 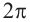 точку
точку
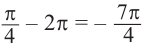 .
.
Один из промежутков, удовлетворяющих неравенству, расположен между наименьших но абсолютному значению корней соответствующего уравнения, т.е. между точками 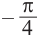 и
и 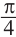 .
.
Приняв во внимание периодичность 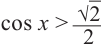 функции, получим следующие решения неравенства
функции, получим следующие решения неравенства 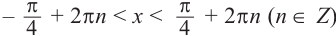 .
.
По графику решение неравенства 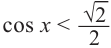 будет:
будет:
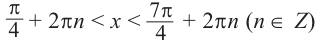 .
.
Пример 4.
Решим неравенства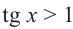 и
и 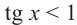 .
.
Решение:
В одной системе координат построим графики функций 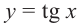 и у = 1.
и у = 1.
Найдём абсциссу точки пересечения , расположенной в интервале 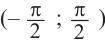 решив уравнение
решив уравнение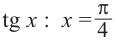 . Функция
. Функция 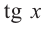 возрастает на промежутке
возрастает на промежутке 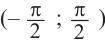 tg х = 1 при
tg х = 1 при 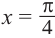 . Тогда, если
. Тогда, если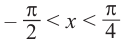 , то tg х < 1. Если
, то tg х < 1. Если 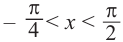 , то tg х > 1.
, то tg х > 1.
Так как функция 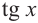 имеет период
имеет период 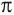 , то решение неравенства
, то решение неравенства 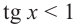 будет
будет 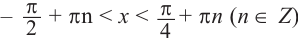 , а решение неравенства
, а решение неравенства
tg х > 1 будет 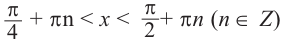 .
.
Пример 5.
Решим неравенства 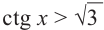 и
и 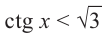 .
.
Решение:
На одной координатной плоскости построим графики функций 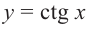 и
и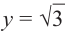 . Абсциссу точки пересечения графиков на промежутке (0;
. Абсциссу точки пересечения графиков на промежутке (0; 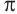 ) найдём из уравнения
) найдём из уравнения 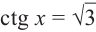 :
: 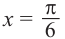 Функция ctg х убывает на промежутке (0;
Функция ctg х убывает на промежутке (0; 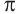 ) и при
) и при 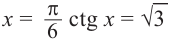 . Тогда, если
. Тогда, если 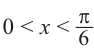 , то
, то 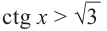 , а
, а
если 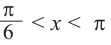 , то
, то 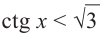 .
.
Это говорит о том , что условию неравенства 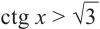 удовлетворяют
удовлетворяют 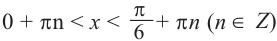 , а условию неравенства
, а условию неравенства
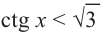
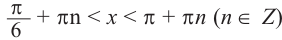 .
.
Для решения тригонометрических неравенств:
1) В одной системе координат постройте графики функций из левой и правой частей неравенства;
2) Решите соответствующие уравнения. Найдите абсциссы для нескольких точек пересечения, расположенных близко к началу координат и отметьте их на графике;
3) Определите какой-либо интервал, удовлетворяющий неравенству;
4) Принимая во внимание периодичность функции, запишите все решения.
Пример 6.
Решите неравенство  на интервале
на интервале  .
.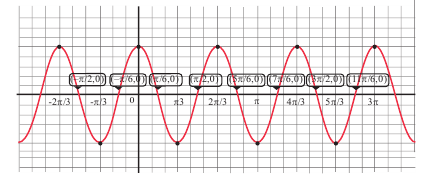
Решение:
1.Построим график функции 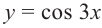 .
.
Как видно из графика, значения 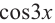 меньше 0 или равные 0 соответствуют точкам, расположенным на оси абсцисс (прямой у = 0 ) или ниже её. Решениями неравенства из интервала
меньше 0 или равные 0 соответствуют точкам, расположенным на оси абсцисс (прямой у = 0 ) или ниже её. Решениями неравенства из интервала 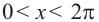 являются промежутки
являются промежутки 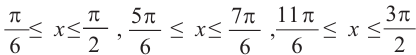
Пример 7.
Решим неравенство 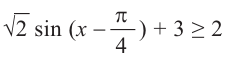 на интервале
на интервале  .
.
Решение:
1. Построим графики функций 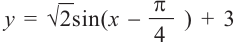 и
и 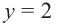 при помощи графкалькулятора.
при помощи графкалькулятора.
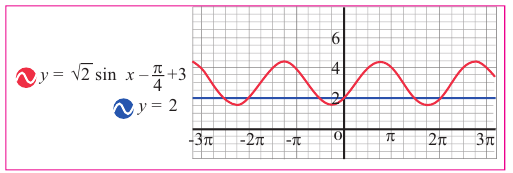
Решением неравенства являются абсциссы всех точек, которые расположены на прямой у = 2 и выше неё. Это точки 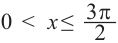 из интервала
из интервала 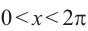 .
.
А общее решение неравенства имеет вид 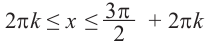 .
.
Проверка: На интервале решения для проверки выберем одну точку, напри-л
мер 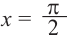 проверим правильность решения:
проверим правильность решения:
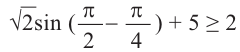
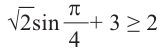
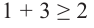
Пример 8.
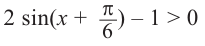
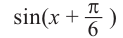
Решение:
Пусть 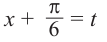
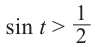
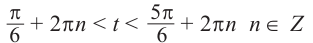
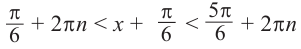
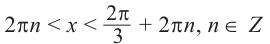

Пример решении задачи:
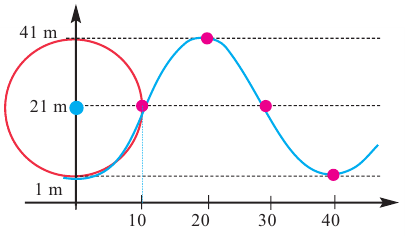
Карусель, радиусом 20 м за каждые 40 секунд совершает один оборот. Самое низкое сиденье находится на высоте 1 м.
а)Изобразите график, соответствующий задаче.

б)Запишите функцию зависимости движения человека, находящегося на сиденье карусели в виде 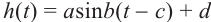 .
.
в)В какие секунды за один полный оборот человек на карусели, окажется на высоте выше 21 м?
Решение:
а) Изобразим схематично решение задачи. Отметим на окружности точки, соответствующие каждой четвёртой части оборота при движении карусели. Соединим эти точки и получим график, в виде синусоиды, движения карусели за один оборот (360°).
б)Из графика видно, что с 10 но 30 секунду человек на карусели, будет находится на высоте от 21 ми более.
в)По данным задачи и графику запишем формулу функции.
Зная период, найдём частоту b: 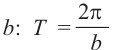
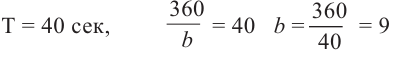
Найдём амплитуду и среднюю линию, зная максимальное и минимальное значения. 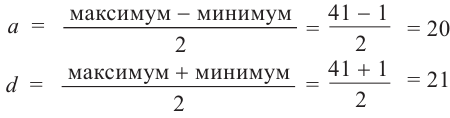 Найдём фазу смещения с. Функция синуса принимает наибольшее значение в одной четвёртой периода. Однако можно заметить, что максимум функции достигается с задержкой на 10 секунд (на 20-ой секунде), а значит сдвиг но фазе с = 10.
Найдём фазу смещения с. Функция синуса принимает наибольшее значение в одной четвёртой периода. Однако можно заметить, что максимум функции достигается с задержкой на 10 секунд (на 20-ой секунде), а значит сдвиг но фазе с = 10.
Формула имеет вид 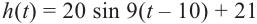 .
.
Решение неравенств
Понятия неравенства с одной переменной и его способы решения:
Определение:
Если два выражения с переменной соединить одним из знаков 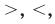
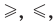 то получим неравенство с переменной. В общем виде неравенство с одной переменной
то получим неравенство с переменной. В общем виде неравенство с одной переменной 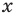 (например, для случая «больше») записывают так:
(например, для случая «больше») записывают так: 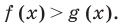
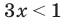 линейное неравенство;
линейное неравенство;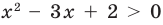 квадратное неравенство;
квадратное неравенство;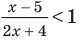 дробное неравенство
дробное неравенство
Решением неравенства с переменной называется значение переменной, которое обращает заданное неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
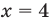 одно из решений неравенства
одно из решений неравенства 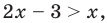 так как при
так как при 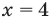 получаем верное неравенство:
получаем верное неравенство: 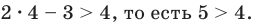
Область допустимых значений (ОДЗ):
Областью допустимых значений (или областью определения) неравенства называется общая область определения для функций  которые стоят в левой и правой частях неравенства.
которые стоят в левой и правой частях неравенства.
Для неравенства 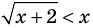 ОДЗ:
ОДЗ: 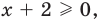 то есть
то есть 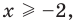 так как область определения функции
так как область определения функции 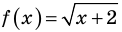 определяется условием:
определяется условием: 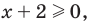 а областью определения функции
а областью определения функции 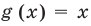 является множество всех действительных чисел.
является множество всех действительных чисел.
Два неравенства называется равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго и наоборот, каждое решение второго неравенства является решением первого.
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не меняя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного неравенства).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное задан ному (на ОДЗ заданного неравенства).
- Метод интервалов (решения неравенств вида
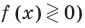
Решите неравенство 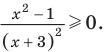
Пусть 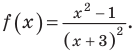
ОДЗ: 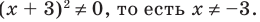
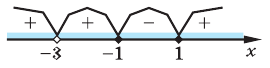
Нули функции 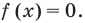
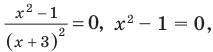
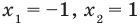 ( входят в ОДЗ)
( входят в ОДЗ)
Ответ: 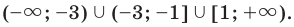
Схема поиска плана решения неравенства

Объяснение и обоснование:
Понятия неравенства с переменной и его решение
Если два выражения с переменной соединить одним из знаков 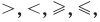 то получаем неравенство с переменной.
то получаем неравенство с переменной.
Аналогично уравнению, неравенство с переменной (например, со знаком 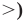 чаще всего понимают как аналитическую запись задачи о нахождении тех значений аргументов, при которых значение одной из заданных функций больше, чем значение другой заданной функции. Поэтому в общем виде неравенство с одной переменной
чаще всего понимают как аналитическую запись задачи о нахождении тех значений аргументов, при которых значение одной из заданных функций больше, чем значение другой заданной функции. Поэтому в общем виде неравенство с одной переменной 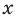 (например, для случаев «больше») записывают так:
(например, для случаев «больше») записывают так: 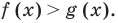
Напомним, что решением неравенства называется значение переменной, которое обращает это неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
Например, решениями неравенства 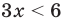 являются все значения
являются все значения 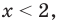 для неравенства
для неравенства  решениями являются все действительные числа
решениями являются все действительные числа 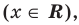 а неравенство
а неравенство 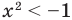 не имеет решений, поскольку значение
не имеет решений, поскольку значение 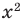 не может быть отрицательным числом.
не может быть отрицательным числом.
Область допустимых значений (ОДЗ) неравенства
Область допустимых значений (ОДЗ) неравенства определяется аналогично ОДЗ уравнения. Если задано неравенство 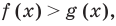 то общая область определения функций
то общая область определения функций 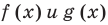 называется областью допустимых значений этого неравенства (иногда используются также термины « область определения неравенства» или «множество допустимых значений неравенства»). Например, для неравенства
называется областью допустимых значений этого неравенства (иногда используются также термины « область определения неравенства» или «множество допустимых значений неравенства»). Например, для неравенства 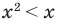 областью допустимых значений являются все действительные числа (это можно записать, например, так: ОДЗ:
областью допустимых значений являются все действительные числа (это можно записать, например, так: ОДЗ: 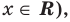 поскольку функции
поскольку функции 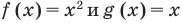 имеют области определения
имеют области определения 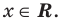
Понятно, что каждое решение заданного неравенства входит как в область определения функции 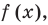 так и в область определения функции
так и в область определения функции 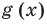 (иначе мы не сможем получить верное числовое неравенство). Таким образом, каждое решение неравенства обязательно входит в ОДЗ этого неравенства. Это позволяет в некоторых случаях применить анализ ОДЗ неравенства для его решения.
(иначе мы не сможем получить верное числовое неравенство). Таким образом, каждое решение неравенства обязательно входит в ОДЗ этого неравенства. Это позволяет в некоторых случаях применить анализ ОДЗ неравенства для его решения.
Например, в неравенстве 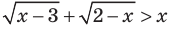 функция
функция 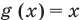 определена при всех действительных значениях
определена при всех действительных значениях  а функция
а функция 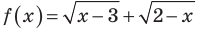 — только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Таким образом, ОДЗ этого неравенства задается системой
— только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Таким образом, ОДЗ этого неравенства задается системой 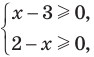 из которой получаем систему
из которой получаем систему 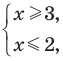 не имеющую решений. Таким образом, ОДЗ заданного неравенства не содержит ни одного числа, поэтому это неравенство не имеет решений.
не имеющую решений. Таким образом, ОДЗ заданного неравенства не содержит ни одного числа, поэтому это неравенство не имеет решений.
В основном при решении неравенств различных видов приходится применять один из двух методов решения: равносильные преобразования неравенств или так называемый метод интервалов.
Равносильные неравенства
С понятием равносильности неравенств вы знакомы еще из курса алгебры 9 класса. Как и для случая равносильных уравнений, равносильность неравенств мы будем рассматривать на определенном множестве.
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго, и наоборот, каждое решение второго неравенства является решением первого.
Договоримся, что в дальнейшем все равносильные преобразования неравенств будем выполнять на ОДЗ заданного неравенства. Укажем, что в том случае, когда ОДЗ заданного неравенства является множество всех действительных чисел, мы не всегда будем его записывать (как не записывали ОДЗ при решении линейных или квадратных неравенств). И в других случаях главное — не записать ОДЗ при решении неравенства, а действительно учесть ее при выполнении равносильных преобразований заданного неравенства.
Общие ориентиры выполнения равносильных преобразований неравенств аналогичны соответствующим ориентирам выполнения равносильных преобразований уравнений.
Как указывалось выше, выполняя равносильные преобразования неравенств, необходимо учитывать ОДЗ заданного неравенства — это и есть первый ориентир для выполнения равносильных преобразований неравенств.
По определению равносильности неравенств необходимо обеспечить, чтобы каждое решение первого неравенства было решением второго, и наоборот, каждое решение второго неравенства было решением первого. Для этого достаточно обеспечить сохранение верного неравенства на каждом шаге решения не только при прямых, а и при обратных преобразованиях. Это и есть второй ориентир для решения неравенств с помощью равносильных преобразований. Действительно, каждое решение неравенства обращает его в верное числовое неравенство, и если верное неравенство сохраняется, то решение каждого из неравенств будет также и решением другого, таким образом, неравенства будут равносильны (соответствующие ориентиры схематически представлены в пункте 5 табл. 38).
Например, чтобы решить с помощью равносильных преобразований неравенство достаточно учесть его ОДЗ:
достаточно учесть его ОДЗ:  и условие положительности дроби (дробь будет положительной тогда и только тогда, когда числитель и знаменатель дроби имеют одинаковые знаки), а также учесть, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением верного неравенства.
и условие положительности дроби (дробь будет положительной тогда и только тогда, когда числитель и знаменатель дроби имеют одинаковые знаки), а также учесть, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением верного неравенства.
Решение:
Данное неравенство равносильно совокупности двух систем: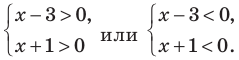
Тогда получаем 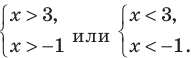
Таким образом, 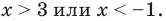
Ответ: 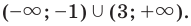
Комментарий:
Заметим, что при записи условия положительности дроби — совокупности систем (2) — мы неявно учли ОДЗ неравенства (1). Действительно, если 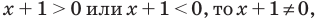 поэтому в явном виде ОДЗ заданного неравенства не записано при оформлении решения. Кроме выделенных общих ориентиров, для выполнения равносильных преобразований неравенств можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности неравенств обобщим также формулировки простейших теорем о равносильности неравенств, известных из курса алгебры 9 класса.
поэтому в явном виде ОДЗ заданного неравенства не записано при оформлении решения. Кроме выделенных общих ориентиров, для выполнения равносильных преобразований неравенств можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности неравенств обобщим также формулировки простейших теорем о равносильности неравенств, известных из курса алгебры 9 класса.
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не изменяя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований заданного неравенства.
Замечание. Для обозначения перехода от заданного неравенства к неравенству, равносильному ему, можно применять специальный значок  но его использование при оформлении решений не является обязательным (хотя иногда мы будем его использовать, чтобы подчеркнуть, что было выполнено именно равносильное преобразование).
но его использование при оформлении решений не является обязательным (хотя иногда мы будем его использовать, чтобы подчеркнуть, что было выполнено именно равносильное преобразование).
Метод интервалов
Решение неравенств методом интервалов опирается на свойства функций, связанные с изменением знаков функции. Объясним эти свойства, используя графики известных нам функций, например функций  (рис. 100).
(рис. 100).
Рассматривая эти графики, замечаем, что функция может изменить свой знак только в двух случаях:
- если график разрывается (как в случае функции
 (рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0); - если график без разрыва переходит из нижней полуплоскости в верхнюю (или наоборот). Но тогда график пересекает ось
 (как в случае функции
(как в случае функции  (рис. 100,6).
(рис. 100,6).
На оси  значения функции равны нулю. (Напомним, что значения аргумента, при которых функция равна нулю, называют нулями функции.) Таким образом, любая функция может поменять свой знак только в нулях или в точках, где разрывается график функции (в так называемых точках разрыва функции ).
значения функции равны нулю. (Напомним, что значения аргумента, при которых функция равна нулю, называют нулями функции.) Таким образом, любая функция может поменять свой знак только в нулях или в точках, где разрывается график функции (в так называемых точках разрыва функции ). 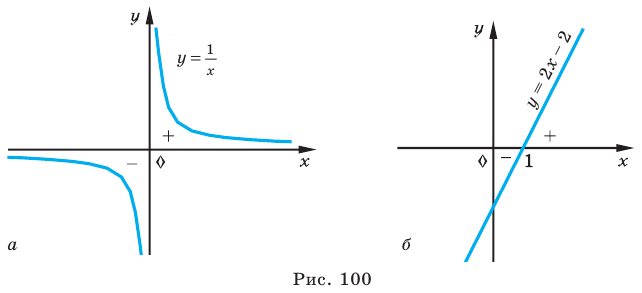
Точки, в которых разрывается график функции  мы выделяем, как правило, когда находим область определения этой функции. Например, если
мы выделяем, как правило, когда находим область определения этой функции. Например, если 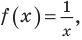 то ее область определения
то ее область определения 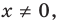 и именно в точке 0 график этой функции разрывается (рис. 100, а). Если же на каком-нибудь промежутке области определения график функции не разрывается и функция не равна нулю, то по приведенному выше выводу она не может на этом промежутке поменять свой знак. Таким образом, если отметить нули функции на ее области определения, то область определения разобьется на промежутки, внутри которых знак функции измениться не может (и поэтому этот знак можно определить в любой точке из этого промежутка).
и именно в точке 0 график этой функции разрывается (рис. 100, а). Если же на каком-нибудь промежутке области определения график функции не разрывается и функция не равна нулю, то по приведенному выше выводу она не может на этом промежутке поменять свой знак. Таким образом, если отметить нули функции на ее области определения, то область определения разобьется на промежутки, внутри которых знак функции измениться не может (и поэтому этот знак можно определить в любой точке из этого промежутка).
В таблице 39 приведено решение дробно-рационального неравенства 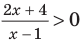 методом интервалов; комментарии, объясняющий каждый этап решения; план решения неравенств вида
методом интервалов; комментарии, объясняющий каждый этап решения; план решения неравенств вида 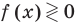 методом интервалов.
методом интервалов.
Пример №1
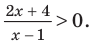
Решение:
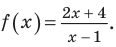
1. ОДЗ:  то есть
то есть 
Рассмотрим функцию, стоящую в левой части этого неравенства, и обозначим ее через 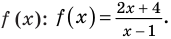 Решением неравенства
Решением неравенства  могут быть только числа, которые входят в область определения функции
могут быть только числа, которые входят в область определения функции  то есть числа, входящие в ОДЗ неравенства. Поэтому первым этапом решения неравенства методом интервалов будет нахождение его ОДЗ.
то есть числа, входящие в ОДЗ неравенства. Поэтому первым этапом решения неравенства методом интервалов будет нахождение его ОДЗ.
1. Найти ОДЗ неравенства.
2. Нули 
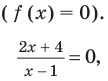
тогда 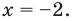
Нас интересуют те промежутки области определения функции 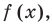 на которых эта функция положительна. Как было отмечено выше, функция
на которых эта функция положительна. Как было отмечено выше, функция 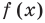 может поменять знак в своих нулях, поэтому вторым этапом решения неравенства
может поменять знак в своих нулях, поэтому вторым этапом решения неравенства 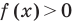 будет нахождение нулей функции (для этого приравниваем функцию
будет нахождение нулей функции (для этого приравниваем функцию 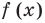 к нулю и решаем полученное уравнение).
к нулю и решаем полученное уравнение).
2. Найти нули
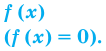
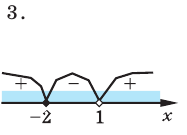
Если теперь отметить нули на области определения функции 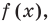 то область определения разбивается на промежутки, внутри каждого из которых функция
то область определения разбивается на промежутки, внутри каждого из которых функция 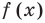 не меняет свой знак. Поэтому знак функции на каждом промежутке можно определить в любой точке этого промежутка. Это и является третьим этапом решения.
не меняет свой знак. Поэтому знак функции на каждом промежутке можно определить в любой точке этого промежутка. Это и является третьим этапом решения.
3. Отметить нули на ОДЗ и найти знак функции в каждом промежутке, на которые разбивается ОДЗ.
4 Ответ: 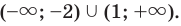
Из рисунка видно, что решением неравенства является объединение промежутков 
4. Записать ответ, учитывая знак неравенства.
Приведем пример решения более сложного дробно-рационального неравенства методом интервалов и с помощью равносильных преобразований.
Пример №2
Решите неравенство
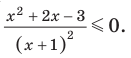
1 способ (метод интервалов)
Решение:
Пусть 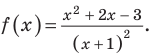
1 ОДЗ: 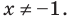
2. Нули
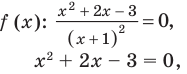
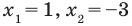 (принадлежат ОДЗ).
(принадлежат ОДЗ).
3. Отмечаем нули функции на ОДЗ и находим знак 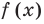 в каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
в каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
Ответ: 
Комментарий:
Данное неравенство имеет вид  и для его решения можно применить метод интервалов. Для этого используем план, приведенный выше и на с. 232.
и для его решения можно применить метод интервалов. Для этого используем план, приведенный выше и на с. 232.
При нахождении нулей 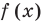 следим за тем, чтобы найденные значения принадлежали ОДЗ (или выполняем проверку найденных корней уравнения
следим за тем, чтобы найденные значения принадлежали ОДЗ (или выполняем проверку найденных корней уравнения 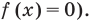
Записывая ответ к нестрогому неравенству, следует учесть, что все нули функции должны войти в ответ (в данном случае — числа -3 и 1).
2 способ (с помощью равносильных преобразований)
Комментарий:
Выберем для решения метод равносильных преобразований неравенства. При выполнении равносильных преобразований мы должны учесть ОДЗ данного неравенства, то есть учесть ограничение 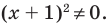
Но если 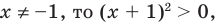 и тогда в данной дроби знаменатель положителен. Если выполняется данное неравенство, то числитель дроби
и тогда в данной дроби знаменатель положителен. Если выполняется данное неравенство, то числитель дроби 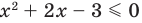 (и наоборот, если выполняется последнее неравенство, то на ОДЗ дробь
(и наоборот, если выполняется последнее неравенство, то на ОДЗ дробь 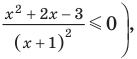 то есть данное неравенство равносильно на ОДЗ неравенству
то есть данное неравенство равносильно на ОДЗ неравенству 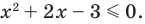
Чтобы решить полученное квадратное неравенство, найдем корни квадратного трехчлена 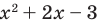 и построим эскиз графика функции
и построим эскиз графика функции 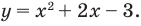 Решение квадратного неравенства:
Решение квадратного неравенства: 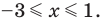
Поскольку все преобразования были равносильными только на ОДЗ, то мы должны выбрать те решения квадратного неравенства, которые удовлетворяют ограничению ОДЗ.
Решение:
ОДЗ: 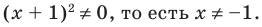
Тогда 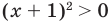 и данное неравенство на его ОДЗ равносильно неравенству
и данное неравенство на его ОДЗ равносильно неравенству 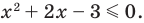 Поскольку
Поскольку 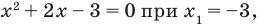
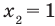 (эти значения
(эти значения 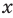 принадлежат ОДЗ), получаем
принадлежат ОДЗ), получаем 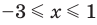 (см. рисунок). -3
(см. рисунок). -3
Учитывая ОДЗ, получаем ответ.
Ответ: 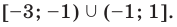
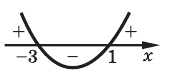
Уравнения и неравенства с модулями
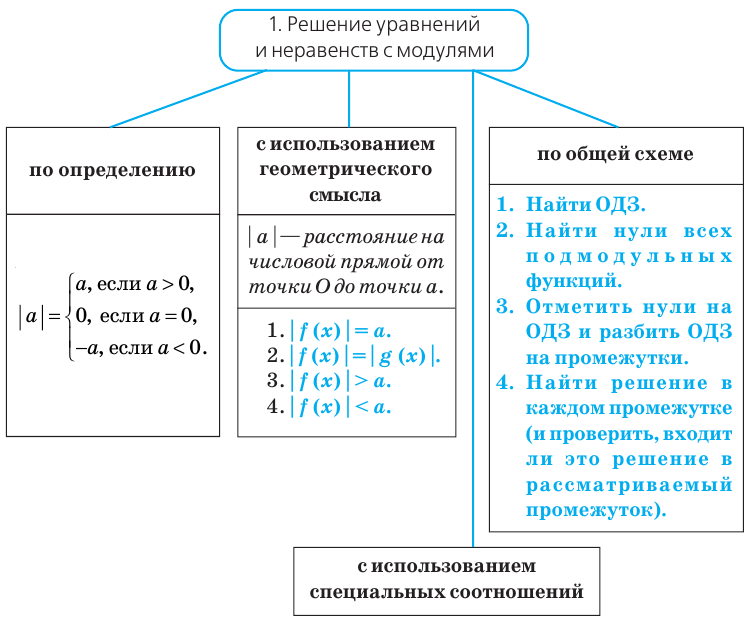
Использование геометрического смысла модуля ( при 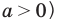
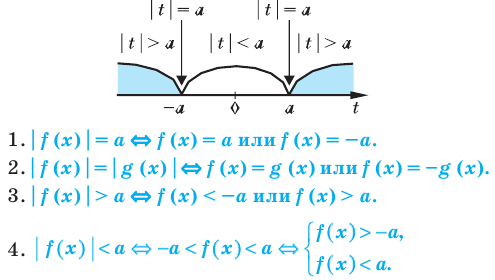
Обобщение:
Использование специальных соотношений:
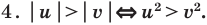 Тогда
Тогда 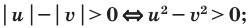 знак разности модулей двух выражений совпадает со знаком разности их квадратов.
знак разности модулей двух выражений совпадает со знаком разности их квадратов.
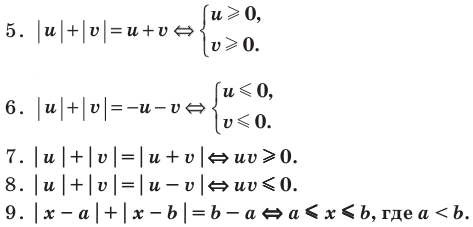
Объяснение и обоснование:
Решение любых уравнений или неравенств с модулем
Решать любое уравнение или неравенство с модулем можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений (табл. 40).
В зависимости от выбранного способа решения получаем разные записи решения.
Пример №3
Решите уравнение 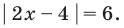
1 способ (по определению модуля)
Решение:
- Если
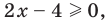 то получаем уравнение
то получаем уравнение 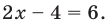 Тогда
Тогда 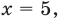 что удовлетворяет и условию (1).
что удовлетворяет и условию (1). - Если
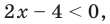 то получаем уравнение
то получаем уравнение 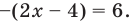 Тогда
Тогда 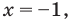 что удовлетворяет и условию (2).
что удовлетворяет и условию (2).
Ответ: 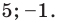
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая: 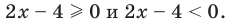 По определению модулем положительного (неотрицательного) числа является само это число, а модулем отрицательного числа является противоположное ему число. Поэтому при
По определению модулем положительного (неотрицательного) числа является само это число, а модулем отрицательного числа является противоположное ему число. Поэтому при 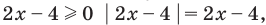 а при
а при 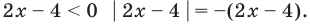
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
2 способ (использование геометрического смысла модуля)
Решение:
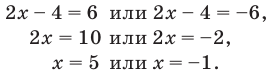
Ответ: 5; -1.
Комментарий:
С геометрической точки зрения 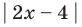 — это расстояние от точки 0 до точки
— это расстояние от точки 0 до точки 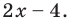 По условию уравнения оно равно 6, но расстояние 6 может быть отложено от 0 как вправо (получаем число 6), так и влево (получаем число -6). Таким образом, равенство
По условию уравнения оно равно 6, но расстояние 6 может быть отложено от 0 как вправо (получаем число 6), так и влево (получаем число -6). Таким образом, равенство 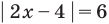 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 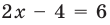 или
или 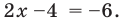
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств с модулями — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида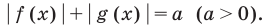
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции  будут положительными, а где — отрицательными. То есть фактически мы должны решить неравенства
будут положительными, а где — отрицательными. То есть фактически мы должны решить неравенства 
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции  а решение неравенства (2) — с нахождения его ОДЗ (то есть области определения функции
а решение неравенства (2) — с нахождения его ОДЗ (то есть области определения функции 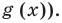 Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций
Чтобы начать одновременно решать оба неравенства, необходимо найти общую область определения для функций 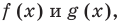 то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы).
то есть найти ОДЗ данного уравнения (это и есть первый из ориентиров необходимой схемы).
Чтобы продолжить решение неравенств 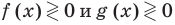 методом интервалов, необходимо найти нули функций
методом интервалов, необходимо найти нули функций 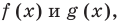 то есть найти нули всех подмодульных функций (это и есть второй ориентир). Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир). В каждом из полученных промежутков знаки функций
то есть найти нули всех подмодульных функций (это и есть второй ориентир). Если далее применить схему метода интервалов одновременно для двух неравенств, необходимо на ОДЗ отметить нули подмодульных функций и разбить ОДЗ на промежутки (это третий ориентир). В каждом из полученных промежутков знаки функций 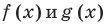 не могут измениться. Тогда мы можем найти знаки подмодульных функций на каждом промежутке (в любой точке этого промежутка), раскрыть знаки модулей и найти решение данного уравнения в каждом из этих промежутков (это и есть четвертый ориентир общей схемы).
не могут измениться. Тогда мы можем найти знаки подмодульных функций на каждом промежутке (в любой точке этого промежутка), раскрыть знаки модулей и найти решение данного уравнения в каждом из этих промежутков (это и есть четвертый ориентир общей схемы).
Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.
Примеры решения задач:
Пример №4
Решите уравнение 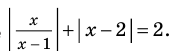
Решение:
1. ОДЗ: 
2. Нули подмодульных функций: 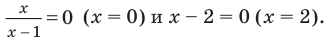
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные функции имеют знаки*, показанные на рисунке.
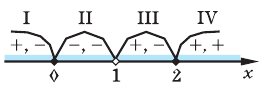
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках 1 и 3, удобно для решения объединить эти промежутки).
Промежутки 1 и 3 :  Учитывая знаки подмодульных функций на этих промежутках и определение модуля, получаем, что в этих промежутках данное уравнение равносильно уравнению
Учитывая знаки подмодульных функций на этих промежутках и определение модуля, получаем, что в этих промежутках данное уравнение равносильно уравнению 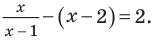 Отсюда
Отсюда 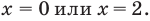 В рассмотренные промежутки полученные значения не входят, таким образом, в этих промежутках корней нет.
В рассмотренные промежутки полученные значения не входят, таким образом, в этих промежутках корней нет.
Промежуток 2: 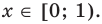 (Следует обратить внимание на то, чтобы не пропустить значение
(Следует обратить внимание на то, чтобы не пропустить значение 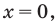 которое принадлежит ОДЗ.) В этом промежутке получаем уравнение
которое принадлежит ОДЗ.) В этом промежутке получаем уравнение 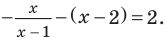 Отсюда
Отсюда 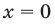 — корень, поскольку принадлежит этому промежутку.
— корень, поскольку принадлежит этому промежутку.
Промежуток 4: 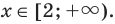 (И в этом промежутке необходимо не забыть значение
(И в этом промежутке необходимо не забыть значение 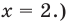 Получаем уравнение
Получаем уравнение 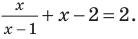 Отсюда
Отсюда 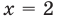 — корень, поскольку принадлежит этому промежутку. Объединяя все решения, которые мы получили в каждом промежутке, имеем решение данного уравнения на всей ОДЗ.
— корень, поскольку принадлежит этому промежутку. Объединяя все решения, которые мы получили в каждом промежутке, имеем решение данного уравнения на всей ОДЗ.
Ответ: 0; 2.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 40. Обоснуем, например, соотношение 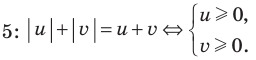
Запишем заданное равенство в виде 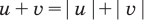 и проанализируем его, опираясь на известные из 6 класса правила действий над числами с одинаковыми и с разными знаками. Чтобы сложить два числа
и проанализируем его, опираясь на известные из 6 класса правила действий над числами с одинаковыми и с разными знаками. Чтобы сложить два числа  мы сложили их модули, таким образом, эти числа имеют одинаковые знаки. Если бы эти числа были оба отрицательными, то и их сумма была бы тоже отрицательна, но и
мы сложили их модули, таким образом, эти числа имеют одинаковые знаки. Если бы эти числа были оба отрицательными, то и их сумма была бы тоже отрицательна, но и 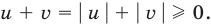 Тогда получаем, что числа
Тогда получаем, что числа 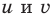 — оба
— оба
неотрицательные. Наоборот, если 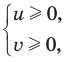 то выполняется равенство
то выполняется равенство 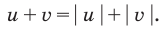 Таким образом, действительно, уравнение
Таким образом, действительно, уравнение 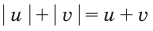 равносильно системе неравенств
равносильно системе неравенств 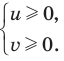
- Заказать решение задач по высшей математике
Пример №5
Решите уравнение 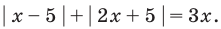
Решение:
Поскольку 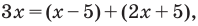 то данное уравнение имеет вид
то данное уравнение имеет вид 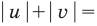
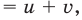 но это равенство может выполняться тогда и только тогда, когда числа
но это равенство может выполняться тогда и только тогда, когда числа  — оба неотрицательные. Таким образом, данное уравнение равносильно системе
— оба неотрицательные. Таким образом, данное уравнение равносильно системе
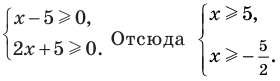
Таким образом, 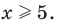
Ответ: 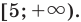
Комментарий:
Если обозначить 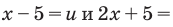
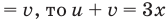 и данное уравнение имеет вид
и данное уравнение имеет вид 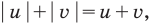 а по соотношению 5 такое уравнение равносильно системе
а по соотношению 5 такое уравнение равносильно системе 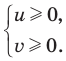
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким но системе
При решении неравенств с модулями рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений с модулями.
Пример №6
Решите неравенство 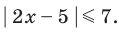
Решение:
Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству 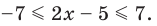 Тогда
Тогда 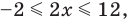 таким образом,
таким образом,
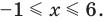
Ответ: 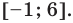
Комментарий:
Неравенство вида 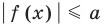 (где
(где 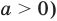 удобно решать, используя геометрический смысл модуля. Поскольку заданное неравенство — это неравенство вида
удобно решать, используя геометрический смысл модуля. Поскольку заданное неравенство — это неравенство вида 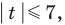 а модуль числа — это расстояние на координатной прямой от точки, изображающей данное число, до точки 0, то заданному неравенству удовлетворяют все точки, находящиеся в промежутке
а модуль числа — это расстояние на координатной прямой от точки, изображающей данное число, до точки 0, то заданному неравенству удовлетворяют все точки, находящиеся в промежутке 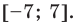 Таким образом,
Таким образом, 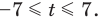 Если возникают затруднения с решением двойного неравенства (1), то его заменяют на равносильную систему
Если возникают затруднения с решением двойного неравенства (1), то его заменяют на равносильную систему 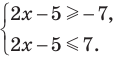
Пример №7
Решите неравенство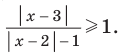
Решение:
1. ОДЗ: 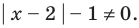 Тогда
Тогда 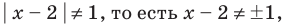 таким образом:
таким образом:
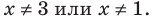
2. Нули подмодульных функций: 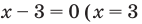 — не принадлежит ОДЗ) и
— не принадлежит ОДЗ) и
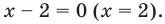
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке (на каждом из промежутков первый знак — это знак функции  а второй — знак функции
а второй — знак функции 
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: 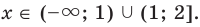 Учитывая знаки подмодульных функций в этих промежутках и определение модуля, получаем, что при
Учитывая знаки подмодульных функций в этих промежутках и определение модуля, получаем, что при 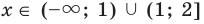 заданное неравенство равносильно неравенству
заданное неравенство равносильно неравенству 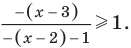 Тогда
Тогда 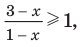 то есть
то есть 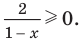 Отсюда
Отсюда 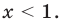 В промежутки, которые мы рассмотрели, входят все значения
В промежутки, которые мы рассмотрели, входят все значения 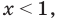 таким образом, в этом случае решением будет
таким образом, в этом случае решением будет 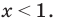
Промежуток III: 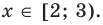 На этом промежутке получаем неравенство
На этом промежутке получаем неравенство 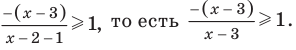 Но при любом значении
Но при любом значении 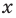 из III промежутка последнее неравенство обращается в неверное неравенство
из III промежутка последнее неравенство обращается в неверное неравенство 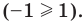 Таким образом, в промежутке III неравенство (1) решений не имеет.
Таким образом, в промежутке III неравенство (1) решений не имеет.
Промежуток IV: 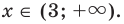 В этом промежутке получаем неравенство
В этом промежутке получаем неравенство 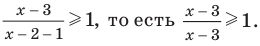 Как видим, при любом
Как видим, при любом  из IV промежутка неравенство (1) обращается в верное числовое неравенство
из IV промежутка неравенство (1) обращается в верное числовое неравенство  Таким образом, решением неравенства (1) в IV промежутке есть любое число из этого промежутка
Таким образом, решением неравенства (1) в IV промежутке есть любое число из этого промежутка 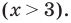
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ: 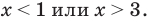
Ответ: 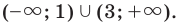
Укажем, что для решения некоторых неравенств с модулями удобно применять также специальные соотношения, приведенные в таблице 40.
Пример №8
Решите неравенство 
Решение:
Поскольку 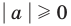 и функция
и функция 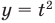 монотонно возрастает на множестве неотрицательных чисел, то все разности модулей в неравенстве можно заменить на разности их квадратов (то есть воспользоваться соотношением 4:
монотонно возрастает на множестве неотрицательных чисел, то все разности модулей в неравенстве можно заменить на разности их квадратов (то есть воспользоваться соотношением 4: 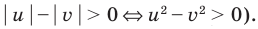 Получаем неравенство, равносильное заданному
Получаем неравенство, равносильное заданному
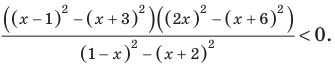
Раскладывая на множители все разности квадратов, имеем: 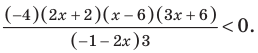
Далее методом интервалов (см. рисунок)получаем
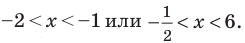
Ответ: 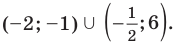
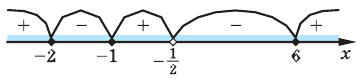
Общая схема, предложенная в таблице 40, может быть использована не только при решении уравнений или неравенств с модулями, но и при выполнении преобразований выражений с модулями.
Например, для построения графика функции 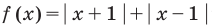 удобно сначала по общей схеме раскрыть знаки модулей, а уже потом строить график функции
удобно сначала по общей схеме раскрыть знаки модулей, а уже потом строить график функции 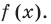
Оформление решения подобного примера может быть таким.
Пример №9
Постройте график функции 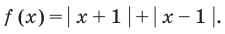
Решение:
1. Область определения функции: 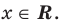
2. Нули подмодульных функций: 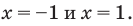
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке также указаны знаки подмодульных функций в каждом из промежутков). 4. Тогда
 Таким образом,
Таким образом, 
Строим график этой функции (см. рисунок).
Решение тригонометрических неравенств
Примеры решения простейших тригонометрических неравенств:
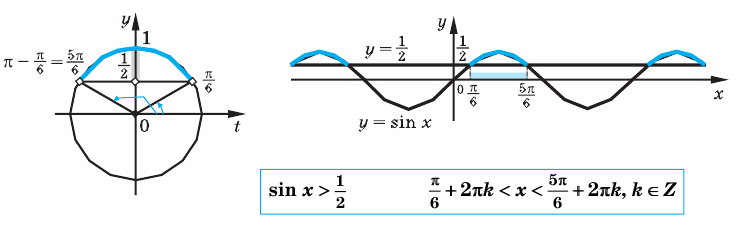
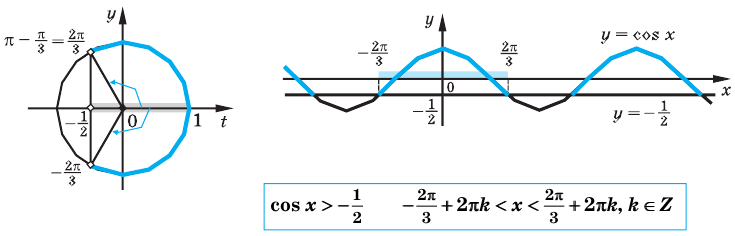
Способы решения более сложных тригонометрических неравенств:
а) Использование равносильных преобразований и, в частности, сведение тригонометрического неравенства к алгебраичкому неравенству по схеме: 1) к одному аргументу, 2) к одной функции, 3) замена переменной (аналогично схеме решения тригонометрических уравнений, приведенной на с. 170) и последующее решение полученных простейших тригонометрических неравенств.
б) Использование метода интервалов (после сведения неравенства к виду  по схеме:
по схеме:
- Найти ОДЗ неравенства.
- Найти общий период (если он существует) для всех функций, входящих в неравенство, то есть период функции
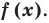
- Найти нули функции:
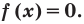
- Отметить нули функции на ОДЗ на одном периоде и найти знак функции
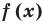 в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде). - Записать ответ, учитывая знак заданного неравенства и период функции
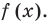
Объяснение и обоснование:
Решение простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами считают неравенства вида 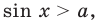
 (на месте знака
(на месте знака  может стоят любой из знаков неравенства:
может стоят любой из знаков неравенства: 
Чтобы рассуждения по нахождению решений этих неравенств были более наглядными, используют единичную окружность или графики соответствующих функций, как это показано в первом пункте таблицы 41.
Пример №10
Объясним более детально решение неравенства 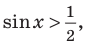 приведенное в пункте 1 таблицы 41, с использованием единичной окружности (рис. 101).
приведенное в пункте 1 таблицы 41, с использованием единичной окружности (рис. 101).
Решение:
Поскольку 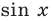 — это ордината соответствующей точки
— это ордината соответствующей точки 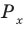 единичной окружности, то при всех значениях
единичной окружности, то при всех значениях  удовлетворяющих данному неравенству, ордината точки
удовлетворяющих данному неравенству, ордината точки  больше
больше 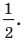 Все такие точки на единичной окружности лежат выше, чем прямая
Все такие точки на единичной окружности лежат выше, чем прямая 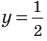 (они изображены на рисунке синей дугой
(они изображены на рисунке синей дугой  без крайних точек, поскольку в крайних точках
без крайних точек, поскольку в крайних точках 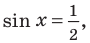 а не больше
а не больше 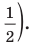 Если, записывая ответ, двигаться против часовой стрелки, то точка
Если, записывая ответ, двигаться против часовой стрелки, то точка  будет началом дуги
будет началом дуги  а точка
а точка  — ее концом. Сначала запишем ответ на одном периоде (напомним, что для синуса период равен
— ее концом. Сначала запишем ответ на одном периоде (напомним, что для синуса период равен 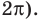 Для точек
Для точек 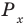 выделенной дуги
выделенной дуги 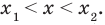 Поскольку точка
Поскольку точка 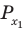 находится в правой полуплоскости, то можно взять
находится в правой полуплоскости, то можно взять 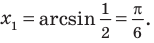 Тогда
Тогда 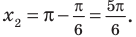 Таким образом, на одном периоде решениями заданного неравенства являются:
Таким образом, на одном периоде решениями заданного неравенства являются: 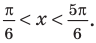
Через период  значения синуса повторяются, поэтому все остальные решения заданного неравенства получаем прибавлением к найденным решениям чисел вида
значения синуса повторяются, поэтому все остальные решения заданного неравенства получаем прибавлением к найденным решениям чисел вида 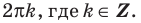
Ответ: 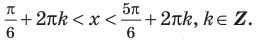
Для решения неравенства 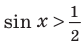 можно воспользоваться также графиками функций
можно воспользоваться также графиками функций 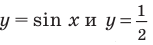 (рис. 102).
(рис. 102).
Решениями неравенства 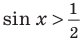 будут те и только те значения
будут те и только те значения 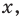 для которых соответствующие точки графика функции
для которых соответствующие точки графика функции 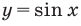 находятся выше прямой
находятся выше прямой 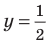 (на рисунке 102 соответствующие части графика функции выделены синими линиями). Чтобы найти абсциссы точек пересечения этих графиков:
(на рисунке 102 соответствующие части графика функции выделены синими линиями). Чтобы найти абсциссы точек пересечения этих графиков: 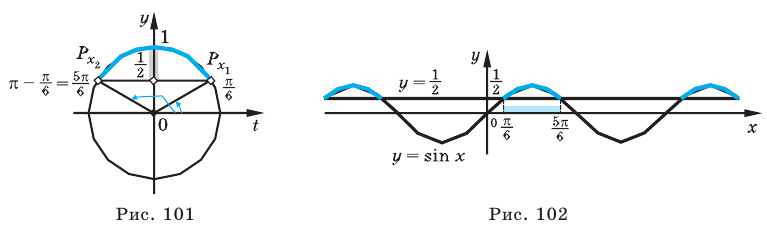
Достаточно решить уравнение 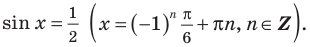 Учитывая периодичность функции
Учитывая периодичность функции  достаточно записать решение данного неравенства на одном периоде. На отрезке длиной
достаточно записать решение данного неравенства на одном периоде. На отрезке длиной  можно взять, например, такие абсциссы точек пересечения графиков функций
можно взять, например, такие абсциссы точек пересечения графиков функций 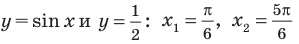 (все другие абсциссы точек пересечения отличаются от них на
(все другие абсциссы точек пересечения отличаются от них на  Тогда на одном периоде решениями данного неравенства являются:
Тогда на одном периоде решениями данного неравенства являются: 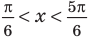 (абсциссы выделенных точек графика
(абсциссы выделенных точек графика  Все остальные решения данного неравенства получаются прибавлением к найденным решениям чисел вида
Все остальные решения данного неравенства получаются прибавлением к найденным решениям чисел вида 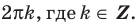
Ответ: 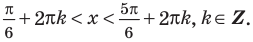
Аналогично можно получить и решения других видов простейших неравенств, приведенных в пункте 1 таблицы 41.
Пример №11
Решите неравенство 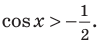
Решение:
Поскольку  — это абсцисса соответствующей точки
— это абсцисса соответствующей точки 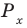 единичной окружности, то при всех значениях
единичной окружности, то при всех значениях 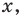 которые удовлетворяют данному неравенству, абсцисса точки
которые удовлетворяют данному неравенству, абсцисса точки 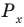 больше
больше 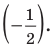 Все такие точки на единичной окружности (рис. 103) лежат справа от прямой
Все такие точки на единичной окружности (рис. 103) лежат справа от прямой 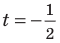 (они изображены на рисунке синей дугой
(они изображены на рисунке синей дугой 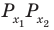 без крайних точек, поскольку в крайних точках
без крайних точек, поскольку в крайних точках 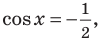 не больше
не больше 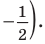 Если, записывая ответ, двигаться против часовой стрелки, то точка
Если, записывая ответ, двигаться против часовой стрелки, то точка  будет началом дуги
будет началом дуги 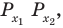 а точка
а точка 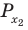 — ее концом. Сначала запишем ответ на одном периоде (напомним, что для косинуса он равен
— ее концом. Сначала запишем ответ на одном периоде (напомним, что для косинуса он равен  Для точек
Для точек  выделенной дуги
выделенной дуги 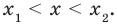 Поскольку точка
Поскольку точка 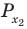 находится в верхней полуплоскости, то можно взять
находится в верхней полуплоскости, то можно взять 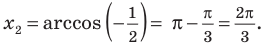 Учитывая симметричность (относительно оси
Учитывая симметричность (относительно оси  точек
точек 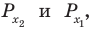 получаем
получаем 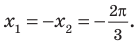
Таким образом, на одном 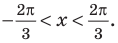 Через период
Через период  решениями данного неравенства являются
решениями данного неравенства являются  . Через период 2л значения косинуса повторяются. Поэтому все остальные решения данного неравенства получаем прибавлением к найденным решениям чисел вида
. Через период 2л значения косинуса повторяются. Поэтому все остальные решения данного неравенства получаем прибавлением к найденным решениям чисел вида  где
где 
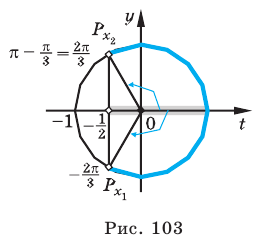
Ответ: 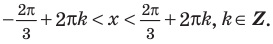
Рассуждения при использовании графической иллюстрации решения неравенства 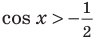 полностью аналогичны приведенным выше рассуждениям по решению неравенства
полностью аналогичны приведенным выше рассуждениям по решению неравенства 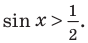
Пример №12
Решите неравенство 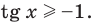
Решение:
Период тангенса равен 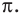 Поэтому сначала найдем решения этого неравенства на промежутке длиной
Поэтому сначала найдем решения этого неравенства на промежутке длиной 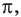 например, на промежутке
например, на промежутке 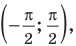 а потом используем периодичность тангенса. Для выделения тех точек
а потом используем периодичность тангенса. Для выделения тех точек 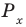 правой полуокружности, значения
правой полуокружности, значения 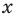 которых удовлетворяют данному неравенству, воспользуемся линией тангенсов (рис. 104). Сначала выделим на линии тангенсов значения тангенсов, большие или равные (-1) (на рисунке они выделены синей линией), а потом для каждой точки линии тангенсов найдем соответствующую точку
которых удовлетворяют данному неравенству, воспользуемся линией тангенсов (рис. 104). Сначала выделим на линии тангенсов значения тангенсов, большие или равные (-1) (на рисунке они выделены синей линией), а потом для каждой точки линии тангенсов найдем соответствующую точку 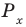 на правой полуокружности (для этого достаточно соединить центр окружности с выделенной точкой на линии тангенсов и взять точку пересечения проведенного отрезка с окружностью). Множество соответствующих точек
на правой полуокружности (для этого достаточно соединить центр окружности с выделенной точкой на линии тангенсов и взять точку пересечения проведенного отрезка с окружностью). Множество соответствующих точек 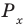 единичной окружности выделено на рисунке синей дугой
единичной окружности выделено на рисунке синей дугой 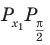 (обратите внимание: точка
(обратите внимание: точка 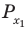 принадлежит рассмотренному множеству, а точка
принадлежит рассмотренному множеству, а точка 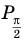 —нет).
—нет).
Поскольку точка 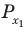 находится в правой полуплоскости, то можно взять
находится в правой полуплоскости, то можно взять 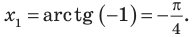 Таким образом, на одном периоде решениями данного неравенства являются
Таким образом, на одном периоде решениями данного неравенства являются 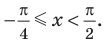 Через период
Через период  значение тангенса повторяется. Поэтому все остальные решения данного неравенства получаем прибавлением к найденным решениям чисел вида
значение тангенса повторяется. Поэтому все остальные решения данного неравенства получаем прибавлением к найденным решениям чисел вида 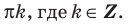
Ответ: 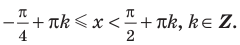
Заметим, что при решении данного неравенства с использованием графиков достаточно, как и в предыдущих случаях, на одном периоде (например, на промежутке 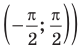 записать те абсциссы, для которых соответствующие точки графика функции
записать те абсциссы, для которых соответствующие точки графика функции 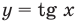 находятся выше прямой
находятся выше прямой 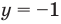 или на самой прямой. (На рисунке в таблице 41 соответствующие части графика функции
или на самой прямой. (На рисунке в таблице 41 соответствующие части графика функции 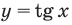 выделены синими линиями.)
выделены синими линиями.)
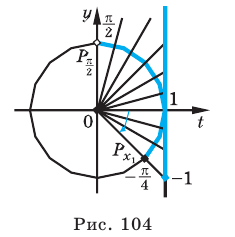
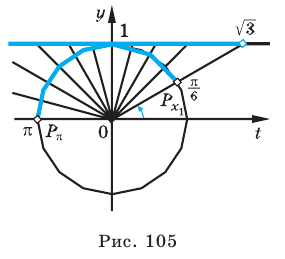
Пример №13
Решите неравенство 
Решение:
Период котангенса равен  Поэтому сначала найдем решение этого неравенства на промежутке длиной
Поэтому сначала найдем решение этого неравенства на промежутке длиной 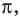 например на промежутке
например на промежутке 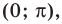 а потом воспользуемся периодичностью котангенса. Для выделения тех точек
а потом воспользуемся периодичностью котангенса. Для выделения тех точек 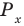 верхней полуокружности, значения
верхней полуокружности, значения 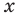 которых удовлетворяют данному неравенству, воспользуемся линией котангенсов (рис. 105).
которых удовлетворяют данному неравенству, воспользуемся линией котангенсов (рис. 105).
Сначала выделим на линии котангенсов значения котангенсов, меньшие, чем 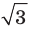 (на рисунке 105 они выделены синей линией), а потом для каждой точки линии котангенсов найдем соответствующую точку
(на рисунке 105 они выделены синей линией), а потом для каждой точки линии котангенсов найдем соответствующую точку 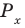 на верхней полуокружности (для этого достаточно соединить центр окружности с выделенной точкой на линии котангенсов и взять точку пересечения проведенного отрезка с окружностью). Множество соответствующих точек
на верхней полуокружности (для этого достаточно соединить центр окружности с выделенной точкой на линии котангенсов и взять точку пересечения проведенного отрезка с окружностью). Множество соответствующих точек 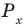 единичной окружности обозначено на рисунке 105 синей дугой
единичной окружности обозначено на рисунке 105 синей дугой 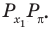 Поскольку точка
Поскольку точка 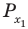 находится в верхней полуплоскости, то можно взять
находится в верхней полуплоскости, то можно взять 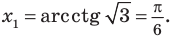
Таким образом, на одном периоде решениями данного неравенства являются
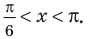 Через период
Через период 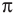 значение котангенса повторяется. Таким образом, все остальные решения данного неравенства получаем прибавлением к найденным решениям чисел вида
значение котангенса повторяется. Таким образом, все остальные решения данного неравенства получаем прибавлением к найденным решениям чисел вида 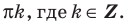 Ответ:
Ответ: 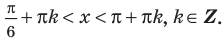 Аналогично предыдущим случаям при решении неравенства
Аналогично предыдущим случаям при решении неравенства 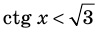 с использованием графиков достаточно на одном периоде (например, на промежутке
с использованием графиков достаточно на одном периоде (например, на промежутке  записать те абсциссы, для которых соответствующие точки графика функции
записать те абсциссы, для которых соответствующие точки графика функции 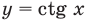 находятся ниже прямой
находятся ниже прямой 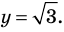 (На рисунке в таблице 41 соответствующие части графика функции
(На рисунке в таблице 41 соответствующие части графика функции 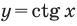 выделены синими линиями.)
выделены синими линиями.)
Способы решения более сложных тригонометрических неравенств
Способы решения более сложных тригонометрических неравенств также проиллюстрируем на примерах.
Пример №14
Решите неравенство: 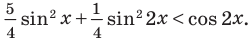
Решение:
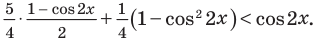
Тогда 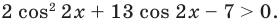 Замена:
Замена: 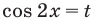 дает неравенство
дает неравенство
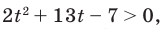 решение которого:
решение которого:
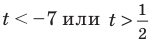 (см. рисунок).
(см. рисунок).
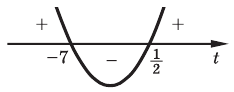
Обратная замена дает: 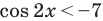 (решений нет) или
(решений нет) или 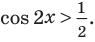 Тогда
Тогда
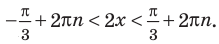
Таким образом,
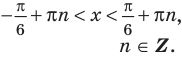
Комментарий:
Используем равносильные преобразования данного неравенства. Для этого приведем его к алгебраическому по схеме, аналогичной схеме решения
- к одному аргументу
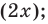
- к одной функции
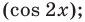
- проведем замену переменной
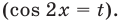 После обратной замены решим полученные простейшие тригонометрические неравенства.
После обратной замены решим полученные простейшие тригонометрические неравенства.
Решая более сложные тригонометрические неравенства, можно также применить метод интервалов, немного изменив его. Необходимость коррекции известной схемы решения неравенств  методом интервалов (с. 232) связана с тем, что в случае, когда функция
методом интервалов (с. 232) связана с тем, что в случае, когда функция  — тригонометрическая, она, как правило, имеет бесконечное множество нулей (которые получаются при целых значениях параметра). Поэтому, если пытаться обозначить нули на ОДЗ, придется обозначить бесконечное их множество, что невозможно. Избежать этого можно, если найти период функции
— тригонометрическая, она, как правило, имеет бесконечное множество нулей (которые получаются при целых значениях параметра). Поэтому, если пытаться обозначить нули на ОДЗ, придется обозначить бесконечное их множество, что невозможно. Избежать этого можно, если найти период функции  (если он существует) и рассмотреть знак функции на каждом промежутке внутри одного периода.
(если он существует) и рассмотреть знак функции на каждом промежутке внутри одного периода.
Таким образом, метод интервалов для решения тригонометрических неравенств 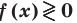 может применяться по схеме:
может применяться по схеме:
- Найти ОДЗ неравенства.
- Найти период функции
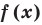 (если он существует).
(если он существует). - Найти нули функции
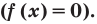
- Отметить нули на ОДЗ внутри одного периода и найти знак функции в каждом из промежутков, на которые разбивается ОДЗ (внутри одного периода).
- Записать ответ (учитывая знак заданного неравенства и период функции
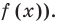
Пример №15
Решите неравенство 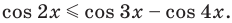
Решение:
Решим данное неравенство методом интервалов. Для этого приведем его к виду 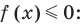
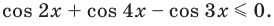
1. ОДЗ: 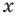 — любое действительное число.
— любое действительное число.
2. Как мы знаем, период функции  равен
равен 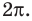 Тогда период функции
Тогда период функции 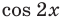 будет
будет 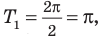 период функции
период функции 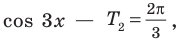 а период функции
а период функции 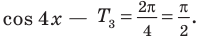
На отрезке длиной  периоды
периоды 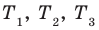 помещаются целое число раз. Тогда
помещаются целое число раз. Тогда  будет общим периодом для всех этих трех функций, и поэтому
будет общим периодом для всех этих трех функций, и поэтому 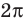 является периодом функции
является периодом функции 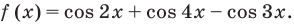
3.Найдем нули этой функции: 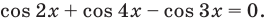
Тогда 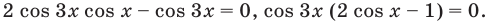
Отсюда 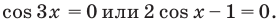 Решая последние уравнения, получаем
Решая последние уравнения, получаем 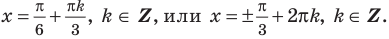
4. Отметим все нули на периоде длиной  например на отрезке от 0 до
например на отрезке от 0 до  и получим 9 промежутков (см. рисунок).
и получим 9 промежутков (см. рисунок).

Находим знаки функции  на каждом из промежутков. Для этого удобно записать функцию
на каждом из промежутков. Для этого удобно записать функцию  в виде произведения:
в виде произведения: 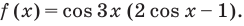
Ответ (записывается с учетом периода): 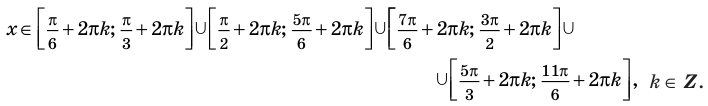
Замечание. При решении тригонометрических неравенств методом интервалов часто приходится находить знак функции в большом количестве промежутков. Для того чтобы уменьшить объем работы, можно предложить такой способ: следить за тем, через какой нуль мы проходим при переходе от одного интервала к другому и изменяется ли знак заданной функции в этом нуле.
В случае, когда функция 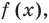 которая стоит в левой части неравенства, записана в виде произведения
которая стоит в левой части неравенства, записана в виде произведения 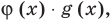 необходимо обращать внимание на то, что знак произведения не меняется, если одновременно оба множителя (функции
необходимо обращать внимание на то, что знак произведения не меняется, если одновременно оба множителя (функции 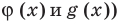 меняют знаки на противоположные.
меняют знаки на противоположные.
Практически для использования этого свойства в случае, если левая часть неравенства записана как произведение нескольких функций, нули каждого множителя отмечают на промежутке разным цветом (так, как это сделано на рисунке к задаче 6), или, если множителей только два, нули первого множителя обозначают под осью, а нули второго — над осью.
Если у функций-множителей нет одинаковых нулей, то знак функции  меняется автоматически при переходе через каждый нуль (при условии, что только одна из функций-множителей меняет знак при переходе через этот нуль). В этом случае для нахождения всех знаков функции
меняется автоматически при переходе через каждый нуль (при условии, что только одна из функций-множителей меняет знак при переходе через этот нуль). В этом случае для нахождения всех знаков функции 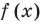 на периоде достаточно найти ее знак только в одном промежутке, а в других расставить знаки, чередуя их. Если же у функций-множителей есть одинаковые нули, то при переходе через такой нуль знак произведения может не меняться, и это учитывается при расстановке знаков.
на периоде достаточно найти ее знак только в одном промежутке, а в других расставить знаки, чередуя их. Если же у функций-множителей есть одинаковые нули, то при переходе через такой нуль знак произведения может не меняться, и это учитывается при расстановке знаков.
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x – их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
