В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема пирамиды
- 1. Общая формула
- 2. Объем правильной треугольной пирамиды
-
3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
- Примеры задач
Формула вычисления объема пирамиды
1. Общая формула
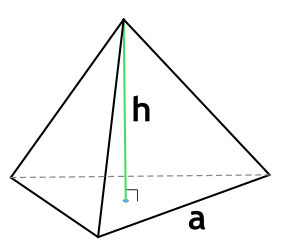
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.


- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:
![]()
3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
![]()
4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
![]()
С учетом этого, объем фигуры считается так:
![]()
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:![]()
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:![]()

{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
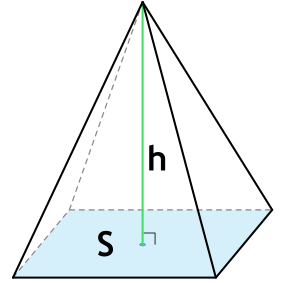
{V= dfrac{1}{3} S cdot h}
S – площадь основания пирамиды
h – высота пирамиды
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
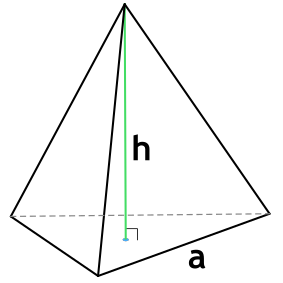
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
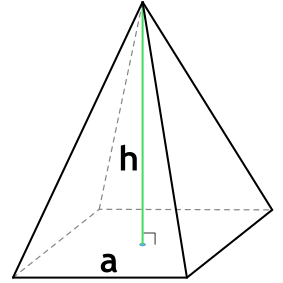
{V= dfrac{1}{3} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
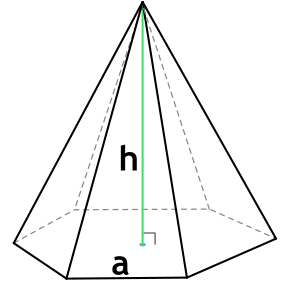
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a – длина стороны основания пирамиды
h – высота пирамиды
n – число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a – длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.
Пирамида – это многогранник, основанием которого является многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор объема пирамиды
У пирамиды есть ребра. Можно сказать, что они тянутся к точке, называемой вершиной данной пирамиды. Ее основанием может быть произвольный многоугольник. Грань — это фигура, которая образуется в результате объединения двух ближайших ребер со стороной основания. Гранью пирамиды является треугольник. Расстояние от вершины пирамиды до середины стороны основания называется апофемой. Высотой пирамиды называется длина перпендикуляра, опущенного из вершины к центру ее основания.
Типы пирамид
Различают следующие типы пирамид.
- Прямоугольная — у нее ребро образует угол в 90 градусов с основанием.
- Правильная — ее основание — какой-либо правильный многоугольник, а вершина проецируется в центр этого основания.
- Тетраэдр — пирамида, у которой в основании лежит треугольник.
Формулы объема пирамиды
Объем пирамиды находится несколькими способами.
По площади основания и высоте пирамиды
Простое умножение одной трети площади основания на высоту пирамиды и является ее объемом.
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания пирамиды;
hh — высота данной пирамиды.
Площадь основания пирамиды равна 100 см2100text{ см}^2, а высота ее равна 30 см30text{ см}. Найдите объем тела.
Решение
Sосн=100S_{text{осн}}=100
h=30h=30
Все величины нам известны, подставляем их численные значения в формулу и находим:
V=13⋅Sосн⋅h=13⋅100⋅30=1000 см3V=frac{1}{3}cdot S_{text{осн}}cdot h=frac{1}{3}cdot 100cdot 30=1000text{ см}^3
Ответ
1000 см3.1000text{ см}^3.
Формула объема правильной треугольной пирамиды
Этот способ подходит, если пирамида правильная и треугольная.
V=h⋅a243V=frac{hcdot a^2}{4sqrt{3}}
hh — высота пирамиды;
aa — сторона основания пирамиды.
Вычислите объем правильной треугольной пирамиды, если в ее основании лежит равносторонний треугольник, в котором сторона равна 5 см5text{ см}, а высота пирамиды равна – 19 см19text{ см}.
Решение
a=5a=5
h=19h=19
Просто подставляем данные величины в формулу для объема:
V=h⋅a243=19⋅5243≈68.6 см3V=frac{hcdot a^2}{4sqrt{3}}=frac{19cdot 5^2}{4sqrt{3}}approx68.6text{ см}^3
Ответ
68.6 см3.68.6text{ см}^3.
Формула объема правильной четырехугольной пирамиды
V=13⋅h⋅a2V=frac{1}{3}cdot hcdot a^2
hh — высота пирамиды;
aa — сторона основания пирамиды.
Дана правильная четырехугольная пирамида. Вычислите ее объем, если ее высота равна 7 см7text{ см}, a сторона основания составляет – 2 см2text{ см}.
Решение
a=2a=2
h=7h=7
По формуле вычисляем:
V=13⋅h⋅a2=13⋅7⋅22≈9.3 см3V=frac{1}{3}cdot hcdot a^2=frac{1}{3}cdot 7cdot 2^2approx9.3text{ см}^3
Ответ
9.3 см3.9.3text{ см}^3.
Формула объема тетраэдра
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Длина ребра тетраэдра равна 13 см13text{ см}. Найдите его объем.
Решение
a=13a=13
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅13312≈259 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 13^3}{12}approx259text{ см}^3
Ответ
259 см3.259text{ см}^3.
Формула объема пирамиды как определитель
Наверное, самый экзотический способ вычисления объема данного тела.
Пусть даны векторы, на которых построена пирамида как на сторонах. Тогда ее объем будет равен одной шестой смешанного произведения векторов. Последний в свою очередь равен определителю составленному из координат этих векторов. Итак, если пирамида построена на трех векторах:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующей пирамиды это такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем пирамиды через смешанное произведение векторов, координаты которых такие: a⃗=(2,3,5)vec{a}=(2,3,5) , b⃗=(1,4,4)vec{b}=(1,4,4), c⃗=(3,5,7)vec{c}=(3,5,7).
Решение
a⃗=(2,3,5)vec{a}=(2,3,5)
b⃗=(1,4,4)vec{b}=(1,4,4)
c⃗=(3,5,7)vec{c}=(3,5,7)
По формуле:
V=16⋅∣235144357∣=16⋅(2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7)=16⋅(56+36+25−60−40−21)=16⋅(−4)=−23≈−0.7V=frac{1}{6}cdotbegin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=frac{1}{6}cdot(2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 – 5cdot4cdot3 – 2cdot4cdot5 – 3cdot1cdot7) =frac{1}{6}cdot( 56 + 36 + 25 – 60 – 40 – 21)=frac{1}{6}cdot(-4)=-frac{2}{3}approx-0.7
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=0.7 см3V=0.7text{ см}^3
Ответ
0.7 см3.0.7text{ см}^3.
Не знаете, где можно оформить заказ контрольных работ недорого? Наши эксперты помогут вам с решением работ по объемам фигур!
Тест по теме “Объем пирамиды”
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что считает калькулятор
Калькулятор объема пирамиды — это онлайн инструмент, который используется для быстрого расчета объема пирамиды по ее известным параметрам. Объем пирамиды представляет собой объем пространства, которое занимает эта фигура в трехмерном пространстве.
Калькулятор объема пирамиды может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов таких геометрических фигур. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов, например, в архитектуре, инженерии, физике и т.д.
Где можно применить калькулятор объема пирамиды
Калькулятор объема пирамиды можно применить в различных сферах, где требуется вычислить объем пирамиды, например:
- Строительство: при проектировании зданий и сооружений инженерам и архитекторам часто нужно вычислить объем пирамиды, например, для расчета объема кровли или фундамента.
- Геометрия: в математике пирамиды являются важным объектом изучения, и вычисление их объема – одна из основных задач геометрии.
- Производство: в производстве может потребоваться вычислить объем пирамиды для расчета необходимых материалов, например, для производства упаковки.
- Учебные цели: калькулятор объема пирамиды может быть использован студентами и учениками при изучении геометрии или математики.
- Игры и развлечения: калькулятор объема пирамиды может быть использован в играх и развлечениях, где требуется решить задачу по вычислению объема пирамиды.
В целом, калькулятор объема пирамиды может быть полезен во всех ситуациях, где требуется вычислить объём данной фигуры.
В чем преимущество пирамиды
Пирамида — многогранник, основание которого является многоугольником, а остальные грани – треугольниками, имеющими общую вершину.
Пирамидальная форма имеет несколько преимуществ:
- Стабильность. Пирамида имеет широкое основание и суживающийся верх, что делает ее очень стабильной. Это свойство делает пирамиду идеальным выбором для многих инженерных и архитектурных конструкций.
- Эффективность использования пространства. Пирамидальная форма позволяет использовать пространство более эффективно. Благодаря своей форме пирамида может поместить больше материала на меньшей площади, чем другие формы.
- Видимость. Пирамиды обычно имеют значительную высоту и суживающуюся вершину, что делает их легко заметными издалека. Это свойство делает пирамиды идеальным выбором для монументальных сооружений, таких как пирамиды в Египте или Латинской Америке.
- Эстетика. Пирамидальная форма может быть очень эстетичной и привлекательной. Она может использоваться в различных областях, таких как дизайн зданий, декоративное искусство, упаковка продуктов и многое другое.
В целом, пирамидальная форма имеет множество преимуществ, которые делают ее полезной в различных областях. Однако, как и любая другая форма, она может иметь свои недостатки в зависимости от контекста, в котором она используется.
Как вычислить объем пирамиды
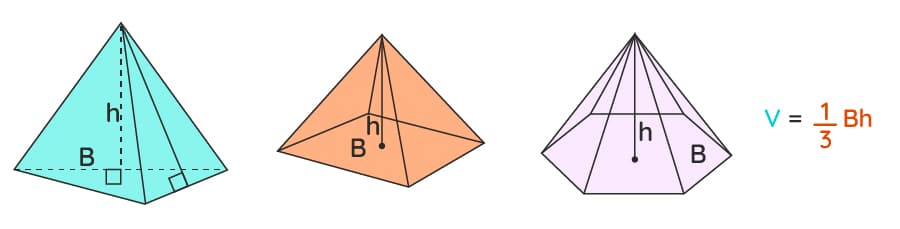
Калькулятор объема пирамиды использует стандартные математические формулы для расчета объема пирамиды с основанием любой формы.
Как вычислить объем пирамиды по высоте и площади основания
Формула расчета объема пирамиды, которая основана на ее высоте и площади основания, выглядит следующим образом:
V = 1/3 * S * h
где: V – объем пирамиды S – площадь основания пирамиды h – высота пирамиды
Для того, чтобы вычислить объем пирамиды, нужно знать ее высоту и площадь основания. Подставьте известные значения в соответствующие поля калькулятора и получите необходимое значение объема.
Например, для пирамиды с площадью основания 20см2 и высотой 5см расчёт объема будет выглядеть таким образом:
V = 1/3 * S * h = 1/3 * 20 * 5 = 33.3см3
Как вычислить объем пирамиды с правильным многоугольным основанием
Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр вписанной в основание окружности.
Объем пирамиды с правильным многоугольным основанием можно вычислить по формуле:
V = (n * a2 * h) / (12 * tan(180о/n))
где h – высота пирамиды, а – сторона основания, n – количество сторон в основании
Например, объем правильной многоугольной пирамиды с высотой 100см, стороной основания 12см и количеством сторон 6 равен:
V = (n * a2 * h) / (12 * tan(180о/n)) = (6 * 122 * 100) / (12 * tan(180о/6)) = 12470.7658см3
Как вычислить объем правильной треугольной пирамиды
Правильная треугольная пирамида – это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Объем пирамиды с правильным треугольным основанием можно вычислить по формуле:
V = h * a² / 4 * √3
где h – высота пирамиды, а – сторона основания
Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания и длину ее высоты, и затем использовать вышеуказанную формулу.
Например, объем правильной треугольной пирамиды с высотой 100см и стороной основания 12см равен:
V = h * a² / 4 * √3 = 100 * 12² / 4 * √3 = 2078.461см3
Как вычислить объем правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Объем пирамиды с правильным четырехугольным основанием можно вычислить по формуле:
V = 1 / 3 * h * a²
где h – высота пирамиды, а – сторона основания.
Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания и длину ее высоты, и затем использовать вышеуказанную формулу.
Например, объем правильной четырехугольной пирамиды с высотой 100см и стороной основания 12см равен:
V = 1 / 3 * h * a² = 1 / 3 * 100 * 12² = 4800см3
Как вычислить объем тетраэдра
Тетраэдр – пирамида, у которой все грани – равносторонние треугольники.
Объем пирамиды с правильным треугольным основанием можно вычислить по формуле:
V = a3 * √2 / 12
где а – сторона основания.
Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания, и затем использовать вышеуказанную формулу.
Например, объем тетраэдра со стороной основания 12см равен:
V = a3 * √2 / 12 = 123 * √2 / 12 = 203.6468см3
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемы вопросе о пирамиде и ее параметрах.
Как найти площадь основания пирамиды?
Площадь основания пирамиды зависит от ее формы. Если основание пирамиды имеет форму прямоугольника, площадь вычисляется по формуле S = a * b, где a и b – длины сторон прямоугольника. Если основание пирамиды имеет форму треугольника, площадь вычисляется по формуле S = (a * b * sin(α)) / 2, где a и b – длины сторон треугольника, α – угол между ними.
Как определить высоту пирамиды?
Высоту пирамиды можно определить с помощью теоремы Пифагора. Для этого необходимо построить прямую, проходящую через вершину пирамиды и перпендикулярную к основанию. Затем нужно измерить длину этой прямой и длину отрезка, соединяющего середины двух сторон основания. Высота пирамиды равна квадратному корню из разности квадратов этих длин.
Как найти боковую поверхность пирамиды?
Боковая поверхность пирамиды состоит из треугольников, каждый из которых имеет общую вершину в вершине пирамиды и стороны, соединяющие эту вершину с точками на основании. Площадь каждого такого треугольника можно вычислить по формуле S = (a * h) / 2, где a – длина стороны основания, h – высота боковой грани. Общая площадь боковой поверхности пирамиды равна сумме площадей всех ее боковых граней.
Как вычислить полную поверхность пирамиды?
Для вычисления полной поверхности пирамиды нужно сложить площади всех ее боковых граней и площадь ее основания. Формула для вычисления площади боковой грани зависит от формы пирамиды. Например, если пирамида имеет правильную многоугольную основу, то ее боковые грани будут равными равнобедренными треугольниками. Площадь такой грани можно вычислить по формуле: Sбок = (1/2) * Периметр основания * Высота боковой грани, где Периметр основания – периметр многоугольной основы пирамиды, Высота боковой грани – расстояние от вершины пирамиды до середины ребра ее основания.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
![]()
Объём правильной пирамиды. Продолжаем рассматривать задачи с пирамидами. На блоге уже рассмотрены задания с правильными пирамидами, в этих статьях шла речь о нахождении элементов и площади поверхности. Здесь разберём примеры связанные с понятием объёма. Для решения подобных заданий обязательно нужно знать формулу объёма пирамиды:
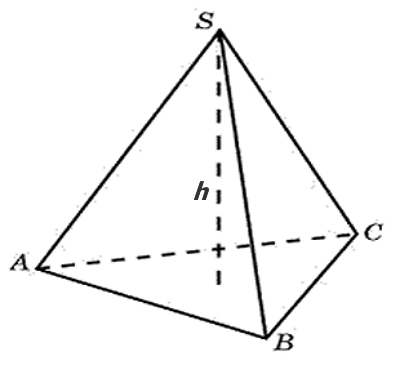
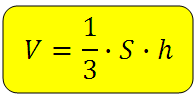
S – площадь основания пирамиды
h – высота пирамиды
Основанием может быть любой многоугольник. Но в большинстве задач на ЕГЭ речь в условии, как правило, идёт о правильных пирамидах. Напомню одно из её свойств:
Вершина правильной пирамиды проецируется в центр её основания
Посмотрите на проекцию правильной треугольной, четырёхугольной и шестиугольной пирамид (ВИД СВЕРХУ):

Можете посмотреть ещё одну статью на блоге, где разбирались задачи связанные с нахождением объёма пирамиды. Рассмотрим задачи:

27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна корню из трёх.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды
h – высота пирамиды
Найдём площадь основания пирамиды, это правильный треугольник. Воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, объём пирамиды равен:

Ответ: 0,25

27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен корню из трёх.

Такие понятия как высота пирамиды и характеристики её основания связаны формулой объёма:

S – площадь основания пирамиды
h – высота пирамиды
Сам объём нам известен, площадь основания можем найти, так как известны стороны треугольника, который является основанием. Зная указанные величины без труда найдём высоту.
Для нахождения площади основания воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, подставив данные значения в формулу объема можем вычислить высоту пирамиды:

Высота равна трём.
Ответ: 3

27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды
h – высота пирамиды
Высота нам известна. Необходимо найти площадь основания. Напомню, что вершина правильной пирамиды проецируется в центр её основания. Основанием правильной четырёхугольной пирамиды является квадрат. Мы можем найти его диагональ. Рассмотрим прямоугольный треугольник (выделен синим):

Отрезок соединяющий центр квадрата с точкой В это катет, который равен половине диагонали квадрата. Этот катет можем вычислить по теореме Пифагора:
![]()
Значит BD = 16. Вычислим площадь квадрата воспользовавшись формулой площади четырёхугольника:

Следовательно:

Таким образом, объём пирамиды равен:

Ответ: 256

27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Высота пирамиды и её и объём известны, значит можем найти площадь квадрата, который является основанием. Зная площадь квадрата, мы сможем найти его диагональ. Далее рассмотрев прямоугольный треугольник по теореме Пифагора вычислим боковое ребро:

Найдём площадь квадрата (основания пирамиды):

Вычислим диагональ квадрата. Так как его площадь равна 50, то сторона будет равна корню из пятидесяти и по теореме Пифагора:

Точка О делит диагональ BD пополам, значит катет прямоугольного треугольника ОВ = 5.
Таким образом, можем вычислить чему равно боковое ребро пирамиды:
![]()
Ответ: 13

245353. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Как уже неоднократно было сказано – объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды
h – высота пирамиды
Боковое ребро перпендикулярное основанию равно трём, это означает, что высота пирамиды равна трём. Основания пирамиды – это многоугольник, площадь которого равна:
![]()
Таким образом:

Ответ: 27
![]()
27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Посмотреть решение
27110. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 6. Найдите объем пирамиды.

Посмотреть решение
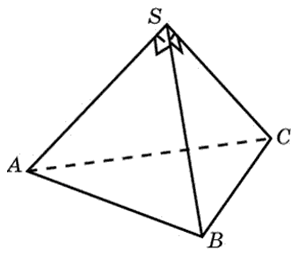
27111. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Посмотреть решение
27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.

Посмотреть решение
27114. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

Посмотреть решение
27176. Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
Посмотреть решение
27179. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Посмотреть решение
27181. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450. Найдите объем пирамиды.

Посмотреть решение
На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
