Как найти давление газа в цилиндре

Давление газа в цилиндре двс и в цилиндре компрессора

Таблица 2

Относительное перемещение поршня (в долях хода поршня)	Давление газа в цилиндре ДВС (в долях от РДmax) при движении поршня	Давление газа в цилиндре компрессора (в долях от РКmax) при движении поршня
Вниз	вверх	вниз	вверх
0	0,863	0,863	1,0	1,0
0,02	1,0	0,5	–	–
0,05	0,863	0,318	–	–
0,1	0,602	0,204	0,30	1,0
0,2	0,340	0,114	-0,1	1,0
0,3	0,238	0,073	-0,1	0,55
0,4	0,170	0,045	-0,1	0,38
0,5	0,130	0,025	-0,1	0,27
0,6	0,10	0,014	-0,1	0,18
0,7	0,082	0,005	-0,1	0,12
0,8	0,068	0,001	-0,1	0,08
0,9	0,034	0	-0,1	0,04
1,0	0	0	-0,1	-0,1

1. Определение закона движения механизма

1.1 Определение
размеров сдвоенного кривошипно-ползунного
механизма

Проектирование
кривошипно-ползунного механизма ведется
по средней скорости поршня (ползуна).
При этом известными являются следующие
параметры (табл. 1.1): средняя скорость
поршня V_ср=6.4
м/с, частота вращения вала кривошипа
n=16 c^-1,
отношение длин шатуна и кривошипа
=l_AB/l_OA
=l_AC/l_OA
=4.5.

Время одного
оборота вала t=1/n =0.0625 с, а расстояние,
которое проходит поршень за один оборот,
S равно 4^.l_OA.
Но V_ср=S/t.
Нетрудно заметить, что l_OA=V_ср/(4^.n)

l_ОА=0.1
м 
l_АC=
l_АВ=0.45
м.

Ход поршня
Н=2l_OA=0.2м.

Получив размеры
звеньев, выбираем масштаб для построения
механизма:

1.2 Построение
диаграмм движущих сил и сил сопротивления

Траекторию точки
А кривошипа разбиваем на 12 равны частей
и нашли соответствующие положения точек
В и С ползунов. По
заданным индикаторным диаграммам (табл.
1.2) для ДВС и компрессора строим диаграммы
соответственно движущих сил и сил
сопротивления. Сила, действующая на
поршень пропорциональна ординатам
соответствующей кривой индикаторной
диаграммы.

По заданному
максимальному давлению в цилиндре
компрессора определяем максимальное
давление в цилиндре ДВС, связанное с
ним соотношением:

P_д^max=
P_к^max(d_k/d_д)²/(h_дh_k)=6.938
МПа.

Определяем масштабы
давлений:

Далее по известным
максимальным давлениям в цилиндрах и
площадям поршней находим максимальную
движущую силу F_Дmax
и максимальную
силу сопротивления F_Kmax
.

=0.0113м²

Определяем масштабы
сил:

Таким образом,
построив диаграммы сил и определив их
масштаб, находим силу в любом положении
механизма. Значения сил представлены
в таблице3

Таблица3

величина	размерн.	0	2	4	6	8	10
z Fд	мм	59	52	17	7	5	3
Fд	кН	67	53,4	19,3	8	5,7	3,4
z Fк	мм	5	5	5	5	1	4
Fк	кН	5,32	5,32	5,32	5,32	1,1	4,3

величина	размерн.	12	14	16	18	20	22
z Fд	мм	0	0	0	1	5	20
Fд	кН	0	0	0	1,14	5,7	22,7
z Fк	мм	11	28	49	49	19	5
Fк	кН	11,7	29,8	52,1	52,1	20,2	5,32

1.3 Определение
приведенного момента движущих сил

Приведение моментов
сил осуществляется на основе метода
приведения сил. В основу метода положено
равенство элементарных работ реальных
сил, действующих в механизме и суммарного
приведенного момента всех сил.

Момент приведенный
от движущих сил определяется из
соотношения:

,
где V_qb
– передаточная функция.

Значения передаточных
функций представлены в распечатке из
программы AR200,
которая приложена к данной работе.

1.4 Определение
приведенного момента сил сопротивления

Момент приведенный
от сил сопротивления определяется из
соотношения:

,
где V_qc
– передаточная
функция.

Значения передаточных
функций приведены в распечатке из
программы AR200,
которая приложена к данной работе.

1.5 Определение
суммарного приведенного момента

Суммарный приведенный
момент определяется как сумма приведенного
момента движущих сил и приведенного
момента сил сопротивления:

Таблица4

величина	Размерн	0	1	2	3	4	5
Мпр Fд	Н*м	0	3.56	1.2	0.81	0.35	0.01
Мпр Fк	Н*м	-0.53	-0.41	-0.21	0	-0.04	-0.33
Мпр сум	Н*м	-0.53	3.15	0.99	0.81	0.31	-0.32

величина	Размерн	6	7	8	9	10	11
Мпр Fд	Н*м	0	0	0	-0.16	-0.38	-1.17
Мпр Fк	Н*м	-1.17	-2.9	-3.1	0	1.2	-0.51
Мпр сум	Н*м	-1.17	-2.9	-3.9	-0.16	0.82	1.68

Вычисляем масштаб
графика суммарного приведенного момента
и масштаб этого графика по оси абсцисс:

Моментами, от
действия сил тяжести звеньев пренебрегаем,
так как их величина очень незначительна
– менее 5 % от максимального суммарного
приведенного момента.

1.6 Построение
графика суммарной работы

Построение графика
работы движущих сил производится путем
графического интегрирования графика
приведенного момента движущих сил.

Отрезок интегрирования
ОК выбираем равным 50 мм.

Построение графика
работы сил сопротивления производится
путем графического интегрирования
графика приведенного момента сил
сопротивления.

Отрезок интегрирования
ОК выбираем равным 50 мм.

Построение графика
суммарной работы производится путем
графического интегрирования графика
суммарного приведенного момента.

Отрезок интегрирования
ОК выбираем равным 50 мм.

Масштаб графика
работы определим по соотношению:

1.7 Определение
приведенного момента инерции II
группы звеньев механизма ДВС

Приведение моментов
инерции осуществили на основе метода
приведения масс. В основу метода положено
равенство кинетической энергии всех
звеньев механизма и звена динамической
модели. В этом случае закон движения
последнего будет таким же, как и закон
движения начального звена реального
механизма.

Суммарный приведенный
момент инерции всего механизма равен
сумме приведенных моментов инерции
всех его звеньев. Суммарный приведенный
момент инерции второй группы звеньев
(поршней 3 и 5 и шатунов 2 и 4) рассчитывается
по формуле:

,

где I_3П^пр
– приведенный
момент инерции поршня ДВС при его
поступательном движении;

где I_5П^пр
– приведенный момент инерции поршня
компрессора при его поступательном
движении;

I_2П^пр
– приведенный момент инерции шатуна 2
при его поступательном движении;

I_4П^пр
– приведенный момент инерции шатуна 4
при его поступательном движении;

I_2Вр^пр
– приведенный момент инерции шатуна 2
при его вращательном движении;

I_4Вр^пр
– приведенный момент инерции шатуна 4
при его вращательном движении.

Приведенные моменты
инерции элементов при поступательном
движении рассчитываются по формулам:

, где

V_i
– скорость
поступательного движения звена [м/с];

₁
– угловая скорость кривошипа 1 [рад/с];

m_i
– масса звена [кг].

Приведенные моменты
инерции шатунов 2 и 4 при их вращательном
движении рассчитываются по формуле:

,
где

_i
– угловая
скорость звена [рад/с];

I_is
-момент
инерции звена относительно оси, проходящей
через центр тяжести [кгм²].

Суммарный приведенный
момент инерции всего механизма

=
+
, где
– приведенный момент инерции первой
группы звеньев. Расчеты выполнены и
представлены в программе AR200.

Вычислим масштаб
графика суммарного приведенного момента
инерции II
группы звеньев:

1.8 Построение
приближенного графика кинетической
энергии II
группы звеньев механизма.

Кинетическую
энергию T_II
звеньев 2, 3, 4, 5 выразим через
J_II^пр
:Закон измененияw₁
еще не известен. Поэтому для определения
T_II
воспользуемся приближенным равенством
w₁=w_ср
(допущение
Мерцалова), поскольку коэффициент
неравномерности δ мал. Тогда

Так как w_ср
=const
, то T_II
можно считать пропорциональной J_II^пр,
а построенную кривую J_II^пр(φ)
принять за приближенную кривую T_II(φ),
вычислив масштаб μ_Т
мм/Дж. Масштаб графика T_II(φ)
:

1.9 Построение
приближенного графика кинетической
энергии I
группы звеньев

T_I=T-T_II

Следовательно,
при построении кривой T_I(φ)
необходимо из ординат кривой T(φ)
в каждом положении механизма вычесть
отрезки, изображающие T_II.
Длины вычитаемых отрезков в миллиметрах
равны

Где

y_TII
– ордината взятая из графика T_II(φ),
мм

μ_T
– масштаб графика T_II(φ),
мм/Дж

μ_A
– масштаб графика T(φ)б
мм/Дж

Кривая T_I(φ^*)
– приближенная т.к. получена вычитанием
из точной кривой T(φ)
приближенных значений T_II.

№ позиции	Отрезки
0,24	115.38	29.54
2	105	26.88
4	104.2	26.68
6	96.36	24.67
8	86.7	22.2
10	95.1	24.35
12	115.38	29.54
14	128.4	32.87
16	117.6	30.11
18	96.36	24.67
20	100.2	25.65
22	118.5	30.34

Таблица5

1.10 Определение
необходимого момента инерции маховых
масс.

Построив кривую
T_I(φ^*),
найдем на ней точки соответствующие
T_Imax
и T_Imin.
Тогда максимальное изменение кинетической
энергии I
группы звеньев за цикл :

Необходимый момент
инерции J_I^пр
подсчитывается по формуле:

Допущение что
w₁=w_ср
не вносит
заметной ошибки в расчет т.к. значение
коэффициента неравномерности мало
(1/90).

Момент инерции
маховика можем вычислить из следующего
соотношения:

,
где

–
момент инерции вращающихся звеньев,
приведенных к звену 1 (задан в исходных
данных)

1.11 Построение
графика угловой скорости

Чтобы
найти угловую скорость начального звена
необходимо знать начальные условия,
которые для установившегося движения
заранее неизвестны. Поэтому воспользуемся
тем, что при малых значениях коэффициента
неравномерности δ верхняя часть графика
T_I(φ^*),
изображающая изменение кине­тической
энергии T_I,
приближенно изображает также изменение
угловой скорости.

Масштаб графика
угловой скорости :

Чтобы перейти от
изменения угловой скорости к ее полному
значению, необходимо определить положения
оси абсцисс графика w₁(φ^**).
Для этого через середину отрезка,
изображающего разность (w_1max–w_1min) проводят горизонтальную штриховую
линию, которая является линией средней
угловой скоростиw_1ср.

Соседние файлы в папке 106-й вариант

• #

  04.03.20144.1 Кб38._Моя Записка.doc

• #

  04.03.201411.73 Кб39зубья1.mcd

• #

  04.03.201453.83 Кб33Мом.инерции1.frw

• #
• #
• #

  04.03.2014174.06 Кб47ЧистовикТММ1.cdw

• #

  04.03.2014153 Кб35ЧистовикТММ2.cdw

• #

  04.03.2014151.95 Кб39ЧистовикТММ3.cdw

• #

  04.03.201499.12 Кб36ЧистовикТММ4.cdw

Давление газов на поршень определяется по индикаторной диаграмме, которая строится по результатам теплового расчёта либо снимается с двигателя внутреннего сгорания. Для этого индикаторную диаграмму p=f(α) лучше представить в развёрнутом виде [рис. 1]. Значения давления газов при этом снимаются через определённые угловые интервалы.

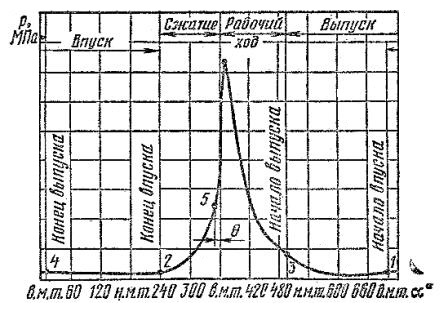
Рис. 1. Развёрнутая индикаторная диаграмма четырёхтактного двигателя p=f(α).

Сила давления газов на поршень определяется из выражения

P_r=F_п(p_r-p₀)H

* где F_п=(πD²)4 – площадь поршня (м²); p_r – давление газов на поршень, определяемое по индикаторной диаграмме в данный момент (Па); p₀ – давление газов под поршнем, то есть в картере двигателя (Па).

Из-за того, что давление газов в цилиндре двигателя является величиной переменной, сила давления газов на поршень –  функция P_r=f(α) угла поворота коленчатого вала [рис. 2].

Рис. 2. Изменение силы давления газов P_r, силы инерции P_i и суммарной силы P в зависимости от угла поворота коленчатого вала.

17*

Условие задачи:

В цилиндре находится газ, удерживаемый в объеме 1 м³ силой тяжести поршня и силой атмосферного давления. При нагревании объем газа возрастает в 2 раза, и газ совершает работу 110 кДж. Найти массу поршня, если его площадь 0,005 м². (p_{атм}=100) кПа.

Задача №5.4.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(V_1=1) м³, (V_2=2V_1), (A=110) кДж, (S=0,005) м², (p_{атм}=100) кПа, (m-?)

Решение задачи:

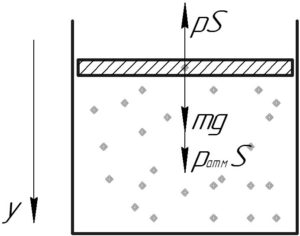На поршень действуют три силы: сила давления газа (pS), сила атмосферного давления (p_{атм}S) и сила тяжести (mg) (смотрите схему). Если газ нагревают медленно, то поршень в каждый момент времени будет находиться в равновесии. Запишем первый закон Ньютона в проекции на ось (y):

[{p_{атм}}S + mg = pS]

Откуда выразим давление газа в цилиндре (p):

[p = {p_{атм}} + frac{{mg}}{S};;;;(1)]

Видно, что давление газа меняться в течение процесса нагревания не будет, значит мы имеем дело с изобарным процессом ((p=const)). Если газ нагревать изобарно, то он будет расширяться. Работу газа при изобарном расширении определяют по известной формуле:

[A = pleft( {{V_2} – {V_1}} right)]

Известно, что объем газа увеличивается в 2 раза, то есть (V_2=2V_1). Учитывая ранее полученную формулу (1), имеем:

[A = left( {{p_{атм}} + frac{{mg}}{S}} right)left( {2{V_1} – {V_1}} right)]

[A = left( {{p_{атм}} + frac{{mg}}{S}} right){V_1}]

В этом равенстве известно всё, кроме искомой массы поршня (m), поэтому осталось только выразить её, чем мы сейчас и займёмся.

[{p_{атм}} + frac{{mg}}{S} = frac{A}{{{V_1}}}]

[frac{{mg}}{S} = frac{A}{{{V_1}}} – {p_{атм}}]

[m = frac{S}{g}left( {frac{A}{{{V_1}}} – {p_{атм}}} right)]

Произведём расчёт численного ответа задачи:

[m = frac{{0,005}}{{10}} cdot left( {frac{{110 cdot {{10}^3}}}{1} – 100 cdot {{10}^3}} right) = 5;кг]

Ответ: 5 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

5.4.31 Газ изобарно увеличился в объеме в три раза при давлении 3000 кПа. Определить
5.4.33 Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают
5.4.34 Определите работу, совершаемую одним молем газа за цикл, если

Как изменится давление газа в цилиндре

Динамика изменения давления газа зависит от причин, вызывающих изменения данной величины, а также от условий, при которых происходит увеличение или уменьшение давления газа. Все эти факторы имеют молекулярную природу.

Физический смысл величины давления газа кроется во внутримолекулярных явлениях, происходящих в веществе. Как известно, частицы газа находятся в постоянном беспорядочном движении, называемом броуновским. Каждая частица на пути своей траектории сталкивается как с другими частицами газа, так и со стенками сосуда, в котором находится газ.

Удар молекул о стенки сосуда порождает изменение импульса частицы. Из второго закона Ньютона известно, что изменение импульса материальной точки за некоторый промежуток времени эквивалентен действию некоторой силы, вызывающей данное изменение или порожденное изменением импульса. Определение же величины давления подразумевает отношение силы, действующей на некоторую поверхность, к величине площади данной поверхности.

Таким образом, именно удары молекул о стенки сосуда приводят к появлению давления как макроскопического явления. Отсюда следует и возможность изменения давления газа.

Нагрев или охлаждение вещества газа, в первую очередь, приводит к увеличению или уменьшению скорости движения его частиц, ибо в этом заключается суть величины температуры тела. Изменение скорости приводит к изменениям в перепадах импульса при ударах молекул о стенки сосуда, что порождает смену давления газа.

Однако стоит заметить, что давление в данном случае изменится лишь в том случае, если стенки, ограничивающие сосуд, неподвижные. Если же объем сосуда может изменяться в зависимости от внешних условий, то колебания температуры не приведут к изменениям в давлении газа.

Так как макроскопическое давление газа вызывается суммарным числом ударов о стенки сосуда, то, изменяя количество ударов, можно изменить и величину давления. Такой эффект обнаруживается при изменении объема сосуда, содержащего в себе газ. Чем меньше размер сосуда, тем меньше длина свободного пробега частиц вещества, что приводит к более частым их столкновениям как друг с другом, так и со стенками сосуда. Собственно говоря, крайним случаем уменьшения давления за счет увеличения объема сосуда является мысленный эксперимент по удалению стенок емкости с газом на бесконечные расстояния. В этом случае давление газа стремится к нулю.

Концентрация частиц вещества определяется по их количеству, которое приходится на единичный объем. То есть увеличить концентрацию можно, увеличив общее число частиц газа при постоянной величине объема сосуда. Увеличение количества атомов газа вновь приводит к более частым столкновениям и, как следствие, к увеличению давления. Поэтому более разреженные газы имеют меньшее давление и вес.

Видео по теме