Как найти кристаллическую массу

2.1 Основные расчетные формулы в гравиметрических методах анализа.

Содержание
определяемого вещества обычно вычисляют
в граммах или процентах. Расчет ведут
с помощью аналитического фактора F
– отношения молекулярной массы
определяемого вещества (М_А)
к молекулярной массе его гравиметрической
(весовой) формы (М_гр.ф.)

(29)

При вычислении
гравиметрического фактора в числителе
указывают формулу определяемого
вещества, в знаменателе- формулу его
весовой(гравиметрической формы),
m,n-стехиометрические
коэффициенты. Например,

Расчет определяемого
вещества в граммах

q_A
= m_гр.ф∙F
(30)

Расчет определяемого
вещества в процентах

(31)

2.1.1 Расчет навески
определяемого вещества

При определении
кристаллических осадков

,
(32)

где М_А
и М_гр.ф.
– молекулярные веса определяемого
вещества и

гравиметрической
формы соответственно;

m,n-
стехиометрические коэффициенты.

При определении
аморфных осадков

(33)

Опытным путем было
найдено, что 0,5 – 0,3 – практически удобная
масса весовой формы вещества для
кристаллических осадков (г); 0,1-0,2-
практически удобная масса весовой формы
вещества для аморфных осадков(г).

Объем осадителя
находим по формуле

,

(34)

где 1,5- const-
коэффициент, найденный практическим
путем

(берется
с учетом того, что осадитель по обыкновению

является
летучим веществом);

М_В–
молекулярный вес осадителя;

М_А–
молекулярный вес определяемого вещества;

а- навеска
определяемого вещества, г;

С- процентная
концентрация;

ρ- плотность
г/см³.

Примеры решения
задач.

Пример 1

Из навески глины
0,5340 г. после соответствующей обработки
получено 0,2345 г CaO.
Рассчитать массовую долю CaCO₃
в глине.

Решение

Найдем аналитический
фактор

Зная аналитический
фактор, можем найти % содержание

Пример 2

При определении
Fe
в препарате сульфата железа (III)
взвешивали BaSO₄
.Написать
выражение для гравиметрического фактора.

Решение

Между Fe
и BaSO₄
существует стехиометрическое соотношение

2M(Fe)
1MFe₂(SO₄)₃
3M(SO₄^2-)3M(BaSO₄)

Пример 3

Навеску алюминиевого
сплава массой 0,14252 г растворили в колбе
вместимостью 200 мл. Из 20,00 мл этого
раствора получили осадок оксихинолината
алюминия Al(C₉H₆ON)₃,массой
0,2012 г. Вычислить массовую долю (%) алюминия
в сплаве.

Решение

Найдем аналитический
фактор

Преобразуя несколько
формул, найдем % содержание алюминия в
сплаве

Тогда

Пример 4

Вычислить число
молекул воды в кристаллогидрате хлорида
магния, если из навески его массой 0,5000
г. получается 0,2738 г Mg₂P₂
O₇.

Решение

Кристаллогидрат
магния:

Определяемое
вещество

Гравиметрическая
форма

Считаем фактор
пересчета

Здесь навеска –
это q.
Значит

2M()
=

M()=

Число молекул в
кристаллогидрате находим

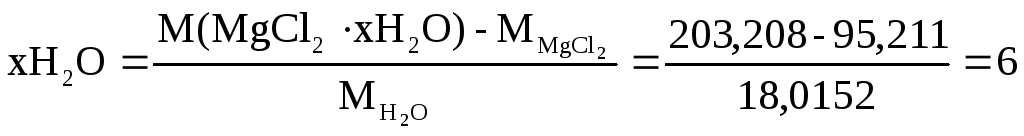
Значит соль

Пример 5

Рассчитать массу
навески апатито- нефелиновой руды,
содержащей 30 % P₂O₅
необходимую для получения 0,9 г осадка.

Решение

Определяемое
вещество

Гравиметрическая
форма

Рассчитаем фактор
пересчета

Пример 6

Из навески каменного
угля массой 2,6248 г. после соответствующей
обработки получили 0,3248 г. BaSO₄
. Вычислить
массовую долю (%) серы в угле. Пересчитать
массовую долю серы на сухое вещество,
если содержание влаги составило 2,58%.

Решение

Считаем

Тогда

Массовая доля (%)
серы в сухом веществе

,

где b
– содержание влаги в %.

Пример 7

Какой объем раствора
карбоната натрия (массовая доля 17,7%
ρ=1,19г/см³)
требуется для осаждения 0,2 г. кальция
при полуторакратном избытке осадителя?

Решение

,

где 105,988 – молекулярный
вес

;

40,08 – молекулярный
вес кальция.

Пример 8

Какой объем 4% (по
массе) раствора оксихинолина C₉H₇NO
, плотностью 1 г/см³.
Необходим для осаждения Al³⁺
из раствора, содержащего 100 мг
(достаточен
избыток осадителя в 10 %)

Решение

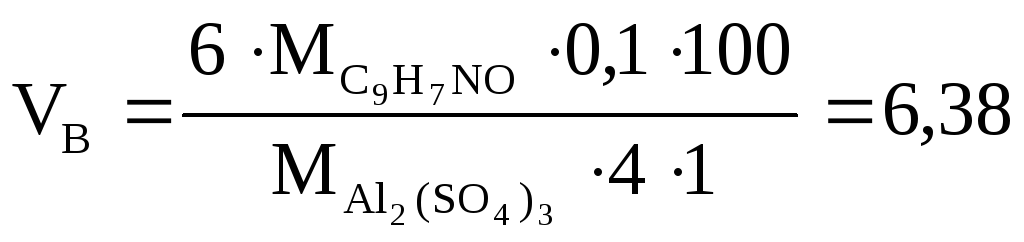мл

X=0,638

мл

Пример 9

При определении
оксидов щелочных металлов из образца
силикатной породы массой 1,2505 г выделили
смесь NaCl
и КCl
массой 0,1500 г. После многократной обработки
этой смеси серной кислотой получили
сульфаты Na₂SO₄
и К₂SO₄
массой
0,1800 г. Вычислить массовые доли (%) Na₂O
и К₂O
в силикатной породе.

Решение

ω_х
– массовая доля Na₂O
в образце

ω_у
– массовая доля К₂O

I
уравнение

II
уравнение

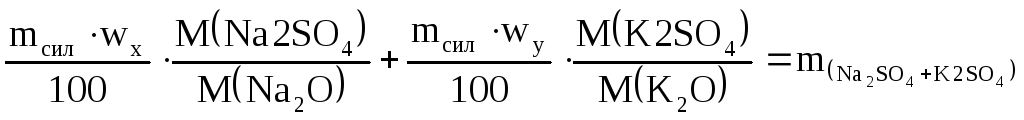
Подставляем
числовые значения

в I
уравнение

во II
уравнение

Решаем систему
уравнений и находим

ω=
ω_х
= 4,28 %

ω=
ω_у
= 2,48 %

Пример 10

Образец содержит
2% К₂SO₄
и 5% КNO₃.
Рассчитать массу навески образца,
необходимую для получения 0,3 г KClO₄.

Решение

Содержание в виде
доли

К₂SO₄
= 0,02 КNO₃
= 0,05

Масса навески
m_обр.

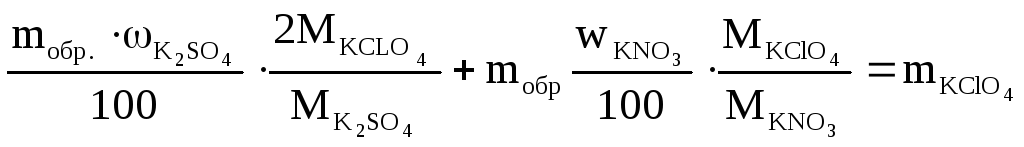
Подставим
числовые значения, получаем

m_обр
=ассчитатРасчитать

Отсюда
m_обр
= 2,992 = 3,0 г

Пример 11

Навеску
инсектицида массой 0,2795 г, содержащую
линдан С₆Н₆Сl₆
(M
= 290,8 г/моль) и ДДТ С₁₄Н₉Сl₅
(М = 354,5 г/моль), сожгли в токе кислорода
до СО₂,
Н₂О
и HCl.

Из поглотительного
раствора получили осадок AgCl
массой 0,7161 г. Вычислить
массовые доли (%) линдана и ДДТ в препарате.

Решение

Обозначим m_x
– масса линдана,

(m_инсект
– m_x)
– масса ДДТ

Составляем расчетное
уравнение

Подставляем
числовые значения

Решая уравнение,
находим

m_x
= 0.1615 г

И далее

ω=

ω=

Пример 12

Вычислить
эмпирическую формулу фосфорита, если
в результате анализа получили содержание:
54,58% СаО; 1,86% F;
3,44% Cl;
41,61% P₂O₅.

Решение

Находим молярное
соотношение (%) компонентов

СаО : F
: Cl
: P₂O₅
=

=

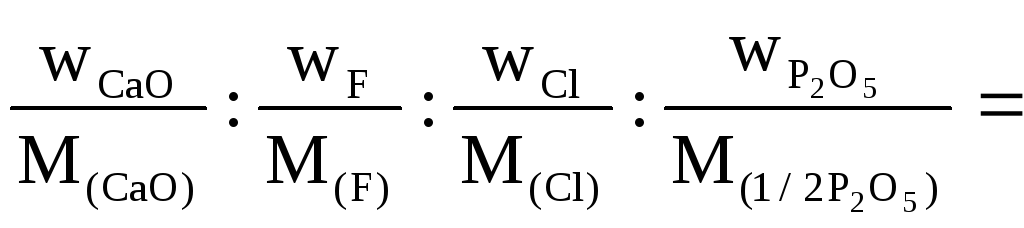
Наименьшее число
0,09703 принимаем за единицу и выражаем
полученное соотношение целыми числами,
учитывая, что n
(Ca)
= n(CaO)

n(PO₄)^3-
= n(1/2 P₂O₅)
:Ca : F : Cl : PO= 10:
1 : 1 : 6

Эмпирическая
формула фосфорита

Са₁₀(РО₄)₆
ClF
или 3Са₃(РО₄)₂
· Са · Cl
· F

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вы уже познакомились с несколькими уроками, основная тема которых — это явление плавления: “Плавление и отвердевание кристаллических тел”, “График плавления и отвердевания кристаллических тел”, “Удельная теплота плавления”.

В данном уроке для решения задач вам пригодятся вышеупомянутые материалы. Также мы будем использовать данные формулы:

• $Q = cm(t_2 — t_1)$
• $Q = qm$
• $eta = frac{A_п}{A_з}$
• $A = Fs$

Табличные значения различных величин вы можете найти в следующих уроках:

• Плотность
• Удельная теплоемкость
• Энергия топлива. Удельная теплота сгорания
• Удельная теплота плавления

Задача №1

Кусок алюминия массой $10 space кг$, взятый при температуре плавления $660 degree C$, полностью расплавился. Какое для этого потребовалось количество теплоты?

Дано:
$m = 10 space кг$
$t = 660 degree C$
$lambda = 8.9 cdot 10^5 frac{Дж}{кг}$

$Q — ?$

Показать решение и ответ

Скрыть

Задача №2

Во сколько раз больше теплоты идет на плавление $2 space кг$ чугуна, чем на нагревание чугуна той же массы на $1 degree C$? Удельная теплота плавления чугуна $96 frac{кДж}{кг}$.

$frac{Q_1}{Q_2} — ?$

Показать решение и ответ

Скрыть

Задача №3

На рисунке 1 дан график изменения температуры твердого тела при нагревании.

Определите по этому графику:

1. При какой температуре плавится это тело?
2. Как долго длилось нагревание от $60 degree C$ до точки плавления?
3. Как долго длилось плавление?
4. До какой температуры было нагрето вещество в жидком состоянии?

Показать решение и ответ

Скрыть

Задача №4

Определите объем глицерина, если при его кристаллизации выделилось $240 space кДж$ энергии. Плотность глицерина $1200 frac{кг}{м^3}$, удельная теплота плавления $1.99 cdot 10^5 frac{Дж}{кг}$.

$V — ?$

Показать решение и ответ

Скрыть

Задача №5

Определите плотность льда при температуре $0 degree C$, если известно, что для плавления льда объемом $1 space дм^3$ требуется количество теплоты, равное $301.5 space кДж$.

$rho — ?$

Показать решение и ответ

Скрыть

Задача №6

На рисунке 2 изображены графики зависимости температуры от времени для слива свинца (I) и плитка олова (II) одинаковой массы. Количество теплоты, получаемой каждым телом в единицу времени, одинаково.

Определите по графику:

1. У какого слитка температура плавления выше?
2. Какой металл обладает большей удельная теплоемкость?
3. У какого металла больше удельная теплота плавления?

Показать решение и ответ

Скрыть

Задача №7

В $5 space кг$ воды при температуре $40 degree C$ опустили $3 space кг$ льда. Сколько льда растает?

Дано:
$m_в = 5 space кг$
$t_1 = 40 degree C$
$m_л = 3 space кг$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$lambda_л = 3.4 cdot 10^5 frac{Дж}{кг}$

$m_{л1} — ?$

Показать решение и ответ

Скрыть

В медный калориметр весом $200 space г$ налито $100 space г$ воды при $16 degree C$ для обоих тел. В воду бросили кусочек льда при $0 degree C$ весом $9.3 space г$, который целиком расплавился. Окончательная температура воды и калориметра после этого установилась $9 degree C$. Определите на основании этих данных удельную теплоту плавления льда.

$lambda_л — ?$

Показать решение и ответ

Скрыть

Задача №9

Сколько требуется сжечь каменного угля в печи, чтобы расплавить $100 space т$ чугуна, взятого при температуре $20 degree C$, если КПД печи составляет $40 %$? Удельная теплота плавления чугуна $0.96 cdot 10^5 frac{Дж}{кг}$

Показать решение и ответ

Скрыть

Задача №10

В водопаде высотой $32 space м$ ежесекундно падает $3.5 space м^3$ воды. Какое количество энергии можно получить в час от этого водопада? Какое количество каменного угля нужно сжигать каждый час, чтобы получить то же самое количество энергии?

$Q — ?$
$m — ?$

Показать решение и ответ

Скрыть

Кристаллическая масса

Cтраница 1

Кристаллическая масса и находящаяся над ней бурая жидкость при соприкосновении с ледяной водой быстро вспыхивают. Кристаллы плавятся при О С, причем получается красно-бурый раствор, теряющий двуокись хлора. Темно-бурый раствор образуется также при добавлении хлората калия к безводной кислоте, а перхлорат калия может быть перекристаллизован без изменений как из безводной, так и из 70 % – нон кислоты.
 [1]

Кристаллическая масса, растворимая в четыреххлористом углероде и петролеином эфире.
 [2]

Кристаллическая масса лактата передается плунжерным насосом 12 на чугунный фильтрпресс, где лактат отжимается от-маточника, промывается холодной водой и подсушивается сжатым воздухом, нагнетаемым под давлением 2 ати.
 [3]

Сырая кристаллическая масса выгружается из кристаллизаторов на транспортер вручную лопатами, через борт кристаллизатора.
 [4]

Коричнево-желтая кристаллическая масса, хорошо растворимая в воде, этиловом спирте и диэтиловом эфире. Растворы реактива окрашены в желтый цвет, кислые на лакмус.
 [5]

Кристаллическая масса лактата передается плунжерным насосом 12 на чугунный фильтрпресс, где лактат отжимается от маточника, промывается холодной водой и подсушивается сжатым воздухом, нагнетаемым под давлением 2 ати.
 [6]

Снежно-белая искристая кристаллическая масса; чрезвычайн гигроскопичная.
 [7]

Кристаллическая масса глауберовой соли, выгружаемая из центрифуг, все еще содержит жидкую фазу со значительным содержанием сульфата цинка, который можв. Промывные воды, содержащие цинковые соединения, отводятся в канализацию.
 [8]

Белая, слоистая кристаллическая масса, по эластичности напоминающая изделия из рога, лишь с трудом поддается растиранию в порошок.
 [9]

Кристаллическую массу отделяют и промывают небольшим количеством метилового спирта. Выход продукта 1 8 г; при разбавлении маточного раствора водой получают еще 0 2 г продукта. После перекристаллизации из 4 – 5 частей метилового спирта получают соединение, плавящееся при 90; при дальнейшем нагревании происходит слабый взрыв.
 [10]

Кристаллическую массу разбивают стеклянной палочкой и фильтруют через фильтр из стеклянной ткани ( примечание 4) на воронке Бюхнера диаметром 18 см. Твердую массу отжимают почти досуха большой плоской стеклянной пробкой или дном конической колбы емкостью 125 мл. Когда большая часть маточного раствора будет отделена ( примечание 5), твердый осадок переносят по частям в 4-литровый стакан, на три четверти заполненный мелко наколотым льдом. После прибавления каждой порции лед перемешивают, чтобы облегчить растворение вещества. Перемешивание рекомендуется производить деревянной палочкой с плоским концом. Вся операция должна занимать не более 10 мин.
 [11]

Кристаллическую массу высушивают на глиняной тарелке, растворяют в теплом эфире и, добавляя лигроин, дают медленно охлаждаться. Так, получают бензоилпроизводное хлоргептиламина. Для отщеплении бензоила продукт нагревают в течение 5 час.
 [12]

Кристаллическую массу размешивают с водой и подщелачивают 10 % – ным-раствором едкого натра до совсем слабой реакции на фенолфталеин. Нужно перемешивать продолжительное время и внимательно следить, чтобы не оставалось комочков. Бели раствор после длительного размешивания все еще остается щелочным, то его отфильтровывают от нерастворимого в щелочи остатка.
 [13]

Кристаллическую массу отфильтровывают и перекрнсталлизовывают.
 [14]

Кристаллическую массу отделяют на воронке Бюхнера, промывают охлажденным изопропиловым спиртом и сушат в вакуум-шкафу при 20 С до постоянной массы.
 [15]

Страницы:  

   1

   2

   3

   4

Выделить растворённое вещество из раствора можно путём выпаривания воды. В некоторых случаях образуются гидраты в кристаллическом виде или кристаллогидраты. Они содержат молекулы воды, которые называются кристаллизационной водой.

Общее описание

Кристаллогидраты образуются благодаря взаимодействию катионов кристаллической решётки вещества с молекулами воды. Это возможно, если связь между катионами и анионами кристалла более слабая.

К кристаллогидратам в первую очередь относятся соли. Типичными кристаллогидратами являются природные минералы – гипс, карналлит, алебастр, бура. Также кристаллогидраты образуют кислоты и основания.

Рис. 1. Кристаллогидраты.

Название вещества зависит от количества молекул воды. Для этого используют приставки, обозначающие число:

• 1 – моно;
• 2 – ди;
• 3 – три;
• 4 – тетра;
• 5 – пента;
• 6 – гекса;
• 7 – гепта;
• 8 – окта;
• 9 – нона;
• 10 – дека.

Рис. 2. Строение молекулы кристаллогидрата.

Например, кристаллогидрат FeSO4, содержащий одну молекулу воды, называется моногидрат сульфата железа (II). Если в кристаллогидрате семь молекул воды, он называется гептагидрат сульфата железа (II).

Вода из кристаллогидрата в большинстве случаев удаляется ступенчато. Например, при нагревании медного купороса, он переходит в тригидрат, затем в моногидрат. При нагревании до 250°С медный купорос полностью обезвоживается до сульфата меди (II).

Формула кристаллогидрата состоит из двух частей. Сначала записывается формула вещества. Через точку (знак умножения) указывается количество молекул воды. Например, ZnSO4 ∙ 7H2O, CuSO4 ∙ H2O, Na2CO3·10H2O, H2SO4 · H2O.

Рис. 3. Пентагидрат сульфата меди (II) и сульфат меди (II).

Расчёт массы вещества

При прокаливании кристаллогидраты разлагаются на сухое вещество и воду. Чтобы вычислить массовую долю вещества используется следующая формула:

ω(сух. в-ва) = m(сух. в-ва) / m(кр-та).

Для расчёта массовой доли воды применяется схожая формула:

ω(H2O) = m(H2O) / m(кр-та).

Рассмотрим решение задачи с применением формулы.

Необходимо вычислить массовую долю кристаллизационной воды в тригидрате нитрата меди (II) (Cu(NO3)2 ∙ 3H2O).

Решение:

Сначала запишем молярные массы воды и нитрата меди (II):

• M (Cu(NO3)2) = 187,5 г/моль;
• M (H2O) = 18 г/моль.

В 1 моле кристаллогидрата содержится 1 моль нитрата меди (II) и 3 моль воды, поэтому получаем по формуле m = n ∙ M массу воды и массу соли в кристаллогидрате:

• m (H2O) = 3 ∙ 18 = 54 г;
• m (Cu(NO3)2) = 1 ∙ 187,5 = 187,5 г.

Высчитаем общую массу вещества:

m (Cu(NO3)2 ∙ 3H2O) = 187,5 + 54 = 241,5 г.

Остаётся вычислить массовую долю воды:

ω(H2O) = m(H2O) / m(кр-та) = 54 / 241,5 = 0,22 или 22 %.

Ответ: массовая доля воды в тригидрате нитрата меди (II) 22 %.

Некоторые вещества невозможно обезводить без разложения. Например, соединение BeC2O4·H2O устойчиво только в форме кристаллогидрата.

Что мы узнали?

Кристаллогидратами называются вещества, содержащие молекулы воды за счёт их притяжения катионами кристаллической решётки. В формуле кристаллогидратов, а также в названии вещества указывается количество воды. Например, CuSO4 ∙ H2O – моногидрат сульфата меди (II). Если известны массы воды и сухого вещества, можно вычислить их массовую долю.