Как найти соотношение сторон квадрата

Как найти соотношение сторон квадрата

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

  1. Все углы квадрата — прямые, все стороны квадрата — равны.
    AB=BC=CD=AD;
    angle A= angle B=angle C=angle D=90^{circ }.
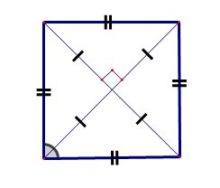
  2. Диагонали квадрата равны и пересекаются под прямым углом.
    AC=BD, AC perp BD.
  3. Диагонали квадрата делятся точкой пересечения пополам.
    AO=OC, BO=OD.
  4. Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
    angle BAC=angle DAC, angle ABD=angle CBD, angle BCA=angle DCA,
    angle CDB=angle ADB.
  5. Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:
    triangle AOB=triangle BOC=triangle COD=DOA.

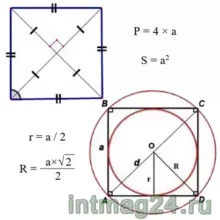
Периметр квадрата P в 4 раза больше его стороны и равен: P=4a.

Площадь квадрата равна квадрату его стороны: S=a^2.

Теорема 1. Диагональ квадрата равна произведению его стороны на sqrt{2}, то есть
d=sqrt{2} cdot a.

Доказательство:

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

AC^{2}=AB^{2}+BC^{2};

AC^{2}=a^{2}+a^{2}=2a^{2}, AC=asqrt{2}, что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

displaystyle r=frac{1}{2}cdot a

Доказательство:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.

Тогда OP perp AB, ON perp CD, поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

2r=a, r=a/2, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

R=frac{sqrt{2}}{2}cdot a.

Доказательство:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

По теореме 1:d=asqrt{2}.

Тогда R=afrac{sqrt{2}}{2}, что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

P=4a=4sqrt{2}R=8r.

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

  1. Все стороны равны и среди внутренних углов есть прямой угол.
  2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна sqrt{8}.

Решение:

Мы знаем, что d=sqrt{2} cdot a. Тогда a=genfrac{}{}{}{0}{displaystyle d}{displaystyle sqrt{2}}= 2.

Ответ: 2.

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

displaystyle d=sqrt{2}cdot a Rightarrow a=frac{d}{sqrt{2}}Rightarrow a=frac{1}{sqrt{2}}.

Тогда по формуле площади квадрата:

displaystyle S=a^{2}=left (frac{1}{sqrt{2}} right )^{2}=frac{1}{2}=0,5.

Второй способ решения:

Воспользуемся формулой для площади ромба:

displaystyle S=frac{1}{2}d_{1}d_{2}=frac{1}{2}d^{2}=0,5.

Ответ: 0,5

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной sqrt{8}.

Решение:

Рисунок к задаче 2

Радиус описанной окружности равен половине диагонали квадрата, поэтому

displaystyle R=frac{d}{2}=afrac{sqrt{2}}{2}=sqrt{8}cdot frac{sqrt{2}}{2}=2.

Ответ: 2.

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса 4.

Решение:

Рисунок к задаче 3

Диаметр окружности равен стороне квадрата: a=2r=8.

Ответ: 8.

Задача 5. Радиус вписанной в квадрат окружности равен 14sqrt{2}. Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

a=2r=28sqrt{2}.

Диагональ найдем, зная сторону квадрата:

d=asqrt{2}=28sqrt{2}cdot sqrt{2}=56.

Ответ: 56.

Задача 6. Радиус вписанной в квадрат окружности равен 11sqrt{2}. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

displaystyle r=frac{a}{2}; R=frac{d}{2}; d=asqrt{2}.

Поэтому R=rsqrt{2}=11sqrt{2}cdot sqrt{2}=22.

Ответ: 22.

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата: a=sqrt{S}=sqrt{9}=3.

Периметр квадрата со стороной 3 равен: P=4a=12.

Ответ: 12.

Задача 8. Найдите площадь квадрата, в который вписан круг площадью 4pi .

Решение:

Площадь круга S_{kp}=pi r^{2}=4pi , откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными sqrt{2}.

 

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна sqrt{2}., то сторона малого квадрата равна 2sqrt{2}. А сторона квадрата ABCD равна 2sqrt{2}cdot sqrt{2}=4.

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите r sqrt{10}.

Решение:

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна sqrt{10}. Тогда радиус вписанной окружности равен genfrac{}{}{}{0}{displaystyle sqrt{10}}{displaystyle 2}. В ответ запишем r sqrt{10}.

Ответ: 5.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник
Квадрат
Квадрат со стороной '"`UNIQ--postMath-00000001-QINU`"' и диагональю '"`UNIQ--postMath-00000002-QINU`"'
Квадрат со стороной a и диагональю d
Рёбра 4
Символ Шлефли {4}
Вид симметрии Диэдрическая группа (D4)
Площадь a2
Внутренний угол 90°
Свойства
Выпуклый многоугольник, Изогональная фигура, изотоксальная фигура
Логотип Викисклада Медиафайлы на Викискладе

Квадра́т (от лат. quadratus, четырёхугольный[1]) — правильный четырёхугольник, то есть плоский четырёхугольник, у которого все углы и все стороны равны. Каждый угол квадрата — прямой {displaystyle (90^{circ })}[2].

Варианты определения[править | править код]

Квадрат может быть однозначно охарактеризован разными способами[3][4].

  • Четырёхугольник, диагонали которого равны и взаимно перпендикулярны, причём точка пересечения делит их пополам.
  • Четырёхугольник, являющийся одновременно прямоугольником и ромбом.
  • Прямоугольник, у которого длины двух смежных сторон равны.
  • Прямоугольник, у которого диагонали пересекаются под прямым углом.
  • Ромб, у которого диагонали равны.
  • Ромб, у которого два соседних угла равны.
  • Ромб, один из углов которого — прямой (прочие углы, как легко доказать, тогда также прямые).
  • Параллелограмм, у которого длины двух смежных сторон равны, а угол между ними — прямой.
  • Параллелограмм, у которого диагонали равны, а угол между ними — прямой.
  • Дельтоид, все углы которого прямые.

Свойства[править | править код]

Основной источник: [4]

Далее в этом разделе a обозначает длину стороны квадрата, d — длину диагонали, R — радиус описанной окружности, r — радиус вписанной окружности.

Стороны и диагонали[править | править код]

Диагонали квадрата равны, взаимно перпендикулярны, делятся точкой пересечения пополам и сами делят углы квадрата пополам (другими словами, являются биссектрисами внутренних углов квадрата). Длина каждой диагонали {displaystyle d=a{sqrt {2}}.}

Периметр квадрата P равен:

{displaystyle P=4a=4{sqrt {2}}R=8r}.

Вписанная и описанная окружности[править | править код]

Вписанная и описанная окружности для квадрата

Центр описанной и вписанной окружностей квадрата совпадает с точкой пересечения его диагоналей.

Радиус вписанной окружности квадрата равен половине стороны квадрата:

{displaystyle r={frac {a}{2}}.}

Радиус описанной окружности квадрата равен половине диагонали квадрата:

{displaystyle R={frac {sqrt {2}}{2}}a.}

Из этих формул следует, что площадь описанной окружности вдвое больше площади вписанной.

Площадь[править | править код]

  • Площадь квадрата

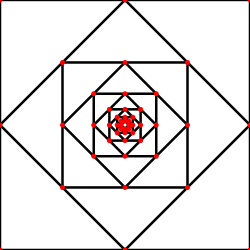
  • Соединив середины сторон квадрата, получаем квадрат вдвое меньшей площади

    Соединив середины сторон квадрата, получаем квадрат вдвое меньшей площади

Площадь S квадрата равна

{displaystyle S=a^{2}=2R^{2}=4r^{2}={1 over 2}d^{2}}.

Из формулы {displaystyle S=a^{2},} связывающей сторону квадрата с его площадью, видно, почему возведение числа во вторую степень традиционно называется «возведением в квадрат», а результаты такого возведения называются «квадратными числами» или просто квадратами. Аналогично корень 2-й степени называется квадратным корнем.

Квадрат имеет два замечательных свойства[5].

  1. Из всех четырёхугольников с заданным периметром квадрат имеет наибольшую площадь.
  2. Из всех четырёхугольников с заданной площадью квадрат имеет наименьший периметр.

К уравнению квадрата; здесь {displaystyle R=2,x_{0}=y_{0}=0}

Уравнение квадрата[править | править код]

В прямоугольной системе координат уравнение квадрата с центром в точке {displaystyle {x_{0},y_{0}}} и диагоналями, параллельными осям координат (см. рисунок), может быть записано в виде[6]:

{displaystyle |x-x_{0}|+|y-y_{0}|=R,}

где R — радиус описанной окружности, равный половине длины диагонали квадрата. Сторона квадрата тогда равна {displaystyle R{sqrt {2}},} его диагональ равна {displaystyle 2R,} а площадь квадрата равна {displaystyle 2R^{2}.}

Уравнение квадрата с центром в начале координат и сторонами, параллельными осям координат (см. рисунок), может быть представлено в одной из следующих форм:

  1. {displaystyle |x-y|+|x+y|=a} (легко получается применением поворота на 45° к предыдущему уравнению)
  2. {displaystyle max(x^{2},y^{2})=r^{2}}
  3. (в полярных координатах[7]) {displaystyle quad r(varphi )=min left({frac {r}{|cos varphi |}},{frac {r}{|sin varphi |}}right)}

Математические проблемы[править | править код]

С квадратами связаны ряд проблем, часть из которых до сих пор не имеет решения.

  • Квадратура круга — древняя проблема построения циркулем и линейкой квадрата, равновеликого по площади заданному кругу. В 1882 году Фердинанд Линдеман доказал, что это невозможно.

Пример квадрирования квадрата {displaystyle 112times 112}

  • Квадрирование квадрата — задача о разбиении квадрата на конечное число меньших квадратов, без «дырок», причём длины сторон квадратов должны отличаться друг от друга (в идеале должны быть все различны). Найден ряд решений этой задачи.
  • Долгое время математики пытались доказать, что непрерывное отображение отрезка прямой в квадрат невозможно, пока Джузеппе Пеано не построил свой контрпример.
  • Гипотеза Тёплица: на всякой замкнутой плоской жордановой кривой можно отыскать четыре точки, образующие вершины квадрата. Не доказана и не опровергнута.
  • Разбиение квадрата сеткой одинаковых более мелких квадратов также приводит к множеству проблем, используемых, в частности, в теории латинских и греко-латинских квадратов, магических квадратов, в игре судоку.

Симметрия[править | править код]

Квадрат обладает наибольшей осевой симметрией среди всех четырёхугольников. Он имеет:

  • одну ось симметрии четвёртого порядка — ось, перпендикулярную плоскости квадрата и проходящую через его центр;
  • четыре оси симметрии второго порядка (то есть относительно них квадрат отражается сам в себя), из которых две проходят вдоль диагоналей квадрата, а другие две — параллельно сторонам.

Применение[править | править код]

В математике[править | править код]

Единичный квадрат используется как эталон единицы измерения площади, а также в определении площади произвольных плоских фигур. Фигуры, у которых можно определить площадь, называются квадрируемыми.

Теорема Пифагора первоначально формулировалась геометрически: площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Квадратами являются грани куба — одного из пяти правильных многогранников.

В математической физике символ квадрата может означать «оператор Д’Аламбера» (даламбериан) — дифференциальный оператор второго порядка:

{displaystyle square u:={frac {partial ^{2}u}{partial x^{2}}}+{frac {partial ^{2}u}{partial y^{2}}}+{frac {partial ^{2}u}{partial z^{2}}}-{frac {1}{c^{2}}}{frac {partial ^{2}u}{partial t^{2}}}}

Из теоремы Бойяи — Гервина следует, что любой многоугольник равносоставлен квадрату, то есть его можно разрезать на конечное число частей, из которых составляется квадрат (и обратно)[8].

Графы:
K4 полный граф часто изображается как квадрат с шестью рёбрами.

Орнаменты и паркеты[править | править код]

  • Мозаики, включающие квадраты

  • «Пифагорова мозаика»

  • Bond brick hexagonal tiling.png

  • Square rhombic tiling.png

Мозаики, орнаменты и паркеты, содержащие квадраты, широко распространены.

Другие применения[править | править код]

Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратная доска для международных шашек поделена на 100 квадратов двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат.

Квадратный флаг Лима поделён на два чёрных и два жёлтых квадрата, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине.

Графика[править | править код]

Символы со сходным начертанием: ロ · ⼝ · ⼞

Ряд символов имеют форму квадрата.

  • Символы Юникода U+25A0 — U+25CF
  • U+20DE ◌⃞ COMBINING ENCLOSING SQUARE
  • ロ (Японский иероглиф «Ро» (катакана))
  • 口 (Китайский иероглиф «рот»)
  • 囗 (Китайский иероглиф «ограда»)

В Latex для вставки символа квадрата служат конструкции Box или square.

В HTML, чтобы заключить произвольный текст в квадрат или прямоугольник, можно использовать конструкцию:

  • <span style=”border-style: solid; border-width: 1.5px 1.5px 1.5px 1.5px; padding-left: 4px; padding-right: 4px;”>text</span>; результат: text.

Вариации и обобщения[править | править код]

Многомерное пространство[править | править код]

Квадрат можно рассматривать как двумерный гиперкуб.

Неевклидова геометрия[править | править код]

В неевклидовой геометрии квадрат (в более широком смысле) — многоугольник с четырьмя равными сторонами и равными углами. По величине этих углов можно судить о кривизне плоскости — в евклидовой геометрии и только в ней углы прямые, в сферической геометрии углы сферического квадрата больше прямого, в геометрии Лобачевского — меньше.

Построение квадрата с использованием циркуля и линейки

Складывание квадрата из произвольного куска бумаги

См. также[править | править код]

  • Алгоритм «движущиеся квадраты»
  • Квадрат Полибия
  • Квадратная матрица
  • Квадратриса
  • Первая теорема Тебо
  • Площадь произвольного четырёхугольника

Примечания[править | править код]

  1. ↑ Квадрат // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — С. 561. — 1600 с.
  2. ↑ Квадрат // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 776. — 1184 с.
  3. ↑ Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
  4. ↑ 1 2 Каплун, 2014, с. 171—173.
  5. ↑ Понарин Я. П. Элементарная геометрия: В 2 т. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — С. 117, 119. — 312 с. — ISBN 5-94057-171-9.
  6. ↑ Уравнение квадрата в декартовой системе координат. Дата обращения: 9 ноября 2021. Архивировано 9 ноября 2021 года.
  7. ↑ What is the polar equation for a square, if any?
  8. ↑ Болтянский В. Г. Третья проблема Гильберта. — М.: Наука, 1977. — 208 с. Архивировано 28 июня 2021 года.

Литература[править | править код]

  • Каплун А. И. Математика, Учебно-практический справочник. — Ростов н/Д.: ООО “Феникс”, 2014. — 240 с. — ISBN 978-5-222-20926-3.

Ссылки[править | править код]

  • Квадрат, геометрическая фигура // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Источник

Квадрат– прямоугольник, у которого все стороны равны. Квадрат  является  правильным четырёхугольником, у которого все углы равны и все стороны равны.
Квадрат — это частный случай четырехугольника, параллелограмма, прямоугольника и ромба, поэтому квадрат также обладает всеми их свойствами.

Свойства квадрата

  • Все стороны квадрата равны;
  • Все углы равны и составляют 90°;
  • Диагонали квадрата равны и перпендикулярны;
  • Диагонали  квадрата являются биссектрисами углов.

Признаки квадрата

  1. Если четырёхугольник является прямоугольником и ромбом, то он – квадрат.
  2. Если у прямоугольника две смежные стороны равны, то он – квадрат.
  3. Если диагональ прямоугольника является биссектрисой его углов, то он – квадрат.
  4. Если у ромба есть прямой угол, то он – квадрат.
  5. Если диагонали ромба равны, то он – квадрат.

Основные формулы

Периметр: 

Площадь по стороне квадрата. Площадь квадрата равна квадрату его стороны:

Площадь по диагоналям квадрата. Площадь квадрата равна половине произведения диагоналей:Сторона и диагональ связаны соотношениями: 

где: P-периметр,  S-площадь квадрата, a-сторона, d-диагональ.

Квадрат и окружность

  • Вокруг квадрата можно описать окружность.
  • В квадрат можно вписать окружность.

У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.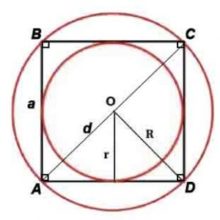

Радиус описанной окружности:

Радиус вписанной окружности:

Калькулятор для квадрата поможет вычислить все характеристики квадрата (сторона, диагональ, периметр, площадь, радиус вписанной и описанной окружности) по одной из известных величин. 

Источник

A square is a quadrilateral with four equal sides. There are numerous items around us that are square in shape. Each square shape is distinguished by its equal sides and inner angles that are equal to 90°. A square is a closed two-dimensional (2D) form having four sides. It has four equal and parallel sides. A square is a rectangle with equal-length adjacent sides. This indicates that it is a quadrilateral with equal-length sides. Every angle in a square is a right angle. Rhombus also has all four side equal but unlike all its angle are not equal

What is a Square?

A square is a closed two-dimensional quadrilateral that is made up of two pairs of parallel lines. All four sides of a square are equal and opposite sides of a square are parallel to each other and the interior angles of a square are equal to 90°. The basic figure of a square is shown below.

Square

Definition of Square

A square is defined as a quadrilateral that has:

  • All four sides are equal.
  • All four angles are equal and the measure of each angle is 90°.
  • Opposite pairs of lines are parallel to each other.

How is a Square Different from a Rhombus?

Square and Rhombus both are Equilateral Quadrilaterals, i.e. both have equal all four sides. The difference between them is that all angles in a square are equal and right angles, but on the other hand all the angles of a rhombus need not be equal.

Hence, Rhombus with right angles is called a Square.

Thus, “Every Square is a Rhombus but all Rhombus are not Squares.”

Real-Life Examples of Square

A square is a very common shape and can be seen in a variety of objects which we use in our daily lives. Various Square-shaped objects are chess boards, carrom boards, Ludo, etc.

Real-Life Examples of Square

Properties of Square

A square is a closed regular quadrilateral. There are various properties of the square some general properties of the square are given below:

  • Square is a quadrilateral with 4 sides and 4 vertices.
  • All four sides of the square are equal.
  • Opposite pairs of sides of a square are parallel to each other.
  • Each interior angle of a square is 90°.
  • Diagonals of a square are perpendicular bisectors of each other.
  • Diagonals of a square are of equal length.
  • Sum of all interior angles of a square is 360°.
  • Diagonals of a square divide it into two congruent triangles.

Formulas of a Square

We know that a square is a four-sided figure with equal sides. There are three basic square formulas that are commonly used in geometry. The first one is to calculate its area, the second is to calculate its perimeter and the third is the diagonal of a square formula. Let us learn these square formulas in detail.

Area of Square

Area of a square is defined as the total space occupied inside its boundaries. The formula for calculating the area of a square is given as

Area of square = a2 

where a is the side of the square

Perimeter of Square

Perimeter of a square is defined as the length of all its boundaries. Suppose the length of the sides of a square is ‘a’ then its perimeter is given by

Perimeter of Square = Sum of all sides of the square 

                                 = a + a + a + a 

Perimeter of square = 4a units

As a result, 4a is the perimeter of a square with each side’s length equal to ‘a’ units.

Diagonal of Square

The diagonals of the square are equal to a√2, where a is the side of the square. The length of both diagonals of a square is equal to each other. The relation between diagonals and sides of a square is given by Pythagoras Theorem.

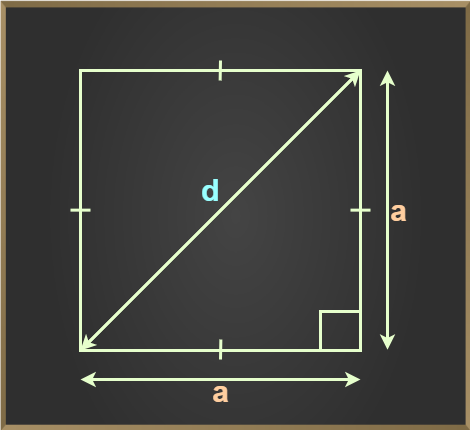
Diagonal of square

By Pythagoras Theorem, Hypotenuse2 = Base2 + Perpendicular2

Hence, 

Diagonal2 = Side2 + Side2

d2 = s2 + s2

d2 = 2s2

d = s√2

where,
d is the length of the diagonal of a square
s is the side of the square.

Area of Square (when diagonal is given)

If the diagonal of a square is given then the area of the square is given by 

Area = d2/2.

where d is the diagonal of the square.

Solved Examples on Square

Example 1: A square has one of its sides measuring 24 cm. Calculate its area and perimeter.

Solution: 

Given, Side of the square = 24 cm

Area of the square: = a2 where, a is the side of the square.

Therefore , Area of the square = a × a 

= 24 × 24 

= 576 sq cm 

Perimeter of the square =  Sum of all sides of square

= a + a + a + a

= 4a 

= 4 × 24 

= 96 cm

 Hence the area of square is 576 sq. cm and the perimeter of square is 96 cm.

Example 2: Find the length of the sides of a square with a perimeter of 56 cm.

Solution:

Given perimeter of the square = 56 cm

Lets suppose length of each side of the square = ‘a’ cm

Therefore, perimeter = 4a cm

56 = 4a 

Or a = 56/4

a = 14 cm

Thus, length of each side of square is 14 cm.

Example 3: Find the area of a square whose side is 5m.

Solution: 

Given, side (a) = 5 m

Area of the square = a × a

= 5 × 5

= 25 sq m 

Example 4: Find the sum of adjacent sides of a square given the perimeter of the square is 16 cm.

Solution:

Given the perimeter of the square = 16 cm

Considering length of each side = ‘a’ cm, the perimeter = 4a cm

Perimeter of Square = Sum of all sides of square

= a + a + a + a

= 4a units

So, 16 = 4a

Or a = 16/4

= 4 cm

Since all sides of a square are of same length, then for the sum of adjacent sides, we can write the sum,

= a + a 

= 2a

Therefore, the sum of adjacent sides of the square = 2 × 4 = 8 cm.

Example 5: Find the area of a square park whose perimeter is 420 ft.

Solution:   

Given: Perimeter of the square park = 420 ft

As we know that, Perimeter of a square = 4 × side

4 × side = 420

Side = 420/4

Side = 105 ft

Formulae for the Area of a square = side2

Hence, Area of the square park = 1052 

= 105 × 105

= 11025 ft2

Thus, the area of a square park whose perimeter is 420 ft is 11025 ft2.

Example 6: A rectangular floor is 40 m long and 30 m wide. Square tiles, each of 4 m side lengths, are to be used to cover the floor. What will be the total number of tiles which will be required to cover the floor?

Solution: 

Given, Length of the floor = 40 m, Breadth = 30 m

Area of the rectangular floor = length × breadth = 40 m × 30 m = 1200 sq. m

Side length of one tile = 4 m

Area of one tile = side × side

= 4 m × 4 m

= 16 sq. m

Now number of tiles needed = Total area of floor / area of one tile 

= 1200 /16

= 75 tiles 

Total 75 tiles are needed to cover the area of rectangular floor of 1200 sq m.

Example 7:  Find the area of a square park whose diagonal is 15 m.

Solution: 

Given: Diagonal of the square park = 15 m

Area of a square formula when diagonal is given = d2 / 2 

Hence, Area of the square park = 152/ 2

= (15 × 15) / 2

= 225 / 2

= 112.5 sq. m

Thus, the area of a square park whose diagonal is 15 m is 112.5 sq. m.

FAQs on Square

Question 1: What is a square?

Answer:

A square is a polygon, with all sides equal and opposite sides parallel to each other. Angles in a square are equal and the measure of each angle is 90 degrees.

Question 2: What is the formula for the area and perimeter of a square?

Answer:

Area of a square is the region occupied by it. It is equal to the square of its sides.

Area = (side)2

Perimeter of a square is given by adding all its sides.

Perimeter = 4 x side.

Question 3: Can a Rhombus be considered a Square?

Answer:

No, a rhombus is not a square, but every square can be considered a rhombus.

Question 4: Is a square a polygon?

Answer:

Square is a closed figure formed by four straight lines So it is considered a quadrilateral. Every quadrilateral is a polygon. So a square is a polygon.

Question 5: Is a square different from a rectangle?

Answer:

Yes, a square is different from Rectangle. In a square, all its sides are equal whereas in a rectangle only its opposite sides are equal.

Related Resources

  • Rhombus
  • Area of Rhombus
  • Area of Triangle

Источник

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

  • Длины всех сторон квадрата равны.
  • Все углы квадрата прямые.
  • Диагонали квадрата равны.
  • Диагонали пересекаются под прямым углом.
  • Диагонали квадрата являются биссектрисами углов.
  • Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

или

Из равенства (1) найдем d:

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

или

Из формулы (5) найдем R:

или, умножая числитель и знаменатель на , получим:

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.Конец доказательства

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).Конец доказательства

Смотрите также:

  • Площадь квадрата онлайн

Источник

Добавить комментарий