Содержание
- Как найти напряжение резистора через общий ток
- Как найти напряжение на резисторе: пример нескольких подходов и проблем
- Как найти напряжение на последовательном резисторе ?
- Как найти напряжение на резисторе параллельно ?
- Как найти напряжение на резисторе в цепи RL?
- Как найти максимальное напряжение на резисторе?
- Как найти напряжение на резисторе в комбинированной цепи?
- Как найти среднеквадратичное напряжение на резисторе?
- Как найти напряжение на нагрузочном резисторе?
- Последние посты
- О НАС
Как найти напряжение резистора через общий ток
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:


Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.
Источник
Как найти напряжение на резисторе: пример нескольких подходов и проблем
В этой статье обсуждалось, как легко найти напряжение на резисторе, например, в последовательной комбинации, параллельной комбинации и других комбинациях цепей.
Напряжение на любом резисторе можно определить:
- Различные законы или правила цепи, такие как закон Кирхгофа, правило деления тока или деления напряжения.
- Эквивалентное сопротивление требуемой части схемы.
- Путем определения характеристик или функций всей цепи или ее части.
Как найти напряжение на последовательном резисторе ?
Цепь последовательного резистора имеет только один путь или ветвь для протекания токов цепи. Все резисторы подключены к одному пути или ветви схемы в этом типе соединения схемы.
Падение напряжения на любом последовательное сочетание сопротивлений может варьироваться в зависимости от общего или отдельного номинала резистора.
Предполагая, что к последовательной комбинации подключено более одного резистора, вся комбинация сопротивлений может быть заменена одним резистором эквивалентного сопротивления. Предположим, резистор в последовательная схема имеет одинаковые значения. В этом случае падение напряжения (или падение электрического потенциала) на каждом резисторе можно определить, поскольку ток, протекающий через каждый резистор в цепи, одинаков.
Общее падение напряжения в любой цепи последовательного резистора равно сумме падений напряжения или потенциала на каждом отдельном резисторе в комбинации последовательных цепей.
В каком типе комбинации резисторов общее напряжение цепи делится между различными резисторами последовательная схема комбинация. Величина напряжения на каждом резисторе зависит от значения сопротивления соответствующего резистора, чтобы найти величину тока, протекающего через резистор.
Предположим, что есть несколько резисторов, соединенных в последовательную цепь, и [латекс] V_1, V_2, V_3 … V_n [/латекс] является отдельным резистором. падение напряжения на каждом резисторе в последовательной цепи комбинации, то общее падение напряжения в последовательной цепи можно обозначить как
[латекс] V =V_1 +V_2 +V_3 . . . +В_н[/латекс]
Чтобы определить общее или общее эквивалентное сопротивление последовательной комбинации n резисторов, используйте формулу:
[латекс] R_e = R_1+ R_2 + R_3……+R_n [/латекс]
Где [латекс] R_e [/латекс] — эквивалентное или общее сопротивление комбинации последовательных сопротивлений.
[латекс] R_1, R_2, R_3. . . . .R_n [/latex] сопротивление отдельных резисторов, соединенных в последовательную цепь из n резисторов.
Как найти напряжение на резисторе параллельно ?
Любая цепь может быть образована последовательно или параллельно комбинацией последовательного и параллельная цепь дизайн.
Игровой автомат падение напряжения (или электрического потенциала падение) на параллельном резисторе можно легко определить или рассчитать по формуле учитывая характеристики параллельной цепи сопротивления, поскольку падение напряжения или падение электрического потенциала на каждом пути или ветви в параллельной комбинации одинаково.
Ток, протекающий через каждую ветвь в комбинации параллельных цепей, можно определить по общему сопротивлению на пути или ветви цепи. Общий ток в цепи равен сумме мгновенных токов, протекающих через отдельные ветви в комбинации параллельных цепей. Если к параллельной цепи подключено более одного резистора, то эти резисторы можно заменить только одним резистором эквивалентной величины.
Цепь называется комбинацией параллельных цепей резистора, когда несколько сопротивлений соединяют два узла цепи, обеспечивая несколько путей для протекания тока.
Ток через каждое сопротивление также можно определить по формуле текущее правило делителя поскольку ток во всей цепи разделяется на все ветви в любой параллельной цепи резистора. Общая мощность, рассеиваемая в параллельной комбинации, пропорциональна сумме отдельных мгновенных мощностей, рассеиваемых любым регистром в параллельной комбинации цепей.
Как известно, общее напряжение в комбинации параллельных цепей сопротивления имеет ту же величину, что и постоянное падение электрического потенциала на каждом пути или ветви параллельной цепи сопротивления.
Предположим, что если в параллельном соединении сопротивлений имеется несколько ветвей, то [latex] V_1, V_2, V_3, V_n [/latex] являются индивидуальным падением напряжения на общем сопротивлении каждой ветви в параллельном соединении.
Тогда [латекс] V_1 =V_2 = V_3 . . .= В_н[/латекс]
Например, предположим, что более одного резистора соединены параллельно. Значения сопротивления могут быть одинаковыми или разными в любом параллельная цепь комбинация. Предположим, что два резистора одинакового сопротивления соединены параллельно друг с другом. В этом случае токи, протекающие через них, будут одинаковыми по величине и с эквивалентным сопротивлением и правилом деления тока. Применив закон Ома, мы можем получить напряжение на каждом сопротивлении параллельно.
Предположим, что два резистора [латекс] R_1 [/латекс] и [латекс] R_2 [/латекс] имеют разное сопротивление и соединены параллельно. Ток, протекающий через каждое сопротивление, может быть независим друг от друга.
После расчета тока через каждую ветвь по правилу деления тока и нахождения значения эквивалентного сопротивления всей цепи можно рассчитать с помощью закона Ома, можно определить напряжение на каждом сопротивлении.
Уравнение эквивалентного сопротивления в параллельная комбинация с резистором:
Где [латекс] R_e [/латекс] -> Эквивалент сопротивление параллели Комбинация контуров.
[latex]R_1, R_2, R_3….R_n [/latex] -> Различные резисторы, соединенные параллельно.
Когда два параллельных резистора (R) имеют одинаковое значение, эквивалентное сопротивление обоих резисторов составляет половину одного резистора (R).
Поскольку [латекс] frac<1>= frac<1> + frac<1> => frac<1> = frac<2> => R_e = frac<2>. [/латекс]
Как найти напряжение на резисторе в цепи RL?
Цепь RL содержит по крайней мере один резистор и катушку индуктивности в схеме параллельно или комбинация серий.
Падение напряжения на резисторе в цепи RL можно получить (или определить), применив закон Кирхгофа. Генерируется дифференциальное уравнение первого порядка, состоящее из падения напряжения на катушке индуктивности и резисторе.
Для любой RL-цепи падение напряжения на резисторе можно определить по протекающему через него току вместе с известным номиналом резистора с помощью закона Ома.
Для цепи серии RL
[латекс] V_r (s)= frac Vin (s) [/latex]
Для параллельной цепи RL
[латекс] I_r (s) = frac> [/latex]
Как найти максимальное напряжение на резисторе?
Каждый резистор имеет максимальную номинальную мощность, что означает, что это максимальная мощность, которую можно передать конкретному резистору без его повреждения.
Из текущего соотношения сил ([латекс]P = I^2R[/латекс], где R в этом случае считается постоянным) и, подавая максимальную мощность на резистор с учетом максимальной номинальной мощности этого конкретного резистора, можно измерить максимальное напряжение на резисторе.
Как найти напряжение на резисторе в комбинированной цепи?
Комбинированная схема представляет собой комбинацию или смесь как последовательных, так и параллельных цепей вместе.
- Анализ комбинированной цепи возможен путем разрыва возможной комбинации параллельной и последовательной цепей.
- И после разбивки всей комбинации на разные части анализ или эквивалент этих конкретных частей можно рассчитать отдельно.
- Затем можно рассчитать общий эквивалент всей комбинации цепей после объединения эквивалентов всех частей (которые рассчитывались отдельно).
- Применяя закон Ома, закон Кирхгофа, можно определить падение напряжения на любом компоненте цепи.
Как найти среднеквадратичное напряжение на резисторе?
Среднеквадратичное значение напряжения означает среднеквадратичное напряжение Цепь переменного тока, где среднеквадратичное значение обозначает эквивалентную рассеиваемую мощность цепи постоянного тока.
В одном из AC цепи, среднеквадратичное напряжение может быть рассчитано по размаху напряжения цепи переменного тока. Закон Ома, закон Кирхгофа и другие законы цепи могут быть применены к цепи переменного тока для расчета мгновенного напряжения или тока через резистор.
Пусть [latex] V_r[/latex] будет мгновенным напряжением на резисторе, тогда [latex]V_r = V_p sin omega t [/latex]
И [latex] I_r [/latex] — мгновенный ток через резистор, тогда [latex]I_r = frac =Vmax/R sin omega t = I_p sin omega t [/latex]
Таким образом, напряжение на резисторе можно определить как [латекс] V_r = I_p R sin omega t [/латекс]
Как найти напряжение на нагрузочном резисторе?
Нагрузочный резистор представляет собой пассивный элемент схемы с двумя выводами, которые имеют некоторое значение сопротивления.
Падение напряжения на сопротивлении нагрузки можно определить, определив комбинацию цепей и применив требуемые законы цепи, такие как закон Ома, закон Кирхгофа и т. д. При необходимости эквивалентную цепь можно создать с помощью простых расчетов.
Я получил высшее образование в области прикладной электроники и приборостроения. Я любопытный человек. У меня есть интерес и опыт в таких предметах, как преобразователи, промышленные приборы, электроника и т. д. Мне нравится узнавать о научных исследованиях и изобретениях, и я верю, что мои знания в этой области будут способствовать моим будущим усилиям. Идентификатор LinkedIn — https://www.linkedin.com/in/sneha-panda-aa2403209/
Последние посты
В английском языке глагол may относится к модальным вспомогательным глаголам. Давайте здесь узнаем, как глагол «может» может быть изменен в пассивный залог. Модальный вспомогательный глагол.
Электрическое поле создается за счет заряженной частицы. В этой статье будет выяснено, является ли электрическое поле скалярной или векторной величиной. Электрическое поле является вектором, так как оно имеет.
О НАС
Мы являемся группой профессионалов отрасли из различных областей образования, таких как наука, инженерия, английская литература, и создаем универсальное образовательное решение, основанное на знаниях.
Источник
Загрузить PDF
Загрузить PDF
Если вам необходимо найти напряжение на сопротивлении (резисторе), первым делом необходимо определить тип электрической цепи. Для лучшего понимания основных терминов, используемых в физике и электротехнике, начните с первого раздела. Если же вы знакомы с терминологией, пропустите его и перейдите к описанию типа электрической цепи.
-

1
Рассмотрим понятие электрического тока. Воспользуемся аналогией: представьте, что вы поместили несколько зерен кукурузы в воду, текущую по трубе. Поток эквивалентен электрическому току, а зерна служат аналогией электронов.[1]
Говоря о потоке, мы описываем его количеством зерен, пересекших поперечное сечение трубы за одну секунду. При рассмотрении электрического тока мы измеряем его в амперах, соответствующих определенному (очень большому) количеству электронов, пересекающих сечение провода за одну секунду. -

2
Рассмотрим понятие электрического заряда. Каждый электрон имеет “отрицательный” электрический заряд. Это означает, что электроны притягиваются, или движутся по направлению к положительному заряду и отталкиваются, или движутся от отрицательного заряда. Каждый электрон обладает отрицательным зарядом, поэтому они отталкиваются друг от друга, стремясь разойтись в стороны.
-

3
Ознакомьтесь с понятием напряжения. Напряжение между двумя точками соответствует разности электрических зарядов, размещенных в этих точках. Чем больше эта разница, тем сильнее данные точки притягиваются друг к другу. Рассмотрим понятие напряжения на примере обычной электрической батарейки:
- Внутри батарейки происходят химические реакции, в результате которых образуются свободные электроны. Эти электроны движутся к отрицательному полюсу батарейки, удаляясь от ее положительного полюса (эти полюса соответствуют отрицательной и положительной клеммам батарейки). Чем дольше длится данный процесс, тем большее напряжение возникает между полюсами.
- Если вы соедините проволокой отрицательный и положительный полюса, у скопившихся электронов появится возможность покинуть отрицательный полюс. Они начнут перетекать к положительному полюсу, создавая электрический ток. Чем выше напряжение, тем больше электронов переместится к положительному полюсу за единицу времени.
-

4
Рассмотрим понятие электрического сопротивления. Его название точно отображает смысл. Чем выше сопротивление какого-либо объекта, тем тяжелее электронам пройти через него. В результате уменьшается ток, поскольку за единицу времени через проводник проходит меньшее число электронов.
- Сопротивлением, или резистором называется что-либо, увеличивающее сопротивление электрической цепи. “Резистор” можно приобрести в магазине электротоваров, но в цепи его роль может выполнять и любой другой объект, обладающий сопротивлением, например, лампа накаливания.
-

5
Запомните закон Ома. Он представляет собой простое соотношение между током, напряжением и сопротивлением. Запишите или запомните это соотношение — оно пригодится вам при расчете электрических цепей:
- Ток равен напряжению, поделенному на сопротивление
- Это записывается следующим образом: I = V / R
- Подумайте о том, что происходит, если вы увеличиваете V (напряжение) или R (сопротивление). Соответствует ли это приведенным выше объяснениям?
Реклама
-

1
Ознакомьтесь с понятием последовательного соединения. Такое соединение легко определить — оно представляет собой набор расположенных в ряд сопротивлений. Ток течет по этим сопротивлениям, последовательно проходя через каждое из них.
- Величина тока одинакова в любой точке цепи.[2]
- При расчете напряжения неважно, где именно в цепи расположен тот или иной резистор. Можно поменять их местами, напряжение на каждом из них останется неизменным.
- В качестве примера рассмотрим цепь, состоящую из трех последовательно соединенных сопротивлений: R1, R2 и R3. Пусть цепь питается от 12-вольтовой батарейки. Найдем напряжение на каждом сопротивлении.
- Величина тока одинакова в любой точке цепи.[2]
-

2
Сначала рассчитаем общее сопротивление. Сложим все сопротивления, включенные в цепь. В результате получим общее сопротивление резисторов, соединенных последовательно.
- Пусть три резистора R1, R2 и R3 имеют сопротивления 2 Ома, 3 Ома и 5 Ом соответственно. Тогда общее сопротивление составит 2 + 3 + 5 = 10 Ом.
-

3
Найдем ток. Используем закон Ома для всей цепи. Как мы помним, при последовательном соединении ток одинаков в любой точке цепи. Поэтому достаточно один раз определить ток и использовать найденную величину во всех последующих расчетах.
- Согласно закону Ома, I = V / R. Напряжение в цепи составляет 12 вольт, а общее сопротивление – 10 Ом. Отсюда находим I = 12 / 10 = 1,2 ампера.
-

4
Применим закон Ома, чтобы найти напряжение на резисторах. При помощи простых преобразований можно выразить напряжение через ток и сопротивление, переписав закон Ома следующим образом:
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-

5
Рассчитаем напряжение на каждом резисторе. Нам известны их сопротивления, протекающий через них ток, и в нашем распоряжении есть равенство, связывающее ток и сопротивление с напряжением. Подставляя в это равенство численные значения, находим ответ. Для нашего примера это выглядит следующим образом:
- Напряжение на резисторе R1 = V1 = (1,2A)(2Ома) = 2,4 вольта.
- Напряжение на резисторе R2 = V2 = (1,2A)(3Ома) = 3,6 вольта.
- Напряжение на резисторе R3 = V3 = (1,2A)(5Ом) = 6,0 вольт.
-

6
Проверим полученный ответ. При последовательном соединении сумма напряжений на каждом сопротивлении должна равняться общему напряжению в цепи.[3]
Сложите найденные напряжения, проверив, равна ли их сумма полному напряжению. Если нет, проверьте решение и найдите ошибку.- В нашем примере 2,4 + 3,6 + 6,0 = 12 вольт, что соответствует общему напряжению в цепи.
- Если ответ немного не совпадает с точным значением (например, 11,97 вместо 12), это, вероятно, вызвано тем, что вы на каком-то этапе округлили полученные величины. В этом случае ответ верен.
- Помните о том, что напряжение соответствует разности зарядов или количества электронов. Представьте себе, что вы подсчитываете число электронов, продвигаясь вдоль цепи. Если вы правильно сосчитаете их, то в результате получите разность зарядов между начальной и конечной точками цепи.
Реклама
-

1
Ознакомьтесь с понятием параллельного соединения. Представьте себе, что вы подсоединили провод к одному полюсу батарейки и расщепили его вдоль на две половины. Эти две части провода идут параллельно друг другу и затем вновь соединяются в один провод перед вторым полюсом батарейки. Если разместить на обеих ветках провода по резистору, они будут соединены «параллельно».[4]
- Параллельно можно соединить любое количество сопротивлений. Данное описание годится и для цепи, состоящей из сотни параллельных проводов.
-

2
Рассмотрим, как течет ток. При параллельном соединении он проходит через все ветки цепи. Ток будет течь через левый провод, пересекая расположенный на нем резистор; одновременно ток будет проходить и через правый провод с резистором. Пройдя через обе ветки, ток достигнет положительного полюса; ни на каком участке цепи ток не будет течь в обратном направлении.
-

3
Зная общее напряжение, найдем напряжение на каждом резисторе. Сделать это очень просто, если известно общее напряжение в цепи. При параллельном соединении напряжение на каждой ветке будет равно общему напряжению в цепи.[5]
Предположим, что наша цепь состоит из двух параллельно соединенных сопротивлений и питается 6-вольтовой батарейкой. В этом случае напряжение и на левом, и на правом сопротивлении составит 6 вольт. При этом каждая ветка может содержать любое число резисторов. Чтобы понять это, вернемся к последовательному соединению, рассмотренному выше:- Как мы помним, при последовательном соединении общее напряжение представляет собой сумму напряжений на каждом сопротивлении.
- Будем считать, что каждая ветка цепи представляет собой набор резисторов, соединенных последовательно. Таким образом, вычислив сумму напряжений на всех сопротивлениях одной из веток, мы найдем общее напряжение.
- Поскольку в нашем случае ток, текущий по каждой ветке, проходит через один резистор, напряжение на этом резисторе и будет общим напряжением в цепи.
-

4
Найдем общий ток в цепи. Если в условии задачи не указано общее напряжение, понадобятся некоторые дополнительные вычисления. Начнем с нахождения общего тока, протекающего по цепи. При параллельном соединении общий ток равен сумме токов, проходящих через каждую ветку цепи.[6]
- В математической записи это означает: Iобщий = I1 + I2 + I3…
- Для лучшего понимания представьте себе водопроводную трубу, разделенную на два рукава. Общее количество воды равно сумме воды, протекающей по каждому рукаву.
-

5
Найдем общее сопротивление цепи. При параллельном соединении резисторы не так сильно снижают ток через цепь, поскольку каждый из них вносит вклад в сопротивление лишь своей ветки цепи. Фактически чем больше ответвлений цепи, тем легче току пройти через нее. Чтобы найти общее сопротивление, необходимо решить относительно Rобщее следующее уравнение:
- 1 / Rобщее = 1 / R1 + 1 / R2 + 1 / R3 …
- Предположим, что цепь состоит из двух резисторов сопротивлением 2 Ома и 4 Ома, соединенных параллельно. Тогда 1 / Rобщее = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rобщее → Rобщее = 1/(3/4) = 4/3 = ~1,33 Ома.
-

6
Вычислим напряжение. Как мы помним, общее напряжение в цепи равно напряжению на одной из ее веток. Воспользуемся законом Ома. Рассмотрим конкретный случай:
- Через цепь течет ток силой 5 ампер. Общее сопротивление цепи равно 1,33 Ома.
- Согласно закону Ома, I = V / R, откуда V = IR
- V = (5A)(1,33Ом) = 6,65 вольт.
Реклама
Советы
- Если вы имеете дело со сложной цепью, состоящей из последовательно и параллельно соединенных сопротивлений, рассмотрите сначала два соседних резистора. Найдите их общее сопротивление, пользуясь правилами для последовательного или параллельного соединения, в соответствии с тем, как соединены данные резисторы. После этого можно рассматривать два данных резистора как одно сопротивление. Продолжайте таким образом объединять резисторы до тех пор, пока у вас не получится простая цепь, состоящая из параллельно либо последовательно соединенных сопротивлений.[7]
- Напряжение на сопротивлении часто называют «падением напряжения».
- Усвойте терминологию:
- Цепь — набор элементов (например, резисторов, конденсаторов и катушек), соединенных проводами так, что через них может проходить электрический ток.
- Резисторы — элементы, оказывающие сопротивление протекающему через них току и понижающие его силу
- Ток — поток электрического заряда через проволоку и элементы цепи, измеряется в амперах (А)
- Напряжение — работа, затрачиваемая на перемещение единичного заряда, измеряется в вольтах (В)
- Сопротивление — мера сопротивления прохождению электрического тока, измеряется в омах (Ом)
Реклама
Об этой статье
Эту страницу просматривали 167 213 раз.
Была ли эта статья полезной?
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
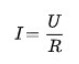
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
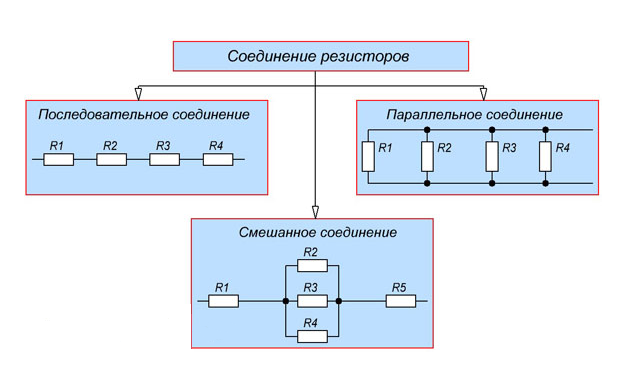
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
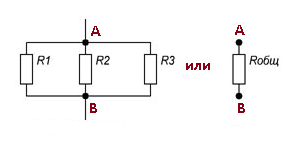
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
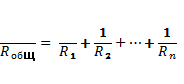
и рассчитывается по формуле:
![]()
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
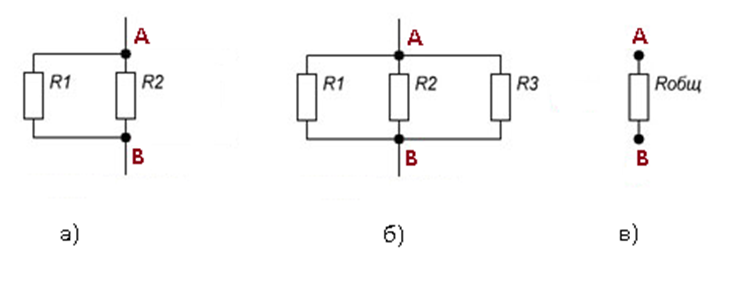
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
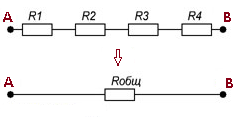
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
![]()
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
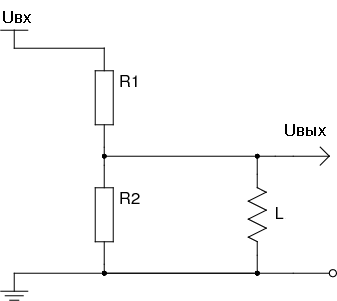
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
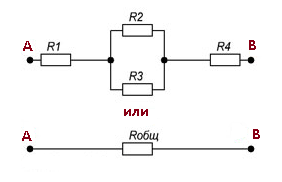
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
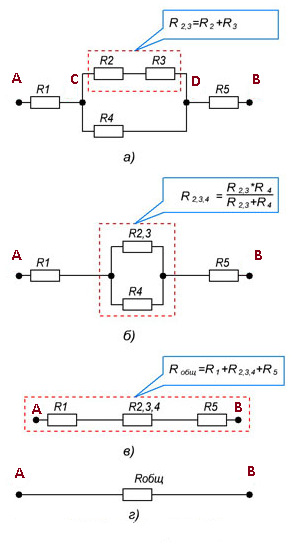
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Download Article
Download Article
Before you can calculate the voltage across a resistor, you’ll first have to determine what kind of circuit you are using. If you need a review of the basic terms or a little help understanding circuits, start with the first section. Otherwise, jump ahead to the type of circuit you have to solve.
-

1
Learn about current. Let’s think about current by using an analogy: imagine you pour a bag of corn kernels into a bowl. Each corn kernel is an electron, and the stream of kernels flowing into the bowl is the current.[1]
When talking about the flow, you describe it by saying how many kernels are flowing each second. When talking about a current, you measure it in amperes (amps), or a certain (very large) number of electrons flowing per second. -

2
Think about electrical charge. Electrons have a “negative” electrical charge. This means they attract (or flow toward) objects with a positive charge, and repel (or flow away from) objects with a negative charge. Since they’re all negative, electrons are always trying to push away from other electrons, spreading out wherever they can.
Advertisement
-

3
Understand voltage. Voltage measures the difference in electrical charge between two points. The greater the difference, the more energetically the two sides attract each other. Here’s an example with an everyday battery:
- Inside a battery, chemical reactions happen that produces a buildup of electrons. The electrons go to the negative end, while the positive end stays mostly empty. (These are called the negative and positive terminals.) The longer this goes on, the larger the voltage between the two ends.
- When you connect a wire between the negative and positive ends, the electrons at the negative end suddenly have somewhere to go. They shoot toward the positive end, creating a current. The larger the voltage, the more electrons move to the positive end each second.
-

4
Figure out resistance. Resistance is exactly what it sounds like. The more resistance something has, the harder it is for the electrons to push through. This slows the current, since fewer electrons can push through each second.
- A resistor is anything in the circuit that adds resistance. You can buy an actual “resistor” at an electronics store, but in a circuits problem it might represent a light bulb or anything else with resistance.
-

5
Memorize Ohm’s Law. There’s a very simple relationship between current, voltage, and resistance.[2]
Write this down or memorize it; you’ll use it often when solving circuit problems:- Current = voltage divided by resistance
- This is usually written: I = V / R
- Think about what happens when you increase V (voltage) or R (resistance). Does this match what you learned in the explanations above?
Advertisement
-

1
Understand a series circuit. A series circuit is easy to identify. It’s just one loop of wire, with everything arranged in a row. The current flows around the entire loop, going through each resistor or element in order.
- The current is always the same at any point along the circuit.[3]
- When calculating voltage, it doesn’t matter where the resistor is on the circuit. You can pick up the resistors and move them around, and you’ll still have the same voltage across each one.
- We’ll use an example circuit with three resistors in series: R1, R2, and R3. This is powered by a 12 volt battery. We’ll find the voltage across each one.
- The current is always the same at any point along the circuit.[3]
-

2
Calculate the total resistance. Add together all resistance values on the circuit. The answer is the total resistance of the series circuit.
- For example, the three resistors R1, R2, and R3 have resistances of 2 Ω (ohms), 3 Ω, and 5 Ω respectively. The total resistance is 2 + 3 + 5 = 10 ohms.
-

3
Find the current. Use Ohm’s Law to find the current of the entire circuit. Remember, the current is the same anywhere on a series circuit. Once we calculate the current this way, we can use it for all our calculations.
- Ohm’s Law says that the current I = V / R. The voltage across the whole circuit is 12 volts, and the total resistance is 10 ohms. The answer is I = 12 / 10 = 1.2 amperes.
-

4
Adjust Ohm’s Law to solve for voltage. With basic algebra, we can change Ohm’s Law to solve for voltage instead of current:[4]
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-

5
Calculate the voltage across each resistor. We know the resistance, we know the current, and we have our equation. Plug in the numbers and solve. Here’s our example problem solved for all three resistors:
- Voltage across R1 = V1 = (1.2A)(2Ω) = 2.4 volts.
- Voltage across R2 = V2 = (1.2A)(3Ω) = 3.6 volts.
- Voltage across R3 = V3 = (1.2A)(5Ω) = 6.0 volts.
-

6
Check your answer. In a series circuit, the sum of all your answers must equal the total voltage.[5]
Add up every voltage you calculated and see if you get the voltage of the entire circuit. If you didn’t, go back and check for mistakes.- In our example, 2.4 + 3.6 + 6.0 = 12 volts, the voltage across the whole circuit.
- If your answer is slightly off (for instance, 11.97 instead of 12), you probably rounded a number at some point. Your answer is still correct.
- Remember, voltage measures the differences in charge, or numbers of electrons. Imagine counting the number of new electrons you see as you travel along the circuit. If you count them correctly, you’re going to end up with the total change in electrons from the beginning to the end.
Advertisement
-

1
Understand parallel circuits. Imagine a wire leaving one end of a battery, then splitting into two separate wires. These two wires run parallel to each other, then join up again before they reach the other end of the battery. If there’s a resistor on the left wire and a resistor on the right wire, those two resistors are connected “in parallel.”[6]
- You can have any number of wires in a parallel circuit. These instructions will still work for a circuit that splits into one hundred wires and comes back together.
-

2
Think about how the current flows. In a parallel circuit, the current flows across each path available to it. Current will flow through the wire on the left, cross the left resistor, and reach the other end. At the same time, current will flow through the wire on the right, cross the right resistor, and reach the end. No part of the current doubles back or flows through two parallel resistors.
-

3
Use the total voltage to find the voltage across each resistor. If you know the voltage across the whole circuit, the answer is surprisingly easy. Each parallel wire has the same voltage as the entire circuit.[7]
Let’s say a circuit with two parallel resistors is powered by a 6 volt battery. The voltage across the left resistor is 6 volts, and the voltage across the right resistor is 6 volts. It doesn’t even matter how much resistance there is. To understand why, think back to the series circuits described above:- Remember that adding voltage drops in a series circuit always results in the total voltage across the circuit.
- Think of each path the current takes as a series circuit. The same holds true for this: if you count up all the voltage drops, you’ll end up with the total voltage.
- Since the current through each of the two wires only passes through one resistor, the voltage across that resistor must equal the total voltage.
-

4
Calculate the total current of the circuit. If the problem doesn’t tell you what the total voltage of the circuit is, you’ll need to complete a few more steps. Start by finding the total current passing through the circuit. In a parallel circuit, the total current is equal to the sum of the current running through each parallel path.[9]
- In mathematical terms: Itotal = I1 + I2 + I3…
- If you’re having trouble understanding this, imagine a water pipe split into two paths. The total amount of water flow is just the amount of water flow in each pipe, added together.
-

5
Compute the total resistance of the circuit. Resistors are not as effective in a parallel circuit, because they only block the current going along one wire. In fact, the more wires there are, the easier it is for the current to find a way through. To find the total resistance, solve for Rtotal in this equation:[9]
- 1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 …
- For example, a circuit has a 2 ohm and a 4 ohm resistor in parallel. 1 / Rtotal = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rtotal → Rtotal = 1/(3/4) = 4/3 = ~1.33 ohms.
-

6
Find the voltage from your answers. Remember, once we find the total voltage of the circuit, we have found the voltage across any one of the parallel wires. Solve for the whole circuit using Ohm’s law.[10]
Here’s an example:- A circuit has 5 amperes of current running through it. The total resistance is 1.33 ohms.
- According to Ohm’s Law, I = V / R, therefore V = IR
- V = (5A)(1.33Ω) = 6.65 volts.
Advertisement
Add New Question
-
Question
What is the percentage of applied voltage that will be dropped across r3=70 if r1=80 and r2=50?

It would be 35%. The higher the resistance, the higher the voltage drop. The ratio of resistances here is 80:50:70. Solving for 70 ohms, we get 35%.
-
Question
What is the voltage of a 60 ohm resistor if the circuit voltage is 150 volts with two parallel 30 ohm resistors and one 60 ohm resister in the series?

Assuming you intend to ask what is the voltage drop across the 60 ohm resistor, the answer is 120v. The two parallel 30 ohm resistors have an equivalent resistance of 15 ohms. 1/(1/30 + 1/30) = 15. The total resistance appears as 75 ohms to the 150v source. Find the circuit current by I = E/R or I = 150/75 = 2 amps. Find the voltage drop for the 60 ohm resistor with E = I x R or E = 2 x 60 = 120V drop across the 60 Ohm resistor.
-
Question
What becomes the Voltage if we use 2 resistors of 4W in parallel?

As any other data is not provided, the voltage across two resistors of 4w in parallel is the same.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you have a complicated circuit that involves resistors in series and resistors in parallel, pick two nearby resistors. Find the total resistance across them using the rules for resistors in parallel or in series, as appropriate. Now you can treat them as a single resistor. Keep doing this until you have a simple circuit with resistors either in parallel or in series.[11]
-
The voltage across a resistor is often called a “voltage drop.”
-
Understand the terminology:
- Circuit – composed of elements (e.g. resistors, capacitors, and inductors) connected by wires and wherein current can pass through
- Resistors – elements that can reduce or resist current
- Current – flow of charge into wires; unit: Ampere, A
- Voltage – work done per unit charge; unit: Voltage, V
- Resistance – measurement of the opposition of an element to electric current; unit: Ohm, Ω
Advertisement
References
About This Article
Article SummaryX
To calculate voltage across a resistor in a series circuit, start by adding together all of the resistance values in the circuit. Then, divide the voltage across the circuit by the total resistance to find the current. Once you have the current, calculate voltage for the individual resistors by multiplying the current by the resistance. For example, in a series circuit with 3 resistors of 2, 3 and 5 Ohms, and a voltage of 12 volts, the current would be 12 divided by 10, or 1.2 amperes. For the 2 Ohm resistor, the voltage would be 1.2 times 2, or 2.4 volts. If you want to learn how to calculate voltage in a parallel circuit, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 914,976 times.
Reader Success Stories
-

Mohd Rodzi Mohamad
Aug 26, 2016
“This article is very neatly and clearly explained with illustrations of pictures for better comprehension. Very…” more
Did this article help you?
«Не знаешь Ома – сиди дома» — пословица старых электриков. Действительно, этот закон очень важен для понимания того, как связаны напряжение, ток и сопротивление, или проще говоря — от чего зависит ток и мощность нагрузки и как их рассчитать.
Для понимания этих базовых вещей нужно знать закон Ома для участка цепи и закон Ома для полной цепи. Главное различие между ними, что первый распространяется на отдельный участок или элемент и учитывает только его сопротивление и приложенное к нему напряжение, а второй учитывает и внутреннее сопротивление источника питания. Давайте разберёмся подробнее.
Закон Ома для участка цепи
Самый простой и всем известный со школы вариант — закон Ома для участка цепи. Его определение звучит следующим образом:
В виде формулы это выглядит так:
I=U/R,
где I — ток, U — напряжение, R— сопротивление.
То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.
Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:
U=IR
Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:
R=U/I
К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».
Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.
Как запомнить эти формулы?
В виде формулы это выглядит так:
I=U/R,
где I — ток, U — напряжение, R— сопротивление.
То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.
Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:
U=IR
Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:
R=U/I
К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».
Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.
Как запомнить эти формулы?
Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.
Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.
Как пользоваться треугольником? Всё просто — закройте пальцем величину, которую нужно найти, а оставшиеся не закрытыми буквы нужно умножить или разделить друг на друга, что подробно проиллюстрировано ниже.
Есть еще одна шпаргалка в виде круга разделенного на сегменты, где перечислены все необходимые формулы, кроме перечисленных выше, добавлены и формулы для вычисления мощности.
Примеры
Итак, чтобы научиться рассчитывать напряжение на участке цепи, решим простенькую задачу. У нас есть цепь, состоящая из 3 резисторов и идеального источника с напряжением 12В постоянного тока. Пусть участком цепи у нас будет резистор R2, найдём напряжение на нём.
Дано:
U= 12 В;
R1= 1 кОм;
R2= 2 кОм;
R3= 3 кОм;
Найти:
I — ?;
U(R2) — ?;
По закону Ома чтобы найти напряжение нужно знать ток через участок цепи и его сопротивление.
U=IR
Последнее у нас известно, поэтому нужно найти ток в цепи, элементы соединены последовательно, поэтому ток через каждый из них одинаков, и чтобы найти его силу — нужно сначала найти общее сопротивление всех элементов, но сначала переведём его в Омы:
R1 = 1 кОм = 1000 Ом; R2 = 2 кОм = 2000 Ом; R3 = 3 кОм = 3000 Ом.
Теперь найдём общее сопротивление:
Rобщ=R1+R2+R3=1000+2000+3000= 6000 Ом
Тогда ток в цепи равен:
I= U/R = 12/6000 = 0,002 А
И наконец падение напряжения на резисторе R2:
U(R2) = I*U(R2) = 0,002*2000=4В
Итого, на выводах резистора R2 будет 4 вольта.
Закон Ома для полной цепи
Определение закона Ома для полной цепи вы видите ниже, жирным выделено основное отличие от закона для участка цепи.
В формуле добавляется внутреннее сопротивление источника питания, а напряжение заменяется на ЭДС:
I=E/(R+r),
где I – ток, E – ЭДС, R – сопротивление, r- внутреннее сопротивление источника.
Внутреннее сопротивление источника обуславливается его устройством, например, сечением вторичной обмотки трансформатора, химическим составом, степенью заряда и состоянием электродов аккумуляторов и батареек и так далее. На схеме условно рисуется в виде резистора внутри источника, но на самом деле никакого «внутреннего» или «скрытого» сопротивления там нет, как было отмечено выше.
Почему важно учитывать внутреннее сопротивление источника? Всё очень просто — вы замечали, как погасают лампочки в автомобиле, когда стартер запускает двигатель? Это происходит из-за просадок на проводах и в аккумуляторе от высоких пусковых токов. В принципе, подобное мы наблюдаем, когда лампы накаливания «просаживаются» по яркости во время пуска мощной нагрузки, например, электродвигателей.
Примеры
Давайте проанализируем, как влияет внутреннее сопротивление источника на напряжение нагрузки. Допустим, что у нас есть какой-то источник с внутренним сопротивлением (r) в 1 Ом и ЭДС (E) в 12 Вольт. И есть 3 разных нагрузки, с сопротивлением (R) каждой из них: 10, 5 и 1 Ом соответственно. Нагрузку будем подключать по очереди, по одной для каждого расчета.
Рассчитаем ток первой нагрузки:
I1=E/(R1+r)=12/(10+1)=1.09 А
Рассчитаем напряжение на нагрузке:
U1=I1*R1=1.09*10=10.9 В
Сразу видим, что на нагрузке уже не 12, а 10 вольт, посчитаем другие варианты:
Рассчитаем ток второй нагрузки:
I2=E/(R2+r)=12/(5+1)=2 А
Рассчитаем напряжение на нагрузке:
U2=I2*R2=2*5=10 В
Рассчитаем ток третей нагрузки:
I3=E/(R3+r)=12/(1+1)=6 А
Рассчитаем напряжение:
U3=I3*R3=6*1=6 В
Как вы можете видеть на внутреннем сопротивлении падает какое-то напряжение, и падение напряжение прямо пропорционально току нагрузки. При этом до нагрузки доходит всё меньше и меньше напряжения.
Сделаем то же самое, но для источника с внутренним сопротивлением 0.1 Ома. Рассчитаем ток первой нагрузки:
I1=E/(R1+r)=12/(10+0,1)=1.18 А
Рассчитаем напряжение:
U1=I1*R1=1.18*10=11.8 В
Ток второй нагрузки:
I2=E/(R2+r)=12/(5+0,1)=2,35 А
Рассчитаем напряжение на нагрузке:
U2=I2*R2=2,35*5=11.75 В
Рассчитаем ток третей нагрузки:
I3=E/(R3+r)=12/(1+0,1)=10,9 А
Рассчитаем напряжение:
U3=I3*R3=10,9*1=10,9 В
Для удобства соберем все результаты расчётов в одну таблицу.
Из таблицы мы видим, что чем меньше внутреннее сопротивление источника — тем меньше просаживается напряжение под нагрузкой.
Заключение
Георг Симон Ом жил в 1786-1854 годах, в 1826 году вывел теоретически и подтвердил с помощью опытов закон выражающий связь напряжения, тока и сопротивления. Этот закон назвали в честь открывателя — законом Ома, а также единицу измерения электрического сопротивления.
Закон Ома — один из важнейших и основополагающих в электротехнике, он широко используется при расчетах электрических схем.
Пишите в комментариях, понравился ли вам такой формат теоретической статьи и какие статьи хотите увидеть в будущем?
