Запасы
играют как положительную, так и
отрицательную роль в деятельности
логистической системы. Положительная
роль заключается в том, что они обеспечивают
непрерывность процессов производства
и сбыта продукции, являясь своеобразным
буфером, сглаживающим непредвиденные
колебания спроса, нарушение сроков
поставки ресурсов, повышают надежность
логистического менеджмента.
Негативной
стороной создания запасов является то,
что в них иммобилизуются значительные
финансовые средства, которые могли бы
быть использованы предприятием на
другие цели, например, инвестиции в
новые технологии, исследование рынка,
улучшение экономических показателей
деятельности предприятия. Кроме того,
большие уровни запасов готовой продукции
препятствуют улучшению ее качества,
так как предприятие, прежде всего,
заинтересовано в реализации уже имеющейся
продукции до вложения инвестиций в
повышении ее качества. Исходя из этого,
возникает проблема обеспечения
непрерывности логистических и
технологических процессов при минимальном
уровне затрат, связанных с формированием
и управлением различными видами запасов
в логистической системе.
Один из
методов эффективного управления запасами
– определение оптимальных партий
поставок груза, который позволяет
оптимизировать расходы на транспортировку,
хранение груза, а также избежать избытка
или недостатка груза на складе.
Оптимальный
размер партии qопределяется
по критерию минимума затрат на
транспортировку продукции и хранение
запасов.
Величина
суммарных затрат рассчитывается по
формуле (3.1);
С= +
+ (3.1)
(3.1)
Где
 – затраты на транспортировку за расчетный
– затраты на транспортировку за расчетный
период (год), у.е;
 – затраты на хранение запаса за расчетный
– затраты на хранение запаса за расчетный
период (год), у.е.
Величина
 определяется по формуле:
определяется по формуле:
 =n*
=n* (3.2)
(3.2)
Где n-
количество партий, доставляемых за
расчетный период,
n= (3.3)
(3.3)
 – тариф на перевозку одной партии ,
– тариф на перевозку одной партии ,
у.е./партия.
Затраты на
хранение определяются по формуле (3.4):
 =
=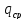 *
*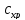
Где qср
– средняя величина (в тоннах), которая
определяется из предположения, что
новая партия завозится после того, как
предыдущая полностью израсходована. В
этом случае средняя величина рассчитывается
по следующей формуле:
 *=
*= (3.5)
(3.5)
Подставив
выражения
 и
и в формулу (3.1), получим:
в формулу (3.1), получим:
С= *
* +
+ *
* (3.6)
(3.6)
Функция
общих затрат С имеет минимум в точке,
где ее первая производная по qравна нулю, т.е.
 =-
=- *
* +
+ =0(3.7)
=0(3.7)
Решив
уравнение (3.7) относительно qполучим оптимальный размер партии
поставки:
q*=sqr(2Q* /
/ ) (3.8)
) (3.8)
В качестве
размеров годового объема потребления
продукции принемаем данные, полученные
в результате прогнозирования методом
простого среднего: Q=98
тыс. т/год; тариф на перевозку одной
партии =80
=80
у.е./т; расходы, связанные с хранением
запаса =5
=5
у.е./т.
Подставив
данные значения, получим:
q= =
=
1770,9 (т)
При этом
общие затраты составляют:
С= *80
*80
+ (у.е.)
(у.е.)
Решение
данной задачи графическим способом
заключается в построении графиков
зависимости
 (q),
(q), (q)
(q)
и С(q), предварительно
выполнив необходимые расчеты по
определению ,
, и С.
и С.
Определим
значения
 ,
,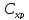 и С при измененииqв
и С при измененииqв
пределах от 400 до 800 с шагом 100. Результаты
расчетов занесем в табл.3.1.
Таблица
3.1
Значения ,
, иС
иС
|
Размер партии q Затраты, у.е. |
400 |
500 |
600 |
700 |
800 |
|
|
19600 |
15680 |
13066,7 |
11200 |
9800 |
|
|
1000 |
1250 |
1500 |
1750 |
200 |
|
С |
20600 |
16930 |
14566,7 |
12950 |
11800 |
По данным
табл.3.1 построены графики зависимости
затрат (транспортных, складских и
суммарных) от размера партии (рис.3.1).

Анализ
графиков на рис.3.1 показывает, что
Произведем
расчет оптимального размера партии в
условиях дефицита при величине расходов,
связанных с дефицитом
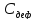 =15
=15
у.е/т.
В условиях
дефицита значение q*,
рассчитанное по формуле (3.8) корректируется
на коэффициентk, учитывающий
расходы, связанные с дефицитом.
q*=k* (3.9)
(3.9)
Коэффициент
kрассчитывают по формуле
(3.10):
K=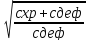 (3.10)
(3.10)
 –
–
величина расходов, связанных с дефицитом;
Принимаем
 –
–
=15у.е./т
Подставим
значения, получим:
K=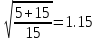
q=
1.15*1770.9= 2036,5 (т)
Из этого
следует, что в условиях возможного
дефицита размер оптимальной партии
поставки необходимо увеличить на 15%.
Соседние файлы в папке курсач docx283
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оптимизация текущего запаса заключается в выборе наиболее экономичного размера партии (заказа).
Размер оптимальной партии в модели Уилсона определяется по формуле:
EOQ = [(2 x Qsg x OPR) : C]1 / 2,
где Qsg – потребность в материальных ресурсах на бюджетный период (квартал, полугодие, год).
Оптимальное число поставок в бюджетный период:
N = Qs : EOQ.
Оптимальный интервал времени между поставками:
t = 360 : N.
Средний уровень запаса:
Зср = 0,5 x EOQ – [(OPR x Qpg) : (2
x C)]1 / 2.
Пример 36. Годовая потребность предприятия в сырье вида “С” составляет 10 000 усл. ед. Расходы, связанные с организацией заказа на поставку одной партии материальных ресурсов (продукции), – 12 тыс. руб. Издержки по содержанию единицы сырья на складе в год – 0,023 тыс. руб. Определить размер оптимальной партии, промежуток времени между поставками. Как изменится размер оптимальной партии при увеличении годовой потребности в сырье на 30%, а издержек по содержанию единицы сырья на 15%?
Решение:
По условию Qsg = 1000 усл. ед.; OPR = 12 тыс. руб.; C = 0,023 тыс. руб.
- Размер оптимальной партии:
EOQ = [(2 x Qsg x OPR) : C]Ѕ = [(2 x 10 000 x12) : 0,023]1 / 2 = 3230 (усл. ед.).
- Оптимальное число поставок в год:
N = Qsg : EOQ = 10 000 : 3230 = 3,10 (партии).
Оптимальный интервал времени между поставками:
t = 360 : N = 360 : 3,1 = 116 (дней).
- Определим размер оптимальной партии и количество партий, если годовая потребность увеличится на 30%:
EOQ = [(2 x Qsg x OPR) : C]1 / 2 = [(2 x 10 000 x 1,30 x 12) : 0,023]1 / 2 = 3683 (усл. ед.).
Оптимальное число поставок в год:
N = Qsg : EOQ = 10 000 x 1,30 : 3683 = 3,53 (партии).
Оптимальный интервал времени между поставками:
t = 360 : N = 360 : 3,53 = 102 (дня).
Увеличение потребности в сырье на 30% приведет к увеличению размера оптимальной партии на 14,02% [(3683 : 3230 – 1)x 100%].
- Определим размер оптимальной партии и количество партий, если годовая потребность останется на том же уровне, а издержки по содержанию единицы сырья изменятся на 15%:
EOQ = [(2 x Qsg x OPR) : C]1 / 2 = [(2 x 10 000 x 12) : (0,023 x 1,15)]1 / 2 = 3012 (усл. ед.).
Оптимальное число поставок в год:
N = Qsg : EOQ = 10 000 : 3012 = 4,32 (партии).
Оптимальный интервал времени между поставками:
t = 360 : N = 360 : 4,32 = 83 (дня).
Если потребность в сырье останется на том же уровне, а издержки по содержанию единицы сырья увеличатся на 15%, то это приведет к уменьшению размера оптимальной партии на -6,75% [(3012 : 3230 – 1)x 100%].
- Определим размер оптимальной партии и количество партий, если годовая потребность увеличится на 30%, а издержек по содержанию единицы сырья на 15%:
EOQ = [(2 x Qsg x OPR) : C]1 / 2 = [(2 x 10 000 x 1,30 x 12) : (0,023 x 1,15)]1 / 2 = 3435 (усл. ед.).
Оптимальное число поставок в год:
N = Qsg : EOQ = 10 000 x 1,30 : 3435 = 3,78 (партии).
Оптимальный интервал времени между поставками:
t = 360 : N = 360 : 3,78 = 95 (дней).
Увеличение потребности в сырье на 30%, а издержек по содержанию единицы сырья на 15% приведет к увеличению размера оптимальной партии на 6,35% [(3435 : 3230 – 1) x 100%].
Модель EOQ
Для определения оптимальной величины заказа закупки сырья и материалов в единичный (бюджетный) период времени (неделя, квартал, год) используют модель EOQ. Применение этой модели предусматривает выполнение следующих условий:
- производственное потребление материалов является абсолютно равномерным в течение бюджетного периода и задано заранее;
- не учитывается время от момента заказа до поступления запасов на склад.
Для осуществления расчетов необходимо знать информацию:
- потребность запасов сырья и материалов за бюджетный период в физических единицах в соответствии с производственной программой:
Qsр = Kh x H,
где
Kh – производственная программа в натуральных единицах;
H – норма расхода сырья для производства единицы продукции;
- стоимость 1 ед. сырья – Z;
- затраты на содержание 1 ед. запаса в течение бюджетного периода на складе – Сс;
- иммобилизационные издержки на 1 ед. сырья. Эти издержки соответствуют возможному доходу от вложения средств, направленных на закупку сырья и материалов, в банк по наиболее доходному безрисковому вложению – Cим;
- операционные издержки по заказу – затраты на закупку форм отчетности, транспортировку, доставку на склад, заработную плату сотрудников службы сбыта, по коммунальным платежам и прочие управленческие расходы – OPR.
На основе этой информации определяются:
-
затраты на хранение единицы сырья в течение бюджетного периода:
С = Сc + Cим;
-
определяется страховой запас сырья и материалов на конец бюджетного периода, расчет осуществляется в процентном отношении от потребности в сырье и материалов в следующий период:
Qsкi – 1 = Qsi x р,
где р – доля в процентах;
-
определяется страховой запас сырья и материалов на начало периода, его величина соответствует запасу сырья на конец предшествующего периода.
Qsнi = Qsкi – 1;
-
определяется потребность в сырье на бюджетный период:
Qsg = Qsp + Qsk – Qsн;
-
определяется оптимальный размер заказа закупки сырья и материалов в натуральных единицах по формуле:
EOQ = [(2 x Qsg x OPR) : C]1 / 2 ,
где EOQ показывает необходимое количество закупки материальных ресурсов в натуральных единицах за один раз;
-
определяется количество заявок на сырье и материалы:
N = Qs : EOQ;
-
определяются совокупные издержки по возобновлению и содержанию запасов материала за бюджетный период:
ISΔ = N x OPR + (Qsн + Qsk)
x 0,5 x Cc.
Рассмотрим использование этой модели на следующем примере.
Пример 37. Определить издержки организации, связанные с обеспечением производственного процесса сырьем и материалами, если известны объемы производства, нормы расхода сырья и цена сырья. Исходные данные представлены в табл. 2.16.
| Показатель | I квартал | II квартал | III квартал | IV квартал |
|---|---|---|---|---|
| 1. Объем производства, усл. ед. | 1000 | 1200 | 1300 | 1300 |
| 2. Норма расхода сырья на 1 ед. продукции, усл. ед. | 2 | 2 | 2 | 2 |
| 3. Цена сырья, тыс. руб. | 3 | 3 | 3 | 3 |
| 4. Безрисковая ставка, % | 2 | 2 | 3 | 3 |
| 5. Операционные издержки по заказу, OPR, тыс. руб. | 40 | 40 | 40 | 40 |
| 5.1. Индекс роста операционных издержек | 1,00 | 1,05 | 1,10 | 1,15 |
| 5.2. Индексированные операционные издержки по заказу, тыс. руб. (стр. 5 x стр. 5.1) OPRi | 40 | 42 | 44 | 46 |
| 6. Затраты на содержание 1 единицы запаса на складе, Сс, тыс. руб. | 0,3 | 0,3 | 0,3 | 0,3 |
| 6.1. Индекс роста затрат | 1,00 | 1,10 | 1,12 | 1,15 |
| 6.2. Индексированные издержки содержания единицы запаса на складе | 0,3 | 0,33 | 0,336 | 0,345 |
| 7. Иммобилизационные издержки на 1 ед. сырья, Сим (стр. 3 x стр. 4 : 100%) | 0,6 | 0,6 | 0,9 | 0,9 |
| 8. Затраты на содержание единицы сырья на складе, тыс. руб. С (стр. 7 x стр. 6.2) | 0,36 | 0,39 | 0,426 | 0,435 |
| 9. Потребность в сырье на производство, усл. ед., Qs (стр. 1 x стр. 2) | 2000 | 2400 | 2600 | 2600 |
| 10. Страховой запас на конец бюджетного периода, усл. ед. Qsk (стр. 9 x 0,5) | 1000 | 1200 | 1300 | 1300 |
| 11. Запас сырья на начало бюджетного периода, усл. ед. QSH | 500 | 1000 | 1200 | 1300 |
| 12. Потребность в сырье на бюджетный период, усл.ед. (стр. 9 + стр. 10 + стр. 11), Qsg | 2500 | 2600 | 2700 | 2600 |
| 13. Оптимальный размер заказа закупки сырья и материалов за бюджетный период, усл. ед. EOQ = [(2 x Qsg x OPR) : C]1 / 2, [2 x стр. 12 x стр. 5.2 : стр 8]1 / 2 | 745 | 748 | 747 | 742 |
| 14. Количество заявок на поставку сырья и материалов, N (стр. 12 : стр. 13) | 3 | 3 | 4 | 4 |
| 14.1 Период времени между поставками, дн. (90 : стр. 14) | 30 | 30 | 22,5 | 22,5 |
| 15. Издержки по возобновлению запасов, тыс. руб. (стр 14 x стр 5.2) | 120 | 126 | 176 | 184 |
| 16. Издержки на хранение запасов, тыс. руб. ((стр. 10 + стр. 11) : 2) x стр. 6.2) | 225 | 363 | 420 | 448,5 |
| 17. Издержки по возобновлению и хранению запасов, тыс.руб. (стр. 15 x стр. 16) | 345 | 489 | 596 | 632,5 |
| 18. Издержки на закупку сырья, тыс. руб. (стр. 12 x стр. 3) | 7500 | 7800 | 8100 | 7800 |
| 19. Общие затраты на бюджетный период на сырье, тыс. руб.(стр. 17 x стр. 18) | 7845 | 8289 | 8696 | 8432,5 |
Энциклопедия
28 августа 2012
0 комментариев
Размер партии – это величина последовательно произведенного товара без перерывов либо переключений в технологическом процессе.
В чем значимость определения оптимального размера партии?
Оптимальный размер партии приводит к уменьшению потерь по складу, процентов на имущество, расходов по перенастройке. Следовательно, разделение объема товаров, производимого за год, на доли приводит к значительному снижению расходов.
Наилучшему размеру партии для производителя противодействует выгодный размер партии для реализации. Расходы по перенастройке становятся при данном варианте расходами по регистрации заказа.
В чем заключается особенность серийного производства?
Серийное производство оптимально для групп товаров сходных по технологическим процессам при изготовлении. Спустя некоторое время возникает необходимость в перенастройке к выпуску иного товара. Вышеприведенный рисунок демонстрирует, что продукция А, В, С производится последовательно на одной технологической линии.
Перерыв в технологическом процессе для пуска в производство нового товара приводит к простою и появлению не связанных с размером партии расходов – постоянные серийные затраты. Это расходы на перенастройку и наладку производственных мощностей.
При увеличении размера партии увеличиваются и постоянные серийные затраты. В пересчете на единицу продукции эти расходы сокращаются при увеличении размера партии, производимой без перерывов или перенастройки технологического процесса – дигрессивное поведение затрат.
Серийное производство требует четкой координации объема производства, серии и последовательности изготовления товаров. Потребности в разных товарах должны исполняться предприятием без задержек.
Каковы варианты удовлетворения годовой потребности в товаре?
У бизнесмена есть несколько вариантов насыщения потребности в товаре в течение года:
1) Единственная партия равная объему годовой потребности:
увеличение пропорциональных серийных затрат, а именно расходов по складу и процентов на имущество;
единичные расходы на перенастройку;
низкий уровень постоянных серийных затрат;
вероятность не насыщения потребностей по другим видам товаров.
2) Некоторое количество партий, насыщающих годовую потребность:
уменьшение складских расходов и расходов на имущество;
увеличение расходов на перенастройку.
Итак, главная задача – поиск наиболее эффективного размера партии, при котором единица произведенного товара будет приносить минимальные постоянные и пропорциональные серийные затраты.
Какие расходы являются основными при серийном производстве?
При серийном изготовлении товаров на предприятии появляются расходы, нуждающиеся в более полном рассмотрении:
A) Расходы по складу:
складские расходы – заработная плата, расходы на поддержание функциональности складских площадей;
калькуляционные проценты – это расходы коррелирующие с объемами хранящегося на складе имущества.
Обе позиции могут быть снижены путем спланированного сокращения объема товаров на сладе. Нижний предел в данном случае – это страховой запас.
Уменьшение складских расходов и калькуляционных процентов вызывает противодействие со стороны увеличивающихся расходов на перенастройку технологического процесса и вероятности не насыщения потребности в определённом виде товаров. Выход из этой ситуации – поиск оптимального размера партии.
Б) Расходы на перенастройку:
зависят от продолжительности процесса перенастройки;
не зависят от размера партии;
в пересчете на единицу товара уменьшаются с увеличением размера партии;
состоят из: 1) затрат простоя; 2) затрат на необходимые технические средства и оборудование; 3) заработной платы; 4) вспомогательных расходов.
Этапы нахождения оптимального размера партии
Чтобы найти наиболее приемлемый вариант размера партии нужно:
1. Найти количество партий:
где n – количество партий, M – годовой объем реализуемого товара, m –наиболее приемлимый размер партии, произведенный без перерыва либо перенастройки технологического процесса.
2. Вычислить постоянные серийные затраты всех серий:
где KF– общие постоянные затраты на перенастройку всех серий, Kf– серийные затраты для одной партии.
3. Рассчитать размер суммарных складских расходов (склад и проценты):
где KL– размер суммарных складских расходов, Kl– ставка расходов по складу и калькуляционных процентов в пересчёте на единицу товара за период.
4. Определить суммарные затраты (K):
5. Минимизация суммарных затрат приводит нас к функции:
6. Наиболее приемлемый размер партии (m) находится при сведении уравнения к дифференциальному виду:
7. Постановка условия
8. Решение уравнения относительно m
Рассмотри на примере. Прогнозируемая реализация в будущем году составит 400 000 единиц товара T. Размер постоянных серийных затрат достигает 6 000 ДМ. Расходы по складу равны 20 ДМ на единицу товара за год. Вычислим наиболее приемлемый вариант размера партии.
Итак, минимизация затрат будет достигнута при размере партии в 15 491 шт. товара.
Есть ли допущения в формуле расчета оптимального размера партии?
Допущения в формуле расчета наиболее приемлемого размера партии:
бесконечность скорости процесса производства;
постоянность скорости реализации;
не учитывались складских потерь;
неизменность постоянных серийных затрат;
прямо пропорциональное изменение прочих расходов по производству;
не учитывались ограничение по складским площадям.
Является ли расчет оптимального размера партии целесообразным на сегодняшний день?
Не стоит отказываться от расчета оптимального размера партии под предлогом чрезмерного расходования трудовых ресурсов. Конечно, нет необходимости определять оптимальный размер партии для каждого вида продукции, но для А и B товаров эти расчёты необходимы.
Для начала производится расчет оптимального размера партии для A-товаров, составляющих 5 процентов от объема всей продукции, но дающих около 75 процентов в переводе на доходность. Улучшение планирования и регулировки производства А-товаров приведет к значительному уменьшению затрат.
Внедрение оптимизации размера партии в сочетании с ABC-анализом значительно уменьшит производственные расходы. Этот эффект будет более значимым при повышении эффективность и снижении расходов склада.
Широкое распространение и активное использование персональных компьютеров облегчает задачи по поиску оптимального размера партии.
Размер партии – это величина последовательно произведенного товара без перерывов либо переключений в технологическом процессе.
В чем значимость определения оптимального размера партии?
Оптимальный размер партии приводит к уменьшению потерь по складу, процентов на имущество, расходов по перенастройке. Следовательно, разделение объема товаров, производимого за год, на доли приводит к значительному снижению расходов.
Наилучшему размеру партии для производителя противодействует выгодный размер партии для реализации. Расходы по перенастройке становятся при данном варианте расходами по регистрации заказа.
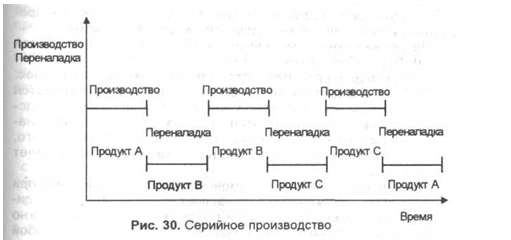
В чем заключается особенность серийного производства?
Серийное производство оптимально для групп товаров сходных по технологическим процессам при изготовлении. Спустя некоторое время возникает необходимость в перенастройке к выпуску иного товара. Вышеприведенный рисунок демонстрирует, что продукция А, В, С производится последовательно на одной технологической линии.
Перерыв в технологическом процессе для пуска в производство нового товара приводит к простою и появлению не связанных с размером партии расходов – постоянные серийные затраты. Это расходы на перенастройку и наладку производственных мощностей.
При увеличении размера партии увеличиваются и постоянные серийные затраты. В пересчете на единицу продукции эти расходы сокращаются при увеличении размера партии, производимой без перерывов или перенастройки технологического процесса – дигрессивное поведение затрат.
Серийное производство требует четкой координации объема производства, серии и последовательности изготовления товаров. Потребности в разных товарах должны исполняться предприятием без задержек.
Каковы варианты удовлетворения годовой потребности в товаре?
У бизнесмена есть несколько вариантов насыщения потребности в товаре в течение года:
1) Единственная партия равная объему годовой потребности:
- увеличение пропорциональных серийных затрат, а именно расходов по складу и процентов на имущество;
- единичные расходы на перенастройку;
- низкий уровень постоянных серийных затрат;
- вероятность не насыщения потребностей по другим видам товаров.
2) Некоторое количество партий, насыщающих годовую потребность:
- уменьшение складских расходов и расходов на имущество;
- увеличение расходов на перенастройку.
Итак, главная задача – поиск наиболее эффективного размера партии, при котором единица произведенного товара будет приносить минимальные постоянные и пропорциональные серийные затраты.
Какие расходы являются основными при серийном производстве?
При серийном изготовлении товаров на предприятии появляются расходы, нуждающиеся в более полном рассмотрении:
A) Расходы по складу:
- складские расходы – заработная плата, расходы на поддержание функциональности складских площадей;
- калькуляционные проценты – это расходы коррелирующие с объемами хранящегося на складе имущества.
Обе позиции могут быть снижены путем спланированного сокращения объема товаров на сладе. Нижний предел в данном случае – это страховой запас.
Уменьшение складских расходов и калькуляционных процентов вызывает противодействие со стороны увеличивающихся расходов на перенастройку технологического процесса и вероятности не насыщения потребности в определённом виде товаров. Выход из этой ситуации – поиск оптимального размера партии.
Б) Расходы на перенастройку:
- зависят от продолжительности процесса перенастройки;
- не зависят от размера партии;
- в пересчете на единицу товара уменьшаются с увеличением размера партии;
- состоят из: 1) затрат простоя; 2) затрат на необходимые технические средства и оборудование; 3) заработной платы; 4) вспомогательных расходов.
Этапы нахождения оптимального размера партии
Чтобы найти наиболее приемлемый вариант размера партии нужно:
1. Найти количество партий:
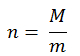
где n – количество партий, M – годовой объем реализуемого товара, m –наиболее приемлимый размер партии, произведенный без перерыва либо перенастройки технологического процесса.
2. Вычислить постоянные серийные затраты всех серий:
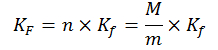
где KF– общие постоянные затраты на перенастройку всех серий, Kf– серийные затраты для одной партии.
3. Рассчитать размер суммарных складских расходов (склад и проценты):
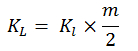
где KL– размер суммарных складских расходов, Kl– ставка расходов по складу и калькуляционных процентов в пересчёте на единицу товара за период.
4. Определить суммарные затраты (K):
![]()
5. Минимизация суммарных затрат приводит нас к функции:
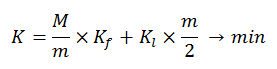
6. Наиболее приемлемый размер партии (m) находится при сведении уравнения к дифференциальному виду:
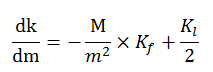
7. Постановка условия
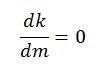
8. Решение уравнения относительно m
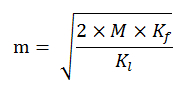
Рассмотри на примере. Прогнозируемая реализация в будущем году составит 400 000 единиц товара T. Размер постоянных серийных затрат достигает 6 000 ДМ. Расходы по складу равны 20 ДМ на единицу товара за год. Вычислим наиболее приемлемый вариант размера партии.

Итак, минимизация затрат будет достигнута при размере партии в 15 491 шт. товара.
Есть ли допущения в формуле расчета оптимального размера партии?
Допущения в формуле расчета наиболее приемлемого размера партии:
- бесконечность скорости процесса производства;
- постоянность скорости реализации;
- не учитывались складских потерь;
- неизменность постоянных серийных затрат;
- прямо пропорциональное изменение прочих расходов по производству;
- не учитывались ограничение по складским площадям.
Является ли расчет оптимального размера партии целесообразным на сегодняшний день?
Не стоит отказываться от расчета оптимального размера партии под предлогом чрезмерного расходования трудовых ресурсов. Конечно, нет необходимости определять оптимальный размер партии для каждого вида продукции, но для А и B товаров эти расчёты необходимы.
Для начала производится расчет оптимального размера партии для A-товаров, составляющих 5 процентов от объема всей продукции, но дающих около 75 процентов в переводе на доходность. Улучшение планирования и регулировки производства А-товаров приведет к значительному уменьшению затрат.
Внедрение оптимизации размера партии в сочетании с ABC-анализом значительно уменьшит производственные расходы. Этот эффект будет более значимым при повышении эффективность и снижении расходов склада.
Широкое распространение и активное использование персональных компьютеров облегчает задачи по поиску оптимального размера партии.
Определение оптимального размера партии
Дмитрий Езепов, менеджер по закупкам компании «Мидвест» © ЛОГИСТИК&система www.logistpro.ru
Одной из самых трудных задач для любого менеджера по закупкам является подбор оптимального размера заказа. Однако реальных инструментов, облегчающих ее решение, очень мало. Конечно, есть формула Вильсона, которая в теоретической литературе преподносится в качестве такого инструмента, но на практике ее использование необходимо корректировать
Автор этой статьи, работая в нескольких крупных торговых фирмах в Минске, нигде не видел, чтобы формула Вильсона применялась на практике. Ее отсутствие в арсенале менеджеров по закупкам никак нельзя объяснить недостатком у них аналитических навыков и умений, так как современные компании уделяют большое внимание квалификации своих сотрудников.
Попробуем выяснить, почему «наиболее распространенный инструмент в управлении запасами» не выходит за рамки научных публикаций и учебников. Ниже представлена известная формула Вильсона, с помощью которой рекомендуется рассчитывать экономичный объем заказа:
![]()
где Q – объем партии закупки;
S – потребность в материалах или готовой продукции за отчетный период;
О – постоянные затраты, связанные с выполнением одного заказа;
С – затраты на хранение единицы запасов за отчетный период.
Суть данной формулы сводится к тому, чтобы рассчитать, какие должны быть размеры партий (все одинаковые), чтобы доставить заданный объем товаров (то есть общую потребность на отчетный период) в течение данного периода. При этом сумма постоянных и переменных издержек должна быть минимальной.
В решаемой задаче есть по крайней мере четыре начальных условия: 1) заданный объем, который требуется доставить до пункта назначения; 2) заданный период; 3) одинаковые размеры партий; 4) заранее утвержденный состав постоянных и переменных затрат. Такая постановка задачи имеет мало общего с реальными условиями ведения бизнеса. Емкость и динамику рынка заранее не знает никто, поэтому размеры заказываемых партий всегда будут разными. Задавать период для планирования закупок тоже нет смысла, так как коммерческие компании обычно существуют значительно дольше отчетного периода. Состав затрат также подвержен изменениям из-за влияния многих факторов.
Другими словами, условия применения формулы Вильсона в реальности просто не существуют или по крайней мере встречаются очень редко. Нужно ли коммерческим компаниям решение задачи с такими исходными условиями? Думается, что нет. Именно поэтому «распространенный инструмент» реализуется только на бумаге.
МЕНЯЕМ УСЛОВИЯ
В рыночных условиях активность продаж непостоянна, что неизбежно влияет на процесс снабжения. Поэтому как частота, так и размеры закупаемых партий никогда не совпадают с их плановыми показателями в начале отчетного периода. Если же ориентироваться исключительно на план или долгосрочный прогноз (как в формуле Вильсона), то неизбежно возникнет одна из двух ситуаций: либо переполнение склада, либо дефицит продукции. Результатом и того, и другого всегда будет уменьшение чистой прибыли. В первом случае – из-за увеличения расходов на хранение, во втором – из-за дефицита. Поэтому формула расчета оптимального размера заказа должна быть гибкой по отношению к ситуации на рынке, то есть опираться на максимально точный краткосрочный прогноз продаж.
Общие затраты на закупку и хранение запасов состоят из суммы этих же затрат для каждой закупаемой партии. Следовательно, минимизация стоимости доставки и хранения каждой партии в отдельности ведет к минимизации процесса снабжения в целом. А так как расчет объема каждой партии требует именно краткосрочного прогноза продаж (а не на весь отчетный период), то необходимое условие гибкости формулы расчета оптимального размера партии (ОРП) по отношению к ситуации на рынке выполняется. Такое условие задачи соответствует как цели коммерческой фирмы (минимизация затрат), так и реальным условиям ведения бизнеса (изменчивость конъюнктуры рынка). Определения постоянных и переменных затрат для подхода минимизации поставок с точки зрения каждой партии в отдельности приведены во врезке «Виды затрат» на стр. 28.
СОБСТВЕННО РАСЧЕТ
Если допустить, что кредит погашается по мере уменьшения стоимости запасов через плановые промежутки времени (дни, недели, месяц и др.)(1), то, используя формулу суммы членов арифметической прогрессии, можно рассчитать общую стоимость хранения одной партии запасов (плату за пользование кредитом):
![]()
где K – расходы на хранение запасов;
Q – объем партии закупки;
p – цена закупки единицы товара;
t – время нахождения запаса на складе, которое зависит от краткосрочного прогноза интенсивности продаж;
r – процентная ставка в плановую единицу времени (день, неделя и др.).
Таким образом, общие затраты на доставку и хранение партии заказа составят:
![]()
где Z – общие затраты на доставку и хранение партии.
Минимизировать абсолютную величину стоимости доставки и хранения одной партии нет смысла, так как дешевле было бы просто отказаться от закупок, поэтому следует перейти к относительному показателю затрат на единицу запаса:

где z – стоимость пополнения и хранения единицы запаса.
Виды затрат
Постоянные затраты остаются затратами, которые фирма несет независимо от объема партии. Обозначим их как R (от англ. replenishment – пополнение). Переменные затраты К (от англ. keep – держать) – это затраты на хранение партии. Они зависят не только от стоимости хранимых запасов, но и от времени их нахождения на складе (t). Время t обычно измеряется в каких-либо плановых единицах: днях, неделях, месяцах и др. Для простоты в качестве стоимости хранения запасов возьмем процентную ставку за пользование кредитом (r) в такую же плановую единицу времени, в которой измеряется время t.
Если закупки осуществляются часто, то период продаж для одной партии получается небольшой, и интенсивность продаж в течение этого времени будет относительно постоянной2. Исходя из этого время нахождения запаса на складе рассчитывают как:
![]()
где ![]() – краткосрочный прогноз средних продаж за плановую единицу времени (день, неделю, месяц и др.).
– краткосрочный прогноз средних продаж за плановую единицу времени (день, неделю, месяц и др.).
Обозначение ![]() не случайно, так как в качестве прогноза обычно выступают средние продажи в прошлом с учетом различных корректировок (дефицит на складе в прошлом, наличие тенденции и др.).
не случайно, так как в качестве прогноза обычно выступают средние продажи в прошлом с учетом различных корректировок (дефицит на складе в прошлом, наличие тенденции и др.).
Таким образом, подставляя формулу (5) в формулу (4), получим целевую функцию минимизации стоимости доставки и хранения единицы запаса:
![]()
Приравнивая первую производную к нулю:
![]()
находим оптимальный размер партии (ОРП) с учетом краткосрочного прогноза продаж:
![]()
НОВАЯ ФОРМУЛА ВИЛЬСОНА
Формально с математической точки зрения формула (8) – та же формула Вильсона (числитель и знаменатель разделены на одну и ту же величину в зависимости от принятой плановой единицы времени). И если интенсивность продаж не будет меняться, скажем, в течение года, то, заменив ![]() годовой потребностью в товаре и r – годовой процентной ставкой, мы получим результат, который будет идентичен расчету ЭОЗ. Однако с функциональной точки зрения формула (8) демонстрирует совершенно иной подход к решаемой задаче. В ней учитывается оперативный прогноз продаж, что делает расчет гибким относительно ситуации на рынке. Остальные параметры формулы ОРП в случае необходимости могут оперативно корректироваться, что также является неоспоримым преимуществом перед классической формулой расчета ЭОЗ.
годовой потребностью в товаре и r – годовой процентной ставкой, мы получим результат, который будет идентичен расчету ЭОЗ. Однако с функциональной точки зрения формула (8) демонстрирует совершенно иной подход к решаемой задаче. В ней учитывается оперативный прогноз продаж, что делает расчет гибким относительно ситуации на рынке. Остальные параметры формулы ОРП в случае необходимости могут оперативно корректироваться, что также является неоспоримым преимуществом перед классической формулой расчета ЭОЗ.
На политику закупок компании влияют и другие, часто более значимые факторы, чем интенсивность продаж (текущие остатки на собственном складе предприятия, минимальный размер партии, условия доставки и др.). Поэтому, несмотря на то что в предлагаемой формуле устранена основная преграда для расчета оптимального размера заказа, ее использование может быть лишь вспомогательным инструментом эффективного управления запасами.
Высокопрофессиональный менеджер по закупкам опирается на целую систему статистических показателей, в которой формула ОРП играет существенную, но далеко не решающую роль. Однако описание такой системы показателей эффективного управления запасами является отдельной темой, которую мы будем освещать уже в следующих номерах журнала •
1- В реальности так не происходит, поэтому стоимость хранения запасов будет выше. 2- В реальности нужно обращать внимание не на частоту заказа, а на стабильность продаж в рамках краткосрочного периода прогноза продаж. Просто обычно, чем меньше период, тем меньше проявляется сезонность и тенденция.
Ольга Владиславовна Алёхина
Эксперт по предмету «Логистика»
Задать вопрос автору статьи
Определение 1
Управление запасами – это логистическая функция, которая заключается в определении оптимального количества товарно-материальных ценностей, находящихся на временном хранении в складских помещениях, и в принятии мер по его поддержанию на данном уровне.
Основы расчета параметров поставок
Для того чтобы предприятие бесперебойно и успешно функционировало в течение определенного периода, необходимо закупить конкретное количество материальных ресурсов данного вида. Эта необходимость базируется на существовании у хозяйственной системы предприятия потребностей, которые должны быть своевременно и правильно рассчитаны.
Процедура закупок необходимых предприятию товаров называется поставкой. Поставки играют важную роль в управлении запасами, поскольку они определяют количество, номенклатуру и частоту входящего потока системы запасов материальных ресурсов и готовой продукции.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Основными параметрами поставки являются величина и количество заказываемых партий. Эти параметры, как показывает современная практика, оказывает существенное влияние на размер логистических издержек предприятия.
Важнейшими параметрами поставки являются размер заказа и интервал времени между заказами. В связи с этим перед закупочной логистикой любого предприятия стоит задача по определению того размера заказа, который обеспечивает предприятию наименьшую сумму общих затрат на создание и поддержание запаса по данному виду материальных ресурсов.
Кроме того, особое место отводится форме поставок. Она характеризуются конкретным способом товародвижения и режимом реализации продукции. В настоящее время в сфере управления запасами наиболее известными являются складская и транзитная формы поставок. Они друг от друга отличаются наличием (использованием) складских помещений и, соответственно, временем хранения материалов.
В общем случае размер партии не определяет закупочную цену единицы материальных ресурсов. Отсюда следует, что размер заказа по большей части определяется следующими категориями логистических затрат:
«Управление запасами: расчет параметров поставок» 👇
- расходы, которые связаны с доставкой заказанной партии;
- расходы, которые связаны с управлением логистической системой в части размещения заказа, приемки поступивших материалов, оформления документов и т. д.;
- расходы, которые связаны с хранением среднего остатка материальных ресурсов на складе.
Первые две группы логистических затрат относительно размера партии считаются условно-постоянными затратами. Это означает отсутствие прямой зависимости между этими затратами и величиной заказа. Следовательно, эти логистические затраты могут быть объединены в одну группу и называться расходами, которые связаны с заказом.
Третья группа логистических затрат (расходы, которые связаны с хранением) возрастают прямо пропорционально увеличению размера заказа (и, соответственно, среднего запаса ресурсов). Это дает основание обозначать их как условно-переменные расходы по отношению к размеру заказа.
Общие логистические затраты предприятия на создание и содержание товарно-материальных запасов состоят из двух слагаемых. Первое слагаемое представлено произведением условно-постоянных расходов на количество заказов за определенный период времени. Второе слагаемое представлено произведением условно-переменных расходов на средний размер товарно-материального запаса предприятия.
Для того чтобы определить интервал времени между заказами, логисты предприятия умножают количество рабочих дней в периоде на размер запаса предприятия, а затем полученное значение делят на потребность предприятия в данном виде материальных ресурсов на этот период.
Определение оптимального размера заказываемой партии
Условно-постоянные логистические затраты с увеличением размера партии будут распределяться на большее количество изделий. Прямым следствием этого является снижение затрат данной категории в расчете на единицу изделия. Это важный фактор, который поможет определить оптимальный размер заказа, при котором обеспечивается минимальный уровень общих затрат.
В данном случае нужно принять во внимание, что количество заказов за определенный период времени равен отношению потребности предприятия в данном виде материальных ресурсов на этот период к размеру запаса. Тогда имеет смысл дифференцировать уравнение общих затрат на создание и содержание запасов относительно размера запаса и приравнять производную к нулю.
Тогда оптимальный размер заказываемой партии будет равен квадратному корню из удвоенного произведения условно-постоянных затрат на потребность предприятия в ресурсах, которое поделено на величину условно-переменных затрат. Этот метод сейчас известен в логистике как метод Уилсона, который впервые предложил эту формулу в 1934 году.
В реальных условиях хозяйствования размер заказа преимущественно определяют исходя из следующих факторов:
- вместимость тары;
- грузоподъемность транспортного средства;
- величина партии, которая установлена поставщиком во время отгрузки продукции.
В качестве фактора, который способен существенно ограничить оптимизацию объема поставок материальных ресурсов, зачастую выступает время доставки материала от поставщика. Для предприятия желательно организовать доставку материалов как можно скорее, однако в реальности этот процесс может занимать несколько дней и даже недель.
Таким образом, значительное место в управлении товарно-материальными запасами предприятия отводится расчету параметров поставок. Предприятию важно установить оптимальные размер заказа и интервал времени между заказами. Благодаря этому будут минимизированы финансовые издержки предприятия, вызванные порчей излишних запасов или недополученной прибылью вследствие отсутствия нужных товарных позиций.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме


