Как найти единственное решение системы уравнений

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #

учимся
программировать

Программированию нельзя научить, можно только научится

Главная » Уроки по Численным методам » Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений

Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений

Система линейных уравнений:

(1)

Здесь и (i =1..m, j=1..n) – заданные, а – неизвестные действительные числа.
Матричной записью системы линейных уравнений называется выражение вида:
=, или кратко: = (2),
где:

=

=

столбец свободных членов

Упорядоченная совокупность n вещественных чисел (c1, c2. cn) называется решением системы(1), если в результате подстановки этих чисел вместо соответствующих переменных x1, x2. xn каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c1, c2. cn)T такой, что AC = B.

СЛУ называется совместной, или разрешимой, если она имеет, по крайней мере, одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
Матрица
,
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.

Вопрос о совместности системы (1) решается следующей теоремой.

Теорема Кронекера-Капелли

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.

Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Пример. Исследовать систему линейных уравнений

Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем
.
Ранг матрицы системы =3, так как матрица имеет три ненулевых строки,
а ранг расширенной матрицы =4.
Тогда согласно теореме Кронекера-Капелли система не имеет решений.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, – так называемые системы крамеровского типа:
a11 x1 + a12 x2 +. + a1n xn = b1,
a21 x1 + a22 x2 +. + a2n xn = b2, (3)
. . . . . .
an1 x1 + an1 x2 +. + ann xn = bn.

Системы (3) решаются одним из следующих способов:
1) методом Гаусса, или методом исключения неизвестных;
2) по формулам Крамера;
3) матричным методом.

Матричный метод

Если матрица А системы линейных уравнений невырожденная, т.е. det A=0, то матрица А имеет обратную, и решение системы (3) совпадает с вектором . Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.

Задание 1: Решить систему уравнений матричным способом в Excel

Ход решения:

1. Сначала надо записать систему в матричном виде и ввести ее на лист Excel:

, здесь ,

1. Затем надо с помощью Excel найти обратную матрицу для матрицы А.
2. Далее полученную матрицу нужно умножить на матрицу В.
3. В результате получим ответ:

Задание 2: Самостоятельно решить матричным способом систему уравнений

Ответ для самопроверки:

Урок по теме “Решение систем линейных уравнений, содержащих параметры”

Разделы: Математика

Если в задаче меньше трех переменных, это не задача; если больше восьми – она неразрешима. Энон.

Задачи с параметрами встречаются во всех вариантах ЕГЭ, поскольку при их решении наиболее ярко выявляется, насколько глубоки и неформальны знания выпускника. Трудности, возникающие у учащихся при выполнении подобных заданий, вызваны не только относительной их сложностью, но и тем, что в учебных пособиях им уделяется недостаточно внимания. В вариантах КИМов по математике встречается два типа заданий с параметрами. Первый: «для каждого значения параметра решить уравнение, неравенство или систему». Второй: «найти все значения параметра, при каждом из которых решения неравенства, уравнения или системы удовлетворяют заданным условиям». Соответственно и ответы в задачах этих двух типов различаются по существу. В первом случае в ответе перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. Во втором – перечисляются все значения параметра, при которых выполнены условия задачи. Запись ответа является существенным этапом решения, очень важно не забыть отразить все этапы решения в ответе. На это необходимо обращать внимание учащихся.
В приложении к уроку приведен дополнительный материал по теме «Решение систем линейных уравнений с параметрами», который поможет при подготовке учащихся к итоговой аттестации.

• систематизация знаний учащихся;
• выработка умений применять графические представления при решении систем уравнений;
• формирование умения решать системы линейных уравнений, содержащих параметры;
• осуществление оперативного контроля и самоконтроля учащихся;
• развитие исследовательской и познавательной деятельности школьников, умения оценивать полученные результаты.

Урок рассчитан на два учебных часа.

Ход урока

1. Организационный момент

Сообщение темы, целей и задач урока.

1. Актуализация опорных знаний учащихся

Проверка домашней работы. В качестве домашнего задания учащимся было предложено решить каждую из трех систем линейных уравнений

а) б) в)

графически и аналитически; сделать вывод о количестве полученных решений для каждого случая

Ответы:

Заслушиваются и анализируются выводы, сделанные учащимися. Результаты работы под руководством учителя в краткой форме оформляются в тетрадях.

В общем виде систему двух линейных уравнений с двумя неизвестными можно представить в виде: .

Решить данную систему уравнений графически – значит найти координаты точек пересечения графиков данных уравнений или доказать, что таковых нет. Графиком каждого уравнения этой системы на плоскости является некоторая прямая.

Возможны три случая взаимного расположения двух прямых на плоскости:

1. если (если хотя бы один из знаменателей равен нулю, последнее неравенство надо понимать как ), то прямые пересекаются в одной точке; в этом случае система имеет единственное решение

1. если то прямые не имеют общих точек, т.е. не пересекаются; а значит, система решений не имеет

1. если то прямые совпадают. В этом случае система имеет бесконечно много решений

К каждому случаю полезно выполнить рисунок.

Сегодня на уроке мы научимся решать системы линейных уравнений, содержащие параметры. Параметром будем называть независимую переменную, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству. Решить систему уравнений с параметром – значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество решений системы.

Решение задачи с параметром зависит от вопроса, поставленного в ней. Если нужно просто решить систему уравнений при различных значениях параметра или исследовать ее, то необходимо дать обоснованный ответ для любого значения параметра или для значения параметра, принадлежащего заранее оговоренному в задаче множеству. Если же необходимо найти значения параметра, удовлетворяющие определенным условиям, то полного исследования не требуется, и решение системы ограничивается нахождением именно этих конкретных значений параметра.

Пример 1. Для каждого значения параметра решим систему уравнений

1. Система имеет единственное решение, если

В этом случае имеем

1. Если а = 0, то система принимает вид

Система несовместна, т.е. решений не имеет.

1. Если то система запишется в виде

Очевидно, что в этом случае система имеет бесконечно много решений вида x = t; где t-любое действительное число.

• при система имеет единственное решение
• при а = 0 — нет решений;
• при а = 3 — бесконечно много решений вида где t R

Пример 2. При каких значениях параметра a система уравнений

• имеет единственное решение;
• имеет множество решений;
• не имеет решений?

• система имеет единственное решение, если
• подставим в пропорцию значение а = 1, получим , т.е. система имеет бесконечно много решений;
• при а = -1 пропорция примет вид: . В этом случае система не имеет решений.

• при система имеет единственное решение;
• при система имеет бесконечно много решений;
• при система не имеет решений.

Пример 3. Найдем сумму параметров a и b, при которых система

имеет бесчисленное множество решений.

Решение. Система имеет бесчисленное множество решений, если

То есть если a = 12, b = 36; a + b = 12 + 36 =48.

1. Закрепление изученного в ходе решения задач

1. № 15.24(а) [1]. Для каждого значения параметра решите систему уравнений

1. № 15.25(а) Для каждого значения параметра решите систему уравнений

1. При каких значениях параметра a система уравнений

а) не имеет решений; б) имеет бесконечно много решений.

Ответ: при а = 2 решений нет, при а = -2 бесконечное множество решений

1. Практическая работа в группах

Класс разбивается на группы по 4-5 человек. В каждую группу входят учащиеся с разным уровнем математической подготовки. Каждая группа получает карточку с заданием. Можно предложить всем группам решить одну систему уравнений, а решение оформить. Группа, первой верно выполнившая задание, представляет свое решение; остальные сдают решение учителю.

Карточка. Решите систему линейных уравнений

при всех значениях параметра а.

Ответ: при система имеет единственное решение ; при нет решений; при а = -1бесконечно много решений вида , (t; 1- t) где t R

Если класс сильный, группам могут быть предложены разные системы уравнений, перечень которых находится в Приложении1. Тогда каждая группа представляет классу свое решение.

Отчет группы, первой верно выполнившей задание

Участники озвучивают и поясняют свой вариант решения и отвечают на вопросы, возникшие у представителей остальных групп.

1. При каком значении k система имеет бесконечно много решений?
2. При каком значении p система не имеет решений?

1. При каком значении k система имеет бесконечно много решений?
2. При каком значении p система не имеет решений?

1. Итоги урока

Решение систем линейных уравнений с параметрами можно сравнить с исследованием, которое включает в себя три основных условия. Учитель предлагает учащимся их сформулировать.

При решении следует помнить:

1. для того, чтобы система имела единственное решение, нужно, чтобы прямые, отвечающие уравнению системы, пересекались, т.е. необходимо выполнение условия;
2. чтобы не имела решений, нужно, чтобы прямые были параллельны, т.е. выполнялось условие,
3. и, наконец, чтобы система имела бесконечно много решений, прямые должны совпадать, т.е. выполнялось условие.

Учитель оценивает работу на уроке класса в целом и выставляет отметки за урок отдельным учащимся. После проверки самостоятельной работы оценку за урок получит каждый ученик.

При каких значениях параметра b система уравнений

• имеет бесконечно много решений;
• не имеет решений?

Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.

• Найдите b и k,
• найдите координаты точки пересечения этих графиков.

Решите систему уравнений при всех значениях m и n.

Решите систему линейных уравнений при всех значениях параметра а (любую на выбор).

1. Алгебра и начала математического анализа: учеб. для 11 кл. общеобразоват. учреждений : базовый и профил. уровни / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин – М. : Просвещение, 2008.
2. Математика : 9 класс : Подготовка к государственной итоговой аттестации / М. Н. Корчагина, В. В. Корчагин – М. : Эксмо, 2008.
3. Готовимся в вуз. Математика. Часть 2. Учебное пособие для подготовки к ЕГЭ, участию в централизованном тестировании и сдаче вступительных испытаний в КубГТУ / Кубан. гос. технол. ун-т; Ин-т совр. технол. и экон.; Сост.: С. Н. Горшкова, Л. М. Данович, Н.А. Наумова, А.В. Мартыненко, И.А. Пальщикова. – Краснодар, 2006.
4. Сборник задач по математике для подготовительных курсов ТУСУР: Учебное пособие / З. М. Гольдштейн, Г. А. Корниевская, Г. А. Коротченко, С.Н. Кудинова. – Томск: Томск. Гос. ун-т систем управления и радиоэлектроники, 1998.
5. Математика: интенсивный курс подготовки к экзамену/ О. Ю. Черкасов, А.Г.Якушев. – М.: Рольф, Айрис-пресс, 1998.

Когда система уравнений имеет единственное решение

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

[spoiler title=”источники:”]

http://urok.1sept.ru/articles/522505

http://toehelp.ru/theory/math/lecture14/lecture14.html

[/spoiler]

1. Системы линейных уравнений с параметром

Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а² – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1 способ. Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а₁ = b/b₁ ≠ c/c₁). Тогда имеем:

1/1 = (а² – 3)/1 ≠ а/2 или систему

{а² – 3 = 1,
{а ≠ 2.

Из первого уравнения а² = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ. Решаем методом подстановки.

{2 – у + (а² – 3)у = а,
{х = 2 – у,

или

{(а² – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а² – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а² – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а₁ = b/b₁ = c/c₁). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а < 4) или ни одного (при а > 4).

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х² = 1.

Решение.

Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1). Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а: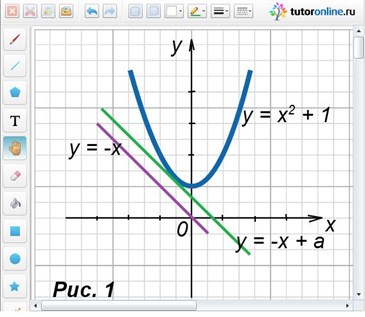

1,25 = 0,5 + а;

а = 0,75.

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а²х – а² – а + 2ах – 2а – 2 = 2;

а²х + 3ах = 2 + а² + 3а + 2.

Квадратный трехчлен а² + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а² + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а² + 3а не должно быть равным нулю, поэтому,

а² + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.

{х² + у² = 9,
{у – |х| = а.

Решение.

Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы

х² + у² = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.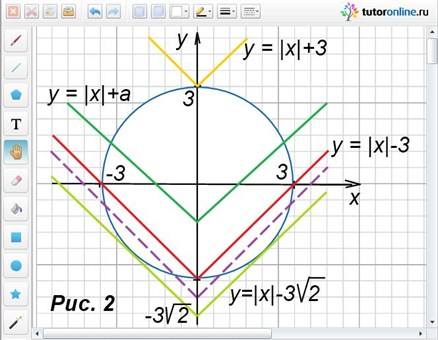

Ответ: а = 3.

 Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.