Конденсаторы часто применяются в электрических схемах, помогая трансформировать электросигнал под определенные характеристики. Используя их основное свойство — накапливать электрический заряд, можно регулировать прохождение тока по цепи, убирать нежелательные пульсации напряжения или повысить энергоэффективность сети. При решении подобных задач в расчет берутся конкретные параметры того или иного электронакопителя, а также общие процессы, связанные с зарядом и разрядом конденсаторов.
- Заряд конденсатора
- Процессы зарядки и разрядки конденсаторов
- Емкость и энергия конденсатора
- Как зарядить конденсатор
- Время, необходимое для зарядки конденсатора
- Заряд конденсатора: формула
- Время разряда конденсатора
Заряд конденсатора
Устройство обычного конденсатора состоит из двух пластин (обкладок), подключаемых к выходам цепи, и диэлектрика между ними. При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.
Емкость конденсатора определяется по формуле:
C = S • ε • ε0 / d,
где S – площадь обкладок, ε — диэлектрическая проницаемость прокладки, ε0 — диэлектрическая постоянная (8,85•10-12 Ф/м), d – расстояние между пластинами.
Конденсируемый же заряд равняется произведению емкости конденсатора на напряжение в цепи: q = С × U.
Процессы зарядки и разрядки конденсаторов
При включении конденсатора в цепь через него начинает проходить ток. С движением электронов по проводнику на одной обкладке устройства скапливается отрицательный заряд, а на другой (при недостатке электронов) — положительный. Между пластинами образуется индуктивное поле, создающее разность потенциалов определенного значения. В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.
Когда цепь размыкается и на конденсатор не подается напряжение, он может сохранять заряд на протяжение определенного времени, а затем с исчезновением электрического поля между пластинами заряд начнет перетекать в проводник. Процесс разряда конденсатора характеризуется переходом электронов с одной обкладки на другую. Конденсатор разряжается полностью, когда количество свободных электронов на обеих пластинах сравнивается. При этом все электродинамические процессы в цепи прекращаются.
Емкость и энергия конденсатора
Конденсатор, как и всякий объект, получающий электрический заряд, обладает энергией. Для его зарядки требуется определенная работа, которая идет на разделение заряженных частиц — именно она считается энергией конденсаторного устройства. Ее можно увидеть, если заряженный конденсатор присоединить, например, к светодиоду. Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.
Для определения энергии конденсатора в расчет берут количество заряда, толщину диэлектрика и напряженность электрического поля. Последняя является векторной величиной и представляет собой силу, действующую на точечный заряд.
Поскольку заряды на обкладках равны между собой по модулю, во внимание принимается только значение напряженности одной из них, а значит, эта величина делится пополам — Е/2. Общая же энергия определяется по формуле:
Wp = qEd/2.
Произведение напряженности на расстояние между пластинами само себе представляет разность потенциалов или напряжение — U = E × d. Таким образом, энергию можно выразить через заряд и напряжение на конденсаторе. Формула будет иметь следующий вид:
Wp = qU/2.
Учитывая, что заряд и напряжение находятся в зависимости от емкости конденсатора, можно вывести еще пару формул энергии:
Wp = q2/2C
Wp = CU2/2
Как зарядить конденсатор
Для зарядки конденсатора требуется генератор электротока. Возникающие при этом процессы удобнее разобрать на примере простой цепи, включающей в себя конденсатор (С) и резистор (R).
Зарядка конденсатора от источника постоянной ЭДС
В соответствии с законом Ома разность потенциалов, возникающая на резисторе и конденсаторе, суммарно равна электродвижущей силе генератора тока. Математически это можно представить следующими формулами:
UC = q/C – напряжение конденсатора;
UR = IR – напряжение резистора;
ε = UC + UR – ЭДС источника.
Для пояснения зарядного процесса определим равенство
IR = ε – q / C.
Эта формула представляет динамические изменения заряда силы тока. Более конкретно это может быть выражено уравнением:
I = dq / dt.
Изменение заряда во времени можно подставить к сопротивлению. Соответственно, получаем
R • dq / dt = ε – q / C.
В строгом смысле это уравнение предписывает бесконечное время зарядки конденсаторного устройства. Однако этим можно пренебречь, если учесть, что заряд фактически дискретен и может быть подвержен случайным изменением и флуктуациям. Таким образом, в данном выражении имеются в виду усредненная динамика зарядного процесса. На его основании можно записать изменение ЭДС и составляющих напряжений обоих элементов цепи:
dε = d(IR) + d(q/C).
Фактически ЭДС генератора не меняется во времени, а значит, dε = 0, а емкость конденсатора и сопротивление обладают постоянными значениями, поэтому их можно обозначить без d:
R • dI = — 1/C • dq.
Поделив данное уравнение на временной период, за который заряжается конденсатор, можно вывести выражение, учитывающее корреляцию между динамикой заряда и силой тока:
dI / dt = –I/RC.
Это уравнение означает отношение скорости, с которой уменьшается сила тока к ее фактическому значению.
В начале процесса заряда конденсатора значение q равняется нулю. В этот момент при наибольшей разнице напряжений источника питания и электронакопителя сила тока имеет максимальное значение. По мере увеличения заряда значение I постепенно падает. Когда конденсатор заряжается полностью, его напряжение сравнивается с ЭДС генератора, а сила тока принимает значение 0. Соответственно, электродинамический процесс прекращается.
Дополнительно можно рассмотреть, как в процессе зарядки трансформируется энергия. Вполне очевидно, что генератор тока является причиной возникновения электротока в цепи и, следовательно, заряда электронакопителя.
В этом усматривается некое противоречие: когда конденсатор получает от генератора тока заряд q, это значит, что ЭДС выполнила работу равную заряду (А = qe), однако энергия самого накопителя определяется по формуле W = q2 / 2C = qε / 2, что составляет только половину от работы, произведенной источником питания. Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.
Дифференциальные расчеты для малых отрезков времени процесса зарядки показывают, что энергия от генератора, действительно, разделяется на электрическую, идущую на заряд конденсаторного устройства, и тепловую. При этом сопротивление цепи само по себе никак не влияет на количество выделяемой теплоты, которое равняется энергии конденсатора.
Заряд конденсатора, ток
При подключении конденсатора к источнику тока в начале зарядки заряд на пластинах практически отсутствует. Максимальное значение I в этой ситуации объясняется минимальным сопротивлением. С увеличением заряженных частиц, возрастает сопротивление индуктивного поля, которое препятствует прохождению тока по проводнику.
Период времени, за начальную точку которого берут момент наибольшей силы тока, а за конечную полное прекращение движения заряженных частиц, носит название переходного периода зарядки конденсатора.
Начальный момент зарядки конденсатора характеризуется нулевым напряжением между его пластинами. Показатель U начинает возрастать с появлением на обкладках разноименно заряженных частиц. Большая сила тока в начале процесса обусловливает большую скорость увеличения напряжения. По мере ее падения рост напряжения замедляется, достигнув максимального значения при полной зарядке электронакопителя.
График увеличения напряжения имеет вид параболы, будучи противоположным графику снижения силы тока.
Математически динамическую взаимозависимость тока, напряжения и емкости конденсатора можно выразить следующим образом:
I = С • dV / dt.
Время, необходимое для зарядки конденсатора
Время зарядки конденсатора определяется его емкостью, электродвижущей силой генератора тока, напряжением и сопротивлением в цепи.
Заряд конденсатора описывается как экспоненциальный процесс. Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:
τ = q / I0 = RC.
Зависимость динамики напряжения от длительности зарядки определяется по следующей формуле:
U(t) = UC • (1 – e-t/τ).
Значение высчитывается с привлечением основания натурального логарифма (е), которое относится к функции экспоненты и равняется приблизительно 2,718. При этом UC обозначает напряжение ЭДС источника.
Процент заряда по постоянной времени τ определяется в соответствии с формулой:
(1 — 1/еτ) • 100%.
Таким образом, конденсатор достигает почти полной зарядки за 5 τ.
• 1 τ — 63,2%;
• 2 τ — 86,5%
• 3 τ — 95,1%
• 4 τ — 98,2%
• 5 τ — 99,3%
Учитывая экспоненциальный характер увеличения напряжения конденсатора, можно сказать, что время его зарядки до уровня ЭДС генератора длится бесконечно долго.
Заряд конденсатора: формула
Конденсатор заряжается довольно быстро. Обычно для этого достаточно нескольких миллисекунд. Равенство напряжения электродвижущей силы источника питания и электронакопителя определяет максимальный заряд конденсатора. Формула заряда может быть определена с учетом общих параметров конденсатора:
q = Uεε0S/d.
Также можно принять во внимание конструкционные особенности конденсатора. Так, для цилиндрического накопителя заряд равняется:
q = U2πεε0l/ln(r2/r1),
где l – высота цилиндров, r2 – радиус наружной пластины, r1 — радиус внутренней пластины.
Время разряда конденсатора
Если конденсатор переключить на нагрузку резистора, он сам станет источником питания и будет отдавать заряд в цепь. Движение тока при этом начинается от пластины с отрицательным зарядом на положительно заряженную пластину и далее по контуру. Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:
IC = UC / R.
Отдавая заряд, конденсатор будет терять напряжение. Соответственно будет уменьшаться и сила тока. Снижение обоих показателей идет по экспоненциальной кривой с замедлением скорости падения. Это значит, что динамику разрядки конденсатора можно описать, как и в случае зарядки, при помощи постоянной времени τ.
Изменение основных электрических показателей при заряде и разряде конденсатора играют ключевую роль в электротехнике и радиоэлектронике. Эта функциональность в полной мере проявляется в цепях переменного тока, где оба процесса сменяют друг друга с определенной периодичностью. На частотно-зависимых качествах электронакопителей основан принцип действия таких электроустановок, как колебательные контуры, реле времени, цепи обратной связи, частотные фильтры и другие.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 3 чел.
Средний рейтинг: 5 из 5.
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
$F=k{|q_1|·|q_2|}/{r^2}$
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
То есть $1$ Кл$= 1А·с$.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
$k=9·10^9H·м^2$/$Кл^2$
Часто его записывают в виде $k={1}/{4πε_0}$, где $ε_0=8.85×10^{-12}Кл^2$/$H·м^2$ – электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
$C={q}/{φ}$
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
$C={q}/{U}={ε_{0}εS}/{d}$
где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_{0}$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора выражается формулами
$E_n={qU}/{2}={q^2}/{2C}={CU^2}/{2}$
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:
$ω={εε_{0}E^2}/{2}$
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Напряженность электрического поля
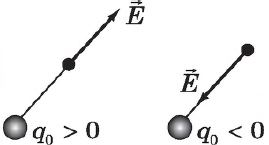
Напряженность электрического поля — векторная характеристика поля, сила, действующая на единичный покоящийся в данной системе отсчета электрический заряд.
Напряженность определяется по формуле:
$E↖{→}={F↖{→}}/{q}$
где $E↖{→}$ — напряженность поля; $F↖{→}$ — сила, действующая на помещенный в данную точку поля заряд $q$. Направление вектора $E↖{→}$ совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.
Единицей напряженности в СИ является вольт на метр (В/м).
Напряженность поля точечного заряда. Согласно закону Кулона, точечный заряд $q_0$ действует на другой заряд $q$ с силой, равной
$F=k{|q_0||q|}/{r^2}$
Модуль напряженности поля точечного заряда $q_0$ на расстоянии $r$ от него равен
$E={F}/{q}=k{|q_0|}/{r^2}$
Вектор напряженности в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд.
Силовые линии электрического поля
Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.
Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой в каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.
Линии напряженности положительно заряженного шарика;
Линии напряженности двух разноименно заряженных шариков;
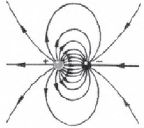
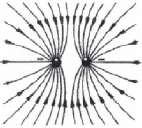
Линии напряженности двух одноименно заряженных шариков
Линии напряженности двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами.
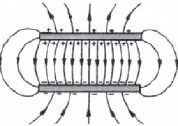
Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства однородно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.
В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересечение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.
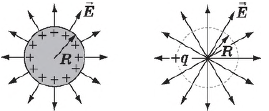
Поле заряженного шара. Напряженность поля заряженного проводящего шара на расстоянии от центра шара, превышающем его радиус $r≥R$, определяется по той же формуле, что и поля точечного заряда. Об этом свидетельствует распределение силовых линий, аналогичное распределению линий напряженности точечного заряда.
Заряд шара распределен равномерно по его поверхности. Внутри проводящего шара напряженность поля равна нулю.
Особенности формулы заряда q
Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.
Что такое электрический заряд q
Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.
Понятие из учебного пособия
Формула нахождения заряда
Определить искомую величину можно из физико-математической формулы силы тока. В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон.
Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.
Как вычислять с помощью законов
Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.
Закон сохранения
Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.
Закон Кулона
Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.
Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.
Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.
Образец решения задач по теме «Электрический заряд»
Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.
Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?
Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.
Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон. Задача состоит в определении первоначальных зарядов шаров.
Чтобы решить вторую задачу, нужно использовать ту же формулу Кулона, но немного видоизмененную: F=kq2/r2. Затем вывести из правила показатель q2. Он будет равен Fr2/k. Подставив известные значения и выполнив несложные расчеты, получится цифры в 10^-7 или 10 микрокулон.
В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.
Источник
Электрический заряд, напряжение, напряженность, потенциал
Любой физический объект в окружающем нас мире состоит из огромного количества элементарных частиц, обладающих зарядами. Элементарная частица протон имеет элементарный электрический заряд, которому приписывают (условно) положительный знак, элементарная частица электрон имеет элементарный отрицательный заряд.
Электрический заряд
Под электрическим зарядом понимают физическую величину, которая характеризует способность тел (объектов) вступать в электрическое взаимодействие. Электрический заряд обозначается через q (иногда для обозначения используют заглавную букву Q) и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].
Электрический заряд – дискретная величина, кратная элементарному электрическому заряду одного электрона (по модулю) e = 1,60217*10 -9 Кл.
С физической точки зрения 1 кулон [Кл] соответствует электрическому заряду, проходящему через поперечное сечение проводника при силе тока 1 Ампер за 1 секунду.
Заряды существуют в двух видах: положительные (+) и отрицательные (-). Одноименные заряды отталкиваются, а разноименные – притягиваются.
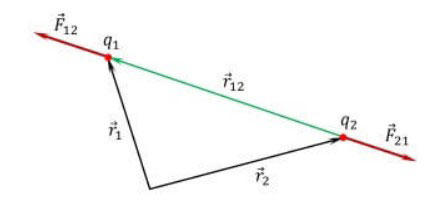
Сила взаимодействия зарядов направлена вдоль прямой, соединяющей их, пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними (рисунок 1).
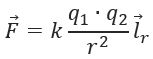
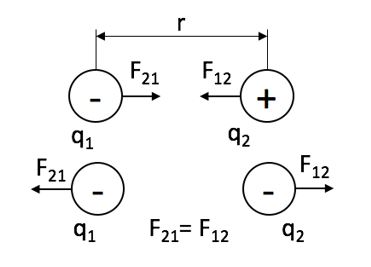Рис. 1. Сила взаимодействия зарядов
где k – коэффициент пропорциональности, зависящий от выбора системы единиц;
– единичный вектор, направленный вдоль прямой, соединяющей заряды q1 и q2.
Силу взаимодействия двух зарядов 
принято называть кулоновской силой в честь ученого-физика Шарля Кулона, обнаружевшего ее существование.
Если объект (система) не обменивается зарядами с окружающей средой, его называют электрически изолированным. В такой системе сумма электрических зарядов (положительных и отрицательных) не меняется со временем, то есть наблюдается закон сохранения заряда.
Большинство тел в природе электрически нейтральны, так как содержат заряды обоих типов в одинаковом количестве. Положительные и отрицательные заряды попарно нейтрализуют действие друг друга. Для перехода тела в заряженное состояние необходимо пространственно перераспределить в нем заряды, сконцентрировав одноименные заряды в одной области тела. Это возможно сделать, например, при помощи трения или взаимодействия с другим заряженным объектом (рисунок 2).
Рис. 2. Переход незаряженного объекта в заряженное состояние
Электрический заряд порождает в окружающем его пространстве непрерывную материю, называемую электрическим полем. Благодаря электрическому полю заряды имеют возможность взаимодействовать между собой. В электротехнике электрическое поле характеризуется двумя величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика).
Напряженность электрического поля
Напряженность электрического поля – это векторная физическая количественная характеристика электрического поля. Ее величина показывает силу, которая действует на пробный точечный единичный положительный заряд, помещенный в некоторую точку электрического поля.
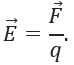
Под точечным зарядом понимают упрощенную модель положительного заряда, в которой его формой и размером можно пренебречь.
Вектор напряженности 
по направлению совпадает с вектором силы , с которой электрическое поле действует на положительный точечный заряд, помещенный в заданную точку поля (рисунок 3).
Рис. 3. Вектор напряженности E , созданной зарядом q, в точке А
Величина напряженности поля в точке А определяется согласно формуле
где r – расстояние от заряда q до точки А, k – коэффициент пропорциональности, зависящий от выбора системы единиц.
Электрическое поле графически изображается линиями напряженности электрического поля, которые условно принято обозначать исходящими из положительно заряженных элементов и входящими в отрицательно заряженные заряды (рисунок 4).
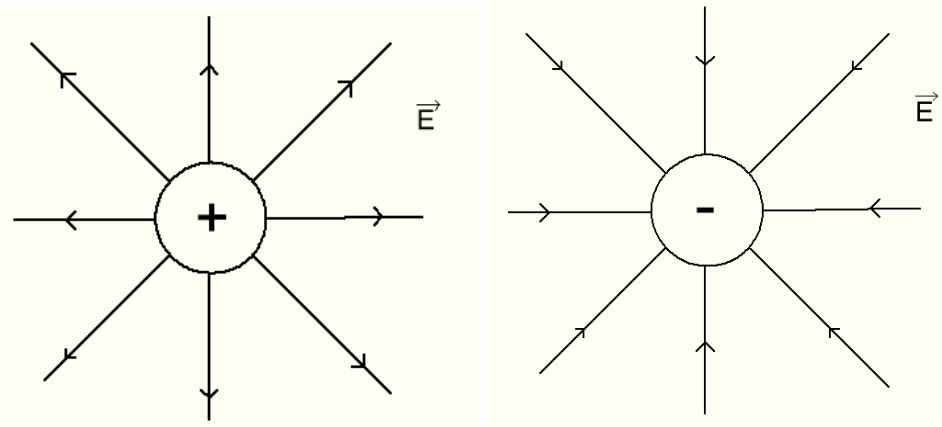а) изолированные заряды 
б) взаимодействующие заряды
Рис. 4. Распределение линий напряженности для изолированных (а) и взаимодействующих (б) зарядов
Потенциал, напряжение
Физическую величину, равную отношению потенциальной энергии W электрического заряда в электростатическом поле к величине самого заряда q, называют потенциалом φ электрического поля
Потенциал – это скалярная величина, которая показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку. Единицей измерения электрического потенциала является вольт, [В].
При этом важно отметить, что работа сил электростатического поля при перемещении заряда из одной точки электрического поля в другую не зависит от формы траектории перемещения, а зависит только от начального и конечного положения заряда, а также от его величины.
Если имеется некоторая система, состоящая из N точечных зарядов, то потенциал ее электрического поля φ будет равен алгебраической сумме потенциалов полей каждого входящего в него заряда, то есть
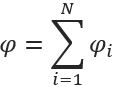
Напряжение электрического поля – это разность потенциалов между двумя точками этого поля (рисунок 5).
Напряжение (U) — это работа (А) совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.
U = A/q [Дж/Кл] или [В]
Рис. 5. Графическая интерпретация напряжения электрического поля
Напряжение является относительной величиной, то есть всегда определяется относительно некоторого уровня. Нулевой уровень выбирается произвольно и не влияет на итоговое значение напряжения, так как соответствует разности потенциалов в двух точках (то есть изменению потенциальной энергии). Для простоты расчетов в качестве нулевого уровня в большинстве случаев принимают потенциал заземленного проводника или земли.
Как уже было отмечено ранее электрическое напряжение – это разность потенциалов двух точек, следовательно его значение определяется по формуле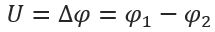 
В системе СИ за единицу измерения напряжения принимается вольт, [В]. Физически величина напряжения, равная 1 вольту, соответствует работе 1 джоуль при перемещении заряда в 1 кулон.
Источник
Напряжение как найти величину заряда
Характеристикой тока в цепи служит величина, называемая силой тока ( I ). Сила тока – физическая величина, характеризующая скорость прохождения заряда через проводник и равная отношению заряда q, прошедшeгo через пoперeчное сечение проводника за промежуток времени t, к этому промежутку времени: I = q/t . Единица измерения силы тока – 1 ампер (1 А).
Определение единицы силы тока основано на магнитном действии тока, в частности на взаимодействии параллельных проводников, по которым идёт электрический ток. Такие проводники притягиваются, если ток по ним идёт в одном направлении, и отталкиваются, если направление тока в них противоположное.
За единицу силы тока принимают такую силу тока, при которой отрезки параллельных проводников длиной 1 м, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 2*10 -7 Н. Эта единица и называется ампером (1 А).
Зная формулу силы тока, можно получить единицу электрического заряда: 1 Кл = 1А * 1с.
Амперметр
Прибор, с помощью которого измеряют силу тока в цепи, называется амперметром. Его работа основана на магнитном действии тока. Основные части амперметра магнит и катушка. При прохождении по катушке электрического тока она в результате взаимодействия с магнитом, поворачивается и поворачивает соединённую с ней стрелку. Чем больше сила тока, проходящего через катушку, тем сильнее она взаимодействует с магнитом, тем больше угол поворота стрелки. Амперметр включается в цепь последовательно с тем прибором, силу тока в котором нужно измерить, и потому он имеет малое внутреннее сопротивление, которое практически не влияет на сопротивление цепи и на силу тока в цепи.
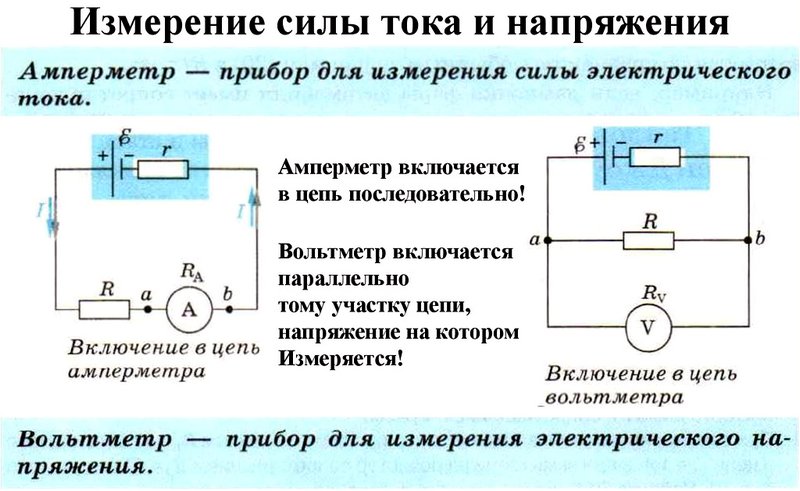
У клемм амперметра стоят знаки «+» и «—», при включении амперметра в цепь клемма со знаком «+» присоединяется к положительному пoлюсу источника тока, а клемма со знаком «—» к отрицательному пoлюсу истoчникa тока.
Напряжение
Источник тока создаёт электрическое поле, которое приводит в движение электрические заряды. Характеристикой источника тока служит величина, называемая напряжением. Чем оно больше, тем сильнее созданное им поле. Напряжение характеризует работу, которую совершает электрическое поле по перемещению электрического заряда.
Напряжение ( U ) — это физическая величина, равную отношению работы (А) электрического поля по перемещению электрического заряда к заряду (q): U = A/q .
Возможно другое определение понятия напряжения. Если числитель и знаменатель в формуле напряжения умножить на время движения заряда (t), то получим: U = At/qt. В числителе этой дроби стоит мощность тока (Р), а в знаменателе — сила тока (I). Получается формула: U = Р/I , т.е. напряжение — это физическая величина, равная отношению мощности электрического тока к силе тока в цепи.
Единица напряжения: [U] = 1 Дж/1 Кл = 1 В (один вольт).
Вольтметр
Напряжение измеряют вольтметром. Он имеет такое же устройство, что и амперметр и такой же принцип действия, но он подключается параллельно тому участку цепи, напряжение на котором хотят. Внутреннее сопротивление вольтметра достаточно большое, соответственно проходящий через него ток мал по сравнению с током в цепи.
У клемм вольтметра стоят знаки «+» и «—», при включении вольтметра в цепь клeмма со знаком «+» присоединяется к положительному полюсу источника тока, а клеммa со знаком «—» к отрицательному полюсу источника тока.
Формулы и определения.
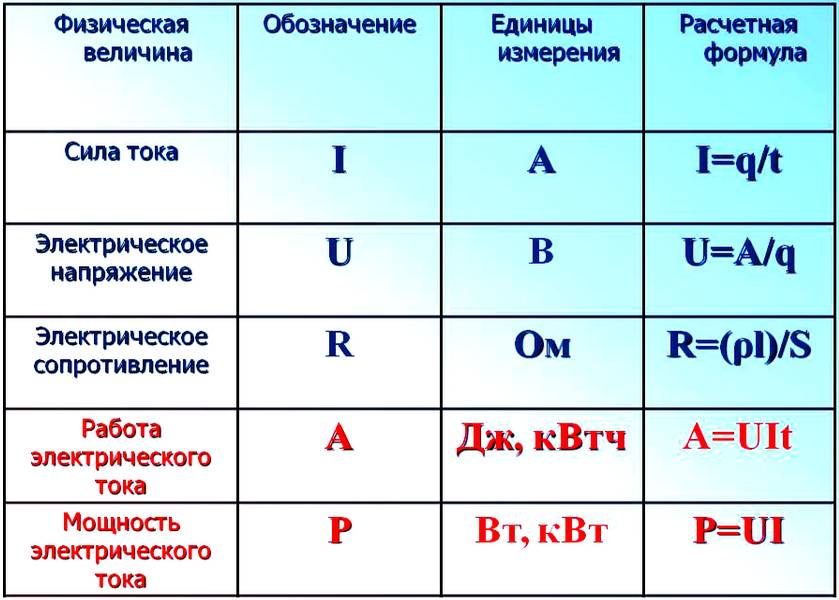
1. Все проводники, используемые в электрических цепях, имеют условные обозначения для изображения на схемах и могут образовывать последовательные, параллельные и смешанные соединения.
2. Мощность тока – физическая величинa, хаpактеpизующая скорость превращения электрической энергии в другие её виды. Единица для измерения – 1 ватт (1 Вт). Измерительный прибор – ваттметр.
3. Сила тока – физическaя вeличина, характеpизующaя скоpость прохождения заряда через проводник и равная отношению заряда, пpoшедшего через попеpeчное сечение проводника, ко времени перемещения. Единица – 1 ампер (1 А). Измерительный прибор – амперметр (подключают последовательно).
4. Электрическое напряжение – физическaя вeличина, характеризующая электрическое поле, создающее ток, и равная отношению мощности тока к его силе. Единица – 1 вольт (1 В). Измерительный прибор – вольтметр (подключают параллельно)
5. Работа тока – физичeская величинa, хаpактеpизующая количество электроэнергии, превратившейся в другие виды энергии. Единица – 1 джоуль (1 Дж). Измерительный прибор – электрический счётчик, использующий единицу 1 киловатт-час (1 кВт·ч).
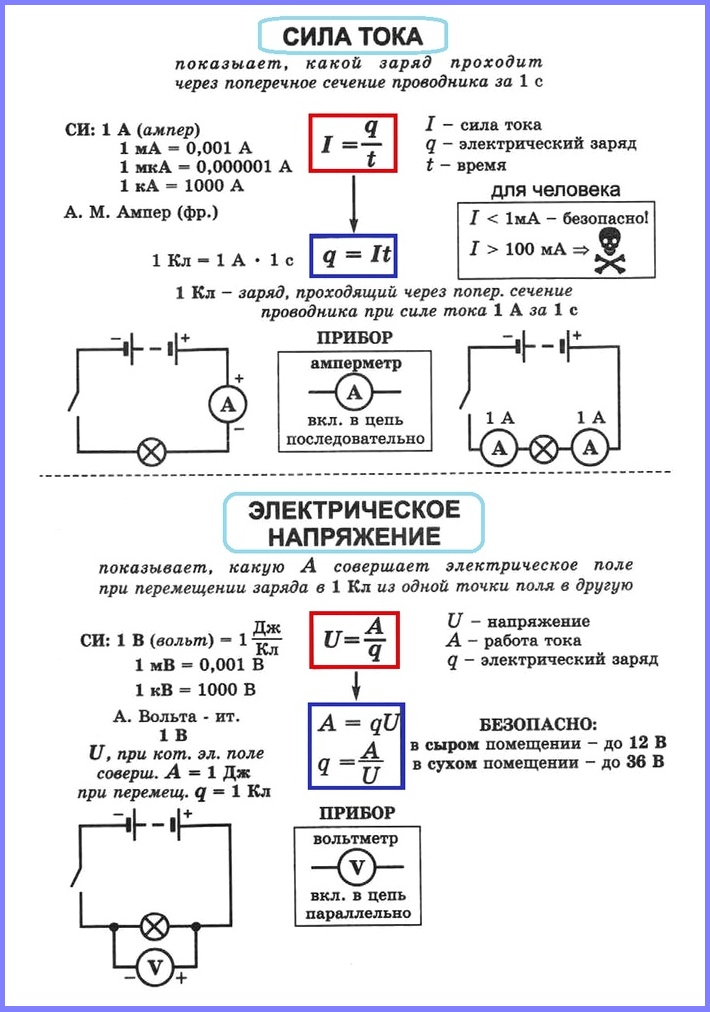
Конспект урока «Сила тока. Напряжение».
Источник
Закон Кулона
Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?
Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806). Он воспользовался крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.
Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается, и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы). С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними.
В те времена еще не было приборов для точного определения величины заряда, но Кулон сумел приготовить небольшие шарики с известным соотношением зарядов. Если заряженный проводящий шарик, рассуждал он, привести в соприкосновение с точно таким же незаряженным шариком, то имевшийся на первом заряд в силу симметрии распределится поровну между двумя шариками.
Это дало ему возможность получать заряды, составлявшие 1/2, 1/4 и т.д. от первоначального.
Несмотря на некоторые трудности, связанные с индуцированием зарядов, Кулону удалось доказать, что сила, с которой одно заряженное тело действует на другое малое заряженное тело, прямо пропорциональна электрическому заряду каждого из них.
Другими словами, если заряд любого из этих тел удвоить, то удвоится и сила; если же удвоить одновременно заряды обоих тел, то сила станет вчетверо больше. Это справедливо при условии, что расстояние между телами остается постоянным.
Изменяя расстояние между телами, Кулон обнаружил, что действующая между ними сила обратно пропорциональна квадрату расстояния: если расстояние, скажем, удваивается, сила становится вчетверо меньше.
Итак, заключил Кулон, сила, с которой одно малое заряженное тело (в идеальном случае -точечный заряд, т.е. тело, подобно материальной точке не имеющее пространственных размеров) действует на другое заряженное тело, пропорциональна произведению их зарядов Q1 и Q2 и обратно пропорциональна квадрату расстояния между ними:
Здесь k -коэффициент пропорциональности.
Это соотношение известно как закон Кулона; его справедливость подтверждена тщательными экспериментами, гораздо более точными, чем первоначальные трудно воспроизводимые опыты Кулона. Показатель степени 2 установлен в настоящее время с точностью 10 -16 , т.е. он равен 2 ± 2?10 -16 .
Коль скоро мы теперь имеем дело с новой величиной — электрическим зарядом, мы можем подобрать такую единицу измерения, чтобы постоянная к в формуле равнялась единице. И действительно, такая система единиц еще недавно широко использовалась в физике.
Речь идет о системе СГС (сантиметр-грамм-секунда), в которой используется электростатическая единица заряда СГСЭ. По определению два малых тела, каждое с зарядом 1 СГСЭ, расположенные на расстоянии 1 см друг от друга, взаимодействуют с силой 1 дина.
Теперь, однако, заряд чаще всего выражают в системе СИ, где его единицей является кулон (Кл).
Точное определение кулона через электрический ток и магнитное поле мы приведем позднее.
В системе СИ постоянная k имеет величину k = 8,988?10 9 Нм 2 /Кл 2 .
Заряды, возникающие при электризации трением обычных предметов (расчески, пластмассовой линейки и т.п.), по порядку величины составляют микрокулон и меньше (1 мкКл = 10 -6 Кл).
Заряд электрона (отрицательный) приблизительно равен 1,602?10 -19 Кл. Это наименьший известный заряд; он имеет фундаментальное значение и обозначается символом е, его часто называют элементарным зарядом.
е = (1,6021892 ± 0,0000046)?10 -19 Кл, или е ? 1,602?10 -19 Кл.
Поскольку тело не может приобрести или потерять долю электрона, суммарный заряд тела должен быть целым кратным элементарного заряда. Говорят, что заряд квантуется (т.е. может принимать лишь дискретные значения). Однако, поскольку заряд электрона е очень мал, мы обычно не замечаем дискретности макроскопических зарядов (заряду 1 мкКл соответствуют примерно 10 13 электронов) и считаем заряд непрерывным.
Формула Кулона характеризует силу, с которой один заряд действует на другой. Эта сила направлена вдоль линии, соединяющей заряды. Если знаки зарядов одинаковы, то силы, действующие на заряды, направлены в противоположные стороны. Если же знаки зарядов различны, то действующие на заряды силы направлены навстречу друг другу.
Заметим, что в соответствии с третьим законом Ньютона сила, с которой один заряд действует на другой, равна по величине и противоположна по направлению силе, с которой второй заряд действует на первый.
Закон Кулона можно записать в векторной форме подобно закону всемирного тяготения Ньютона:
где F12 — вектор силы, действующей на заряд Q1 со стороны заряда Q2, 
— расстояние между зарядами, 
— единичный вектор, направленный от Q2 к Q1.
Следует иметь в виду, что формула применима лишь к телам, расстояние между которыми значительно больше их собственных размеров. В идеальном случае это точечные заряды. Для тел конечного размера не всегда ясно, как отсчитывать расстояние r между ними, тем более что распределение заряда может быть и неоднородным. Если оба тела — сферы с равномерным распределением заряда, то r означает расстояние между центрами сфер. Важно также понимать, что формула определяет силу, действующую на данный заряд со стороны единственного заряда. Если система включает несколько (или много) заряженных тел, то результирующая сила, действующая на данный заряд, будет равнодействующей (векторной суммой) сил, действующих со стороны остальных зарядов. Постоянная к в формуле Закона Кулона обычно выражается через другую константу, ?0, так называемую электрическую постоянную, которая связана с k соотношением k = 1/(4??0). С учетом этого закон Кулона можно переписать в следующем виде:
где с наивысшей на сегодня точностью
Запись большинства других уравнений электромагнитной теории упрощается при использовании ?0, поскольку 4? в окончательном результате часто сокращается. Поэтому мы будем обычно использовать Закон Кулона, считая, что:
Закон Кулона описывает силу, действующую между двумя покоящимися зарядами. Когда заряды движутся, между ними возникают дополнительные силы, и их мы обсудим в последующих главах. Здесь же рассматриваются только покоящиеся заряды; этот раздел учения об электричестве называется электростатикой.
Продолжение следует. Коротко о следующей публикации:
Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, либо возникающий при изменении магнитного поля.
Закон Кулона.
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов. Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
.
где |q1| и |q2| — модули зарядов; r — расстояние между ними; k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.
Заряд в 1 Кл очень велик. Сила взаимодействия двух точечных зарядов по 1 Кл каждый, расположенных на расстоянии 1 км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой 1 т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в 1 А — вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент k в законе Кулона при его записи в СИ выражается в Н · м 2 /Кл 2 . Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
Часто его записывают в виде , где ɛ0 =8,85 · 10 — 12 Kл 2 /H·м 2 — электрическая постоянная. В среде с диэлектрической проницаемостью ɛ закон Кулона имеет вид:
.
Закон Кулона простым языком
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.
Рисунок 1. Закон Кулона
История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).
Рис. 2. Крутильные весы
У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r 2
Рис. 3. Взаимодействие точечных зарядов
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r 2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).
Рис. 4. Большой адронный коллайдер
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
История открытия
Взаимодействия двух точечных зарядов рассмотренным выше законом в первый раз были доказаны в 1785 Шарлем Кулоном. Доказать правдивость сформулированного закона физику удалось с использованием крутильных весов, принцип действия которых также был представлен в статье.
Кулон также доказал, что внутри сферического конденсатора нет электрического заряда. Так он пришёл к утверждению, что величину электростатических сил можно менять путём изменения расстояния между рассматриваемыми телами.
Таким образом, закон Кулона по-прежнему является главнейшим законом электростатики, на основе которого было сделано немало величайших открытий. В рамках данной статьи была представлена официальная формулировка закона, а также подробно описаны его составляющие части.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r2
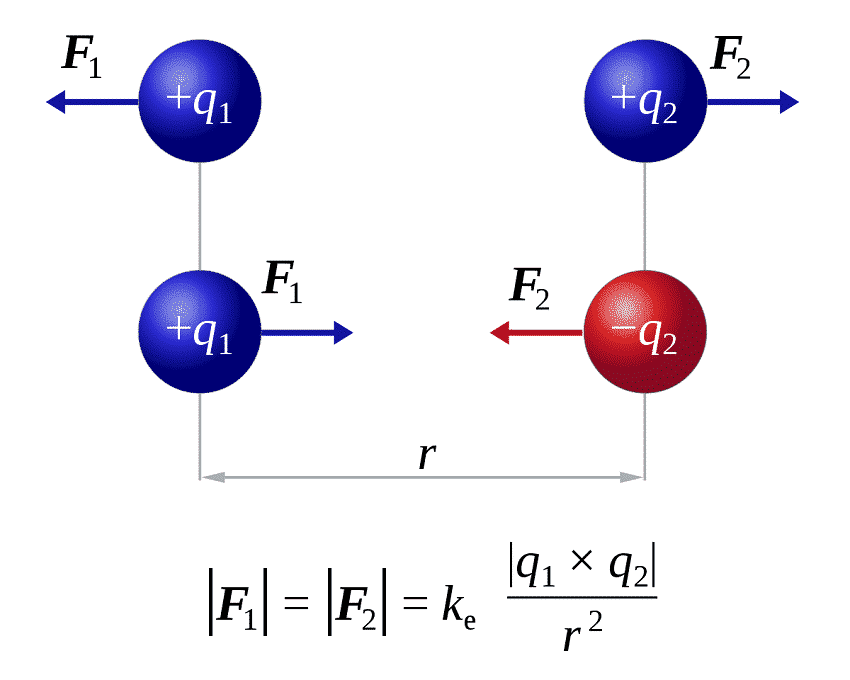
Рис. 3. Взаимодействие точечных зарядов
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 — 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 1018 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент пропорциональности k и электрическая постоянная
В формуле закона Кулона есть параметры k — коэффициент пропорциональности или 
— электрическая постоянная. Электрическая постоянная
представлена во многих справочниках, учебниках, интернете, и её не нужно считать! Коэффициент пропорциональности в вакууме на основе
можно найти по известной формуле:
Здесь 
— электрическая постоянная,
— число пи,
— коэффициент пропорциональности в вакууме.
Дополнительная информация! Не зная представленные выше параметры, найти силу взаимодействия между двумя точечными электрическими зарядами не получится.
Формулировка и формула закона Кулона
Чтобы подытожить вышесказанное, необходимо привести официальную формулировку главного закона электростатики. Она принимает вид:
Сила взаимодействия двух покоящихся точечных зарядов в вакууме прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Причём произведение зарядов необходимо брать по модулю!
В данной формуле q1 и q2 — это точечные заряды, рассматриваемые тела; r2 — расстояние на плоскости между этими телами, взятое в квадрате; k — коэффициент пропорциональности (
для вакуума).
Закон Кулона в диэлектриках и для зарядов в веществе.
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Если два точечных заряда находятся в веществе, то сила их взаимного действия будет меньше, чем в вакууме. Для зарядов в веществе закон Кулона выглядит так:
[large boxed { F = frac{1}{varepsilon} cdot k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила взаимодействия зарядов в веществе;
(|q| ; |Q| left( text{Кл}right) ) – величины зарядов;
(r left( text{м}right) ) – расстояние между зарядами;
( k = 9cdot 10^{9} ) – постоянная величина;
( varepsilon ) – диэлектрическая проницаемость вещества, для разных веществ различается, ее можно найти в справочнике физики;
Два заряда -q и +Q, расположенные в вакууме на расстоянии r, притягиваются сильнее, нежели те же заряды, расположенные на таком же расстоянии в диэлектрике
Силы, с которыми заряды действуют друг на друга в веществе, отличаются от сил взаимодействия в вакууме в ( varepsilon ) раз:
[large boxed { F_{text{(в диэлектрике)}} = frac{1}{varepsilon} cdot F_{text{(в вакууме)}} } ]
Где закон Кулона применяется на практике
Основной закон электростатики — это важнейшее открытие Шарля Кулона, которое нашло своё применение во многих областях.
Работы известного физика использовались в процессе изобретения различных устройств, приборов, аппаратов. К примеру, молниеотвод.
При помощи молниеотвода жилые дома, здания защищают от попадания молнии во время грозы. Таким образом, повышается степень защиты электрического оборудования.
Молниеотвод работает по следующему принципу: во время грозы на земле постепенно начинают скапливаться сильные индукционные заряды, которые поднимаются вверх и притягиваются к облакам. При этом на земле образуется немаленькое электрическое поле. Вблизи молниеотвода электрическое поле становится сильнее, благодаря чему от острия устройства зажигается коронный электрический заряд.
Далее образованный на земле заряд начинает притягиваться к заряду облака с противоположным знаком, как и должно быть согласно закону Шарля Кулона. После этого воздух проходит процесс ионизации, а напряжённость электрического поля становится меньше возле конца молниеотвода. Таким образом, риск попадания молнии в здание минимален.
Обратите внимание! Если в здание, на котором установлен молниеотвод, попадёт удар, то пожара не произойдёт, а вся энергия уйдёт в землю.
На основе закона Кулона было разработано устройство под названием “Ускоритель частиц”, которое пользуется большим спросом сегодня.
В данном приборе создано сильное электрическое поле, которое увеличивает энергию попадающих в него частиц.
Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера
Рис. 4. Большой адронный коллайдер
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Устройство крутильных весов
Такие весы содержат перекладину — тонкий стеклянный стержень, расположенный горизонтально. Он подвешен на тонкой вертикально натянутой упругой проволоке.
На одном конце стержня находится небольшой металлический шарик. К другому концу прикреплен груз, который используется, как противовес.
Еще один металлический шарик, прикрепленный ко второй палочке из стекла, можно располагать неподалеку от первого шарика. Для этого в верхней крышке корпуса весов проделано отверстие.
Устройство крутильных весов, использованных Кулоном для обнаружения силы взаимодействия зарядов
Если наэлектризовать шарики, они начнут взаимодействовать. А прикрепленная к проволоке перекладина, на которой находится один из шариков, будет поворачиваться на некоторый угол.
На корпусе весов на уровне палочки располагается шкала с делениями. Угол поворота связан с силой взаимного действия шариков. Чем больше угол поворота, тем больше сила, с которой шарики действуют друг на друга.
Чтобы сдвинувшийся шарик вернуть в первоначальное положение, нужно закрутить проволоку на некоторый угол. Так, чтобы сила упругости скомпенсировала силу взаимодействия шариков.
Для закручивания проволоки в верхней части весов есть рычажок. Рядом с ним расположен диск, а на нем – еще одна угловая шкала с делениями.
По нижней шкале определяют точку, в которую необходимо вернуть шарик. Верхней шкалой пользуются, чтобы установить угол, на который нужно рычажком закрутить проволоку.
С помощью крутильных весов Шарль Кулон выяснил, как именно сила взаимного действия зависит от величины зарядов и расстояния между зарядами.
В те годы единиц для измерения заряда не было. Поэтому ему пришлось изменять заряд одного шарика с помощью метода половинного деления.
Когда он касался заряженным шариком второго такого же шарика, заряды между ними распределялись поровну. Таким способом, можно было уменьшать заряд одного из шариков, участвующих в опыте, в 2, 4, 8, 16 и т. д. раз.
Так опытным путем Кулон получил закон, формула которого очень похожа на закон всемирного тяготения.
В память о его заслугах, силу взаимодействия зарядов называют Кулоновской силой.
Это прибор, разработанный Кулоном в 1777 году, помог вывести зависимость силы, названной в последствии в его честь. С его помощью изучается взаимодействие точечных зарядов, а также магнитных полюсов.
Крутильные весы имеют небольшую шёлковую нить, расположенную в вертикальной плоскости, на которой висит уравновешенный рычаг. На концах рычага расположены точечные заряды.
Под действием внешних сил рычаг начинает совершать движения по горизонтали. Рычаг будет перемещаться в плоскости до тех пор, пока его не уравновесит сила упругости нити.
В процессе перемещений рычаг отклоняется от вертикальной оси на определённый угол. Его принимают за d и называют углом поворота. Зная величину данного параметра, можно найти крутящий момент возникающих сил.
Крутильные весы Шарля Кулона выглядят следующим образом:
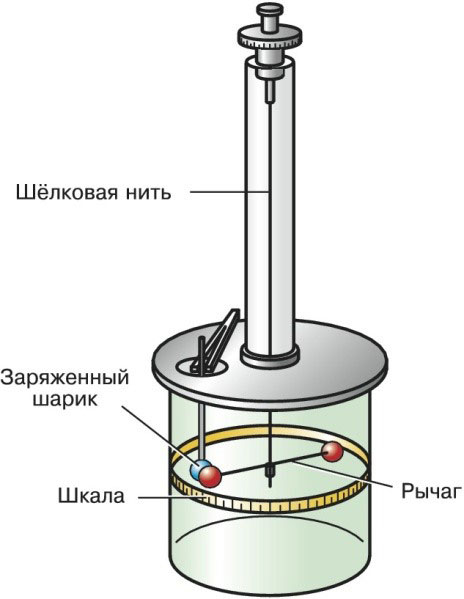
Направление сил в законе Кулона.
Как и говорилось выше, направление взаимодействующих сил двух точечных электрических зарядов зависит от их полярности. Т.е. одноимённые заряды будут отталкиваться, а разноимённые притягиваться.
Кулоновские силы также можно назвать радиус-вектором, т.к. они направлены вдоль линии, проведённой между ними.
В некоторых физических задачах даются тела сложной формы, которые не получается принять за точечный электрический заряд, т.е. пренебречь его размерами. В сложившейся ситуации рассматриваемое тело необходимо разбить на несколько мелких частей и рассчитывать каждую часть по отдельности, применяя закон Кулона.
Полученные при разбиении вектора сил суммируются по правилам алгебры и геометрии. В результате получается результирующая сила, которая и будет являться ответом для данной задачи. Данный способ решения часто называют методом треугольника.
Прямая и обратная пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| 1 | 2 | 4 | 8 | 16 |
| 5 | 10 | 20 | 40 | 80 |
Скорость v = 5 км/чВремя t (ч)Путь s (км)
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| 5 | 15 | 45 | 90 |
| 10 | 30 | 90 | 180 |
Время t = 2 чСкорость v (км/ч)Расстояние s (км)
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
- Область определения — множество всех действительных чисел, кроме x = 0.
D(y): (-∞; 0) U (0; +∞).
- Область значений — все действительные числа, кроме y = 0.
Е(у): (-∞; 0) U (0; +∞).
- Не имеет наибольших и наименьших значений.
- Является нечетной, и ее график симметричен относительно начала координат.
- Непериодическая.
- Ее график не пересекает оси координат.
- Не имеет нулей.
- Если k > 0 (аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
- При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные — (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные — (-∞; 0).
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| 10 | 20 | 40 | 80 |
| 12 | 6 | 3 | 1,5 |
Путь s = 120 кмСкорость v (км/ч)Время t (ч)
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Каким прибором измеряется электрический заряд?
Прибор, который определяет электрический заряд носит название электроскоп.
Электроскоп (от греческих слов «электрон» и skopeo – наблюдать, обнаруживать) — прибор для индикации наличия электрического заряда.
Принцип действия электроскопа основан на том, что на одноименно заряженные тела действуют силы взаимного отталкивания.
Измерить электрический заряд можно также с помощью электрометра, в простейшем случае состоящий из металлического стержня и стрелки, которая способна вращаться вокруг горизонтальной оси
Вы спросите чем электрометр отличается от электроскопа? Электроскоп и электрометр это приборы для обнаружения зарядов. У электрометра имеется стрелка которая позволяет еще и оценить(измерить) электрический заряд.
Т.е.электроскоп находит заряд, а электрометр еще и измеряет силу заряда (метр -измерять, вычислять)
Закон Амонтона-Кулона
Познакомимся с законом, который позволяет вычислять силу трения. Он был открыт французом Г.Амонтоном и проверен его соотечественником Ш.Кулоном, поэтому называется законом Амонтона-Кулона.
Рассмотрим тело, лежащее на опоре (см. левую часть чертежа). Тело действует на опору своим весом W, который направлен вниз. По третьему закону Ньютона опора реагирует на тело силой R, равной по модулю весу тела и противоположно направленной. По правилу параллелограмма силу реакции R можно представить суммой силы нормальной реакции N по перпендикуляру к поверхности и силы тангенциальной реакции T вдоль поверхности. Эта составляющая реакции – сила трения покоя.
Если мы расположим опору горизонтально, то она тоже будет реагировать на тело согласно третьему закону Ньютона (см. среднюю часть чертежа). В этом случае, как и ранее, сила реакции опоры R будет равной по модулю весу тела W и противоположно направленной. Наряду с этим, сила реакции одновременно будет и силой нормальной реакции, а сила тангенциальной реакции, сила трения, будет отсутствовать. Если теперь к телу приложить внешнюю силу F, направленную вдоль поверхности, то мы снова вызовем появление силы тангенциальной реакции. В этом случае она будет силой трения скольжения (см. правую часть чертежа).
Опыты показывают: при движении одного тела по поверхности другого модуль силы трения скольжения пропорционален модулю силы нормальной реакции опоры, выражаясь законом Амонтона-Кулона:
Иначе говоря, закон Амонтона-Кулона указывает на пропорциональность двух сил: тангенциальной реакции опоры (силы трения скольжения) и нормальной реакции опоры (силы давления).
Опыты показывают: закон Амонтона-Кулона можно применять как для расчёта силы трения скольжения, так и максимальной силы трения покоя. Коэффициенты трения скольжения (максимальные коэффициенты трения покоя) определяются экспериментально и могут быть, например, такими:
| Дерево по дереву: 0,25 | Резина по бетону: 0,75 |
| Дерево по металлу: 0,2 – 0,5 | Резина по льду: 0,15 – 0,25 |
Физический смысл коэффициента трения заключается в том, что он показывает долю возникающей силы трения скольжения (или максимальной силы трения покоя) от силы нормальной реакции опоры.
Задача. Рабочий прижимает брусок к стене, как показано на рисунке. Как нужно изменить вектор силы, чтобы брусок не скользил по стене?
Решение. В левой части чертежа показано, что рука прижимает брусок. В правой части показано, как он передаёт силу руки на стену. По третьему закону Ньютона возникает ответная сила реакции, которую представим нормальной и тангенциальной силами:
Проектируя последнее равенство на оси, получим следующие уравнения:
Чтобы брусок не скользил по стене, модуль действующей силы трения должен быть меньше её расчётного значения: T mN . Тогда имеем:
F·sin(a) m·F·cos(a) => tg(a) m
Ответ: рабочий должен уменьшить угол a так, чтобы его тангенс был меньше коэффициента трения скольжения бруска по стене; покой или скольжение бруска не зависят от модуля силы давления на брусок.
Применение электризации
1.Электрофильтры.
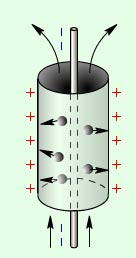
Для очистки воздуха от пыли, например, при производстве цемента, очистки частиц дыма на ТЭС используют электрофильтры. Наэлектризованные частицы пыли притягиваются к заряженному элементу внутри фильтра.
2. Равномерное распыление краски краскопультом.
Электростатическая покраска используется для покрытия металлических поверхностей, например, в покрасочном цехе автомобильных кузовов. Для равномерного распыления краски на краскопульт подают отрицательный заряд, а кузову автомобиля сообщают положительный заряд. Отрицательно заряженные капельки краски равномерно распределяются по поверхности кузова, образуя прочный, ровный слой.
3. Изготовление наждачной бумаги.
4. Генератор высокого напряжения Ван де Граафа.
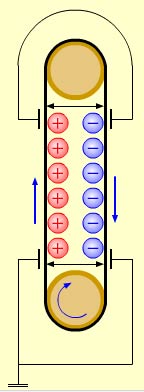
Электризация нашла практическое применение в науке и технике. До недавнего времени в ядерных исследованиях на ускорителях элементарных частиц широко применялся генератор Ван-дер-Ваальса. С его помощью удавалось генерировать напряжение до нескольких миллионов вольт. Генератор разработан в 1929 году американским физиком Робертом Ван-дер-Ваальсом. Используется электризация трением. Заряд переносится на движущейся ленте и многократно снимается с нее на полый металлический проводник.
5. Очистка зерна.
6. Дактилоскопия.
7. Лазерный принтер и ксерокс.
Электризация тел при облучении нашла применение в ксерокопирование и лазерном принтере.
8. Медицина.
При работе люстры Чижевского образуется большое количество отрицательных ионов кислорода. При вдыхании воздуха ионы кислорода отдают электрические заряды эритроцитам крови, а затем – клеткам. Вследствие чего улучшается обмен веществ в организме.
Учет электризации:
- Перевозка топлива.
- Электризация нитей на ткацкой фабрике.
- Электризация самолета во время полета.
- Электризация одежды.
Связь с гравитацией
Интересно, что у различных законов физики есть некоторые общие черты. Вспомним закон тяготения. Сила гравитации также обратно пропорциональны квадрату расстояния, но уже между массами , и невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество как два разных проявления одной и той же сущности.
Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Как можно говорить, что одно действует сильнее другого? Ведь все зависит от того, какова масса и каков заряд. Рассуждая о том, насколько сильно действует тяготение, вы не вправе говорить: “Возьмем массу такой-то величины”, потому что вы выбираете ее сами. Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Вопрос: каково отношение силы тяготения к электрической силе? Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число?
Люди ищут этот огромный коэффициент в других явлениях природы. Они перебирают всякие большие числа, а если вам нужно большое число, почему не взять, скажем, отношение диаметра Вселенной к диаметру протона – как ни удивительно, это тоже число с 42 нулями. И вот говорят: может быть, этот коэффициент и равен отношению диаметра протона к диаметру Вселенной? Это интересная мысль, но, поскольку Вселенная постепенно расширяется, должна меняться и постоянная тяготения. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.
Закон Кулона в квантовой механике [ править | править код ]
В квантовой механике закон Кулона формулируется не при помощи понятия силы, как в классической механике, а при помощи понятия потенциальной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частицы, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она вычисляется в классической механике [4] . Это утверждение не следует из остальных аксиом квантовой механики, а получено путём обобщения опытных данных.
Так, оператор Гамильтона атома с зарядом ядра Z имеет вид:
H=−ℏ22m∑j∇j2−Ze2∑j1rj+∑i>je2rij.{displaystyle H=-{frac {hbar ^{2}}{2m}}sum _{j}nabla _{j}^{2}-Ze^{2}sum _{j}{frac {1}{r_{j}}}+sum _{i>j}{frac {e^{2}}{r_{ij}}}.}
Здесь m — масса электрона, е — его заряд, rj{displaystyle r_{j}}
— абсолютная величина радиус-вектора j-го электрона r→j{displaystyle {vec {r}}_{j}}
, а rij=|r→i−r→j|{displaystyle r_{ij}=|{vec {r}}_{i}-{vec {r}}_{j}|}
. Первое слагаемое выражает кинетическую энергию электронов, второе слагаемое — потенциальную энергию кулоновского взаимодействия электронов с ядром и третье слагаемое — потенциальную кулоновскую энергию взаимного отталкивания электронов. Суммирование в первом и втором слагаемом ведется по всем Z электронам. В третьем слагаемом суммирование идёт по всем парам электронов, причём каждая пара встречается однократно
Закон Кулона с точки зрения квантовой электродинамики
Согласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частицами. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частицами, тем меньшее время нужно виртуальным фотонам для преодоления этого расстояния и следовательно, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при больших расстояниях в обмене участвуют только длинноволновые фотоны. Таким образом, с помощью квантовой электродинамики можно вывести закон Кулона .
Закон Кулона для зарядов в вакууме
Рассмотрим два точечных заряда, которые находятся в вакуум.
Два положительных заряда q и Q, расположенных в вакууме на расстоянии r, отталкиваются. Силы отталкивания направлены вдоль прямой, соединяющей заряды
На рисунке 2 сила (large F_{Q} ) – это сила, с которой положительный заряд Q отталкивает второй положительный заряд q. А сила (large F_{q} ) принадлежит заряду q, с такой силой он отталкивает заряд Q.
Примечание: Точечный заряд – это заряженное тело, размером и формой которого можно пренебречь.
Силы взаимодействия зарядов, по третьему закону Ньютона, равны по величине и направлены противоположно. Поэтому, для удобства можно ввести обозначение:
[large F_{q} = F_{Q} = F]
Для силы взаимодействия зарядов в вакууме Шарль Кулон сформулировал закон так:
Два точечных заряда в вакууме,
взаимодействуют с силой
прямо пропорциональной
произведению величин зарядов
и обратно пропорциональной
квадрату расстояния между ними.
Формула для этого закона на языке математики запишется так:
[large boxed { F = k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;
(|q| left( text{Кл}right) ) – величина первого заряда;
(|Q| left( text{Кл}right) ) – величина второго заряда;
(r left( text{м}right) ) – расстояние между двумя точечными зарядами;
(k ) – постоянная величина, коэффициент в системе СИ;
Сила – это вектор. Две главные характеристики вектора – его длина и направление.
Формула позволяет найти одну из характеристик вектора F — модуль (длину) вектора.
Чтобы определить вторую характеристику вектора F – его направление, нужно воспользоваться правилом: Мысленно соединить два неподвижных точечных заряда прямой линией. Сила, с которой они взаимодействуют, будет направлена вдоль этой прямой линии.
Сила Кулона – это центральная сила, так как она направлена вдоль прямой, соединяющей центры тел.
Степень точности закона Кулона
Закон Кулона — экспериментально установленный факт. Его справедливость неоднократно подтверждалась всё более точными экспериментами. Одним из направлений таких экспериментов является проверка того, отличается ли показатель степени r в законе от 2. Для поиска этого отличия используется тот факт, что если степень точно равна двум, то поле внутри полости в проводнике отсутствует, какова бы ни была форма полости или проводника
Такие опыты впервые провел Кавендиш и повторил Максвелл в усовершенствованном виде, получив для максимального отличия показателя в степени от двух величину 121600{displaystyle {frac {1}{21600}}}
Эксперименты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, показали, что показатель степени в законе Кулона равен 2 с точностью до (3,1±2,7)×10−16{displaystyle (3,1pm 2,7)times 10^{
Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были использованы измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10−8 см, показатель степени в законе Кулона отличается от 2 не более чем на 10−9
Коэффициент k{displaystyle k}
в законе Кулона остается постоянным с точностью до 15⋅10−6 .
Факторы, влияющие на трение
В настоящее время установлено, что коэффициент трения в разной степени зависит от трех факторов:
- материала трущихся тел и характера смазки, плёнки, имеющейся на поверхности;
- конструкции фрикционного сочленения: размера поверхности, геометрического очертания, в основном от отношения площадей трения контактирующих деталей — коэффициента взаимного перекрытия;
- режима работы: температуры, скорости, нагрузки, в основном температурного поля, возникающего в тонком поверхностном слое.
Источники:
- https://www.asutpp.ru/zakon-kulona.html
- https://odinelectric.ru/knowledgebase/zakon-kulona-opredelenie-i-formula
- https://formulki.ru/electromagnetism/zakon-kulona
- https://izamorfix.ru/matematika/algebra/proportsionalnost.html
- https://zakon-oma.ru/kulon-edinica-izmereniya-elektricheskogo-zaryada.php
- https://fizclass.ru/elektricheskij-zaryad-vzaimodejstvie-elektricheskix-zaryadov-zakon-kulona/
- http://fizmat.by/kursy/jelektrichestvo/Kulon
- https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9A%D1%83%D0%BB%D0%BE%D0%BD%D0%B0
- https://wiki2.org/ru/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9A%D1%83%D0%BB%D0%BE%D0%BD%D0%B0
- https://wiki2.org/ru/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%90%D0%BC%D0%BE%D0%BD%D1%82%D0%BE%D0%BD%D0%B0_%E2%80%94_%D0%9A%D1%83%D0%BB%D0%BE%D0%BD%D0%B0
Предыдущая
ИнформацияМагнитный поток – что это: обозначение и единица измерения, формула, скорость изменения потока, направление вектора магнитной индукции
Следующая
ИнформацияПостоянные магниты в физике, их описание и принцип действия
