Ответы Mail.ru
Домашние задания
Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика
Другие предметы
Вопросы – лидеры.
Срочно! Не могу разобраться с ответом
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Sonia Bychkova
Ученик
(214),
закрыт
12 лет назад
Дополнен 12 лет назад
последовательное
Лучший ответ
Ох Ой
Мастер
(2371)
12 лет назад
Общее сопротивление будет 3+2=5
Сила тока будет 1.5/5=0,3А
Остальные ответы
Роза Марковна
Просветленный
(35806)
12 лет назад
Какое соединение?
Похожие вопросы
Как найти показание амперметра? физика
В схеме E1 = 2 В, E2 = 4 В,
R1 = 0,5 Ом. Падение потенциала на сопротивлении
R2 равно 1 В. Найдите показание амперметра.
Сопротивле-ниями элементов и амперметра пренебречь.
Хотя бы конечную формулу пожалуйста.


То, что в решении получился отрицательный ответ, значит лишь то, что выбрано не то направление тока. Меняя знак мы получаем правильный ответ.
Итоговый ответ: 6 А.
Как найти показания амперметра формула

По закону Ома, ток в замкнутом контуре равен алгебраической сумме ЭДС, действующих в контуре, деленному на полное сопротивление цепи.
Алгебраическая сумма ЭДС равна Е=12В-10В+2В=4В
Полное сопротивление цепи равно R=r1+r2+r3+R1234+R56
R1234 состоит из двух папаллельно включенных цепочек из двух последовательно включенных сопротивлений (R1,R2 и R3,R4 соответственно)
Полное сопротивление цепи равно 4+1+4+7.2+1=17,2 Ом
Амперметр А» показывает полный ток в цепи, и он покажет 4В/17,2Ом=»0,232558А» или примерно 0,233А
Чтобы найти показания амперметра А1, найдем напряжение на R56. U56=I2*R56=I2*1
Ток I1=U56/2=I2/2=0.116279А или примерно 0,116 А
Показание вольтметра равно разности падения напряжения на сопротивлениях R2 и R4. Чтобы найти эти значения, найдем падение напряжения на всей цепочке сопротивлений R1R2R3R4. U1234=I2*R1234=I2*7,2
Падение напряжения на R2 U2=U1234/(R1+R2)*R2=I2*7,2*12/18=I2*7,2*2/3
Падение напряжения на R4 U4=U1234/(R3+R4)*R4=I2*7,2*8/12=I2*7,2*2/3
Разность напряжений на R2 и R4 равна U2-U4=I2*7,2*2/3-I2*7,2*2/3=0, следовательно, показания вольтметра будут равны нулю.
Ответ: амперметр А2 покажет ток примерно 0,233А, амперметр А1 примерно 0,116А, а вольтметр покажет 0
Приветствую всех читателей на нашем сайте и сегодня в рамках курса “Электроника для начинающих” мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр, амперметр и др.

Измерение тока.
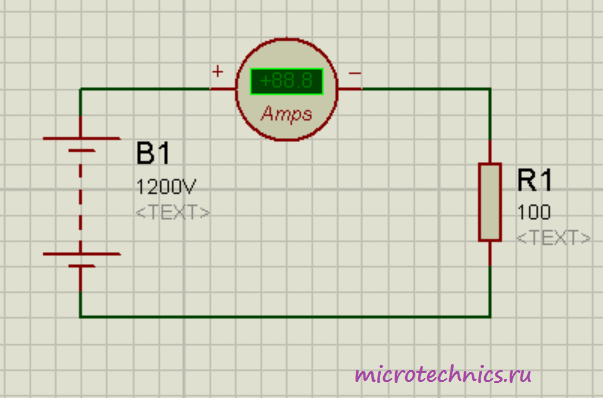
И начнем мы с измерения тока. Прибор, используемый для этих целей, называется амперметр и в цепь он включается последовательно. Рассмотрим небольшой примерчик:
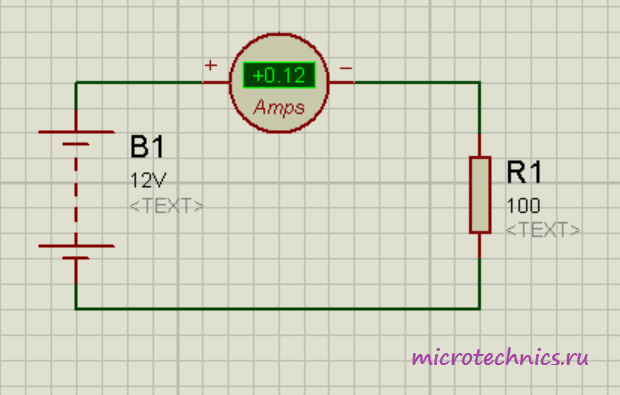
Как видите, здесь источник питания подключен напрямую к резистору. Кроме того, в цепи присутсвует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи должна быть равна:
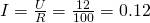
Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 🙂
Важным параметром этого прибора является его внутреннее сопротивление 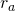 . Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
. Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
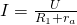
Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.
При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:
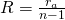
В этой формуле n – это коэффициент шунтирования – число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.
Пусть максимальное значение, которое может измерить амперметр составляет 1А. А схема, силу тока в которой нам нужно определить имеет следующий вид:
 Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
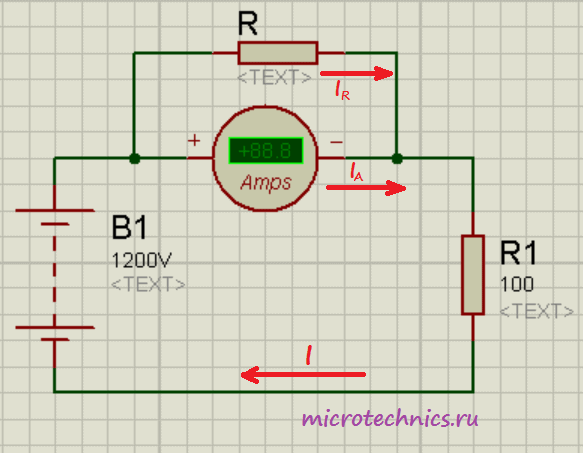 В данной задаче нам необходимо измерить ток
В данной задаче нам необходимо измерить ток 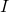 . Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
. Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
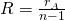
В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.
Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:
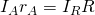
Выразим ток шунта через ток амперметра:
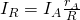
Измеряемый ток равен:
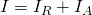
Подставим в это уравнение предыдущее выражение для тока шунта:
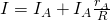
Но сопротивление шунта нам также известно (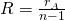 ). В итоге мы получаем:
). В итоге мы получаем:
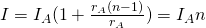
Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нам и нужно измерить 🙂
С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.
Измерение напряжения.
Прибор, предназначенный для измерения напряжения называется вольтметр, и, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся с чем это связано:
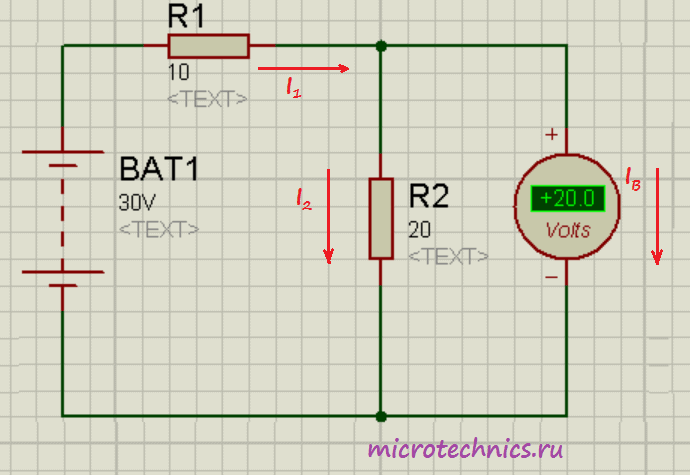 Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
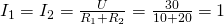
Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с 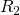 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (
. Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (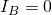 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку
), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку 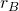 имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе
имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе 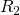 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:
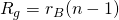
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример 😉
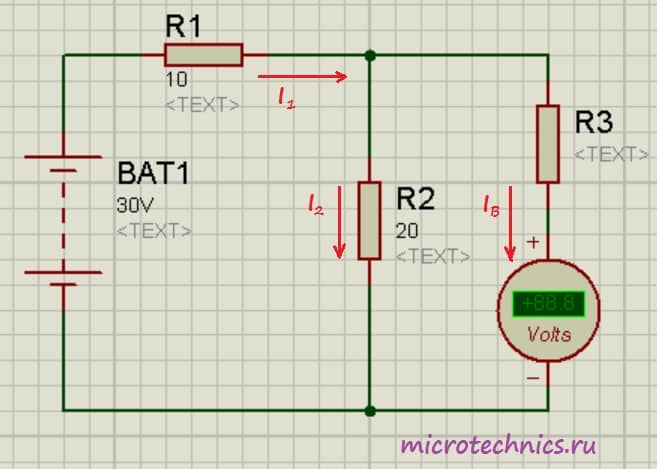 Здесь мы добавили в цепь добавочное сопротивление
Здесь мы добавили в цепь добавочное сопротивление 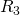 . Перед нами стоит задача измерить напряжение на резисторе
. Перед нами стоит задача измерить напряжение на резисторе 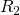 :
: 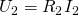 . Давайте определим, что при таком включении будет на экране вольтметра:
. Давайте определим, что при таком включении будет на экране вольтметра:
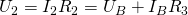
Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:
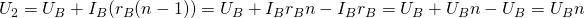
Таким образом: 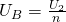 . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
. То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
В завершении статьи пару слов об измерении сопротивления и мощности.
Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи – омметр – и мощности – ваттметр.
В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями и заходите к нам на сайт! До скорых встреч!
Приветствую всех читателей на нашем сайте и сегодня в рамках курса “Электроника для начинающих” мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр, амперметр и др.

Измерение тока.
И начнем мы с измерения тока. Прибор, используемый для этих целей, называется амперметр и в цепь он включается последовательно. Рассмотрим небольшой примерчик:

Как видите, здесь источник питания подключен напрямую к резистору. Кроме того, в цепи присутсвует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи должна быть равна:
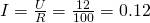
Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 🙂
Важным параметром этого прибора является его внутреннее сопротивление 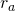 . Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
. Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
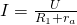
Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.
При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:
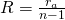
В этой формуле n – это коэффициент шунтирования – число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.
Пусть максимальное значение, которое может измерить амперметр составляет 1А. А схема, силу тока в которой нам нужно определить имеет следующий вид:
 Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
 В данной задаче нам необходимо измерить ток
В данной задаче нам необходимо измерить ток 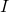 . Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
. Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
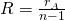
В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.
Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:
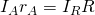
Выразим ток шунта через ток амперметра:
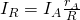
Измеряемый ток равен:
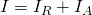
Подставим в это уравнение предыдущее выражение для тока шунта:
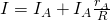
Но сопротивление шунта нам также известно (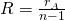 ). В итоге мы получаем:
). В итоге мы получаем:
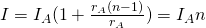
Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нам и нужно измерить 🙂
С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.
Измерение напряжения.
Прибор, предназначенный для измерения напряжения называется вольтметр, и, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся с чем это связано:
 Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
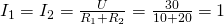
Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с 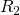 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (
. Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (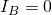 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку
), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку 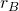 имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе
имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе 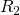 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:
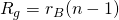
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример 😉
 Здесь мы добавили в цепь добавочное сопротивление
Здесь мы добавили в цепь добавочное сопротивление 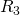 . Перед нами стоит задача измерить напряжение на резисторе
. Перед нами стоит задача измерить напряжение на резисторе 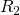 :
: 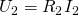 . Давайте определим, что при таком включении будет на экране вольтметра:
. Давайте определим, что при таком включении будет на экране вольтметра:
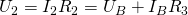
Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:
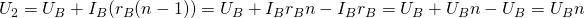
Таким образом: 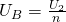 . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
. То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
В завершении статьи пару слов об измерении сопротивления и мощности.
Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи – омметр – и мощности – ваттметр.
В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями и заходите к нам на сайт! До скорых встреч!
Идеальные и реальные вольтметры и амперметры в цепях постоянного тока



По закону Ома, ток в замкнутом контуре равен алгебраической сумме ЭДС, действующих в контуре, деленному на полное сопротивление цепи.
Алгебраическая сумма ЭДС равна Е=12В-10В+2В=4В
Полное сопротивление цепи равно R=r1+r2+r3+R1234+R56
R1234 состоит из двух папаллельно включенных цепочек из двух последовательно включенных сопротивлений (R1,R2 и R3,R4 соответственно)
Полное сопротивление цепи равно 4+1+4+7.2+1=17,2 Ом
Амперметр А» показывает полный ток в цепи, и он покажет 4В/17,2Ом=»0,232558А» или примерно 0,233А
Чтобы найти показания амперметра А1, найдем напряжение на R56. U56=I2*R56=I2*1
Ток I1=U56/2=I2/2=0.116279А или примерно 0,116 А
Показание вольтметра равно разности падения напряжения на сопротивлениях R2 и R4. Чтобы найти эти значения, найдем падение напряжения на всей цепочке сопротивлений R1R2R3R4. U1234=I2*R1234=I2*7,2
Падение напряжения на R2 U2=U1234/(R1+R2)*R2=I2*7,2*12/18=I2*7,2*2/3
Падение напряжения на R4 U4=U1234/(R3+R4)*R4=I2*7,2*8/12=I2*7,2*2/3
Разность напряжений на R2 и R4 равна U2-U4=I2*7,2*2/3-I2*7,2*2/3=0, следовательно, показания вольтметра будут равны нулю.
Ответ: амперметр А2 покажет ток примерно 0,233А, амперметр А1 примерно 0,116А, а вольтметр покажет 0
Приветствую всех читателей на нашем сайте и сегодня в рамках курса “Электроника для начинающих” мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр, амперметр и др.

Измерение тока.
И начнем мы с измерения тока. Прибор, используемый для этих целей, называется амперметр и в цепь он включается последовательно. Рассмотрим небольшой примерчик:

Как видите, здесь источник питания подключен напрямую к резистору. Кроме того, в цепи присутсвует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи должна быть равна:
Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи
На чтение 18 мин Просмотров 22 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- Амперметр. Измерение силы тока
- Содержание
- Амперметр
- Амперметр в электрической цепи
- Правила подключения амперметра в электрическую цепь
- Измерение силы тока амперметром
- Безопасные и опасные пределы значений силы тока
- Это интересно: амперметр и Minecraft
- Упражнения
- Упражнение №1
- Упражнение №2
- Упражнение №3
- Упражнение №4
- Как найти показания амперметра формула
- Ответ
- Измерение тока.
- Измерение напряжения.
- Измерение тока.
- Измерение напряжения.
Амперметр. Измерение силы тока
Содержание
Сила тока $I$ — важная характеристика в электричестве. Она напрямую зависит от величины электрического заряда $q$, переносимого частицами, и от времени $t$, за которое этот заряд проходит через поперечное сечение проводника.
Далеко не всегда есть возможность заглянуть внутрь проводника, измерить переносимый заряд и рассчитать силу тока по формуле $I = frac$. Зато есть возможность измерить силу тока с помощью специального прибора.
Этот прибор называется амперметром. В данном уроке вы узнаете, как с его помощью измерять силу тока и как правильно подключать его к электрической цепи.
Амперметр
Амперметр — это прибор для измерения силы тока в электрической цепи.
По принципу работы и внешнему виду амперметр очень похож на гальванометр. Его устройство изменено, чтобы можно было не просто фиксировать наличие тока в цепи, но и измерять его силу.
В каких единицах градуируют шкалу амперметра? Так как он измеряет силу тока, то и его шкала будет проградуирована в амперах.
Различные виды амперметров могут отличаться друг от друга в зависимости от сферы использования. На рисунке 1, а изображен демонстрационный амперметр. Такие приборы чаще всего используют в школе при демонстрации опытов.
На рисунке 1, б представлен амперметр, который чаще используют для лабораторных работ.
Как вы видите, эти два амперметра рассчитаны на измерение определенного диапазона значений силы тока. Шкала первого амперметра покажет максимальное значение в $3 space А$, а второго — в $2 space А$. Превышать эти значения не рекомендуется, так как приборы могут выйти из строя.
Амперметр в электрической цепи
Амперметр — измерительный прибор. Поэтому, когда мы подключаем его к электрической цепи, он не будет влиять на величину силы тока. Он будет лишь показывать ее значение.
На схемах электрических цепей амперметр обозначается специальным условным знаком — кружочком с буквой “А” (рисунок 2).
Правила подключения амперметра в электрическую цепь
- Амперметр необходимо включать в цепь последовательно с тем прибором/проводником, силу тока в котором нужно измерить (рисунок 3)
- У амперметра имеется две клеммы для подсоединения проводников. Клемму, на которой стоит знак “+” нужно соединять с проводом, идущим от положительного полюса источника тока. И, соответственно, клемму, на которой стоит знак “-” нужно соединять с проводом, идущим от отрицательного полюса источника тока (рисунок 4).
- Нельзя подключать амперметр к цепи, в которой нет потребителя (приемника) тока (рисунок 5). Это может привести к выходу прибора из строя.
Измерение силы тока амперметром
Первое правило подключения амперметра в цепь говорит о его последовательном подключении. А есть ли разница, где именно при таком подсоединении мы расположим амперметр?
Давайте соберем электрическую цепь. Она будет состоять из источника тока, ключа, электрической лампочки и амперметра (рисунок 6).
После замыкания цепи, зафиксируем силу тока, которую показал амперметр.
А теперь давайте переместим амперметр в цепи так, чтобы он стоял после лампы, а не до нее (рисунок 7).
Амперметр покажет нам ту же величину силы тока, что и в предыдущем случае.
А теперь подключим в цепь сразу два амперметра (рисунок 8). И что мы увидим? Они будут показывать одинаковые значения силы тока, точно такие же, как и в предыдущих опытах.
В цепи с последовательным подключением проводников (так, что конец одного проводника соединяется с началом другого) сила тока во всех участках цепи одинакова.
Почему она одинакова? Дело в том, что заряд, который проходит через любое поперечное сечение проводников цепи за $t = 1 space с$, одинаков. Ведь ток равномерно протекает по всем проводам цепи, нигде не накапливаясь. Его течение можно сравнить с протеканием воды по трубам.
Безопасные и опасные пределы значений силы тока
Работа с электрическими цепями может быть опасной при несоблюдении правил безопасности. Если мы говорим о постоянном токе (величина силы тока и его направление со временем не изменяются), то эффекты воздействия такого тока на человеческий организм приведены в таблице 1.
| $I$, $мА$ | Воздействие на человеческий организм |
| 0 — 3 | Не ощущается |
| 4 — 7 | Зуд. Ощущение нагревания |
| 8 — 10 | Усиление нагревания |
| 11 — 25 | Еще большее усиление нагревания, незначительные сокращения мышц рук |
| 26 — 80 | Сильное ощущение нагревания. Сокращения мышц рук. Судороги, затруднение дыхания. |
| 81 — 100 | Паралич дыхания |
Таблица 1. Действие постоянного тока на организм человека
Это интересно: амперметр и Minecraft
Упражнения
Упражнение №1
При включении в цепь амперметра так, как показано на рисунке 9, а, сила тока была $0.5 space А$. Каковы будут показания амперметра при включении его в ту же цепь так, как изображено на рисунке 9, б?
Сила тока будет точно такая же. Амперметр покажет значение в $0.5 space А$. Это объясняется тем, что в данной электрической цепи все элементы соединены последовательно. В этом случае сила тока на всех участках цепи одинакова.
Упражнение №2
Как можно проверить правильность показаний амперметра с помощью другого амперметра, точность показаний которого проверена?
Можно собрать цепь, как на рисунке 6, используя точный амперметр. Зафиксировать значение силы тока, которое он покажет. Потом заменить его другим — тем, правильность показаний которого мы хотим проверить. Далее останется просто сравнить показания этого амперметра с полученными ранее.
Можно сделать это и другим способом. Для этого нужно собрать цепь, как на рисунке 8 с последовательным соединений всех элементов. Мы уже знаем, что в такой цепи два исправных амперметра должны показывать одинаковые значения. Главное при такой проверке — это отметить для себя, какой амперметр показывает точные результаты измерений, чтобы не запутаться.
Упражнение №3
Рассмотрите амперметры, данные на рисунке 1. Определите цену деления шкалы каждого амперметра. Какую наибольшую силу тока они могут измерять? Перерисуйте шкалу амперметра (смотрите рисунок 1, а) в тетрадь и покажите, каково будет положение стрелки при силе тока $0.3 space А$ и $1.5 space А$.
Шкала демонстрационного амперметра с рисунка 1, а будет иметь цену деления, равную $0.2 space А$.
Шкала лабораторного амперметра с рисунка 1, б будет иметь цену деления, равную $0.05 space А$.
На рисунке 10, а мы изобразили шкалу демонстрационного амперметра, который показывает значение $I = 0.3 space А$,а на рисунке 10, б — $I = 1.5 space А$.
Упражнение №4
Имеется точный амперметр. Как, пользуясь им, нанести шкалу на другой, ещё не проградуированный амперметр?
Для этого нужно подключить оба амперметра в электрическую сеть. Например, как на рисунке 8.
Сначала перед замыканием ключа на пустую шкалу амперметра нанесем первую отметку — $0 space А$.
Замыкаем цепь. Точный амперметр покажет нам какое-то определенное значение силы тока. Его стрелка отклонится. Например, она покажет значение в $1 space А$. Стрелка второго амперметра тоже отклонится. Отметим ее положение — $1 space А$. Мы можем так сделать, потому что сила тока при последовательном соединении элементов в цепи на всех ее участках одинакова.
Затем можно, используя линейку, самостоятельно нанести дополнительную отметки на шкале амперметра, выбрав удобную для вас цену деления.
Источник
Как найти показания амперметра формула
найти показания амперметр и вольтметра в цепи. E1=12в E2=10В,E3=2 В, r1=4ом,r2=1 ом,r3=4 Ом, R1=6 Ом,R2=12 Ом,R3=4 Ом,R4=8 Ом,R5=2 Ом,R6=2Ом
помогите решить пожалуйста,не знаю что делать с 3 источниками ЭДС,получится что только один будет гнать напряжение(который 12в)?

- Попроси больше объяснений
- Следить
- Отметить нарушение
Ответ
По закону Ома, ток в замкнутом контуре равен алгебраической сумме ЭДС, действующих в контуре, деленному на полное сопротивление цепи.
Алгебраическая сумма ЭДС равна Е=12В-10В+2В=4В
Полное сопротивление цепи равно R=r1+r2+r3+R1234+R56
R1234 состоит из двух папаллельно включенных цепочек из двух последовательно включенных сопротивлений (R1,R2 и R3,R4 соответственно)
Полное сопротивление цепи равно 4+1+4+7.2+1=17,2 Ом
Амперметр А» показывает полный ток в цепи, и он покажет 4В/17,2Ом=»0,232558А» или примерно 0,233А
Чтобы найти показания амперметра А1, найдем напряжение на R56. U56=I2*R56=I2*1
Ток I1=U56/2=I2/2=0.116279А или примерно 0,116 А
Показание вольтметра равно разности падения напряжения на сопротивлениях R2 и R4. Чтобы найти эти значения, найдем падение напряжения на всей цепочке сопротивлений R1R2R3R4. U1234=I2*R1234=I2*7,2
Падение напряжения на R2 U2=U1234/(R1+R2)*R2=I2*7,2*12/18=I2*7,2*2/3
Падение напряжения на R4 U4=U1234/(R3+R4)*R4=I2*7,2*8/12=I2*7,2*2/3
Разность напряжений на R2 и R4 равна U2-U4=I2*7,2*2/3-I2*7,2*2/3=0, следовательно, показания вольтметра будут равны нулю.
Ответ: амперметр А2 покажет ток примерно 0,233А, амперметр А1 примерно 0,116А, а вольтметр покажет 0
Приветствую всех читателей на нашем сайте и сегодня в рамках курса “Электроника для начинающих” мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр, амперметр и др.

Измерение тока.
И начнем мы с измерения тока. Прибор, используемый для этих целей, называется амперметр и в цепь он включается последовательно. Рассмотрим небольшой примерчик:

Как видите, здесь источник питания подключен напрямую к резистору. Кроме того, в цепи присутсвует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи должна быть равна:
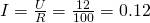
Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 🙂
Важным параметром этого прибора является его внутреннее сопротивление 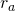 . Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
. Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
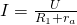
Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.
При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:
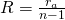
В этой формуле n – это коэффициент шунтирования – число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.
Пусть максимальное значение, которое может измерить амперметр составляет 1А. А схема, силу тока в которой нам нужно определить имеет следующий вид:
 Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
 В данной задаче нам необходимо измерить ток
В данной задаче нам необходимо измерить ток 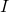 . Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
. Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
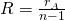
В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.
Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:
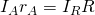
Выразим ток шунта через ток амперметра:
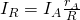
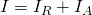
Подставим в это уравнение предыдущее выражение для тока шунта:
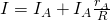
Но сопротивление шунта нам также известно (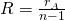 ). В итоге мы получаем:
). В итоге мы получаем:
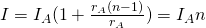
Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нам и нужно измерить 🙂
С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.
Измерение напряжения.
Прибор, предназначенный для измерения напряжения называется вольтметр, и, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся с чем это связано:
 Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
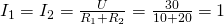
Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с 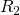 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (
. Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (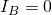 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку
), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку 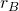 имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе
имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе 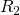 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:
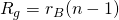
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример 😉
 Здесь мы добавили в цепь добавочное сопротивление
Здесь мы добавили в цепь добавочное сопротивление 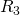 . Перед нами стоит задача измерить напряжение на резисторе
. Перед нами стоит задача измерить напряжение на резисторе 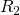 :
: 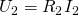 . Давайте определим, что при таком включении будет на экране вольтметра:
. Давайте определим, что при таком включении будет на экране вольтметра:
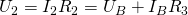
Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:
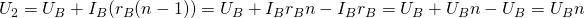
Таким образом: 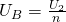 . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
. То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
В завершении статьи пару слов об измерении сопротивления и мощности.
Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи – омметр – и мощности – ваттметр.
В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями и заходите к нам на сайт! До скорых встреч!
Приветствую всех читателей на нашем сайте и сегодня в рамках курса “Электроника для начинающих” мы будем изучать основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр, амперметр и др.

Измерение тока.
И начнем мы с измерения тока. Прибор, используемый для этих целей, называется амперметр и в цепь он включается последовательно. Рассмотрим небольшой примерчик:

Как видите, здесь источник питания подключен напрямую к резистору. Кроме того, в цепи присутсвует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи должна быть равна:
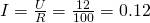
Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 🙂
Важным параметром этого прибора является его внутреннее сопротивление 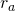 . Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
. Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится сопротивление, и мы получим следующее значение:
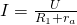
Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.
При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:
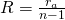
В этой формуле n – это коэффициент шунтирования – число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.
Пусть максимальное значение, которое может измерить амперметр составляет 1А. А схема, силу тока в которой нам нужно определить имеет следующий вид:
 Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
 В данной задаче нам необходимо измерить ток
В данной задаче нам необходимо измерить ток 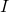 . Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
. Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и мы получим нужное нам значение. Для реализации нашей задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
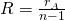
В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.
Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:
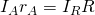
Выразим ток шунта через ток амперметра:
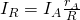
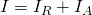
Подставим в это уравнение предыдущее выражение для тока шунта:
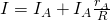
Но сопротивление шунта нам также известно (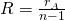 ). В итоге мы получаем:
). В итоге мы получаем:
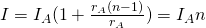
Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нам и нужно измерить 🙂
С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.
Измерение напряжения.
Прибор, предназначенный для измерения напряжения называется вольтметр, и, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся с чем это связано:
 Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
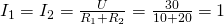
Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с 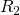 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (
. Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (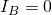 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку
), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку 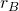 имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе
имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток и, в связи с этим напряжение на резисторе 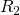 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:
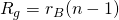
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример 😉
 Здесь мы добавили в цепь добавочное сопротивление
Здесь мы добавили в цепь добавочное сопротивление 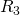 . Перед нами стоит задача измерить напряжение на резисторе
. Перед нами стоит задача измерить напряжение на резисторе 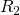 :
: 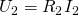 . Давайте определим, что при таком включении будет на экране вольтметра:
. Давайте определим, что при таком включении будет на экране вольтметра:
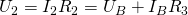
Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:
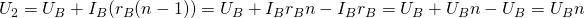
Таким образом: 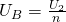 . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
. То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно увеличить пределы измерения вольтметра 🙂
В завершении статьи пару слов об измерении сопротивления и мощности.
Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи – омметр – и мощности – ваттметр.
В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями и заходите к нам на сайт! До скорых встреч!
Источник
Условие задачи:
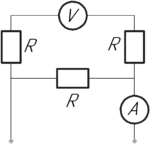 Определите показание амперметра в электрической цепи, изображенной на рисунке, если показание вольтметра (U=250) В, а сопротивление каждого резистора (R) и внутреннее сопротивление вольтметра равны по 1 кОм.
Определите показание амперметра в электрической цепи, изображенной на рисунке, если показание вольтметра (U=250) В, а сопротивление каждого резистора (R) и внутреннее сопротивление вольтметра равны по 1 кОм.
Задача №7.5.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(U=250) В, (R=1) кОм, (I-?)
Решение задачи:
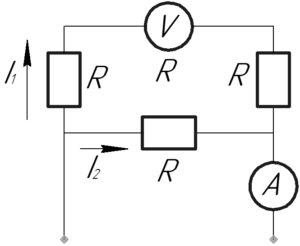 Так как из условия задачи нам известно показание вольтметра (U), то зная внутреннее сопротивление вольтметра, а оно такое же, как у резисторов, то есть равно (R), очень легко определить ток (I_1), который течет по верхней ветви, благодаря закону Ома для участка цепи:
Так как из условия задачи нам известно показание вольтметра (U), то зная внутреннее сопротивление вольтметра, а оно такое же, как у резисторов, то есть равно (R), очень легко определить ток (I_1), который течет по верхней ветви, благодаря закону Ома для участка цепи:
[I_1 = frac{U}{R};;;;(1)]
Очевидно, что верхняя ветвь, состоящая из последовательно соединенных двух резисторов и вольтметра (все имеющие одинаковое сопротивление (R)), и нижняя ветвь, состоящая из одного резистора, соединены параллельно, то они находятся под одинаковым напряжением, поэтому верно записать:
[{I_1} cdot 3R = {I_2} cdot R]
Откуда имеем:
[{I_2} = 3{I_1}]
[{I_2} = frac{{3U}}{R};;;;(2)]
Очевидно, что ток (I), который показывает амперметр, равен сумме токов (I_1) и (I_2), то есть:
[I = {I_1} + {I_2}]
Учитывая выражения (1) и (2), имеем:
[I = frac{U}{R} + frac{{3U}}{R}]
[I = frac{{4U}}{R}]
Посчитаем численный ответ:
[I = frac{{4 cdot 250}}{{1 cdot {{10}^3}}} = 1;А]
Ответ: 1 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.49 Вольтметр, внутреннее сопротивление которого равно 50 кОм, подключенный к источнику
7.5.51 Какой величины надо взять дополнительное сопротивление, чтобы можно было включить
7.1.1 Определить силу тока, проходящего через сопротивление 15 Ом, если напряжение на нем
Окончательно для токов ![]() ,
, ![]() получим (рис. 1.8)
получим (рис. 1.8)
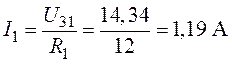 ;
;
 .
.
5. Ток ![]() определим из
определим из
уравнения, составленного по первому закону Кирхгофа для узла 1 (рис.1.6)
![]() .
.
6. Из уравнений, составленных по первому закону
Кирхгофа, для узлов 3 и 2 (рис. 1.6) определим токи ![]() и
и
![]() :
:
![]() ;
;
![]() .
.
Задача 1.3.
Определить показание амперметра, установленного в
ветви с источником ЭДС (рис. 1.12), если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Внутренним сопротивлением амперметра можно пренебречь (![]() ).
).
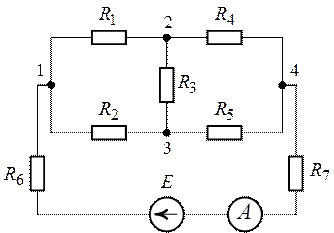
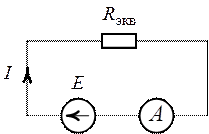
Рис. 1.12. Рис.
1.13.
Решение.
1. Методом свертывания цепи преобразуем схему рис.
1.12 к виду, приведенному на рис. 1.13.
Заменим треугольник сопротивлений, подключенный к
точкам 1, 2 и 3 (рис. 1.12), эквивалентной звездой с вершинами 1, 2 и 3 (рис.
1.14).
Величины сопротивлений эквивалентной звезды:
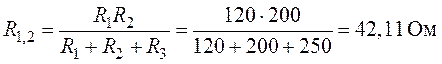 ;
;
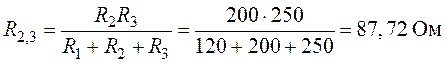 ;
;
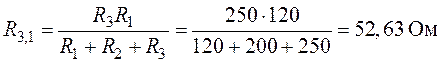 .
.
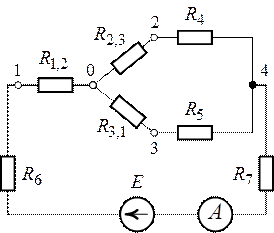

Рис. 1.14. Рис.
1.15.
Сопротивление ![]() соединено
соединено
последовательно с ![]() , а сопротивление
, а сопротивление ![]() последовательно с
последовательно с ![]() (рис. 1.14). Участок цепи с сопротивлениями
(рис. 1.14). Участок цепи с сопротивлениями
![]() и
и ![]() включен
включен
параллельно участку с сопротивлениями ![]() и
и
![]() (рис. 1.14).
(рис. 1.14).
Общее сопротивление обоих участков схемы (рис. 1.15)
равно:
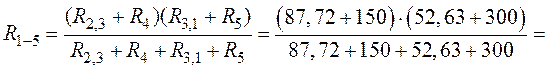
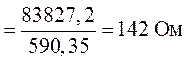 .
.
Сопротивления ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1.15) включены последовательно.
(рис. 1.15) включены последовательно.
Эквивалентное сопротивление всей цепи (рис. 1.13)
![]()
![]() .
.
2. Показание амперметра соответствует току ![]() (рис. 1.13):
(рис. 1.13):
 .
.
Задача 1.4.
Определить величину источника тока, установленного на
входе цепи (рис. 1.16), если показание амперметра в разветвленной части схемы
составляет ![]() . Сопротивления резисторов
. Сопротивления резисторов ![]() равны
равны ![]() .
.
Внутреннее сопротивление источника ![]() . Внутренним сопротивлением
. Внутренним сопротивлением
амперметра можно пренебречь (![]() ).
).
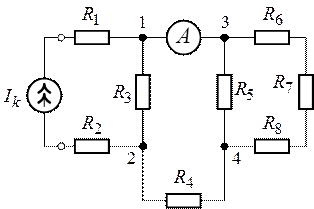

Рис. 1.16. Рис.
1.17.
Решение.
1. Пользуясь методом свертывания, приведем участок
цепи (рис. 1.16) относительно узлов 3 и 4 к виду, представленному на рис. 1.17.
Общее сопротивление участка цепи
 .
.
2. Напряжение ![]() между
между
узлами 1 и 2 (рис. 1.17)
![]() .
.
3. Ток ![]() в ветви с
в ветви с
сопротивлением ![]() (рис. 1.17)
(рис. 1.17)
 .
.
4. Ток источника ![]() на
на
входе цепи определим на основании первого закона Кирхгофа:
![]() .
.
Задача 1.5.
В схеме (рис. 1.18) найти токи, применив метод
пропорционального пересчета, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
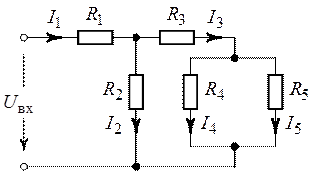
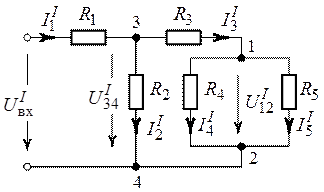
Рис. 1.18. Рис.
1.19.
Решение.
1. В рассматриваемой цепи зададим ток в одной из
удаленных от источника ветвей, например, с сопротивлением ![]() , равным
, равным ![]() и
и
определим некоторое напряжение источника на входе цепи ![]() ,
,
при котором ![]() (рис. 1.19)
(рис. 1.19)
2. Определим токи ![]() (рис.
(рис.
1.19)
Напряжение ![]()
![]() .
.
Ток ![]() равен:
равен: 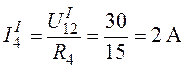 .
.
Ток ![]() определим как
определим как
сумму токов ![]() и
и ![]()
![]() .
.
Напряжение на сопротивлении ![]()
![]() .
.
Напряжение ![]() между узловыми
между узловыми
точками 3 и 4
![]() .
.
Ток ![]() определим как
определим как
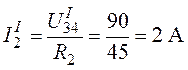 .
.
Ток ![]() на входе цепи
на входе цепи
определим как сумму токов ![]() и
и ![]() :
:
![]() .
.
Напряжение на сопротивлении ![]()
![]() .
.
Напряжение на входе цепи
![]() .
.
3. Определим коэффициент пересчета как отношение
напряжения на входе цепи, заданного по условию задачи ![]() ,
,
к найденному при расчетах ![]() :
:
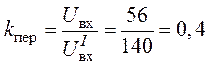 .
.
4. Действительные токи в ветвях цепи найдем как
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задачи для
самостоятельного решения
Задача 1.6. Определить
эквивалентное сопротивление электрической цепи, представленной на рис. 1.20,
относительно зажимов 1 и 2, в которой сопротивления ![]() равны
равны
![]() .
.
О т в е т: ![]() .
.
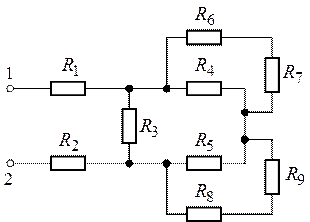
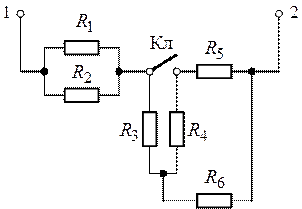
Рис. 1.20. Рис.
1.21.
Задача 1.7. Определить
эквивалентное сопротивление цепи (рис.1.21) между входными зажимами 1 и 2 при
разомкнутом и замкнутом положениях ключа (![]() ),
),
если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: при разомкнутом ключе ![]() ; при замкнутом ключе
; при замкнутом ключе ![]() .
.
Задача 1.8. Определить
токи в ветвях цепи (рис. 1.22), если задано ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Задача 1.9. В
схеме (рис. 1.23) определить токи во всех ветвях, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
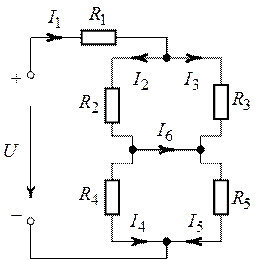
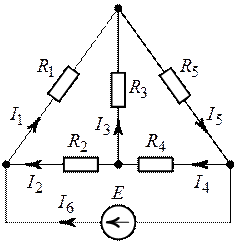
Рис. 1.22. Рис.
1.23.
Задача 1.10. Определить
токи во всех ветвях схемы (рис. 1.24), если задано ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Задача 1.11. В
электрической схеме рис. 1.25 определить токи во всех ветвях, если задано ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.

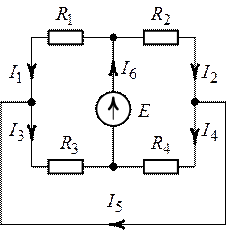
Рис. 1.24.
Рис. 1.25.
Задача 1.12. Определить
показание амперметра для схемы рис. 1.26, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Принять ![]() .
.
О т в е т: ![]() .
.
Задача 1.13. Определить
показание амперметра для схемы рис. 1.27, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Принять ![]() .
.
О т в е т: ![]() .
.
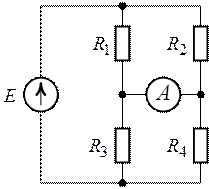
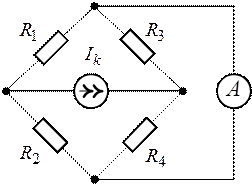
Рис. 1.26.
Рис. 1.27.
Задача 1.10. Показание
амперметра (рис. 1.28), установленного в разветвленной части схемы, составляет ![]() . Найти величину источника тока
. Найти величину источника тока ![]() , если
, если ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Сопротивление источника считать
. Сопротивление источника считать ![]() , амперметра
, амперметра ![]() .
.
О т в е т: ![]() .
.
Задача 1.11. Найти
все токи в ветвях цепи, схема которой приведена на рис. 1.29, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Принять сопротивление источника
. Принять сопротивление источника ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.

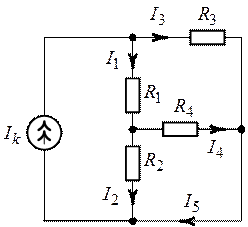
Рис. 1.28. Рис.
1.29.
Задача 1.12. Определить
показание амперметра в схеме (рис. 1.30), если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Принять ![]() .
.
О т в е т: ![]() .
.
Задача 1.13. Методом
пропорционального пересчета найти все токи в схеме рис. 1.31, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
В расчетах принять ток в сопротивлении ![]() равным
равным
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
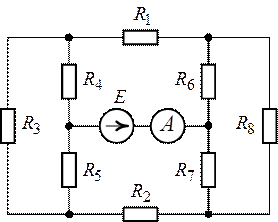
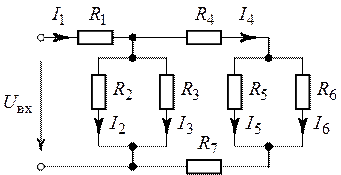
Рис. 1.30. Рис.
1.31.
2.
РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ С ПОМОЩЬЮ ПРЯМОГО ПРИМЕНЕНИЯ ЗАКОНОВ КИРХГОФА
Законы Кирхгофа лежат в основе расчета сложных цепей содержащих несколько
источников энергии. С помощью двух законов Кирхгофа устанавливаются соотношения
между токами и ЭДС в ветвях электрической цепи и напряжениями на элементах
цепи.
Задача 2.1.
Пользуясь законами Кирхгофа, рассчитать токи в
ветвях схемы рис.2.1, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Решение.
1. Цепь рис. 2.1 содержит три ветви (![]() ), два узла (
), два узла (![]() ).
).
Цепь питает два источника ЭДС ![]() и
и ![]() . Источники тока в цепи отсутствуют (
. Источники тока в цепи отсутствуют (![]() ).
).
Выберем произвольно положительные направления токов в
ветвях схемы и обозначим их как указано на рис. 2.2.
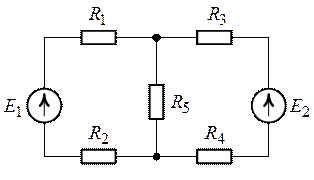

Рис. 2.1.
Рис. 2.2.
2. Определим достаточное количество уравнений для
расчета цепи по законам Кирхгофа.
По первому закону Кирхгофа:
![]() .
.
По второму закону Кирхгофа:
![]()
![]() .
.
Достаточное количество уравнений равно трем, что
соответствует количеству неизвестных токов, обозначенных в ветвях схемы как ![]() ,
, ![]() и
и
![]() (рис. 2.2).
(рис. 2.2).
3. Составим систему уравнений по первому и второму
закону Кирхгофа. Одно уравнение по первому закону Кирхгофа, например, для узла
1 и два уравнения по второму закону Кирхгофа для двух независимых контуров. Положительные
направления обхода контуров соответствуют направлениям, указанным на рис. 2.2.
для узла 1: ![]() ;
;
для контура ![]() :
: ![]() ;
;
для контура ![]() :
: ![]() .
.
4. После подстановки числовых значений имеем:

5. Решение системы получим с помощью определителей:
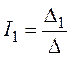 ;
; 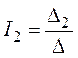 ;
;
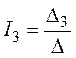 ,
,
где![]() – главный
– главный
определитель системы, ![]() ,
, ![]() ,
,
![]() – алгебраические дополнения.
– алгебраические дополнения.
Главный определитель системы равен:
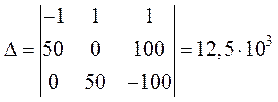 .
.
Дополнительные определители равны:
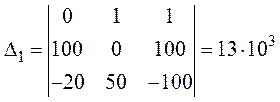 ;
;
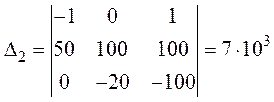 ;
;
 .
.
6. Токи в ветвях:
 ;
; 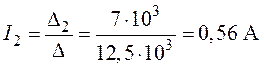 ;
;
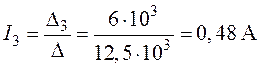 .
.
Задача 2.2.
Рассчитать с использованием законов Кирхгофа токи в
ветвях схемы изображенной на рис. 2.3, если известны ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Выполнить правильность расчета цепи
. Выполнить правильность расчета цепи
путем проверки баланса мощностей.
