Площадь параллелограмма
Параллелограммом называют геометрическую фигуру, которая имеет парные противоположные стороны (расположенные на параллельных прямых).
К свойствам параллелограмма принято относить: противоположные стороны этого четырехугольника равные; противоположные углы параллелограмма имеют одинаковые величины; диагонали в точке пресечения делятся пополам; углы, находящиеся в одной стороне параллелепипеда, составляют 180°; каждая из диагоналей делит параллелепипед на два совершенно одинаковых треугольника; сума всех углов параллелограмма составляет 360; центр симметрии параллелограмма – точка пересечения диагоналей.
Прямоугольником называют параллелограмм, у которого все углы прямые (равны 90 градусам).
Площадь параллелограмма находят с помощью формулы S = hxa, где S – площадь, h – высота, опущенная с угла параллелограмма на противоположную сторону, a – сторона к которой была проведена высота.
Доказательство:
Представленный на рисунке параллелограмм ABCD не является прямоугольником, так как один из его углов острый. На данном четырехугольнике острый угол – DCF. Опустим
перпендикуляр c вершины параллелепипеда А на сторону СВ – AE. Следовательно, получим трапецию, площадь которой равняется сумме площадей треугольника AEB и параллелограмма ABCD. Также опустим перпендикуляр DF, который берет свое начало с вершины D к одной из сторон – CD. Площадь трапеции AECD, которая образовалась, равняется сумме площадей треугольника DFC и прямоугольника AEFD. Треугольники, которые возникли после опущения сторон DFC и AEB равны, а также имеют одинаковое значение площадей. Из этого мы можем сделать вывод, что площадь параллелограмма ABCD равняется площади прямоугольника AEFD, иначе говоря, площадь равна произведению отрезков AE и AD, где AE – высота представленного параллелограмма, которая соответствует стороне AD. Исходя из всего вышесказанного, можно сказать S = hxa. Теорема доказана.
Также существуют такие формулы для расчета площади параллелограмма:
- Площадь параллелограмма можно найти если известна длина, сторона параллелепипеда и высота, которая опущена на эту сторону: SABCD=ADxhAD.
- Площадь параллелограмма можно найти при известных двух сторонах и углом, который образуют эти стороны: SABCD=АВxADxsinα.
- Площадь параллелограмма можно найти при известных диагоналях параллелограмма и углом, который они образуют: SABCD=АСxВDxsinβ.
- При известном радиусе полупериметра (p) и вписанной окружности (r): SABCD=pxr.
Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.
-
Формула вычисления площади
-
По длине стороны и высоте
- По двум сторонам и углу между ними
- По двум диагоналям и углу между ними
-
По длине стороны и высоте
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По двум сторонам и углу между ними
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:
S = a ⋅ b ⋅ sin α
По двум диагоналям и углу между ними
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:
S = 1/2 ⋅ d 1 ⋅ d 2 ⋅ sin α
Примеры задач
Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.
Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см2.
Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.
Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см2.
Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.
Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см2.
Как найти площадь параллелограмма
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти площадь параллелограмма
Чтобы найти площадь параллелограмма воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
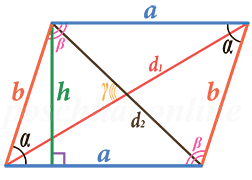
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.
Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):
- длину стороны a и длину высоты h
- длины сторон a и b, и угол α
- длины сторон a и b, и угол β
- длины сторон a и b, и длину любой из диагоналей (d1 или d2)
- длины диагоналей d1 и d2, и угол между ними γ
Подставьте значения в соответствующие поля и получите результат.
Зная длину стороны a и длину высоты h
Чему равна площадь параллелограмма если сторона
a = ,
а высота
h = ?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
S = a⋅h
Пример
Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:
S = 8 ⋅ 4 = 32 см2
Зная длины сторон a и b, и угол α
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а угол между ними
α = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?
Формула
S = a⋅b⋅sinα
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:
S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и угол β
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а угол между ними
β = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?
Формула
S = a⋅b⋅sin(180 – β)
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:
S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и длину диагонали (d1 или d2)
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а диагональ
d =
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?
Формула
S = 2√p⋅(p-a)⋅(p-b)⋅(p-d), где p=(a+b+d)/2
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:
p = (8 + 5 +11)/2 = 12
S = 2√12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅√12⋅4⋅7⋅1 = 2⋅√336 = 36.66 см2
Зная длины диагоналей d1 и d2, и угол между ними γ
Чему равна площадь параллелограмма если диагональ
d1 = ,
диагональ
d2 = ,
а угол между ними
γ = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины диагоналей d1 и d2, и угол между ними γ?
Формула
S = ½⋅d1⋅d2⋅sinγ
Пример
Если диагональ параллелограмма d1 = 11 см, диагональ d2 = 7 см, а ∠γ = 45° то:
S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см2
См. также
В прошлой статье предложила решить 4 задачки на тему площадь параллелограмма. Задания простые. Несколько заданий требуют несложных размышлений.
Посмотрим как они решаются.
Во всех четырех задачах требуется найти площадь параллелограмма ABCD.
Задание №1
Задание на знание базовой формулы нахождения площади параллелограмма (произведение высоты и стороны параллелограмма, к которой эта высота проведена):
Высота, в данном случае, отрезок ВЕ, а сторона, к которой проведена высота это AD.
В параллелограмме противолежащие стороны равны. Значит AD=BC=8.
ОТВЕТ: 32
Задание №2
В этом задании уже понадобится знание формулы вычисления площади параллелограмма через синус угла (площадь параллелограмма вычисляется как произведение смежных сторон на синус угла между ними):
Остается только найти угол между сторонами параллелограмма из исходных данных.
Заметим, что углы BCA и CAD накрест лежащие углы при параллельных прямых ВС и AD и секущей АС .
Тогда из рисунка видно, что угол BAD является суммой углов BAC и CAD:
Не забываем, что AD=ВС=12. Остается только подставить все значения в формулу и найти площадь.
Синус угла 60 градусов – табличное значение.
ОТВЕТ: 60√3
Задание №3
В этом задании знаем высоты, но не знаем ни одной стороны. Попробуем найти любую из сторон параллелограмма.
Рассмотрим образовавшийся прямоугольный треугольник ВАЕ:
В этом треугольнике один острый угол равен 60 градусов, значит второй острый угол равен 90-60=30 градусов.
А в прямоугольном треугольнике против угла 30 градусов лежит катет равный половине гипотенузы. Т.е. гипотенуза АВ в два раза больше противолежащего катета ВЕ:
Не забываем что в параллелограмме CD=AB=8. Воспользуемся формулой вычисления площади параллелограмма:
где BF – высота, СD – сторона, к которой проведена высота.
ОТВЕТ: 48
Задание №4
Сторона параллелограмма по сути нам известна (AD=AE+ED=10+4=14).
Попробуем найти высоту.
Для этого сначала посмотрим на образовавшийся выпуклый четырехугольник BEDF, в котором два угла прямые. С учетом, что сумма углов выпуклого четырехугольника равна 360 градусов, можно найти угол FDE (или тот же угол CDA, обозначенный другими буквами ):
Помним, что сумма углов параллелограмма, прилежащих одной стороне, равна 180 градусов. Значит:
Рассмотрим треугольник АВЕ (прямоугольный). Если один его острый угол равен 45 градусов, то второй:
По признаку равнобедренного треугольника получаем, что треугольник АВЕ – равнобедренный с равными сторонами АЕ и ВЕ:
ВЕ, в свою очередь, является высотой параллелограмма АВСD. Значит:
ОТВЕТ: 140
Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
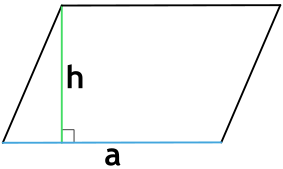
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними
{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
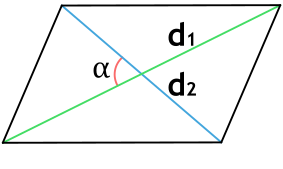
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
